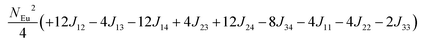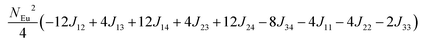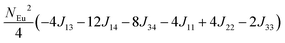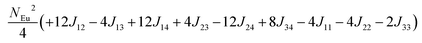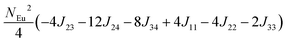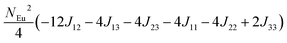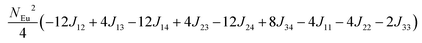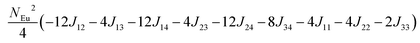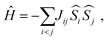DOI:
10.1039/C8QI01099D
(Research Article)
Inorg. Chem. Front., 2019,
6, 137-147
Synthesis, crystal and electronic structure, physical properties and 121Sb and 151Eu Mössbauer spectroscopy of the Eu14AlPn11 series (Pn = As, Sb)
Received
11th October 2018
, Accepted 11th November 2018
First published on 16th November 2018
Abstract
The pnictides Eu14AlAs11 and Eu14AlSb11 were synthesized from the elements in sealed niobium ampoules. They crystallize in the tetragonal crystal system (Eu14AlAs11: a = 1627.6(2), c = 2180.0(4) pm; Eu14AlSb11: a = 1725.6(2), c = 2289.7(7) pm) with space group I41/acd, isostructural to Ca14AlSb11 and can be described as Zintl phases. The Al atoms are surrounded by four pnictogen atoms, forming [AlPn4]9− tetrahedra. Additionally isolated Pn3− anions and linear Pn37− trimers can be found in the crystal structure. The compounds can be described according to (Eu2+)14(AlPn9−)(Pn3−)4(Pn37−). Eu14AlAs11 and Eu14AlSb11 both exhibit an antiferromagnetic transition at TN = 10.5(1) K and 12.5(1) K, respectively. For the antimonide, the magnetic transition has been confirmed by additional heat capacity measurements. Resistivity investigations indicate that Eu14AlSb11 is a semiconductor with a band gap of Eg = 0.28(5) eV close to room temperature. According to the Zintl formalism, the Eu atoms are divalent, which has been confirmed by magnetic susceptibility and additional 151Eu Mössbauer spectroscopic studies. The measurements conducted at 6 K, below the magnetic ordering temperature, show a full hyperfine field splitting with complex spectra underlining the recorded magnetic data. Furthermore, 121Sb Mössbauer spectroscopic studies have been conducted to study the different antimonide entities in the title compounds.
1. Introduction
Zintl phases can be positioned between intermetallic compounds and insulating valence compounds from an electronic perspective.1 Usually they contain an electropositive alkali or alkaline-earth metal, which formally reduces the more electronegative element, which can be a triele, tetrele or a pnictogen for example. A more precise definition classifies Zintl compounds as materials in which both ionic and covalent bonding exists. Besides the ‘classical’ binary Zintl phases numerous ternary compounds, meanwhile also containing transition metals, have been reported.2 Usually Zintl compounds exhibit semiconducting properties, although also metallic compounds have been reported. The semiconducting properties make Zintl compounds an important class of materials for e.g. thermoelectric applications.3 Yb14MnSb11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4,5 or Yb9Mn4.2Sb9
4,5 or Yb9Mn4.2Sb9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 are prominent examples for antimony containing high zT thermoelectric materials. Recently we have reported on the first compound in the ternary system Eu–Al–Sb, Eu5Al2Sb6,7 which crystallizes isotypically to Sr5Al2Sb6.8,9 Further investigations lead to the discovery of another prominent composition amongst antimonide Zintl phases: Eu14AlSb11, which crystallizes in the Ca14AlSb11 type structure.10 Of this 14–1–11 composition numerous compounds have been reported: A14AlSb11 (A = Ca,10,11 Sr,11 Ba11) Ca14MnX11 (X = P,12 As,13 Sb,13 Bi14), Sr14MnX11 (X = As,13 Sb,13 Bi14), Ba14MnX11 (X = As,13 Sb,13 Bi14), Ba14InP11,15 Eu14MnX11 (X = P,16 As,16 Sb,17 Bi18), Eu14InX11 (X = Sb,18 Bi18), Yb14MnX11 (X = Sb,19 Bi19) and finally Yb14MSb11 (M = Al,20 Zn20,21).
6 are prominent examples for antimony containing high zT thermoelectric materials. Recently we have reported on the first compound in the ternary system Eu–Al–Sb, Eu5Al2Sb6,7 which crystallizes isotypically to Sr5Al2Sb6.8,9 Further investigations lead to the discovery of another prominent composition amongst antimonide Zintl phases: Eu14AlSb11, which crystallizes in the Ca14AlSb11 type structure.10 Of this 14–1–11 composition numerous compounds have been reported: A14AlSb11 (A = Ca,10,11 Sr,11 Ba11) Ca14MnX11 (X = P,12 As,13 Sb,13 Bi14), Sr14MnX11 (X = As,13 Sb,13 Bi14), Ba14MnX11 (X = As,13 Sb,13 Bi14), Ba14InP11,15 Eu14MnX11 (X = P,16 As,16 Sb,17 Bi18), Eu14InX11 (X = Sb,18 Bi18), Yb14MnX11 (X = Sb,19 Bi19) and finally Yb14MSb11 (M = Al,20 Zn20,21).
Here we report on Eu14AlSb11 and the isostructural arsenide Eu14AlAs11, so far unknown elemental combinations of the Ca14AlSb11 type structure. We have investigated the crystal structure, physical properties (magnetism and electrical resistivity), along with 121Sb and 151Eu Mössbauer spectroscopic measurements of the bulk material. Theoretical calculations have been used to elucidate the electronic and magnetic structures of Eu14AlSb11 and finally Bader charges were calculated in comparison with the strontium compound Sr14AlSb11.
2. Experimental
2.1. Synthesis
Starting materials for the syntheses of Eu14AlAs11 and Eu14AlSb11 were europium ingots (Alfa Aesar, 99.9%), aluminium turnings (Koch Chemicals, 99.99%), as well as arsenic (Klepin, 99.9%) and antimony pieces (VWR International, 99.9%). The europium ingots were stored under argon; impurities on the surface were removed prior to the synthesis. The argon was purified over molecular sieves, silica gel and a titanium sponge (873 K). The elements were weighed in the ideal atomic ratio and arc-welded22 in niobium tubes in a dried argon atmosphere of about 800 mbar. The metal tubes were subsequently placed in the water-cooled sample chamber of a high-frequency furnace (Hüttinger Elektronik, Freiburg, type TIG 1.5/300) under flowing argon.23 The temperature was controlled by a Sensor Therm Methis MS09 pyrometer with an accuracy of ±50 K. The samples were rapidly heated to 1273 K, after 10 min the temperature was reduced to 1123 K and the samples were dwelled for two hours. After the annealing step, the samples were cooled to room temperature within two hours. The samples were obtained as brittle polycrystalline pieces with metallic lustre and could easily be separated from the crucible material. No reaction with the container material was observed. The compounds showed moderate sensitivity to moisture and were therefore stored under dry argon atmosphere. The corresponding bismuth compound could not be obtained under the given synthetic conditions (1273 K); the main components were Eu16Bi11 (Ca16Sb11 type)24 and Eu4Bi3 (anti-Th3P4 type).25 Reactions carried out at lower temperatures (943 K) yielded Eu16Bi11 as major product.
2.2. EDX data
Semiquantitative EDX analysis of the single crystal that has been investigated on the diffractometer was carried out by use of a Zeiss EVO® MA10 scanning electron microscope in variable pressure mode with EuF3, Al2O3 and Sb as standards. The experimentally observed compositions (Eu14AlSb11: 49(2) at% Eu, 8(2) at% Al, 43(2) at% Sb) were close to the theoretical (53.9 at% Eu, 3.8 at% Al, 42.3 at% Sb) and refined ones. The irregularly shaped crystals contained no impurity elements heavier than sodium (detection limit of the instrument). The deviations observed are related to the conchoidal fractures.
2.3. Powder X-Ray diffraction
The polycrystalline samples were characterized by Guinier powder patterns using CuKα1 radiation and α-quartz (a = 491.30 and c = 540.46 pm) as an internal standard. The Guinier camera was equipped with an imaging plate technique (Fujifilm, BAS-READER 1800). Least-squares refinements led to the lattice parameters listed in Table 1. To ensure correct indexing, the experimental patterns were compared to calculated ones using the refined atomic positions (vide infra) obtained from the single crystal X-ray diffraction.26
Table 1 Lattice parameters of the M14AlPn11 (M = Ca, Sr, Ba, Eu, Yb; Pn = As, Sb; Ca14AlSb11 type, space group I41/acd, Z = 8) members
| Compound |
a (pm) |
c (pm) |
V (nm3) |
Lit. |
|
This work, P powder data, SC single crystal data.
|
| Eu14AlAs11P |
1627.6(2) |
2180.0(4) |
5.7750 |
|
| Ca14AlSb11P |
1667.6(5) |
2242.3(7) |
6.2356 |
10
|
| Ca14AlSb11P |
1667.2(6) |
2243(1) |
6.7905 |
11
|
| Sr14AlSb11P |
1749.3(4) |
2348.0(8) |
7.1850 |
11
|
| Ba14AlSb11P |
1829.3(2) |
2422.2(9) |
8.1055 |
11
|
| Eu14AlSb11P |
1725.6(3) |
2289.7(7) |
6.8183 |
|
| Eu14AlSb11SC |
1726.49(4) |
2292.24(6) |
6.8326 |
|
| Yb14AlSb11P |
1656.1(2) |
2210.2(3) |
6.0635 |
20
|
2.4. Single crystal X-ray diffraction
Single crystals of Eu14AlSb11 were isolated from the crushed sample. The crystal fragments were glued to thin quartz fibres using beeswax and investigated by Laue photographs on a Buerger camera (white Mo radiation, Fujifilm imaging plate, BAS-1800) in order to check their quality for intensity data collection. The intensity data set was collected at room temperature using a Stoe IPDS II (graphite-monochromatized MoKα radiation; oscillation mode) diffractometer. Numerical absorption correction was applied to the data set. Details about the data collection and the crystallographic parameters are summarized in Tables 2–4.
Table 2 Crystallographic data and details of the room temperature single crystal structure refinement of Eu14AlSb11 (Ca14AlSb11 type, space group I41/acd, Z = 8)
| Lattice parameter/pm |
a = 1726.49(4) |
|
c = 2292.24(6) |
| Volume, V/nm3 |
6.8326 |
| Molar Mass/g mol−1 |
3493.7 |
| Calc. density, Dx/g cm−3 |
6.79 |
| Abs. coeff. μ/mm−1 |
33.8 |
|
F(000)/e |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648 648 |
| Crystal size/μm3 |
20 × 30 × 35 |
| Transmission ratio (min/max) |
0.019/0.045 |
| Detector distance/mm |
80 |
| Exposure time/min |
10 |
| Integr. parameters A/B/EMS |
13.0/−1.0/0.030 |
|
θ range/° |
2.4–32.1 |
| Range in hkl |
−25, +21; ±25; ±34 |
| Total no. reflections |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201 201 |
| Independent reflections/Rint |
2971/0.1598 |
| Reflections with I ≥ 3σ(I)/Rσ |
1826/0.0487 |
| Data/parameters |
2971/62 |
| Goodness-of-fit on F2 |
1.16 |
|
R
1/wR2 for I ≥ 3σ(I) |
0.0345/0.0571 |
|
R
1/wR2 for all data |
0.0805/0.0695 |
| Extinction coefficient |
40(20) |
| Largest diff. peak/hole/e Å−3 |
+2.74/−2.94 |
Table 3 Atomic coordinates and isotropic displacement parameters Ueq (pm2) Eu14AlSb11 (Ca14AlSb11 type, space group I41/acd, Z = 8). Standard deviations are given in parentheses
| |
Wyckoff site |
x
|
y
|
z
|
U
eq
|
| Eu1 |
32g |
0.04391(3) |
0.07244(3) |
0.17137(2) |
216(1) |
| Eu2 |
32g |
0.02100(3) |
0.37660(4) |
0.00263(3) |
242(1) |
| Eu3 |
16e |
0.35607(5) |
0 |
1/4 |
215(2) |
| Eu4 |
32g |
0.34128(4) |
0.06830(4) |
0.09267(2) |
252(2) |
| Al |
8a |
0 |
1/4 |
3/8 |
209(1) |
| Sb1 |
16f |
0.13305(4) |
0.38305(4) |
1/8 |
200(2) |
| Sb2 |
32g |
0.36509(5) |
0.25319(4) |
0.06209(3) |
212(2) |
| Sb3 |
32g |
0.13138(5) |
0.02507(4) |
0.04697(3) |
210(2) |
| Sb4 |
8b |
0 |
1/4 |
1/8 |
237(3) |
Table 4 Interatomic distances (in pm) in the structure of Eu14AlSb11 (Ca14AlSb11 type, space group I41/acd, Z = 8). Standard deviations are smaller or equal to ±0.1 pm. All distances <400 pm are listed
| Eu1 |
1 |
Sb3 |
330.6 |
Eu2 |
1 |
Sb2 |
325.7 |
Eu3 |
2 |
Sb3 |
323.7 |
| 1 |
Sb1 |
332.5 |
1 |
Sb3 |
329.2 |
2 |
Sb2 |
344.6 |
| 1 |
Sb3 |
332.9 |
1 |
Sb3 |
339.0 |
2 |
Sb1 |
351.0 |
| 1 |
Sb4 |
333.2 |
1 |
Sb1 |
340.9 |
2 |
Eu4 |
380.3 |
| 1 |
Sb2 |
336.0 |
1 |
Sb4 |
357.4 |
2 |
Eu1 |
391.5 |
| 1 |
Sb2 |
340.7 |
1 |
Al |
367.0 |
2 |
Eu2 |
396.5 |
| 1 |
Eu4 |
370.8 |
1 |
Sb2 |
380.4 |
|
|
|
| 1 |
Eu1 |
389.5 |
1 |
Eu4 |
391.2 |
|
|
|
| 1 |
Eu3 |
391.5 |
1 |
Eu3 |
396.5 |
|
|
|
| |
| Eu4 |
1 |
Sb2 |
329.4 |
Al |
4 |
Sb2 |
274.0 |
Sb1 |
1 |
Sb4 |
324.9 |
| 1 |
Sb1 |
331.3 |
4 |
Eu2 |
367.0 |
2 |
Eu4 |
331.3 |
| 1 |
Sb3 |
332.0 |
|
|
|
2 |
Eu1 |
332.5 |
| 1 |
Sb3 |
334.5 |
|
|
|
2 |
Eu2 |
340.9 |
| 1 |
Sb2 |
355.4 |
|
|
|
2 |
Eu3 |
351.0 |
| 1 |
Eu1 |
370.8 |
|
|
|
|
|
|
| 1 |
Eu3 |
380.3 |
|
|
|
|
|
|
| 1 |
Sb3 |
384.5 |
|
|
|
|
|
|
| 1 |
Eu2 |
391.2 |
|
|
|
|
|
|
| |
| Sb2 |
1 |
Al |
274.0 |
Sb3 |
1 |
Eu3 |
323.7 |
Sb4 |
2 |
Sb1 |
324.9 |
| 1 |
Eu2 |
325.7 |
1 |
Eu2 |
329.2 |
4 |
Eu1 |
333.2 |
| 1 |
Eu4 |
329.4 |
1 |
Eu1 |
330.6 |
4 |
Eu2 |
357.4 |
| 1 |
Eu1 |
336.0 |
1 |
Eu4 |
332.0 |
|
|
|
| 1 |
Eu1 |
340.7 |
1 |
Eu1 |
332.9 |
|
|
|
| 1 |
Eu3 |
344.6 |
1 |
Eu4 |
334.5 |
|
|
|
| 1 |
Eu4 |
355.4 |
1 |
Eu2 |
339.0 |
|
|
|
| 1 |
Eu2 |
380.4 |
1 |
Eu4 |
384.5 |
|
|
|
CCDC 1867337 contains the supplementary crystallographic data for this paper.
2.5. Physical property measurements
The powdered samples of Eu14AlAs11 and Eu14AlSb11 were packed in polyethylene (PE) capsules and attached to the sample holder rod of a Vibrating Sample Magnetometer unit (VSM) for measuring the magnetization M(T,H) in a Quantum Design Physical Property Measurement System (PPMS). The sample was investigated in the temperature range of 2.5–300 K with magnetic fields up to 80 kOe. For the heat capacity measurement of Eu14AlSb11, one piece of the sample was fixed to a pre-calibrated heat capacity puck using Apiezon N grease and investigated in the temperature range of 2.0 to 75 K. A cold pressed tablet of Eu14AlSb11 (Ø 4.5 mm, Archimedes density 93(1)%) was annealed at 773 K for 4 weeks. The sintered material was used for the resistivity experiments. The measurements were carried out in the AC transport (ACT) mode27 of the PPMS. The ACT puck was modified by a van-der-Pauw press contact assembly purchased from Wimbush Science & Technology. The probes are spring contacts, gold plated over nickel; the distance between the pins was set to 2 mm. The resistivity was measured between 2–300 K with a data point every 0.1 K up to 25 K and one data point every 1 K up to 300 K. The AC frequency was set to 17 Hz with a measurement time of 1 s. The recorded data of channel 1 & 2 was converted according to the van-der-Pauw equation given in the Quantum Design Application Note 1076-304.
2.6. Mössbauer spectroscopy
The 21.53 keV transition of 151Eu with an activity of 130 MBq (2% of the total activity of a 151Sm:EuF3 source) and a Ba121mSnO3 source were used for the 151Eu and 121Sb Mössbauer spectroscopic experiments, which were conducted in the usual transmission geometry. The measurements were performed with a commercial helium-bath cryostat and a liquid nitrogen-bath cryostat. The temperature of the absorber was set to 6 K, 78 K or RT, while the source was kept at room temperature. The temperature was controlled by a resistance thermometer (∼0.5 K accuracy). The samples were enclosed in small PVC containers, the required sample mass was calculated based on the work by Long et al.28 Fitting of the spectrum was performed with the WinNormos program package.29 The obtained fitting parameters are listed in Table 5.
Table 5 Fitting parameters of the 121Sb and 151Eu Mössbauer spectroscopic measurements of Eu11AlAs11 and Eu14AlSb11 at RT, 78 K and 6 K. δ = isomer shift, ΔEQ = electric quadrupole splitting, Γ = experimental line width, BHF = hyperfine field
| Compound |
δ/mm s−1 |
ΔEQ/mm s−1 |
Γ/mm s−1 |
B
HF
|
|
Fixed during fitting procedure due to strong correlations.
Isomeric shift of Eu3+ in Eu2O3.
Hyperfine field increment of 0.1 T.
Four signals used.
|
|
Eu
14
Al
121
Sb
11
, 78 K
|
| #1 |
−9.6(1) |
−10.5(7) |
3.08a |
— |
| #2 |
−8.2(1) |
+6.4(5) |
3.08a |
— |
| #3 |
−8.1(1) |
0a |
3.08a |
— |
|
151
Eu
14
AlAs
11
, 6 K
|
| #1 |
−10.2(2) |
−2.9(7) |
2.7a |
17.7(6) |
| #2 |
−10.5(2) |
−1.2(8) |
2.7a |
19.1(6) |
| #3 |
−9.1(4) |
+0.3(9) |
2.7a |
17.5(6) |
| #4 |
−10.8(1) |
+4.1(4) |
2.7a |
17.6(3) |
| #5 (2%) |
+1.05b |
— |
2.7a |
— |
|
151
Eu
14
AlAs
11
, 6 K – hyperfine field distribution fit
|
| #1 |
−10.5(1) |
+0.9(7) |
2.7a |
20(7)c |
| #2 (2%) |
+1.05b |
— |
2.7a |
— |
|
151
Eu
14
AlAs
11
, RT
|
| #1 |
−9.5(1) |
— |
2.7a |
— |
| #2 |
−10.5(1) |
— |
2.7a |
— |
| #3 |
−12.8(1) |
— |
2.7a |
— |
| #4 |
−11.8(1) |
— |
2.7a |
— |
| #5 (2%) |
+1.05b |
— |
2.7a |
— |
|
151
Eu
14
AlAs
11
, RT – isomeric shift distribution fit: Δδ = 1.0(1) mm s
−1
|
| #1 |
−11(1)d |
— |
2.7a |
— |
| #2 |
+1.05b |
— |
2.7a |
— |
|
151
Eu
14
AlSb
11
, 6 K
|
| #1 |
−10.7(1) |
−1.1(2) |
2.7a |
18.1(1) |
| #2 |
−8.6(1) |
+6.6(1) |
2.7a |
20.0(1) |
| #3 |
−12.3(1) |
−2.1(2) |
2.7a |
11.2(1) |
| #4 |
−11.2(1) |
−0.5(2) |
2.7a |
21.2(1) |
| #5 (2%) |
+1.05b |
— |
2.7a |
— |
|
151
Eu
14
AlSb
11
, 6 K – hyperfine field distribution fit
|
| #1 |
−10.7(1) |
−0.5(1) |
2.7a |
21(8)c |
| #2 (2%) |
+1.05b |
— |
2.7a |
— |
|
151
Eu
14
AlSb
11
, RT
|
| #1 |
−9.87(2) |
— |
2.7a |
— |
| #2 |
−10.88(2) |
— |
2.7a |
— |
| #3 |
−12.99(4) |
— |
2.7a |
— |
| #4 |
−12.04(2) |
— |
2.7a |
— |
| #5 (2%) |
+1.05b |
— |
2.7a |
— |
|
151
Eu
14
AlSb
11
, RT – isomeric shift distribution fit: Δδ = 1.0(1) mm s
−1
|
| #1 |
−11(1)d |
— |
2.7a |
— |
| #2 |
+1.05b |
— |
2.7a |
— |
2.7. Theoretical methodology
Electronic structure calculations of Eu14AlSb11 and Sr14AlSb11 were performed using the projector augmented wave method (PAW) of Blöchl30,31 coded in the Vienna ab initio simulation package (VASP).32,33 All VASP calculations employed the generalized gradient approximation (GGA) with exchange and correlation treated by Perdew–Burke–Ernzerhof (PBE).34 To describe the electron correlation associated with Eu 4f states, an on-site Hubbard repulsion U parameter35 was applied with an effective Ueff = 6 eV on the Eu atom. The cutoff energy for the plane wave calculations was set to 500 eV and the Brillouin zone integration was carried out using 3 × 3 × 2 Γ-centered k-point meshes. The Bader charge analysis was based on VASP calculations with subsequent calculations with the Bader program developed by the Henkelman group.36–38
3. Results and discussion
3.1. Crystal chemistry
Eu14AlAs11 and Eu14AlSb11 crystallize in the tetragonal crystal system with space group I41/acd and lattice parameters of a = 1627.6(2) and c = 2180.0(4) pm for the arsenide and a = 1725.6(2) and c = 2289.7(7) pm for the antimonide. Both compounds are isostructural to Ca14AlSb11, which forms the respective prototype.10 The Zintl phase can be described using ionic constituents according to (Eu2+)14(AlPn49−)(Pn3−)4(Pn37−) with Pn37− being a linear tripnictide anion. An extended view as central projection of the unit cell of Eu14AlPn11 is shown in Fig. 1 (top and bottom). In the unit cell, isolated Pn3− and tetrahedral [AlPn4]9− anions (Fig. 2, top) are found besides the aforementioned Pn37− tripnictide anions (Fig. 2, bottom). The structure of Eu14AlSb11 has been refined from single crystal X-ray diffraction data and will subsequently be used for the structural discussion. The interatomic Al–Sb distances within the tetrahedral [AlSb4]9− units are 274 pm and therefore slightly longer than the sum of the covalent radii (125 + 141 = 266 pm (ref. 39)), yet in good agreement with the distances found in Ca14AlSb11 (272 pm).10 The distances within the linear Sb37− triantimonide anion are 325 pm, which is significantly longer than the sum of the covalent radii (2 × 141 = 282 pm (ref. 39)) of the element and also longer compared to antimony–antimony single bonds observed in other Zintl phases e.g., dimorphic BaSb2 (CaSb2 type: 291 pm;40 BaSb2 type: 291–296 pm (ref. 41)) or EuSb2 (CaSb2 type: 293 pm (ref. 42)). The observed distance, however, is again comparable to the one found in Ca14AlSb11 (320 pm)10 or Sr14AlSb11 (330 pm).11 In contrast to e.g. Sr5Al2Sb6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 or Eu5Al2Sb6,7 no higher dimensional antimonidoaluminate polyanion can be found. The four crystallographically independent Eu cations are found in between the anions and exhibit coordination numbers of nine (Eu1, Eu2 and Eu4) and twelve (Eu3) (Fig. 3) with Eu–Al distances of 367 pm and Eu–Sb distances of 324–357 and 380–385 pm. The interatomic Eu–Sb distances are close to the sum of the covalent radii (Eu + Sb = 326 pm (ref. 39)), suggesting bonding contributions between the Eu and Sb atoms, however, the Eu–Al distances are significantly longer compared to Eu + Al = 310 pm. The Eu–Eu distances of 371–401 pm are in line to slightly longer compared to the sum of the covalent radii of Eu + Eu = 370 pm.
43 or Eu5Al2Sb6,7 no higher dimensional antimonidoaluminate polyanion can be found. The four crystallographically independent Eu cations are found in between the anions and exhibit coordination numbers of nine (Eu1, Eu2 and Eu4) and twelve (Eu3) (Fig. 3) with Eu–Al distances of 367 pm and Eu–Sb distances of 324–357 and 380–385 pm. The interatomic Eu–Sb distances are close to the sum of the covalent radii (Eu + Sb = 326 pm (ref. 39)), suggesting bonding contributions between the Eu and Sb atoms, however, the Eu–Al distances are significantly longer compared to Eu + Al = 310 pm. The Eu–Eu distances of 371–401 pm are in line to slightly longer compared to the sum of the covalent radii of Eu + Eu = 370 pm.
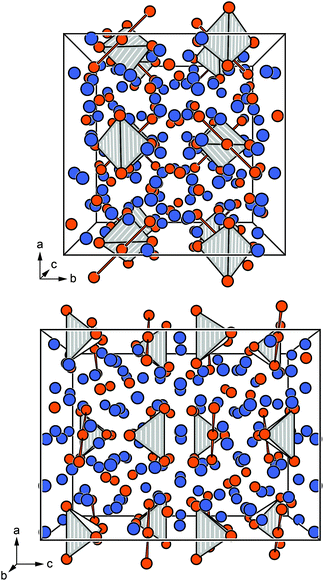 |
| | Fig. 1 Extended view of the unit cell of Eu14AlPn11 along [100] (top) and [010] (bottom). The bonding within the Pn37− tripnictide and the tetrahedral coordination environments of the [AlPn4]9− surrounding the Al atoms are highlighted. Eu atoms are depicted in blue, Al atoms as white circles and Pn atoms in orange. | |
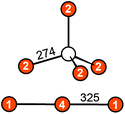 |
| | Fig. 2 Anions in the Zintl phase Eu14AlSb11: (top) tetrahedral [AlSb4]9− unit; (bottom) linear Sb37− triantimonide entity. The interatomic distances are given in pm. Al atoms are depicted as white circles and Sb atoms in orange. | |
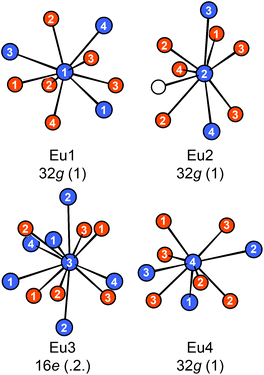 |
| | Fig. 3 Coordination environments surrounding the four crystallographically independent Eu atoms in Eu14AlSb11. The Wyckoff sites and local site symmetries are given. Eu atoms are depicted in blue, Al atoms as white circles and Sb atoms in orange. | |
3.2. Magnetic measurements
High-field magnetic susceptibility measurements of Eu14AlAs11 and Eu14AlSb11 were conducted in zero-field cooled (ZFC) mode at 10 kOe (Fig. 4 and 5, top panel) and indicate antiferromagnetic ordering at low temperatures and paramagnetic behaviour above the Neél-temperature. A Curie–Weiss fit of the reciprocal magnetic susceptibility in the paramagnetic region (75–300 K) was used to determine the effective magnetic moment and the paramagnetic Curie temperatures (Eu14AlAs11: μeff = 7.71(1) μB/Eu, θP = +18.3(1) K; Eu14AlSb11: μeff = 7.93(1) μB/Eu, θP = −1.9(1) K). The magnetic moments are in line with the calculated magnetic moment of a free Eu2+ ion (μcalc = 7.94 μB), indicating that all europium atoms are divalent. To confirm the magnetic ground state zero-field-cooled/field-cooled measurements (ZFC/FC) were conducted at an external field of 100 Oe. Fig. 4 and 5 (middle panel) show that the antiferromagnetic transition already observed in the high-field measurements can be seen again at TN = 10.5(1) and TN = 12.5(1) K for the arsenide and the respective antimonide. A second anomaly causing a bifurcation between the ZFC and FC curve can be observed at ∼7 K. Subsequently, heat capacity measurements (depicted in red in Fig. 5, middle panel) were conducted for Eu14AlSb11. They confirm the antiferromagnetic transition to be intrinsic and in line with the susceptibility measurements (T = 11.8(1) K). The observed bifurcation has to be attributed to traces of impurities since no peak signal is observed around 7 K in the specific heat. Finally, magnetization isotherms for both compounds were recorded (Fig. 4 and 5, bottom panel). The isotherms at 50 and 100 K show a linear field dependency in line with paramagnetic behaviour. For the arsenide, the 20 and 10 K isotherms show a pronounced curvature, since they are close to the magnetic transition. The 3 K isotherm finally exhibits an S-shaped character, which is a so-called meta-magnetic step (antiparallel to parallel spin realignment). The critical field was determined to be Hcrit = 8.2(1) kOe. The isotherm at 10 K for Eu14AlSb11 also shows a curved trace with a tendency for saturation at high fields. The 3 K isotherm finally exhibits again an S-shaped character, underlining the antiferromagnetic ground state (Hcrit = 17.0(1) kOe). The saturation magnetization reaches μsat = 5.8(1) μB per Eu2+ atom for Eu14AlAs11 and μsat = 6.6(1) μB per Eu2+ atom for Eu14AlSb11 at 3 K and 80 kOe. This is, in both cases, only slightly lower than the expected saturation magnetization of 7 μB according to gJ × J.
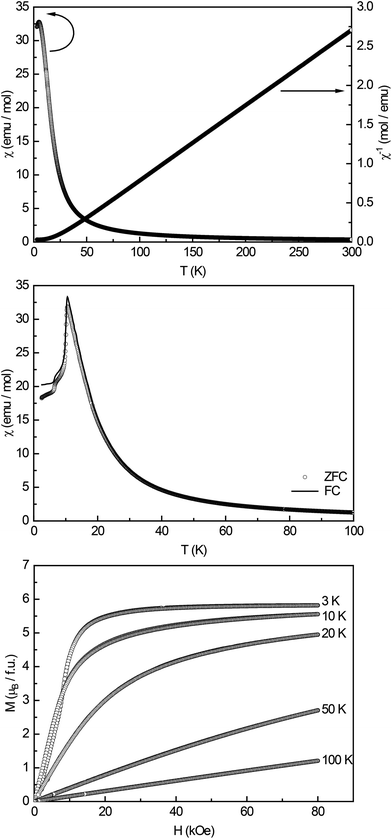 |
| | Fig. 4 Magnetic properties of Eu14AlAs11: (top) temperature dependence of the magnetic susceptibility (χ and χ−1 data) measured at 10 kOe; (middle) magnetic susceptibility in zero-field-cooled/field-cooled (ZFC/FC) mode, measured at 100 Oe in the low-temperature range; (bottom) magnetization isotherms recorded at 3, 10, 20, 50 and 100 K. | |
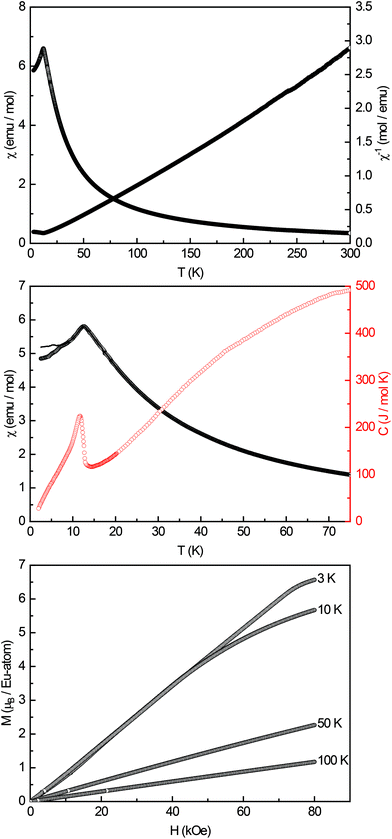 |
| | Fig. 5 Magnetic properties of Eu14AlSb11: (top) temperature dependence of the magnetic susceptibility (χ and χ−1 data) measured at 10 kOe; (middle) magnetic susceptibility in zero-field-cooled/field-cooled (ZFC/FC) mode, measured at 100 Oe in the low-temperature range, in red the heat capacity measurement in zero-field between 2–75 K is shown; (bottom) magnetization isotherms recorded at 3, 10, 50 and 100 K. | |
3.3. Electrical resistivity
The temperature dependence of the electrical resistivity of Eu14AlSb11 is depicted in Fig. 6. The measured resistivity increases with decreasing temperature, therefore exhibits the typical behaviour of a semiconductor. From the high temperature region of this measurement, two band gaps were extracted using the relation ρ ∝ eEg/2kT for semiconductors. In Fig. 6 (inset) the Arrhenius plot is depicted. The data between 250 and 300 K yielded a band gap of Eg = 0.28(5) eV (red) whereas the fit between 150–250 K resulted in Eg = 0.13(5) eV (green).
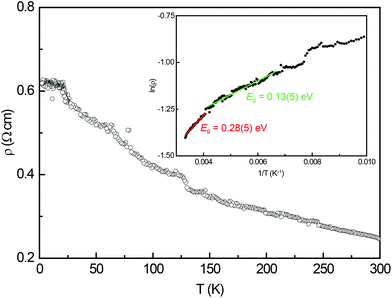 |
| | Fig. 6 Temperature dependence of the electrical resistivity of Eu14AlSb11. The inset depicts the Arrhenius plot used to determine the band gap. | |
3.4.
121Sb and 151Eu Mössbauer spectroscopy
To further proof the presence of Eu2+ in Eu14AlAs11 and Eu14AlSb11, 151Eu Mössbauer spectra were recorded at 6 K and RT. The obtained fitting parameters are listed in Table 5. We want to note, that fitting the obtained spectra with only one signal is not possible in all cases. Since the Eu14AlPn11 compounds exhibit four crystallographic Eu sites (Fig. 3), in principle four signals with respective ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 could be used for fitting the Mössbauer data. A similar fit using three signals has already been performed for Eu5Al2Sb6.7
2 could be used for fitting the Mössbauer data. A similar fit using three signals has already been performed for Eu5Al2Sb6.7
The calculated Bader charges (vide infra) for the Eu atoms suggest a distribution of isomeric shifts, both at RT and 6 K. The RT spectra of Eu14AlAs11 and Eu14AlSb11 can be fitted using four signals (Fig. 7, left). The refined isomeric shifts range from δ = −9.5 to −13 mm s−1, in line with Eu2+ cations. Due to strong correlations, the line width was fixed to typical values of Γ = 2.7 mm s−1.7,44–49 Alternatively, the experimental spectra can be reproduced using an isomeric shift distribution (Fig. 7, right), yielding an average shift of δ = −11(1) mm s−1 along with Δδ = 1.0(1) mm s−1 for the arsenide and δ = −10.7(3) mm s−1 (Δδ = 1.0(1) mm s−1) for the antimonide. The Eu3+ impurities (<3%) that were observed in the 6 K spectra were added with a fixed percental contribution to the RT spectra.
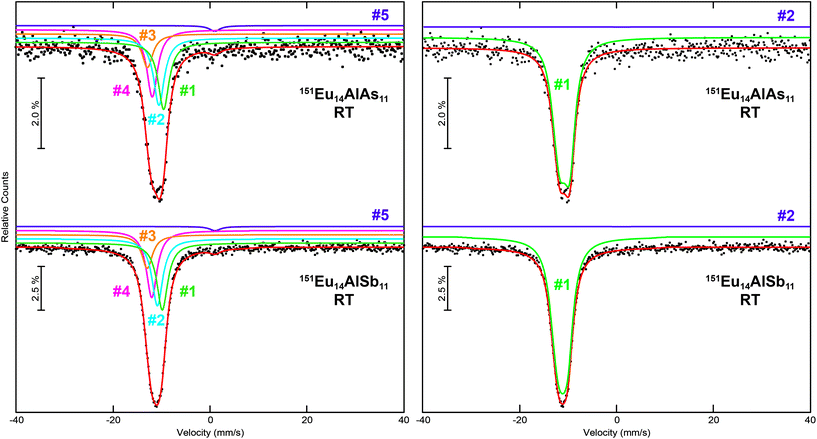 |
| | Fig. 7 Experimental (data points) and simulated (continuous lines) 151Eu Mössbauer spectra of Eu14AlAs11 and Eu14AlSb11 at room temperature. The red line corresponds to the sum of the different signals used for fitting. In the left panels, the fits using five signals are shown, they are labelled according to Table 5; in the right panels, the fits utilizing isomeric shift distributions are depicted. The purple signals are Eu3+ impurities. | |
The 6 K spectra were recorded below the respective Néel temperatures, hence, a full hyperfine field splitting was observed. Again, the 151Eu Mössbauer spectra of Eu14AlAs11 and Eu14AlSb11 were fitted with two possibilities. Fig. 8 (left) shows the fits using four signals for the respective Eu sites along with a fifth signal for the Eu3+ impurity, most likely originating from surface oxidation. The main signals of the arsenide show isomer shifts of δ = −10.2(2), −10.5(2), −9.1(4) and −10.8(1) mm s−1, the impurity signal is found at δ = +1.05 mm s−1. For the antimonide isomer shifts of δ = −10.7(1), −8.6(1), −12.3(1) and −11.2(1) mm s−1 are found, the impurity signal is located at δ = +1.05 mm s−1. As a consequence of the non-cubic site symmetry of the europium atoms, the signals in both compounds show quadrupole splitting. For the antimonide, Eu1 and Eu4 exhibit similar (distorted) coordination environments (both 32g, 1); with ΔEQ = −1.1(2) mm s−1 and ΔEQ = −2.1(2) mm s−1. Eu3 shows a rather symmetric coordination environment (16e, .2.) with an electric quadrupole splitting of ΔEQ = −0.5(2) mm s−1. Eu2 finally shows a highly distorted coordination environment (32g, 1), in line with a rather large quadrupole splitting ΔEQ = +6.6(1) mm s−1. In addition, significant magnetic hyperfine field splittings (Bhf = 18.1(1), 11.2(1), 21.2(1) and 20.0(1) T) were observed. The hyperfine fields are in line with other semiconducting and intermetallic europium compounds.7,44–49 The areas of the four signals were again fixed with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio, corresponding to the respective site multiplicities of the crystal structure (16e and 3× 32g). On the right hand side of Fig. 8, fits of the 151Eu Mössbauer spectra of Eu14AlAs11 and Eu14AlSb11 at 6 K, utilizing hyperfine field distributions, are depicted. An averaged isomeric shift of δ = −10.5(1) mm s−1 for Eu14AlAs11 and of δ = −10.7(1) mm s−1 for Eu14AlSb11 was refined. The obtained field distribution is illustrated in the histogram on the very right.
2 ratio, corresponding to the respective site multiplicities of the crystal structure (16e and 3× 32g). On the right hand side of Fig. 8, fits of the 151Eu Mössbauer spectra of Eu14AlAs11 and Eu14AlSb11 at 6 K, utilizing hyperfine field distributions, are depicted. An averaged isomeric shift of δ = −10.5(1) mm s−1 for Eu14AlAs11 and of δ = −10.7(1) mm s−1 for Eu14AlSb11 was refined. The obtained field distribution is illustrated in the histogram on the very right.
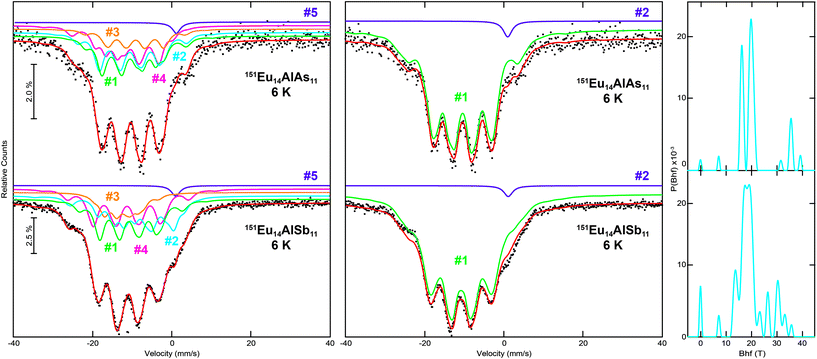 |
| | Fig. 8 Experimental (data points) and simulated (continuous lines) 151Eu Mössbauer spectra of Eu14AlAs11 and Eu14AlSb11 at 6 K. The red line corresponds to the sum of the different signals used for fitting. In the left panels, the fits using five signals are shown, they are labelled according to Table 5; in the middle panels, the fits utilizing hyperfine field distributions are depicted. On the right, the hyperfine field distributions are shown. The purple signals are Eu3+ impurities. | |
The 121Sb Mössbauer spectra of Eu14AlSb11 was measured at 78 K and is depicted in Fig. 9 along with the respective fits. The crystal structure contains four crystallographic antimonide sites (2× 32g, 16f and 8b) of which two sites (Sb1 and Sb4) are forming the Sb37− anion (16f and 8b), while the other two sites (Sb2 and Sb3) are Sb3− anions. These sites differ, however, in their crystal chemical environment. Sb3 is an isolated Sb3− anion, while Sb2 contributes to the [AlSb4]9− unit. Therefore, the spectrum was fitted using three signals, one for each Sb3− anion and one signal for the Sb37− (≡Sb2.33−) anion. The area ratio of the three signals was fixed to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Sb2
3 (Sb2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb3
Sb3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Sb1/4) ≡ Sb3−
(Sb1/4) ≡ Sb3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb3−
Sb3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb2.33−). While for the ‘Sb2.33−’ anions an isomer shift of δ = −9.6(1) mm s−1 was found, the Sb3− signals exhibit isomer shifts of δ = −8.2(1) mm s−1 and −8.1(1) mm s−1 (Table 5). For the latter ones, the observed isomer shifts are in line with other antimonides containing formally Sb3− anions, e.g. the binary alkali metal antimonides Li3Sb,50 A3Sb (A = Na, K, Rb),51 the III–V semiconductors AlSb, GaSb and InSb,52 the MT2Sb2 (M = Eu, Yb; T = Mn, Zn) series,53 the antimonide oxides RETSbO (RE = La–Sm, Gd; T = Mn, Zn)54 or the half-Heusler phases YbTSb (T = Ni, Pd, Pt, Cu, Ag, Au)55 and ScTSb (T = Ni, Pd, Pt)56 and M5Al2Sb6 (M = Sr, Eu)7 all with isomer shifts around δ ∼−8 mm s−1. Antimonide dumbbells and linear triantimonide units in contrast are rather rare with respect to 121Sb Mössbauer spectroscopic investigations. With respect to the dumbbells, the investigations of α-Zn13Sb10
Sb2.33−). While for the ‘Sb2.33−’ anions an isomer shift of δ = −9.6(1) mm s−1 was found, the Sb3− signals exhibit isomer shifts of δ = −8.2(1) mm s−1 and −8.1(1) mm s−1 (Table 5). For the latter ones, the observed isomer shifts are in line with other antimonides containing formally Sb3− anions, e.g. the binary alkali metal antimonides Li3Sb,50 A3Sb (A = Na, K, Rb),51 the III–V semiconductors AlSb, GaSb and InSb,52 the MT2Sb2 (M = Eu, Yb; T = Mn, Zn) series,53 the antimonide oxides RETSbO (RE = La–Sm, Gd; T = Mn, Zn)54 or the half-Heusler phases YbTSb (T = Ni, Pd, Pt, Cu, Ag, Au)55 and ScTSb (T = Ni, Pd, Pt)56 and M5Al2Sb6 (M = Sr, Eu)7 all with isomer shifts around δ ∼−8 mm s−1. Antimonide dumbbells and linear triantimonide units in contrast are rather rare with respect to 121Sb Mössbauer spectroscopic investigations. With respect to the dumbbells, the investigations of α-Zn13Sb10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 and M5Al2Sb6 (M = Sr, Eu)7 can be found in the literature with reported isomer shifts of δ ∼–9 mm s−1. For linear triantimonides so far no distinct Mössbauer spectroscopic investigations have been reported. The 121Sb Mössbauer spectra of Eu14MnSb11 and Yb14MnSb11 were fitted with two signals, one for the sample and one for an Sb2O3 impurity.58
57 and M5Al2Sb6 (M = Sr, Eu)7 can be found in the literature with reported isomer shifts of δ ∼–9 mm s−1. For linear triantimonides so far no distinct Mössbauer spectroscopic investigations have been reported. The 121Sb Mössbauer spectra of Eu14MnSb11 and Yb14MnSb11 were fitted with two signals, one for the sample and one for an Sb2O3 impurity.58
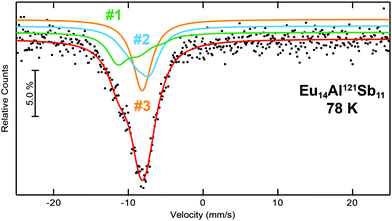 |
| | Fig. 9 Experimental (data points) and simulated (continuous lines) 121Sb Mössbauer spectrum of Eu14AlSb11 at 78 K. The red line corresponds to the sum of the different signals used for fitting. The fit using three signals is shown, they are labelled according to Table 5. | |
3.5. First principle calculations
To investigate the magnetic interactions in Eu14AlSb11, Eu–Eu pairs for interatomic distances less than 5.0 Å are considered, and nine spin exchange interactions were evaluated by performing mapping analysis of ten magnetic models. The nine spin exchange paths include Eu1–Eu2 (J12), Eu1–Eu3 (J13), Eu1–Eu4 (J14), Eu2–Eu3 (J23), Eu2–Eu4 (J24), Eu3–Eu4 (J34), Eu1–Eu1 (J11), Eu2–Eu2 (J22) and Eu4–Eu4 (J44). The magnetic models include one ferromagnetic (FM) model and nine ferrimagnetic (Fi1–Fi9) models (see Table 6). The relative energies, per formula unit (f. u.), of the ten magnetic models determined from our VASP calculations are summarized in Table 7. The energies of these models can also be approximated in terms of the spin Hamiltonian,
in which, Jij is the spin exchange parameter for the interaction between the spin site i and j. By applying this energy expression for spin dimers with N unpaired spins per spin site and mapping the relative energy of the ten models determined by VASP calculations onto the corresponding relative energies determined from the above exchange energies, we obtained the values of Jij listed in Table 7. The magnitudes of these parameters are similar as those for Eu5Al2Sb6,7 consistent with the near zero Weiss constant (θp = −1.9(1) K) and low ordering temperature (TN = 12.5(1) K). Eu3–Eu4 and Eu1–Eu1 interactions are ferromagnetic while the rest (seven) are antiferromagnetic (AFM) with four of them stronger than the two FM ones. Therefore, antiferromagnetic interactions dominate, which is consistent with the negative Weiss constant and the AFM transition observed in the magnetic measurements. The two FM interactions may account for the behaviour of the isotherms at 10 K and 3 K. Because of the complexity of the crystal structure, it is not easy to predict the magnetic ground state.
Table 6 The spin arrangement of the ten magnetic structure models. + indicates spin up, − indicates spin down, ± indicates that neighboring Eu atoms have opposite spins
| Models |
Arrangement of the spins |
| Eu1 |
Eu2 |
Eu3 |
Eu4 |
| Fi1 |
+ |
− |
+ |
+ |
| Fi2 |
+ |
+ |
− |
− |
| Fi3 |
+ |
− |
− |
+ |
| Fi4 |
− |
+ |
+ |
+ |
| Fi5 |
+ |
± |
+ |
+ |
| Fi6 |
+ |
− |
+ |
− |
| Fi7 |
± |
+ |
+ |
+ |
| Fi8 |
+ |
+ |
+ |
± |
| Fi9 |
+ |
+ |
− |
+ |
| |
| FM |
+ |
+ |
+ |
+ |
Table 7 Total energies and spin exchange energy expressions for the ten magnetic structure models of Eu14AlSb11. NEu = 7
| Models |
Energya (meV per f. u.) |
Spin exchange energy expression (meV) |
|
Total energy relative to model FM from VASP calculation.
|
| Fi1 |
−52.69 |
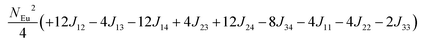
|
| Fi2 |
−51.84 |
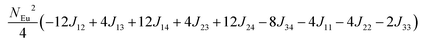
|
| Fi3 |
−40.38 |
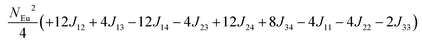
|
| Fi4 |
−30.34 |
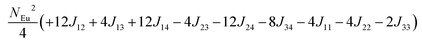
|
| Fi5 |
−26.91 |
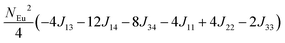
|
| Fi6 |
−18.86 |
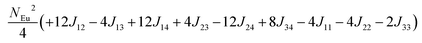
|
| Fi7 |
−14.00 |
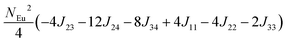
|
| Fi8 |
−13.90 |
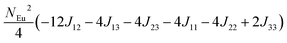
|
| Fi9 |
−5.94 |
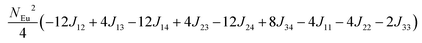
|
| FM |
0.00 |
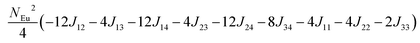
|
|
J (meV) |
|
J
12 = −0.053, J13 = −0.089, J14 = −0.021, J23 = −0.078, J24 = −0.100, J34 = +0.053, J11 = +0.012, J22 = −0.006, J44 = −0.028 |
The spin-polarized density of states (DOS) curve for the FM state was plotted in Fig. 10. There is a small band gap (∼0.07 eV for FM and ∼0.3 eV for the most stable magnetic model, Fi1) at the Fermi level, consistent with the large electrical resistivity. The majority spin states of Eu-f are all occupied, while its minority spin states are all unoccupied, indicating a high spin 4f7 (Eu2+) configuration. The calculated Bader effective charges for Eu14AlSb11 and Sr14AlSb11 are listed in Table 8. In both, Eu14AlSb11 and Sr14AlSb11, Eu, Sr and Al atoms have positive charges while Sb atoms have negative charges. The charges on Eu atoms are all between +1 and +2, which indicates that Eu3+ can be ruled out, in accordance with the 151Eu Mössbauer result that solely found Eu2+. However, the fact that the effective charges on Eu atoms are less than +2 indicates the presence of some partial covalent bonding interactions between Eu and Sb.
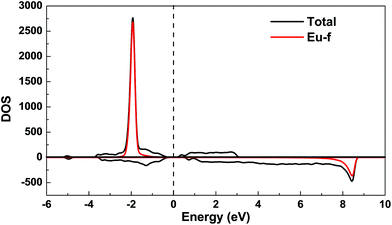 |
| | Fig. 10 Total and partial spin polarized density of states (DOS) of Eu14AlSb11 for ferromagnetic model. The Fermi level is denoted by the dashed line. | |
Table 8 Bader charges in Eu14AlSb11 and Sr14AlSb11
| Eu14AlSb11 |
Atom |
Eu1 |
Eu2 |
Eu3 |
Eu4 |
Al |
Sb1 |
Sb2 |
Sb3 |
Sb4 |
| Charge |
+1.16 |
+1.20 |
+1.13 |
+1.17 |
+1.35 |
−1.52 |
−1.70 |
−1.70 |
−1.11 |
| Sr14AlSb11 |
Atom |
Sr1 |
Sr2 |
Sr3 |
Sr4 |
Al |
Sb1 |
Sb2 |
Sb3 |
Sb4 |
| Charge |
+1.30 |
+1.33 |
+1.28 |
+1.32 |
+1.15 |
−1.69 |
−1.80 |
−1.91 |
−1.28 |
4. Conclusions
The Zintl phases Eu14AlAs11 and Eu14AlSb11 crystallize isostructural to Ca14AlSb11 and were synthesized from the elements in niobium ampoules in an induction furnace and subsequently structurally characterized by powder and single crystal X-ray diffraction. In the tetragonal crystal structure, the Al atoms are tetrahedrally surrounded by Pn atoms forming isolated [AlPn4]9− entities. Additionally, linear Pn37− triantimonide and spherical Pn3− anions are found. The four crystallographically independent Eu sites are located in between the different anionic species. In each compound, one magnetic ordering phenomena at TN = 10.5(1) K (Eu14AlAs11) and TN = 12.5(1) K (Eu14AlSb11) was observed in the susceptibility measurements and confirmed by heat capacity measurements in the case of the antimonide. 151Eu Mössbauer spectroscopic studies confirmed the divalent oxidation state of all europium atoms. Measurements at 6 K, therefore below TN, showed a hyperfine field splitting for all Eu sites due to magnetic ordering. The calculated densities of states using the ferromagnetic model indicate the presence of a band gap in accordance with the semiconducting behaviour found by electrical resistivity measurements. Based on the spin exchange parameters calculated using mapping analysis, the spin exchange interactions in Eu14AlSb11 are similar to Eu5Al2Sb5 and much smaller than other magnetically ordered rare-earth compounds. In addition, antiferromagnetic interactions dominate in Eu14AlSb11 with some weak ferromagnetic interactions. Bader charge analysis confirms the divalent oxidation state of Eu, but also indicates significant covalent interactions involving the Eu atoms.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank Dipl.-Ing. Jutta Kösters for the single crystal intensity data collection. Boniface P. T. Fokwa and Yuemei Zhang thank San Diego Supercomputer Center for providing computing resources.
References
-
S. M. Kauzlarich, Chemistry, Structure, and Bonding of Zintl Phases and Ions, VCH Publishers, 1996 Search PubMed.
-
O. Janka and S. M. Kauzlarich, in Encyclopedia of Inorganic and Bioinorganic Chemistry, John Wiley & Sons, Ltd, 2013 Search PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- S. R. Brown, S. M. Kauzlarich, F. Gascoin and G. J. Snyder, Chem. Mater., 2006, 18, 1873–1877 CrossRef CAS.
-
J.-A. Paik, B. Brandon, T. Caillat, R. Ewell and J. P. Fleurial, Proceedings of Nuclear and Emerging Technologies for Space 2011, 2011, paper 3695, 1–10.
- S. K. Bux, A. Zevalkink, O. Janka, D. Uhl, S. Kauzlarich, J. G. Snyder and J.-P. Fleurial, J. Mater. Chem. A, 2014, 2, 215–220 RSC.
- M. Radzieowski, T. Block, T. Fickenscher, Y. Zhang, B. P. T. Fokwa and O. Janka, Mater. Chem. Front., 2017, 1, 1563–1572 RSC.
- G. Cordier and M. Steher, Z. Naturforsch., B: J. Chem. Sci., 1988, 43, 463–466 CAS.
- A. Zevalkink, Y. Takagiwa, K. Kitahara, K. Kimura and G. J. Snyder, Dalton Trans., 2014, 43, 4720–4725 RSC.
- G. Cordier, H. Schäfer and M. Stelter, Z. Anorg. Allg. Chem., 1984, 519, 183–188 CrossRef CAS.
- S. L. Brock, L. J. Weston, M. M. Olmstead and S. M. Kauzlarich, J. Solid State Chem., 1993, 107, 513–523 CrossRef CAS.
- H. Kim and S. M. Kauzlarich, J. Solid State Chem., 2005, 178, 1935–1939 CrossRef CAS.
- A. Rehr, T. Y. Kuromoto, S. M. Kauzlarich, J. Delcastillo and D. J. Webb, Chem. Mater., 1994, 6, 93–99 CrossRef CAS.
- T. Y. Kuromoto, S. M. Kauzlarich and D. J. Webb, Chem. Mater., 1992, 4, 435–440 CrossRef CAS.
- W. Carrillo-Cabrera, M. Somer, K. Peters and H. G. von Schnering, Chem. Ber., 1996, 129, 1015–1023 CrossRef.
- A. C. Payne, M. M. Olmstead, S. M. Kauzlarich and D. J. Webb, Chem. Mater., 2001, 13, 1398–1406 CrossRef CAS.
- A. Rehr and S. M. Kauzlarich, J. Alloys Compd., 1994, 207, 424–426 CrossRef.
- J. Y. Chan, M. E. Wang, A. Rehr, S. M. Kauzlarich and D. J. Webb, Chem. Mater., 1997, 9, 2131–2138 CrossRef CAS.
- J. Y. Chan, M. M. Olmstead, S. M. Kauzlarich and D. J. Webb, Chem. Mater., 1998, 10, 3583–3588 CrossRef CAS.
- I. R. Fisher, S. L. Bud'ko, C. Song, P. C. Canfield, T. C. Ozawa and S. M. Kauzlarich, Phys. Rev. Lett., 2000, 85, 1120–1123 CrossRef CAS PubMed.
- A. P. Holm, T. C. Ozawa, S. M. Kauzlarich, S. A. Morton, G. Dan Waddill and J. G. Tobin, J. Solid State Chem., 2005, 178, 262–269 CrossRef CAS.
- R. Pöttgen, T. Gulden and A. Simon, GIT Labor-Fachz., 1999, 43, 133–136 Search PubMed.
- D. Kußmann, R.-D. Hoffmann and R. Pöttgen, Z. Anorg. Allg. Chem., 1998, 624, 1727–1735 CrossRef.
- E. A. Leon-Escamilla, W.-M. Hurng, E. S. Peterson and J. D. Corbett, Inorg. Chem., 1997, 36, 703–710 CrossRef CAS.
- R. J. Gambino, J. Less-Common Met., 1967, 12, 344–352 CrossRef CAS.
- K. Yvon, W. Jeitschko and E. Parthé, J. Appl. Crystallogr., 1977, 10, 73–74 CrossRef.
- L. J. van der Pauw, Philips Res. Rep., 1958, 13, 1–9 Search PubMed.
-
G. J. Long, T. E. Cranshaw and G. Longworth, Mössbauer Effect Reference and Data Journal, 1983, vol. 6, pp. 42–49 Search PubMed.
-
R. A. Brand, WinNormos for Igor6, Version for Igor 6.2 or above: 22.02.2017, Universität Duisburg, Duisburg (Germany), 2017 Search PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
-
J. Emsley, The Elements, Clarendon Press, Oxford University Press, Oxford, New York, 1998 Search PubMed.
- B. Eisenmann, C. Gieck and U. Rößler, Z. Kristallogr. – New Cryst. Struct., 2001, 216, 36 CAS.
- F. Emmerling, N. Längin, F. Pickhard, M. Wendorff and C. Röhr, Z. Naturforsch., B: J. Chem. Sci., 2004, 59, 7–16 CAS.
- F. Hulliger and R. Schmelczer, J. Solid State Chem., 1978, 26, 389–396 CrossRef CAS.
- G. Cordier and M. Stelter, Z. Naturforsch., 1988, 43, 463–466 CAS.
- R. Müllmann, B. D. Mosel, H. Eckert, G. Kotzyba and R. Pöttgen, J. Solid State Chem., 1998, 137, 174–180 CrossRef.
- D. Kußmann, R. Pöttgen, U. C. Rodewald, C. Rosenhahn, B. D. Mosel, G. Kotzyba and B. Künnen, Z. Naturforsch., B: J. Chem. Sci., 1999, 54, 1155–1164 Search PubMed.
- S. Seidel, O. Niehaus, S. F. Matar, O. Janka, B. Gerke, U. C. Rodewald and R. Pöttgen, Z. Naturforsch., B: J. Chem. Sci., 2014, 69, 1105–1118 CAS.
- J.-P. Schmiegel, T. Block, B. Gerke, T. Fickenscher, R. S. Touzani, B. P. T. Fokwa and O. Janka, Inorg. Chem., 2016, 55, 9057–9064 CrossRef CAS PubMed.
- I. Schellenberg, M. Eul and R. Pöttgen, Monatsh. Chem., 2011, 142, 875–880 CrossRef CAS.
- M. Radzieowski, F. Stegemann, T. Block, J. Stahl, D. Johrendt and O. Janka, J. Am. Chem. Soc., 2018, 140, 8950–8957 CrossRef CAS PubMed.
- P. E. Lippens, J.-C. Jumas and J. Olivier-Fourcade, Hyperfine Interact., 2004, 156, 327–333 CrossRef.
- K. Kitadai, M. Takahashi and M. Takeda, J. Radioanal. Nucl. Chem., 2003, 255, 311–314 CrossRef CAS.
- P. E. Lippens, Solid State Commun., 2000, 113, 399–403 CrossRef CAS.
- I. Schellenberg, M. Eul, W. Hermes and R. Pöttgen, Z. Anorg. Allg. Chem., 2010, 636, 85–93 CrossRef CAS.
- I. Schellenberg, T. Nilges and R. Pöttgen, Z. Naturforsch., B: J. Chem. Sci., 2008, 63, 834–840 CAS.
- M. Ratikanta, R. Pöttgen, R.-D. Hoffmann, T. Fickenscher, M. Eschen, H. Trill and B. D. Mosel, Z. Naturforsch., B: J. Chem. Sci., 2002, 57, 1215–1223 Search PubMed.
- T. Harmening, H. Eckert and R. Pöttgen, Solid State Sci., 2009, 11, 900–906 CrossRef CAS.
- R. P. Hermann, F. Grandjean, T.-C. Chen, D. E. Brown, C. E. Johnson, G. J. Snyder and G. J. Long, Inorg. Chem., 2007, 46, 767–770 CrossRef CAS PubMed.
- R. P. Hermann, F. Grandjean, D. Kafle, D. E. Brown, C. E. Johnson, S. M. Kauzlarich and G. J. Long, Inorg. Chem., 2007, 46, 10736–10740 CrossRef CAS PubMed.
|
| This journal is © the Partner Organisations 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  b,
Boniface P. T.
Fokwa
b,
Boniface P. T.
Fokwa
 b and
Oliver
Janka
b and
Oliver
Janka
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4,5 or Yb9Mn4.2Sb9
4,5 or Yb9Mn4.2Sb9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 are prominent examples for antimony containing high zT thermoelectric materials. Recently we have reported on the first compound in the ternary system Eu–Al–Sb, Eu5Al2Sb6,7 which crystallizes isotypically to Sr5Al2Sb6.8,9 Further investigations lead to the discovery of another prominent composition amongst antimonide Zintl phases: Eu14AlSb11, which crystallizes in the Ca14AlSb11 type structure.10 Of this 14–1–11 composition numerous compounds have been reported: A14AlSb11 (A = Ca,10,11 Sr,11 Ba11) Ca14MnX11 (X = P,12 As,13 Sb,13 Bi14), Sr14MnX11 (X = As,13 Sb,13 Bi14), Ba14MnX11 (X = As,13 Sb,13 Bi14), Ba14InP11,15 Eu14MnX11 (X = P,16 As,16 Sb,17 Bi18), Eu14InX11 (X = Sb,18 Bi18), Yb14MnX11 (X = Sb,19 Bi19) and finally Yb14MSb11 (M = Al,20 Zn20,21).
6 are prominent examples for antimony containing high zT thermoelectric materials. Recently we have reported on the first compound in the ternary system Eu–Al–Sb, Eu5Al2Sb6,7 which crystallizes isotypically to Sr5Al2Sb6.8,9 Further investigations lead to the discovery of another prominent composition amongst antimonide Zintl phases: Eu14AlSb11, which crystallizes in the Ca14AlSb11 type structure.10 Of this 14–1–11 composition numerous compounds have been reported: A14AlSb11 (A = Ca,10,11 Sr,11 Ba11) Ca14MnX11 (X = P,12 As,13 Sb,13 Bi14), Sr14MnX11 (X = As,13 Sb,13 Bi14), Ba14MnX11 (X = As,13 Sb,13 Bi14), Ba14InP11,15 Eu14MnX11 (X = P,16 As,16 Sb,17 Bi18), Eu14InX11 (X = Sb,18 Bi18), Yb14MnX11 (X = Sb,19 Bi19) and finally Yb14MSb11 (M = Al,20 Zn20,21).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648
648![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201
201![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 or Eu5Al2Sb6,7 no higher dimensional antimonidoaluminate polyanion can be found. The four crystallographically independent Eu cations are found in between the anions and exhibit coordination numbers of nine (Eu1, Eu2 and Eu4) and twelve (Eu3) (Fig. 3) with Eu–Al distances of 367 pm and Eu–Sb distances of 324–357 and 380–385 pm. The interatomic Eu–Sb distances are close to the sum of the covalent radii (Eu + Sb = 326 pm (ref. 39)), suggesting bonding contributions between the Eu and Sb atoms, however, the Eu–Al distances are significantly longer compared to Eu + Al = 310 pm. The Eu–Eu distances of 371–401 pm are in line to slightly longer compared to the sum of the covalent radii of Eu + Eu = 370 pm.
43 or Eu5Al2Sb6,7 no higher dimensional antimonidoaluminate polyanion can be found. The four crystallographically independent Eu cations are found in between the anions and exhibit coordination numbers of nine (Eu1, Eu2 and Eu4) and twelve (Eu3) (Fig. 3) with Eu–Al distances of 367 pm and Eu–Sb distances of 324–357 and 380–385 pm. The interatomic Eu–Sb distances are close to the sum of the covalent radii (Eu + Sb = 326 pm (ref. 39)), suggesting bonding contributions between the Eu and Sb atoms, however, the Eu–Al distances are significantly longer compared to Eu + Al = 310 pm. The Eu–Eu distances of 371–401 pm are in line to slightly longer compared to the sum of the covalent radii of Eu + Eu = 370 pm.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 could be used for fitting the Mössbauer data. A similar fit using three signals has already been performed for Eu5Al2Sb6.7
2 could be used for fitting the Mössbauer data. A similar fit using three signals has already been performed for Eu5Al2Sb6.7

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio, corresponding to the respective site multiplicities of the crystal structure (16e and 3× 32g). On the right hand side of Fig. 8, fits of the 151Eu Mössbauer spectra of Eu14AlAs11 and Eu14AlSb11 at 6 K, utilizing hyperfine field distributions, are depicted. An averaged isomeric shift of δ = −10.5(1) mm s−1 for Eu14AlAs11 and of δ = −10.7(1) mm s−1 for Eu14AlSb11 was refined. The obtained field distribution is illustrated in the histogram on the very right.
2 ratio, corresponding to the respective site multiplicities of the crystal structure (16e and 3× 32g). On the right hand side of Fig. 8, fits of the 151Eu Mössbauer spectra of Eu14AlAs11 and Eu14AlSb11 at 6 K, utilizing hyperfine field distributions, are depicted. An averaged isomeric shift of δ = −10.5(1) mm s−1 for Eu14AlAs11 and of δ = −10.7(1) mm s−1 for Eu14AlSb11 was refined. The obtained field distribution is illustrated in the histogram on the very right.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Sb2
3 (Sb2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb3
Sb3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Sb1/4) ≡ Sb3−
(Sb1/4) ≡ Sb3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb3−
Sb3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb2.33−). While for the ‘Sb2.33−’ anions an isomer shift of δ = −9.6(1) mm s−1 was found, the Sb3− signals exhibit isomer shifts of δ = −8.2(1) mm s−1 and −8.1(1) mm s−1 (Table 5). For the latter ones, the observed isomer shifts are in line with other antimonides containing formally Sb3− anions, e.g. the binary alkali metal antimonides Li3Sb,50 A3Sb (A = Na, K, Rb),51 the III–V semiconductors AlSb, GaSb and InSb,52 the MT2Sb2 (M = Eu, Yb; T = Mn, Zn) series,53 the antimonide oxides RETSbO (RE = La–Sm, Gd; T = Mn, Zn)54 or the half-Heusler phases YbTSb (T = Ni, Pd, Pt, Cu, Ag, Au)55 and ScTSb (T = Ni, Pd, Pt)56 and M5Al2Sb6 (M = Sr, Eu)7 all with isomer shifts around δ ∼−8 mm s−1. Antimonide dumbbells and linear triantimonide units in contrast are rather rare with respect to 121Sb Mössbauer spectroscopic investigations. With respect to the dumbbells, the investigations of α-Zn13Sb10
Sb2.33−). While for the ‘Sb2.33−’ anions an isomer shift of δ = −9.6(1) mm s−1 was found, the Sb3− signals exhibit isomer shifts of δ = −8.2(1) mm s−1 and −8.1(1) mm s−1 (Table 5). For the latter ones, the observed isomer shifts are in line with other antimonides containing formally Sb3− anions, e.g. the binary alkali metal antimonides Li3Sb,50 A3Sb (A = Na, K, Rb),51 the III–V semiconductors AlSb, GaSb and InSb,52 the MT2Sb2 (M = Eu, Yb; T = Mn, Zn) series,53 the antimonide oxides RETSbO (RE = La–Sm, Gd; T = Mn, Zn)54 or the half-Heusler phases YbTSb (T = Ni, Pd, Pt, Cu, Ag, Au)55 and ScTSb (T = Ni, Pd, Pt)56 and M5Al2Sb6 (M = Sr, Eu)7 all with isomer shifts around δ ∼−8 mm s−1. Antimonide dumbbells and linear triantimonide units in contrast are rather rare with respect to 121Sb Mössbauer spectroscopic investigations. With respect to the dumbbells, the investigations of α-Zn13Sb10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 and M5Al2Sb6 (M = Sr, Eu)7 can be found in the literature with reported isomer shifts of δ ∼–9 mm s−1. For linear triantimonides so far no distinct Mössbauer spectroscopic investigations have been reported. The 121Sb Mössbauer spectra of Eu14MnSb11 and Yb14MnSb11 were fitted with two signals, one for the sample and one for an Sb2O3 impurity.58
57 and M5Al2Sb6 (M = Sr, Eu)7 can be found in the literature with reported isomer shifts of δ ∼–9 mm s−1. For linear triantimonides so far no distinct Mössbauer spectroscopic investigations have been reported. The 121Sb Mössbauer spectra of Eu14MnSb11 and Yb14MnSb11 were fitted with two signals, one for the sample and one for an Sb2O3 impurity.58