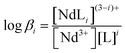DOI:
10.1039/C7NJ03925E
(Paper)
New J. Chem., 2018,
42, 708-716
Complexation thermodynamics of tetraalkyl diglycolamides with trivalent f-elements in ionic liquids: spectroscopic, microcalorimetric and computational studies†
Received
19th October 2017
, Accepted 29th November 2017
First published on 29th November 2017
Abstract
The thermodynamics of lanthanide complexation with a series of diglycolamides (DGAs) containing varying alkyl chain lengths (methyl, ethyl, n-butyl and n-hexyl) was studied in [C4mim][Tf2N], a room temperature ionic liquid. The stability constants, enthalpies and entropies of complexation were determined by spectrophotometry and calorimetry. All the DGA ligands formed a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Nd3+/DGA) complex as the limiting species, and their stability constants increased linearly with increasing alkyl chain length. The stability constants of the Nd3+/DGA complexes are orders of magnitude higher in [C4mim][Tf2N] as compared to those observed in aqueous medium. For all the complexes, the enthalpy of complexation was negative with a positive entropy change, indicating that the complexation was driven by both enthalpy and entropy. The enthalpy changes observed in [C4mim][Tf2N] medium were more exothermic than those in the aqueous medium. Fluorescence lifetime data indicated that the complexation proceeded via the replacement of water molecules from the primary coordination sphere of the metal ion. DFT calculations were performed on the structures of the different Nd3+/tetramethyl DGA (TMDGA) complexes, and the corresponding free energies in both gas and solution phases were calculated. Insights into the structural features by DFT studies confirmed that the nature of Ln3+/DGA complexes formed in [C4mim][Tf2N], n-dodecane, and aqueous medium and that in the crystalline state is identical.
3 (Nd3+/DGA) complex as the limiting species, and their stability constants increased linearly with increasing alkyl chain length. The stability constants of the Nd3+/DGA complexes are orders of magnitude higher in [C4mim][Tf2N] as compared to those observed in aqueous medium. For all the complexes, the enthalpy of complexation was negative with a positive entropy change, indicating that the complexation was driven by both enthalpy and entropy. The enthalpy changes observed in [C4mim][Tf2N] medium were more exothermic than those in the aqueous medium. Fluorescence lifetime data indicated that the complexation proceeded via the replacement of water molecules from the primary coordination sphere of the metal ion. DFT calculations were performed on the structures of the different Nd3+/tetramethyl DGA (TMDGA) complexes, and the corresponding free energies in both gas and solution phases were calculated. Insights into the structural features by DFT studies confirmed that the nature of Ln3+/DGA complexes formed in [C4mim][Tf2N], n-dodecane, and aqueous medium and that in the crystalline state is identical.
1. Introduction
During the last decade and half, a new class of diamide extractants, namely diglycolamides (DGAs), containing an ether linkage between two amide groups (Fig. 1), has received particular attention from separation scientists engaged in the field of actinide partitioning.1–5 Extensive studies have been carried out with DGA ligands pertaining to the selective complexation and separation of lanthanides (Lns) and actinides (Ans) from various aqueous streams. The basic studies include aqueous complexation with water-soluble DGA ligands for selective stripping of Ans,6–8 spectroscopy, synthesis of solid complexes9–13 and theoretical calculations with these ligands.14–17 The applied studies extensively focused on the evaluation of DGA extractants for actinide partitioning from nuclear waste solutions.1,2 Amongst the various DGA ligands, the most efficient actinide partitioning studies have been accomplished using TODGA (N,N,N′,N′-tetra-n-octyl diglycolamide)18–22 and T2EHDGA (N,N,N′,N′-tetra-2-ethylhexyl diglycolamide).23,24 TODGA has been extensively studied in different laboratories, and hot runs have been demonstrated at the European Union program on actinide recycling by separation and transmutation (ACSEPT) at ITU, Karlsruhe.19,25
 |
| | Fig. 1 Molecular structures of tetraalkyl diglycolamides (TRDGA) and the cationic and anionic components of [C4mim][Tf2N]. | |
Apart from applied research, the fascinating chemistry of DGAs has caught the imagination of researchers, as is evident from a large number of publications in basic chemistry studies.10,15,26,27 The complexation of DGA ligands with metal ions is intriguing as these ligands display a high affinity for trivalent actinide ions as compared to the hexavalent actinide ions. The distribution ratios of Ans in solvent extraction with the TODGA/n-dodecane system generally decrease in the order: An3+/Ln3+ > An4+ ≫ AnO22+ > AnO2+, which is quite different from those of other known neutral extractants, such as CMPO (octyl(phenyl)-N,N-diisobutylcarbamoylmethyl phosphine oxide), TRPO (trialkylphosphine oxide), DMDBTDMA (N,N′-dimethyl-N,N′-dibutyltetradecyl malonamide), etc.28 The extraction ability of the latter neutral extractants usually decreases in the order: An4+ ≅ AnO22+ > An3+/Ln3+ > AnO2+, which is explained on the basis of the effective charges on these metal ions. Moreover, an analysis based on solvent extraction experiments showed some inconsistencies in the extracted complexes of An3+, wherein a varying number of 2–4 TODGA molecules were observed in the extracted complexes.5,29 On the other hand, aqueous complexation of Ln3+/Am3+ with TMDGA (N,N,N′,N’-tetramethyl diglycolamide) and their crystal structures have confirmed the coordination of three DGA ligands in tridentate mode.9–11 A similar observation has been made in the solution phase of the Eu3+/TODGA extracted complex in n-dodecane by EXAFS measurements.26 Another report involved studies on M3+/TODGA complexes (M = Eu and Cm) in ethanol by time-resolved laser fluorescence measurements and the suggested analogous species.13
It is important to note that all the studies pertaining to DGA complexation have been made in a molecular solvent, either in aqueous medium or in solvents such as methanol, ethanol or acetonitrile.9–11,13,30 In contrast to this, a study on the complexation of DGAs with Ln3+ or An3+ in room temperature ionic liquids (RTILs) has been unknown until recently,31 though extensive solvent extraction-based separation studies have been performed in RTILs with these ligands.32 One of the major advantages of a RTIL-based solvent is the unusually high extraction of metal ions as compared to that observed with molecular diluents.33–35 This has been explained on the basis of a cation-exchange mechanism prevailing in the case of RTILs as the diluents as compared to a solvation mechanism operative in the case of the conventional molecular diluents.36–38 Interestingly, however, there are reports in which an analogous extraction behavior of metal ions has been reported both in RTILs and in molecular solvents.39
Despite numerous studies conducted on the use of RTILs for metal ion separations, fundamental studies on the thermodynamics of the interactions of metal ions with ligands in RTILs are rare. A few studies have been devoted to the fundamental understanding of the energetics of the Ln/An complexation in RTILs with simple ligands such as nitrates, chlorides, etc.40–45 To the best of our knowledge, only limited studies on the complexation of Lns with organic ligands in RTILs have been reported.45,46 The only study on DGA/Ln3+ complexation in a RTIL deals with relatively long alkyl chain derivatives of DGA (>C-5) in [C8mim][Tf2N] (3-octyl-1-methylimidazolium bis(trifluoromethanesulfonyl)imide).31 In the reported study, a RTIL having a larger alkyl chain length ([C8mim]) was used due to limited solubility of the higher alkyl chain DGA ligands in [C4mim][Tf2N].
The present study deals with the DGA ligands having smaller substituents such as methyl, ethyl, n-butyl and n-hexyl so that the ligand substituent effect can be better understood. [C4mim][Tf2N] (1-butyl-3-methyl imidazolium bis(trifluoromethanesulfonyl)imide) was chosen as the RTIL for this study because it has physico-chemical properties (such as water immiscibility and viscosity) favourable to applications in separation processes and has been widely studied as a solvent in biphasic separations.33–35 Furthermore, [C4mim][Tf2N] shows good solubility of lower alkyl chain DGA, e.g., tetramethyl to tetrahexyl DGA, and metal/ligand complexes. To gain insights into the nature of the Ln3+/DGA complexes formed in the RTIL, systematic studies were performed to obtain thermodynamic parameters, viz. the equilibrium constant, the enthalpy and entropy of complexation, structural factors, etc. The stability constants of Ln3+/DGA complexes were determined by spectrophotometric titration, whereas microcalorimetric titrations were performed to estimate the complexation heat. To understand the nature of the complexes, fluorescence spectroscopy and DFT calculations were also performed. The present fundamental study is of utmost importance to understand the extraction behaviour of metal ions in RTILs and paraffinic solvents (which have been well reported).
2. Result and discussion
2.1. Stability constants of Nd3+/DGA complexes: absorption spectroscopy
Fig. 2 shows the representative spectrophotometric titration data of Nd3+ with TMDGA, TEDGA and TBDGA. A similar spectrophotometric titration of Nd3+ with THDGA was also performed (Fig. S1 in the ESI†). The initial solution contained ∼10 mmol L−1Nd(Tf2N)3. As the aliquots of DGA were added stepwise, the intensity of the absorption band at 575 nm, corresponding to the hypersensitive 4I9/2 → 4G5/2 and 2G7/2 transitions of Nd3+, changed significantly.47 The changes consist of three stages. In the first stage, as the quantity of the ligand increased, the absorption band at 575 nm shifted to around 580 nm, indicating the formation of an ML complex. In the second stage, the intensity of the 580 nm absorption band decreased with a simultaneous red-shift in the absorption band. In the third step, the absorption band at 583 nm splits into a triplet upon addition of the ligand. No further spectral change was observed after this point even in the presence of excess ligand (CL/CNd = 10), suggesting the formation of a limiting complex. A factor analysis of the absorption spectra indicated the presence of four absorbing species, i.e., the free Nd3+ and three successive Nd3+/L complexes. The de-convoluted spectra of all the absorbing species are shown in the bottom part of Fig. 2. The spectra were fitted with the model described by eqn (2), and the calculated stability constants of the NdL3+, NdL23+ and NdL33+ complexes are listed in Table 1.
 |
| | Fig. 2 Representative spectrophotometric titrations of Nd3+ with TMDGA, TEDGA and TBDGA in [C4mim][Tf2N] (top), and the deconvoluted spectra of the Nd3+, Nd(L)3+, Nd(L)23+ and Nd(L)33+ species (Bottom). Cuvette: 25 μmole Nd(Tf2N)3 (2 mL); titrant: 100 μmole mL−1 ligand in [C4mim][Tf2N]; temperature: 25 °C. | |
Table 1 Stability constant data for DGA/Ln3+/An3+ at 25 °C
| M3+/DGA |
Complexa,b |
Medium |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β |
Ref.c |
|
L denotes the respective DGA ligand.
The equilibrium reactions are given in the ESI.
p.w. means present work.
|
| Nd3+/TMDGA |
NdL3+ |
[C4mim][Tf2N] |
4.40 ± 0.07 |
p.w. |
| NdL23+ |
7.99 ± 0.14 |
| NdL33+ |
10.5 ± 0.13 |
| Nd3+/TMDGA |
NdL3+ |
1 M NaNO3 |
3.53 ± 0.10 |
9
|
| NdL23+ |
5.84 ± 0.19 |
| NdL33+ |
6.80 ± 0.19 |
| Eu3+/TMDGA |
EuL3+ |
1 M NaNO3 |
3.43 ± 0.08 |
10
|
| EuL23+ |
5.59 ± 0.06 |
| EuL33+ |
6.48 ± 0.10 |
| Am3+/TMDGA |
AmL3+ |
1 M NaNO3 |
3.71 ± 0.01 |
11
|
| AmL23+ |
5.95 ± 0.06 |
| AmL33+ |
6.93 ± 0.03 |
| Nd3+/TEDGA |
NdL3+ |
[C4mim][Tf2N] |
5.28 ± 0.15 |
p.w. |
| NdL23+ |
9.13 ± 0.11 |
| NdL33+ |
11.4 ± 0.19 |
| Am3+/TEDGA |
AmL3+ |
1 M NaNO3 |
2.9 |
48
|
| AmL23+ |
6.07 |
| AmL33+ |
8.33 |
| Nd3+/TBDGA |
NdL3+ |
[C4mim][Tf2N] |
7.16 ± 0.16 |
p.w. |
| NdL23+ |
10.8 ± 0.17 |
| NdL33+ |
12.7 ± 0.14 |
| Nd3+/THDGA |
NdL3+ |
[C4mim][Tf2N] |
8.41 ± 0.32 |
p.w. |
| NdL23+ |
12.5 ± 0.29 |
| NdL33+ |
14.3 ± 0.34 |
| Nd3+/THDGA |
NdL3+ |
[C8mim][Tf2N] |
7.83 ± 0.05 |
31
|
| NdL23+ |
14.4 ± 0.11 |
| NdL33+ |
19.3 ± 0.11 |
It is worth mentioning that, to the best of our knowledge, this is the first report on the determination of stability constants of a lanthanide with TMDGA, TEDGA and TBDGA in any type of RTIL. However, complexation studies have been performed earlier with TMDGA in aqueous medium, where stability constants and crystal structures of Nd3+/TMDGA, Eu3+/TMDGA and Am3+/TMDGA have been reported (Table 1). Apart from this, the aqueous complexation of TEDGA with Am3+ has also been studied with respect to the selective aqueous stripping of Am3+ from the loaded organic phase over lanthanides.48 As summarized in Table 1, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of Nd3+, Eu3+ and Am3+ with TMDGA (in aqueous medium) are in close proximity. This information gives rise to a logical conclusion that the complexation constants obtained for Nd3+ in the present work may be extended to Am3+, which is an important actinide ion from the actinide partitioning point of view.1,2 The log
β values of Nd3+, Eu3+ and Am3+ with TMDGA (in aqueous medium) are in close proximity. This information gives rise to a logical conclusion that the complexation constants obtained for Nd3+ in the present work may be extended to Am3+, which is an important actinide ion from the actinide partitioning point of view.1,2 The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of Nd3+/TMDGA complexes in [C4mim][Tf2N] are several orders of magnitude higher than those in aqueous nitrate medium. This observation is in line with Nd3+/nitrate complexation in [C4mim][Tf2N], where stability of the Nd3+/NO3− complexes in RTIL are many orders of magnitude stronger than those observed in aqueous medium.40 A probable explanation for this unusual complexation was given based on the competition between nitrate ions and water molecules present in the primary hydration sphere of the metal ions. It is easier for the ligands to replace the water molecules from the primary coordination sphere when the metal ions are present in a hydrophobic medium such as an RTIL than when present in an aqueous medium (vide infra). When we compare the stability constants of Nd3+/DGA in [C4mim][Tf2N], the log
β values of Nd3+/TMDGA complexes in [C4mim][Tf2N] are several orders of magnitude higher than those in aqueous nitrate medium. This observation is in line with Nd3+/nitrate complexation in [C4mim][Tf2N], where stability of the Nd3+/NO3− complexes in RTIL are many orders of magnitude stronger than those observed in aqueous medium.40 A probable explanation for this unusual complexation was given based on the competition between nitrate ions and water molecules present in the primary hydration sphere of the metal ions. It is easier for the ligands to replace the water molecules from the primary coordination sphere when the metal ions are present in a hydrophobic medium such as an RTIL than when present in an aqueous medium (vide infra). When we compare the stability constants of Nd3+/DGA in [C4mim][Tf2N], the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β value increased linearly with increasing alkyl chain length of the DGA, i.e., log
β value increased linearly with increasing alkyl chain length of the DGA, i.e., log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βTMDGA < log
βTMDGA < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βTEDGA < log
βTEDGA < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βTBDGA < log
βTBDGA < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βTHDGA (Fig. 3). This behaviour may be ascribed to the increasing +I effect on the ligand upon increasing alkyl chain length. Table 1 also includes the log
βTHDGA (Fig. 3). This behaviour may be ascribed to the increasing +I effect on the ligand upon increasing alkyl chain length. Table 1 also includes the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for THDGA in [C8mim][Tf2N].31 It is intriguing to note that while the log
β values for THDGA in [C8mim][Tf2N].31 It is intriguing to note that while the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1 value is lower in [C8mim][Tf2N] as compared to that obtained in [C4mim][Tf2N], the log
β1 value is lower in [C8mim][Tf2N] as compared to that obtained in [C4mim][Tf2N], the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β2 and log
β2 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β3 values show the opposite trend. This feature might have arisen due to the different solvation power of the metal ion and the ligands in the two RTILs.
β3 values show the opposite trend. This feature might have arisen due to the different solvation power of the metal ion and the ligands in the two RTILs.
 |
| | Fig. 3 Stability constants of the Nd3+/DGA complexes in [C4mim][Tf2N] at 25 °C. | |
2.2. Enthalpy of complexation: microcalorimetry
Fig. 4 shows the overall heat of reaction, obtained from the microcalorimetric titrations, and the speciation of Nd3+/DGA complexes as a function of volume of the ligand added to the metal ion solution. The measured heat, in conjunction with the equilibrium constants determined by spectrophotometry (vide supra), was used to calculate the enthalpy of complexation using the Hyperquad program.49 As summarized in Table 2, the enthalpies of complexation for all the three complexes (with the four TRDGA ligands), viz. Nd(L)3+, Nd(L)23+ and Nd(L)33+, are exothermic and are in line with the enthalpy changes observed for Nd3+/TMDGA complexes in aqueous medium.9 However, the enthalpy change observed in [C4mim][Tf2N] medium was more exothermic than that in the aqueous medium, indicating a more favourable complexation reaction in the RTIL. This enthalpy trend in the two complexing media viz., aqueous and RTIL, may arise due to the differences in the degree of hydration/solvation of the ligand in these media. In the case of TMDGA, being more hydrated in aqueous medium, more energy is required to dehydrate the ligand before complexation, resulting in a lower exothermic enthalpy. The entropies of complexation, calculated from the enthalpies (obtained in calorimetry) and Gibbs free energies (calculated from the stability constant values), are all positive, indicating that the complexation processes are both enthalpy and entropy driven. The large positive entropies of complexation probably result from the release of the water molecules from the primary coordination sphere of Nd3+ upon complexation with the ligand. An important observation from Table 2 is that the stepwise enthalpy of complexation remains unchanged with values of ΔH1 = 9.5 ± 0.6 kJ mol−1, ΔH2 = 5.9 ± 0.9 kJ mol−1 and ΔH3 = 3.7 ± 0.7 kJ mol−1 (where, ΔH1, ΔH2 and ΔH3 represent the enthalpy changes for the stepwise complex formation reactions) DGA ligands. This is an indication that the complexation reactions are more entropy driven, and a higher positive entropy is obtained with increasing chain length of DGA. It looks like the shorter alkyl chain DGAs form more organized complexes, whereas the longer alkyl chain DGAs bring more disruption in the system while re-organizing their chain around the metal ion resulting in a higher entropy.
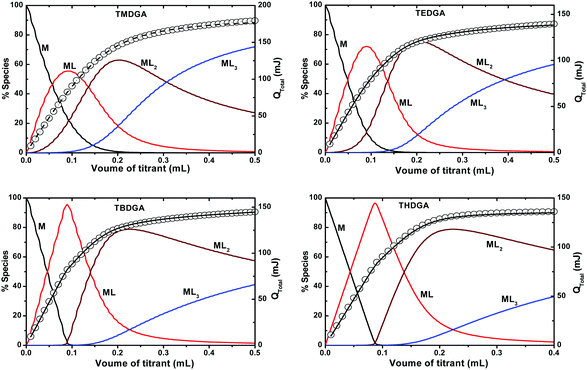 |
| | Fig. 4 Calorimetric titrations of Nd3+/DGA in [C4mim][Tf2N]. The left y-axis: speciation of Nd3+(solid lines) as a function of titrant volume. The right y-axis: cumulative heat (○ – experimental, -![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) - -![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) - fitted data) as a function of titrant volume. Cup solution: 8.6 μmole Nd(Tf2N)3 (2.7 mL); titrant: 0.1 mol L−1 DGA; Temperature: 25 °C. - fitted data) as a function of titrant volume. Cup solution: 8.6 μmole Nd(Tf2N)3 (2.7 mL); titrant: 0.1 mol L−1 DGA; Temperature: 25 °C. | |
Table 2 Thermodynamics data for Nd3+/DGA complexation at 25 °C
| DGA/Medium |
Complexa |
ΔG (kJ mol−1) |
ΔH (kJ mol−1) |
ΔS (J mol−1 K−1) |
Ref.b |
|
L denotes the respective DGA ligand.
p.w. = present work.
|
| TMDGA/ |
NdL3+ |
−25.1 |
−10.1 |
50.4 |
|
| [C4mim][Tf2N] |
NdL23+ |
−45.6 |
−17.3 |
94.9 |
p.w. |
|
|
NdL33+ |
−59.9 |
−21.9 |
128 |
|
| TMDGA/ |
NdL3+ |
−20.1 |
−10.9 |
31.0 |
|
| 1 M NaNO3 |
NdL23+ |
−33.3 |
−15.6 |
59.5 |
9
|
|
|
NdL33+ |
−38.8 |
−19.3 |
65.4 |
|
| TEDGA/ |
NdL3+ |
−30.1 |
−8.86 |
71.4 |
|
| [C4mim][Tf2N] |
NdL23+ |
−52.1 |
−14.1 |
127 |
p.w. |
|
|
NdL33+ |
−65.0 |
−17.2 |
161 |
|
| TBDGA/ |
NdL3+ |
−40.9 |
−9.34 |
106 |
|
| [C4mim][Tf2N] |
NdL23+ |
−61.6 |
−15.3 |
155 |
p.w. |
|
|
NdL33+ |
−72.5 |
−18.7 |
180 |
|
| THDGA/ |
NdL3+ |
−48.0 |
−9.71 |
128 |
|
| [C4mim][Tf2N] |
NdL23+ |
−71.3 |
−14.8 |
190 |
p.w. |
|
|
NdL33+ |
−81.6 |
−18.6 |
211 |
|
2.3. Structural features of Ln3+/DGA complexes
After confirming the formation of Nd·L33+ species with all the four DGA ligands, an attempt was made to understand the nature of the complexes and the mode of complexation. Extensive complexation studies on shorter alkyl chain DGAs (TMDGAs) and the crystal structures of the Nd3+/TMDGA complex,9 the Eu3+/TMDGA complex10 and the Am3+/TMDGA complex11 confirmed the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 M/L species, where three DGA ligands are bonded with the metal via two amidic ‘O’ atoms and one etheric ‘O’ atom, without any H2O or nitrate ions in the primary hydration sphere. Similarly, the structural features of Ln3+/TEDGA complexes confirmed the absence of H2O or nitrate in the primary coordination sphere.48 Additionally, structural studies performed on a longer alkyl chain DGA (TODGA) gave similar results.26 Structural features obtained with EXAFS measurements confirmed the formation of a Eu3+/TODGA complex in the solution phase identical to that in the crystalline state of Eu3+/TMDGA.26 In the present work, we assumed a similar coordination mode in [C4mim][Tf2N] and focused on the detailed structural investigation with the help of fluorescence spectroscopy. As will be seen from the DFT studies (vide infra), the structural features do not change with the solvent.
3 M/L species, where three DGA ligands are bonded with the metal via two amidic ‘O’ atoms and one etheric ‘O’ atom, without any H2O or nitrate ions in the primary hydration sphere. Similarly, the structural features of Ln3+/TEDGA complexes confirmed the absence of H2O or nitrate in the primary coordination sphere.48 Additionally, structural studies performed on a longer alkyl chain DGA (TODGA) gave similar results.26 Structural features obtained with EXAFS measurements confirmed the formation of a Eu3+/TODGA complex in the solution phase identical to that in the crystalline state of Eu3+/TMDGA.26 In the present work, we assumed a similar coordination mode in [C4mim][Tf2N] and focused on the detailed structural investigation with the help of fluorescence spectroscopy. As will be seen from the DFT studies (vide infra), the structural features do not change with the solvent.
In order to obtain insight into the structure of the complexes, the presence of water molecules or Tf2N− ions in the primary hydration sphere of the metal centre was probed with the help of Eu3+ lifetime data. The lifetime of Eu(NO3)3 in water and Eu(Tf2N)3 in [C4mim][Tf2N] were found to be around 114 μs and 116 μs, respectively, indicating that in both cases the Eu3+ species are identical, i.e., Eu(H2O)(8-9)3+. The number of water molecules (NH2O) in the primary coordination sphere of Eu3+ was calculated using the equation50
where
τ is the lifetime in ms. The fluorescence decay curve of the limiting EuL
33+ species in [C
4mim][Tf
2N] (with all the DGAs) is shown in
Fig. 5. The decay curves were fitted using mono- and bi-exponential decay equations, which predominantly predicted the presence of single species. It is worth mentioning that only single species were observed in the decay curve as the measurements were performed at the Eu
3+/DGA ratio of 10, where the (Eu·L
3)
3+ species is predominant. The lifetime of Eu
3+ in the complex was in the range of a few ms (2.2 to 2.4 ms), confirming the absence of water molecules in all the Eu
3+/DGA complexes (
Table 3). In the absence of water in the primary hydration sphere of Eu
3+, it is easier to conclude that all the available coordination sites in Eu
3+ will have to be occupied by three tridentate DGA moieties saturating the metal coordination sites. This means that the coordination mode of a DGA in the M/L complex in [C
4mim][Tf
2N] medium is identical to that in the crystalline state
6–8 and in
n-dodecane (as indicated by EXAFS measurements
22), where three DGA ligands are bonded with the metal
via two carbonyl ‘O’ atoms and one etheric ‘O’ atom, satisfying the coordination number of the metal ion. The identical species and the coordination mode in the Eu
3+/TODGA complex were also confirmed by fluorescence spectroscopy in ethanol medium.
13
 |
| | Fig. 5 Emission decay curve for Eu3+ using different DGAs. | |
Table 3 Calculated number of water molecules (nH2O) associated with Eu3+/DGA complexes in different systems
| Systema |
Asymmetry factor (I612/I592)b |
Lifetime (ms) |
N
H2O
|
|
RTIL = [C4mim][Tf2N].
Data obtained from Fig. S2 (ESI).
|
| Eu(NO3)3/H2O |
0.45 |
0.114 |
8.51 |
| Eu(Tf2N)3/RTIL |
0.44 |
0.116 |
8.35 |
| Eu3+/TMDGA |
1.32 |
2.41 |
−0.26 |
| Eu3+/TEDHA |
1.28 |
2.35 |
−0.25 |
| Eu3+/TBDGA |
2.25 |
2.34 |
−0.25 |
| Eu3+/THDGA |
1.32 |
2.24 |
10.23 |
2.4. DFT studies
2.4.1. Optimization of structures of ligand/complexes.
The optimized minimum energy structures of free TMDGA and its complexes with Nd3+ ions in various stoichiometries in the gas phase are displayed in Fig. 6. From the optimized structure of free TMDGA (Fig. 6a), it can be seen that all three donor O atoms (2 of carbonyl O and 1 of ether O) are lying in the same plane and act as a tridentate chelating ligand. Though the structure of the ML3 complex has been obtained by DFT calculations and reported by many authors, including us,27,51 the structures for the stepwise complex formation have not been reported. In the case of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (Fig. 6b) with Nd3+ ions, the metal ion is coordinated to three O atoms where the two carbonyl O atoms show a shorter metal–oxygen (M–O) bond distance of 2.15 Å than that with the lone ether O atom being 2.43 Å. The structure of the 1
1 complex (Fig. 6b) with Nd3+ ions, the metal ion is coordinated to three O atoms where the two carbonyl O atoms show a shorter metal–oxygen (M–O) bond distance of 2.15 Å than that with the lone ether O atom being 2.43 Å. The structure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex (Fig. 6c) shows that the two TMDGA units are coordinating to the central metal ion in a perpendicular manner leading to a hexa-coordinated environment, which results in a slight elongation of the M–O (O of carbonyl) bond to 2.30 Å and the etheric M–O bonds to 2.55 Å. This is due to the accommodation of six O atoms within the first coordination sphere of the Nd3+ ion, which causes steric repulsion among the ligands. The optimized structure of the 1
2 complex (Fig. 6c) shows that the two TMDGA units are coordinating to the central metal ion in a perpendicular manner leading to a hexa-coordinated environment, which results in a slight elongation of the M–O (O of carbonyl) bond to 2.30 Å and the etheric M–O bonds to 2.55 Å. This is due to the accommodation of six O atoms within the first coordination sphere of the Nd3+ ion, which causes steric repulsion among the ligands. The optimized structure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 metal–ligand complex is displayed in Fig. 6d, where nine O donors from three TMDGA units participate in the coordination leading to a nona-coordinated complex resulting in even longer M–O bonds with the carbonyl (2.44 Å) and etheric (2.65 Å) O atoms.
3 metal–ligand complex is displayed in Fig. 6d, where nine O donors from three TMDGA units participate in the coordination leading to a nona-coordinated complex resulting in even longer M–O bonds with the carbonyl (2.44 Å) and etheric (2.65 Å) O atoms.
 |
| | Fig. 6 Optimized structures of TMDGA and its complexes: (a) free TMDGA, (b) Nd3+/TMDGA, (c) Nd3+/(TMDGA)2, and (d) Nd3+/(TMDGA)3 phase at the B3LYP/SVP level of theory. | |
2.4.2. Free energy of complexation in gas and solution phases.
The metal ion–ligand complexation reaction in both gas and solution phases was modeled as| | | M(p) + nTMDGA(p) = M(TMDGA)n·(p), | (2) |
where M is Nd3+ and n ranges from 1 to 3 for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 stoichiometric complexes, and the subscript p represents gas/n-dodecane/ionic liquid/water. The free energy (ΔG) of complexation is a crucial parameter for understanding the complexation stability with the metal ions and can be evaluated using eqn (2) aswhere T is the temperature, R is the gas constant, Δn = the number of product species–reactant species, ΔS is the entropy change and ΔE is described by:
3 stoichiometric complexes, and the subscript p represents gas/n-dodecane/ionic liquid/water. The free energy (ΔG) of complexation is a crucial parameter for understanding the complexation stability with the metal ions and can be evaluated using eqn (2) aswhere T is the temperature, R is the gas constant, Δn = the number of product species–reactant species, ΔS is the entropy change and ΔE is described by:| | | ΔE = EM(TMDGA)n·(p) − (EM(p) + nETMDGA(p)) | (4) |
Here, E is the total electronic energy of the respective chemical species. The value of ΔS is computed using our earlier reported procedure.51 The calculated values of free energy (ΔG) in gas and solution phases are tabulated in Table S1 (ESI†). The free energy was found to be the highest for the Nd3+ ion in the gas phase and the lowest in water for all the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes with TMDGA. The solution phase free energy was found to be reduced drastically due to dielectric screening of the solvents. The free energy of complexation for all the 1
3 complexes with TMDGA. The solution phase free energy was found to be reduced drastically due to dielectric screening of the solvents. The free energy of complexation for all the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes with TMDGA follows the decreasing trend: gas phase > n-dodecane > ionic liquid > water. This is expected as with increasing dielectric constant of the solvent, the dielectric screening is also increased, which in turn reduces the interaction and hence the free energy. It is worth noting that the free energy of complexation is increased with an increase in the number of ligands for all the solvents and in the gas phase. It is the highest with a 1
3 complexes with TMDGA follows the decreasing trend: gas phase > n-dodecane > ionic liquid > water. This is expected as with increasing dielectric constant of the solvent, the dielectric screening is also increased, which in turn reduces the interaction and hence the free energy. It is worth noting that the free energy of complexation is increased with an increase in the number of ligands for all the solvents and in the gas phase. It is the highest with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 metal/ligand stoichiometry for the Nd3+ ion and the lowest with a 1
3 metal/ligand stoichiometry for the Nd3+ ion and the lowest with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metal/ligand stoichiometry and in between for the 1
1 metal/ligand stoichiometry and in between for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 metal/ligand complex. However, the values appear to be much larger than those reported above from the calorimetric studies due to the approximations in the DFT methods, which include, amongst other things, the hydration of the metal ions, which occurs in the ionic liquid case (as seen from the luminescence spectroscopic study). Similar overestimations in the case of DFT calculations are reported in the literature.52 It may be prudent to add here that the successive free energy difference from 1
2 metal/ligand complex. However, the values appear to be much larger than those reported above from the calorimetric studies due to the approximations in the DFT methods, which include, amongst other things, the hydration of the metal ions, which occurs in the ionic liquid case (as seen from the luminescence spectroscopic study). Similar overestimations in the case of DFT calculations are reported in the literature.52 It may be prudent to add here that the successive free energy difference from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to 1
2 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for all the solvents and in the gas phase is reduced due to steric crowding with increasing number of molecules in the first coordination sphere of the metal ion. Thus, density functional theoretical studies not only offer insights at the molecular level, but also help in understanding the correct metal ion stability towards a ligand by incorporating the appropriate metal–ligand stoichiometry, which otherwise is not possible through experimental means alone.
3 for all the solvents and in the gas phase is reduced due to steric crowding with increasing number of molecules in the first coordination sphere of the metal ion. Thus, density functional theoretical studies not only offer insights at the molecular level, but also help in understanding the correct metal ion stability towards a ligand by incorporating the appropriate metal–ligand stoichiometry, which otherwise is not possible through experimental means alone.
2.4.3. Bonding analysis.
Natural population analysis (NPA) was performed to get an insight into the nature of bonding in the complexes of TMDGA with the Nd3+ ion. The residual charge and atomic orbital population on the metal atom in the metal ion complexes were estimated using NPA.53,54 The calculated values are listed in Table S1 (ESI†). There is a considerable charge transfer to the TMDGA molecule, as evident from the residual charge on the metal atom, which in turn leads to a high interaction and free energy. Furthermore, the transfer of charge is more for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 metal–ligand complex compared to the 1
3 metal–ligand complex compared to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metal–ligand complexes. There is an amplification of the electronic population in the s, d and f orbitals of the metal atom after complexation, demonstrating the covalent nature of bonding. Furthermore, the amplification in the s and d orbitals is increased with an increase in the participation of a larger number of ligands. Another interesting point is that as we move from the gas phase to n-dodecane to ionic liquid to water, the transfer of charge is reduced due to the increased dielectric screening of the solvents, which in turn reduces the interaction and hence the free energy, thus causing a reduced stability.
1 metal–ligand complexes. There is an amplification of the electronic population in the s, d and f orbitals of the metal atom after complexation, demonstrating the covalent nature of bonding. Furthermore, the amplification in the s and d orbitals is increased with an increase in the participation of a larger number of ligands. Another interesting point is that as we move from the gas phase to n-dodecane to ionic liquid to water, the transfer of charge is reduced due to the increased dielectric screening of the solvents, which in turn reduces the interaction and hence the free energy, thus causing a reduced stability.
3. Conclusions
An effort has been made to look into the complexation thermodynamics of lanthanides with a series of diglycolamides (DGAs) containing varying alkyl chain lengths (methyl, ethyl, n-butyl and n-hexyl) in [C4mim][Tf2N]. Though the cation exchange mechanism predicts the species of the type MLn3+ (where n can be 2 or 3), all the DGA ligands formed a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Ln3+/DGA) complex, which is similar to the observations made during the previously reported aqueous phase complexation studies.6–8 Poor stripping possibility due to high extraction of the metal ions can be avoided by the use of complexing agents.55 Their stability constants in [C4mim][Tf2N] are orders of magnitude higher than those in the aqueous medium. In a manner similar to that reported previously in the case of the aqueous medium, the complexation reaction in [C4mim][Tf2N] was driven by both enthalpy and entropy. The enthalpy change observed in the [C4mim][Tf2N] medium was more exothermic than that in the aqueous medium. Spectroscopic data and DFT calculations confirmed the formation of 1
3 (Ln3+/DGA) complex, which is similar to the observations made during the previously reported aqueous phase complexation studies.6–8 Poor stripping possibility due to high extraction of the metal ions can be avoided by the use of complexing agents.55 Their stability constants in [C4mim][Tf2N] are orders of magnitude higher than those in the aqueous medium. In a manner similar to that reported previously in the case of the aqueous medium, the complexation reaction in [C4mim][Tf2N] was driven by both enthalpy and entropy. The enthalpy change observed in the [C4mim][Tf2N] medium was more exothermic than that in the aqueous medium. Spectroscopic data and DFT calculations confirmed the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 M/L species where three DGA ligands are bonded with the metal via two amidic ‘O’ atoms and one etheric ‘O’ atom, without any water or Tf2N− ions in the primary coordination sphere. This study reveals that the nature of Ln3+/DGA complexes formed in [C4mim][Tf2N] and n-dodecane or in the crystalline state is identical. It may be mentioned here that different stoichiometries of the extracted complex reported previously5 are a consequence of the diluent nature and ionic liquid medium do not take into consideration factors such as the variation in the nature of the complexed species.
3 M/L species where three DGA ligands are bonded with the metal via two amidic ‘O’ atoms and one etheric ‘O’ atom, without any water or Tf2N− ions in the primary coordination sphere. This study reveals that the nature of Ln3+/DGA complexes formed in [C4mim][Tf2N] and n-dodecane or in the crystalline state is identical. It may be mentioned here that different stoichiometries of the extracted complex reported previously5 are a consequence of the diluent nature and ionic liquid medium do not take into consideration factors such as the variation in the nature of the complexed species.
4. Experimental
4.1. Materials
A series of tetraalkyl diglycolamides (Fig. 1) was synthesized by reacting diglycolyl chloride with the respective dialkyl amines as reported earlier.1 The products were characterized by 1H-NMR, FT-IR and mass spectrometry. The ionic liquid, [C4mim][Tf2N] (Fig. 1), in 99% purity was procured from Iolitec, Germany. Nd(Tf2N)3 and Eu(Tf2N)3 salts were prepared by a metathesis reaction of Nd2O3 or Eu2O3 with trifluoromethane sulfonimide (HTf2N) procured from Sigma Aldrich. Stoichiometric amounts of Eu2O3 or Nd2O3 solids were dissolved in HTf2N solution (0.5 g of HTf2N/10 mL of Milli-Q water) by stirring for an hour at room temperature. The solution was filtered with a 0.2 μm syringe filter, evaporated to dryness, and finally vacuum dried to get a pink powder of Nd(Tf2N)3 and a white powder of Eu(Tf2N)3. Stock solutions of Nd(Tf2N)3 and Eu(Tf2N)3 were prepared by dissolving appropriate amounts of their salts in [C4mim][Tf2N], and their concentrations were confirmed by volumetric titrations with a standard EDTA solution using bromothymol blue as the indicator.
4.2. Spectrophotometry
Spectrophotometric titrations were performed by following the absorption spectra of Nd3+ in [C4mim][Tf2N] in the wavelength region of 560–610 nm, where Nd3+ shows well-defined hypersensitive absorption bands at around 575 nm originating from the 4I9/2 → 4G5/2 and 2G7/2 transitions.47 The spectra were recorded on a double-beam Jasco V-530 spectrophotometer using 10 mm path length quartz cells. The initial concentration of Nd(Tf2N)3 in the cell was ∼10 mmol L−1. In each titration, appropriate aliquots of the titrant (DGA solution in [C4mim][Tf2N]) were added into the cell and mixed thoroughly for about 5 minutes before recording the spectrum. Usually a set of 20–25 spectra was recorded in each titration, and the stability constants of the Nd3+/L complexes were calculated by nonlinear least-squares regression analysis using the HypSpec® program49 based on the following equations:| | | Nd3+ + iL = NdL(3−i)i+ | (5) |
| | 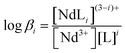 | (6) |
where βi is the stability constant of ith complex and L is the DGA ligand.
4.3. Microcalorimetry
Microcalorimetric titrations at 25 °C were performed on an isothermal titration calorimeter (Nanocalorimeter TAM-III, Thermometric AB, Sweden). It is a twin thermopile heat conduction type calorimeter where the measured differential power signal is dynamically corrected for the thermal inertia of the system.56 Both chemical and electrical calibrations were performed to validate the performance of the instrument. The chemical calibration was carried out by measuring the complexation heat of 18-crown-6 and BaCl2. The obtained ΔH value (31.71 ± 0.04 kJ mol−1) is in good agreement with the literature data.57 The reaction vessel contained 2.7 mL of the solutions of Nd(Tf2N)3 in [C4mim][Tf2N] stirred using a mixing rotor maintained at 100 rpm. The ligand solution in [C4mim][Tf2N] was added into the reaction vessel through a Hamilton 500 μL syringe stepwise (10 μL per addition). About 50 injections were made in each set of titrations. The reaction heats, after correcting the dilution heats that were measured separately in a blank titration, were used in conjunction with the equilibrium constants obtained by spectrophotometry to calculate the enthalpy of complexation using the Hyperquad program.58
4.4. Fluorescence measurements
Luminescence emission spectra were recorded and the lifetime of Eu3+ was determined using a fluorometer (PTI QuantaMaster 400) adapted for time-resolved measurements. The luminescence emission spectra were obtained in the wavelength region of 570–710 nm (0.5 nm per step) by excitation at 395 nm. The signals were acquired and analyzed using PTI FelixGX software from the PTI QuantaMaster. The emission lifetime data were recorded in the time-resolved mode after a delay time of 100 μs to avoid the background contribution from scattered radiation (if any). The emission lifetime data were fitted in the following decay equation by the PTI FelixGX software to get the decay constant.| |  | (7) |
where τi is the lifetime of the ith complex.
4.5. Computational protocol
The minimum energy structures of free TMDGA and its complexes were calculated with the B3LYP hybrid density functional using the split-valence plus polarization (SVP) basis set as available in the TURBOMOLE electronic structure code.59–62 The scalar relativistic effective core potentials (ECPs) were considered for Nd3+ where 28 electrons were kept in its core.63–66 The quintet spin state was used for the Nd complexes during the optimization of structures and energy calculations. The free energy was computed at 298.15 K. The hybrid B3LYP functional was shown to be quite successful in predicting the thermodynamic properties of actinides.67 The water, n-dodecane and ionic liquid ([C4mim][Tf2N]) phases were taken care of by the use of a conductor like screening model for real systems (COSMO-RS).68–72 Dielectric constants of 80, 2.0 and 9.4 were used for water, n-dodecane and the ionic liquid, respectively. The free energy of complexation, ΔG, for the complexation reaction (eqn (2)) was evaluated using standard thermodynamic methods.73–76 As mentioned above, the corresponding values for the water, n-dodecane and ionic liquid phases were mimicked using the equilibrated gas phase geometry by employing the COSMO-RS solvation model.68–72 COSMO-RS incorporates the structure of the solvents by incorporating the surface charge densities through the well-defined sigma potential. The calculation has been performed using D-COSMO-RS74,75 module of Turbomole. The required sigma potential for water has been taken from the Turbomole library, whereas for n-dodecane and [C4mim][Tf2N], the sigma potential was borrowed from COSMO logic.
Conflicts of interest
There are no conflicts of interest.
Acknowledgements
The authors thank Dr P. K. Pujari, Head of the Radiochemistry Division, for his constant encouragement. They are also thankful to Dr R. B. Gujar for his help during the experiments.
References
- S. A. Ansari, P. N. Pathak, P. K. Mohapatra and V. K. Manchanda, Chem. Rev., 2012, 112, 1751–1772 CrossRef CAS PubMed.
- R. Taylor, S. Bourg, J.-P. Glatz and G. Modolo, Nucl. Future, 2015, 11, 38–43 Search PubMed.
- H. Stephan, K. Gloe, J. Beger and P. Muhl, Solvent Extr. Ion Exch., 1991, 9, 435–458 CrossRef CAS.
- H. Stephan, K. Gloe, J. Beger and P. Muhl, Solvent Extr. Ion Exch., 1991, 9, 459 CrossRef CAS.
- Y. Sasaki, Y. Sugo, S. Suzuki and S. Tachimori, Solvent Extr. Ion Exch., 2001, 19, 91–103 CrossRef CAS.
- Y. Sasaki, Y. Sugo, Y. Kitatsuji, A. Kirishima, T. Kimura and G. R. Choppin, Anal. Sci., 2007, 23, 727–731 CrossRef CAS PubMed.
- S. Chapron, C. Marie, G. Arrachart, M. Miguirditchian and S. Pellet-Rostaing, Solvent Extr. Ion Exch., 2015, 33, 236–248 CrossRef CAS.
- Y. Sasaki, Y. Sugo, K. Morita and K. L. Nash, Solvent Extr. Ion Exch., 2015, 33, 625–641 CrossRef CAS.
- G. Tian, S. J. Teat and L. Rao, Inorg. Chem., 2014, 53, 9477–9485 CrossRef CAS PubMed.
- F. Kou, S. Yang, H. Qian, L. Zhang, C. M. Beavers, S. J. Teat and G. Tian, Dalton Trans., 2016, 45, 18484–18493 RSC.
- G. Tian, D. K. Shuh, C. M. Beavers and S. J. Teat, Dalton Trans., 2015, 44, 18469–18474 RSC.
- S. D. Reilly, A. J. Gaunt, B. L. Scott, G. Modolo, M. Iqbal, W. Verboom and M. J. Sarsfield, Chem. Commun., 2012, 48, 9732–9734 RSC.
- A. Wilden, G. Modolo, S. Lange, F. Sadowski, B. B. Beele, A. S. Frech, P. J. Panak, M. Iqbal, W. Verboom, A. Geist and D. Bosbach, Solvent Extr. Ion Exch., 2014, 32, 119–137 CrossRef CAS.
- M. Hirata, P. Guilbaud, M. Dobler and S. Tachimori, Phys. Chem. Chem. Phys., 2003, 5, 691–695 RSC.
- J. Narbutt, A. Wodyńskia and M. Pecul, Dalton Trans., 2015, 44, 2657–2666 RSC.
- M. Kaneko, M. Watanabe and T. Matsumura, Dalton Trans., 2016, 45, 17530–17537 RSC.
- T. Koubsky, J. Fojtikova and L. Kalvoda, Prog. Nucl. Energy, 2017, 94, 208–215 CrossRef CAS.
- S. A. Ansari, P. N. Pathak, M. Husain, A. K. Prasad, V. S. Parmar and V. K. Manchanda, Solvent Extr. Ion Exch., 2005, 23, 463–479 CrossRef CAS.
- D. Magnusson, B. Christiansen, J.-P. Glatz, R. Malmbeck, G. Modolo, D. Purroy and C. Sorel, Solvent Extr. Ion Exch., 2009, 27, 26–35 CrossRef CAS.
- A. Wilden, C. Schreinemachers, M. Sypula and G. Modolo, Solvent Extr. Ion Exch., 2011, 29, 190–212 CrossRef CAS.
- R. B. Gujar, S. A. Ansari, D. R. Prabhu, P. N. Pathak, A. Sengupta, S. K. Thulasidas, P. K. Mohapatra and V. K. Manchanda, Solvent Extr. Ion Exch., 2012, 30, 156–170 CrossRef CAS.
- D. Peterman, A. Geist, B. Mincher, G. Modolo, M. H. Galan, L. Olson and R. McDowell, Ind. Eng. Chem. Res., 2016, 55, 10427–10435 CrossRef CAS.
- R. B. Gujar, S. A. Ansari, P. K. Mohapatra and V. K. Manchanda, Solvent Extr. Ion Exch., 2010, 28, 350–366 CrossRef CAS.
- R. B. Gujar, S. A. Ansari, D. R. Prabhu, D. R. Raut, P. N. Pathak, A. Sengupta, S. K. Thulasidas, P. K. Mohapatra and V. K. Manchanda, Solvent Extr. Ion Exch., 2010, 28, 764–777 CrossRef CAS.
-
G. Modolo, A. Geist and M. Miguirditchian, Minor Actinide Separations in the Reprocessing of Spent Nuclear Fuels: Recent Advances in Europe, in Reprocessing and Recycling of Spent Nuclear Fuel, Woodhead Publishing, Oxford, 2015, pp. 245–287 Search PubMed.
- M. R. Antonio, D. R. McAlister and E. P. Horwitz, Dalton Trans., 2015, 44, 515–521 RSC.
- C. Wang, J. Lan, Q. Wu, Y. Zhao, X. Wang, Z. Chai and W. Shi, Dalton Trans., 2014, 43, 8713–8720 RSC.
- S. A. Ansari, P. N. Pathak, P. K. Mohapatra and V. K. Manchanda, Sep. Purif. Rev., 2011, 40, 43–76 CrossRef CAS.
- Z. Zhu, Y. Sasaki, H. Suzuki, S. Suzuki and T. Kimura, Anal. Chim. Acta, 2004, 527, 163–168 CrossRef CAS.
- P. N. Pathak, S. A. Ansari, S. V. Godbole, A. R. Dhobale and V. K. Manchanda, Spectrochim. Acta, Part A, 2009, 73, 348–352 CrossRef CAS PubMed.
- S. A. Ansari, R. B. Gujar and P. K. Mohapatra, Dalton Trans., 2017, 46, 7584–7593 RSC.
- P. K. Mohapatra, Chem. Proc. Prod. Model., 2015, 10, 135–245 CAS.
- X. Sun, H. Luo and S. Dai, Chem. Rev., 2012, 112, 2100–2128 CrossRef CAS PubMed.
-
I. Billard, Ionic Liquids: New Hopes for Efficient Lanthanide/Actinide Extraction and Separation? in Handbook on the Physics and Chemistry of Rare Earths, Elsevier, B.V., Amsterdam, ch. 256, vol. 43, 2013, pp. 213–273 Search PubMed.
- P. K. Mohapatra, Dalton Trans., 2017, 46, 1730–1747 RSC.
- M. P. Jensen, J. A. Dzielawa, P. Rickert and M. L. Dietz, J. Am. Chem. Soc., 2002, 124, 10664–10665 CrossRef CAS PubMed.
- M. P. Jensen, J. Neuefeind, J. V. Beitz, S. Skanthakumar and L. Soderholm, J. Am. Chem. Soc., 2003, 125, 15466–15473 CrossRef CAS PubMed.
- C. Gaillard, M. Boltoeva, I. Billard, S. Georg, V. Mazan, A. Ouadi, D. Ternova and C. Hennig, ChemPhysChem, 2015, 16, 2653–2662 CrossRef CAS PubMed.
- V. A. Cocalia, M. P. Jensen, J. D. Holbrey, S. K. Spear, D. C. Stepinski and R. D. Rogers, Dalton Trans., 2005, 1966–1971 RSC.
- S. A. Ansari, L. Liu and L. Rao, Dalton Trans., 2015, 44, 2907–2914 RSC.
- C. Gaillard, A. Chaumont, I. Billard, C. Hennig, A. Ouadi and G. Wipff, Inorg. Chem., 2007, 46, 4815–4826 CrossRef CAS PubMed.
- C. Gaillard, A. Chaumont, I. Billard, C. Hennig, A. Ouadi, S. Georg and G. Wipff, Inorg. Chem., 2010, 49, 6484–6494 CrossRef CAS PubMed.
- S. P. Pasilis and A. Blumenfeld, Inorg. Chem., 2011, 50, 8302–8307 CrossRef CAS PubMed.
- A. Chaumont, O. Klimchuk, C. Gaillard, I. Billard, A. Ouadi, C. Hennig and G. Wipff, J. Phys. Chem. B, 2012, 116, 3205–3219 CrossRef CAS PubMed.
- Y. Pan and C. L. Hussey, Inorg. Chem., 2013, 52, 3241–3252 CrossRef CAS PubMed.
- S. A. Ansari, P. K. Mohapatra, W. Verboom, Z. Zhang, P. D. Dau, J. K. Gibson and L. Rao, Dalton Trans., 2015, 44, 6416–6422 RSC.
-
C. K. Jorgensen, Absorption Spectra and Chemical Bonding in Complexes, Pergamon Press, London, 1962 Search PubMed.
- M. C. Charbonnel, C. Berthon, L. Berthon, N. Boubals, F. Burdet, M.-T. Duchesne, P. Guilbaud, N. Mabille, S. Petit and N. Zorz, Procedia Chem., 2012, 7, 20–26 CrossRef CAS.
- P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753 CrossRef CAS PubMed.
- P. P. Barthelemy and G. R. Choppin, Inorg. Chem., 1989, 28, 3354–3357 CrossRef CAS.
- S. M. Ali, S. Pahan, A. Bhattacharyya and P. K. Mohapatra, Phys. Chem. Chem. Phys., 2016, 18, 9816–9828 RSC.
- S. M. Ali, J. M. Joshi, A. K. Singha Deb, A. Boda, K. T. Shenoy and S. K. Ghosh, RSC Adv., 2014, 4, 22911–22925 RSC.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- K. Nakashima, F. Kubota, T. Maruyama and M. Goto, Ind. Eng. Chem. Res., 2005, 44, 4368–4372 CrossRef CAS.
- P. Johansson and I. Wadso, Thermochim. Acta, 1999, 342, 19–29 CrossRef CAS.
- R. M. Izatt, R. E. Terry, B. L. Haymore, L. D. Hansen, N. K. Dalley, A. G. Avondet and J. J. Christensen, J. Am. Chem. Soc., 1976, 98, 7620–7626 CrossRef CAS.
- P. Gans, A. Sabatini and A. Vacca, J. Solution Chem., 2008, 37, 467–476 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Wang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. Schaefer, H. Horn and R. J. Ahlrichs, J. Chem. Phys., 1992, 97, 2751–2777 CrossRef.
- R. Ahlrichs, M. Bar, M. Haser, H. Horn and C. Kolmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS ; TURBOMOLE V6.0 2009, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH.
- M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1989, 90, 1730–1734 CrossRef CAS.
- W. Kuchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535–7542 CrossRef.
- X. Cao and M. Dolg, J. Mol. Struct., 2004, 673, 203–209 CrossRef CAS.
- X. Cao and M. Dolg, J. Mol. Struct., 2002, 581, 139–147 CrossRef CAS.
- G. A. Shamov, G. Schreckenbach and T. N. Vo, Chem. – Eur. J., 2007, 13, 4932–4947 CrossRef CAS PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, WIREs Comput. Mol. Sci., 2011, 1, 699–709 CrossRef CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- M. Renz, M. Kess, M. Diedenhofen, A. Klamt and M. Kaupp, J. Chem. Theory Comput., 2012, 8, 4189–4203 CrossRef CAS PubMed.
- S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110, 2235–2245 CrossRef CAS PubMed.
- S. M. Ali, J. M. Joshi, A. K. Singha Deb, A. Boda, K. T. Shenoy and S. K. Ghosh, RSC Adv., 2014, 4, 22911–22925 RSC.
- S. M. Ali, Comput. Theor. Chem., 2014, 1034, 38–52 CrossRef CAS.
- S. M. Ali, Eur. J. Inorg. Chem., 2014, 1533–1545 CrossRef CAS.
- S. Pahan, A. Boda and S. M. Ali, Theor. Chem. Acc., 2015, 134, 41–57 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: UV-Vis spectrophotometry, luminescence spectroscopy and DFT data. See DOI: 10.1039/c7nj03925e |
|
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Prasanta K.
Mohapatra
a,
Prasanta K.
Mohapatra
 *a,
Sk.
Musharaf Ali
b,
Neetika
Rawat
c,
Bhupinder S.
Tomar
*a,
Sk.
Musharaf Ali
b,
Neetika
Rawat
c,
Bhupinder S.
Tomar
 c,
Andrea
Leoncini
c,
Andrea
Leoncini
 d,
Jurriaan
Huskens
d,
Jurriaan
Huskens
 d and
Willem
Verboom
d and
Willem
Verboom
 d
d
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Nd3+/DGA) complex as the limiting species, and their stability constants increased linearly with increasing alkyl chain length. The stability constants of the Nd3+/DGA complexes are orders of magnitude higher in [C4mim][Tf2N] as compared to those observed in aqueous medium. For all the complexes, the enthalpy of complexation was negative with a positive entropy change, indicating that the complexation was driven by both enthalpy and entropy. The enthalpy changes observed in [C4mim][Tf2N] medium were more exothermic than those in the aqueous medium. Fluorescence lifetime data indicated that the complexation proceeded via the replacement of water molecules from the primary coordination sphere of the metal ion. DFT calculations were performed on the structures of the different Nd3+/tetramethyl DGA (TMDGA) complexes, and the corresponding free energies in both gas and solution phases were calculated. Insights into the structural features by DFT studies confirmed that the nature of Ln3+/DGA complexes formed in [C4mim][Tf2N], n-dodecane, and aqueous medium and that in the crystalline state is identical.
3 (Nd3+/DGA) complex as the limiting species, and their stability constants increased linearly with increasing alkyl chain length. The stability constants of the Nd3+/DGA complexes are orders of magnitude higher in [C4mim][Tf2N] as compared to those observed in aqueous medium. For all the complexes, the enthalpy of complexation was negative with a positive entropy change, indicating that the complexation was driven by both enthalpy and entropy. The enthalpy changes observed in [C4mim][Tf2N] medium were more exothermic than those in the aqueous medium. Fluorescence lifetime data indicated that the complexation proceeded via the replacement of water molecules from the primary coordination sphere of the metal ion. DFT calculations were performed on the structures of the different Nd3+/tetramethyl DGA (TMDGA) complexes, and the corresponding free energies in both gas and solution phases were calculated. Insights into the structural features by DFT studies confirmed that the nature of Ln3+/DGA complexes formed in [C4mim][Tf2N], n-dodecane, and aqueous medium and that in the crystalline state is identical.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of Nd3+, Eu3+ and Am3+ with TMDGA (in aqueous medium) are in close proximity. This information gives rise to a logical conclusion that the complexation constants obtained for Nd3+ in the present work may be extended to Am3+, which is an important actinide ion from the actinide partitioning point of view.1,2 The log
β values of Nd3+, Eu3+ and Am3+ with TMDGA (in aqueous medium) are in close proximity. This information gives rise to a logical conclusion that the complexation constants obtained for Nd3+ in the present work may be extended to Am3+, which is an important actinide ion from the actinide partitioning point of view.1,2 The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of Nd3+/TMDGA complexes in [C4mim][Tf2N] are several orders of magnitude higher than those in aqueous nitrate medium. This observation is in line with Nd3+/nitrate complexation in [C4mim][Tf2N], where stability of the Nd3+/NO3− complexes in RTIL are many orders of magnitude stronger than those observed in aqueous medium.40 A probable explanation for this unusual complexation was given based on the competition between nitrate ions and water molecules present in the primary hydration sphere of the metal ions. It is easier for the ligands to replace the water molecules from the primary coordination sphere when the metal ions are present in a hydrophobic medium such as an RTIL than when present in an aqueous medium (vide infra). When we compare the stability constants of Nd3+/DGA in [C4mim][Tf2N], the log
β values of Nd3+/TMDGA complexes in [C4mim][Tf2N] are several orders of magnitude higher than those in aqueous nitrate medium. This observation is in line with Nd3+/nitrate complexation in [C4mim][Tf2N], where stability of the Nd3+/NO3− complexes in RTIL are many orders of magnitude stronger than those observed in aqueous medium.40 A probable explanation for this unusual complexation was given based on the competition between nitrate ions and water molecules present in the primary hydration sphere of the metal ions. It is easier for the ligands to replace the water molecules from the primary coordination sphere when the metal ions are present in a hydrophobic medium such as an RTIL than when present in an aqueous medium (vide infra). When we compare the stability constants of Nd3+/DGA in [C4mim][Tf2N], the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β value increased linearly with increasing alkyl chain length of the DGA, i.e., log
β value increased linearly with increasing alkyl chain length of the DGA, i.e., log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βTMDGA < log
βTMDGA < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βTEDGA < log
βTEDGA < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βTBDGA < log
βTBDGA < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βTHDGA (Fig. 3). This behaviour may be ascribed to the increasing +I effect on the ligand upon increasing alkyl chain length. Table 1 also includes the log
βTHDGA (Fig. 3). This behaviour may be ascribed to the increasing +I effect on the ligand upon increasing alkyl chain length. Table 1 also includes the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for THDGA in [C8mim][Tf2N].31 It is intriguing to note that while the log
β values for THDGA in [C8mim][Tf2N].31 It is intriguing to note that while the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1 value is lower in [C8mim][Tf2N] as compared to that obtained in [C4mim][Tf2N], the log
β1 value is lower in [C8mim][Tf2N] as compared to that obtained in [C4mim][Tf2N], the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β2 and log
β2 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β3 values show the opposite trend. This feature might have arisen due to the different solvation power of the metal ion and the ligands in the two RTILs.
β3 values show the opposite trend. This feature might have arisen due to the different solvation power of the metal ion and the ligands in the two RTILs.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 M/L species, where three DGA ligands are bonded with the metal via two amidic ‘O’ atoms and one etheric ‘O’ atom, without any H2O or nitrate ions in the primary hydration sphere. Similarly, the structural features of Ln3+/TEDGA complexes confirmed the absence of H2O or nitrate in the primary coordination sphere.48 Additionally, structural studies performed on a longer alkyl chain DGA (TODGA) gave similar results.26 Structural features obtained with EXAFS measurements confirmed the formation of a Eu3+/TODGA complex in the solution phase identical to that in the crystalline state of Eu3+/TMDGA.26 In the present work, we assumed a similar coordination mode in [C4mim][Tf2N] and focused on the detailed structural investigation with the help of fluorescence spectroscopy. As will be seen from the DFT studies (vide infra), the structural features do not change with the solvent.
3 M/L species, where three DGA ligands are bonded with the metal via two amidic ‘O’ atoms and one etheric ‘O’ atom, without any H2O or nitrate ions in the primary hydration sphere. Similarly, the structural features of Ln3+/TEDGA complexes confirmed the absence of H2O or nitrate in the primary coordination sphere.48 Additionally, structural studies performed on a longer alkyl chain DGA (TODGA) gave similar results.26 Structural features obtained with EXAFS measurements confirmed the formation of a Eu3+/TODGA complex in the solution phase identical to that in the crystalline state of Eu3+/TMDGA.26 In the present work, we assumed a similar coordination mode in [C4mim][Tf2N] and focused on the detailed structural investigation with the help of fluorescence spectroscopy. As will be seen from the DFT studies (vide infra), the structural features do not change with the solvent.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (Fig. 6b) with Nd3+ ions, the metal ion is coordinated to three O atoms where the two carbonyl O atoms show a shorter metal–oxygen (M–O) bond distance of 2.15 Å than that with the lone ether O atom being 2.43 Å. The structure of the 1
1 complex (Fig. 6b) with Nd3+ ions, the metal ion is coordinated to three O atoms where the two carbonyl O atoms show a shorter metal–oxygen (M–O) bond distance of 2.15 Å than that with the lone ether O atom being 2.43 Å. The structure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex (Fig. 6c) shows that the two TMDGA units are coordinating to the central metal ion in a perpendicular manner leading to a hexa-coordinated environment, which results in a slight elongation of the M–O (O of carbonyl) bond to 2.30 Å and the etheric M–O bonds to 2.55 Å. This is due to the accommodation of six O atoms within the first coordination sphere of the Nd3+ ion, which causes steric repulsion among the ligands. The optimized structure of the 1
2 complex (Fig. 6c) shows that the two TMDGA units are coordinating to the central metal ion in a perpendicular manner leading to a hexa-coordinated environment, which results in a slight elongation of the M–O (O of carbonyl) bond to 2.30 Å and the etheric M–O bonds to 2.55 Å. This is due to the accommodation of six O atoms within the first coordination sphere of the Nd3+ ion, which causes steric repulsion among the ligands. The optimized structure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 metal–ligand complex is displayed in Fig. 6d, where nine O donors from three TMDGA units participate in the coordination leading to a nona-coordinated complex resulting in even longer M–O bonds with the carbonyl (2.44 Å) and etheric (2.65 Å) O atoms.
3 metal–ligand complex is displayed in Fig. 6d, where nine O donors from three TMDGA units participate in the coordination leading to a nona-coordinated complex resulting in even longer M–O bonds with the carbonyl (2.44 Å) and etheric (2.65 Å) O atoms.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 stoichiometric complexes, and the subscript p represents gas/n-dodecane/ionic liquid/water. The free energy (ΔG) of complexation is a crucial parameter for understanding the complexation stability with the metal ions and can be evaluated using eqn (2) as
3 stoichiometric complexes, and the subscript p represents gas/n-dodecane/ionic liquid/water. The free energy (ΔG) of complexation is a crucial parameter for understanding the complexation stability with the metal ions and can be evaluated using eqn (2) as![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes with TMDGA. The solution phase free energy was found to be reduced drastically due to dielectric screening of the solvents. The free energy of complexation for all the 1
3 complexes with TMDGA. The solution phase free energy was found to be reduced drastically due to dielectric screening of the solvents. The free energy of complexation for all the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes with TMDGA follows the decreasing trend: gas phase > n-dodecane > ionic liquid > water. This is expected as with increasing dielectric constant of the solvent, the dielectric screening is also increased, which in turn reduces the interaction and hence the free energy. It is worth noting that the free energy of complexation is increased with an increase in the number of ligands for all the solvents and in the gas phase. It is the highest with a 1
3 complexes with TMDGA follows the decreasing trend: gas phase > n-dodecane > ionic liquid > water. This is expected as with increasing dielectric constant of the solvent, the dielectric screening is also increased, which in turn reduces the interaction and hence the free energy. It is worth noting that the free energy of complexation is increased with an increase in the number of ligands for all the solvents and in the gas phase. It is the highest with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 metal/ligand stoichiometry for the Nd3+ ion and the lowest with a 1
3 metal/ligand stoichiometry for the Nd3+ ion and the lowest with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metal/ligand stoichiometry and in between for the 1
1 metal/ligand stoichiometry and in between for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 metal/ligand complex. However, the values appear to be much larger than those reported above from the calorimetric studies due to the approximations in the DFT methods, which include, amongst other things, the hydration of the metal ions, which occurs in the ionic liquid case (as seen from the luminescence spectroscopic study). Similar overestimations in the case of DFT calculations are reported in the literature.52 It may be prudent to add here that the successive free energy difference from 1
2 metal/ligand complex. However, the values appear to be much larger than those reported above from the calorimetric studies due to the approximations in the DFT methods, which include, amongst other things, the hydration of the metal ions, which occurs in the ionic liquid case (as seen from the luminescence spectroscopic study). Similar overestimations in the case of DFT calculations are reported in the literature.52 It may be prudent to add here that the successive free energy difference from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to 1
2 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for all the solvents and in the gas phase is reduced due to steric crowding with increasing number of molecules in the first coordination sphere of the metal ion. Thus, density functional theoretical studies not only offer insights at the molecular level, but also help in understanding the correct metal ion stability towards a ligand by incorporating the appropriate metal–ligand stoichiometry, which otherwise is not possible through experimental means alone.
3 for all the solvents and in the gas phase is reduced due to steric crowding with increasing number of molecules in the first coordination sphere of the metal ion. Thus, density functional theoretical studies not only offer insights at the molecular level, but also help in understanding the correct metal ion stability towards a ligand by incorporating the appropriate metal–ligand stoichiometry, which otherwise is not possible through experimental means alone.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 metal–ligand complex compared to the 1
3 metal–ligand complex compared to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metal–ligand complexes. There is an amplification of the electronic population in the s, d and f orbitals of the metal atom after complexation, demonstrating the covalent nature of bonding. Furthermore, the amplification in the s and d orbitals is increased with an increase in the participation of a larger number of ligands. Another interesting point is that as we move from the gas phase to n-dodecane to ionic liquid to water, the transfer of charge is reduced due to the increased dielectric screening of the solvents, which in turn reduces the interaction and hence the free energy, thus causing a reduced stability.
1 metal–ligand complexes. There is an amplification of the electronic population in the s, d and f orbitals of the metal atom after complexation, demonstrating the covalent nature of bonding. Furthermore, the amplification in the s and d orbitals is increased with an increase in the participation of a larger number of ligands. Another interesting point is that as we move from the gas phase to n-dodecane to ionic liquid to water, the transfer of charge is reduced due to the increased dielectric screening of the solvents, which in turn reduces the interaction and hence the free energy, thus causing a reduced stability.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Ln3+/DGA) complex, which is similar to the observations made during the previously reported aqueous phase complexation studies.6–8 Poor stripping possibility due to high extraction of the metal ions can be avoided by the use of complexing agents.55 Their stability constants in [C4mim][Tf2N] are orders of magnitude higher than those in the aqueous medium. In a manner similar to that reported previously in the case of the aqueous medium, the complexation reaction in [C4mim][Tf2N] was driven by both enthalpy and entropy. The enthalpy change observed in the [C4mim][Tf2N] medium was more exothermic than that in the aqueous medium. Spectroscopic data and DFT calculations confirmed the formation of 1
3 (Ln3+/DGA) complex, which is similar to the observations made during the previously reported aqueous phase complexation studies.6–8 Poor stripping possibility due to high extraction of the metal ions can be avoided by the use of complexing agents.55 Their stability constants in [C4mim][Tf2N] are orders of magnitude higher than those in the aqueous medium. In a manner similar to that reported previously in the case of the aqueous medium, the complexation reaction in [C4mim][Tf2N] was driven by both enthalpy and entropy. The enthalpy change observed in the [C4mim][Tf2N] medium was more exothermic than that in the aqueous medium. Spectroscopic data and DFT calculations confirmed the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 M/L species where three DGA ligands are bonded with the metal via two amidic ‘O’ atoms and one etheric ‘O’ atom, without any water or Tf2N− ions in the primary coordination sphere. This study reveals that the nature of Ln3+/DGA complexes formed in [C4mim][Tf2N] and n-dodecane or in the crystalline state is identical. It may be mentioned here that different stoichiometries of the extracted complex reported previously5 are a consequence of the diluent nature and ionic liquid medium do not take into consideration factors such as the variation in the nature of the complexed species.
3 M/L species where three DGA ligands are bonded with the metal via two amidic ‘O’ atoms and one etheric ‘O’ atom, without any water or Tf2N− ions in the primary coordination sphere. This study reveals that the nature of Ln3+/DGA complexes formed in [C4mim][Tf2N] and n-dodecane or in the crystalline state is identical. It may be mentioned here that different stoichiometries of the extracted complex reported previously5 are a consequence of the diluent nature and ionic liquid medium do not take into consideration factors such as the variation in the nature of the complexed species.