Generic maps of optimality reveal two chemomechanical coupling regimes for motor proteins: from F1-ATPase and kinesin to myosin and cytoplasmic dynein
Zhisong
Wang
 ab
ab
aDepartment of Physics, National University of Singapore, Singapore 117542, Singapore. E-mail: phywangz@nus.edu.sg
bNUS Graduate School for Integrative Sciences and Engineering, National University of Singapore, Singapore 117542, Singapore
First published on 14th December 2017
Abstract
Many motor proteins achieve high efficiency for chemomechanical conversion, and single-molecule force-resisting experiments are a major tool to detect the chemomechanical coupling of efficient motors. Here, we introduce several quantitative relations that involve only parameters extracted from force-resisting experiments and offer new benchmarks beyond mere efficiency to judge the chemomechanical optimality or deficit of evolutionary remote motors on the same footing. The relations are verified by the experimental data from F1-ATPase, kinesin-1, myosin V and cytoplasmic dynein, which are representative members of four motor protein families. A double-fitting procedure yields the chemomechanical parameters that can be cross-checked for consistency. Using the extracted parameters, two generic maps of chemomechanical optimality are constructed on which motors across families can be quantitatively compared. The maps reveal two chemomechanical coupling regimes, one conducive to high efficiency and high directionality, and the other advantageous to force generation. Surprisingly, an F1 rotor and a kinesin-1 walker belong to the first regime despite their obvious evolutionary gap, while myosin V and cytoplasmic dynein follow the second regime. This analysis also predicts the symmetries of directional biases and heat productions for the motors, which impose constraints on their chemomechanical coupling and are open to future experimental tests. The verified relations, six in total, present a unified fitting framework to analyze force-resisting experiments. The generic maps of optimality, to which many more motors can be added in future, provide a rigorous method for a systematic cross-family comparison of motors to expose their evolutionary connections and mechanistic similarities.
Insight, innovation, integrationThis study introduces new quantitative benchmarks to judge the chemomechanical optimality or deficit of motor proteins across evolutionarily remote families. Two generic maps of optimality are constructed, and analysing four motor families on the maps reveals two distinct chemomechanical coupling regimes. Overall, this study presents a unified fitting framework for the systematic analysis of force-resisting experiments on many different motor proteins, with the extracted parameters revealing their revolutionary connection and mechanistic similarities. |
Introduction
Motor proteins are ATPases that use chemical energy from ATP hydrolysis to execute diverse cellular functions involving directional transport, force generation, and energy conversion, often with a high efficiency for mechanical work output. The molecular mechanisms for efficient chemomechanical conversion are an area of intensive study for diverse motor protein families. An F1-ATPase rotor1–8 and cytoskeleton-based translational motors9–19 have been modeled at various levels of protein representation. These system-specific models help interpret experimental data and clarify the molecular origin of observed chemomechanical coupling patterns. There are also studies on the fundamental limits20–26 of physical laws on molecular motors. These physical studies are often general but difficult to compare with experiments on specific motors. Generic and quantitative relations that are applicable to different motors and involve only experimentally accessible quantities are rare. These relations allow objective and quantitative comparison of different motor proteins even across families. One example is a recently developed approach27,28 by which energy dissipation within a motor can be extracted from the measured quantities. The extracted internal dissipations29,30 have shown a substantial difference between an F1 rotor and a kinesin-1 walker.A fully experiment-based, quantitative comparison across motor protein families on the same footing offers a rigorous method to expose evolutionary connections and mechanistic similarities between many motor proteins. Previous studies31,32 suggested that motors from kinesin and myosin families, and perhaps also G proteins, share a common ancestor in natural evolution as they possess similar mechanisms for ATP-induced conformational changes and for direction rectification.13,18 On the other hand, motor proteins are presumably optimized through natural evolution, but quantitative evidence of chemomechanical optimality is hardly beyond the single quantity of the measured efficiency.
In this study, we introduce several quantitative relations that allow an experiment-based cross-family comparison of the chemomechanical optimality or deficit of motor proteins on the same footing beyond mere efficiency. These relations are fully expressed with chemomechanical parameters extracted from single-molecule force-resisting experiments, which are a major tool to detect the chemomechanical coupling of efficient motors. These relations are applied to analyze an F1-ATPase rotor and the processive walkers kinesin-1, myosin V and cytoplasmic dynein, which are representative members of four motor protein families. A double-fitting procedure yields the chemomechanical parameters that can be cross-checked for consistency. All the four motors pass the consistency check, confirming the wide applicability of these relations. Using the extracted chemomechanical parameters, two generic maps of optimality are constructed on which virtually any motor can be quantitatively compared. The maps indicate the existence of two chemomechanical coupling regimes and expose a surprising mechanistic similarity between an F1 rotor and a kinesin-1 walker.
Results and discussion
Quantitative relations of efficient motors in terms of experimentally accessible quantities
The rationale behind this study is to quantify the chemomechanical optimality of motor proteins through a new conceptual line based on directionality, which is a motor's probability of moving forward upon fuel consumption minus that of moving backward divided by the total probability of moving forward, backward and futile moving (attempted but failed forward or back motion). Compared to other performance indicators like velocity, directionality possesses upper limits23,24 that can be formulated in a mathematical form involving a motor's energy dissipation but less its kinetic rates explicitly. In general, a motor's velocity is its directionality times step size and an overall rate for fuel turnover as clarified in ref. 24. Thus, the directionality may be interpreted as a measure of a motor's pure direction.26 For an isothermal motor, its pure direction, but not velocity, is subject to a general limit from the 2nd law of thermodynamics as found in ref. 26. In this paper, we hypothesize that a motor protein follows the directionality-based optimality up to the 2nd law limit, and predict its maximum work and efficiency (eqn (1) and (2)) from the directionality-based optimality (eqn (3) and (4)). On this basis, we further predict the power-versus-efficiency relation (eqn (5), which is equivalent to the speed-versus-load relation) and the efficiency-versus-zero-load relation (eqn (7)). Then we compare to the experimental data to test the validity of the directionality-based optimality in real motor proteins across families. The results are rather positive as can be seen throughout this study. We note that the evolutionary optimization of motor proteins is complex and likely involves multiple aspects. This study addresses only the aspect of chemomechanical optimality, which turns out to be an important part of the complex evolutionary optimization of motor proteins.A motor of optimal efficiency satisfies four quantitative relations in terms of directionality (D), maximum work (Wmax), maximum efficiency (ηmax), and energy utilization (ΔGη). All the quantities can be obtained from force-resisting experiments. No kinetic rates are involved (hence they are free of complication from load dependences of catalytic rates that are difficult to measure in experiments).
First, the maximum work of such an optimally efficient motor is related to its directionality at zero load (D0),
| Wmax = 2γdkBT × ln[(1 + D0)/(1 − D0)]. | (1) |
Second, the motor's maximum efficiency is determined by the step partition γd and another constant γe characterizing energy partition,
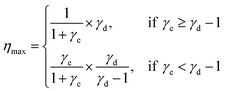 | (2) |
Third, the motor's directionality under a finite opposing load (F) has a distinct load dependence,
| D(F) = tanh[(ΔμD − FdD)/4kBT]. | (3) |
| ΔGη(F) = ΔμD + Fdin. | (4) |
Fitting the D-versus-F data with eqn (3) results in a curve whose shape yields the direction-pertinent displacement dD, and thereby the step partition γd. Extrapolating the fitting curve yields D0 and ΔμD at F → 0, and yields the stall force Fs = ΔμD/dD at D → 0. The fitted ΔμD value leads to a value of γevia the measured Δμ, and the fitted Fs leads to Wmax and ηmaxvia the measured d and Δμ. The resultant D0, γd, γe and Fs can be used to test the Wmax–D0 relation (eqn (1)) and the ηmax-partition relation (eqn (2)).
Similarly, fitting the ΔGη-vs.-F data with eqn (3) results in a curve whose slope yields the displacement din, and thereby the step partition γd again. Extrapolating the fitting curve at F → 0 yields the ΔμD value again. The second fit differs essentially from the first fit, and offers a consistency check: the two independent fits must yield the same ΔμD value, and must yield either dD or din displacement that adds to match the total step size (d = dD + din).
Hence a double-fitting to the stepping ratio-vs.-load data from two different aspects (eqn (3) and (4)) yields self-consistent chemomechanical parameters that fully determine a motor's maximum work and efficiency. With the extracted parameters D0, γd, and γe, eqn (1) and (2) define two generic maps of optimality against which different motors, even evolutionarily remote ones across motor protein families, can be quantitatively assessed for their extent of chemomechanical optimization.
In addition to the above four relations with no rates explicitly involved, two more quantitative relations involving catalytic rates exist for a motor that is optimal not only in efficiency but also in power. There is a power–efficiency relation, which is specified by four parameters (i.e., ATP turnover rate, two rate ratios, and heat production, see eqn (5) in the Methods section). The power-vs.-efficiency data for a motor can be obtained from the speed-vs.-load data measured at a controlled Δμ value. The data for a motor with a tight chemomechanical coupling can be fitted by the power–efficiency relation to yield the load dependence of the motor's ATP turnover. There is also a quantitative relation between the maximum efficiency of an optimal motor and its speed at zero load (eqn (7), see the Methods section). This efficiency–speed relation is useful for analyzing the efficiency–speed trade-off of different motors with evolutionarily conservative ATPase activity. In total, this study presents six quantitative relations that form a unified fitting framework for the analysis of force-resisting experiments, yielding multiple parameters characterizing a motor's chemomechanical coupling.
Quantitative relations are matched by representative motors from four families
The quantitative relations are tested against F1-ATPase, kinesin-1, myosin V and cytoplasmic dynein. F1-ATPase is a membrane-embedded rotor known33,34 to achieve ∼100% efficient energy conversion. Kinesin-1, myosin V and cytoplasmic dynein are cytoskeleton-based processive walkers, which are all involved in intracellular transport but belong to different motor families. Hence, the present analysis covers four distinct families of motor proteins, which is a reason to choose the four motors for this study. Another reason is the fact that the stepping behavior of the four motors had been measured in single-molecule force-resistance experiments over the last three decades, accumulating a wealth of data suitable for testing the relations. In a force-resisting experiment, a single motor protein is tethered to a tip of an atomic force microscope (AFM) or a bead trapped by optical tweezers. The AFM tip or tweezers is adjusted to follow the motor's motion along an immobilized cytoskeletal track, exerts a constant force on the motor and reports its trajectory. If the trajectory data are able to resolve the motor's individual steps, the forward-to-backward stepping ratio can be extracted as a function of the applied force, yielding the directionality-vs.-load data for this study. The trajectories also yield a motor's speed-vs.-load data that can be converted to the power-vs.-efficiency data for this study. In some force-resisting experiments, the chemical potentials for ATP consumption are controlled. Hence the force-resisting experiments are suitable for testing the chemomechanical optimality of motor proteins.Fig. 1–3 analyze the load-dependent directionality and energy utilization of the four motors. A good fitting to the experimental data is obtained and the condition of consistency is well satisfied by all the four motors. Based on the double-fitting procedure, the two independent fittings yield the same ΔμD value for each motor, and yield either dD or din displacement that adds to match the total step size (d = dD + din, with the fitted values for dD and din given in the captions of Fig. 1–3 for the four motors, together with their d values reported from literature). The consistency between the extracted parameters and the good overall fitting suggest that all the four motors follow the load dependences displayed in eqn (3) and (4).
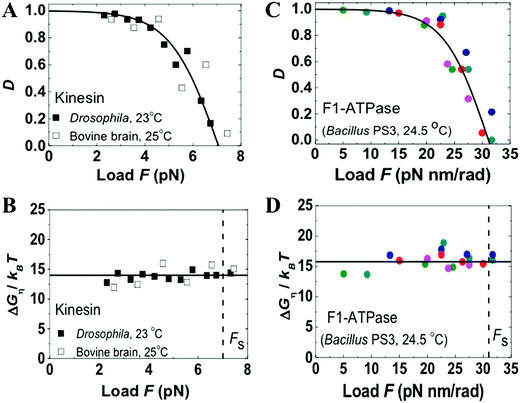 | ||
| Fig. 1 Directionality and utilized energy of kinesin-1 and F1-ATPase. The symbols are the results extracted from the forward-to-backward stepping ratio data reported in ref. 62 and 63 (for kinesin) and in ref. 34 (for F1, various colors for data collected from different individual F1 motors). The species producing the motor samples and the temperature (T) at which the data were collected are indicated. The lines are fits with eqn (3) (panels A and C) and with eqn (4) (panels B and D). The fits yield din = 0, dD = d, and γd = 1.0 for both motors, with the resultant dD values matching the measured step size of d = 120° for F133,34 and d = 8.2 nm for kinesin.60,62 The two fits also yield the same ΔμD = 15.75kBT, D0 = 99.924%, and Fs = 31.2 pN nm rad−1 for F1 and the same ΔμD = 14.0kBT, D0 = 99.818%, and Fs = 7 pN for kinesin. | ||
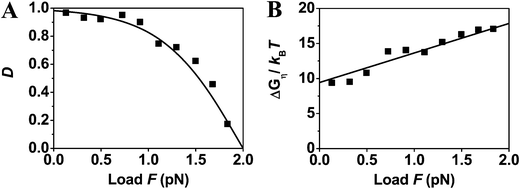 | ||
| Fig. 2 Directionality and utilized energy of myosin V. The symbols are extracted from the forward-to-backward stepping ratio data obtained from ref. 64 (collected at T = 20 °C). The fit with eqn (3) (the line in panel A) yields dD = 19 nm, ΔμD = 9.4kBT; the fit with eqn (4) (the line in panel B) yields din = 17 nm and the same ΔμD value. The dD and dL values add to match the measured step size42 of d = 36 nm and yield γd = 1.9. The fit in panel A also yields D0 = 98.197% and Fs = 2 pN. | ||
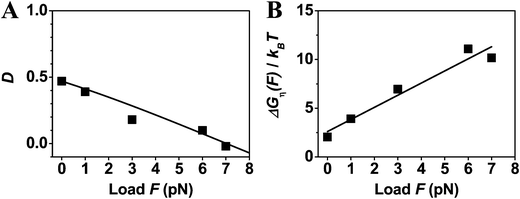 | ||
| Fig. 3 Directionality (panel A) and utilized energy (B) of cytoplasmic dynein. The symbols are the results extracted from the experimental data reported in ref. 35 (collected at T = 25° for dynein from a species of yeast). The ΔGη(F) data in panel B are obtained using the load-dependent step size (d = 9.3 nm for 0 and 1 pN, 8.5 nm for 3 pN, 7.3 nm for 6 pN, and 6.0 nm for 7 pN as counted from the data of step-size distribution reported in ref. 35). The fit with eqn (3) (the line in panel A) yields dD = 1.19 nm and ΔμD = 2.0kBT, Fs = 7 pN; the fit with eqn (4) (the line in panel B) yields din = 5.1 nm and the same ΔμD. The sum of dD and din values is 6.3 nm, which is near to the measured step of 6.0 nm under the stall load. Hence, Wmax = 7 pN × 6.3 nm = 44.1 pN nm. The fits yield D0 = 46.212%, γd = 7.8 at the zero load, and yield γd = 5.0 at the stall load. | ||
Fig. 4 shows the comparison of the extracted step partition, zero-load directionality and maximum work for the four motors. The step partition is a load-independent constant for F1, kinesin, and myosin V in line with their load-independent step size. The step partition for cytoplasmic dynein is load-dependent as its step size35 is reduced by increasing load. The extracted γd value is 1.0 for F1 and kinesin, 1.9 for myosin V, and between 5.0 and 7.8 for cytoplasmic dynein (Fig. 4A). While the γd value rises from F1 to kinesin, myosin V and then dynein, their zero-load directionality and the corresponding energy consumption (ΔμD) both drop successively (Fig. 4B and C). However, the work done over the direction-decoupled displacement din increases from the virtually zero value for F1 and kinesin to the finite values for myosin V and dynein (Fig. 4C). In the order of increasing γd, the four motors appear to shift their balance of energy consumption from sustaining a robust direction to force generation. This is in line with the fact that myosin V and cytoplasmic dynein are evolutionarily related to force-generating motors (muscle myosin and axonemal dynein), but kinesin 1 and F1 are optimal motors for directional transport and energy conversion.
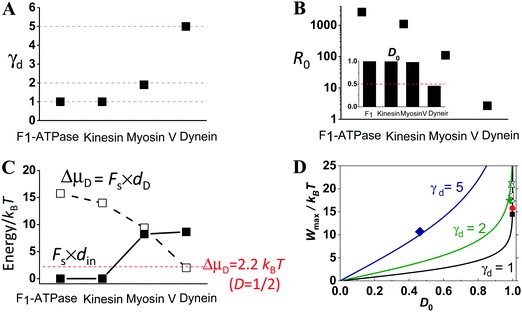 | ||
| Fig. 4 Step partition (panel A), zero-load directionality (panel B), maximum work done over the two portions of the step (panel C), and directionality–work relation (panel D) for the four motors as extracted from Fig. 1–3. In panel B, the R0 data are the zero-load forward-to-backward stepping ratio obtained from the D0 data (inset) following the relation7,26R0 = (1 + D0)/(1 − D0). The lines in panel D extracted using eqn (1) for the γd values of the motors (for dynein, the γd value extracted near the stall load is used for relevance to the maximum work). The filled square, sphere, star and diamond are the D0 and Wmax obtained from Fig. 1–3 for kinesin, F1-ATPase, myosin V, and dynein, respectively. The empty triangles are for kinesin too but obtained from stepping data reported in ref. 65 by the same method as for Fig. 1A (downward, upward, leftward and rightward triangles for bovine brain kinesin 1 at temperature 7, 14, 25 and 35 °C, respectively). | ||
Despite their very different γd and D0 values, the four motors all satisfy the D0–Wmax relation of eqn (1) (Fig. 4D). This is also true for cytoplasmic dynein considering its step partition extracted near the stall load (γd = 5 value), which is relevant to the discussion of the maximum work.
The four motors also follow the efficiency relation of eqn (2) but to a different extent (Fig. 5A). For F1 and kinesin, their actual efficiency and energy partition extracted from experiments lie on the ηmax–γe curve predicted from eqn (2) for their corresponding step partition. Myosin V deviates slightly; dynein deviates the most. As for the optimal γd–γe relation necessary for 100% efficiency, F1 follows it exactly, kinesin and myosin V differ from it slightly, and dynein even more (Fig. 5B).
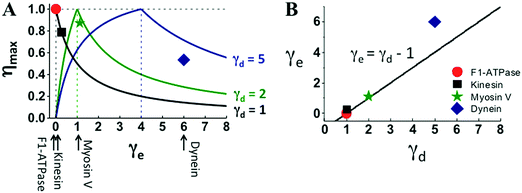 | ||
| Fig. 5 Efficiency–energy partition relation (panel A) and energy partition versus step partition (panel B) of the four motors. The lines in panel A are extracted using eqn (2) for the γd values of the motors, the line in panel B is the γe–γd relation necessary for 100% efficiency. The solid symbols are the motors’ actual efficiency (η = Wmax/Δμ) and energy partition (γe = Δμ/ΔμD − 1) estimated with the Wmax and ΔμD extracted from Fig. 1–3, and with the Δμ values at which the data were obtained. The Δμ value for the F1 data is 65.2 pN nm reported in ref. 34 (obtained at 0.4 μM ATP, 4 μM ADP and 1 mM phosphate). No measured Δμ is available for kinesin-1, myosin V and dynein data shown in Fig. 1–3. A kinesin-1 study62 suggests Δμ ∼ 20kBT (equivalent of 82 pN nm for T = 25 °C), which is used to estimate the η and γe values for the three translational motors (solid symbols). | ||
Power–efficiency relation
In Fig. 6, the power–efficiency relation of eqn (5) is tested against the power-vs.-efficiency data of the F1 rotor, which are converted from the speed-vs.-load data34 measured with a controlled value of Δμ (i.e. power = speed × F and efficiency = F × d/Δμ). If the power is normalized to Δμ times the ATP turnover rate, the resultant dimensionless power versus efficiency follows a curve that is determined by heat production and two rate ratios. The three parameters of F1 likely have a weak dependence on the load. Using their zero-load values from the literature, the normalized power-vs.-efficiency relation can be predicted for F1 without knowing the load dependence of any kinetic rates (Fig. 6A). However, estimating the absolute power requires the load dependence of the ATP turnover rate (ktot), which is assumed to follow a load-dependent function36 involving a coupling length and a branch ratio. The power-vs.-efficiency data of the F1 rotor over a wide range of Δμ values (62–91 pN nm) and ATP concentrations (0.4–250 μM) are well reproduced by the relation of eqn (5) using the coupling length, the branch ratio and the zero-load turnover rate as fitting parameters (Fig. 6B and C). An overall good agreement is obtained with a common coupling length near an experimentally detected ∼40° substep37–39 of F1 and with slightly adjusted values for the branch ratio and the zero-load turnover rate. The coupling length and the branch ratio from the fit provide quantitative information on the load dependence of F1's ATP turnover, which is difficult to measure by experiments.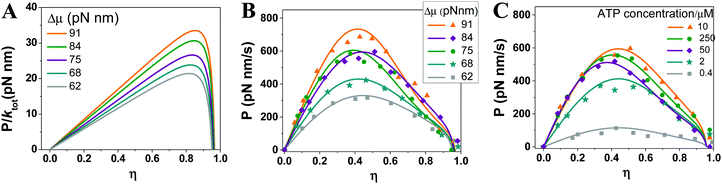 | ||
| Fig. 6 Power output versus efficiency of F1-ATPase. (A) Maximal power predicted using eqn (5) for the various values of fuel energy (Δμ). The following parameters are used: the energy dissipation ΔQin is obtained from ref. 7 as 0.75kBT; the rate ratios (a1 and a2) are assumed to be load-independent and estimated from zero-load rates66 (the ATP hydrolysis rate k1,2 = 140 s−1, the phosphate release rate k2,3 = 210 s−1, the ADP dissociation rate k4,1 = 380 s−1, and the ATP binding rate k3,4 = 4 × 107 s−1 M−1 × [ATP] with ATP concentration [ATP] = 10 μM used to predict the curves shown in panel A). (B and C) Absolute power for various Δμ values but a fixed ATP concentration (10 μM) (B), and for a constant Δμ (75 pN nm) but different ATP concentrations (C). The power-vs.-efficiency data (symbols) are extracted from the speed-vs.-load data reported in ref. 34, where the Δμ values were controlled using various ATP, ADP and phosphate concentrations as Δμ = Δμ0 + kBT × ln([ATP]/[ADP][Pi]). For data in panel B, [ATP] = 10 μM, [ADP] and [Pi] are 2 μM and 100 μM (for Δμ = 91 pN nm), 10 μM and 100 μM (for Δμ = 84 pN nm), 10 μM and 1 mM (for Δμ = 75 pN nm), 50 μM and 1 mM (for Δμ = 68 pN nm), and 100 μM and 2 mM (for Δμ = 62 pN nm). For data in panel C, [Pi] = 1 mM, [ATP] = [ADP] were changed simultaneously as indicated in the figure. The lines are eqn (5) (for the same values of ΔQin and the rates as for panel A) times the ATP turnover rate (ktot), which is assumed to follow a load-dependent function36ktot(F) = ktot(F = 0)/(p + qeFδ/kBT) with p + q = 1. The parameters ktot(F = 0), δ and p are used as fitting parameters. The fitting for all the data yields δ = 36° (near a substep of ∼40° reported in ref. 67). The ktot(0) and p values from the fitting are 63 s−1 and 0.965 (for triangle data), 63 s−1 and 0.94 (diamond), 63 s−1 and 0.94 (sphere), 55 s−1 and 0.90 (star), 44 s−1 and 0.89 (square) for panel B. The ktot(0) and p values are 62 s−1 and 0.94 (triangle), 65 s−1 and 0.92 (sphere), 68 s−1 and 0.89 (diamond), 43 s−1 and 0.94 (star), 12 s−1 and 0.94 (square) for panel C. | ||
Efficiency–speed relation
A quantitative relation exists between a motor's maximum efficiency (ηmax) and maximum speed at zero load (vmax(F = 0)) because the energy partition (γe) affects both the efficiency (by eqn (2)) and the speed (the Methods section). The ηmax–vmax(F = 0) relation is useful for the analysis of evolutionarily close motors within a family. The myosin family was chosen as an example in this study.A study by Purcell et al.40 suggested that compared to myosin V, a group of other myosin motors partition more energy to promote the rate-limiting41 ADP dissociation for higher speed, resulting in less energy for work. According to the consensus chemomechanical coupling pattern42 for myosin V and other motors from the myosin family (see Fig. 8D), the ADP dissociation is not involved in the kinetic pathways for the energy consumption ΔμD (this energy produces direction at zero load but does work at finite loads). Hence, the other myosin motors likely differ from myosin V by higher γe values and higher speeds. For myosin V, which is a processive dimeric member of the myosin family, the double-fitting procedure yields γe ∼ 1 and γd ∼ 2 (Fig. 5), which imply a potential capacity for ∼100% efficiency according to eqn (2). Any higher γe results in a lower efficiency for the value of step partition (γd ∼ 2) that is likely conserved within the myosin family. This rationalizes the negative correlation found by Purcell et al.40 between the measured efficiency and the zero-load speed for nine myosin motors, including processive myosin V, myosin XI and seven non-processive muscle myosins. Fig. 7 shows that the efficiency–speed data of the nine processive and non-processive myosins can be quantitatively reproduced with the ηmax–vmax(F = 0) relation predicted using catalytic rates slightly adjusted from the reported values for myosin V (see the Methods section for details).
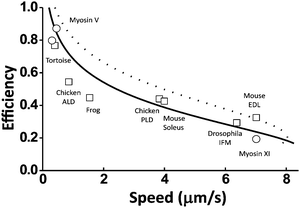 | ||
| Fig. 7 Efficiency versus zero-load speed for multiple motors from the myosin family. The data cover processive myosins (circles, myosin V from ref. 10 and 64, myosin XI from ref. 68) and non-processive muscle myosins (squares, from tortoise,69 chicken (anterior latissimus dorsi),70 frog,69 chicken (posterior latissimus dorsi),70 mouse (soleus),71 drosophila (adult indirect flight muscle),72 and mouse (extensor digitorum muscle)71). The lines are prediction from eqn (7) and (2) (see details in the Methods section). The dashed line is obtained using Δμ = 20kBT and the rates of myosin V as reported in ref. 41: the ADP dissociation rate k1,2 = 12 s−1, the ATP binding rate k2,3 = 2000 s−1 for saturating ATP concentration [ATP] = 2 M, the hydrolysis rate, k3,4 = 250 s−1, and the phosphate release rate k4,1 = 750 s−1. The solid line is obtained with two rates adjusted: k1,2 = 6 s−1 and k4,1 = 2000 s−1. | ||
Generic maps of chemomechanical optimality for cross-family comparisons
The Wmax–D0–γd curves formed by using eqn (1) plotted in Fig. 4D give the highest possible work from a motor of a certain step partition and capable of a certain level of zero directionality. Likewise, the ηmax–γe–γd curves formed by using eqn (2) in Fig. 5A give the highest possible efficiency for a motor of a certain step partition and energy partition. The Wmax–D0–γd and ηmax–γe–γd curves essentially form two separate maps of chemomechanical optimality. As illustrated in Fig. 4D and 5, rotational and translational motors from evolutionarily divergent motor protein families can all be added to the maps for quantitative comparison of chemomechanical optimality on the same footing. The comparison requires five parameters (γd, γe, D0, Wmax, and ηmax), which can all be obtained from single-molecule force-resistance experiments under controlled chemical potentials. (The raw stepping ratio data lead to the D(F) and ΔGη(F) data, which yield γd and ΔμD by the double fitting, and yield D0 and Wmax by extrapolation. These quantities plus the experimentally controlled Δμ further yield ηmax and γe). The two optimality maps can include any motor proteins capable of a minimum level of processivity to allow experimental detection of consecutive steps from which the directionality can be extracted. The optimality maps also have wide applicability because they are largely a consequence of a universal limit26 of the 2nd law of thermodynamics on isothermal motors. The two maps of optimality are not remote inaccessible upper limits but practically feasible ones that are approached by real motors, as can be seen in Fig. 4 and 5.On the two maps, motor proteins across families can be systematically compared for evolutionary optimality and mechanistic connections. Motor proteins are presumably optimized by natural evolution. This biological optimality is based on the chemomechanical optimality permitted by physical laws but can deviate from the latter due to extra requirements from diverse cellular functions of the motors. Indeed, most motor proteins do not necessarily optimize towards ∼100% efficiency; they instead sacrifice their efficiency for speed, force generation or other functional preferences. The two optimality maps (and also the relations of eqn (3) and (4)) provide new quantitative standards beyond mere efficiency to judge a motor's actual extent of chemomechanical optimality/deficit and functional compromise. As can be seen in Fig. 4D and 5A, F1 and kinesin-1 fall on the Wmax–D0–γd and the ηmax–γe–γd curves, but cytoplasmic dynein shows an apparent deviation from the ηmax–γe–γd curves (also from the γe–γd relation necessary for ∼100% efficiency, Fig. 5B). These results indicate, in a rigorous quantitative way, that the biological optimization and the chemomechanical optimality converge for F1 and kinesin-1 but not for cytoplasmic dynein.
Two chemomechanical coupling regimes
The optimality maps reveal two distinct regimes of chemomechanical coupling, which are represented by the γd = 1 motors and the γd > 1 ones. The γd = 1 regime, henceforth called regime I, is characterized by a load-dependent decay of directionality that involves the entire step and accounts for all the work output. Regime II (γd > 1) is characterized by a directionality decay over a portion of step and by extra work done over the other portion independent of directionality. Quantitatively speaking, Wmax = ΔGmin(D0) for regime I but Wmax > ΔGmin(D0) for regime II (or equivalently Wmax = ΔGmin(D0) + Fs × din). On the optimality maps, regime I is represented by a unique Wmax–D0 or ηmax–γe curve, and regime II can be represented by multiple curves (see Fig. 4D and 5A). Surprisingly, F1-ATPase and kinesin 1 both belong to regime I despite one being a rotor and the other a walker. Myosin V and cytoplasmic dynein belong to regime II.The two regimes differ substantially in energy utilization over the partitioned displacements dD and din. The double-fitting procedure for myosin V finds din ∼ 17 nm that matches an experimentally detected ∼16.5 nm on-track sliding motion.43 The value of din ∼ 5 nm found for cytoplasmic dynein also matches a detected on-track sliding.44 These results suggest that the din portion of a motor's step is likely an on-track downhill displacement that is decoupled from a motor's direction but still does work against a load. This amounts to an advantage in force generation, which is consistent with the fact that the two processive motors are evolutionarily linked to muscle myosins and axonemal dyneins.
The nature of energy use over the dD portion is better exposed by the γ = 1 motors F1 and kinesin-1: both motors have a flat ΔGηversus F, i.e., ΔGmin(D(F)) + Fd = constant from near-zero load up to stall load despite typical fluctuations of single-motor measurements (Fig. 1B and D). Thus, the total work rises and ΔGmin(D) drops by an equal amount when D is reduced by an increasing F. This implies a peculiar channel that uses the same energy to produce either direction or work.
A motor from regime I consumes the entire ATP energy (Δμ) by this channel of dual energy utilization. As a consequence, such a motor may use all the energy supply to attain near-unity D0 at zero load and then achieve ∼100% efficiency near the stall load. This is proven by the F1 rotor that has a D0 of ∼99.92% and ∼100% efficiency. Kinesin-1 is another motor from regime I with a high D0 (∼99.82%) and a reasonably high efficiency (∼80%). This finding that F1 and kinesin belong to the same chemomechanical regime conducive to high efficiency plus high directionality implies a profound mechanistic similarity in energy conversion and direction rectification between the two seemingly unrelated motors in evolution. Motors from regime II unlikely access high directionality and high efficiency together, as suggested by the lower D0 of myosin V and cytoplasmic dynein (Fig. 4B). Besides, the two regimes require different energy partitions for a motor to approach ∼100 efficiency: γe = 0 for regime I; γe = γd − 1 > 0 for regime II (Fig. 5B).
Bias symmetry and heat symmetry
A motor matching the multiple optimality standards (eqn (1)–(4)) should possess symmetric directional biases and symmetric heat productions, which impose mechanistic constraints to the underlying chemomechanical coupling and may be measured by future experiments.A motor's directionality is determined by two complementary directional biases. Take a bipedal motor for example: one bias is preferential dissociation of the motor's rear leg over the front leg from the track, which is quantified by the back–front dissociation probability ratio (α). The other bias is preferential binding of the dissociated leg to the front site over the back site, and is quantified by the forward–backward binding probability ratio (β). The two biases produce a motor's directionality as D = (αβ − 1)/[(α + 1)(β + 1)] (see the Methods section for derivation). A motor attains the optimal directionality when both biases are equal, i.e., α = β. This bias symmetry is ensured by equal heat productions along the motor's kinetic pathway for the rear leg dissociation and reverse binding and along the pathway for the forward binding and reverse dissociation. The bias symmetry and the heat symmetry are necessary conditions for the optimality relations of eqn (1) and (2), which are matched by the four motors analyzed in this study (Fig. 1–3).
Considering the equal biases for F1, kinesin-1 and myosin V (a reasonable assumption for their high D0 values, see Fig. 4D), their zero-load biases are α = β ∼ 2500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1000
1, 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 100
1, and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. These predictions might be verified by future experiments in which the steps are resolved45 to measure the biases. For F1 and kinesin-1, the heat production from internal friction has been successfully measured.29,30 New experiments detecting heat–bias correlation might help identify the molecular origin of chemomechanical deficiency, and probably also test the predicted heat symmetry. Besides, it is interesting to note that the level of biases for myosin V has been achieved by artificial bipedal nanomotors.46,47
1, respectively. These predictions might be verified by future experiments in which the steps are resolved45 to measure the biases. For F1 and kinesin-1, the heat production from internal friction has been successfully measured.29,30 New experiments detecting heat–bias correlation might help identify the molecular origin of chemomechanical deficiency, and probably also test the predicted heat symmetry. Besides, it is interesting to note that the level of biases for myosin V has been achieved by artificial bipedal nanomotors.46,47
A subtlety exists for cytoplasmic dynein, whose D0 (∼50%) coincides with a general limit23 of D ≤ 50% for motors missing either bias. This motor's low directionality might be explained if it possesses a single high bias, or if it possesses two weak biases (∼3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for equal biases). This uncertainty may be resolved by future experiments. F1, kinesin and myosin V are apparently above the directionality limit (Fig. 4B), which is consistent with their energy consumption for direction (ΔμD) being apparently beyond that for the limit, ΔGmin(D = 50%) = 2.2kBT (dynein's ΔμD is near the value, see Fig. 4C). These results suggest the presence of two biases in the three motors, which is in line with previous studies on F1,3 kinesin13,48,49 and myosin V.18 Two complementary biases are also achieved in artificial nanomotors,47,50–55 with an autonomous bipedal motor47 reaching a D value (above ∼59%) already better than that of dynein.
1 for equal biases). This uncertainty may be resolved by future experiments. F1, kinesin and myosin V are apparently above the directionality limit (Fig. 4B), which is consistent with their energy consumption for direction (ΔμD) being apparently beyond that for the limit, ΔGmin(D = 50%) = 2.2kBT (dynein's ΔμD is near the value, see Fig. 4C). These results suggest the presence of two biases in the three motors, which is in line with previous studies on F1,3 kinesin13,48,49 and myosin V.18 Two complementary biases are also achieved in artificial nanomotors,47,50–55 with an autonomous bipedal motor47 reaching a D value (above ∼59%) already better than that of dynein.
A recent study by Belyy et al.56 reports that the binding of a dynactin complex to mammalian dynein activates its processive motility and raises its force output. According to eqn (1), a motor's maximum work (equivalent of force generation for a fixed step size) depends on both directionality and step partition. Data analysis in Fig. 3 indicates a low directionality (D0 < 0.5) but a high step partition (γd ∼ 5 near stall load) for dynein from yeast. For mammalian dynein, the activation of processive motility by dynactin probably suggests an increase in directionality, which likely results in a higher force. This possibility can be examined by measuring the stepping ratio for dynactin-bound mammalian dynein, which might be considered for future experiments. An analysis of the stepping ratio-vs.-load data with the fitting equations given by this study will elucidate whether the dynactin complex can modify dynein's directionality or/and step partition, and thereby switch the chemomechanical coupling regime of this motor.
Conclusions
A total of six quantitative relations have proven valid for analyzing the force–resistance experiments across motor protein families, yielding multiple parameters characterizing a motor's chemomechanical coupling. These relations form the maps of optimality that serve as generic and quantitative benchmarks to assess evolutionary optimality and reveal mechanistic connections across motor families. Two chemomechanical coupling regimes are identified from the optimality maps. Remarkably, the F1 rotor and kinesin-1 walker, despite their obvious evolutionary gap, belong to the same regime conducive to high efficiency plus high directionality. Myosin V and cytoplasmic dynein belong to the other chemomechanical regime, which is advantageous to force generation. The analysis of the four motors based on the optimality maps also predicts the symmetries of directional biases and heat productions, which impose constraints on the underlying chemomechanical coupling and are open to future experimental tests. Besides, the verified relations (six in total) combine to form a unified fitting framework that can be used to analyze force-resisting experiments of many more motor proteins in future.This study provides quantitative evidence (extracted from experimental data) that the directionality-based chemomechanical optimality is a real and important element of the evolutionary optimization of motor proteins across families. This does not mean that all motor proteins follow the directionality-based chemomechanical optimality, as biological optimization often is not single-dimensional but involves a balance of multiple aspects. Understanding of the complex optimization benefits from the understanding of individual dimensions. Depending on their cellular functions, many motor proteins can deviate from the chemomechanical optimality quantified in this study. The deviation carries important information about the motor, and can be quantified using the fitting equations and optimality maps, which are presented in a format easy for experimenters to use. The extent to which a motor matches or deviates from the directionality-based chemomechanical optimality can be systematically extracted from load-dependent stepping experiments, which can be done on many more motors in future (desirably with controlled chemical potentials).
At last, this study presents a new conceptual framework to understand motor proteins. The new framework does not contradict traditional kinetic modelling; instead, it provides extra restrictions to reduce the number of independent rates for a kinetic model if a motor is experimentally verified to follow the directionality-based optimality. Hence a fruitful area for future study is the integration of this framework with other approaches including kinetic, mechanical and structural models to cover more aspects of the evolutionary optimization of motor proteins.
Methods
Mapping motor proteins to a common kinetic diagram for directionality analysis
Both translational and rotational motor proteins achieve directional motion along a periodic array of identical binding ‘stations’ that each retains a motor in a well-defined position during the motor's motion. A station can be made of a molecular binding site or multiple ones collectively. For translational motors kinesin 1, myosin V and cytoplasmic dynein that are all dimers, the stations are identified with the periodic binding sites for individual motor heads along microtubule or actin filaments. For translational motor F1, the stations are hosted by the three pairs of (αβ) subunits that form a pseudo-hexagon with the rotatory γ subunit in the center. The inter-site motion of a motor is characterized by two types of states: ‘station’ states in which the motor forms contacts with only one station, and intermediate ‘bridge’ states in which the motor forms contacts with two adjacent stations. The motor's inter-site motion is decided by the transitions between the two types of states, which are essentially captured by a common four-state diagram as shown in Fig. 8A.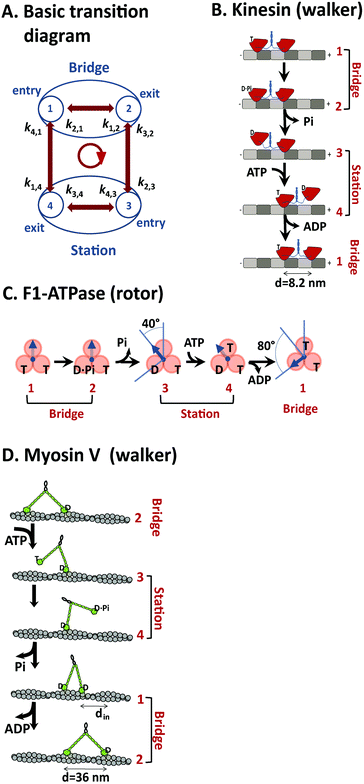 | ||
| Fig. 8 A generic kinetic diagram suitable for analyzing efficient motors (panel A), and the mapping of the kinetic diagram to translational motors kinesin-1 (B), myosin V (D), and the rotational motor F1-ATPase (C) according to their consensus chemomechanical coupling patterns from the literature (ref. 67 for F1, ref. 48 for kinesin, and ref. 42 for myosin V). A major feature of the kinetic diagram in panel A is the differentiation of two types of states (station and bridge, see explanation in the main text), which are assigned to the three motors in panels B–D. The forward step of the motors is represented by the transition cycle indicated by an arrowed circle at the center of panel A. In panel B, the motor domains of a kinesin dimer are shown in red, the soft necklinkers and the coiled-coil dimerization domain in blue, α and β tubulins of the microtubule track in grey and dark grey. In panel C, the rotary γ-subunit of F1 is shown by arrow, and the stator (αβ) subunits by spheres. In panel D, the motor domains of myosin V are shown by green spheres, the IQ motifs of the rigid necks by small green bars in tandem, and the helical actin track by grey spheres. The labels are T for ATP (adenosine triphosphate), D for ADP (adenosine diphosphate) and Pi for phosphate. The step size of the three motors is shown. For myosin V, an on-track sliding is indicated (a feature shared by cytoplasmic dynein44 that is the fourth motor discussed in this study). | ||
In the kinetic diagram, two states are ‘doorway’ states (marked as states 1 and 2) by which a motor enters or exits a bridge state formed between two adjacent stations. The other two states of the kinetic diagram (states 3 and 4) are doorway states by which the motor enters or exits a station state. For bipedal translational motors, which cover all the three translational motors in this study, their two-leg bound states are bridge states and the one-leg states are station states. For F1, the station and bridge states are assigned to the two long-paused angles of the γ subunit in its full 120° rotational step. As shown in Fig. 8B–D, the four states of the kinetic diagram can be assigned to the experimentally detected mechanical and nucleotide states for kinesin 1, F1, and myosin V according to their consensus chemomechanical cycles. A forward inter-site step is represented by the transition cycle 1 → 2 → 3 → 4 → 1 (arrowed circle in Fig. 8A).
A motor's directionality (D) is defined23,24 as the probability for its forward inter-site step minus that for the backward inter-site divided by the total probability for the forward step, backward step, and futile steps that are attempted but failed forward or backward step returning the motor to its previous location. A kinetic–thermodynamic study24 found that a motor's D is entirely decided by the entropy productions along the transitions between a station and a bridge. For the kinetic diagram in Fig. 8A, the steady-state solution, which quantifies a motor's sustained operation, readily reproduces the D expression of ref. 24, i.e., D = [exp(ΔS2,3/kB) − 1] × [exp(ΔS4,1/kB) − 1]/[exp(ΔS2,3/kB + ΔS4,1/kB) − 1]. Here kB is the Boltzmann constant, and ΔS2,3 and ΔS4,1 are entropy productions along the transition pathways 2 ↔ 3 and 4 ↔ 1, which are henceforth called D-pertinent pathways. The intra-station or intra-bridge pathways 1 ↔ 2 and 3 ↔ 4 are called D-uncoupled pathways. A motor may undergo a center-of-mass displacement by the D-uncoupled transition pathways, and this is likely true for myosin V (Fig. 8D, 1 ↔ 2 transitions). But the center-of-mass displacement in 1 ↔ 2 and 3 ↔ 4 transitions occurs without involving any leg dissociation or binding. For a bipedal walker, only the dissociation and binding of its legs contribute to the walker's directionality, as shown by the D–entropy relation (for a rigorous derivation of the relation, see ref. 24).
The neat D–entropy relation identifies the energy cost for the direction D as the heat production along the two D-pertinent pathways, i.e., ΔQD = T(ΔS2,3 + ΔS4,1), in an isothermal environment of temperature T. Following the D–entropy relation, the maximization of D for a fixed amount of heat yields an equal-entropy condition ΔS2,3 = ΔS4,1 = ΔQD/2T. The equal entropies are a necessary condition for producing the highest possible D at a certain price of heat or for producing a certain D with the lowest heat.
The neat D–entropy relation, which is a basis for this study, holds not only for the simplified four-state diagram but also for the complex transition schemes that involve intermediate states between the four doorway states and even more doorway states entering or exiting a station or bridge. As found in ref. 24, any motor-relevant kinetic schemes, however complex they may be, must support cyclic fuel consumption/inter-station motion, hence allowing their many transitions to be grouped into two D-pertinent pathways unambiguously. Two effective entropy productions can be defined accordingly to preserve the neat D–entropy relation. Therefore, the conclusions of this study are not limited by the four-state diagram. This kinetic scheme is suitable for studying efficient motors in optimal operation, which is the purpose of this study. Including more states into the kinetic scheme is necessary to account for spurious pathways of motors under less optimal conditions or in mutated versions, as has been done by many previous studies. Besides, the D–entropy relation is independent of step size, and thus is applicable to motors with fixed steps or variable ones (e.g., cytoplasmic dynein).
Directionality-based relations
Consider a motor that partitions the free-energy change of an ATP hydrolysis Δμ to the D-pertinent pathways by an amount ΔμD and to the D-uncoupled pathways by Δμin, with the energy conservation Δμ = ΔμD + Δμin. As a motor's D-pertinent pathways and D-uncoupled ones must combine to form complete kinetic cycles for the inter-site motion over the motor's full step size (see the arrowed cycle in Fig. 8A for example), the two types of kinetic pathways involve displacements dD and din that are each a portion of the motor's step size d, namely d = dD + din. A motor works along both types of pathways under a load F, i.e., WD = FdD and Win = Fdin. The total work (W = Fd = WD + Win) is capped by the stall force Fs, which is however determined only by the D-pertinent pathways under the condition D → 0 at F → Fs. Considering the energy constraint ΔμD = ΔQD + FdD for the D-pertinent pathways, maximizing the stall force (efficiency) amounts to minimizing the energy cost ΔQD for the motor's directionality. The D–entropy relation yields the minimal energy cost for a certain D, ΔQD,min(D) = 4kBT × arctanh(D), which holds under the equal-entropy condition ΔS2,3 = ΔS4,1 = ΔQD/2T. The ΔQD,min(D) reproduces the 2nd-law required least energy26 for D, namely ΔQD,min(D) = ΔGmin(D). Thus the maximal force that a motor can produce at D is Fmax(D) = [ΔμD − ΔGmin(D)]/dD. The Fmax(D) relation at D = 0 yields the maximum stall force Fs,max = ΔμD/dD and the maximum work Wmax = Fs,maxd = γdΔμD. The Fmax(D) relation at Fmax = 0 yields the zero-load directionality D0 = tanh(ΔμD/4kBT). As this D0–ΔμD relation and the Wmax = γdΔμD relation both hold for arbitrary ΔμD, combining the two relations yields Wmax = γdΔGmin(D0), i.e., eqn (1).Eqn (2) follows from eqn (1)via the relation ΔμD = ΔGmin(D0) and the energy partition γe = (Δμ − ΔμD)/ΔμD. Eqn (3) is the inversed Fmax(D) relation for an optimal motor generating at the maximal force (i.e., F = Fmax). For such a motor, the utilized energy ΔGη(F) = ΔGmin(D(F)) + Fd yields eqn (4) through the Fmax(D) relation plus the step partition d = dD + din.
Directionality–bias relation, bias symmetry, and heat symmetry
A motor's directionality can be expressed24 in terms of cyclic fluxes as D = (Jc+ − Jc−)/(Jc+ + Jc− + Jc0,α + Jc0,β). Here, Jc+ and Jc− are the fluxes for the forward step (i.e., transition cycle 1 → 2 → 3 → 4 → 1 on the four-state diagram) and the backward step (1 → 4 → 3 → 2 → 1); Jc0,α and Jc0,β are the fluxes for the futile steps (4 → 1 → 4 and 3 → 2 → 3). The two biases (α,β) can be identified along the D-pertinent pathways as α = J2,3/J1,4 and β = J4,1/J3,2. Here, Ji,j = piki,j is the transition flux due to the i → j transition with ki,j being the rate and pi the occupation probability for the i-th state. Using the relations24,26 between transition fluxes and cyclic fluxes (J2,3 = Jc+ + Jc0,β, J3,2 = Jc− + Jc0,β, J4,1 = Jc+ + Jc0,α, and J1,4 = Jc− + Jc0,α), the directionality can be rewritten as D = (J2,3 − J3,2)/(J2,3 + J1,4). Applying the steady-state condition J4,1 + J3,2 = J2,3 + J1,4 yields D in terms of two biases. The bias–directionality relation was derived in ref. 47 from a statistical perspective. Here, it is re-derived in order to show that a bias symmetry comes from the equal-entropy relation for an optimal motor. The entropy production57,58 accompanying the net forward flux along a pathway from the i-th to j-th states is generally ΔSi,j = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ji,j/Jj,i). The equal-entropy condition, ΔS2,3 = ΔS4,1, yields J2,3/J3,2 = J4,1/J1,4 and Jc0,α = Jc0,β, J4,1= J2,3, J3,2= J1,4, hence equal biases α = β. The equal entropies amount to symmetric heat productions along the two D-coupled pathways, i.e., Q2,3 = Q4,1 with Q2,3 = TΔS2,3 and Q4,1 = TΔS4,1.
ln(Ji,j/Jj,i). The equal-entropy condition, ΔS2,3 = ΔS4,1, yields J2,3/J3,2 = J4,1/J1,4 and Jc0,α = Jc0,β, J4,1= J2,3, J3,2= J1,4, hence equal biases α = β. The equal entropies amount to symmetric heat productions along the two D-coupled pathways, i.e., Q2,3 = Q4,1 with Q2,3 = TΔS2,3 and Q4,1 = TΔS4,1.
Power–efficiency relation
A motor moving against a load F has an efficiency η = Fd/Δμ and a power P = Fv with v as the motor's speed. Hence a motor's power–efficiency relation is decided by its v-vs.-F relation. The steady-state solution to the four-state kinetic diagram yields the maximal speed,7 which in turn yields the maximal power as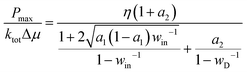 | (5) |
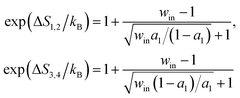 | (6) |
In eqn (5) and (6), win = exp(ΔQin/kBT) with ΔQin = T(ΔS1,2 + ΔS3,4) as the heat production along the D-uncoupled pathways; wD = exp(ΔQD/2kBT). Based on the energy conservation (i.e., Δμ = Fd + ΔQin + ΔQD), the heat production ΔQD is related to ΔQin as ΔQD = (1 − η)Δμ − ΔQin. ktot is the joint rate for the cycle of transitions producing a full forward step (i.e., state 1 → 2 → 3 → 4 → 1). Hence 1/ktot = 1/k1,2 + 1/k2,3 + 1/k3,4 + 1/k4,1. For motor proteins with a tight chemomechanical coupling, the four forward transitions for the forward-stepping cycle k1,2, k2,3, k3,4, and k4,1 correspond to the four processes of the fuel turnover cycle, namely ATP binding, hydrolysis, phosphate release and ADP dissociation. Hence ktot is the overall ATP turnover rate for a motor of tight chemomechanical coupling. This joint forward-step rate can be re-organized as 1/ktot = 1/kc + 1/kd with kc as the joint rate for the forward transitions along the two D-uncoupled pathways (i.e., 1/kc = 1/k1,2 + 1/k3,4) and kd as the joint rate for forward transitions along the D-pertinent pathways (1/kd = 1/k2,3 + 1/k4,1). a1 and a2 are two rate ratios a1 = kc/k3,4 and a2 = kc/kd.
For the F1 rotor, its ATP binding rate is k3,4, hydrolysis rate is k1,2, phosphate release rate is k2,3, and ADP dissociation rate is k4,1 according to the consensus chemomechanical coupling scheme shown in Fig. 8C. The load may affect each of the rates, but the load dependences are likely cancelled in the rate ratios. It is a good approximation to assume load-independent ratios a1 and a2. It is also reasonable to assume a load-independent ΔQin for F1, because this energy dissipation occurs in the transition pathways of ATP binding and hydrolysis that are not coupled to any displacement (see Fig. 8C). A previous study7 shows that a ΔQin value of ∼0.75kBT explains the measured zero-load speed34 of F1 within a large rate uncertainty. Estimating the absolute power also requires the load dependence of the ATP turnover rate ktot, which is unclear for this motor. As an approximation, we assume F1's ktot to follow a load-dependent function previously adopted for the studies13,16,17,36 of kinesin-1 (also a motor known for tight chemomechanical coupling59,60), namely ktot(F) = ktot(F = 0)/(p + qeFδ/kBT), in which δ is a coupling length and p is a branch ratio with p + q = 1. The absolute power in Fig. 6B and C is estimated using ktot(F = 0), δ and p as fitting parameters.
Efficiency–speed relation
The speed of an optimal motor at zero load follows eqn (5) as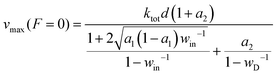 | (7) |
Consider a reference value for the energy partition γe0, thereby a reference efficiency ηmax0 by eqn (2). The values of ΔQin, ΔQD, and the four forward rates at γe0 decide the value of vmax(F = 0) at ηmax0. When the energy partition changes from γe0 to a higher value γe, ΔQin and ΔQD change as ΔQD = Δμ/(1 + γe) and ΔQin = Δμγe/(1 + γe), i.e., more energy is partitioned to the D-uncoupled pathways. A motor's speed at zero load is likely not limited by the rates for the D-coupled pathways (k2,3 and k4,1), but by the rates for the D-uncoupled pathways (k1,2 and k3,4), since the former pathways contribute to the motor's direction that is maximal at zero load. Hence a reasonable assumption is that the partition change affects only the rates k1,2 and k3,4. Following the spirit of Bell's equation61 or the Arrhenius equation, the two rates are assumed to change as k1,2(γe)/k1,2(γe0) = exp{[ΔS1,2(γe) − ΔS1,2(γe0)]/kB} and k3,4(γe)/k3,4(γe0) = exp{[ΔS3,4(γe) − ΔS3,4(γe0)]/kB}. Here ΔS1,2(γe0) and ΔS1,2(γe) are entropy productions at the reference and new partition, which are calculated from the corresponding ΔQin values by eqn (6). However, calculating ΔS1,2(γe) from eqn (6) requires the a1 value at γe, which in turn requires the values of k1,2 and k3,4 at γe in the first place. Re-organize the rates as k1,2(γe) = ρ1,2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ΔS1,2/kB), k3,4(γe) = ρ3,4 exp(ΔS3,4/kB) with ρ1,2 = k1,2(γe0) exp[−ΔS1,2(γe0)/kB] and ρ3,4 = k3,4(γe0) exp[−ΔS3,4(γe0)/kB]. Applying the two rates to a1 = k1,2/(k1,2 + k3,4) and further using ΔQin = T(ΔS1,2 + ΔS3,4) yields ΔS1,2 in terms of a1. Plugging the obtained relation into the left-side relation in eqn (6) produces a closed equation for a1, which yields the a1 value at γe as
exp(ΔS1,2/kB), k3,4(γe) = ρ3,4 exp(ΔS3,4/kB) with ρ1,2 = k1,2(γe0) exp[−ΔS1,2(γe0)/kB] and ρ3,4 = k3,4(γe0) exp[−ΔS3,4(γe0)/kB]. Applying the two rates to a1 = k1,2/(k1,2 + k3,4) and further using ΔQin = T(ΔS1,2 + ΔS3,4) yields ΔS1,2 in terms of a1. Plugging the obtained relation into the left-side relation in eqn (6) produces a closed equation for a1, which yields the a1 value at γe as 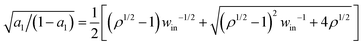 with ρ = ρ1,2/ρ3,4. The solution further yields ΔS1,2(γe) and ΔS3,4(γe), and thereby k1,2(γe) and k3,4(γe). Then the joint rate ktot is obtained at γe, and the speed at the corresponding efficiency ηmax is calculated from eqn (7).
with ρ = ρ1,2/ρ3,4. The solution further yields ΔS1,2(γe) and ΔS3,4(γe), and thereby k1,2(γe) and k3,4(γe). Then the joint rate ktot is obtained at γe, and the speed at the corresponding efficiency ηmax is calculated from eqn (7).
For myosin V and other myosin motors, k1,2, k2,3, k3,4, and k4,1 correspond to ADP dissociation, ATP binding, hydrolysis, and phosphate release, respectively (Fig. 8D). Hence the ADP dissociation, known as the rate-limiting process,41 is indeed in the D-uncoupled pathways. Fig. 7 shows the ηmax–vmax(F = 0) relation predicted for myosin motors by the above procedures using myosin V as the reference, i.e., γe0 = 1. The rates at this γe0 value are taken from those of myosin V reported in ref. 41: k1,2 = 12 s−1, k2,3 = 0.9 μM−1 s−1 × [ATP] = 2000 s−1 for saturating ATP concentration [ATP] = 2 M, k3,4, = 250 s−1, and k4,1 = 750 s−1. The speed–efficiency correlation predicted using these rates (the dashed line in Fig. 7) has a speed limit because the rate-limiting process becomes the phosphate release (k4,1) at low efficiency (i.e., high γe). Raising this rate to 2000 s−1 removes the speed limit (solid line in Fig. 7). The ADP dissociation rate is also adjusted to k1,2 = 6 s−1 for the solid line to show that a better agreement in magnitude with experimental data is readily available.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Ministry of Education of Singapore under grants R-144-000-325-112 and R-144-000-372-114.References
- H. Wang and G. Oster, Energy transduction in the F1 motor of ATP synthase, Nature, 1998, 396, 279–282 CrossRef CAS PubMed.
- T. Elston, H. Wang and G. Oster, Energy transduction in ATP synthase, Nature, 1998, 391, 510–513 CrossRef CAS PubMed.
- G. Oster and H. Wang, Reverse engineering a protein: the mechanochemistry of ATP synthase, Biochim. Biophys. Acta, 2000, 1458, 482–510 CrossRef CAS.
- Y. Q. Gao, W. Yang, M. Karplus and A. Structure-Based, Model for the Synthesis and Hydrolysis of ATP by F1-ATPase, Cell, 2005, 123, 195–205 CrossRef CAS PubMed.
- E. Gerritsma and P. Gaspard, Chemomechanical coupling and stochastic thermodynamics of the F1-ATPase molecular motor with an applied external torque, Biophys. Rev. Lett., 2010, 5, 163–208 CrossRef CAS.
- E. Zimmermann and U. Seifert, Efficiencies of a molecular motor: a generic hybrid model applied to the F1-ATPase, New J. Phys., 2012, 14, 103023 CrossRef.
- R. Z. Hou and Z. S. Wang, Role of directional fidelity in multiple extreme performance of F1-ATPase motor, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022703 CrossRef PubMed.
- K. Kawaguchi, S. I. Sasa and T. Sagawa, Nonequilibrium dissipation-free transport in F1-ATPase and the thermodynamic role of asymmetric allosterism, Biophys. J., 2014, 106, 2450–2457 CrossRef CAS PubMed.
- M. E. Fisher and A. B. Kolomeisky, The force exerted by a molecular motor, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 6597–6602 CrossRef CAS.
- A. E. M. Clemen, M. Vilfan, J. Jaud, J. S. Zhang, M. Barmann and M. Rief, Force-dependent stepping kinetics of myosin-V, Biophys. J., 2005, 88, 4402–4410 CrossRef CAS PubMed.
- Q. Shao and Y. Q. Gao, On the hand-over-hand mechanism of kinesin, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8072–8077 CrossRef CAS PubMed.
- S. Liepelt and R. Lipowsky, Kinesin's network of chemomechanical motor cycles, Phys. Rev. Lett., 2007, 98, 258102 CrossRef PubMed.
- Z. S. Wang, M. Feng, W. W. Zheng and D. G. Fan, Kinesin is an evolutionarily fine-tuned molecular ratchet-and-pawl device of decisively locked directionality, Biophys. J., 2007, 93, 3363–3372 CrossRef CAS PubMed.
- C. Hyeon and J. N. Onuchic, Internal strain regulates the nucleotide binding site of the kinesin leading head, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2175–2180 CrossRef CAS PubMed.
- P. Xie, S. X. Dou and P. Y. Wang, Limping of homodimeric kinesin motors, J. Mol. Biol., 2007, 366, 976–985 CrossRef CAS PubMed.
- D. G. Fan, W. W. Zheng, R. Hou, F. Li and Z. S. Wang, Modelling motility of the kinesin dimer from molecular properties of individual monomers, Biochemistry, 2008, 47, 4733–4742 CrossRef CAS PubMed.
- W. W. Zheng, D. Fan, M. Feng and Z. S. Wang, Load-resisting capacity of kinesin, Phys. Biol., 2009, 6, 036002 CrossRef PubMed.
- Y. Xu and Z. S. Wang, Comprehensive physical mechanism of two-headed biomotor myosin V, J. Chem. Phys., 2009, 131, 245104(9) Search PubMed.
- R. Z. Hou and Z. S. Wang, Coordinated molecular “fishing” in heterodimeric kinesin, Phys. Biol., 2010, 7, 036003 CrossRef PubMed.
- A. Parmeggiani, F. Julicher, A. Ajdari and J. Prost, Energy transduction of isothermal ratchets: generic aspects and specific examples close to and far from equilibirum, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 2127–2140 CrossRef CAS.
- M. Esposito, K. Lindenberg and C. Van den Broeck, Universality of efficiency at maximum power, Phys. Rev. Lett., 2009, 102, 130602 CrossRef PubMed.
- U. Seifert, Efficiency of autonomous soft nanomachines at maximum power, Phys. Rev. Lett., 2011, 106, 020601 CrossRef PubMed.
- A. Efremov and Z. S. Wang, Maximum directionality and systematic classification of molecular motors, Phys. Chem. Chem. Phys., 2011, 13, 5159–5170 RSC.
- A. Efremov and Z. S. Wang, Universal optimal working cycles of molecular motors, Phys. Chem. Chem. Phys., 2011, 13, 6223–6233 RSC.
- C. Van den Broeck, N. Kumar and K. Lindenberg, Efficiency of Isothermal Molecular Machines at Maximum Power, Phys. Rev. Lett., 2012, 108, 210602 CrossRef PubMed.
- Z. S. Wang, R. Z. Hou and A. Efremov, Directional fidelity of nanoscale motors and particles is limited by the 2nd law of thermodynamics-via a universal equality, J. Chem. Phys., 2013, 139, 035105 CrossRef PubMed.
- T. Harada and S.-i. Sasa, Equality Connecting Energy Dissipation with a Violation of the Fluctuation-Response Relation, Phys. Rev. Lett., 2005, 95, 130602 CrossRef PubMed.
- T. Harada and S.-i. Sasa, Energy dissipation and violation of the fluctuation-response relation in nonequilibrium Langevin systems, Phys. Rev., 2006, E 73, 026131 Search PubMed.
- S. Toyabe, T. Okamoto, T. Watanabe-Nakayama, H. Taketani, S. Kudo and E. Muneyuki, Nonequilibrium energetics of a single F1-ATPase molecule, Phys. Rev. Lett., 2010, 104, 198103 CrossRef PubMed.
- T. Ariga, M. Tomishige and D. Mizuno, Nonequilibrium Energetics of Molecular Motor Kinesin, 2017, arXiv:1704.05302 [physics.bio-ph].
- F. J. Kull, R. D. Vale and R. J. Fletterick, The case for a common ancester: kinesin and myosin motor proteins and g proteins, J. Muscle Res. Cell Motil., 1998, 19, 877–886 CrossRef CAS PubMed.
- E. P. Sablin and R. J. Fletterick, Nucleotide switches in molecular motors: structural analysis of kinesins and myosins, Curr. Opin. Struct. Biol., 2001, 11, 716–724 CrossRef CAS PubMed.
- R. Yasuda, H. Noji, K. Kinosita and M. Yoshida, F1-ATPase is a highly efficient molecular motor that rotates with discrete 120° steps, Cell, 1998, 93, 1117–1124 CrossRef CAS PubMed.
- S. Toyabe, T. M. Watanabe, T. Okamoto, S. Kudo and E. Muneyuki, Thermodynamic efficiency and mechanochemical coupling of F1-ATPase, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17951–17956 CrossRef CAS PubMed.
- A. Gennerich, A. P. Carter, S. L. Reck-Peterson and R. D. Vale, Force-induced bidirectional stepping of cytoplasmic dynein, Cell, 2007, 131, 952–965 CrossRef CAS PubMed.
- M. J. Schnitzer, K. Visscher and S. M. Block, Force production by single kinesin motors, Nat. Cell Biol., 2000, 2, 718–723 CrossRef CAS PubMed.
- R. Yasuda, H. Noji, M. Yoshida, K. Kinosita and H. Itoh, Resolution of distinct rotational substeps by submillisecond kinetic analysis of F1-ATPase, Nature, 2001, 410, 898–904 CrossRef CAS PubMed.
- K. O. Takayuki Nishizaka, Hiroyuki Noji, Shigeki Kimura, Eiro Muneyuki, Masasuke Yoshida and Kazuhiko Kinosita Jr, Chemomechanical coupling in F1-ATPase revealed by simultaneous observation of nucleotide kinetics and rotation, Nat. Struct. Mol. Biol., 2004, 11, 142–148 Search PubMed.
- H. R. Hendrik Sielaff, Siegfried Engelbrecht, Wolfgang Junge and H. Sielaff, et al., Functional halt positions of rotary FOF1-ATPase correlated with crystal structures, Biophys. J., 2008, 95, 4979–4987 CrossRef CAS PubMed.
- T. J. Purcell, N. Naber, K. Franks-Skiba, A. R. Dunn, C. C. Eldred, C. L. Berger, A. Málnási-Csizmadia, J. A. Spudich, D. M. Swank, E. Pate and R. Cooke, Nucleotide Pocket Thermodynamics Measured by EPR Reveal How Energy Partitioning Relates Myosin Speed to Efficiency, J. Mol. Biol., 2011, 407, 79–91 CrossRef CAS PubMed.
- E. M. De la Cruz, A. L. Wells, S. S. Rosenfeld, E. M. Ostap and H. L. Sweeney, The kinetic mechanism of myosin V, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13726–13731 CrossRef CAS.
- D. Vale, Myosin V motor proteins: marching stepwise towards a mechanism, J. Cell Biol., 2003, 163, 445–450 CrossRef PubMed.
- T. Okada, H. Tanaka, A. H. Iwane, K. Kitamura, M. Ikebe and T. Yanagida, The diffusive search mechanism of processive myosin class-V motor involves directional steps along actin subunits, Biochem. Biophys. Res. Commun., 2007, 354, 379–384 CrossRef CAS PubMed.
- A. P. Carter, Crystal clear insights into how the dynein motor moves, J. Cell Sci., 2013, 126, 705–713 CrossRef CAS PubMed.
- H. Isojima, R. Iino, Y. Niitani, H. Noji and M. Tomishige, Direct observation of intermediate states during the stepping motion of kinesin-1, Nat. Chem. Biol., 2016, 12, 290–298 CrossRef CAS PubMed.
- J. Bath, S. J. Green, K. E. Allen and A. J. Turberfield, Mechanism for a Directional, Processive, and Reversible DNA Motor, Small, 2009, 5, 1513–1516 CrossRef CAS PubMed.
- M. H. Liu, J. Cheng, S. R. Tee, S. Sreelatha, I. Y. Loh and Z. S. Wang, Biomimetic Autonomous Enzymatic Nanowalker of High Fuel Efficiency, ACS Nano, 2016, 10, 5882–5890, DOI:10.1021/acsnano.6b01035.
- R. D. Vale and R. A. Milligan, The way things move: looking under the hood of molecular motor proteins, Science, 2000, 288, 88–95 CrossRef CAS PubMed.
- A. Gennerich and R. D. Vale, Walking the walk: how kinesin and dynein coordinate their steps, Curr. Opin. Cell Biol., 2009, 21, 59–67 CrossRef CAS PubMed.
- J. Cheng, S. Sreelatha, R. Z. Hou, A. Efremov, R. C. Liu, J. R. van der Maarel and Z. S. Wang, Bipedal nanowalker by pure physical mechanisms, Phys. Rev. Lett., 2012, 109, 238104 CrossRef PubMed.
- M. H. Liu, R. Z. Hou, J. Cheng, I. Y. Loh, S. Sreelatha, J. N. Tey, J. Wei and Z. S. Wang, Autonomous synergic control of a nanomotor, ACS Nano, 2014, 8, 1792–1803 CrossRef CAS PubMed.
- I. Y. Loh, J. Cheng, S. R. Tee, A. Efremov and Z. S. Wang, From bistate molecular switches to self-directed track-walking nanomotors, ACS Nano, 2014, 8, 10293–10304 CrossRef CAS PubMed.
- J. Cheng, S. Sreelatha, I. Y. Loh, M. Liu and Z. S. Wang, A bioinspired design principle for DNA nanomotors: mechanics-mediated symmetry breaking and experimental demonstration, Methods, 2014, 67, 227–233 CrossRef CAS PubMed.
- Q. Y. Yeo, I. Y. Loh, S. R. Tee, Y. H. Chiang, J. Cheng, M. H. Liu and Z. S. Wang, A DNA bipedal nanowalker with a piston-like expulsion stroke, Nanoscale, 2017, 9, 12142–12149 RSC.
- R. Z. Hou, I. Y. Loh, H. Li and Z. S. Wang, Mechanical-kinetic modelling of a molecular walker from a modular design principle, Phys. Rev. Appl., 2017, 7, 024020 CrossRef.
- V. Belyy, M. A. Schlager, H. Foster, A. E. Reimer, A. P. Carter and A. Yildiz, The mammalian dynein–dynactin complex is a strong opponent to kinesin in a tug-of-war competition, Nat. Cell Biol., 2016, 18, 1018–1024 CrossRef CAS PubMed.
- T. L. Hill, Free Energy Transduction and Biochemical Cycle Kinetics, Springer, New York, 1989 Search PubMed.
- U. Seifert, Entropy Production along a Stochastic Trajectory and an Integral Fluctuation Theorem, Phys. Rev. Lett., 2005, 95, 040602 CrossRef PubMed.
- W. Hua, E. C. Young, M. L. Fleming and J. Gelles, Coupling of kinesin steps to ATP hydrolysis, Nature, 1997, 388, 390–393 CrossRef CAS PubMed.
- M. J. Schnitzer and S. M. Block, Kinesin hydrolyses one ATP per 8-nm step, Nature, 1997, 388, 386–390 CrossRef CAS PubMed.
- G. I. Bell, Models for the specific adhesion of cells to cells, Science, 1978, 200, 618–627 CAS.
- M. Nishiyama, H. Higuchi and T. Yanagida, Chemomechanical coupling of the forward and backward steps of single kinesin molecules, Nat. Cell Biol., 2002, 4, 790–797 CrossRef CAS PubMed.
- N. J. Carter and R. A. Cross, Mechanics of the kinesin step, Nature, 2005, 435, 308–312 CrossRef CAS PubMed.
- N. M. Kad, K. M. Trybus and D. Warshaw, Load and Pi control flux through the branched kinetic cycle of myosin V, J. Biol. Chem., 2008, 283, 17477–17484 CrossRef CAS PubMed.
- Y. Taniguchi, M. Nishiyama, Y. Ishii and T. Yanagida, Entropy rectifies the Brownian steps of kinesin, Nat. Chem. Biol., 2005, 1, 342–347 CrossRef CAS PubMed.
- J. A. B. Scanlon, M. K. Al-Shawi, N. P. Le and R. K. Nakamoto, Determination of the partial reactions of rotational catalysis in F1-ATPase, Biochemistry, 2007, 46, 8785–8797 CrossRef CAS PubMed.
- D. Okuno, R. Iino and H. Noji, Rotation and structure of FoF1-ATP synthase, J. Biochem., 2011, 149, 655–664 CrossRef CAS PubMed.
- M. Tominaga, H. Kojima, E. Yokota, H. Orii, R. Nakamori, E. Katayama, M. Anson, T. Shimmen and K. Oiwa, Higher plant myosin XI moves processively on actin with 35 nm steps at high velocity, EMBO J., 2003, 22, 1263–1272 CrossRef CAS PubMed.
- R. C. Woledge, The energetics of tortoise muscle, J. Physiol., 1968, 197, 685–707 CrossRef CAS.
- J. A. Rall and B. A. Schottelius, Energetics of contraction in phasic and tonic skeletal muscles of the chicken, J. Gen. Physiol., 1973, 62, 303–323 CrossRef CAS PubMed.
- N. P. Smith, C. J. Barclay and D. S. Loiselle, The efficiency of muscle contraction, Prog. Biophys. Mol. Biol., 2005, 88, 1–58 CrossRef CAS PubMed.
- F. O. Lehmann and N. Heymann, Dynamics of in vivo power output and efficiency of Nasonia asynchronous flight muscle, J. Biotechnol., 2006, 124, 93–107 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2018 |
