Excited state C–N bond dissociation and cyclization of tri-aryl amine-based OLED materials: a theoretical investigation

Abstract

Tri-aryl amines (TAA) such as triphenylamine (TPA) are widely used for designing chromophores for dye-sensitized solar cells (DSSC) and organic light-emitting diodes (OLED). These materials degrade over time and hence result in reduced performance. Therefore, exploring the associated mechanistic pathways and factors controlling the degradation is necessary for future development of durable TAA-based devices. Hence, in this study, the complete active space self-consistent-field (CASSCF) method coupled with second order N-electron valence perturbation theory (NEVPT2) calculations was carried out to understand the excited state phenomena occurring in TAA using TPA and N,N-diphenyl-2-naphthylamine (DPNA) as model systems. The results indicated the presence of a conical intersection between ground and first excited singlet states with C–N bond dissociation, which acts as a channel for the excited molecules to dissociate and form radical fragments (phenyl/naphthyl). This occurrence is unusual for non-saturated bonds with delocalization. The resulting radical fragments formed intra-molecular products and subsequently yielded five- and six-membered cyclized products depending on the type of aryl groups. The significant findings from this study throw light on the photostability of TAA-based OLED devices as well as on the possible route to synthesize cyclic amines such as carbazoles.

---

Introduction

Harnessing the energy from sunlight and developing artificial lighting systems with high efficiency are the two leading areas of research in current energy applications with many potential challenges.^1–9 The development of organic light-emitting diodes (OLEDs) has caused revolutionary transition in lighting technology. OLEDs incorporate organic molecules’ hole/electron transport layers;^10–12 several organic molecules/moieties, such as triphenylamine (TPA),^13–22 carbazole (Cbz),^23–26 and perylene-based systems,^27–30 have been designed to improve their efficiency. Over the past decade, intense research in these fields has led to the fabrication of devices with high efficiencies and lifetimes. Ageing of these devices is mainly caused by the formation of different photochemical/electrochemical products.^31–35 Among OLEDs, the operational lifetime of blue light-emitting OLEDs is greatly reduced due to degradation of functional molecules and accumulation of defects.^32,36–38 The degradation of functional molecules occurs due to charge carriers and excitons. In charge carrier-induced degradation, radical cations/anions formed by holes/electrons can lead to bond rupture within the molecule or radical reactions between surrounding molecules.^{31,32,39–42} Exciton-induced degradation occurs via direct degradation of the molecule in excited states or by bimolecular quenching reactions. Bimolecular quenching occurs either by exciton–exciton combination, leading to “hot molecule”, or by exciton–polaron interaction. In the former case, two excitons combine to form high lying excited states, which then undergo internal conversion to form highly vibrationally excited ground state (hot molecule). These hot molecules can dissociate either directly or by absorption of photons. Exciton–polaron interactions lead to energy transfer from exciton to radical cation/anion, creating an excited polaron/radical.³³ Kondakov et al. have studied the degraded products of 4,4′-bis(N-carbazolyl)-1,1′-biphenyl carbazole (CPB)⁴³ and N,N′-di(1-naphthyl)-N,N′-diphenyl-(1,1′-biphenyl)-4,4′-diamine (NPD).⁴⁴ They identified that singlet excitons pave the way for their fragmentation. Similarly, hole transport materials (HTM), such as 4,4′-cyclohexylidenebis[N,N-bis(4-methylphenyl)benzenamine] (TAPC),³⁹ tris(4-carbazoyl-9-ylphenyl)amine (TCTA),⁴⁵ and phenanthroline and anthracene derivatives,⁴¹ show degradation in the aged samples of these devices. It is noted from these studies that C–N bond dissociation is the most predominant mechanism for NPD and CBP with C–C bond breaking between aryl groups as a minor pathway. They have also identified products, which are the fragments of these molecules along with cross-conjugated structures between the fragments. These fragments form defects, which can decrease the lifetime of devices. Several theoretical studies have also been carried out to understand the mechanism of degradation for TAPC and carbazole-based systems.^39,46–48 Recently, Freidzon et al.⁴⁸ predicted the operational stability of phosphorescent OLED host molecules using multi-reference CASSCF/XMCQDPT2 methods. They reported that the bond dissociation energy between C–N bonds can be directly correlated to the stability of OLED molecules.⁴⁸

Triphenylamine (TPA) has been the most exploited basic unit in the molecular architecture of OLED and DSSC.^13–22 The nitrogen atom connected to three aromatic rings forms the basic skeleton in these materials. The lone pair electrons of N-atom delocalizes over the aromatic rings, leading to multiple resonance structures, which in turn makes these structures strong electron donors and hole transporting materials. Functionalization of TPA creates a potential window to enhance the efficiency of these devices. However, ageing and presence of non-emissive spots are common in TPA-based OLED devices.³² Experimental studies have revealed that NPD degrades into various fragments in the singlet excited states.⁴³ Kondakov et al.⁴⁴ have identified the products using mass spectrometry and concluded that C–N bond dissociation in the excited state is the plausible mechanism. However, studies conducted by Bell et al.⁴⁹ reported the formation of five- and six-membered cyclized products, resembling a carbazole unit. They concluded that during excitation, there is bond formation between the carbon atoms present in the adjacent phenyl/naphthyl rings attached to N-atom in NPD. These two experiments directly provided contrasting observations, in which the former showed the preference for C–N dissociation and the latter demonstrated the formation of C–C bond, leading to cyclization. However, both results indicate that degradation occurs directly in the first excited state and not through “hot molecule” mechanism or charge carriers.

Very few studies have been carried out to understand the degradation mechanism of OLED materials when compared to the studies on engineering of these devices. Understanding the degradation mechanism of these materials is as important as the technical aspects to improve lifetime and efficiency. Finding the dissociation channels will help design new materials to avoid energy loss and minimize the rate of accumulation of e-waste on global scale. Therefore, in this study, we systematically explored the excited state degradation channels of TPA and DPNA as models for NPD and other TPA-based devices. The objectives of this study are to investigate the following questions: (i) Why does C–N bond dissociation occur in excited states? (ii) Is C–N bond dissociation or cyclization preferred in excited state? (iii) Is bond dissociation energy (BDE) an appropriate parameter to predict the feasibility of dissociation in excited states?

Computational details

Electronically excited molecules return to ground state through emission of light in the form of florescence or phosphorescence or via non-radiative decay. The latter occurs either by radiation-less deactivation (conversion of excited energy to vibrational energy, leading to the loss of energy as heat) or through conical intersection (CI)/avoided crossing. Technically, the devices will be constructed to avoid deactivation by lattice vibrations and therefore, studying CI is of utmost importance since it is independent of device parameters and highly dependent on the electronic structure of the molecule. To explore the potential energy surface (PES) of excited states near CI, post Hartree–Fock methods, such as multireference configuration interaction (MRCI),⁵⁰ complete active space self-consistent field (CASSCF),⁵¹ complete active space 2nd order perturbation theory (CASPT2)⁵² and equation-of-motion coupled-cluster methods (EOM-CC),^53,54 are useful to account for degeneracy of energy states at CI. Standard DFT cannot correctly describe CI between the ground and excited states,⁵⁵ but spin-flip extension (SF-TDDFT)^56–58 can be used for exploring CI. Although MRCI, CASSCF, CASPT2 and EOM-CC methods are computationally demanding, they can properly predict the localized and delocalized states.

In this study, we used the CASSCF method for geometry optimization and frequency calculations. TPA and DPNA were used as model systems for TAA in this study. The active spaces used for TPA and DPNA are (14,13) and (12,11), where the first and second terms in the brackets represent the number of electrons and number of orbitals in the active space, respectively. The choice of the active space is based on the careful speculation of proper π, π* and lone pair orbitals. The contour images of the selected orbitals in the active space are given in ESI† (S1 and S2). Increase in active space beyond these values did not improve the quality of the results and therefore, these active spaces were used throughout this study. It is pertinent that these combinations provided better convergence in excited states. Calculation of non-adiabatic couplings (NAC) between the states is important, especially near degenerate states. However, it requires enormous computational time and memory for larger molecules with large active space and therefore was not attempted in this study. The basis set used in this study was cc-pVTZ,⁵⁹ since it is known from previous studies^60–62 that it provides sensibly accurate results. In addition, the configuration space functions (CSFs) are very large (81 675 CSFs for DPNA) and the solutions require considerable computational cost and time, which justifies the choice of the basis set used in this study. The calculations were carried out with state averaged CASSCF (SA-CASSCF) for generating PES along the dissociation mode and state specific CASSCF (SS-CASSCF) for reporting the energetics of optimized structures at stationary points in the reaction path. To account for the dynamic correlation correction, NEVPT2⁶³ with fully internally contracted wavefunction (FIC) was used over CASSCF calculations with resolution of identity (RI) approximation. Since we are interested in the region around CI, the SA-CASSCF energies were not corrected for dynamic correlation, whereas all SS-CASSCF energies were corrected for the same using NEVPT2 approach. The bond lengths and bond angles were represented with two and one decimal places, respectively, since CASSCF has less accuracy in predicting geometrical parameters. All calculations were carried out using ORCA program package.⁶⁴

Results and discussion

1. Relaxed PES scan

The optimized geometries of TPA and DPNA at the CASSCF/cc-pVTZ level of theory are given in Fig. 1.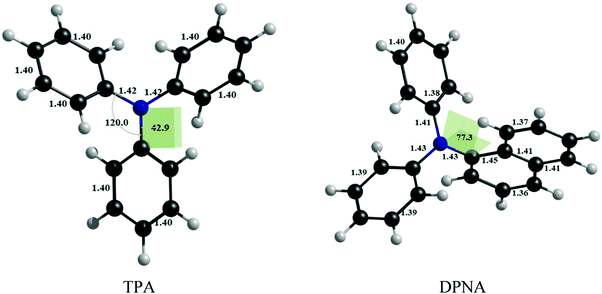

Fig. 1 Optimized geometries of TPA at CAS(14,13)/cc-pVTZ and DPNA at CAS(12,11)/cc-pVTZ level of theory.

TPA shows symmetrical bond parameters around nitrogen, whereas DPNA shows distorted geometry, which could be due to steric hindrance by the naphthyl ring. The absorption maxima of TPA and DPNA are calculated to be 263 and 265 nm, respectively, at the CASSCF/cc-pVTZ level of theory with inclusion of NEVPT2 correction and solvation contribution (methanol) using SMD model. The excitation occurs from HOMO to LUMO, wherein the lone pair of nitrogen (n) and the π-orbitals of phenyl ring hybridize to form HOMO and the π*-orbitals of phenyl ring contribute to LUMO. It is observed that the calculated adsorption value is in good agreement with the experimental excitation energy of TPA (298 nm) in methanol despite the use of moderate active space and RI-approximation. This finding justifies the choices of computational methodology and active space employed for the calculations.

The primary objective of this study is to map the potential energy surface of TPA and DPNA that leads to exciton-induced degradation. However, predicting the decay mode, including all excited states, requires complete knowledge of the PES of all states along all degrees of freedom, which is computationally tedious. On the other hand, direct dynamics affords another possible way to understand PES. Nevertheless, it requires more sampling and a larger timescale to observe rare events, especially for molecules containing several degrees of freedom. This led us to use a prior good guess about the decay channel. Previous experiments conducted on NPD indicate that C–N bond dissociation is observed with the formation of fragmented products. Hence, we started our calculation by studying the PES of TPA and DPNA along C–N bond. Relaxed surface scan along the C–N bond was carried out for both structures, and the results are presented in Fig. 2(a and b). In this figure, S0, S1, S2, S3 and T1 represent ground, first, second, and third excited singlet states and first triplet state, respectively. In this figure, the characters E, M and I, included within the brackets, represent equilibrium, maximum, and inflection points, respectively. The point D indicates the dissociation limit. The dissociation limit was calculated up to 4.5 Å but is cropped to 3.5 Å in the figure for simplicity.

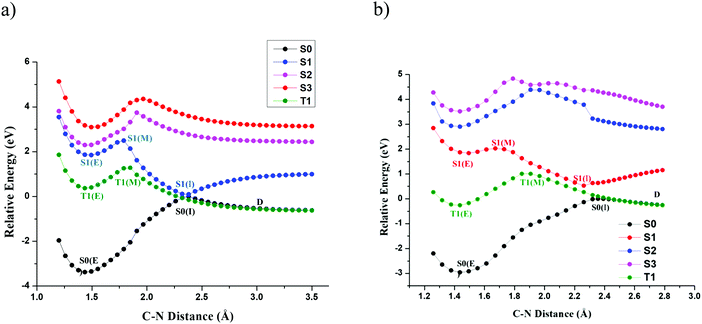Fig. 2 Relaxed PES scans of C–N bond of (a) TPA at SA-CAS(14,13)/cc-pVTZ and (b) DPNA at SA-CAS(12,11)/cc-pVTZ.

For SA-CASSCF energy, two singlet states (S0 and S1) and one triplet state with equal weights were used. Since these states have degenerate energy levels at CI, they were used to compute SA-CASSCF energy. Instead of SA-CASSCF energy, individual energetics of each state was used to plot potential energy surface scans. It is observed from the plot that elongation of the bond distance from the equilibrium value of 1.42 Å increases the energy of all states. However, S0 state reaches a maximum S0(I) at 2.38 Å for TPA and 2.36 Å for DPNA. These two points were used as reference points to construct their respective PESs. After reaching S0(I), the PES of S0 decreases exponentially and reaches constant dissociation limit D. The energy of all excited states reaches a maximum and subsequently decreases to constant values except for S1. The S1 state of TPA (DPNA) reaches stationary point S1(M), which is similar to a 2D-transition state (TS) at 1.73 Å (1.67 Å). S1(M) lies above S1(E) by 12.96 kcal mol⁻¹ (4.36 kcal mol⁻¹) for TPA (DPNA). It is well-known that S1(M) is not a TS as it has not been optimized along all degrees of freedom. However, it provides a clear picture of the presence of high-energy TS. Details of the TS associated with S1(M) are discussed in the next section. After S1(M), the energy of S1 decreases slowly and reaches S1(I) at 2.38 Å (2.36 Å) for TPA (DPNA). The energy difference values between S1(I) and S0(I) are 0.097 eV and 0.53 eV for TPA and DPNA, respectively. Then, S1 exponentially rises and reaches saturation. The triplet state T1 behaves in a similar manner to S1, reaching a maximum T1(M) (located at 1.84 Å (1.91 Å) for TPA (DPNA)) and decreases to intersect with S0 at 2.26 Å for TPA and 2.43 Å for DPNA. PESs of the other two excited states S2 and S3 are high in energy. In addition, they do not convey any physically significant event along C–N coordinate and therefore, they are not considered for further analysis.

Two important observations need to be addressed here. The presence of inflection point in TPA and DPNA can be seen from the examination of both S0 and S1 states. Near this point, both S0 and S1 surfaces look like inverted cones placed over the tip of each other. At this inflection point, the difference in the energies of S0 and S1 for TPA is almost close to zero, which leads to conical intersection (CI). In case of DPNA, inclusion of NEVPT2 correction still reduces the energy difference to 0.35 eV. This energy difference between S0 and S1 is small enough for the electron to jump from one state to another. A clearer graph of the CI and dissociation limit for both molecules in kcal mol⁻¹ is given in ESI.† Once S1(I) is reached, both the molecules may revert to the ground state. Particularly, TPA has higher probability to relax back to ground state than DPNA, since it has the lowest energy gap between S0 and S1 states. It is also possible that the molecule can reach the dissociation point D, where the ground and first triplet states are degenerate. This indicates that at dissociation limit, the fragments have both ionic and radical nature.

The presence of transition state in S1 surface determines whether the molecule can reach CI. While the activation energies are comparatively lower than the thermal reaction barriers, the number of molecules that cross this barrier will be very few since most of the molecules undergo other competitive processes such as emission of light or deactivation through vibrational coupling. Also, after relaxing to S1(E), most of the molecules in excitonic form can occupy the lowest vibrational state and a smaller number of molecules are populated in high energy states at room temperature. These molecules can only attain favourable energy along the reaction mode by collision with other nearby molecules, which is dependent on the lifetime of the excited states and vibrational coupling. Since the molecules in the solid state contain weaker phonon coupling than those in the solution phase, it can be safely assumed that the exciton formation at the interface of OLEDs has less possibility to reach CI. These molecules can reach CI only if they are vibrationally excited, which is the case when S1 is formed by the internal conversion from S2 or higher electronic excited states. The transition from S2 to S1 occurs by the coupling between the lowest vibrational state of S2 and the highest vibrational state of S1 and results in the formation of vibrationally excited first singlet state. Such configurations allow the possibility for molecules to gain enough energy to cross the barrier height and reach CI. Therefore, from relaxed PES scans, it can be argued that direct excitation with light to higher energy states provides more possibility for molecular degradation rather than exciton formation through other methods.

2. Intra-molecular reactions of TPA

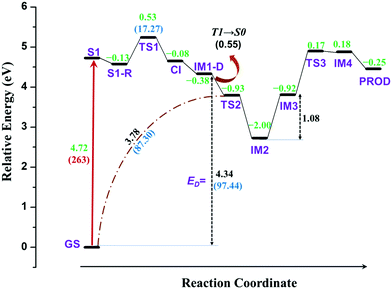
PES, discussed in the previous section, provides conclusive evidence that TPA undergoes dissociation of C–N bond through a conical intersection between first excited singlet and ground states. However, it does not give any clue about how cyclization occurs in such molecules. The dissociated fragments are triplet in nature with each unpaired electron residing on different fragments, which can react with neighbouring molecules to produce a wide array of products in accordance with a previous experimental report.⁴⁵ However, there is still a question that remains to be answered: Would the dissociated fragments react with each other to form intra-molecular rearranged products?

To answer this question, the reaction was further carried out from the dissociated molecular fragments in triplet state. The overall reaction path is schematically depicted in Fig. 3. The complete energy profile of intra-molecular reactions of TPA after excitation is presented in Fig. 4.

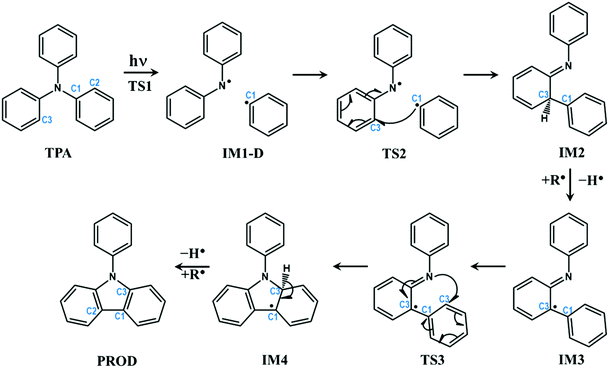Fig. 3 Schematic representation of intra-molecular reactions occurring in TPA-based systems after excitation. The carbon atoms undergoing changes are highlighted with numbering.

Fig. 4 Complete reaction energy profile of TPA after excitation obtained at SS-CAS(14,13)(SMD)/NEVPT2/cc-pVTZ//SS-CAS(14,13)/cc-pVTZ level of theory with methanol as solvent. The values in green represent the relative energy in eV of all the structures with respect to S1. The values in black depict the difference in energy in eV between consecutive structures, as indicated in the figure. The values in blue denote the energy in kcal mol⁻¹ for the corresponding energy in eV. The values in red indicate the excitation wavelength in nm.

The profile completely displays the events that occur after the excitation of the molecule. All structures including the transition states were optimized and the energies were corrected for dynamic correlation. The calculations were carried out with SMD solvation model with methanol as solvent. The optimized geometries corresponding to each structure with structural parameters are given in ESI† (S3). The electron density isosurfaces of HOMO and LUMO of important structures and transition states are depicted in ESI† (S5). Initially, TPA is directly excited to the S1 state with energy equivalent to 263 nm (4.72 eV). Subsequently, the molecule relaxes to S1-R, and the energy is 0.13 eV lower than that of S1. It can be observed from ESI† (Fig. S3) that the bond lengths of three C–N bonds differ. One of the bonds is shortened to 1.34 Å and other two are elongated to ≈1.45 Å. This indicates that these bonds are weaker and prone to dissociation. Hence, an attempt to identify the transition state was carried out in the S1 state, which yielded TS1. As discussed in the previous section, S1-R must be vibrationally excited to reach the transition state TS1, which is 17.27 kcal mol⁻¹ higher in energy than S1-R. The geometrical parameters of TS1 reveal that the C1–N bond starts to break at 1.73 Å. Then, TS1 leads directly to CI, which lies below S1 by 0.08 eV; the distance between the two fragments is 2.38 Å. The molecule then dissociates completely at IM1-D, where the two fragments are 3.73 Å apart. The geometry of IM1-D was optimized using CASSCF with state averaging of both S0 and T1 states since both are nearly degenerate at this point. The geometry at IM1-D is energetically lower than S1 by 0.38 eV, which indicates that the formation of IM1-D is thermodynamically favourable. Another significant observation from Fig. 4 is that IM1-D exhibits 97.44 kcal mol⁻¹ higher energy than GS, which represents the dissociation energy of TPA to form diphenylamino and phenyl radicals. The accuracy of this reported energy is dependent on the inclusion of correlation energies at GS, which conversely relies on the span of active space used for CASSCF calculation. However, CASSCF accurately describes the electronic state at dissociation due to the presence of higher static correlation. On the other hand, DFT predicts the correlation energies at GS with good accuracy and fails at dissociation limit. Therefore, CASSCF/NEVPT2 with proper active space provides more accurate dissociation energy as compared to DFT. Also, IM1-D has more radical nature than ionic nature due to the dominance of triplet state, which is observed from the occupation numbers of HOMO and LUMO orbitals (1.005 and 0.999, respectively). Also, the spin matrix indicates the presence of positive and significantly larger spin values (≈0.5) in both the orbitals.

After dissociation of the molecule, the fragments can migrate to nearby sites and react with them. However, there is a possibility that the fragments react with themselves to give new products. To explore this, the reaction was further carried out by allowing the phenyl radical to react with phenyl groups of another fragment to form a C–C bond. The carbon atom represented as C2 in Fig. 3 is nearest to the phenyl radical. The radical attack occurs viaTS2 with C1–C2 bond distance of 2.17 Å. TS2 lies below S1 and IM1-D by about 0.93 and 0.55 eV, respectively. An interesting observation is that TS2 is singlet in nature with energy gap of 1.36 eV between singlet and triplet states, indicating that IM-D is not the reactant for TS2. The precursor of TS2 is then optimized and it is found to be GS, implying that TS2 is the transition state for C1–N bond breaking and C1–C2 bond formation from GS in a concerted step with barrier height of 87.3 kcal mol⁻¹. Such a large barrier prohibits the molecule from undergoing dissociative re-arrangement. However, excitation of the molecule opens the channel that directly leads to the formation of TS2 and paves the way for the reaction. In addition, TS2 provides a path for the molecule to return to GS and avoid degradation. Also, the formation of TS2 from IM1-D is spin-forbidden as it is T1 → S0 interconversion and therefore could be the rate determining step for the overall reaction.

TS2 directly enables the formation of IM2, which is lower than S1 by 2.00 eV, and IM2 is the most stable intermediate when compared to those of all steps. Here, an imine and saturated carbon (C2) are formed with C=N length of 1.37 Å. The backward barrier height for IM2 is 1.07 eV (24.67 kcal mol⁻¹), which implies that it can revert to GS through TS2 at device operational conditions and it also avoids degradation. IM2 is thermodynamically stable and has less propensity to undergo further reaction. However, in the presence of phenyl and diphenylamino radicals from nearby molecules, IM2 can lose its H-atom, as a radical, from C2 to form IM3. The resulting radical is near a tertiary carbon; it conjugates with nearby C=N and stabilizes the structure. Although, IM3 is less stable than IM2 by about 1.08 eV (24.90 kcal mol⁻¹), it is still favourable at room temperature.

The delocalization of the radical over C=N results in the activation of nitrogen (C˙–C=N ↔ C=C–N˙) and leads to the subsequent attack of the same over the phenyl ring, as shown in Fig. 3. This results in the transition state TS3, which is 1.09 eV higher than IM3 with N–C3 distance of 1.98 Å. This is a cyclization reaction and facilitates the formation of a five-membered ring structure IM4 with a radical centre at C1. IM4 is less stable than IM3 by 1.1 eV due to steric hindrance in the cyclic system. After the formation of IM4, it can either go back to more stable IM3 or encounter nearby radicals and undergo radical abstraction reaction from C1. The abstraction can lead to the formation of a product (PROD), which is well-known as 9-phenyl carbazole. The formation of PROD is exothermic by about 0.07 eV due to the restoration of the π-conjugated system.

3. Intra-molecular reactions of DPNA

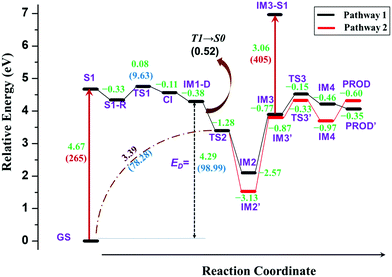
In the previous section, the degradation of TPA was explained in detail. The substitution of TPA at any phenyl groups will lead to similar dissociation channels with different energetics. However, excited state dissociation of DPNA was also studied to answer the following questions: (i) How does naphthyl fragment behave with reference to phenyl radical? (ii) How does a fused ring system alter the CI band gap? (iii) Could the extension of the ring system change the reaction pathway and result in the formation of different products?

A previous experimental study⁴⁹ has shown that DPNA-related systems can end up with six-membered cyclic products compared to a five-membered one. In this study, an attempt has been made to understand the unusual behaviour of the degradation channel of DPNA. Two possible mechanisms (pathways 1 and 2) are arrived at based on the calculations carried out on the scheme, which are presented in Fig. 5 and 6.

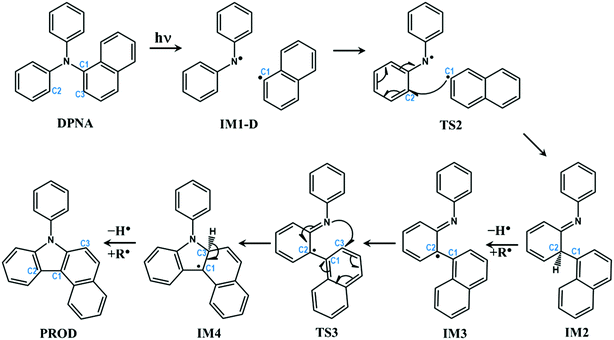Fig. 5 Schematic representation of intra-molecular reactions occurring in DPNA-based systems after excitation (pathway 1). The carbon atoms undergoing changes are highlighted with numbering.

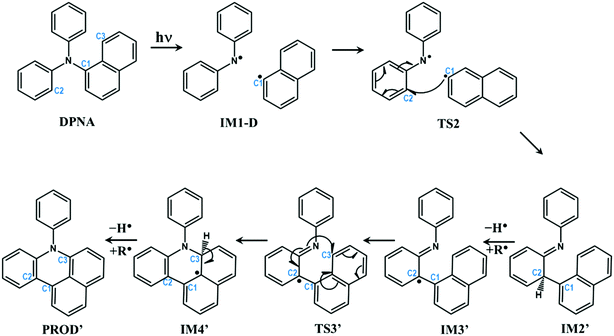Fig. 6 Schematic representation of intra-molecular reactions occurring in DPNA-based systems after excitation (pathway 2). The carbon atoms undergoing changes are highlighted with numbering.

The complete energy profiles obtained for the two mechanisms are shown in Fig. 7.

Fig. 7 Complete reaction energy profile of DPNA after excitation obtained at SS-CAS(12,11)(SMD)/NEVPT2/cc-pVTZ//SS-CAS(12,11)/cc-pVTZ level of theory with methanol as solvent. The values in green represent the relative energy in eV of each structure with respect to S1. The values in black depict the difference in energy in eV between consecutive structures as indicated in the figure. The values in blue denote the energy in kcal mol⁻¹ for the corresponding energy in eV. The values in red indicate the excitation wavelength in nm.

The optimized geometries corresponding to Fig. 5 and 6 with important geometrical parameters are shown in ESI† (S4). The electron density isosurfaces of HOMO and LUMO for important structures in the dissociation channel and transition states are given in ESI† (S6). The mechanism represented in Fig. 5 is similar to that of TPA and hence is not explained in detail. There are no significant differences in the geometrical parameters along the reaction coordinate in the mechanistic pathways of TPA and DPNA. Nevertheless, the energetics of pathway 1 is different from that of TPA. When compared to the result for TPA, the relaxed geometry of DPNA (S1-R) in the first excited state is more stable by 0.33 eV with respect to S1 due to higher delocalization. Also, the geometry of S1-R shows that the naphthyl ring is away from nitrogen by 1.49 Å, which is the longest bond. Therefore, the search for transition state was carried out along N–C1, which yields TS1. It is stabilized by delocalization and results in lower barrier height of 9.6 kcal mol⁻¹. This indicates that increasing the delocalization reduces activation energy, which is attainable at room temperature. CI for DPNA is 0.11 eV lower than S1 and yields IM1-D, which is 4.29 eV (98.99 kcal mol⁻¹) higher than GS. The formation of TS2 from IM1-D is more favoured for DPNA in contrast to TPA since it exhibits energy that is 1.28 eV lower than that of IM1-D. Also, TS2 is 3.39 eV higher than GS, indicating that it is more stable compared to TPA. As noted in the previous section, TS2 facilitates the fragments to revert to the ground state. The intermediate IM2 is more stable by 2.57 eV with respect to S1 and it is more inert compared to TPA. The abstraction of hydrogen from C2 position results in IM3, which is less stable by 1.7 eV (39.2 kcal mol⁻¹) than IM2. This finding indicates that the conversion is thermodynamically less feasible at room temperature. IM3 leads to TS3 with activation energy of 0.62 eV (14.29 kcal mol⁻¹), which is lower by 11.1 kcal mol⁻¹ than that of TPA. Another interesting feature about TS3 is that the first singlet state lies at 0.64 eV above the ground state, suggesting a possible conical intersection at the transition state (similar to cis to trans isomerization of azobenzene). TS3 yields IM4, which is 0.46 eV lower than S1 and is also more stable than TPA. Finally, the abstraction of hydrogen occurs at C3; this results in product (PROD), which is 9-naphthyl carbazole. PROD is more stable compared to its TPA counterpart due to increased delocalization. Still, compared to GS, it is 4.07 eV less stable and therefore, such product formation is only possible through excitation.

Pathway 2 is indistinguishable from pathway 1 until TS2 and then, it deviates since the separated naphthyl fragment can have two possible configurations with the fused ring present above C1–C2–N plane and vice versa. In other words, the fused ring is present trans to the hydrogen at C2 in pathway 2. This leads to IM2′, which is 0.56 eV (12.91 kcal mol⁻¹) lower than IM2. Next step is the abstraction of hydrogen from C2 position to form IM3′, which is more stable than IM3 by 0.1 eV. At this point, C3 carbon in the naphthyl ring, as represented in Fig. 6, is nearer to nitrogen (3.40 Å) than the C3 carbon involved in pathway 1. Therefore, the radical attack of nitrogen occurs over C3 carbon through transition state TS3′. This transition state is lower in energy than the same in pathway 1 by 0.18 eV. In TS3′, the C3–N bond distance is 2.02 Å and it does not have any low lying excited states as compared to pathway 1. TS3′ yields IM4′, where a fused six-membered ring is formed between the naphthyl and phenyl ring of DPNA. IM4′ is lower in energy than IM4 by 0.51 eV and has saturated carbon at C3 position. The hydrogen from C3 carbon is abstracted in the next step to give the product PROD′, which is less stable than PROD by 0.25 eV. This could be due to the presence of pyrrolic-type resonance structures in PROD, which are absent in PROD′. This final product is similar to the fused six-membered ring system observed by Bell et al.⁴⁹

Conclusion

The CASSCF/NEVPT2 study on the excited state degradation mechanisms of TPA and DPNA has been carried out to understand the degradation of TAA with TPA and DPNA as model systems. The important findings obtained from this study are as follows:

1. The observed dissociation of TAAs can be explained by the presence of conical intersection between the first excited singlet state and ground state (in both TPA and DPNA, along C–N coordinate), which acts as the channel for the fragmentation of molecules to undergo further reactions.

2. Once the molecule reaches CI, it can either revert to the equilibrium geometry or reach the dissociation point depending on the momentum of the molecule at CI. However, the average lifetime of the dissociated fragments determines how many molecules will undergo further cyclization reaction, since the next step involves less favourable triplet to singlet conversion.

3. Even with the presence of CI, the quantum yield of the dissociated products is low. This is explained by the presence of transition state in first excited singlet state. The barrier height of the transition state determines the probability for the molecule to reach CI. Also, comparison of the activation energies of TPA and DPNA reveals that increasing the conjugation of the phenyl ring leads to reduction in activation energy and results in easier degradation of the material. This conclusion is supported by the experimental evidence, wherein many products are formed with naphthyl radicals.

4. Since the barrier height of TS1 decreases with increase in conjugation, materials with extended delocalization can easily pass through the barrier even in the vibrational ground state. Avoiding such modifications can lead to a long life of TAA-based materials. However, this also indicates that reduced barrier height is favourable for the synthesis of cyclized products from TAAs.

5. Both IM1-D and TS2 act as direct channels for the molecule to return to the starting structure. Controlling the energetics of these two structures through chemical modification helps reduce the degradation of the material. Once the molecule reaches IM2, it has very less probability of returning to ground state.

6. After the absorption of light, the molecule is fragmented after crossing CI. These fragments can abstract hydrogen from nearby molecules or form intra-molecular products. However, it should be noted that the hydrogens of neutral/ionic TPA are bonded to sp² carbon atoms and therefore not available for abstraction reactions. Hence, such abstraction can happen from the intra-molecular products, which contain hydrogen attached to sp³ carbon atom. Conclusively, the formation of both types of products occurs simultaneously and both can be observed in the degraded material. Without the formation of cyclized products, there is less possibility for the fragmentation of material.

In summary, the present study is one among few reported on the degradation of OLED materials. It is evident from the above findings that there is a necessity to model OLED materials from the view point of probability of undergoing degradation in excited state and other means. The findings open a new avenue for better understanding OLED degradation. They also provide a hint for an easy route for the synthesis of cyclic amines, such as carbazoles, from TAA. Such possibilities need to be explored in future studies for possible application in organic synthesis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author J. Vijaya Sundar acknowledges Indian Institute of Technology Madras (IITM), Chennai for providing Institute Post-Doctoral Fellowship (IPDF) and computational facility.

References

1. M. Grätzel, Solar Energy Conversion by Dye-Sensitized Photovoltaic Cells, Inorg. Chem., 2005, 44, 6841–6851.
2. D. Gust, T. A. Moore and A. L. Moore, Mimicking Photosynthetic Solar Energy Transduction, Acc. Chem. Res., 2001, 34, 40–48.
3. P. V. Kamat, Meeting the Clean Energy Demand: Nanostructure Architectures for Solar Energy Conversion, J. Phys. Chem. C, 2007, 111, 2834–2860.
4. N. L. Panwar, S. C. Kaushik and S. Kothari, Role of renewable energy sources in environmental protection: a review, Renewable Sustainable Energy Rev., 2011, 15, 1513–1524.
5. A. Steinfeld, Solar thermochemical production of hydrogen—a review, Sol. Energy, 2005, 78, 603–615.
6. M. M. Farid, A. M. Khudhair, S. A. K. Razack and S. Al-Hallaj, A review on phase change energy storage: materials and applications, Energy Convers. Manage., 2004, 45, 1597–1615.
7. V. Balzani, A. Credi and M. Venturi, Photochemical Conversion of Solar Energy, ChemSusChem, 2008, 1, 26–58.
8. N. Yeh and J.-P. Chung, High-brightness LEDs-energy efficient lighting sources and their potential in indoor plant cultivation, Renewable Sustainable Energy Rev., 2009, 13, 2175–2180.
9. A. De Almeida, B. Santos, B. Paolo and M. Quicheron, Solid state lighting review – potential and challenges in Europe, Renewable Sustainable Energy Rev., 2014, 34, 30–48.
10. E. F. Schubert, Light-emitting diodes, E. Fred Schubert, 2018.
11. K. Müllen and U. Scherf, Organic light emitting devices: synthesis, properties and applications, John Wiley & Sons, 2006.
12. A. Mishra, M. K. R. Fischer and P. Bäuerle, Metal-free organic dyes for dye-sensitized solar cells: from structure: property relationships to design rules, Angew. Chem. Int. Ed., 2009, 48, 2474–2499.
13. H. Tian, X. Yang, R. Chen, R. Zhang, A. Hagfeldt and L. Sun, Effect of different dye baths and dye-structures on the performance of dye-sensitized solar cells based on triphenylamine dyes, J. Phys. Chem. C, 2008, 112, 11023–11033.
14. J. Preat, D. Jacquemin and E. A. Perpète, Design of new triphenylamine-sensitized solar cells: a theoretical approach, Environ. Sci. Technol., 2010, 44, 5666–5671.
15. P. Agarwala and D. Kabra, A review on triphenylamine (TPA) based organic hole transport materials (HTMs) for dye sensitized solar cells (DSSCs) and perovskite solar cells (PSCs): evolution and molecular engineering, J. Mater. Chem. A, 2017, 5, 1348–1373.
16. A. Mahmood, Triphenylamine based dyes for dye sensitized solar cells: a review, Sol. Energy, 2016, 123, 127–144.
17. G. Li, K.-J. Jiang, Y.-F. Li, S.-L. Li and L.-M. Yang, Efficient structural modification of triphenylamine-based organic dyes for dye-sensitized solar cells, J. Phys. Chem. C, 2008, 112, 11591–11599.
18. J. Huang, Y. Jiang, J. Yang, R. Tang, N. Xie, Q. Li, H. S. Kwok, B. Z. Tang and Z. Li, Construction of efficient blue AIE emitters with triphenylamine and TPE moieties for non-doped OLEDs, J. Mater. Chem. C, 2014, 2, 2028–2036.
19. N. N. Ghosh, A. Chakraborty, S. Pal, A. Pramanik and P. Sarkar, Modulating triphenylamine-based organic dyes for their potential application in dye-sensitized solar cells: a first principle theoretical study, Phys. Chem. Chem. Phys., 2014, 16, 25280–25287.
20. H. H. Fong, K. C. Lun and S. K. So, Hole transports in molecularly doped triphenylamine derivative, Chem. Phys. Lett., 2002, 353, 407–413.
21. C. Ego, A. C. Grimsdale, F. Uckert, G. Yu, G. Srdanov and K. Müllen, Triphenylamine-Substituted Polyfluorenema Stable Blue-Emitter with Improved Charge Injection for Light-Emitting Diodes, Adv. Mater., 2002, 14, 809–811.
22. P. Cias, C. Slugovc and G. Gescheidt, Hole transport in triphenylamine based OLED devices: from theoretical modeling to properties prediction, J. Phys. Chem. A, 2011, 115, 14519–14525.
23. N. Koumura, Z.-S. Wang, M. Miyashita, Y. Uemura, H. Sekiguchi, Y. Cui, A. Mori, S. Mori and K. Hara, Substituted carbazole dyes for efficient molecular photovoltaics: long electron lifetime and high open circuit voltage performance, J. Mater. Chem., 2009, 19, 4829–4836.
24. D. Kim, J. K. Lee, S. O. Kang and J. Ko, Molecular engineering of organic dyes containing N-aryl carbazole moiety for solar cell, Tetrahedron, 2007, 63, 1913–1922.
25. H. Jiang, J. Sun and J. Zhang, A review on synthesis of carbazole-based chromophores as organic light-emitting materials, Curr. Org. Chem., 2012, 16, 2014–2025.
26. K. Brunner, A. van Dijken, H. Börner, J. J. A. M. Bastiaansen, N. M. M. Kiggen and B. M. W. Langeveld, Carbazole compounds as host materials for triplet emitters in organic light-emitting diodes: tuning the HOMO level without influencing the triplet energy in small molecules, J. Am. Chem. Soc., 2004, 126, 6035–6042.
27. C. Zafer, M. Kus, G. Turkmen, H. Dincalp, S. Demic, B. Kuban, Y. Teoman and S. Icli, New perylene derivative dyes for dye-sensitized solar cells, Sol. Energy Mater. Sol. Cells, 2007, 91, 427–431.
28. Y. Shibano, T. Umeyama, Y. Matano and H. Imahori, Electron-donating perylene tetracarboxylic acids for dye-sensitized solar cells, Org. Lett., 2007, 9, 1971–1974.
29. C. Li, J. Yum, S. Moon, A. Herrmann, F. Eickemeyer, N. G. Pschirer, P. Erk, J. Schöneboom, K. Müllen and M. Grätzel, An improved perylene sensitizer for solar cell applications, ChemSusChem, 2008, 1, 615–618.
30. S. Ferrere and B. A. Gregg, New perylenes for dye sensitization of TiO₂, New J. Chem., 2002, 26, 1155–1160.
31. Y. Zhang, M. Sims, S. Li and H. Aziz, Triplet-induced degradation: an important consideration in the design of solution-processed hole injection materials for organic light-emitting devices, Org. Electron., 2017, 48, 217–222.
32. S. Schmidbauer, A. Hohenleutner and B. König, Chemical Degradation in Organic Light-Emitting Devices: Mechanisms and Implications for the Design of New Materials, Adv. Mater., 2013, 25, 2114–2129.
33. G. Niu, X. Guo and L. Wang, Review of recent progress in chemical stability of perovskite solar cells, J. Mater. Chem. A, 2015, 3, 8970–8980.
34. M. Jørgensen, K. Norrman and F. C. Krebs, Stability/degradation of polymer solar cells, Sol. Energy Mater. Sol. Cells, 2008, 92, 686–714.
35. A. Hinsch, J. M. Kroon, R. Kern, I. Uhlendorf, J. Holzbock, A. Meyer and J. Ferber, Long-term stability of dye-sensitised solar cells, Prog. Photovoltaics Res. Appl., 2001, 9, 425–438.
36. S. Winter, S. Reineke, K. Walzer and K. Leo, Organic Optoelectronics and Photonics III, International Society for Optics and Photonics, 2008, vol. 6999, p. 69992N.
37. I. R. de Moraes, S. Scholz, B. Lüssem and K. Leo, Analysis of chemical degradation mechanism within sky blue phosphorescent organic light emitting diodes by laser-desorption/ionization time-of-flight mass spectrometry, Org. Electron., 2011, 12, 341–347.
38. S. W. Culligan, A. Chen, J. U. Wallace, K. P. Klubek, C. W. Tang and S. H. Chen, Effect of Hole Mobility Through Emissive Layer on Temporal Stability of Blue Organic Light-Emitting Diodes, Adv. Funct. Mater., 2006, 16, 1481–1487.
39. S.-C. Dong, L. Xu and C. W. Tang, Chemical degradation mechanism of TAPC as hole transport layer in blue phosphorescent OLED, Org. Electron., 2017, 42, 379–386.
40. Q. Wang and H. Aziz, Degradation of organic/organic interfaces in organic light-emitting devices due to polaron–exciton interactions, ACS Appl. Mater. Interfaces, 2013, 5, 8733–8739.
41. S. Scholz, D. Kondakov, B. Lüssem and K. Leo, Degradation mechanisms and reactions in organic light-emitting devices, Chem. Rev., 2015, 115, 8449–8503.
42. D. Y. Kondakov, T. D. Pawlik, W. F. Nichols and W. C. Lenhart, Free-radical pathways in operational degradation of OLEDs, J. Soc. Inf. Disp., 2008, 16, 37–46.
43. D. Y. Kondakov, W. C. Lenhart and W. F. Nichols, Operational degradation of organic light-emitting diodes: mechanism and identification of chemical products, J. Appl. Phys., 2007, 101, 24512.
44. D. Y. Kondakov, Role of chemical reactions of arylamine hole transport materials in operational degradation of organic light-emitting diodes, J. Appl. Phys., 2008, 104, 84520.
45. V. Sivasubramaniam, F. Brodkorb, S. Hanning, O. Buttler, H. P. Loebl, V. van Elsbergen, H. Boerner, U. Scherf and M. Kreyenschmidt, Degradation of HTL layers during device operation in PhOLEDs, Solid State Sci., 2009, 11, 1933–1940.
46. T. Zhu and T. Van Voorhis, Charge Recombination in Phosphorescent Organic Light-Emitting Diode Host–Guest Systems through QM/MM Simulations, J. Phys. Chem. C, 2016, 120, 19987–19994.
47. M. Hong, M. K. Ravva, P. Winget and J.-L. Bredas, Effect of substituents on the electronic structure and degradation process in carbazole derivatives for blue OLED host materials, Chem. Mater., 2016, 28, 5791–5798.
48. A. Y. Freidzon, A. A. Safonov, A. A. Bagaturyants, D. N. Krasikov, B. V. Potapkin, A. A. Osipov, A. V. Yakubovich and O. Kwon, Predicting the Operational Stability of Phosphorescent OLED Host Molecules from First Principles: a Case Study, J. Phys. Chem. C, 2017, 121, 22422–22433.
49. B. M. Bell, M. B. Clark Jr, D. D. Devore, T. S. De Vries, R. D. Froese, K. C. Gray, D. H. K. Jackson, T. F. Kuech, H.-Y. Na and K. L. Kearns, Degradation of hole transport materials via exciton-driven cyclization, ACS Appl. Mater. Interfaces, 2017, 9, 13369–13379.
50. P. J. Knowles and H.-J. Werner, An efficient method for the evaluation of coupling coefficients in configuration interaction calculations, Chem. Phys. Lett., 1988, 145, 514–522.
51. M. A. Robb and U. Niazi, The unitary group approach in configuration interaction (CI) methods, Comput. Phys. Rep., 1984, 1, 127–236.
52. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The multi-state CASPT2 method, Chem. Phys. Lett., 1998, 288, 299–306.
53. A. I. Krylov, Equation-of-Motion Coupled-Cluster Methods for Open-Shell and Electronically Excited Species: the Hitchhiker's Guide to Fock Space, Annu. Rev. Phys. Chem., 2008, 59, 433–462.
54. R. J. Bartlett, Coupled-cluster theory and its equation-of-motion extensions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 126–138.
55. M. Ben-Nun, J. Quenneville and T. J. Martínez, Ab initio Multiple Spawning:  Photochemistry from First Principles Quantum Molecular Dynamics, J. Phys. Chem. A, 2000, 104, 5161–5175.
56. N. Minezawa and M. S. Gordon, Optimizing Conical Intersections by Spin-Flip Density Functional Theory: Application to Ethylene, J. Phys. Chem. A, 2009, 113, 12749–12753.
57. Y. Shao, M. Head-Gordon and A. I. Krylov, The spin-flip approach within time-dependent density functional theory: theory and applications to diradicals, J. Chem. Phys., 2003, 118, 4807–4818.
58. X. Zhang and J. M. Herbert, Analytic derivative couplings for spin-flip configuration interaction singles and spin-flip time-dependent density functional theory, J. Chem. Phys., 2014, 141, 64104.
59. K. A. Peterson and T. H. Dunning Jr, Accurate correlation consistent basis sets for molecular core–valence correlation effects: the second row atoms Al–Ar, and the first row atoms B–Ne revisited, J. Chem. Phys., 2002, 117, 10548–10560.
60. M. Swart and J. G. Snijders, Accuracy of geometries: influence of basis set, exchange–correlation potential, inclusion of core electrons, and relativistic corrections, Theor. Chem. Acc., 2003, 110, 34–41.
61. K. A. Peterson, D. E. Woon and T. H. Dunning, Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H + H₂ → H₂ + H reaction, J. Chem. Phys., 1994, 100, 7410–7415.
62. M. Dallos, H. Lischka, R. Shepard, D. R. Yarkony and P. G. Szalay, Analytic evaluation of nonadiabatic coupling terms at the MR-CI level. II. Minima on the crossing seam: formaldehyde and the photodimerization of ethylene, J. Chem. Phys., 2004, 120, 7330–7339.
63. R. W. A. Havenith, P. R. Taylor, C. Angeli, R. Cimiraglia and K. Ruud, Calibration of the n-electron valence state perturbation theory approach, J. Chem. Phys., 2004, 120, 4619–4625.
64. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.

---

Footnote

† Electronic supplementary information (ESI) available: Structures of optimized geometries reported in this work with important geometrical parameters and contours of orbitals in active space are given. The HOMO and LUMO pictures of important structures taking part in the reaction are also provided. The PES in kcal mol⁻¹ for both molecules around the conical intersection is also provided. See DOI: 10.1039/c8cp06314a

---