Ab initio quantum-chemical computations of the absorption cross sections of HgX2 and HgXY (X, Y = Cl, Br, and I): molecules of interest in the Earth's atmosphere†
Sebastian P.
Sitkiewicz
 a,
Daniel
Rivero
b,
Josep M.
Oliva-Enrich
b,
Alfonso
Saiz-Lopez
b and
Daniel
Roca-Sanjuán
a,
Daniel
Rivero
b,
Josep M.
Oliva-Enrich
b,
Alfonso
Saiz-Lopez
b and
Daniel
Roca-Sanjuán
 *c
*c
aKimika Fakultatea, Euskal Herriko Unibertsitatea UPV/EHU and Donostia International Physics Center (DIPC), P.K. 1072, 20080 Donostia, Euskadi, Spain
bDepartment of Atmospheric Chemistry and Climate, Institute of Physical Chemistry Rocasolano, CSIC, 28006 Madrid, Spain
cInstitut de Ciència Molecular, Universitat de València, P.O. Box 22085, 46071 València, Spain. E-mail: Daniel.Roca@uv.es
First published on 26th November 2018
Abstract
The electronic-structure properties of the low-lying electronic states and the absorption cross sections (σ(E)) of mercury halides HgCl2, HgBr2, HgI2, HgBrCl, HgClI, and HgBrI have been determined within the UV-vis spectrum range (170 nm ≤ λphoton ≤ 600 nm) by means of the DKH3-MS-CASPT2/SO-RASSI quantum-chemical methodology (with the ANO-RCC basis set) and a semi-classical computational strategy based on nuclear sampling for simulating the band shapes. Computed band energies show a good agreement with the available experimental data for HgX2 with errors around 0.1–0.2 eV; theoretical and σ(E) are within the same order of magnitude. For the mixed HgXY compounds, the present computed data allow us to interpret previously proposed absorption bands estimated from the spectra of the parent molecules HgX2 and HgY2, measured in methanol solution. The analyses performed on the excited-state electronic structure and its changes around the Franck–Condon region provide a rationale on the singlet–triplet mixing of the absorption bands and the heavy-atom effect of the Hg compounds. Furthermore, the present benchmark of HgX2 and HgXY absorption σ values together with the previous benchmark of the electronic-structure properties of HgBr2 [see S. P. Sitkiewicz, et al., J. Chem. Phys., 2016, 145, 244304] has been helpful to set up a methodological and computational protocol which shall be used for predicting the atmospheric absorption and photolysis properties of several Hg compounds present in the atmospheric cycle of Hg.
1 Introduction
Due to its volatile nature, much research on mercury (Hg) has over the past two decades focused on its atmospheric dispersal and cycling. Anthropogenic emissions to the atmosphere are essentially in the elemental Hg(0) form which is oxidized to divalent Hg(II),1,2 the reactive form that is deposited to Earth's surface mostly by rain and becomes bioaccumulative species. The harmful effects of mercury on the environment are already well known and can affect our health, animal life, and the ecosystems on Earth, as happened in the human disaster of Minimata (Japan) in 1956. Relevant oxidation products are Hg(II)XY, with X, Y representing halogen atoms or oxygen species such as BrO, O, OH, or NO2. These species are reduced in the atmosphere, which competes with deposition. However, the mechanism of the corresponding process is still poorly understood. Literature is scarce on experimental and theoretical information on the kinetics and thermodynamics of atmospheric mercury oxidative processes, and basically absent in the case of the response to irradiation under atmospheric conditions.3–8 This last aspect is highly relevant since a source of reduction could be via light absorption. In this context, accurate theoretical methods for computing UV-vis absorption spectra and effective σ(E) of mercury derivatives are necessary in order to predict elemental mercury atmospheric processes.Among the Hg(II)XY compounds, mercury halides (which from now on we denote as HgX2 and HgXY, with X, Y = Cl, Br, and I) are probably the systems for which more experimental data have been reported to date regarding electronic-structure and spectroscopic properties. Hence, these systems can be used in the benchmarks of computational strategies to establish accurate approaches with a predictive character for more complicated systems.
So far, for the mercury species of interest in this work, the gas-phase absorption spectra have been experimentally measured for HgCl2, HgBr2, and HgI2.9–12 Their similarities in the visible and near UV part of the energy spectrum are the occurrence of three absorption bands: an initial low-intensity and broad band at low energies (band a), a high-intensity and sharp band at higher energies (band b), and an even sharper band in the close vicinity of band b but at slightly higher energies (band c). These bands are red-shifted upon increasing the atomic number of the halogen atoms in HgX2. According to the four available experimental studies, the energy positions of the band maxima (nm) for HgCl2, HgBr2, and HgI2, in this order, are the following: (i) 202,11 22511/22912/221,9 and 2629/27110 for band a, (ii) 182,11 19811/19712/194,9 and 22511/2199/22510 for band b, and (iii) not reported (out of the range of measured energies),11 18311/183,12 and 20811/2019/20810 for band c.
For the mixed halide compounds – HgBrCl, HgClI, and HgBrI – absorption spectra have been derived from measurements in methanol solutions (not in the gas phase). Griffiths and Anderson calculated the σ(E) data of these systems from the measured spectra of mixed methanol solutions of HgX2 + HgY2, where the HgXY are formed.13,14 We shall use this data for comparisons with the results obtained in our computations. It can be easily seen in the HgXY experimental spectra, reported only in the range 200–340 nm, that low-intensity absorption signals spread over the two a-type bands of the parent molecules HgX2 and HgY2 and a higher-intensity and sharper band appears in between the b-type bands of the parent molecules.13,14
From a theoretical viewpoint, we should emphasize that the study of the excited-state electronic-structure properties of Hg compounds is in general quite complex, especially when spectroscopic accuracy is desired. Firstly, the use of multireference methods is required to correctly describe the multiconfigurational character of the excited states.15,16 Secondly, relativistic effects in molecules with heavy atoms such as Hg and I have to be accounted for – both scalar relativistic effects (through the choice of a proper Hamiltonian and a suitable basis set), and spin–orbit coupling (SOC) (since this type of interaction is also relevant for the excited states and often ground states).16–21 Most of the computational studies on the mercury halides found in the literature were focused on the ground-state electronic structure,19,20,22–25 with some exceptions such as the work of Wadt published in 1980.15 This author determined the electronic-structure of the ground and low-lying excited states of HgCl2 and HgBr2 on the basis of a moderate-size configuration interaction (CI) method, named POL(1) CI, and a double-ζ plus polarization quality basis set with effective core potentials (ECPs). According to his calculations, bands a, b, and c were assigned to the transition from the 11Σ+g ground state to the 11Πu, 11Σ+u, and 21Σ+u singlet states, respectively. However, in his work the SOC effect was not considered and the scalar relativistic effects were accounted for with approximated ECPs. Recently, we carried out an extensive theoretical analysis on the electronic states of IBr and HgBr2 in order to establish a useful and highly accurate theoretical methodology for predicting vertical absorption energies (ΔE) and associated oscillator strengths (f) of the Hg-based systems.16 On the basis of the results, we confirmed some of Wadt's predictions. In addition, we concluded that, for HgBr2, band a has a complex nature, originating from several singlet–singlet and singlet–triplet transitions to low-lying coupled Σ and Π states. Band b corresponds to a pure singlet–singlet transition to the 11Σ+u state. Meanwhile, band c occurs due to the transition to the 13Σ−u0+ state (contrary to Wadt's computations, in which such a transition was spin-symmetry forbidden).15,16
In the present work, we have used the previously established16 high-level multireference multiconfigurational methodology – complete-active-space self-consistent field/multi-state complete-active-space second-order perturbation theory/spin–orbit restricted-active-space state-interaction (CASSCF/MS-CASPT2/SO-RASSI) – for the electronic-structure computations of the HgXY halides with two objectives. Firstly, the study aims to characterize and interpret the red shifts of the transition bands upon changing the X atom to a heavier halogen atom and the spectral modifications arising for the asymmetric structures (with distinct X and Y halogen atoms) as compared to the σ(E) of the symmetric HgX2 molecules. Secondly, we have gone one step further from the conventional determination of theoretical absorption properties, based on ΔE and associated f at one (equilibrium) geometry from the Franck–Condon region, and we have computed the absorption-spectra band shapes of the symmetric and asymmetric HgXY molecules in the UV-vis part of the energy spectrum (up to 170 nm) with relevance to atmospheric chemistry. In order to achieve this goal, we have used a nuclear-ensemble computational approach able to predict, with relatively good accuracy, absorption spectra with physically-meaningful band shapes, as proposed by Barbatti and co-workers.26–28 The same computational methodology has been recently used in other work,29 extending the study to other Hg(II)XY species, which has evaluated the impact that efficient atmospheric photoreduction of Hg(II) has over the global Hg cycle. This study together with the present one allows us to conclude that gaseous Hg(II) photolysis can dominate global atmospheric mercury reduction and lead to substantial changes in atmospheric mercury lifetime, transport, and deposition.
2 Computational details
In the first part of this section, details are given on the used CASSCF/MS-CASPT2/SO-RASSI30–32 quantum-chemical methodology for computing the ΔE, which are also named vertical excitation energies, and f between electronic states of HgX2 and HgXY. In the second part, the nuclear-ensemble computational approach for determining σ(E) is described.2.1 Quantum-chemical methodology
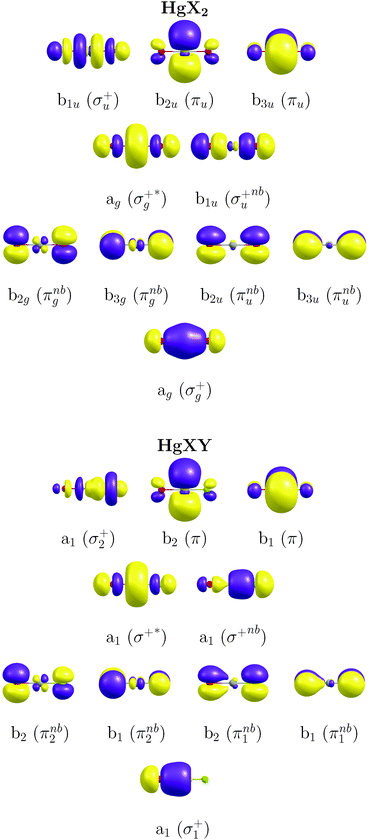
The CASSCF/MS-CASPT231,33–35/SO-RASSI36,37 methodology with the third-order Douglas–Kroll and Hess (DKH3) Hamiltonian38–41 and the atomic-natural-orbital relativistic-correlation-consistent (ANO-RCC) basis set of valence quadruple-ζ plus polarization quality (hereafter, ANO-RCC-VQZP)42 have been used in the present study as calibrated in our previous work on IBr and HgBr2.16 Highly accurate ΔE and f were obtained with this methodology showing a good agreement with the experimental values with errors around 0.2 eV. We summarize here the details of the methodology and describe the adaptation done for the presently-studied molecules. Regarding the active-space selection, in our previous work we already discussed the proper CAS for these systems (necessary for the description of transitions in the energetic range of interest).16 In this study we have chosen the (12,10) active space corresponding to 12 active electrons distributed over 10 natural orbitals (NOs) of the following character: σ/σ*-type (Hg 6s ± Cl 3pz/Br 4pz/I 5pz and Hg 6pz ± Cl 3pz/Br 4pz/I 5pz), σnb-type (Cl 3pz/Br 4pz/I 5pz), πnb-type (Cl 3px/y/Br 4px/y/I 5px/y) and π (Hg 6px/y) (see Fig. 1; note the additional parity symmetry in the case of HgX2 systems and also note the asymmetric effects in AO contributions for mixed HgXY molecules). The σ*-type orbital related to the Hg 6pz ± Cl 3pz/Br 4pz/I 5pz atomic orbital contributions was included in the active space, although it was not significantly occupied in any of the excited-state wavefunctions. Two last NOs of non-bonding character, consisting of Br 4dxz/yz + Br 4dxz/yz AOs and used in our first benchmark study with CAS(12,12),16 were shown to be not necessary for the determination of the absorption spectra and were therefore omitted in the present computations.The previous benchmark study16 included also comparisons of the suitability of all-electron basis sets (ANO-RCC-VQZP42 and Sapporo-DKH3-QZP43,44) against basis sets with electron-core potentials (Def2QZVP45 and aug-cc-pVQZ-PP46–49), the number of state-average (SA) roots in the SA-CASSCF wavefunction optimizations, the ionization potential electron affinity (IPEA)50 parameter of the CASPT2 method and the single- and multi-state approaches of this method. Furthermore, the role of SOC in the computed vertical transitions was also analyzed. The basis sets with ECPs (the first two) provided poor descriptions in some cases with strong SOC, and therefore they are not adequate for an accurate determination of the electronic transitions in the systems studied here. The ANO-RCC basis set was shown to be particularly efficient due to its general contraction scheme, which makes it more flexible in the characterization of the excited states. Meanwhile, 8 state-averaged (SA)-CASSCF roots in all the irreducible representations (IrReps) of the D2h point group were found to provide a good description of the electronic states of interest. The IPEA shift of 0.25 a.u. of the CASPT2 method improved the transition energies by 0.2–0.4 eV with respect to the results obtained with the non-modified zeroth-order Hamiltonian of CASPT2. The single- and multi-state approaches of CASPT2 gave rise to basically the same energies, although the latter provided a better description of the relative intensity of the absorption bands in HgBr2. Finally, the benchmark showed that a description based on the spin–orbit (SO) states rather than spin-free (SF) states is mandatory for these halogen/mercury molecular systems since some bands (such as band c) arise as the result of the SOC. All these established parameters have been also employed in the present study for accurately determining ΔE and f in the HgXY molecules. An imaginary shift with a value of 0.2 a.u. was also used to minimize the effect of weakly-interacting intruder states.51 Oscillator strengths (f) were similarly computed as described in the previous work.16 All the electronic-structure computations were carried out using the MOLCAS 8 quantum-chemistry software.52
2.2 Semi-classical spectrum simulations using geometry ensembles
Whereas the main features of a typical UV-Vis spectrum normally come from the electronic transitions from the ground state to the excited states at the Franck–Condon equilibrium geometry, the actual shape of the observed electronic absorption bands originates from more subtle transitions between vibrational states of different electronic states.53,54 For such band-shape determination, detailed information on the vibrational part of the wavefunction corresponding to each of the excited states is required. Some approaches are available to determine the rovibrational patterns of one or a few low-lying electronic states in diatomic and triatomic molecules.55 However, we are interested in a huge number of SO states (see Section 2.1) spanning all the wavelengths of relevance in the atmosphere (170 nm ≤ λphoton ≤ 600 nm), and it must be taken into account that the electronic-structure determinations of the studied mercury compounds require one to account for relativistic effects such as scalar relativity and SOC. In addition, we pursue a common and general approach valid also for molecules in which the number of degrees of freedom do not allow us to determine the full dimensionality of the PES, such as those studied in a related study.29 Therefore, the vibrational states and couplings can only be estimated by using approximate strategies. An adequate computational strategy, which was previously used in other theoretical studies by Barbatti and co-workers and which has been also employed here, is based on generating a representative ensemble of sampled geometries Rk around the ground-state equilibrium structure and combining the computed ΔE and f (obtained separately for each geometry) to build up the bands.26,27,56,57 A semi-classical approach was then used (based on an average of the data obtained from the ground-state geometrical ensemble), which allows to approximate the vibrational structure of the absorption bands. No nuclear wavefunction of the excited electronic states is required and high-level quantum-chemistry methodologies such as CASSCF/MS-CASPT2/SO-RASSI can be used in the electronic-structure calculations, which was a mandatory condition in our study as described above. Furthermore, such methodology allows for the automation of the computations which is of great importance for carrying out the present study and upcoming works on Hg compounds with larger molecular size.Hence, the absorption cross sections (σ(E)) were computed for each photon energy E separately, by using the following equation:26
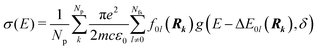 | (1) |
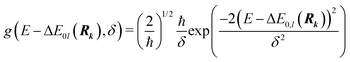 | (2) |
On the energetic scale E, each of the Gaussian functions is centered at the vertical transition energy to a particular l-th exicted state, ΔE0,l(Rk), and δ is the phenomenological broadening. These computations do not take into account the temperature or the refractive index of the medium. Thus, vibrationally cold molecules in the gaseous phase are considered. In the present work, the statistical error of the sampling (δσ(E)) is measured as the standard deviation for the particular sampled photon energy E, in a slightly different manner to the one presented in the study of Crespo-Otero and Barbatti26,27
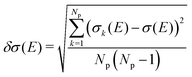 | (3) |
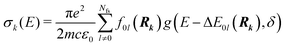 | (4) |
Sampling of the nuclear coordinates Rk was done according to the Wigner distribution58 for the optimized ground spin-free (SF) states and using the corresponding vibrational harmonic frequencies of the normal modes.26,27,59 The optimization and vibrational analysis were carried out numerically, at the same level of theory used in the electronic-structure calculations of the excited states [DKH3-CASPT2(12,10)/ANO-RCC-VQZP] with the MOLCAS 8 program. The sampled geometries Rk were generated with the 1.4 NEWTON-X program,28,60,61 using the obtained information on the equilibrium structures, whereas the calculation of σ(E) was done with an in-house program. At each of the sampled geometries, the MS-CASPT2 computations of ΔE and f were performed with the Cs symmetry constraint on the wavefunction (all three atoms were placed in the XOY plane). For each of the IrRep belonging to the Cs point group, A′ and A′′, we chose Nfs = 10 for the number of SF states in the CASSCF/CASPT2 computations because it includes all relevant SF transitions up to 170 nm. Finally, Np = 100 geometries were used along with a broadening of the Gaussian shape functions of δ = 0.05 eV, adequate for the triatomic systems studied in this work.
Benchmark computations were also carried out varying the number of sampled geometries and the method used to generate the ground-state minimum geometry and associated frequencies. Thus, nuclear ensembles of 20, 50, 75, and 100 geometries were generated from the CASPT2 equilibrium structure and frequencies and tested. In addition, absorption spectra were also computed, using sampling based on the equilibrium structures and frequencies obtained with the coupled-cluster method including single and double excitations (CCSD) and density functional theory (DFT) with the PBE0 functional, both with the Def2QZVP basis set and using the Gaussian09 (revision C.01) program.62 The atomic masses of the Hg, Cl, Br, and I atoms used in the computations are 201.9706, 34.9688, 78.9183, and 126.9045 Da, which correspond to the most abundant isotopes. For both tests, see a short discussion presented in Section SII of the ESI.†
3 Results and discussion
In this section, we firstly present the computed geometrical parameters (bonds and angles) and vibrational frequencies of the normal modes for the compounds studied in this work and compare them with data from the literature.19,20,63,64 Secondly, the electronic structures of the low-lying SF and SO electronic states are analyzed and discussed in detail, focusing separately on the symmetric HgX2 and mixed HgXY halides (X, Y = Cl, Br, and I). Finally, the computed σ(E) are compiled and compared with the experimental spectra.3.1 Equilibrium ground-state structures
The theoretical and experimental data available in the literature for the mercury–halogen bond distances (RHgX) together with those computed in this work with the CASPT2/ANO-RCC-VQZP methodology are compiled in Tables SI and SII (see ESI†). In this section, we will focus only on the main trends. For the HgX2 molecules, experimental measurements using the electron diffraction technique and compiled by Hargittai63 give rise to equilibrium geometries with Hg–X bond lengths of 2.240, 2.374, and 2.558 Å for X = Cl, Br, and I, respectively. Other experimental data deviate by up to 0.04 Å.63 In contrast, for the mixed HgXY halides, no experimental geometry data is available. Regarding the theoretical studies, two main groups of work can be highlighted in which the DFT method and CCSD with perturbative triplet excitations [CCSD(T)] are used. Kim et al. carried out benchmark computations with several DFT functionals and analyzed the effect of including SOC.20 The authors conclude that the PBE0 functional produces good estimations of the equilibrium structure. On the other hand, Balabanov and Peterson reported high-level ab initio CCSD(T) data with aug-cc-pVXZ-PP basis sets and analyzed the effects of basis sets, SOC, scalar relativity (SR) effects, and core–valence correlation (CV).19 Corrections for the CV electron correlation were found to produce the strongest changes although with small differences of up to 0.009 Å.19 Meanwhile, SR and SOC yielded non-significant contributions, which agrees with the almost pure singlet nature of the 11Σ+g ground electronic state as determined in our previous work.16,19The CASPT2 results were computed in the present study by using the all-electron ANO-RCC-VQZP basis set which was shown to be more accurate for the determinaton of the geometrical and electronic-structure properties of the HgBr2 molecule as compared to the Def2QZVP and aug-cc-pVQZ-PP basis sets containing ECPs.16 SOC was not considered for the geometry determination due to the negligible effect for the ground-state geometrical parameters. As compared with the best estimations obtained in the literature at the CCSD(T)/CBS(TQ) level and including CV, SO, and SR corrections, the CASPT2 results show in all cases shorter bond lengths with an average difference of 0.014 Å. As compared with the experimental data, CCSD(T) slightly overestimates the bond distances, while CASPT2 underestimates them.
In general, all methodological approaches considered here predict linear structures for the ground-state equilibrium of the HgXY compounds, which is in agreement with the experimental observations.16,19,20,63 The behaviour is different for some low-lying excited states which show bent structures.15,16 This is the case of the low-lying singlet and triplet Σ+u and Πu electronic states, which become A1 and B1/B2 states in C2v symmetry, respectively, with bond angles around 90°.15,16
From the comparison of the different bond distances compiled in Tables SI and SII (ESI†), heavy atom effects can be quantified. The Hg–X bond length in the symmetric compounds (HgX2) increases by 0.13 Å from X = Cl to Br and by 0.17 Å from X = Br to I. For the mixed molecules (HgXY), the change in the Y atom slightly affects the distance of the Hg–X bond and the resulting differences are of order ±0.01 Å.
Regarding the vibrational normal modes, the documented experimental data correspond to UV, Raman, and IR measurements.65–76 The symmetric stretching (νsym), asymmetric stretching (νasym), and bending (νbend) normal modes frequencies are compiled in Tables SI and SII (ESI†) together with the corresponding theoretical values from the literature (selected DFT19,20 and CC19 methods) and those computed in this study with the CASPT2 method. In general, CASPT2/ANO-RCC-VQZP values of νsym, νasym, and νbend are larger than the best estimations obtained with the CCSD(T) method. Both theoretical findings are slightly larger than the experimental data. However, the differences are not qualitatively significant and therefore the trends are the same in all cases. It can be easily seen that vibrational frequencies decrease upon increasing the atomic number of the halogen atom. The νbend normal mode is much less affected than νsym and νasym. In the HgX2 molecules, substitution of the Hg–Cl bonds with Hg–Br implies a decrease of all frequencies almost twice bigger than that obtained by changing Br for I. This trend is also observed in the case of the mixed HgXY halides for the νbend normal mode, whereas it is not found for νsym and νasym, most probably because the last two frequencies are much more affected by the other halogen atom.
3.2 Vertical electronic transitions
Tables 1 and 2 compile the electronic-structure data obtained for the symmetric HgBr2 and asymmetric HgBrCl molecules, respectively, at the DKH3-SOC-MS-CASPT2(12,10)/ANO-RCC-VQZP level of theory. Analogous tables for the other compounds can be found in the ESI† (see Tables SIII–SVI). In the corresponding calculations, the highest Abelian symmetry point-group of the HgX2/HgXY molecules was used, the D2h/C2v point group (in SA-CASSCF procedures 8 roots per IrRep were used). The point group was later translated by using correlation tables to the full D∞h/C∞v group. The first five columns show the orbital nature and spectroscopic properties of the SF states, while the remaining columns compile the information for the SO states, with SF contributions and SO-based spectroscopic properties. Only symmetry allowed and relevant electronic transitions are included in such tables for both the pure HgX2 and mixed HgXY halides. Triplet states which mix with singlet SF states or which give rise to important SO states for the absorption spectra are also added. Data corresponding to other secondary and non-allowed electronic transitions can be found in Tables SVII–SXVI in the ESI.† To facilitate comparisons between non-mixed and mixed halides, Table 2 and Tables SV, SVI (ESI†) also show the relationships between SF states of the mixed halides and those of the HgX2 molecules (which are established taking into account the nature (orbital excitations) of the main configuration state function of each SF state). Note that the gerade-like electronic transitions are not symmetry forbidden in the C2v compounds. For the representation of the SO states, two types of notations are used, one in which the information about the main SF state contributing to the SO state is indicated and another in which the focus is only on the Ω number and the energetic order of the states (for example, 11Πu1 and (2)1u, respectively; see more details in our previous work).16| SF state | (D∞h) | Weight [%] | Excitation | ΔE [eV] | f [a.u.] | SO state/Ω state | Weight [%] | SF state | ΔE [eV] | f [a.u.] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11Σ+ | (11Σ+g) | 95 | 0.00 | 11Σ+0+ | (1)0+ | 100 | 11Σ+ | 0.00 | |||
| 13Π | (13Πg) | 86 | πnb2 → σ+* | 4.86 | 13Π1 | (1)1 | 88 | 13Π | 4.83 | 0.00053 | |
| 12 | 11Π | ||||||||||
| 13Π0+ | (2)0+ | 100 | 13Π | 5.01 | 0.00118 | ||||||
| 11Π | (11Πg) | 84 | πnb2 → σ+* | 5.15 | 0.00318 | 11Π1 | (2)1 | 86 | 11Π | 5.21 | 0.00267 |
| 11 | 13Π | ||||||||||
| 2 | 13Σ+ | ||||||||||
| 23Π | (13Πu) | 83 | πnb1 → σ+* | 5.70 | 23Π1 | (3)1 | 93 | 23Π | 5.70 | 0.00053 | |
| 4 | 21Π | ||||||||||
| 23Π0+ | (3)0+ | 100 | 23Π | 5.79 | 0.00073 | ||||||
| 13Σ+ | (13Σ+u) | 85 | σ+nb → σ+* | 5.84 | 13Σ+1 | (4)1 | 94 | 13Σ+ | 5.88 | 0.00019 | |
| 2 | 21Π | ||||||||||
| 2 | 11Π | ||||||||||
| 21Π | (11Πu) | 83 | πnb1 → σ+* | 6.00 | 0.01676 | 21Π1 | (5)1 | 92 | 21Π | 6.04 | 0.01579 |
| 5 | 23Π | ||||||||||
| 2 | 13Σ+ | ||||||||||
| 21Σ+ | (11Σ+u) | 63 | πnb2 → π | 6.66 | 0.05102 | 21Σ+0+ | (4)0+ | 94 | 21Σ+ | 6.66 | 0.04221 |
| 23 | σ+nb → σ+* | 5 | 13Σ+ | ||||||||
| 23Σ+ | (23Σ+u) | 72 | πnb2 → π | 6.66 | 23Σ+1 | (6)1 | 70 | 23Σ+ | 6.44 | 0.00007 | |
| 11 | πnb1 → π | 29 | 13Σ− | ||||||||
| 13Δ | (13Δu) | 80 | πnb2 → π | 6.80 | 13Δ1 | (7)1 | 100 | 13Δ | 6.73 | 0.00064 | |
| 10 | πnb1 → π | ||||||||||
| 33Σ+ | (13Σ+g) | 38 | πnb1 → π | 6.95 | 33Σ+1 | (8)1 | 88 | 33Σ+ | 6.95 | 0.00003 | |
| 38 | σ+1 → σ+* | 6 | 13Δ | ||||||||
| 13 | πnb2 → π | ||||||||||
| 13Σ− | (13Σ−u) | 80 | πnb2 → π | 6.99 | 13Σ−0+ | (5)0+ | 94 | 13Σ− | 7.02 | 0.01252 | |
| 10 | πnb1 → π | 6 | 21Σ+ | ||||||||
| 13Σ−1 | (9)1 | 67 | 13Σ− | 7.25 | 0.00051 | ||||||
| 28 | 23Σ+ | ||||||||||
| 3 | 33Σ+ | ||||||||||
| 31Σ+ | (21Σ+g) | 55 | πnb1 → π | 7.51 | 0.00683 | 31Σ+0+ | (6)0+ | 91 | 31Σ+ | 7.50 | 0.00499 |
| 28 | σ+1 → σ+* | 9 | 23Σ− | ||||||||
| 23Δ | (13Δg) | 77 | πnb1 → π | 7.62 | 23Δ1 | (11)1 | 100 | 23Δ | 7.48 | 0.00024 | |
| 10 | πnb2 → π | ||||||||||
| 43Σ+ | (23Σ+g) | 49 | σ+1 → σ+* | 7.64 | 43Σ1+ | (10)1 | 64 | 43Σ+ | 7.45 | 1.1 × 10−6 | |
| 38 | πnb1 → π | 34 | 23Σ− | ||||||||
| 23Σ− | (13Σ−g) | 76 | πnb1 → π | 7.81 | 23Σ−1 | (7)0+ | 88 | 23Σ− | 7.85 | 0.00259 | |
| 11 | πnb2 → π | ||||||||||
| 41Σ+ | (31Σ+g) | 50 | σ+1 → σ+* | 8.14 | 1.54965 | 41Σ+0+ | (9)0+ | 98 | 41Σ+ | 8.16 | 1.58677 |
| 26 | πnb1 → π | ||||||||||
| 33Π | (23Πu) | 63 | σ+1 → π | 8.19 | 33Π1 | (12)1 | 49 | 33Π | 8.03 | 0.00601 | |
| 29 | σ+nb → π | 31 | 31Π | ||||||||
| 14 | 23Σ− | ||||||||||
| 5 | 43Σ+ | ||||||||||
| 33Π0+ | (8)0+ | 99 | 33Π | 8.00 | 0.00001 | ||||||
 ) < b2u(πu)/b3u(πu) < b1u(σ+u). In the ground-state Hartree–Fock wavefunction, the first 6 MOs are occupied while the others are empty. As can be seen in Fig. 1, σu and πu/g-type orbitals are more localized than σg-type ones either on the Hg atom or on the X halogen atoms. Based on the orbital energy order, the predicted lowest-energy electronic transition is πnbg →
) < b2u(πu)/b3u(πu) < b1u(σ+u). In the ground-state Hartree–Fock wavefunction, the first 6 MOs are occupied while the others are empty. As can be seen in Fig. 1, σu and πu/g-type orbitals are more localized than σg-type ones either on the Hg atom or on the X halogen atoms. Based on the orbital energy order, the predicted lowest-energy electronic transition is πnbg → 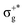 , which gives rise to the 11Πg state. Next, πnbu →
, which gives rise to the 11Πg state. Next, πnbu → 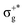 gives rise to 11Πu. πnbg → πu produces a set of three electronic states Σ+u, Δu, and Σ−u. Similarly, πnbu → πu generates Σ+g, Δg, and Σ−g states. At high energies (see Table 1), 21Σ+u, which mainly corresponds now to the σnb+u →
gives rise to 11Πu. πnbg → πu produces a set of three electronic states Σ+u, Δu, and Σ−u. Similarly, πnbu → πu generates Σ+g, Δg, and Σ−g states. At high energies (see Table 1), 21Σ+u, which mainly corresponds now to the σnb+u → 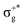 excitation plus some contribution from the πnbg → πu one, is the most probable transition. The 11Σ+u and 11Πu states follow, with a decrease of f of one order of magnitude each. Taking into account now the distinct multiplicities, it can be readily seen that for equivalent states, singlet–triplet energy splitting is not larger than 0.1 eV in Πu, Δu, and Σ−u. This is not the case for Σ+u, where the configuration state functions represented by the σ+nbu →
excitation plus some contribution from the πnbg → πu one, is the most probable transition. The 11Σ+u and 11Πu states follow, with a decrease of f of one order of magnitude each. Taking into account now the distinct multiplicities, it can be readily seen that for equivalent states, singlet–triplet energy splitting is not larger than 0.1 eV in Πu, Δu, and Σ−u. This is not the case for Σ+u, where the configuration state functions represented by the σ+nbu → 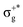 and πnbg → πu excitations are strongly mixed. While the latter dominates the low-energy 11Σ+u state, the former has a higher weight in the low-energy triplet 13Σ+u. The opposite behaviour is found for the high energy 21Σ+u and 23Σ+u states. In general, this qualitative description is maintained for the three HgX2 molecules (see Table 1 and Tables SIII, SIV in the ESI†). The only difference observed is an average decrease of 0.6 eV for ΔE upon increasing the atomic number of the halogen atom, which is ascribed to the lower electronegativity of the X atom and the corresponding energetic increase of the px/y/z atomic orbital (3px/y/z (Cl) < 4px/y/z (Br) < 5px/y/z (I)).
and πnbg → πu excitations are strongly mixed. While the latter dominates the low-energy 11Σ+u state, the former has a higher weight in the low-energy triplet 13Σ+u. The opposite behaviour is found for the high energy 21Σ+u and 23Σ+u states. In general, this qualitative description is maintained for the three HgX2 molecules (see Table 1 and Tables SIII, SIV in the ESI†). The only difference observed is an average decrease of 0.6 eV for ΔE upon increasing the atomic number of the halogen atom, which is ascribed to the lower electronegativity of the X atom and the corresponding energetic increase of the px/y/z atomic orbital (3px/y/z (Cl) < 4px/y/z (Br) < 5px/y/z (I)).
In terms of SO electronic states, it can be seen in Table 1 and Tables SIII, SIV (ESI†) that 11Πu, 11Σ+u, and 21Σ+u contribute predominantly to (2)1u, (2)0+u, and (4)0+u, respectively. While (2)0+u and (4)0+u arise mainly from the respective singlet SF states, (2)1u presents a large participation of triplet states, in particular 13Σ+u and 13Πu. In addition, new probable transitions (with non-negligible f values) appear mainly arising from triplet states (which are forbidden without SOC). This is the case of (1)1u, (1)0+u, (3)1u, and (3)0+u, with f values of 0.004–0.007. The comparison of the SO data for the distinct halogen compounds allows us to analyze the heavy-atom effect, which contributes by increasing the SOC or singlet–triplet mixing. This can be easily seen by analyzing the contributions of singlet and triplet SF states to the SO states. Thus, greater mixing appears in HgI2 as compared to HgBr2 and HgCl2, which in some cases makes transitions more probable and in other cases less probable depending on the relative contribution of singlet and triplet SF states. Significant changes of several orders of magnitude in the f values can be seen, for example, in the transition to the (1)0+u state, with f = 0.00001, 0.00645, and 0.04102 for HgCl2, HgBr2, and HgI2, respectively. The (3)1u SO state also has higher f values for HgI2 and HgBr2 than for HgCl2. Meanwhile, the transition to the (5)1u SO state with a pure triplet character is also more probable for the HgI2 compound than for HgBr2 and is very small in HgCl2.
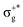 ) of the parent halide with the highest electronegativity halogen atom (similarly for the gerade-like 11Π state, which involves πnb2 → σ+* excitations and is related to the 11Πg state of the parent compounds mainly formed by the πnbg →
) of the parent halide with the highest electronegativity halogen atom (similarly for the gerade-like 11Π state, which involves πnb2 → σ+* excitations and is related to the 11Πg state of the parent compounds mainly formed by the πnbg → 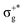 excitations). Secondly, electronic transitions to 41Σ+ (σ+1 → σ+*) related to 31Σ+g (σ+g →
excitations). Secondly, electronic transitions to 41Σ+ (σ+1 → σ+*) related to 31Σ+g (σ+g → 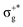 ) show the opposite behaviour and they appear closer to the corresponding states of the non-mixed halide with the lowest electronegativity halogen atom (higher atomic number). Meanwhile, transitions to the set of 21Σ+, 11Δ, and 11Σ− states, which correspond to πnb2 → π NO excitations and are related to the set of 21Σ+u, 11Δu, and 11Σ−u states, respectively, with πnbg → πu relevant excitations, appear in between the corresponding transitions of the parent halides (similarly for the gerade-like states 31Σ+, 21Δ, and 21Σ− (πnb1 → π) related to 21Σ+g, 11Δg, and 11Σ−g (πnbu → πu states of HgX2)).
) show the opposite behaviour and they appear closer to the corresponding states of the non-mixed halide with the lowest electronegativity halogen atom (higher atomic number). Meanwhile, transitions to the set of 21Σ+, 11Δ, and 11Σ− states, which correspond to πnb2 → π NO excitations and are related to the set of 21Σ+u, 11Δu, and 11Σ−u states, respectively, with πnbg → πu relevant excitations, appear in between the corresponding transitions of the parent halides (similarly for the gerade-like states 31Σ+, 21Δ, and 21Σ− (πnb1 → π) related to 21Σ+g, 11Δg, and 11Σ−g (πnbu → πu states of HgX2)).
In general, there are five relevant vertical electronic transitions in the SF description of the mixed halides, ascribed to the energetically ordered 11Π, 21Π, 21Σ+, 31Σ+, and 41Σ+ states. The most intense is the last one, whereas distinct relative intensities appear when the other transitions are compared in the three compounds. In particular, while 31Σ+ is more intense than 21Σ+ in HgClI, their relative intensity decreases in HgBrI, and the opposite trend is found for HgBrCl.
Regarding the energy splitting between related singlet and triplet states, the gaps are higher than those obtained for the non-mixed halides. Singlet–triplet energy splittings are around 0.1 eV for the Δ and Σ− states and 0.3 eV for the Π states. As can be seen in Table 2 and Tables SV, SVI (see ESI†), Σ+ states show a strong mixture of the πnb1/2 → π and σ+1/σ+nb → σ+ configuration state functions, producing, in general, larger gaps. Similarly to the parent HgX2 compounds, inclusion of a less electronegative halogen atom gives rise to a decrease in ΔE, with an average difference of 0.3 eV between HgBrCl and HgClI, of 0.3 eV between HgClI and HgBrI, and of 0.6 eV between HgBrCl and HgBrI. A proportional shift of 0.3 eV is then obtained when changing one halogen atom in the HgXY (X, Y = Cl, Br, and I) halides.
In the SO description of the absorption spectra, many transitions become probable, which arise not only from dominant singlet SF states but also from singlet–triplet mixture and even dominant triplet SF states. As can be seen by comparing Table 2 and Tables SV, SVI (ESI†), this mixing is more pronounced in HgBrI due to the heavy-atom effect. The brightest transition computed corresponds to the (9)0+ SO state which is mainly generated by the singlet 41Σ+ SF state. The other singlet SF states 11Π, 21Π, 21Σ+, and 31Σ+ give rise mainly to the (2)1, (5)1, (4)0+, and (6)0+ SO states, respectively. In general, mixing with other triplet SF states is largely increased in the cases of HgBrI and HgClI. At low energies, below that of the important “singlet” (4)0+ state, the relevant transitions to SO states with dominant triplet character are (2)0+ for HgBrCl, (2)0+, (3)0+, and (6)1 for HgClI and (2)0+, (3)1, (3)0+, and (4)1 for HgBrI. The SO states (2)0+ and (3)0+ are basically pure triplet 13Π and 23Π SF states, respectively. Meanwhile, at higher energies, significant transitions characterized by strong triplet components are (7)0+ and (8)0+ for HgClI and HgBrI. They are mainly formed from the 33Π or 23Σ− SF states.
3.3 Simulated absorption cross sections
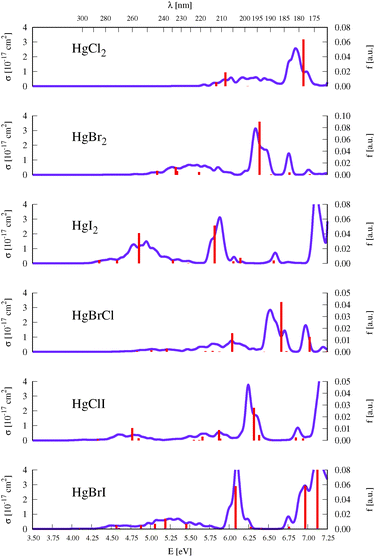
As described above in Section 2, benchmark computations were carried out in this work to establish an accurate semi-classical approach for determining the absorption band shapes of the representative HgBr2 and HgXY molecules. We analyzed the effect of the type of method used for determining the ground-state optimized geometries (and corresponding vibrational modes frequencies), which are required for the generation of the set of nuclear configurations, and the effect of considering a different number of configurations in the nuclear sampling (see eqn (1)). An extended analysis of such benchmarks can be found in Section SIII of the ESI.† In summary, negligible changes are obtained by comparing the σ(E) values obtained by using DFT/PBE0, CCSD, or CASPT2 starting geometries and frequencies (see Fig. S1, ESI†). For the second test, since the studied molecular systems have a small number of degrees of freedom, 100 configurations are clearly enough to produce a converged absorption spectrum (see Fig. S2 (ESI†) which compares the spectra generated by sampling 25, 50, 75, and 100 geometries). On the other hand, the δ value that seems to be more reliable and appropriate is 0.05 eV, since higher values might introduce unphysical band shapes. Also the apparent vibrational resolution that can be obtained with lower δ values is not reliable because the exact vibronic couplings are not computed here with the semi-classical approximation.Fig. 2 displays the σ(E) of all the HgXY halide compounds, computed in the present study with the DKH3-SOC-MS-CASPT2(12,10)/ANO-RCC-VQZP level of theory and the semi-classical approximation for the nuclear sampling. Spectra of the HgBr2 and HgBrCl representatives are displayed in Fig. 3 and 4, respectively, along with the experimental absorption spectra reported in the literature.9,11–13 The analogous figures for the remaining compounds were moved to the ESI† (see Fig. S3–S6) for the sake of a more appropriate organization of the work. Note that for the symmetric HgX2 molecules, experimental spectra correspond to gas-phase data,9–12 whereas for the mixed halides they are obtained from measurements in methanol solution.13 Therefore, for HgXY, the simulated spectra in vacuo are not strictly comparable to the experimental spectra. Dipole moments, which are helpful for a rough qualitative analysis on the possible effects of polar solvents on the band shifts, are compiled in Table SXVI of the ESI.† In general, excited states of HgXY are characterized by larger dipole moments than that of the ground state. This is in part related to the asymmetric AO contributions to the excitations from the halogen atoms to Hg (see Fig. 1). Consequently, general solvatochromic shifts to the red might be expected especially in highly polar solvents. Finally, we shall focus in this section on the UV-vis absorption spectra of interest up to around 170 nm, which includes electronic transitions with energies up to those of the 13Σ−u0+ and 13Σ−0+ states for HgX2 and HgXY, respectively. This corresponds to the bands a, b, and c of HgX2 discussed in Section 1. At higher energies, Rydberg states are present according to the experimental observations.77 Those states might interact with the valence states and affect the computed electronic-transition properties of the latter. Computation of Rydberg states requires basis sets with extra diffuse functions and inclusion of the Rydberg orbitals in the active space, which is out of the scope of our work focused on an accurate determination at lower energies.
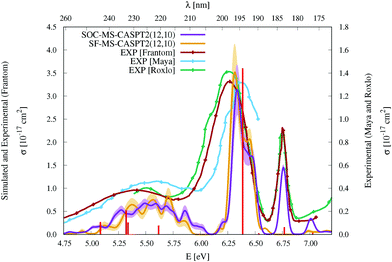 | ||
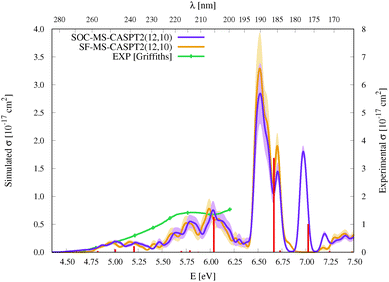
| Fig. 3 Simulated UV-vis absorption cross sections (σ(E)) of HgBr2 both without (SF, orange) and with (SOC, violet) taking into account the spin–orbit coupling between states. Shaded areas represent the statistical error for the sampled photon energies (δσ(E)). Experimental spectra9,11,12 are included for comparison (for a better comparison, the σ(E) values of the spectrum of Frantom et al.12 are shown on the same axis as theoretical ones). Additionally, vertical excitation energies in eV (ΔE) and associated f values between SO states for the optimized ground-state structure of HgBr2 are graphically represented with red sticks (see the discussion in Section 2). | ||
 | ||
| Fig. 4 Simulated UV-vis absorption cross sections (σ(E)) of HgBrCl both without (SF, orange) and with (SOC, violet) taking into account the spin–orbit coupling between states. Shaded areas represent the statistical error for the sampled photon energies (δσ(E)). Experimental spectra13 are included for comparison. Additionally, vertical excitation energies in eV (ΔE) and associated f values between SO states for the optimized ground-state structure of HgBrCl are graphically represented with red sticks (see the discussion in Section 2). | ||
As described in the Introduction, three main bands characterize the UV absorption spectra of the three halogen–mercury compounds (bands a, b, and c). The lowest-energy one (band a) is broad with low intensity. Our computations predict band maxima at approximately 6.20 eV (200 nm), 5.55 eV (223 nm), and 4.95 eV (250 nm) for HgCl2, HgBr2, and HgI2, respectively, which are mainly produced by transitions to 13Πu1, 11Πu1, 13Πu0+, and 13Σ+u1 SO states (see Table 1 and Tables SIII, SIV, ESI†). Therefore, band a involves a certain degree of SOC. For HgCl2, the most intense transition is related to the 11Πu1 state with dominant singlet character (11Πu). The second most intense transition corresponds to 13Πu1 which has mainly triplet character (13Πu). In HgBr2, the transition to the “singlet” 11Πu1 state is still the most intense but now three SO states with triplet dominance have similar σ values: 13Πu1, 13Πu0+, and 13Σ+u1. Finally, in HgI2, the “triplet” 13Πu0+ becomes the most probable transition, and the “singlet” 11Πu1 has a similar f to 13Πu1 and 13Σ+u1. Such intense triplet absorptions are the consequence of SOC and heavy-atom effects which are evident by comparing the spectra generated by SF and SO states (see differences in Fig. 3 and Fig. S3, S4, ESI†). Whereas the SF and SO descriptions are similar in HgCl2 and no significant SOC role can be interpreted from the spectra, band a is clearly more prominent in the SO spectra than in the SF spectra for HgI2.
Band b is much sharper and more intense than band a and, according to our simulations, it has band maxima at 6.85 eV (181 nm), 6.34 eV (196 nm), and 5.88 eV (211 nm) for HgCl2, HgBr2, and HgI2, respectively. This band mainly originates from the electronic transition to the 11Σ+u0+ SO state. As can be seen in Table 1 and Tables SIII, SIV (ESI†), this state is mainly formed by the singlet 11Σ+u SF state with small contributions from states of triplet character (13Σ−u for HgCl2 and HgBr2 and this state plus 13Πu for HgI2). The “singlet” nature of band b and the increasing “triplet” nature of band a in the series Cl, Br, and I allows us to interpret the distinct relative intensity of the two analyzed bands observed experimentally (a large relative intensity difference in HgCl2 and small in HgI2). This is another clear manifestation of the higher SOC for the heavy atom.
In the high-energy part of the spectra, an even sharper band arises (band c), with band maxima at 7.34 eV (169 nm), 6.75 eV (184 nm), and 6.16 eV (201 nm) for HgCl2, HgBr2, and HgI2, respectively. The σ values of this band are the largest in the spectrum of HgCl2, largely decrease for HgBr2, and become very low in HgI2. Band c can be related to the 13Σ−u0+ SO state, which is mainly formed by the triplet 13Σ−u.16 However, subtle contributions seem to affect the band intensity. Firstly, in HgCl2, there is an 8% contribution of the 11Σ+u state which according to the SF properties has very large f value (see Table SIII, ESI†). In HgBr2, the small contribution of the singlet 11Σ+u state in the ground-state optimized geometry (only 1%; see Table 1) seems to underestimate the intensity of the band in the corresponding spectrum in Fig. 3. For HgI2, even though the contribution of the 11Σ+u SF state to the 13Σ−u0+ SO state is higher (2%; see Table SIV, ESI†), this band almost disappears in the absorption spectrum (see Fig. S4, ESI†). Such findings point to greater mixing of the singlet 11Σ+u state in HgBr2 due to the nuclear sampling and a shorter interaction in HgI2. The triplet nature of band c becomes evident when comparing the spectra with and without the SOC effect. It fully disappears in the SF simulated spectra. This confirms our predictions on the nature of this band (which are contrary to Wadt's first predictions).15,16 Finally, it is also worth noticing that in HgI2 a close-lying band at 6.06 eV (205 nm) is present related to the transition to the (5)1u SO state (which is a pure triplet 13Δu). The peak corresponding to this transition cannot be identified in the spectra of the other symmetrical halide compounds.
3.4 HgXY
An intense band is found in the high-energy part of the absorption spectra of HgBrCl, HgClI, and HgBrI with band maxima at 6.52, 6.25 and 6.10 eV, respectively (see Fig. 2). As can be seen by comparing the spectra of the non-mixed and mixed compounds, the energy position of the band for the HgXY molecules is located in between those for the parent HgX2 and HgY2 systems. Such bands correspond to transitions to the (4)0+ SO states with a clearly dominant singlet nature from the 21Σ+ SF state, which mainly involve πnb2 → π orbital excitations similarly to the parent compounds (11Σ+u0+ ≡ (2)0+u).Regarding the low-energy part of the spectra, signals have in general lower intensity and are spread over the range of the low-energy band of the parent non-mixed halides. A lack of differences between the SF and SO simulated spectra clearly indicates that this part of the spectra is not very affected by triplet states in HgBrCl (see Fig. 4) while for the other two compounds, HgClI and HgBrI, there are significant triplet contributions (see Fig. S5 and S6, ESI†). Thus, in HgBrCl, two mainly singlet states, 11Π1 and 21Π1, contribute to the low-energy part of the spectrum, and one “triplet” state, 13Π0+, appears although with low σ values. For HgClI, two “triplet” SO states, 13Π0+ and 23Π0+, have similar intensities to 21Π1. In the case of HgBrI, four “triplet” states, 13Π0+, 23Π1, 23Π0+, and 13Σ1+, and one “singlet” state, 21Π1, are responsible for the low-energy signals.
Finally, as in the case of HgCl2 and HgBr2, the spectra of HgBrCl and HgClI are also characterized by almost pure triplet bands (sharp bands at around 6.7–7.0 eV in the last two compounds). The corresponding electronic transitions are already described in detail in Section 3.2.2 and their nature is once more clearly understood by comparing the SF and SO spectra of Fig. 4 and Fig. S5 (ESI†).
4 Conclusions
In this study, we have extended our previous analysis16 on the nature of the electronic transitions of HgBr2 to analogous analyses for the HgX2 and HgXY mercury halides (with X and Y representing the halogen atoms Cl, Br, and I) within the UV-vis range of the energy spectrum up to around 170 nm, followed by simulations of physically meaningful σ(E).In the first part of the work, in the same manner as in the HgBr2 study, we have assigned the main electronic bands on the basis of ΔE and f computed at the Franck–Condon geometry. We have adapted the previously benchmarked CASSCF/MS-CASPT2/SO-RASSI methodology using the DKH3 Hamiltonian for treating the scalar relativistic effects of the inner electrons and the relativistic-correlation-consistent ANO-RCC-VQZP basis set.16 The main results of this part confirm the experimental trends observed in the HgX2 and HgXY UV-vis spectra9–11,13 and provide new information on the nature of the electronic transitions:
(1) Electronic excitations (up to 170 nm) are almost of the same nature, and upon increasing the atomic number of the halogen atoms (X or Y) in the series Cl, Br, and I, ΔE systematically decreases by 0.3 and 0.6 eV for the HgXY and HgX2 halides, respectively.
(2) The low-energy part of the absorption spectra with low-intensity signals (band a) has some mixing of singlet and triplet states. The sharp band b, which follows at higher energy, corresponds mainly to singlet states, and band c is basically the electronic transition to a pure triplet state (appearing only with SOC corrections).
(3) Stronger singlet–triplet mixing (due to SOC) affects the energetics of the excited states of HgXY halides containing I atoms.
In the second part of this work, we have presented theoretically simulated σ(E) of the studied mercury compounds, which were generated with the semi-classical approach based on computations of ΔE and f for the probed set of geometries (sampled according to the Wigner distribution).26–28 This approach has allowed the determination of the general shapes of the electronic bands (and intensities), while keeping a high-level methodology for the electronic-structure computations of the excited states, namely DKH3-SOC-MS-CASPT2/ANO-RCC-VZQP. For HgX2, where experimental gas-phase electronic spectra are available, despite the differences in σ(E) (within the same order of magnitude), the position and shape of the electronic bands are reproduced properly. This is especially meaningful for the mixed HgXY halides, since no experimental spectra up to 170 nm have been reported (only part of the HgXY spectra is available which is estimated from the spectra of the parent molecules HgX2 and HgY2, measured in methanol solution).13,14
The results of the benchmarking on the simulations related to the choice of geometrical ensembles have shown the correct applicability of the semi-classical approach. It seems to be invariant to the method employed in the geometry optimizations (and computed vibrational frequencies) for generating the Wigner ensemble. This has been useful in simulations of UV-vis spectra of larger mercury-based compounds, for which computationally cheaper methods (for example DFT) could be chosen for producing the geometrical ensembles.29
Overall, the methodological and computational approaches presented in this paper and applied to the HgX2 and HgXY compounds have allowed us to clearly establish the nature of the UV absorption bands of these molecules (orbital excitations, singlet–triplet mixing, and heavy-atom effects) and systematically relate the bands of the HgXY to those of the parent HgX2 and HgY2 compounds. Furthermore, this work has been proved worthy in recent σ(E) predictions in mercury compounds with no available experimental spectra.29
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. P. S. acknowledges the Basque Government for funding through a predoctoral fellowship (PRE 2017 1 0403). D. R.-S. is thankful to the Spanish MINECO/FEDER for financial support through project CTQ2017-87054-C2-2-P and the Ramón y Cajal fellowship with Ref. RYC-2015-19234.References
- F. Wang, A. Saiz-Lopez, A. S. Mahajan, J. C. Gómez Martín, D. Armstrong, M. Lemes, T. Hay and C. Prados-Roman, Atmos. Chem. Phys., 2014, 14, 1323–1335 CrossRef.
- H. M. Horowitz, D. J. Jacob, Y. Zhang, T. S. Dibble, F. Slemr, H. M. Amos, J. A. Schmidt, E. S. Corbitt, E. A. Marais and E. M. Sunderland, Atmos. Chem. Phys., 2017, 17, 6353–6371 CrossRef CAS.
- E. Carriere, H. Guiter and M. Lafitte, Bull. Soc. Chim. Fr., 1948, 25–26 CAS.
- L. G. Hepler and G. Olofsson, Chem. Rev., 1975, 75, 585–602 CrossRef CAS.
- T. S. Dibble, M. J. Zelie and H. Mao, Atmos. Chem. Phys., 2012, 12, 10271–10279 CrossRef CAS.
- T. S. Dibble, M. J. Zelie and Y. Jiao, J. Phys. Chem. A, 2014, 118, 7847–7854 CrossRef CAS.
- R. Ahmad, J. Ali and Q. Faisal, Orient. J. Chem., 2015, 31, 653–659 CrossRef CAS.
- T. S. Dibble and A. C. Schwid, Chem. Phys. Lett., 2016, 659, 289–294 CrossRef CAS.
- J. Maya, J. Chem. Phys., 1977, 67, 4976 CrossRef CAS.
- H. Hofmann and S. R. Leone, J. Chem. Phys., 1978, 69, 3819–3825 CrossRef CAS.
- C. Roxlo and A. Mandl, J. Appl. Phys., 1980, 51, 2969–2972 CrossRef CAS.
- G. Frantom, P. Bletzinger and A. Garscadden, Bull. Am. Phys. Soc., 1980, 25, 461 Search PubMed.
- T. R. Griffiths and R. A. Anderson, Inorg. Chem., 1979, 18, 2506–2511 CrossRef CAS.
- T. R. Griffiths and R. A. Anderson, J. Chem. Soc., Dalton Trans., 1980, 205–208 RSC.
- W. R. Wadt, J. Chem. Phys., 1980, 72, 2469 CrossRef CAS.
- S. P. Sitkiewicz, J. M. Oliva, J. Z. Dávalos, R. Notario, A. Saiz-Lopez, D. R. Alcoba, O. B. Oña and D. Roca-Sanjuán, J. Chem. Phys., 2016, 145, 244304 CrossRef.
- J. Pittner and P. Jungwirth, Chem. Phys. Lett., 2000, 321, 281–286 CrossRef CAS.
- S. Patchkovskii, Phys. Chem. Chem. Phys., 2006, 8, 926–940 RSC.
- N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2003, 119, 12271 CrossRef CAS.
- J. Kim, H. Ihee and Y. S. Lee, J. Chem. Phys., 2010, 133, 144309 CrossRef PubMed.
- R. Li, C. Wei, Q. Sun, E. Sun, M. Jin, H. Xu and B. Yan, J. Quant. Spectrosc. Radiat. Transfer, 2014, 133, 271–280 CrossRef CAS.
- V. Barone, A. Bencini, F. Totti and M. G. Uytterhoeven, Int. J. Quantum Chem., 1995, 61, 361–367 CrossRef.
- P. Schwerdtfeger, P. D. W. Boyd, S. Brienne, J. S. McFeaters, M. Dolg, M. S. Liao and W. H. Eugen Schwarz, Inorg. Chim. Acta, 1993, 213, 233–246 CrossRef CAS.
- A. F. Khalizov, B. Viswanathan, P. Larregaray and P. A. Ariya, J. Phys. Chem. A, 2003, 107, 6360–6365 CrossRef CAS.
- M. Kaupp and H. G. Von Schnering, Inorg. Chem., 1994, 33, 4179–4185 CrossRef CAS.
- M. Barbatti, A. J. A. Aquino and H. Lischka, Phys. Chem. Chem. Phys., 2010, 12, 4959–4967 RSC.
- R. Crespo-Otero and M. Barbatti, Theor. Chem. Acc., 2012, 131, 1–14 Search PubMed.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26–33 Search PubMed.
- A. Saiz-Lopez, S. P. Sitkiewicz, D. Roca-Sanjuán, J. M. Oliva-Enrich, J. Z. Dávalos, R. Notario, M. Jiskra, Y. Xu, F. Wang, C. P. Thackray, E. M. Sunderland, D. J. Jacob, O. Travnikov, C. A. Cuevas, A. U. Acuña, D. Rivero, J. M. C. Plane, D. E. Kinnison and J. E. Sonke, Nat. Commun., 2018, 9, 4796 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- J. Finley, P.-A. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- P.-A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- K. Andersson, P.-A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P.-A. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218 CrossRef CAS.
- D. Roca-Sanjuán, F. Aquilante and R. Lindh, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 585–603 Search PubMed.
- B. Schimmelpfennig, Amfi, an atomic mean-field spin–orbit integral program, 1996.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef.
- M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 2037–2047 CrossRef CAS.
- M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945–10956 CrossRef CAS PubMed.
- D. Peng and K. Hirao, J. Chem. Phys., 2009, 130, 044192 CrossRef PubMed.
- D. Peng and M. Reiher, Theor. Chem. Acc., 2012, 131, 1081 Search PubMed.
- B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P. O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2012, 131, 1124 Search PubMed.
- T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2013, 132, 1363 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296 Search PubMed.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- G. Ghigo, B. O. Roos and P.-A. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- N. Forsberg and P.-A. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204 CrossRef CAS.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P.-A. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS.
- G. Herzberg, Molecular Spectra and Molecular Structure I. Spectra of Diatomic Molecules, Van Nostrand Reinhold Company, New York, 2nd edn, 1950 Search PubMed.
- G. Herzberg, Molecular Spectra and Molecular Structure III. Electronic Spectra and Electronic Structure of Polyatomic Molecules, Van Nostrand Reinhold Company, New York, 2nd edn, 1966 Search PubMed.
- A. G. Császár, M. Hochlaf, L. Forzi and A. Tortaja, European Cooperation in Science and Technology, COST Action Molecules in Motion, accessed November 2018, http://cost-molim.eu.
- J. P. Bergsma, P. H. Berens and K. R. Wilson, J. Phys. Chem., 1984, 88, 612–619 CrossRef CAS.
- S. Mukamel, J. Chem. Phys., 1982, 77, 173–181 CrossRef CAS.
- E. Wigner, Phys. Rev., 1932, 40, 749–759 CrossRef CAS.
- J. P. Dahl and M. Springborg, J. Chem. Phys., 1988, 88, 4535–4547 CrossRef CAS.
- M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, J. Photochem. Photobiol., A, 2007, 190, 228–240 CrossRef CAS.
- M. Barbatti, G. Granucci, M. Ruckenbauer and J. Pittner, NEWTON-X: a package for Newtonian dynamics close to the crossing seam, 2013, http://www.newtonx.org.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision C.01, 2009 Search PubMed.
- M. Hargittai, Chem. Rev., 2000, 100, 2233–2302 CrossRef CAS.
- V. P. Spiridonov, A. G. Gershikov and B. S. Butayev, J. Mol. Struct., 1979, 52, 53–62 CrossRef CAS.
- H. Sponer and E. Teller, Rev. Mod. Phys., 1941, 13, 75–170 CrossRef CAS.
- S. Bell, R. D. McKenzie and J. B. Coon, J. Mol. Spectrosc., 1966, 20, 217–225 CrossRef CAS.
- W. Klemperer and L. Lindeman, J. Chem. Phys., 1956, 25, 397–399 CrossRef CAS.
- A. A. Malt'sev, G. K. Selivanov, V. I. Yampolsky and N. I. Zavalishin, Nature, Phys. Sci., 1971, 231, 157–158 CrossRef.
- I. R. Beattie and J. R. Horder, J. Chem. Soc. A, 1970, 2433–2435 RSC.
- A. Givan and A. Loewenschuss, J. Chem. Phys., 1976, 64, 1967 CrossRef CAS.
- A. Givan and A. Loewenschuss, J. Chem. Phys., 1976, 65, 1851 CrossRef CAS.
- A. Gedanken, B. Raz, U. Even and I. Eliezer, J. Mol. Spectrosc., 1969, 32, 287–295 CrossRef CAS.
- A. Loewenschuss, A. Ron and O. Schnepp, J. Chem. Phys., 1969, 50, 2502–2512 CrossRef CAS.
- W. Klemperer, J. Chem. Phys., 1956, 25, 1066–1069 CrossRef CAS.
- R. J. H. Clark and D. M. Rippon, J. Chem. Soc., Faraday Trans. 2, 1973, 69, 1496–1501 RSC.
- H. Wehrli, Helv. Phys. Acta, 1938, 11, 339 Search PubMed.
- D. Spence, R. Wang and M. A. Dillon, J. Chem. Phys., 1985, 82, 1883–1889 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tables compiling information on the experimental and theoretical bond lengths for the studied compounds; tables compiling information on computed vertical transitions of HgCl2, HgI2, HgClI and HgBrI and the nature of the important electronic states; figures displaying simulated absorption spectra of HgCl2, HgI2, HgClI, and HgBrI; and a section on the benchmark of the computational procedure of simulation of UV-vis spectra of the studied compounds. See DOI: 10.1039/c8cp06160b |
| This journal is © the Owner Societies 2019 |