2D planar penta-MN2 (M = Pd, Pt) sheets identified through structure search
Kexian
Zhao
ab,
Xiaoyin
Li
ab,
Shuo
Wang
b and
Qian
Wang
 *ab
*ab
aCenter for Applied Physics and Technology, College of Engineering, Peking University, Beijing 100871, China. E-mail: qianwang2@pku.edu.cn
bDepartment of Materials Science and Engineering, College of Engineering, Peking University, Beijing 100871, China
First published on 27th November 2018
Abstract
Two-dimensional (2D) metal dinitrides have attracted increasing attention because of their diverse geometry configurations and extraordinary properties. Using the particle swarm optimization (PSO)-based global structure search method combined with first principles calculations, we have identified 2D metal dinitride MN2 (M = Pd, Pt) sheets containing N2 dimers, penta-MN2, which are planar and composed entirely of pentagons. These pentagonal sheets are not only dynamically, thermally and mechanically stable, but also energetically more favorable over the experimentally synthesized pyrite MN2 monolayers. In particular, penta-PtN2 can withstand a temperature as high as 2000 K, showing its potential as a refractory material. In addition, due to its unique atomic configuration, penta-MN2 exhibits intriguing electronic properties. Penta-PdN2 is metallic, while penta-PtN2 is semiconducting with a direct band gap of 75 meV and an ultrahigh carrier mobility. This study expands the family of 2D metal nitrides, and provides new insight into finding new materials using a reliable structure search algorithm rather than chemical and physical intuition.
1. Introduction
Since the discovery of graphene,1 a lot of two-dimensional (2D) materials have been experimentally synthesized and theoretically predicted with many fascinating properties, showing great potential for various applications.2–8 As compared to the widely studied 2D metal oxides and carbides, much less effort has been devoted to the nitrogen analogues, metal nitrides (MNs). Among the recently studied 2D MNs, the sheets can be in very distinct geometry configurations.9–16 For instance, the Ti4N3 sheet has a MXene like geometric structure with multi-atomic layers and atomic N,9 while the tetra-MoN2 sheet has a square lattice with a single-atomic thickness and atomic N,17 and the O-YN2 sheet possesses a buckled monolayer where the metal atoms are sandwiched between the top and bottom layers of N2 dimers.18 Additionally, previous studies reported that the penta-AlN2 sheet has a buckled Cairo pentagonal tiling geometry with N2 dimers,19 whereas the BeN2 sheet is in distorted honeycomb lattice containing N4 cluster units.20 These studies demonstrate that the geometric structures of 2D MNs sensitively depend on the metal species and the atomic ratio of metal/N, exhibiting complexities and diversities.Moreover, the diverse and flexible bonding features of a metal with N/N2 lead to rich physical and chemical properties of MNs. For example, the H-MoN2 sheet displays a robust ferromagnetism with a Curie temperature over 420 K,21 the metallic O-YN2 sheet shows promising potential as an anode material for potassium (K) ion batteries with high K capacity,18 and the penta-AlN2 sheet is a half-metal and presents ferromagnetism as well.19 These advances inspire us to carry out the present study focusing on 2D MN2 (M = Pd, Pt) systems by using the global structure search method and first principles calculations. Our results show that the most stable monolayers are composed of pure pentagons, thus named penta-MN2. They are totally planar, differing from the other hitherto reported 2D pentagon-based materials which have buckled structures.8,20,22–29 We further systematically investigated their physical properties, including melting points, in-plane Young's modulus, ideal strength, band structure, charge distribution, and carrier mobility. In particular, penta-PtN2 possesses ultrahigh melting point over 2000 K and carrier mobility comparable with that of graphene.
2. Computational methods
We use the Crystal structure AnaLYsis by Particle Swarm Optimization (CALYPSO)30 code to search for the ground state structures of 2D PdN2 and PtN2, and this method has been successfully employed to predict numerous structures ranging from elemental crystals to binary and ternary compounds.31 In the global search, the PSO algorithm is used with thirty generations and population size up to thirty, which means a total of 900 structures are produced including the symmetry P4/mbm, Pmmm and so on. It reaches convergence quickly after 14 generations. The unit cells containing 6 atoms and the buffering thickness is set to 0.15 Å to accommodate the buckling of the structures.Density functional theory (DFT) based first-principles calculations are further performed to study the structural and electronic properties as implemented in the Vienna ab initio Simulation Package (VASP)32 with the projector augmented wave potential (PAW)33 to treat the ion-electron interactions. The generalized gradient approximation (GGA)34 with the Perdew–Burke–Ernzerhof (PBE) functional35 is used to describe the exchange and correlation energy. All atoms of system are relaxed with the convergence criteria for the force and total energy set to be 10−2 eV Å−1 and 10−4 eV, respectively. The kinetic energy cutoff is set to be 600 eV for all calculations. The Monkhorst–Pack k-mesh36 is employed to the sample k point of the first Brillouin zone. The k-point grids are set as 9 × 9 × 1 and 25 × 25 × 1 for the geometry optimization and electronic structure calculations, respectively. For eliminating the interaction between adjacent cells in the vertical orientation, a vacuum distance of 20 Å is used. The PHONOPY package is adopted to calculate the phonon dispersion of the structures and verify their dynamic stability.37
In 2D materials, the carrier mobility can be calculated by using the deformation potential (DP) theory38 and given by the expression:
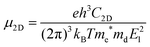 | (1) |
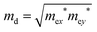 . T is the temperature, which is set to be 300 K in our calculations. El represents the deformation potential constant defined as El = ΔE/(Δlx/lx). ΔE is the energy change of the ith band under proper structure compression or dilatation, lx is the lattice constant along the deformation direction and Δlx is the amount of the deformation. C2D is the elastic modulus of the longitudinal strain in the propagation directions of the longitudinal acoustic wave given by (E − E0)/S0 = C2Dδ2/2, where E is the total energy and S0 is the area of the cell and δ is the applied uniaxial strain.
. T is the temperature, which is set to be 300 K in our calculations. El represents the deformation potential constant defined as El = ΔE/(Δlx/lx). ΔE is the energy change of the ith band under proper structure compression or dilatation, lx is the lattice constant along the deformation direction and Δlx is the amount of the deformation. C2D is the elastic modulus of the longitudinal strain in the propagation directions of the longitudinal acoustic wave given by (E − E0)/S0 = C2Dδ2/2, where E is the total energy and S0 is the area of the cell and δ is the applied uniaxial strain.
3. Results and discussion
3.1 Geometric structures
By performing global structure search, we obtain some low-energy structures of 2D MN2 (M = Pt, Pd). Among them, three energetically most stable isomers are displayed in Fig. 1, where the relative energies of the structures are also listed. The ground-state structures of 2D PdN2 and PtN2 are shown in the bottom panel of Fig. 1. They both have tetragonal structures and P4/mbm symmetry (space group no. 127). From the top views of the structures, one can see that the MN2 monolayers are composed entirely of pentagons, which form a Cairo pentagonal tiling,39 thus the monolayers are termed penta-MN2. While the side views show that the penta-MN2 monolayers are in ideal planar forms which are rare in previously reported pentagonal structures. The optimized lattice constants of penta-PdN2 are a = b = 4.873 Å, while those of penta-PtN2 are a = b = 4.826 Å. In penta-MN2, all N atoms are in dimers and form the N–N bonds. The N–N bond lengths in penta-PdN2 and penta-PtN2 are 1.225 Å and 1.260 Å, respectively, both showing the double bond characters. Specifically in penta-MN2 sheets, the planar geometry structures and the bond angles θN–M–N = 90° and θN–N–M = 120° indicate the square hybridization configurations of M atoms and the regular triangle hybridization configurations of N atoms.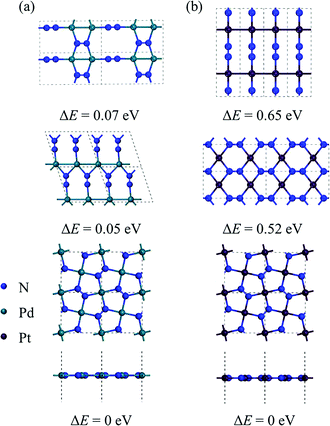 | ||
| Fig. 1 The geometrical structures of low-lying (a) PdN2 and (b) PtN2 and their relative energy. The total energy of the lowest-energy structure (the bottom panel) is set as 0 eV. | ||
3.2 Stability
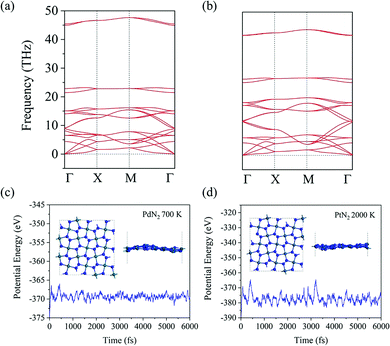
To evaluate the energetic stability, we calculate the cohesive energy of penta-MN2 by following the formula: Ecoh = (2EM + 4EN − EMN2)/6 (EM, EN, and EMN2 are the total energies of a single M atom, a single N atom, and one unit cell of the penta-MN2 monolayer, respectively). The calculated cohesive energies of penta-PdN2 and penta-PtN2 are 4.37 and 5.01 eV per atom, respectively. Using the same calculation methods, we also calculate the cohesive energies of pyrite PdN2 and PtN2, which have the buckled pentagonal structures and have been synthesized experimentally.40–42 The calculated results are 4.24 and 4.87 eV per atom for pyrite PdN2 and PtN2, from which one finds that penta-MN2 are energetically more stable than pyrite MN2. In order to evaluate the dynamic stability, we also calculate the phonon dispersion of penta-MN2, with results shown in Fig. 2(a and b). For both of penta-PdN2 and penta-PtN2, there are no imaginary modes in the entire Brillouin zone, demonstrating that the penta-MN2 monolayers are dynamically stable.We then perform ab initio molecular dynamics (AIMD) simulations to study the thermal stability of penta-MN2. The 3 × 3 × 1 supercells are constructed to reduce the constraint of periodic boundary conditions. For penta-PdN2, the simulations are carried out at a temperature of 700 K, for 6 picoseconds (ps) with a time step of 1 femtosecond (fs). The variations of the total potential energies for the 3 × 3 × 1 penta-PdN2 supercells with respect to simulation time are plotted in Fig. 2(c). We can see that the average values of the total potential energy remain nearly constants during the entire simulations, confirming that penta-MN2 are thermally stable at 700 K. However, when we increase the temperature to 900 K, the structure is found to be seriously disrupted. It suggests that penta-PdN2 has a melting point between 700 and 900 K. Much more interesting is that, using the same method, penta-PtN2 can withstand temperatures as high as 2000 K (see Fig. 2(d)), and it has a melting point between 2000 and 2500 K. Like the case of other metal nitrides such as IrN2 and OsN2,43 penta-PtN2 exhibits potential as a highly refractory material.
It is necessary to estimate the effect of lattice distortion on structural stability as well. Therefore, we calculate the linear elastic constants to investigate the mechanical stability of penta-MN2 under small lattice distortion. The elastic constants are obtained by applying the finite distortion method44 and the results are summarized in Table 1. Here we use the standard Voigt notation45 and the elastic constants C11, C22, C12, and C66 are components of the elastic modulus tensor, corresponding to the second partial derivative of strain energy with respect to strain (all other components are strictly zero for 2D structures). According to Born–Huang criteria,46 for a mechanically stable 2D sheet, its elastic constants need to satisfy C11C22 – C212 > 0, C66 > 0. From the results in Table 1, the elastic constants of penta-PdN2 and penta-PtN2 both meet the criteria, confirming that the penta-MN2 monolayers are mechanically stable.
| Structure | C 11 | C 22 | C 12 | C 66 | E | ν |
|---|---|---|---|---|---|---|
| Penta-PdN2 | 129.2 | 129.2 | 16.9 | 28.9 | 127 | 0.13 |
| Penta-PtN2 | 227.7 | 227.7 | 40.2 | 42.2 | 220 | 0.18 |
3.3 Mechanical properties
With the formula E = (C211 − C212)/C11, we obtain the in-plane Young's moduli of penta-MN2, which are shown in Table 1 as well. The Young's modulus of penta-PtN2 is 220 N m−1, close to 271 N m−1 of the h-BN monolayer45 and 263.8 N m−1 of penta-graphene,8 indicating the good in-plane stiffness of penta-PtN2. Although the Young's modulus of penta-PdN2 (127 N m−1) is smaller than that of penta-PtN2, it is larger than those of the MoS2 monolayer (120 N m−1), germanene (42 N m−1) and silicene (61 N m−1).47,48 The high in-plane stiffness implies the strong bonding in penta-MN2, which is beneficial to the structure stability. In addition, we also calculate the Poisson's ratio of penta-MN2 by ν = C12/C11, and present the results in Table 1. Besides, the ideal strength is also a very important mechanical property of a nanomaterial. Thus, we apply various biaxial tensile strains to the monolayers and calculate the corresponding stress to study the ideal strength of penta-MN2. The calculated results are plotted in Fig. 3(a and b), which show that the strain at the maximum stress is 17.5% for penta-PdN2 and 15.0% for penta-PtN2. The high in-plane Young's modulus and high ideal strength indicate that the penta-MN2 monolayers exhibit excellent mechanical properties.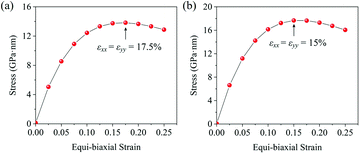 | ||
| Fig. 3 Stress–strain relationship of (a) penta-PdN2 and (b) penta-PtN2 under biaxial tensile strain. The black arrows denote the strain at the maximum stress. | ||
3.4 Electronic properties
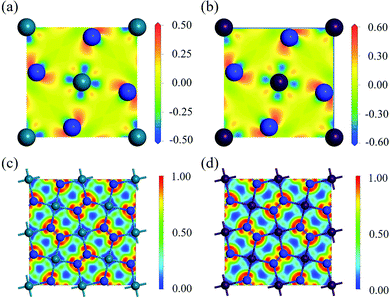
To study the charge distribution of penta-MN2, we calculate the deformation charge density which is defined as the total charge density with the contribution of isolated M and N atoms being subtracted. The slices on the (001) plane are shown in Fig. 4(a and b), where the blue and red regions represent the depletion and accumulation of charge, respectively. It is obvious that the electrons transfer from M to N atoms in penta-MN2 since M is less electronegative as compared with N. Furthermore, the Bader charge analysis49–51 shows that each Pd (Pt) atom transfers 0.66 (0.76) e to each N2 dimer, consistent with the results of deformation charge density.In addition, to get the bonding feature of penta-MN2, we also perform the electron localization function (ELF) analysis, which is widely used to analyze the spatial distribution of electrons. ELF is defined as:
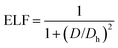 | (2) |
 | (3) |
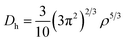 | (4) |
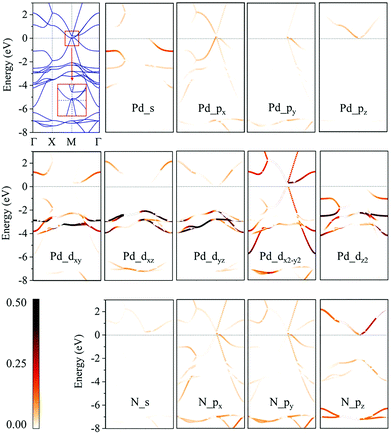
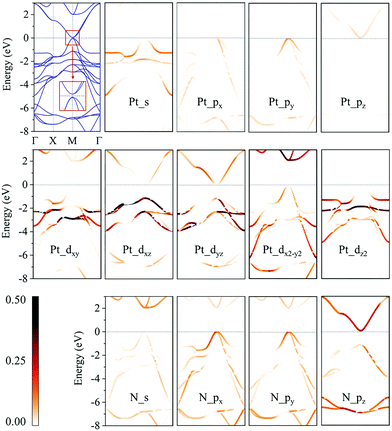
We then calculate the electronic band structures of penta-MN2 to explore the electronic properties. The PBE results for penta-PdN2 and penta-PtN2 are plotted in Fig. 5 and 6, respectively. It is clear that there is no gap between the valence and conduction bands of penta-PdN2, demonstrating its metallic character. However, the band structures of penta-PtN2 show that it is a direct bandgap semiconductor with a small band gap of 75 meV. The valance band maximum (VBM) and conduction band minimum (CBM) are both located at the M point of the first Brillouin zone.
To better understand the electronic properties of penta-MN2, their orbital hybridization forms are studied. The atomic orbital contributions to the band structures of penta-PdN2 and penta-PtN2 are shown in Fig. 5 and 6. The ground state electronic configuration of an isolated N2 dimer is (σ1s)2(σ1s*)2(σ2s)2(σ2s*)2(σ2p)2(π2p)4. Our results show that for both of penta-PdN2 and penta-PtN2, the occupied electronic bands near the Fermi level are mainly contributed by d orbitals of M atoms, because these orbitals have higher energy and transfer electrons to N–N dimers, and they coordinate with unoccupied orbitals of N–N. Meanwhile, the electronic bands in the energy range of −5 to −3 eV for penta-PdN2 and −4 to −2 eV for penta-PtN2 are contributed by d orbitals of M atoms with slight contributions from the p orbitals of N atoms, suggesting that d orbitals of M atoms can hybridize with the π2p of N–N dimers. Also, the deeper occupied bands in the energy range from −8 to −6 eV are mostly contributed by N–N dimers because their energies are much lower than that of the M-d states.
3.5 Carrier mobility
Besides the mechanical and electronic properties, the carrier mobility is also a significant factor to determine the performance of a semiconductor. By using the acoustic-phonon-limited scattering model, we calculate the carrier mobility of penta-PtN2. Due to the tetragonal symmetry of penta-PtN2, the carrier mobility along x and y directions is isotropic. All the calculated results containing effective mass, deformational potential constants, 2D elastic modulus and carrier mobility are summarized in Table 2. We can see that the effective mass of electron and hole are 0.118 m0 and 0.198 m0 for penta-PtN2. According to equation (a), the light effective mass and high 2D elastic modulus lead to ultrahigh carrier mobilities (μe = 219 × 103 cm2 V−1 s−1 and μh = 132 × 103 cm2 V−1 s−1) which are higher than that of phosphorene (1–26 × 103 cm2 V−1 s−1) and even are close to that of graphene (∼200 × 103 cm2 V−1 s−1).53–55 The ultrahigh carrier mobility allows penta-PtN2 to be of potential application in electronic devices.| Carrier type | m*/m0 | E 1 (eV) | C 2D (J m−2) | μ (103 cm2 V−1 s−1) | |
|---|---|---|---|---|---|
| PtN2 | e | 0.118 | 1.401 | 227.7 | 219 |
| h | 0.198 | 1.391 | 227.7 | 132 | |
4. Conclusions
In summary, by using the CALYPSO code, we obtain the 2D ground-state structures of MN2 (M = Pd, Pt), which are composed entirely of pentagons. DFT calculations confirm their dynamical, thermal and mechanical stabilities. Moreover, compared with the experimentally synthesized pyrite MN2, the penta-MN2 monolayers show several distinct characteristics: (1) penta-MN2 monolayers are more stable than the pyrite structures in energy; (2) penta-MN2 show high melting point. Particularly, penta-PtN2 can withstand the temperature over 2000 K before it breaks down; (3) penta-MN2 possess high in-plane Young's modulus and high ideal strength; (4) penta-PtN2 has ultrahigh carrier mobility, with the values of μe = 219 × 103 cm2 V−1 s−1, μh = 132 × 103 cm2 V−1 s−1, which are higher than those of phosphorene and comparable with graphene. These excellent properties of penta-MN2 imply their potential applications in high refractory materials and nanoscale electronic devices. The present study would deepen our understandings on the diversity of geometries and properties of 2D metal nitrides.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by grants from the National Key Research and Development Program of China (2016YFE0127300, and 2017YFA0205003), the National Natural Science Foundation of China (NSFC-51471004, and NSFC-21773004), and supported by the High Performance Computing Platform of Peking University, China.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- C. Zhi, Y. Bando, C. Tang, H. Kuwahara and D. Golberg, Adv. Mater., 2009, 21, 2889–2893 CrossRef CAS.
- H. Liu, Y. Du, Y. Deng and P. D. Ye, Chem. Soc. Rev., 2015, 44, 2732–2743 RSC.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS.
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- S. Cahangirov, M. Topsakal, E. Akturk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804 CrossRef CAS PubMed.
- C. L. Lin, R. Arafune, K. Kawahara, N. Tsukahara, E. Minamitani, Y. Kim, N. Takagi and M. Kawai, Appl. Phys. Express, 2012, 5, 045802 CrossRef.
- S. H. Zhang, J. Zhou, Q. Wang, X. S. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377 CrossRef CAS.
- P. Urbankowski, B. Anasori, T. Makaryan, D. Er, S. Kota, P. L. Walsh, M. Zhao, V. B. Shenoy, M. W. Barsoum and Y. Gogotsi, Nanoscale, 2016, 8, 11385–11391 RSC.
- M. Khazaei, M. Arai, T. Sasaki, C.-Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185–2192 CrossRef CAS.
- I. R. Shein and A. L. Ivanovskii, Comput. Mater. Sci., 2012, 65, 104–114 CrossRef CAS.
- Y. Xie and P. R. C. Kent, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235411 CrossRef.
- G. Gao, G. Ding, J. Li, K. Yao, M. Wu and M. Qian, Nanoscale, 2016, 8, 8986–8994 RSC.
- M. Khazaei, A. Ranjbar, M. Ghorbani-Asl, M. Arai, T. Sasaki, Y. Liang and S. Yunoki, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 205125 CrossRef.
- X. Zhang, Z. Zhang, X. Zhao, D. Wu, X. Zhang and Z. Zhou, J. Mater. Chem. A, 2017, 5, 2870–2875 RSC.
- G. M. Veith, A. R. Lupini, L. Baggetto, J. F. Browning, J. K. Keum, A. Villa, L. Prati, A. B. Papandrew, G. A. Goenaga, D. R. Mullins, S. E. Bullock and N. J. Dudney, Chem. Mater., 2013, 25, 4936–4945 CrossRef CAS.
- C. Zhang, J. Liu, H. Shen, X.-Z. Li and Q. Sun, Chem. Mater., 2017, 29, 8588–8593 CrossRef CAS.
- S. Gong, C. Zhang, S. Wang and Q. Wang, J. Phys. Chem. C, 2017, 121, 10258–10264 CrossRef CAS.
- J. Li, X. Fan, Y. Wei, H. Liu, S. Li, P. Zhao and G. Chen, Sci. Rep., 2016, 6, 33060 CrossRef CAS.
- C. Zhang and Q. Sun, J. Phys. Chem. Lett., 2016, 7, 2664–2670 CrossRef CAS PubMed.
- F. Wu, C. Huang, H. Wu, C. Lee, K. Deng, E. Kan and P. Jena, Nano Lett., 2015, 15, 8277–8281 CrossRef CAS PubMed.
- J. I. Cerda, J. Slawinska, G. Le Lay, A. C. Marele, J. M. Gomez-Rodriguez and M. E. Davila, Nat. Commun., 2016, 7, 13076 CrossRef CAS PubMed.
- J. Chen, G. Schusteritsch, C. J. Pickard, C. G. Salzmann and A. Michaelides, Phys. Rev. Lett., 2016, 116, 025501 CrossRef.
- X. Li, Y. Dai, M. Li, W. Wei and B. Huang, J. Mater. Chem. A, 2015, 3, 24055–24063 RSC.
- A. Lopez Bezanilla and P. B. Littlewood, J. Phys. Chem. C, 2015, 119, 19469–19474 CrossRef CAS.
- A. D. Oyedele, S. Yang, L. Liang, A. A. Puretzky, K. Wang, J. Zhang, P. Yu, P. R. Pudasaini, A. W. Ghosh, Z. Liu, C. M. Rouleau, B. G. Sumpter, M. F. Chisholm, W. Zhou, P. D. Rack, D. B. Geohegan and K. Xiao, J. Am. Chem. Soc., 2017, 139, 14090–14097 CrossRef CAS.
- Y. Wang, Y. Li and Z. Chen, J. Mater. Chem. C, 2015, 3, 9603–9608 RSC.
- M. Yagmurcukardes, H. Sahin, J. Kang, E. Torun, F. M. Peeters and R. T. Senger, J. Appl. Phys., 2015, 118, 104303 CrossRef.
- S. Zhang, J. Zhou, Q. Wang and P. Jena, J. Phys. Chem. C, 2016, 120, 3993–3998 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- Y. Wang, M. Miao, J. Lv, L. Zhu, K. Yin, H. Liu and Y. Ma, J. Chem. Phys., 2012, 137, 224108 CrossRef.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72–80 CrossRef CAS.
- E. Ressouche, V. Simonet, B. Canals, M. Gospodinov and V. Skumryev, Phys. Rev. Lett., 2009, 103, 267204 CrossRef CAS.
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Science, 2006, 311, 1275–1278 CrossRef CAS PubMed.
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, J. M. Zaug, D. Aberg, Y. Meng and V. B. Prakapenka, J. Mater. Res., 2008, 23, 1–5 CrossRef CAS.
- D. Aberg, B. Sadigh, J. Crowhurst and A. F. Goncharov, Phys. Rev. Lett., 2008, 100, 095501 CrossRef PubMed.
- A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. J. Hemley and H. K. Mao, Phys. Rev. Lett., 2006, 96, 155501 CrossRef.
- Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104 CrossRef.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- J. Wang, S. Yip, S. R. Phillpot and D. Wolf, Phys. Rev. Lett., 1993, 71, 4182–4185 CrossRef CAS.
- R. John and B. Merlin, Cryst. Struct. Theory Appl., 2016, 5, 43–55 CAS.
- Q. Peng and S. De, Phys. Chem. Chem. Phys., 2013, 15, 19427–19437 RSC.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- J.-H. Chen, C. Jang, S. Xiao, M. Ishigami and M. S. Fuhrer, Nat. Nanotechnol., 2008, 3, 206 CrossRef CAS.
- R. Fei and L. Yang, Nano Lett., 2014, 14, 2884–2889 CrossRef CAS.
- J. Qiao, X. Kong, Z. X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 4475 CrossRef CAS.
| This journal is © the Owner Societies 2019 |