View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C8CP03398F (Communication) Phys. Chem. Chem. Phys., 2018, 20, 19307-19313

Designing the ammonium cation to achieve a higher hydrophilicity of bistriflimide-based ionic liquids†

A. Mão de Ferro a, P. M. Reis ab, M. R. C. Soromenho ab, C. E. S. Bernardes c, K. Shimizu c, A. A. Freitas c, J. M. S. S. Esperança *ab, J. N. Canongia Lopes *ac and L. P. N. Rebelo ab
aInstituto de Tecnologia Química e Biológica António Xavier, Universidade Nova de Lisboa, Oeiras, 2780-157, Portugal
bLAQV, REQUIMTE, Departamento de Química, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa, Caparica, 2829-516, Portugal. E-mail: jmesp@fct.unl.pt
cCentro de Química Estrutural, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais, Lisboa, 1049-001, Portugal. E-mail: jnlopes@tecnico.ulisboa.pt

Received 19th April 2018 , Accepted 6th June 2018

First published on 6th June 2018

Abstract

In this work, we have found complete water miscibility for a priori, water immiscible (highly hydrophobic) ionic liquids by chemical manipulation of the quaternary ammonium cation grafted with hydroxyethyl moieties. Specifically, we were able to obtain bistriflimide-based ionic liquids completely miscible with water, even below room temperature. The underlying reason is the full integration of the OH groups of the cation in the continuous H-bonded network of water.

Introduction

The bis(trifluoromethyl)sulfonylimide anion, usually named as bistriflimide and represented as [NTf2]−, is a common component of many ionic liquids (ILs). This fact can be explained by the important advantages that it brings to this class of fluids such as high chemical and thermal stability, and low viscosity and melting point temperatures. Another well-known characteristic of the bistriflimide anion is that it produces hydrophobic ILs. For instance, only recently it was discovered that bistriflimide combined with the strongly hydrophilic cholinium cation, melts at around room temperature and becomes miscible with water above 70 °C.1–3 In contrast, the corresponding halide analogue (cholinium chloride) exhibits a melting point which is 200 °C higher and is known to be very hygroscopic.

Bistriflimide-based ionic liquids (BILs) have also attracted interest in the field of energy applications, due to their wide electrochemical window.4 Their potential use in lithium batteries, sodium secondary batteries5–7 and polymeric actuators8 has been broadly reported.

It is however evident that the hydrophobic behaviour of the bistriflimide anion may restrict its utility. For instance, in what concerns bio-applications, e.g. biocatalysis,9 the formulation of ILs incorporating active pharmaceutical ingredients10,11 or in drug delivery media,12,13 hydrophilicity matters. Regarding bio-applications, it is also widely known that BILs depict a higher toxicity than their halide analogues, or even ILs containing [PF6]− or [BF4]− anions.14 This fact alone represents a limitation for the adoption of BILs in certain applications. However, it should be also noted that the toxicity of ILs was found to be more dependent on the length of the alkyl chain of the cation than on the replacement of the bistriflimide anion by a halide.15

The ILs ability of being easily tuned, either by simple exchange of their constituent ions or by modification of the alkyl chains, represents an important advantage. Manipulating the cation in order to break the hydrophobicity of BILs—while keeping their melting points below room temperature—represents a challenge which, to the best of our knowledge, is yet to be attempted.

Taking advantage of the tuning capabilities of the ammonium cation, as well as, its well-known low toxicity behaviour in species with short alkyl chains,15–17 we have explored new synthetic routes aiming to explore how the new functional groups affect the solubility of the ILs and, in particular, how these groups increase the hydrophilicity of the ammonium BILs. Given the high hydrophilicity of the hydroxyethyl group, the natural approach has consisted on exploring the effect of increasing the number of these groups attached to the nitrogen atom of the ammonium cation. As such, instead of cholinium, we have adopted N-ethyl-N-N-dimethyl-N-(2-hydroxyethyl)ammonium, [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH]+, as our starting-point cation in order to increase the chances of obtaining low-melting temperature ILs. The BILs studied in this work incorporate the cations [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH]+, [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH]+, [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1]+, [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4]+, [N2[thin space (1/6-em)]1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH]+, [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH]+, [N2[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH]+ and [N4[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH]+, cf.Fig. 1 for the nomenclature used throughout this work. Note that these ILs have distinct functional groups, number of hydroxyalkyl chains and also distinct alkyl side chain lengths.


image file: c8cp03398f-f1.tif
Fig. 1 Name, acronym, molecular weight, and structural formula of the constituents of the ILs under study.

This study reports on the liquid–liquid equilibrium of BIL systems combined with either water or n-alkyl alcohols (from methanol to hexanol) cf.Table 1. The results are complemented by analyses at a molecular level resulting from Molecular Dynamics (MD) simulations conducted on selected model systems.

Table 1 Matrix showing the binary systems studied (×) in this work. The [NTf2] anion is omitted from the table
Cations C1–C6 alcohols Water
[N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH]+ ×
[N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH]+ × ×
[N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1]+ × ×
[N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4]+ × ×
[N2[thin space (1/6-em)]1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH]+ ×
[N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH]+ ×
[N2[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH]+ ×
[N4[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH]+ ×

Experimental

The liquid–liquid phase equilibria (LLE) measurements were performed using the “cloud point” method, based on the visual detection of the turbidity of solutions contained in 4 mL Pyrex glass cells equipped with magnetic stirrers. All samples were gravimetrically prepared at atmospheric pressure.

The cell was placed in a heating bath and the temperature of the liquid–liquid phase transition was taken upon cooling down to the point at which the first sign of turbidity appeared in the solution. Data were confirmed by repeated cooling-heating cycles (at least three in all cases). For measurements at temperatures between room temperature and ca. 100 °C we have used a water plus ethylene glycol bath. For temperatures below or above this range, the measurements were performed in ethanol or silicone oil baths, respectively. The bath's temperature was measured using a four-wire platinum resistance thermometer coupled to a previously calibrated Yokogawa 756I digital multimeter. The uncertainty of this method is mainly due to the visual determination, which often offered a challenge for extreme mass-fraction concentration values. Overall, taking into account all sources of error, an uncertainty better than 1 K is estimated.

The ionic liquids used in this work were synthesised according to the procedure described in the ESI.† Characterization analysis by NMR and Elemental Analysis indicate an overall purity better than 99 wt% (see ESI†). Each IL was dried under vacuum at least for 48 h at ca. 60 °C before any experiment. The molecular solvents used herein were acquired from different suppliers (purity between brackets): methanol from Riedel-de Haën (99.9 wt%); ethanol from Panreac (99.8 wt%); propanol from Merck (99.5 wt%); and butanol (99.8 wt%), pentanol (99 wt%), and hexanol (98 wt%) from Sigma-Aldrich. Water was of Millipore grade. All molecular solvents, except, obviously, water, were dried with 4 Å molecular sieves and filtered before preparing the binary systems.

Molecular Dynamics (MD) simulations were carried out using the DLPOLY package.18 The [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] and [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] ionic liquids were modeled using the CL&P atomistic force field,19,20 which is based on the OPLS-AA framework21 but was to a large extent developed specifically for encompassing entire homologous series of ionic liquids. Their mixtures with either water or alcohols were modeled using the SPC model22 and OPLS force fields for those types of molecule, respectively. All simulations were carried out at 400 K. The ([N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] plus water) mixture simulations were also carried out at 298 K.

The size of the systems and the duration of the simulations are of particular importance since periodic boundary conditions can induce artificial finite-size effects on the length scales of the nanostructures under scrutiny. The runs were performed with a 2 fs time step and a 1.6 nm cutoff distance. Ewald summation corrections were performed beyond the cutoffs. The simulations were performed using cubic simulation boxes slightly larger than (5 × 5 × 5) nm3. The number of ion pairs and the size of the simulation boxes are presented in Table S1 of ESI.† Equilibrations started from initial low-density configurations, with ions placed randomly in periodic cubic boxes and were subjected to runs under N–p–T ensemble conditions (under the action of Nosé–Hoover barostats and thermostats) for more than 1 ns. Multiple re-equilibrations through the use of temperature annealing and switching off and on of the Coulomb interactions were performed. Further simulation runs were used to produce equilibrated systems at the studied temperatures. Finally, several (at least six) consecutive production stages of 1.0 ns each were performed.

Pair radial distribution functions, g(r), and the statistical tools used in the aggregate analyses (aggregate probability distribution functions, P(na) and number of neighbors analyses, Ni) were computed according to previously described methodologies.23,24

Results and discussion

The following discussion is divided in two sub-sections according to the nature of the solvents used in the binary mixtures. We will first address the experimental LLE data of systems composed of alcohols, and then those composed of water (see Tables S2 and S3 of ESI†).

LLE with n-alkanols

Fig. 2 depicts the temperature-composition phase diagrams of systems composed of n-alkanols and [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2], [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2] or [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2]. Seven systems were found to be completely miscible: [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2], [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2] and [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2] with methanol, [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2] with ethanol and [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] with propanol. The data can be found in Table S2 of the ESI.†
image file: c8cp03398f-f2.tif
Fig. 2 Temperature-composition (IL mass fraction, WIL) phase diagrams showing the LLE behaviour of binary mixtures of linear alcohols (blue circle, ethanol; magenta triangle, propanol; green square, butanol; brown star, pentanol; grey cross, hexanol) with (a) [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], (b) [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2], (c) [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2] and (d) [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2]. Note that the following systems were found to be completely miscible: [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2], [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2] and [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2] with methanol, [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] and [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2] with ethanol, and [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] with propanol.

All systems show upper critical solution temperatures (UCSTs) in the corresponding T–x phase diagrams. The almost symmetric nature of the phase diagrams suggests that the critical solution temperature is achieved at approximately equal mass fraction of the two components.25 UCST-type diagrams were expected for these systems, except for that based on [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2]. In fact, the ether functionality on the ammonium cation was regarded as a particular interesting example to look at, given the fact that lower critical solution temperatures (LCSTs) have been found in systems composed of hydroxyl-functionalized ammonium BILs and ether-functionalized solvents.26 However, when the ether and alcohol moieties are interchanged between the IL and the molecular solvent no LCST behaviour is found– cf.Fig. 2(c).

The results point out to a strong direct relation between the size of the alcohols alkyl chain and its miscibility with a given IL. This trend is independent of the polarity of the functional group in the IL. The fact that the exchange of the hydroxypropyl group by an apolar one ([N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2] vs. [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2]) also results in an IL completely miscible with methanol is also interesting to note.

Despite the importance of the alcohols aliphatic chain on the miscibility with a given IL, it is also perceived from Fig. 2 that the moieties grafted in the cation also play a fair role in the overall miscibility of the IL. For any given alcohol, the UCST's generally follows the trend [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] < [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2] < [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2] ≈ [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2], i.e., suggesting a direct relation between the polarity of the moiety and the miscibility of the IL with a given alcohol. However, when one compares the cases of [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2] versus [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2] mixed with small chain alcohols, a deviation from this general trend is found. This exception might find an explanation at the fact that there is some suppression of the nanostructured nature in ionic liquids with ether-functionalized chains.27

In order to rationalize these results at a molecular level and begin to unveil the mechanisms that may lead to higher IL hydrophilicity, we have performed a series of MD simulations on mixtures of [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] with 1-butanol, 1-pentanol and 1-hexanol. In order to compare the different mixtures at equivalent conditions we conducted the simulation runs at 400 K and xIL = 0.2. This corresponds to single-phase conditions for all mixtures (above the corresponding UCST values) and to volume fractions occupied by the IL component in the 30–45% range, i.e. close to the concentrations corresponding to the immiscibility windows maxima.

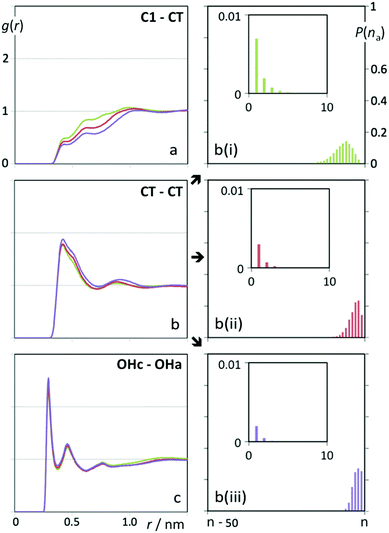
Fig. 3 shows pair radial distribution functions between selected interaction centres in the ionic liquid and the alcohol molecules. Fig. 3a displays correlations between the terminal methyl groups of the alcohol molecules (CT) and the methyl groups of the cation (C1). The absence of a distinct first peak above g(r) = 1 in the 0.5 nm region is a sign that the alkyl chains of the alcohol molecules are never in the vicinity of the charged part of the cation (the nitrogen atom and its four adjacent methyl/methylene groups). The shape of the g(r) function is also similar to the C1–C1 correlation in pure [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] (cf. Fig. 3 of ref. 28) that indicates that the methyl groups of the cations are never close to each other due to the presence of an intercalated counter-ion (the [NTf2]− anion).


image file: c8cp03398f-f3.tif
Fig. 3 Left column: Pair radial distribution functions, g(r), between selected pairs of interaction centres in the [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] ionic liquid and 1-butanol (green), 1-pentanol (red) or 1-hexanol (purple). C1 and OHc correspond to the methyl and hydroxyl groups in the cation, CT and OHa to the terminal methyl and hydroxyl groups in the alcohol molecules. Right column: Discrete probability distribution functions, P(na), of aggregates containing na alcohol alkyl chains. The value n (=600) corresponds to the number of alcohol molecules in the simulation box.

Fig. 3b shows, on the other hand, that there is a strong correlation between the terminal methyl groups from the alcohol molecules. In other words, the alkyl side chains of the alcohol molecules tend to cluster together. Such aggregation can be further appreciated in the three panels on the right column of Fig. 3: the probability distribution functions of finding large aggregates containing most of the alcohol chains present in the simulation box (n) is very large, and the size of such aggregates increases from butanol to hexanol. Such alkyl aggregates percolate the entire simulation box. At the nanoscopic level, the mixture is a bicontinuous phase formed by a polar network (the charged parts of the IL ions) intermeshed with a nonpolar domain (the alkyl side chains of the alcohols). The potential for phase separation is thus very large and it indeed occurs for lower temperatures, where the entropy mixing term is not enough to balance the penalty imposed by the enthalpy term. The bicontinuous character of the mixtures is also similar to the nature of pure ionic liquids with long alkyl side chains. However, phase separation in the latter case is not possible due to the fact that the chains are covalently attached to the ion cores of the IL.

Fig. 3c shows the correlation between the hydroxyl groups in the alcohol molecules (OHa) and those in the choline cations (OHc). The strong correlation between these groups supports the idea that the two nano-segregated domains (the polar network and the alcohol alkyl chains) are able to interact via hydrogen bonding between the OH groups present in both species and thus partially compensate part of their intrinsic antagonism. In fact, similar interactions are also possible between the alcohol OH group and the oxygen atoms of the [NTf2]− anion or the methyl hydrogen atoms of the cation. The corresponding g(r) functions are given as ESI.†

The interaction between the alcohol OH group and the different charged parts of the ionic liquids explains the trends experimentally observed in Fig. 2. In short chain alcohols (ethanol, propanol) the small nonpolar aggregates are better accommodated in the midst of the IL polar network due to the dominant influence of the OH group in such alcohols. In longer alcohols (butanol, pentanol, hexanol) the same amount of H-bonding cannot compensate the existence of much larger non-polar domains and two-phase systems subsist up to higher UCST values. Moreover, the presence of an additional interaction center in the cation—the C2OH or C3OH groups in the choline-based ILs in Fig. 2(a) and (b)versus the C2OC1 and C4 groups in Fig. 2(c) and (d)—also decreases the corresponding UCST values.

Pathway to a higher hydrophilicity

We have shown in the previous section that the presence of small and polar groups in the ammonium cation leads to BILs with high affinity to short-chained n-alkanols. Indeed, the hydrophobicity of ILs is directly related to the length of its aliphatic chains.3,29,30 In what concerns the binary mixtures of water and the ILs with similar sized ammonium cations, [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2], [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2] and [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2], the LLE results indicate that the hydrophilicity is correlated with the polarity of the attached functional group, see Fig. 4. In the case of [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2], the complete immiscibility envelope could not be determined since the (hypothetical) UCST lies above the upper limit of the working temperature range for this type of system (470 K).3 It should be noted that the increment of a CH2 group in the hydroxyethyl chain of [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], to obtain [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2], does not change significantly the phase diagram, cf.Fig. 4. However, when the CH2 increment occurs in the ethyl group – [N3[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], which is an isomer of [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2], a considerably higher hydrophobicity is observed.
image file: c8cp03398f-f4.tif
Fig. 4 Temperature-composition phase diagrams showing the LLE behaviour of binary mixtures of distinct ILs with water. The ILs [N2[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] and [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] were found to be completely miscible with water. The phase diagrams of [Nn[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], with n = 1, 2, and 3, are shown for comparison purposes and were taken from previous studies.3,26 Full circle – [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]3OH][NTf2], full triangle – [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2O1][NTf2], full square – [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]4][NTf2], blue star – [N4[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2], brown cross – [N2[thin space (1/6-em)]1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2], empty circle – [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], empty triangle – [N2[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], empty square – [N3[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2].

Fig. 4 also shows that a significant decrease of the UCST is obtained when a methyl group of ethylcholinium is replaced by a hydroxyethyl group to yield [N2[thin space (1/6-em)]1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2]. When a third hydroxyethyl group is inserted, then the miscibility of the BIL with water depends on the size of the remaining alkyl chain. Therefore, [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] and [N2[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] were found to be completely soluble in water, whereas the lengthening of the remaining alkyl chain to a butyl group, [N4[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2], partially cancels the hydrophilicity given by the three hydroxyethyl chains, forming a BIL which again presents an UCST with water. To the best of our knowledge this is the first example of a bistriflimide based ionic liquid completely soluble in water at room temperature.

The issue of the hydrophilicity at a molecular level can now be addressed if one considers simulations performed on the pure [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] and [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] ionic liquids and on mixtures of the latter with water. Fig. 5 shows probability distribution functions of different types of aggregation in such systems.


image file: c8cp03398f-f5.tif
Fig. 5 Discrete probability distribution functions, P(na), of different types of aggregate in [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2], and [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] pure ILs (top and middle) and in a ([N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] + H2O) aqueous mixture at xIL = 0.05. The depicted aggregates are: cat–ani (green) as the polar network; OHcat–OHcat (light blue) as the choline H-bonding; OHcat–OHH2O (dark blue) as the H-bonding network in the aqueous mixture. The value nT corresponds to the number of ions in the simulation box (700 in the two pure ILs and 320 in the mixture); ncat is the number of cations (350 in the pure ILs, 160 in the mixture); ncat+H2O is the number of cations plus water molecules (3200 in the mixture). The Ni values correspond to the average number of neighbors of a given ion or molecule within an aggregate. Simulations performed at T = 400 K for the pure BILs and at T = 298 K for the mixture. A simulation at 400 K for the mixture was also performed for comparisons purposes and is given as ESI.†

Previous discussions have shown that hydrogen bonding between different species can play a crucial role on the fluid phase behaviour of these systems, namely on the promotion of interactions between the polar network of the ionic liquid and the non-polar domains of 1-alkanols, and the IL hydrophilicity in aqueous solutions. In the case of aqueous solutions of [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] and [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2], partial immiscibility and complete miscibility was observed at room temperature, respectively. Fig. 5 can explain such behaviour.

The top panel clearly shows that the pure [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] ionic liquid is composed of a continuous polar network (all ions belong to such network and each of them has, on average, Ni = 5.93 contact points with its first-shell counterions). The OH groups of the ethanol moiety are either isolated from each other (68%) or form H-bonded clusters with very few OH groups (22% as pairs, 6% as trios, Ni = 0.37). The solubility of [N1[thin space (1/6-em)]1[thin space (1/6-em)]1[thin space (1/6-em)]2OH][NTf2] in water is rather poor because the water molecules are not able to disrupt the continuous polar network and solvate bulky molecular anions such as [NTf2]−.

The middle panel shows a rather different picture. The [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] polar network is still continuous but with a smaller number of first-contact neighbors (Ni = 5.10). However, the three ethanol moieties are now able to form a second continuous network of H-bonded OH groups, each of them establishing two H-bonds to neighbouring OH groups (Ni = 2.12).

The bottom panel shows that in the ([N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] + H2O) mixture with 5% IL mole percentage (57% IL mass percentage), the water molecules also form a continuous H-bonded network where the OH groups from the cation are now fully integrated. In fact, the number of H-bonded clusters formed exclusively by cations is now very small. Moreover, a few ions are now free from the polar network and become solvated by water molecules. This state of affairs is consistent with a situation where as more water is added to the system the IL can become fully solvated. The driving force behind the complete miscibility of this BIL in water is thus its ability to compensate the enthalpy penalty associated with the [NTf2]− anion solvation with an enthalpy gain related to the integration of the cation in the H-bonded water network.

Conclusions

This study reports on the liquid–liquid equilibria of binary mixtures composed of either n-alkyl alcohols (C1 ≤ n ≤ C6) or water and a series of bistriflimide-based ionic liquids with specially-designed quaternary ammonium cations, [Ni[thin space (1/6-em)]j[thin space (1/6-em)]k[thin space (1/6-em)]l].

The results point out to three main conclusions: (i) the polarity of the moiety present in the cation is, in general, correlated with the miscibility of the IL with a given alcohol or water; (ii) adding hydroxyethyl groups to the ammonium cation is an effective way to obtain hydrophilic bistriflimide-based ionic liquids, specifically, [N2[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] and [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] and (iii) MD simulations have shown that in ([N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] + H2O) mixtures of about equimass composition, the OH groups of the cation are fully integrated in the continuous H-bonded network of water. The presence of three anchoring points in [N1[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH[thin space (1/6-em)]2OH][NTf2] stabilizes the molecular ions in the midst of the aqueous medium and allows the complete solubilisation of such BIL.

These results open the door for the use of bistriflimide-based ionic liquids in several processes where their application, e.g. aqueous biphasic systems separations, was previously prevented due to their hydrophobic behaviour.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Fundação para a Ciência e Tecnologia, FCT/MCTES (Portugal) for financial support through a FCT Investigator contract (IF/00355/2012 – J. M. S. S. E), post-doctoral grants SFRH/BPD/94291/2013 (K. S.), SFRH/BPD/94299/2013 (A. A. F.) and SFRH/BPD/101505/2014 (C. E. S. B.), and through projects PTDC/CTM-NAN/121274/2010, UID/QUI/50006/2013, UID/QUI/00100/2013 and UID/Multi/04551/2013. The NMR spectrometers are part of The National NMR Facility, supported by FCT/MCTES (RECI/BBB-BQB/0230/2012).

Notes and references

  1. P. Nockemann, K. Binnemans, B. Thijs, T. N. Parac-Vogt, K. Merz, A. V. Mudring, P. C. Menon, R. N. Rajesh, G. Cordoyiannis, J. Thoen, J. Leys and C. Glorieux, J. Phys. Chem. B, 2009, 113, 1429–1437 CrossRef PubMed.
  2. U. Domanska, A. Marciniak and M. Krolikowski, J. Phys. Chem. B, 2008, 112, 1218–1225 CrossRef PubMed.
  3. A. J. L. Costa, M. R. C. Soromenho, K. Shimizu, I. M. Marrucho, J. M. S. S. Esperança, J. N. C. Lopes and L. P. N. Rebelo, J. Phys. Chem. B, 2012, 116, 9186–9195 CrossRef PubMed.
  4. D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250 Search PubMed.
  5. T. Yamamoto, T. Nohira, R. Hagiwara, A. Fukunaga, S. Sakai, K. Nitta and S. Inazawa, J. Power Sources, 2012, 217, 479–484 CrossRef.
  6. B. Garcia, S. Lavallee, G. Perron, C. Michot and M. Armand, Electrochim. Acta, 2004, 49, 4583–4588 CrossRef.
  7. T. Nohira, T. Ishibashi and R. Hagiwara, J. Power Sources, 2012, 205, 506–509 CrossRef.
  8. S. Imaizumi, H. Kokubo and M. Watanabe, Macromolecules, 2012, 45, 401–409 CrossRef.
  9. F. J. Deive, D. Ruivo, J. V. Rodrigues, C. M. Gomes, M. A. Sanroman, L. P. N. Rebelo, J. M. S. S. Esperança and A. Rodriguez, RSC Adv., 2015, 5, 3386–3389 RSC.
  10. W. L. Hough, M. Smiglak, H. Rodriguez, R. P. Swatloski, S. K. Spear, D. T. Daly, J. Pernak, J. E. Grisel, R. D. Carliss, M. D. Soutullo, J. H. Davis and R. D. Rogers, New J. Chem., 2007, 31, 1429–1436 RSC.
  11. J. M. M. Araujo, C. Florindo, A. B. Pereiro, N. S. M. Vieira, A. A. Matias, C. M. M. Duarte, L. P. N. Rebelo and I. M. Marrucho, RSC Adv., 2014, 4, 28126–28132 RSC.
  12. M. Moniruzzaman, N. Kamiya and M. Goto, J. Colloid Interface Sci., 2010, 352, 136–142 CrossRef PubMed.
  13. M. Moniruzzaman, Y. Tahara, M. Tamura, N. Kamiya and M. Goto, Chem. Commun., 2010, 46, 1452–1454 RSC.
  14. S. Stolte, J. Arning, U. Bottin-Weber, M. Matzke, F. Stock, K. Thiele, M. Uerdingen, U. Welz-Biermann, B. Jastorff and J. Ranke, Green Chem., 2006, 8, 621–629 RSC.
  15. X. F. Wang, C. A. Ohlin, Q. H. Lu, Z. F. Fei, J. Hu and P. J. Dyson, Green Chem., 2007, 9, 1191–1197 RSC.
  16. D. J. Couling, R. J. Bernot, K. M. Docherty, J. K. Dixon and E. J. Maginn, Green Chem., 2006, 8, 82–90 RSC.
  17. S. Tang, G. A. Baker and H. Zhao, Chem. Soc. Rev., 2012, 41, 4030–4066 RSC.
  18. W. Smith and T. R. Forester, The DL_POLY Package of Molecular Simulation Routines (v.2.2), The Council for The Central Laboratory of Research Councils, Daresbury Laboratory, Warrington, 2006 Search PubMed.
  19. J. N. C. Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
  20. J. N. C. Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
  21. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef.
  22. M. Praprotnik, D. Janežič and J. Mavri, J. Phys. Chem. A, 2004, 108, 11056–11062 CrossRef.
  23. K. Shimizu, C. E. S. Bernardes and J. N. C. Lopes, J. Phys. Chem. B, 2014, 118, 567–576 CrossRef PubMed.
  24. C. E. S. Bernardes, K. Shimizu, A. I. M. C. L. Ferreira, L. M. N. B. F. Santos and J. N. C. Lopes, J. Phys. Chem. B, 2014, 118, 6885–6895 CrossRef PubMed.
  25. V. Najdanovic-Visak, J. M. S. S. Esperança, L. P. N. Rebelo, M. N. da Ponte, H. J. R. Guedes, K. R. Seddon, H. C. de Sousa and J. Szydlowski, J. Phys. Chem. B, 2003, 107, 12797–12807 CrossRef.
  26. A. J. L. Costa, M. R. C. Soromenho, K. Shimizu, J. M. S. S. Esperança, J. N. C. Lopes and L. P. N. Rebelo, RSC Adv., 2013, 3, 10262–10271 RSC.
  27. K. Shimizu, C. E. S. Bernardes, A. Triolo and J. N. C. Lopes, Phys. Chem. Chem. Phys., 2013, 15, 16256–16262 RSC.
  28. A. J. L. Costa, M. R. C. Soromenho, K. Shimizu, I. M. Marrucho, J. M. S. S. Esperança, J. N. C. Lopes and L. P. N. Rebelo, ChemPhysChem, 2012, 13, 1902–1909 CrossRef PubMed.
  29. M. Wagner, O. Stanga and W. Schroer, Phys. Chem. Chem. Phys., 2003, 5, 3943–3950 RSC.
  30. F. M. Maia, O. Rodríguez and E. A. Macedo, Fluid Phase Equilib., 2010, 296, 184–191 CrossRef.

Footnote

† Electronic supplementary information (ESI) available: Synthesis, 1H NMR, 19F NMR and elemental analysis; MD simulations details; LLE data. See DOI: 10.1039/c8cp03398f
This journal is © the Owner Societies 2018
Click here to see how this site uses Cookies. View our privacy policy here.