Coordination-induced CO₂ fixation into carbonate by metal oxides

Abstract

Here, we have investigated how coordination induces CO₂ fixation into a carbonate using a cationic yttrium oxide model catalyst. The infrared spectra show that the first three CO₂ molecules are weakly bound to the metal. Subsequent coordination of CO₂ ligands leads to the formation of a carbonate complex and results in a core ion transition. The conversion of Y = O and CO₂ to carbonate is achieved by the donation of electrons from the ligands to the metal. Systematic analyses of the effects of different ligands and metals on the coordination-induced CO₂ fixation demonstrate that the present system serves as an efficient and rational model for adjusting CO₂ fixation and CO₂ emission.

---

1. Introduction

The chemical transformation of carbon dioxide is of considerable interest because CO₂ is a potent greenhouse gas, but is also an abundant renewable resource for the production of fine chemicals and clean fuels.^1,2 Metal complexes are widely involved in the catalytic activation and fixation of the robust CO₂ molecule.^3,4 Advanced surface-science investigations and theoretical calculations have demonstrated the formation of carbonate species (CO₃²⁻) on various metal oxides.^5–7 Vibrational spectroscopic measurements of the interfaces indicate that the 1200–1700 cm⁻¹ spectral region corresponds to the C–O stretching vibrations of CO₂ adsorption products (i.e., CO₂⁻, CO₃²⁻, HCO₃⁻, HCO₂⁻, etc.), which readily become complex and difficult to interpret.⁷ A recent noteworthy development in this endeavor is the use of gas-phase optical spectroscopy coupled with mass spectrometry to understand the direct relationships between structure and function by adding one CO₂ molecule at a time to a metal model catalyst, as well as to clarify the pivotal roles played by the ligands, metals, and charge effects.^8–10

Pioneering infrared photodissociation (IRPD) spectroscopic studies on anionic metal–CO₂ complexes have revealed that the activation of CO₂ can be readily accessed by metal anions, where the excess electrons lead to a deformation of CO₂ from the linear geometry of the neutral molecule to a bent anion, resulting in an elongation of the C–O bond distances.⁹ While the first-row transition metal anions preferentially involve the bidentate configuration [M(η²-CO₂)]⁻, the atomic Bi⁻, Cu⁻, Ag⁻, and Au⁻ anions bind to CO₂ in the form of metalloformates [M(η¹-CO₂)]⁻.^11–17 In particular, the atomic Bi⁻ anion is able to switch from a metalloformate complex to an oxalate product with increasing cluster size.¹⁶ A double metal–oxygen coordination mode has been spectroscopically characterized in a [ClMg(η²-O₂C)]⁻ complex.¹⁸

For the reactions of CO₂ with metal cations, in general, the CO₂ molecules are weakly bound to metal cations in an ‘‘end-on’’ configuration via a charge-quadrupole electrostatic interaction.^8,19–21 However, the early transition metal cations in their +1 charge state have very strong reducing power, and nine of them can reduce CO₂ to CO (i.e. Sc⁺, Y⁺, La⁺; Ti⁺, Zr⁺, Hf⁺; Nb⁺, Ta⁺; W⁺).¹⁹ σ donating ligands, such as CO₂, are able to enhance the reducing power of metal cations. In fact, seven CO₂ molecules were found to be capable of inducing the metal → ligand electron transfer of V⁺.²² The feasibility of CO₂ activation-induced C–C bond formation was demonstrated by the studies on the phenyl yttrium cation [Y(C₆H₅)]⁺, evidencing that the greater oxophilicity of the early transition metals can accelerate the insertion of CO₂ into a metal–carbon bond.²³ So far, the spectroscopic characterization of CO₂ fixation into carbonate by a cationic metal model catalyst has remained elusive in the gas phase. In this work, we report an infrared spectroscopic study on the reaction of CO₂ with a cationic yttrium oxide to investigate the effect of stepwise coordination on the structure and energetics, which provides detailed insights into the microscopic mechanism of coordination-driven CO₂ fixation into carbonate by metal oxides.

2. Experimental method

The experiments were carried out using a homemade infrared photodissociation apparatus, including a laser vaporization supersonic cluster source, a tandem time-of-flight (TOF) mass spectrometer, and a tunable infrared laser source, manufactured by Highlight Technology Corporation, Shanghai, China. The experimental setup has been previously described in detail.²⁴ Briefly, a 532 nm laser beam from a Nd:YAG laser was focused to vaporize a rotating metal rod. The purities of the targets were better than 99.9%. The surface of the rod was polished prior to the experiments to ensure a clean vaporization target. The [YO(CO₂)_n]⁺ complexes were produced by the reactions of the vaporized species with 2% O₂ seeded in CO₂. The stagnation pressure of the reaction gas was approximately 5–8 atm and the gas was introduced into the vacuum region using a pulsed General Valve (Series 9). After the supersonic expansion, the cationic complexes were skimmed into the acceleration region and analyzed using the first stage of the TOF system. The cations of interest were mass-selected and decelerated into the extraction region of the vertical second stage of the TOF system. Here, they interacted with a single pass of the IR photodissociation laser. The dissociation fragments and the remaining parent cations were analyzed using the vertical second stage of the TOF mass spectrometer. Typical spectra were recorded by scanning the infrared laser in increments of 2 cm⁻¹. Infrared photodissociation spectra were acquired by monitoring the fragment ions as a function of the wavelength of the tunable infrared laser.

The tunable infrared laser beam was generated by a KTP/KTA optical parametric oscillator/amplifier system (OPO/OPA, LaserVision) pumped by an injection-seeded Nd:YAG laser (Continuum Surelite EX). The system provided tunable IR output radiation from 700 to 7000 cm⁻¹ with a linewidth of 1 cm⁻¹. The wavelength of the OPO laser output was calibrated using a commercial wavelength meter (Bristol, 821 Pulse Laser Wavelength Meter).

3. Computational method

Quantum chemical calculations were performed using the Gaussian 09 program.²⁵ The structures were optimized by B3LYP hybrid functionals augmented with a dispersion correction (B3LYP-D) together with DZP basis sets for the carbon, oxygen, nitrogen, and hydrogen atoms and the LanL2DZ ECP basis set for the metal atoms. The integral grid used for the B3LYP-D calculations was a pruned (99590) grid (the “ultrafine” grid as defined by Gaussian 09). The harmonic vibrational frequencies were scaled by a factor of 0.964 in order to account for anharmonicities and for the method-dependent systematic errors on the calculated harmonic force constants, which were determined by the ratio of the experimental value (2349 cm⁻¹) to the B3LYP-D calculated one (2437 cm⁻¹) of the free CO₂ molecule. The resulting stick spectra were convoluted by a Gaussian line shape function with a full width at half maximum line width of 5 cm⁻¹, in order to account for line-broadening effects. B2PLYP(full)/def2-TZVP single point calculations on the B3LYP-D/DZP-LanL2DZ structures were carried out to determine relative energies.

4. Results and discussion

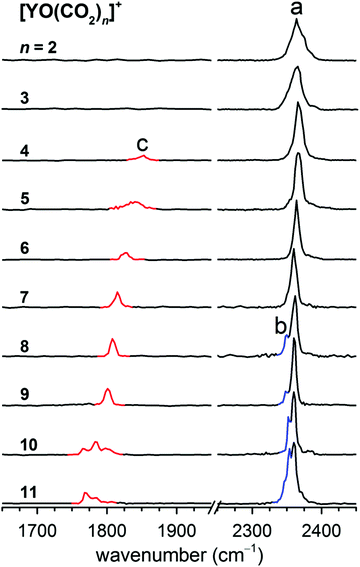
A series of yttrium oxide–CO₂ complexes in the form of [YO(CO₂)_n]⁺ were prepared by a pulsed laser vaporization/supersonic expansion ion source in the gas phase. A typical mass spectrum is shown in Fig. S1 in the ESI,† which was obtained at experimental conditions that favor the formation of cations with relatively high thermodynamic stability. The lowest dissociation energy of [YO(CO₂)]⁺ was calculated to be 85.6 kJ mol⁻¹ at the B2PLYP/def2-TZVP level of theory (Table S1, ESI†). Assuming that internally cold [YO(CO₂)]⁺ is formed, the absorption of at least four photons at around 2350 cm⁻¹ is required to overcome the dissociation limit. The photon fluence generated from the table-top LaserVision system was insufficient to induce the photofragmentation of [YO(CO₂)]⁺ under the experimental conditions. The messenger tagging efficiency of [YO(CO₂)]⁺ was too low to allow the IRPD measurements. Beginning at the n = 2 cluster, the fragmentation was observed. The number densities of the n ≥ 12 clusters were insufficient for the obvious detection of the IR-induced-dissociation fragmentation. The experimental IRPD spectra of the mass-selected [YO(CO₂)_n]⁺ (n = 2–11) are shown in Fig. 1 and the band positions are listed in Table 1. The only fragmentation pathways observed involve the loss of one or more CO₂ molecules. These IRPD spectra were generated by the summing of the yield of the fragment ions as a function of the IR laser wavelength. The spectra for the smaller n = 2–7 clusters were measured in the multiphoton absorption regime and the relative intensities of the bands in the experimental IR spectra may differ significantly from those in the linear absorption spectra. The experimental IRPD spectra comprise three features, labeled a–c in Fig. 1. Band a is present for all of the clusters studied and slightly red-shifts from 2374 cm⁻¹ to 2360 cm⁻¹ upon addition of the CO₂ molecules, which is characteristic of the antisymmetric stretch of CO₂ in the first solvation shell.^8,22 Band b appears as a small shoulder at n = 8 and gains in intensity for the larger clusters, which is close to the antisymmetric stretching vibration of free CO₂ found at 2349 cm⁻¹.^8,22 A new feature (band c) is found in the 1700–1900 cm⁻¹ region for the n = 4–11 clusters and exhibits a progressive red-shift per CO₂ molecule, which is characteristic of the C–O stretch.

Fig. 1 Experimental IRPD spectra of the [YO(CO₂)_n]⁺ (n = 2–11) complexes. The labels denote the antisymmetric stretch of CO₂ in the first solvation shell (band a), in the second solvation shell (band b), and the C–O stretch of CO₃²⁻ (band c).

Table 1 Experimental band positions (in cm⁻¹), calculated scaled harmonic vibrational frequencies of the lowest-lying isomers, and band assignments for [YO(CO₂)_n]⁺ (n = 2–11)

n	Band a		Band b		Band c
	Exp.	Calc.	Exp.	Calc.	Exp.	Calc.
2	2374	2378	—	—	—	—
	2364	2366
3	2366	2373	—	—	—	—
4	2366	2371	—	—	1853	1831
5	2365	2371	—	—	1840	1820
6	2364	2366	—	—	1828	1808
7	2360	2360	—	—	1815	1800
8	2360	2360	2350	2352	1808	1779
9	2360	—	2350	—	1801	—
10	2360	—	2352	—	1785	—
11	2360	—	2354	—	1768	—
Assignment	Antisymmetric stretch of CO2 in the first solvation shell		Antisymmetric stretch of CO2 in the second solvation shell		C–O stretch of CO3^2−

---

Quantum chemical calculations were performed to predict the structures and IR spectra of the [YO(CO₂)_n]⁺ (n = 2–8) clusters. Two types of structure were observed for each cluster. The first type is where all of the CO₂ molecules are weakly solvated with the metal (labeled nS). The second type is where one CO₂ molecule reacts with the metal oxo group to form a carbonate, which coordinates to the metal bidentately (labeled nC). Optimized structures of the nC and nS isomers for [YO(CO₂)_n]⁺ (n = 2–8) are illustrated in Fig. 2 and their calculated harmonic vibrational spectra are shown in Fig. 3. For each cluster up to n = 8, the comparisons of the experimental IRPD spectra to the calculated harmonic vibrational spectra are shown in Fig. S2–S8 in the (ESI†).

Fig. 2 Representatively optimized structures of the [YO(CO₂)_n]⁺ (n = 2–8) complexes (Y, cyan; C, gray; O, red). Relative energies are given in kJ mol⁻¹.

Fig. 3 Calculated harmonic vibrational spectra of the two lowest-energy isomers for [YO(CO₂)_n]⁺ (n = 2–8) with relative energies (kJ mol⁻¹).

The lowest-energy isomer of the [YO(CO₂)₂]⁺ cluster, labeled 2S, is a C_s structure with a ¹A′ ground state (Fig. 2), in which the two CO₂ molecules are terminally bound to the Y atom in an “end-on” linear configuration. The next energetically higher isomer (2C, +14.6 kJ mol⁻¹) involves a CO₃²⁻ carbonate structure. The antisymmetric stretching vibrational frequencies of the CO₂ units in the 2S isomer were predicted to be 2378 and 2366 cm⁻¹ (Table 1 and Fig. S2, ESI†), which are consistent with the experimental values of 2374 and 2364 cm⁻¹. In the calculated harmonic vibrational spectrum of isomer 2C, the band at 1855 cm⁻¹ is attributed to the C–O stretch of the carbonate core ion, which is not seen experimentally. Then, isomer 2S is responsible for the experimental IRPD spectrum of [YO(CO₂)₂]⁺ instead of 2C. Similarly, the calculated harmonic vibrational spectrum of the lowest-lying isomer 3S for the n = 3 cluster agrees best with the experimental spectrum (Fig. S3, ESI†).

For the n = 4 cluster, the carbonate core ionic structure (4C) was calculated to be more stable than the solvated structure (4S) by 19.8 kJ mol⁻¹ (Fig. 2). The antisymmetric stretching vibrational frequencies of the CO₂ units in the 4C isomer were predicted to be 2371 and 2358 cm⁻¹ (Fig. S4, ESI†), which are observed as a broad feature at 2366 cm⁻¹ in the experimental spectrum. The calculated harmonic vibrational spectrum of 4C showed an intense peak at 1831 cm⁻¹, which well reproduced the experimental band c. For the n = 5–8 clusters, the calculated harmonic vibrational spectra of the lowest-lying isomers 5C–8C were consistent with the experimental data (Fig. 1 and 3). In addition to bands a and c, a feature near 2350 cm⁻¹ (band b) in the n = 8 cluster was also reproduced in the simulated IR spectrum of isomer 8C (Fig. 3), which was assigned to the asymmetric stretch of CO₂ in the second solvation shell. It can be seen from Fig. S2–S8 (ESI†) that the carbonate formation could also be manifested in the fingerprint region of the metal oxide stretching. However, below 800 cm⁻¹, an infrared free electron laser is required to achieve efficient photon dissociation.

Ab Initio Molecular Dynamics (AIMD) simulations were carried out to elucidate the dynamic motion of weakly-bonded CO₂ molecules in [YO(CO₂)_n]⁺ (n = 4–6) (see the ESI† for the computational details). Vibrational profiles at a finite temperature were obtained by the Fourier transform of the dipole time correlation function (DTCF), which accounts for anharmonic and dynamic effects. For n = 4, the DTCF spectrum at 250 K indeed reproduced a broad feature centered at 2368 cm⁻¹ (Fig. S9, ESI†), near the experimental peak a. Analogously, the broadening of band a in the n = 5 and 6 clusters was also addressed by the DTCF spectra at 250 K (Fig. S10 and S11, ESI†). Note that the simulation temperature is calculated from the average kinetic energy by treating the atomic motion with Newtonian mechanics in the AIMD simulations and cannot be directly compared to the experimental temperature of the ions, which could be employed to provide a general picture of the temperature effect on the vibrational spectra of weakly bound complexes.²⁶

The agreement between the experimental and theoretical results allows for establishing the structural evolution of [YO(CO₂)_n]⁺ (n = 2–11). For the n = 2 and 3 clusters, the weakly solvated-CO₂ structure is favored. The carbonate motif is formed in the n ≥ 4 clusters. Comparison of the calculated carbonate and weakly-solvated-CO₂ structures with converged solvent conformers for each cluster size is depicted in Fig. 4. The carbonate motif becomes lower in energy than the weakly solvated-CO₂ structure at n = 4, which is consistent with the experimental results.

Fig. 4 Comparison of the energy differences between the carbonate core ion clusters (nC) and weakly-solvated-CO₂ clusters (nS) as a function of the cluster size.

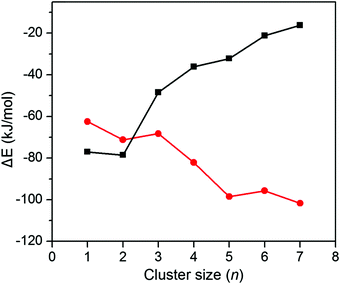
In order to gain further insight into the competition between the carbonate motif and the weakly solvated-CO₂ structure, we calculated the sequential CO₂ solvation energy and sequential carbonation energy for [YO(CO₂)_n]⁺ (n = 1–7) (Fig. 5). As expected, the CO₂ solvation energy decreases with an increase in the cluster size, which is supposed to be one of the reasons for the preference of a carbonate motif in larger clusters. Interestingly, the carbonation energy becomes more and more negative with an increase in the cluster size, suggesting that the CO₂ coordination helps the conversion of Y = O and CO₂ to carbonate. Thus, the preference of carbonate for [YO(CO₂)_n]⁺ (n > 3) is actually the CO₂ fixation into a carbonate motif induced by CO₂ coordination.

Fig. 5 The sequential CO₂ solvation energy (black squares, calculated by [YO(CO₂)_n]⁺ + CO₂ → [YO(CO₂)_n+1]⁺) and sequential CO₂ carbonation energy (red solid circles, calculated by [YO(CO₂)_n]⁺ + CO₂ → [Y(CO₃)(CO₂)_n]⁺) for [YO(CO₂)_n]⁺ (n = 1–7).

Why does the CO₂ coordination help the conversion of Y = O and CO₂ to carbonate? Note that CO₂ forms a dative bond with Y, in which CO₂ donates some electrons to Y. Therefore, with more CO₂ coordination, Y is more electron rich and O is more negatively charged (the calculated natural charges on O change smoothly from −0.93 to −1.08 with n = 2 to 8 in [YO(CO₂)_n]⁺). Kinetically, the conversion of Y = O and CO₂ undergoes a 2 + 2 cycloaddition transition state, and the negative charges on O are beneficial for its nucleophilic attack on the C center of the CO₂ motif. The conversion barriers decrease from 43.1 to 14.4 kJ mol⁻¹ with n = 2 to 5 in [YO(CO₂)_n]⁺ (Table 2). Thermodynamically, the O with more negative charge forms a stronger C–O bond with more ionic contribution. Furthermore, the negative charge on O elevates the orbital energies of the lone pairs, which facilitates the overlapping with the π* orbital of CO₂ to form the four-center six-electron π bond in the carbonate structure. The calculated results show that the gap between the O lone pair and the CO₂ π* orbitals decreases from 0.386 eV to 0.362 eV for n = 2 to 8 in the carbonate motifs of [YO(CO₂)_n]⁺. The increase in the C–O bond strength with an increase in the CO₂ coordination is also illustrated by our optimized structures, where the C–O bond lengths decrease monotonically from 1.393 to 1.367 Å for n = 2 to 8 in the carbonate motifs of [YO(CO₂)_n]⁺.

Table 2 B2PLYP/def2-TZVP calculated barriers for transition states from nS to nC isomers of [YO(CO₂)_n]⁺ (n = 2–5)

Transition states	Barrier (kJ mol^−1)
2S → 2C	43.1
3S → 3C	37.8
4S → 4C	22.8
5S → 5C	14.4

---

Since the CO₂ coordination assists the conversion of Y = O and CO₂ to carbonate by donating electrons to the metal, the coordination-induced CO₂ fixation observed in this work is expected to also be possible for ligands other than CO₂, especially for strong electron donating ligands. To verify this idea, we performed computational studies on the conversion of [YO(CO₂)L]⁺ to [Y(CO₃)L]⁺ (L = CO₂, H₂O, NH₃, and NHC (N,N′-bis(methyl)imidazol-2-ylidene)). Indeed, it can be seen from Fig. 6(a) that with an increase in the donating power of ligand L, the carbonation becomes easier. In particular, for the prototypical carbene ligand of NHC, only one ligand is sufficient to induce the carbonation. The strong electron donating ligands are expected to facilitate the [YO(CO₂)L]⁺ to [Y(CO₃)L]⁺ conversion via a similar mechanism to that discussed above, as shown by the calculated natural charges on O (−0.95 for L = NH₃, and −0.99 for L = NHC), the C–O bond length (1.391 Å for L = NH₃, and 1.386 Å for L = NHC), and the gap between the O lone pair and the CO₂ π* orbitals (0.386 eV for L = NH₃, and 0.379 for L = NHC). Generally, the electron effect of one NHC is equals to around 2–3 CO₂ ligands. Quantum chemical calculations on the [Mg(OH)(CO₂)(H₂O)_n]⁺ system predict that two water molecules are needed to convert the [Mg(OH)]⁺/CO₂ adducts to the magnesium bicarbonate [MgO₂COH]⁺.²⁷ Recently, FT-ICR mass spectrometric and theoretical studies on [ReCO₂(CO)_n]⁺ (n = 0–3) complexes have demonstrated that two CO molecules are required to abstract one oxygen atom from CO₂.²⁸

Fig. 6 (a) Conversion energy for [YO(CO₂)L]⁺ → [Y(CO₃)L]⁺. (b) Conversion energy for nS → nC of [RhO(CO₂)_n]⁺ (n = 2–6).

Considering that the carbonate motif for the late transition metals is less stable, CO₂ fixation for their metal oxides should be harder. Theoretical studies on the [RhO(CO₂)_n]⁺ system have been carried out to explore whether coordination-induced CO₂ fixation is possible for RhO⁺. The calculated results are shown in Fig. 6(b), revealing that six CO₂ ligands are able to induce CO₂ fixation to carbonate. In contrast, four CO₂ ligands are enough for the chemical transformation of CO₂ to carbonate by YO⁺. Thus, the present yttrium oxide–CO₂ model should be valid for a wide range of systems.

5. Conclusions

Infrared spectroscopic studies on the reaction of CO₂ with cationic yttrium oxide indicate that the CO₂ molecules are weakly coordinated to the metal in the n ≤ 3 clusters. A carbonate motif is formed at n = 4, which is retained in all of the lowest-energy isomers of the larger clusters. The experimental observation is consistent with theoretical predictions that the conversion of Y = O and CO₂ to carbonate is achieved by donating electrons from the ligands to the metal. The present system affords a model in clarifying how the coordination induces CO₂ fixation into carbonate by metal oxides, which should have important implications for the catalyst design and the development for the utilization of CO₂.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant numbers 21327901, 21503222, 21673231, 21688102, and 11574040) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant number XDB17000000).

References

1. D. H. Gibson, Chem. Rev., 1996, 96, 2063–2095.
2. T. Sakakura, J.-C. Choi and H. Yasuda, Chem. Rev., 2007, 107, 2365–2387.
3. M. North, R. Pasquale and C. Young, Green Chem., 2010, 12, 1514–1539.
4. X.-B. Lu and D. J. Darensbourg, Chem. Soc. Rev., 2012, 41, 1462–1484.
5. H. J. Freund and M. W. Roberts, Surf. Sci. Rep., 1996, 25, 225–273.
6. U. Burghaus, Prog. Surf. Sci., 2014, 89, 161–217.
7. W. Taifan, J.-F. Boily and J. Baltrusaitis, Surf. Sci. Rep., 2016, 71, 595–671.
8. N. R. Walker, R. S. Walters and M. A. Duncan, New J. Chem., 2005, 29, 1495–1503.
9. J. M. Weber, Int. Rev. Phys. Chem., 2014, 33, 489–519.
10. H. Schwarz, Coord. Chem. Rev., 2017, 334, 112–123.
11. B. J. Knurr and J. M. Weber, J. Am. Chem. Soc., 2012, 134, 18804–18808.
12. B. J. Knurr and J. M. Weber, J. Phys. Chem. A, 2013, 117, 10764–10771.
13. B. J. Knurr and J. M. Weber, J. Phys. Chem. A, 2014, 118, 10246–10251.
14. B. J. Knurr and J. M. Weber, J. Phys. Chem. A, 2014, 118, 4056–4062.
15. B. J. Knurr and J. M. Weber, J. Phys. Chem. A, 2014, 118, 8753–8757.
16. M. C. Thompson, J. Ramsay and J. M. Weber, Angew. Chem., Int. Ed., 2016, 55, 15171–15174.
17. M. C. Thompson, J. Ramsay and J. M. Weber, J. Phys. Chem. A, 2017, 121, 7534–7542.
18. G. B. S. Miller, T. K. Esser, H. Knorke, S. Gewinner, W. Schoellkopf, N. Heine, K. R. Asmis and E. Uggerud, Angew. Chem., Int. Ed., 2014, 53, 14407–14410.
19. G. K. Koyanagi and D. K. Bohme, J. Phys. Chem. A, 2006, 110, 1232–1241.
20. A. Iskra, A. S. Gentleman, A. Kartouzian, M. J. Kent, A. P. Sharp and S. R. Mackenzie, J. Phys. Chem. A, 2017, 121, 133–140.
21. Z. Zhao, X. Kong, D. Yang, Q. Yuan, H. Xie, H. Fan, J. Zhao and L. Jiang, J. Phys. Chem. A, 2017, 121, 3220–3226.
22. A. M. Ricks, A. D. Brathwaite and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 11490–11498.
23. M. Firouzbakht, M. Schlangen, M. Kaupp and H. Schwarz, J. Catal., 2016, 343, 68–74.
24. H. Xie, J. Wang, Z. B. Qin, L. Shi, Z. C. Tang and X. P. Xing, J. Phys. Chem. A, 2014, 118, 9380–9385.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.
26. S.-T. Sun, L. Jiang, J. W. Liu, N. Heine, T. I. Yacovitch, T. Wende, K. R. Asmis, D. M. Neumark and Z.-F. Liu, Phys. Chem. Chem. Phys., 2015, 17, 25714–25724.
27. S. Petrie, Int. J. Mass Spectrom., 2006, 254, 136–144.
28. S. Zhou, J. Li, M. Firouzbakht, M. Schlangen and H. Schwarz, J. Am. Chem. Soc., 2017, 139, 6169–6176.

---

Footnotes

† Electronic supplementary information (ESI) available: Mass spectrum of [YO(CO₂)_n]⁺ (Fig. S1); comparison of the experimental IRPD spectrum to the calculated harmonic vibrational spectra of [YO(CO₂)_n]⁺ (n = 2–8) (Fig. S2–S8); method of molecular dynamics simulations; comparison of the experimental IRPD spectra of [YO(CO₂)_n]⁺ (n = 4–6) to the DTCF spectra at 50 K, 150 K, and 250 K based on AIMD simulations (Fig. S9–S11); B2PLYP/def2-TZVP lowest dissociation energies and the number of IR photons required for the dissociation of [YO(CO₂)_n]⁺ (n = 1–8) (Table S1). See DOI: 10.1039/c8cp02085j

‡ These authors contributed equally to this work.

---