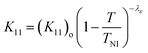Physical model for temperature-dependent dielectric properties of anisotropic nematic liquid crystals†
Received
10th March 2018
, Accepted 17th May 2018
First published on 19th May 2018
Abstract
We derived a new analytic physical model for describing the temperature-dependent dielectric permittivities εe(T) and εo(T) in anisotropic mesophase molecules of nematic liquid crystals (NLCs). These temperature-dependent dielectric properties of NLCs could be explained by a six-parameter dielectric permittivity model, where the analytic dielectric permittivity curves of εe(T), εo(T), and Δε(T) from the model using the six parameters ε*, Aε, Bε, (Δε)o, λε, and T* showed excellent agreement with experimental data. The six-parameter dielectric permittivity model was compared to the conventional four-parameter refractive index model. To systematically investigate the temperature-dependent properties of the refractive indices (ne(T) and no(T)) and dielectric permittivities according to the molecular structure of the NLCs, four similar types of fluorinated phenyl bicyclohexane NLCs were selected. Using the presented models, the temperature-dependent behaviour of these four fluorinated NLCs was discussed, according to the molecular length of the alkyl chains and the positions of the fluorine substituents. In particular, two fitting equations for the temperature-dependent properties of threshold voltage and splay elastic LC constant could also be developed using the physical coefficients extracted from the six-parameter dielectric permittivity model, and these equations coincided well with experimental results.
1 Introduction
Liquid crystals (LCs) are meso-phase materials exhibiting intermediate physical features between solid crystals and isotropic liquids.1–3 Most of these features come from anisotropic molecular geometries of LCs, which can be grouped into rod-like and disc-like.1 Phase transitions of LCs may be brought about in two different ways. The first is a purely thermal process, and is referred to as a thermotropic phase transition, whereas the other is caused by the molecular concentration variation and is called a lyotropic phase transition.1–3 The investigation of LC compounds is a wide field of study, and concerns their chemical structure, physical properties, and electro-optic practical applications.1–8 Because of their dual characteristics of anisotropic physical properties, like ordered and fluidic rheological properties, similar to liquids, and also their effective response to external forces such as electric, magnetic, and optical fields, LCs are applied in many types of electro-optic applications, including well-developed liquid crystal displays (LCDs).1–8 Because of the anisotropic molecular shape, the physical properties of rod-like nematic LCs (NLCs) are uniaxial. They exhibit different electro-optic physical properties with respect to the parallel or perpendicular directions of the average molecular direction of the NLC director. As anisotropic fluids, the uniaxial properties of NLCs are exhibited in a wide range of physical phenomena including their refractive indices (ne and no; extraordinary and ordinary refractive index, respectively) and dielectric permittivities (εe and εo; extraordinary and ordinary dielectric permittivity, respectively), which can be understood if their macroscopic properties are fully characterized.
The order parameter (S) of NLCs is highly dependent on temperature,1–3 as it exhibits thermotropic phase transition behaviour. In addition, within the nematic phase range below the nematic-to-isotropic phase transition temperature of TNI, both the macroscopic values of the refractive indices and the dielectric permittivity values are highly affected by temperature, which results in a temperature-dependent refractive index and dielectric anisotropy (Δn(T) and Δε(T), respectively). Knowledge of these temperature-dependent optical and electrical physical parameters – ne(T), no(T), Δn(T), εe(T), εo(T), and Δε(T) – is essential when developing or designing electro-optic devices utilizing NLCs, including well-commercialized devices such as LCDs.
Among these parameters, the temperature-dependent refractive index can be explained by an analytic model called the four-parameter refractive index model, which was proposed by Li et al.9 The temperature-dependent refractive index properties can be also explained by a model based on the microscopic molecular picture.1–3 However, the analytic equations of the four-parameter refractive index model well describe how the temperature dependencies of the LC parameters affect the refractive indices under varying temperature conditions from examination of the temperature-dependent macroscopic features of density and molecular orientation variation.10,11 With this model, given experimental data, the temperature-dependent properties of the refractive index – ne(T), no(T), and Δn(T) – can be modelled in analytic equations over the whole nematic range. In addition, from the four parameters obtained from the equations, we can also investigate other macroscopic NLC features such as the critical birefringence value of (Δn)o extracted at S = 1,12–14 the crossover temperature (Tco),11 and the detailed temperature gradient behaviour of the extraordinary (dne/dT) and ordinary (dno/dT) refractive indices.15
However, the temperature-dependent dielectric permittivity variation behaviour differs from the temperature-dependent refractive index variation because the anisotropic electron displacement effects in response to a low-frequency electric field are different to those in response to a high-frequency optical field. Both changes of the induced dipole moment and the permanent dipole moment of the NLCs contribute to the thermally-varying dielectric permittivity values (εe(T), εo(T), and Δε(T)), while only the induced dipole moment change contributes to the thermally-varying refractive indices (ne(T), no(T), and Δn(T)).1–3 It is worth noting that the temperature dependencies of the dielectric permittivities in NLC compounds are also totally different from the isotropic solvents model16,17 because the orientational ordering is highly dependent on the temperature in the thermotropic anisotropic fluid of NLCs. Because of the practical need for material information on the temperature-dependent dielectric permittivity values mentioned above, there have been intensive experimental studies and physical explanations based on the microscopic molecular picture for several NLCs to explain the relationship between the positional molecular substituent and different terminal tails on the structures of NLC molecules.18–21 However, there is as yet no report on an appropriate physical analytic model that can explain the temperature-dependent dielectric permittivity values – εe(T), εo(T), and Δε(T) – covering the whole nematic temperature regime and extracting meaningful macroscopic parameters like the four-parameter refractive index model.
In this work, a physical analytic model for describing the temperature-dependent dielectric permittivity values εe(T) and εo(T) in thermotropic NLCs was presented with the newly developed six-parameter dielectric permittivity model. This analytic model will be compared with the conventional four-parameter refractive index model. For LCD applications, the elastic LC constants and the threshold voltage (Vth) are also important as significant physical properties which determine the temperature-dependent electro-optic properties.22–26 We will also show that the temperature dependencies of the splay elastic LC constant (K11) and the threshold voltage (Vth) can be modelled by two analytic equations using the physical parameters extracted from the six-parameter dielectric permittivity model, which cannot be derived from the conventional four-parameter refractive index model. To systemically examine and investigate the effectiveness of these two analytic models for the temperature-dependent refractive indices and dielectric permittivities of NLCs, four fluorinated phenyl bicyclohexane NLCs were selected. These NLCs had similar structures but different molecular lengths of the alkyl chains and different positions of the fluorine substituents.22 Fluorinated LCs have recently been widely applied to LCDs and have attracted much attention owing to several advantageous features, such as high electrical resistance, a good voltage-holding ratio, a broad nematic temperature range, high birefringence, reasonable dielectric anisotropy, tunable polarity, and higher long-term material stability, making them suitable for various electro-optic applications.27–30 The four fluorinated NLCs under investigation in this work have homologous members with the same phenyl bicyclohexane core structure, different fluorine end groups on the benzene ring, and different side-chains substituents on the cyclohexane ring. The chemical structures and phase transition temperatures of the NLCs are listed in Table 1.
Table 1 Molecular structures and phase transition temperatures (TNI) of the four homologous fluorinated phenyl bicyclohexane NLCs investigated in our analysis22
| Abbreviation |
Structure |
T
NI/K |
| 3PBC3,5F2 |
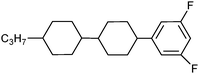
|
361.05 |
| 5PBC3,5F2 |

|
367.35 |
| 3PBC3,4,5F3 |
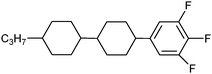
|
365.85 |
| 5PBC3,4,5F3 |
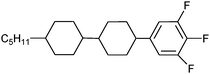
|
373.05 |
The remainder of this paper is structured as follows. First, in Section 2, the four unknown physical parameters will be extracted and the analytic refractive index curves will be compared with the experimental data by employing the four-parameter refractive index model using temperature-dependent refractive index data from the literature.22 The crossover temperature (Tco) and temperature gradients of the extraordinary (dne/dT) and ordinary (dno/dT) refractive indices will be determined based on the four physical parameters A, B, (Δn)o, and β. They will then be discussed based on the molecular structures of the four fluorinated phenyl bicyclohexane NLCs. In the next step, reported in Section 3, we will present the newly derived six-parameter dielectric permittivity model to explain the temperature-dependent electric-responsive properties of the NLCs. The unknown six parameters – ε*, Aε, Bε, (Δε)o, λε, and T* – within the analytic model will be extracted for the four fluorinated phenyl bicyclohexane NLCs from literature data,22 and the analytic curves for the temperature-dependent dielectric permittivity will be compared with the experimental results. According to the molecular structures of the fluorine substituents (di-fluorinated and tri-fluorinated NLCs), the fitting curves based on the six-parameter dielectric permittivity model will be compared with the fitting curves obtained from the conventional four-parameter-based equation. In Section 4, we present the final step, in which we will show that the analytic curves for the temperature-dependent K11 and Vth values can also be obtained by two fitting equations newly developed in this work, using physical parameters from the temperature-dependent dielectric permittivity model and mean field theory.
2 Model for temperature-dependent refractive indices of NLCs
2.1 Four-parameter model for ne(T) and no(T)
The temperature dependence of LC refractive indices can be described by a four-parameter model.9,11 To apply this model, two independent fitting procedure steps are needed which use experimental data of the refractive indices at varying temperatures to extract the four unknown parameters. Vuks12 made a semi-empirical equation correlating the refractive indices with the molecular polarizabilities, assuming that the internal field in an LC is similar in all directions as follows:30| |  | (1) |
where N, αe,o, and 〈n2〉 are the number of molecules per unit volume, the molecular polarizabilities, and the mean value of the square of the refractive index, respectively. 〈n2〉 is determined as:11| | 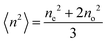 | (2) |
The ordinary and extraordinary refractive indices can be obtained as a function of 〈n〉 and the birefringence (Δn = ne − no) as follows:| |  | (3) |
| |  | (4) |
The mean value of the refractive index can be determined from a linear plot of the experimental data of ne and no, viaeqn (5), considering the temperature-dependent effective molecular density variation as follows:11,15| |  | (5) |
where A and B (<0) denote the refractive index terms determined by the inherent molecular structure and the temperature-dependent molecular density dilution effect, respectively.
According to the Haller approximation method,31 a linearly proportional relationship between the temperature-dependent birefringence and the temperature-dependent order parameter can be formulated as follows:
| | 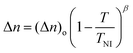 | (6) |
where (Δ
n)
o is the birefringence in the crystalline state (
S = 1), which is the nominally extrapolated birefringence at
T = 0 K.
TNI is the LC clearing temperature, and
β is a characteristic constant of the material. Using a linear curve fitting approach, the values of (Δ
n)
o and
β can be obtained.
Substituting the values of  and (Δn) from eqn (5) and (6) into eqn (3) and (4), the four-parameter refractive index models for ne(T) and no(T) are obtained:11,15
and (Δn) from eqn (5) and (6) into eqn (3) and (4), the four-parameter refractive index models for ne(T) and no(T) are obtained:11,15
| |  | (7) |
| |  | (8) |
Therefore,
eqn (7) and (8) have the four unknown parameters
A,
B, (Δ
n)
o, and
β, which are determined by two fitting steps using the experimental data of

and Δ
n for an NLC.
In Table 2, the fitting results of the four parameters for each fluorinated NLC under investigation are listed. We found that additional molecular length and fluorine substitution strongly impacted the values of the coefficients. The NLC 5PBC3,4,5F3, containing three fluorine substituents and a long tail, possesses the smallest absolute magnitude for all coefficients. On the other hand, 3PBC3,5F2, which had the lowest number of fluorine substituents and the shortest tail, displays a relatively large absolute magnitude for the A, B, and (Δn)o parameters. However, comparing the characteristics of 3PBC3,4,5F3 and 5PBC3,5F2 presented in Table 2 shows that an extra fluorine substitution has a more significant impact than tail length on decreasing the values of all coefficients in the four-parameter refractive index model. As an electron withdrawing group, more fluorine end groups on the benzene ring reduce the delocalized π electron density within the NLC molecules.2,6,8 This results in the reduced amount of the induced polarization of NLCs in response to optical fields. Especially, among the four physical parameters, the A and (Δn)o values are highly affected by the number of fluorine substituents on the benzene ring because the values of the A and (Δn)o parameters can be inherently determined by the delocalized π electron density within the NLC molecular structure.
Table 2 Fitting parameters of A, B, (Δn)o and β for four fluorinated phenyl bicyclohexane NLCs, which are extracted from the temperature-dependent average refractive index22 〈n(T)〉 and birefringence22 (Δn(T)) using eqn (5) and (6), respectively, for the four-parameter refractive index model of eqn (7) and (8). The crossover temperature (Tco) is determined from eqn (11)
| LC material |
A
|
B (×10−3 K−1) |
(Δn)o |
β
|
T
co (K) |
| 3PBC3,5F2 |
1.656 ± 0.01 |
−0.470 ± 0.03 |
0.1140 ± 0.002 |
0.148 ± 0.03 |
354.48 ± 0.01 |
| 5PBC3,5F2 |
1.637 ± 0.02 |
−0.426 ± 0.02 |
0.1137 ± 0.001 |
0.195 ± 0.01 |
359.05 ± 0.02 |
| 3PBC3,4,5F3 |
1.626 ± 0.03 |
−0.412 ± 0.04 |
0.0980 ± 0.003 |
0.149 ± 0.04 |
359.37 ± 0.03 |
| 5PBC3,4,5F3 |
1.598 ± 0.02 |
−0.337 ± 0.01 |
0.0890 ± 0.002 |
0.134 ± 0.02 |
366.31 ± 0.01 |
Fig. 1 shows the analytic curves for temperature-dependent ne(T) and no(T), generated using the four-parameter refractive index model, with the fitted measured results co-plotted. For all four fluorinated NLCs investigated in our work, excellent agreement between the experimental data and the fitting curves could be confirmed, as could the validity of the model of NLC temperature-dependence. As temperature varied, ne(T) and no(T) showed different temperature dependencies. As temperature increased, ne declined steeply and monotonically, whereas no initially decreased smoothly far from TNI but increased again when approaching TNI.
 |
| | Fig. 1 Refractive indices ne and no of the four fluorinated phenyl bicyclohexane NLCs with varying temperature. The experimental data22 is presented as symbols, and the corresponding fitting curves obtained with the four-parameter refractive index model of eqn (7) and (8) are presented as solid lines. | |
The temperature dependence of optical birefringence is shown in Fig. 2. For the fitting curves of Δn(T), eqn (6) and the fitting parameters of (Δn)o and β were used. For all the investigated mesogens, the Δn values displayed a sharp reduction as the temperature rose. In other words, as TNI was approached, the decrease of the order parameter strongly affected the value of Δn(T). In addition, Fig. 2 reveals that no significant difference can be observed in Δn for all mesogens except for 3PBC3,5F2. The NLC of 3PBC3,5F2 shows a slightly higher Δn compared to the other NLCs, which may be due to the relatively higher molecular polarizability anisotropy and induced dipole moment, which can also be observed in the relatively higher values of A and (Δn)o displayed in Table 2. The relationship between Δn and the fitting parameters A and (Δn)o can be explained more clearly with two di-fluorinated NLCs, 5PBC3,5F2 and 3PBC3,5F2. The values of Δn, A, and (Δn)o of 5PBC3,5F2 are slightly lower than those of 3PBC3,5F2. This may originate from the higher thermal dilution effects on the molecular density in 5PBC3,5F2 caused by an extra –CH2 group compared to 3PBC3,5F2. This results in the relatively lower values of A and (Δn)o as shown in Table 2. Furthermore, when we compare the relationship between Δn and the fitting parameters A and (Δn)o between the di-fluorinated and tri-fluorinated NLC groups, the additional fluorine group in both 3PBC3,4,5F3 and 5PBC3,4,5F3 leads to a less symmetric distribution of electron density, as well as less anisotropic electron displacement in response to an optical field along the molecular axis. Consequently, this effect reduces the Δn, A, and (Δn)o values of tri-fluorinated NLCs when compared with di-fluorinated NLCs. The values of Δn are arranged as follows: 3PBC3,5F2 > 5PBC3,5F2 > 3PBC3,4,5F3 > 5PBC3,4,5F3, which is highly related to the values of A and (Δn)o in the four-parameter refractive index model.
 |
| | Fig. 2 Temperature-dependent birefringence (Δn(T)) of the four fluorinated phenyl bicyclohexane NLCs, where the symbols and solid lines respectively represent the experimental data22 and the fitting curves using eqn (6) and the physical parameters listed in Table 2. | |
In the phase transition of NLCs, the first order transition occurs in general. That means that the order parameter (S(T)) of the NLCs is abruptly changed at TNI. However, the Haller approximation method of eqn (6) can show the continuous phase transition behavior even at TNI. Thus, the Δn(T) curves obtained by using the Haller approximation method can give better fitting results for NLCs with higher values of (Δn)o and β, displaying temperature-dependent nonlinear properties of Δn(T) and S(T) more appropriately. Fig. 2 shows that the excellent fitting result of Δn(T) can be obtained for 5PBC3,5F2 with higher values of (Δn)o and β. In the case of 5PBC3,4,5F3, the fitting result of Δn(T) slightly deviates from the measured results because of the relatively lower values of (Δn)o and β, compared with the other NLCs. However, Fig. 1 shows that the fitting results of ne(T) and no(T), obtained by using the (Δn)o and β values extracted from Fig. 2, matched well with the measured results for the four fluorinated NLCs in this work. For better fitting results of Δn(T), ne(T), and no(T), a four-parameter power law expression method32–34 can be employed instead of the simpler Haller approximation method of eqn (6). When we apply the four-parameter power law expression model to describe Δn(T) and S(T), the analytic functions of ne(T) and no(T) will require more fitting parameters than shown in eqn (7) and (8) with the four-parameter refractive index model, which is under investigation as our future work.
2.2 Temperature gradients of refractive indices and crossover temperature
As shown in Fig. 1, the optical properties ne and no of an NLC are inevitably highly sensitive to temperature variations because of its anisotropic fluid nature. This can be explained by the temperature-dependent molecular density variation and order parameter variation described by the four-parameter model. That means that, in general, the optical anisotropy value Δn is also temperature-dependent. When developing LCDs utilizing field-dependent retardation to control transmittance, the temperature-dependent property Δn is more important than the temperature-dependent properties ne and no.11 However, near room temperature, far from TNI, we can make the Δn value be less sensitive to temperature variation depending on the molecular design of the NLC, considering the fact that some NLCs exhibit an initially decreasing behaviour of no as temperature increases from room temperature. Therefore, investigation into the relative behaviour of the temperature-dependent refractive indices dne/dT and dno/dT is also important for thermotropic NLCs possessing less temperature-sensitive Δn properties. Of course, for some specific NLC applications like thermally tunable photonic devices, the temperature-dependent material feature of higher dne/dT and dno/dT values is essential for efficient control.9 From eqn (7) and (8), the temperature gradients of the refractive indices can be expressed as follows:9,11,15| |  | (9) |
| | 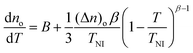 | (10) |
In eqn (9) and (10), the first term of the B value is always negative (i.e. B < 0) for all NLCs as shown in Table 2 for our four fluorinated NLCs because the B value corresponds to the temperature-dependent molecular density effect. Therefore, over the whole nematic temperature regime, dne/dT in eqn (9) is negative, as shown in Fig. 1 and 3. On the other hand, dno/dT can be either positive or negative depending on the relative absolute values of the first and second terms in eqn (10). The sign of the dno/dT value can vary according to the temperature or the material properties of the NLC, as shown in Fig. 1 and 3. Of course, all NLCs eventually exhibit positive behaviour of dno/dT close to TNI because the thermally induced LC ordering variation described by the second term in eqn (10) becomes more dominant. Because of this relationship in the dno/dT behaviour, some NLCs, like the four fluorinated NLCs investigated in our work, exhibit a specific temperature where the value of dno/dT changes from negative to positive as shown in Fig. 3. This point is defined as the crossover temperature (Tco). From eqn (10), the value of Tco is determined from dno/dT = 0, as follows:11,31,35| | 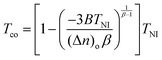 | (11) |
This temperature gradient behaviour occurring at Tco in no(T) cannot be observed in general isotropic liquids. To achieve a low temperature sensitivity of the Δn of a NLC, the Tco condition needs to be close to TNI. For this purpose, as shown in eqn (11), the Tco condition of an NLC can be deduced from the physical parameters constituting the four-parameter refractive index model.
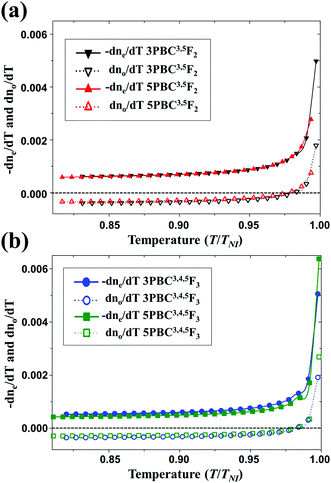 |
| | Fig. 3 Variation of temperature gradient of ne and no for (a) di-fluorinated and (b) tri-fluorinated NLCs, obtained using eqn (9) and (10). | |
From eqn (11) and the physical parameters listed in Table 2, the Tco values for the four fluorinated NLCs were obtained, and are listed also in Table 2. Among the physical parameters affecting the Tco value, eqn (11) shows that a higher TNI value condition is the most dominant factor in achieving a high Tco condition.11,35–37 Among the fluorinated NLCs investigated in this work, the TNI conditions of 5PBC3,4,5F3 (TNI = 373.05 K) and 3PBC3,5F2 (TNI = 361.05 K) were the highest and the lowest, respectively, as shown in Table 1. Consequently, the Tco values exhibited the analogous feature of the highest Tco for 5PBC3,4,5F3 (Tco = 366.31 K) and the lowest Tco for 3PBC3,5F2 (Tco = 354.48 K), as listed in Table 2. However, when considering eqn (11), three parameters – B, (Δn)o, and β – also obviously affect the Tco value. When we compare the Tco values for 3PBC3,4,5F3 and 5PBC3,5F2, which have very similar TNI values to each other (TNI = 365.85 K and 367.35 K for 3PBC3,4,5F3 and 5PBC3,5F2, respectively), the Tco value of 3PBC3,4,5F3 (Tco = 359.37 K) is slightly higher than that of 5PBC3,5F2 (Tco = 359.05 K) even at the lower TNI condition of 3PBC3,4,5F3, because of relative features of these three parameters – B, (Δn)o, and β.
3 Model for temperature-dependent dielectric permittivity values of NLCs
3.1 Six-parameter model for εe(T) and εo(T)
Here we present the six-parameter dielectric permittivity model, which is newly derived in this work and analytically describes the temperature-dependent dielectric properties of NLCs. Considering the macroscopically uniaxial properties of NLCs, the extraordinary and ordinary dielectric permittivity can be expressed in a similar fashion to eqn (3) and (4) presented in Section 2, as follows:| |  | (12) |
| |  | (13) |
where 〈ε〉 = (εe + 2εo)/3 represents the average dielectric constant, and Δε is Δε = (εe − εo).
Before presenting the new model, we should address what happens in the case of deriving the four-parameter-based dielectric permittivity model obtained following a similar derivation procedures as that presented in Section 2. The derivation procedure for the four-parameter dielectric permittivity model and its fitting results using the four fluorinated phenyl bicyclohexane NLCs investigated in this work are presented in the ESI.† The four fitting parameters obtained using the four-parameter dielectric permittivity model are listed in Table S1 (ESI†), for comparison with the values obtained from fitting the six-parameter dielectric permittivity model, which are presented later in this paper. In the case of the dielectric permittivity model described using four physical parameters, a linear relationship between the temperature variation and the average dielectric permittivity of 〈ε(T)〉 is used, much like eqn (5), considering the temperature-dependent density dilution effects. However, the analytic curves of 〈ε(T)〉, εe(T), and εo(T) based on the four-parameter dielectric permittivity model using the four parameters listed in Table S1 (ESI†) showed no appropriate agreement with the measured results. Near TNI, in particular, the disagreement between the measured results and the analytic curves became more severe. In addition, for the NLCs with a higher dielectric permittivity such as the tri-fluorinated NLC group investigated in our work, the four-parameter-based analytic curves for εe(T) and εo(T) did not match the experimental values. For these tri-fluorinated NLC groups, temperature-dependent low-frequency electric displacement effects needed to be considered more than for the di-fluorinated NLC groups.
When deriving our six-parameter dielectric permittivity model, a temperature-dependent nonlinear fluid-like model35–37 was applied for 〈ε(T)〉, instead of the linear relationship used for 〈n(T)〉 in eqn (5). The fluid-like model properly describes the hypothetical critical region around the TNI in agreement with the first-order transition. By considering the importance of the temperature-dependent dipole moment effect in this fluid-like model, the critical behaviour of the dielectric permittivity and pre-transitional (fluctuation) phenomena was predicted and considered for 〈ε(T)〉 of NLCs.38–42 It is worth noting that the fluid-like model is associated with the static dielectric permittivity, the dielectric amplitude, and the classical exponent of the critical specific heat terms.38,41,42 As the first crucial step for deriving the six-parameter dielectric permittivity model, the 〈ε(T)〉 of the NLCs was described by following a fluid-like model as follows:35,38,39
| | | 〈ε(T)〉 = ε* + Aε(T* − T) + Bε(T* − T)α | (14) |
where
ε* is the extrapolated dielectric permittivity at
T*,
T* denotes the extrapolated temperature of the hypothetical continuous phase transition,
Aε is the static dielectric permittivity background term,
Bε corresponds to the dielectric amplitude, and
α is the classical exponent of the specific heat critical exponent which was determined within the limit of experimental error as
α ≈ 0.5.
38,41,42 The values of
ε*,
Aε,
Bε, and
T* can be determined from experimental results of the 〈
ε(
T)〉 values. The second and the third terms in
eqn (14) respectively provide the linear behaviour far from
TNI, and the nonlinear trends near
TNI. Therefore,
eqn (14) fully fits with experimental results in the whole nematic region. It is essential to note that the pre-transitional temperature (
T*) is considered as an important parameter from a theoretical point of view, while due to the first-order phase transition nature of NLCs, defining
T* values in the critical region near the critical point is not possible in direct measurement. Moreover, the temperature width between the
T* and
TNI values can be represented as the metastable region at the nematic-to-isotropic phase transition.
41,42
In the next step, for determining the temperature-dependent dielectric anisotropy of Δε(T), we employed Haller's approximation method31 as the universally utilized semi-empirical technique like that used for Δn(T) in eqn (6):
| |  | (15) |
where (Δ
ε)
o is the dielectric anisotropy in the crystalline state (
S = 1) obtained as the extrapolated dielectric anisotropy at
T = 0 K,
TNI is the LC clearing temperature, and
λε is a characteristic constant of the material. Like the
β parameter used in
eqn (6) for describing the Δ
n(
T) behaviour, the
λε parameter is introduced to reflect the effect of the temperature-dependent order parameter variation on the Δ
ε(
T) behaviour. However, the physical quantity and physical unit of Δ
ε in
eqn (15) are different to those of Δ
n in
eqn (6). Thus, the
λε parameter is newly introduced for the Δ
ε(
T) description in
eqn (15), different to the
β parameter in
eqn (6). Then, the six-parameter dielectric permittivity model can be derived to analytically describe
εe(
T) and
εo(
T) of NLCs by substituting
eqn (14) and (15) into
eqn (12) and (13):
| |  | (16) |
| |  | (17) |
As opposed to the four-parameter models for ne(T) and no(T) shown in eqn (7) and (8), the dielectric permittivity models for εe(T) and εo(T) shown in eqn (16) and (17) have six unknown fitting parameters: ε*, Aε, Bε, T*, (Δε)o, and λε. These parameters are determined by two independent fitting steps using experimental data. In the first step, ε*, Aε, Bε, and T* can be determined by fitting 〈ε(T)〉 in eqn (14) to the measured results. In the second step, (Δε)o and λε can be obtained by fitting the logarithmic form of eqn (15) to the experimental results of Δε(T). Like our previous discussion on the Δn(T) fitting procedure with eqn (6), the four-parameter power law expression method32–34 can be employed in the Δε(T) description for better fitting results of Δε(T), instead of using the Haller's approximation method in eqn (15). Then, the εe(T) and εo(T) equations are described by more physical parameters than the six-parameter dielectric model presented in eqn (16) and (17).
3.2 Temperature gradients of dielectric constants
For the reduced temperature-sensitivity of electro-optic properties in electrically switching LC devices operating near room temperature, investigation into the temperature-gradient properties of εe(T) and εo(T) would be meaningful. In a similar derivation to that of the temperature-gradient refractive indices in eqn (9) and (10), the temperature-gradient properties of εe(T) and εo(T) can be analytically described by the six-parameter dielectric permittivity models (eqn (16) and (17)) as follows:| |  | (18) |
| |  | (19) |
In eqn (19), as opposed to the dno/dT properties, dεo/dT does not exhibit the crossover behaviour within the nematic phase regime, which will be discussed further later.
3.3 Fitting results of the six-parameter dielectric model for four fluorinated NLCs
Fig. 4 and 5 show the analytic curves of 〈ε(T)〉, and εe(T) and εo(T), respectively, for the four fluorinated NLCs investigated in our work. The curves were generated using eqn (15) and the six-parameter dielectric permittivity models of eqn (16) and (17). The six physical parameters extracted using the experimental results are listed in Table 3. As opposed to the analytic curves (the dotted lines in Fig. 4 and 5) generated using the four-parameter dielectric permittivity model, the fitting curves (the solid lines) of 〈ε(T)〉, εe(T), and εo(T), based on the six-parameter dielectric permittivity model, matched the experimental values accurately for the whole nematic phase temperature regime, even near TNI.
 |
| | Fig. 4 Mean values of the temperature-dependent dielectric constants (〈ε(T)〉) of the four fluorinated phenyl bicyclohexane NLCs. The experimental data22 and fitting curves are presented as symbols and solid lines, respectively. The fitting curves are obtained with eqn (14) derived for the six-parameter dielectric model. The fitting curves obtained with eqn (S4) derived for the four-parameter dielectric model are co-plotted with dotted lines for comparison (ESI†). | |
 |
| | Fig. 5 Temperature-dependent dielectric constants (εe(T), εo(T)) of the four fluorinated phenyl bicyclohexane NLCs: (a) di-fluorinated and (b) tri-fluorinated substitutions. The experimental data22 and fitting curves are presented as symbols and solid lines, respectively. The fitting curves represented by the solid lines are obtained with the six-parameter dielectric model of eqn (16) and (17) and the physical parameters listed in Table 3. The fitting curves obtained with the four-parameter dielectric model of eqn (S1) and (S2) and the physical parameters of Table S1 are co-plotted with dotted lines for comparison (ESI†). | |
Table 3 Fitting parameters of ε*, Aε, Bε, T*, (Δε)o and λε for the four fluorinated phenyl bicyclohexane NLCs, which were extracted from the temperature-dependent average dielectric constant22 〈ε(T)〉 and dielectric anisotropy22 (Δε(T)) using eqn (14) and (15), respectively, to obtain the six-parameter dielectric permittivity models of eqn (16) and (17)
| LC material |
ε* |
A
ε
(×10−3 K−1) |
B
ε
(×10−1 K−0.5) |
(Δε)o |
λ
ε
|
T* (K) |
| 3PBC3,5F2 |
3.38 ± 0.05 |
−0.9 ± 0.1 |
0.41 ± 0.07 |
5.25 ± 0.08 |
0.224 ± 0.05 |
361.02 ± 0.10 |
| 5PBC3,5F2 |
3.33 ± 0.04 |
−0.8 ± 0.2 |
0.40 ± 0.10 |
4.46 ± 0.04 |
0.202 ± 0.06 |
367.31 ± 0.08 |
| 3PBC3,4,5F3 |
5.78 ± 0.07 |
−0.1 ± 0.3 |
1.08 ± 0.08 |
15.45 ± 0.03 |
0.238 ± 0.05 |
365.83 ± 0.05 |
| 5PBC3,4,5F3 |
5.35 ± 0.02 |
−0.7 ± 0.1 |
0.90 ± 0.09 |
14.12 ± 0.02 |
0.230 ± 0.04 |
373.02 ± 0.07 |
Our results reveal that all the values of the six parameters, listed in Table 3, strongly depend on the molecular structures of the fluorinated NLCs, including their polar and tail groups. By comparative consideration of the di-fluorinated and tri-fluorinated substitutions, all values of the six parameters for the tri-fluorinated NLCs were larger than those for the di-fluorinated NLCs. Obviously, the reasons behind this behaviour might be attributed to the higher Δε and ε values of the tri-fluorinated NLCs, and their larger total molecular dipole moments compared to the di-fluorinated NLCs. For calculation of the dipole moment values, we used HyperChem™ Release 7.51 according to semi-empirical Austin Model 1 (AM1),43 and the results are listed in Table 4. The dipole moment results showed that an LC structure with extra fluorinated substitutions along the longitudinal molecular axis and a longer tail group can effectively increase the net NLC dipole moment.
Table 4 The calculated dipole moments for the investigated NLCs based on the AM1 calculating method
| LC material |
μ (Debye) |
| 3PBC3,5F2 |
2.71 |
| 5PBC3,5F2 |
2.90 |
| 3PBC3,4,5F3 |
4.12 |
| 5PBC3,4,5F3 |
4.40 |
In the case of the macroscopic values, the longer tail group of NLC reduces the molecular density but enhances the orientational ordering for the nematic phase.2,6,8 As listed in Table 1, the fluorinated NLC with a longer alkyl chain exhibits a higher TNI condition at the same number of fluorine end groups. Accordingly, NLC molecular structures with a shorter tail and extra fluorine substitutions led to increased values of the five physical parameters except T* in our six-parameter dielectric permittivity model, as listed in Table 3. Therefore, 3PBC3,4,5F3, containing three fluorine substituents and a shorter tail length possessed the highest values for ε*, Aε, Bε, (Δε)o, and λε. On other hand, 5PBC3,5F2, containing two fluorine substituents and a longer tail length, displayed the lowest values of the five coefficients.
In terms of T*, a longer alkyl chain in the tail group can contribute to increasing T* and TNI owing to increased molecular ordering effects. When we examined the T* value along with the TNI condition for each NLC, it seemed that NLCs with a shorter tail exhibited a narrower metastable temperature regime, in which T* approached TNI. In the studied NLCs, pre-transitional effects occurred, exhibiting a discontinuity in 〈ε(T)〉 near TNI, which might be interpreted as a consequence of the anti-parallel local ordering of the NLC molecules. The decrease of the 〈ε(T)〉 value with increasing temperature in the nematic phase can be attributed to an increase in the anti-parallel correlation, which results from the rapid reduction in long-range nematic ordering.
When we investigated the Aε and Bε values in more detail, the Bε value was found to be predominant in describing the absolute values of 〈ε(T)〉, εe(T), and εo(T), as well as their temperature-dependent properties. In eqn (14), the third term related to the Bε parameter contributed in a highly nonlinear manner to determining 〈ε(T)〉, whereas the second term contributed linearly. In terms of the molecular structure, the Bε values for tri-fluorinated NLCs were higher than those for the di-fluorinated NLCs because more nonlinear behaviour in 〈ε(T)〉 occurred in NLCs with higher dielectric permittivity conditions of εe, εo, and Δε, owing to a larger electric displacement effect within their molecular structures.
Fig. 6 shows the fitting results for Δε(T) in the four investigated fluorinated NLCs, obtained using eqn (15). Haller's approximation method showed excellent agreement for both types of fluorinated NLCs, which showed that the tri-fluorinated NLCs possessed higher Δε values than the di-fluorinated NLCs. The reason behind this behaviour comes back to taking into account the dipole moment of the NLC molecules. In the presence of more polar groups such as fluorine at the terminal position, a further dipole moment is induced along the longitudinal molecular axis, as discussed previously for the results presented in Table 4.
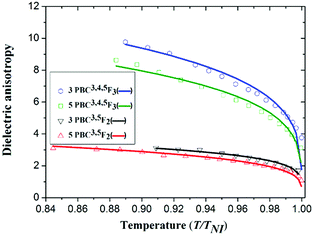 |
| | Fig. 6 Temperature-dependent dielectric anisotropy (Δε(T)) of the four fluorinated phenyl bicyclohexane NLCs, where the symbols and solid lines represent the experimental data22 and fitting curves using eqn (15), respectively. | |
Fig. 7 shows the temperature gradients of εe(T) and εo(T), obtained using eqn (18) and (19). As opposed to the dno/dT behaviour shown in Fig. 3, no crossover behaviour can be seen for the dielectric permittivity values. Considering the uniaxial properties of NLCs and their temperature-dependent order parameter behaviour, the negative properties of dεe/dT for the whole nematic temperature regime are understandable, much like the dne/dT tendency. For both eqn (10) and (19), the last terms are related to the effects of the temperature-dependent order parameter variation on the dno/dT and dεo/dT behaviour, respectively, which contribute as the positive values in determining the signs of dno/dT and dεo/dT. As shown in Tables 2 and 3, the B and β values for the four-parameter refractive index model and the Aε and λε values for the six-parameter dielectric mode have a similar order of magnitude to each other. In eqn (19), the absolute value of the second term described by the Bε parameter is also small. However, for the last terms in eqn (10) and (19), the values of (Δε)o are much larger than those of (Δn)o, as listed in Tables 2 and 3. The dno/dT behaviour can be determined by the competition between the decreasing and increasing no(T) effects of the molecular density and the order parameter with increasing temperature. On the other hand, for the dεo/dT term in eqn (19), the effect of the temperature-dependent order parameter variation is more dominant compared with the temperature-dependent variation of the mean value of the dielectric constant, which results in the positive dεo/dT behaviour for the whole nematic regime without exhibiting the crossover behaviour as shown in Fig. 7. When we compare the dεe/dT and dεo/dT tendencies among the investigated NLCs, the tri-fluorinated NLCs possess greater dεe/dT and dεo/dT values than the di-fluorinated NLCs, which can be explained and analytically modelled by the extracted values from the six-parameter dielectric permittivity model.
 |
| | Fig. 7 Variation of the temperature gradient of εe and εo for (a) di-fluorinated and (b) tri-fluorinated NLCs, obtained using eqn (18) and (19), which are derived from the six-parameter dielectric model. | |
When we applied the six-parameter dielectric model to other NLCs, the fitting results of εe(T), εo(T), and Δε(T) matched also well with the experimental results. In the ESI,† the fitting results of temperature-dependent dielectric constants (Fig. S2, ESI†) and dielectric anisotropies (Fig. S3, ESI†) are presented for three types of aminobenzonitrile NLCs.44 The fitting parameter values of the six-parameter dielectric model for these aminobenzonitrile NLCs are listed in Table S2 (ESI†).
4 Temperature-dependent threshold voltage and splay elastic constant based on the six-parameter dielectric model
4.1 Analytic models for Vth(T) and K11(T)
For understanding and designing the electro-optic properties of LC-based devices including LCDs, characterization of the threshold voltage (Vth) of an NLC is essential. To reorient NLC molecules electrically from the initial NLC geometries determined by the surface alignment conditions, a minimum voltage level is required, which can be explained by the Fréedericksz transition.1,2,6,7,19,20 With an applied voltage condition over the Fréedericksz threshold voltage (Vth), NLCs can start field-induced reorientation with overcoming of the elastic distortion free energy of the NLC layer. Accordingly, the Fréedericksz threshold voltage (Vth) level of an NLC is highly related to the elastic constant of an NLC. When we assume a homogeneously planar LC geometry as representative of the initial LC alignment among several LC modes, the relationship between the splay elastic constant (K11), among the three elastic constants K11, K22, and K33, associated with the splay, twist, and bend NLC deformations, respectively, and the Vth level is described as follows:19,20| |  | (20) |
As shown in eqn (20), the Vth level is inevitably temperature-sensitive because of the temperature-dependence of Δε(T). Several experimental techniques have previously been suggested to delicately measure the Vth and K11 values at a given LC cell condition.1,2,6,7 However, these methods required several sets of measurements with varying temperatures to characterize the temperature-dependent Vth(T) and K11(T). In this work, we will show our approach to obtaining the temperature-dependent Vth(T) and K11(T) properties with two analytic models derived from the temperature-dependent six-parameter dielectric permittivity model, which can give these values under continuously varying temperatures over the whole nematic phase.
It is worthwhile to note that the Vth(T) properties are highly related to low-frequency responsive εe(T), εo(T), and Δε(T) and that the K11(T) properties are highly associated with temperature-dependent dielectric properties when we extract the K11(T) values from eqn (20). Therefore, when we derive the temperature-dependent Vth(T) and K11(T) analytic equations using the Haller approximation method shown in eqn (6), where the temperature-dependent order parameter effects are related to the high-frequency optical response of the refractive index, the fitting results of Vth(T) and K11(T) cannot match with the measurement results, as shown in Fig. S4 and S5 (ESI†), which were presented for comparison with our models. In Fig. S4 and S5 (ESI†), Haller's approximation equation was used for the order parameter (S) as S = (1 − T/TNI)β,31,45 and the analytic equations for Vth(T) and K11(T) were obtained as Vth = (Vth)o (1 − T/TNI)β−λε/2 and K11 = (K11)o(1 − T/TNI)2β, respectively. Note that both these equations are described by the β parameter extracted from the four-parameter refractive index model. However, when we applied the extracted β values listed in Table 2, the fitting results showed no agreement with the experimental data.
In our derivation of Vth(T) and K11(T), instead of Haller's approximation, Vuks’ model was applied, which explains the relationship between the temperature-dependent order parameter and the physical constants of an NLC based on mean field theory: Kii ∼ KiioS2,45,46 where Kiio is the extrapolated elastic constant at T = 0 K. Then, by using eqn (15) and Vuks’ model, eqn (20) can be rearranged into the following new relationship where Vth(T) is expressed by the λε parameter extracted from the six-parameter dielectric permittivity model.
| | 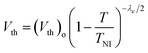 | (21) |
where the value of (
Vth)
o is determined by a linear plot of log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vth
Vth as a function of ln(1 −
T/
TNI). By extrapolating the intercept value in the linear plot to
T = 0 K, the value of (
Vth)
o can be determined, providing (
Vth)
o = π((
K11)
o/
εo(Δ
ε)
o)
1/2.
By using eqn (21), eqn (20) can be rearranged into another form for analytic description of K11(T) as follows:
| | 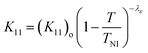 | (22) |
where (
K11)
o =
εo(Δ
ε)
o((
Vth)
o/π)
2. The value of (
K11)
o is determined from a linear plot of ln(
K11) as a function of ln(1 −
T/
TNI) by extrapolating the intercept value in a linear plot to
T = 0 K. Like
eqn (21),
eqn (22) derived for the analytic model of the temperature-dependent
K11(
T) is expressed by the
λε parameter instead of the
β parameter.
4.2 Fitting results of Vth(T) and K11(T) for four fluorinate NLCs
Fig. 8 shows the fitting results of Vth(T) using eqn (21), obtained for the four fluorinated phenyl bicyclohexane NLCs investigated in our work. The fitting parameter (Vth)o, obtained from eqn (21), is listed in Table 5. Contrary to the fitting results shown in Fig. S4 (ESI†), the fitting results in Fig. 8 show that the analytic curves plotted using eqn (21) agree well with the experimental data, and that this agreement is satisfactory over the whole nematic regime. The Vth(T) curves exhibited slowly decreasing and steeply decreasing behaviour with increasing temperature, far from and near to TNI, respectively. When we compare the fitting values of (Vth)o for the four fluorinated NLCs, they can be arranged as: 5PBC3,5F2 > 3PBC3,5F2 > 5PBC3,4,5F3 > 3PBC3,4,5F3, as listed in Table 5. Comparative investigation of the (Vth)o values between di- and tri-fluorinated NLCs showed that larger (Vth)o values were obtained for the di-fluorinated NLCs rather than the tri-fluorinated NLCs. These results can be explained by the smaller dipole moment and dielectric anisotropy within the NLC molecule in the di-fluorinated NLC group, as explained in Section 3. In eqn (21), the temperature-dependent varying behaviour of Vth(T) is highly related to the λε parameter and TNI, and the absolute value of Vth(T) over the whole nematic phase temperature regime is definitely affected by the (Vth)o value newly derived in our work. The analytic curves and the measured results of Vth(T) follow the same sequence as those of (Vth)o for the four fluorinated NLCs: 5PBC3,5F2 > 3PBC3,5F2 > 5PBC3,4,5F3 > 3PBC3,4,5F3, over the whole nematic temperature regime.
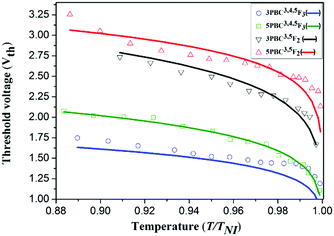 |
| | Fig. 8 Temperature-dependent threshold voltage (Vth(T)) properties of the four fluorinated phenyl bicyclohexane NLCs, where the experimental data22 and fitting curves are presented as symbols and solid lines, respectively. The fitting curves are obtained using eqn (21), where the λε and (Vth)o values listed in Tables 3 and 5, respectively, are used. The λε values are obtained during the fitting procedures for the six-parameter dielectric model of eqn (16) and (17). | |
Table 5 Fitting parameters of (Vth)o and (K11)o for the four fluorinated phenyl bicyclohexane NLCs, which were extracted from eqn (21) and (22) using the λε values listed in Table 3 to obtain the analytic solid line curves in Fig. 8 and 9 showing the temperature-dependent threshold voltage (Vth(T)) and splay LC elastic constant (K11(T)), respectively
| LC material |
(Vth)o (V) |
(K11)o (×10−11 N) |
| 3PBC3,5F2 |
3.54 ± 0.01 |
5.75 ± 0.01 |
| 5PBC3,5F2 |
3.78 ± 0.02 |
5.61 ± 0.05 |
| 3PBC3,4,5F3 |
2.29 ± 0.03 |
6.98 ± 0.03 |
| 5PBC3,4,5F3 |
2.58 ± 0.01 |
8.58 ± 0.02 |
Fig. 9 shows the fitting results of K11(T) using eqn (22) for the four fluorinated NLCs. In Table 5, the (K11)o fitting parameters for eqn (22) are listed. As opposed to the fitting results of Fig. S5 (ESI†) obtained with the analytic model based on the β parameter, well-matched agreements for K11(T) can be observed between the measured results and the analytic model of eqn (22), as shown in Fig. 9. From Fig. 9, it is evident that the NLC structures with more fluorine substitutions along the longitudinal molecular axis provide a higher K11 constant over the whole nematic range and a higher (K11)o value, which would be strongly related with the higher anisotropic intermolecular interaction between the mesogenic LC molecules in the tri-fluorinated NLC group than the di-fluorinated NLC group. When we compare the (K11)o values among the four fluorinated NLCs, these can be arranged as 5PBC3,4,5F3 > 3PBC3,4,5F3 > 3PBC3,5F2 > 5PBC3,5F2, as listed in Table 5. However, the K11(T) values near room temperature far from TNI are arranged as 5PBC3,4,5F3 > 3PBC3,4,5F3 > 5PBC3,5F2 > 3PBC3,5F2, as shown in Fig. 9. Under the NLC structures with the same rigid core part and the same polar end group (the same fluorine group in our work), the end group of a longer alkyl chain enhances the orientational ordering of the nematic phase.1,6,14 In Fig. 9, the K11 value of 5PBC3,4,5F3 is much higher than the others, which can be explained by its relatively larger (K11)o value and the enhanced order parameter by its longer alkyl chain considering the Kii ∼ KiioS2 relationship.45,46
 |
| | Fig. 9 Temperature-dependent splay elastic LC constant (K11(T)) properties of the four fluorinated phenyl bicyclohexane NLCs, where the experimental data22 and fitting curves are presented as the symbols and solid lines, respectively. The fitting curves are obtained using eqn (22), where the λε and (K11)o values listed in Tables 3 and 5, respectively, are used. The λε values were obtained during the fitting procedures for the six-parameter dielectric model of eqn (16) and (17). | |
5 Conclusions
In this work, we presented a new analytic model for describing temperature-dependent dielectric properties with a new six-parameter dielectric permittivity model. To confirm the presented model and to investigate the NLC properties systematically depending on their molecular constitutions, four types of fluorinated phenyl bicyclohexane NLCs with different alkyl chain lengths and different positions of the fluorine substituents were selected. Our model was used to extract six physical parameters ε*, Aε, Bε, T*, (Δε)o, and λε. The conventional four-parameter refractive index model was also applied to the four fluorinated NLCs to extract the four parameters A, B, (Δn)o, and β. The fitting results of the six-parameter dielectric permittivity model derived in our work and the conventional four-parameter refractive index model agreed well with the measured results over the whole nematic phase temperature regime. Furthermore, the models provided analytic curves of 〈n(T)〉, ne(T), no(T), Δn(T), dne/dT, and dno/dT for temperature-dependent refractive index properties and curves of 〈ε(T)〉, εe(T), εo(T), Δε(T), dεe/dT, and dεo/dT for temperature-dependent dielectric permittivity properties. The extracted parameters using the analytic models could provide meaningful physical insight into the molecular design of an NLC by changing the polar group substituents and the alkyl chain length. In the refractive index model, our results show that a larger value of (Δn)o is essentially needed for a larger Δn(T) over the whole nematic temperature region. Similarly, for a larger Δε(T) value, a larger value of (Δε)o is the most important parameter condition among the six physical parameters of the dielectric model. At the same core structure condition, more fluorine end groups of an NLC reduce the value of (Δn)o and increase the value of (Δε)o because of reduction of the induced dipole moment and enhancement of the permanent dipole moment, respectively. Temperature-dependent variation behaviour of the refractive indices and the dielectric constants are highly related to the temperature-dependent order parameter variation. These effects are represented by the β and λε values for the refractive indices and the dielectric constants, respectively, which are highly related to the alkyl chain length of an NLC. Of course, to predict the temperature-dependent refractive or dielectric properties more precisely, the other physical coefficients also need to be considered.
In particular, for the derivation of the six-parameter dielectric permittivity model, a temperature-dependent nonlinear fluid-like model was used for 〈ε(T)〉, whereas a temperature-dependent linear model was used for 〈n(T)〉 in the conventional four-parameter refractive index model. By using physical parameters extracted from the four-parameter refractive index model, the crossover temperature Tco condition according to the molecular constitution could be discussed, which is important for NLC designs possessing less temperature-sensitive birefringence properties, which is a practical need in most NLC applications. However, the six-parameter dielectric permittivity model and the extracted physical parameters revealed that it is difficult to have crossover properties for εo(T) or dεo/dT in general NLCs unlike the case of no(T) and dno/dT.
In addition, by using the six-parameter model, we could present two analytic models for the temperature-dependent properties of Vth(T) and K11(T), which also showed excellent agreement with the experimental data. For the analytic functions of Vth(T) and K11(T), two fitting coefficients were extracted that could provide crucial information on the relative threshold voltages and elastic constants of NLCs. By using the analytic six-parameter dielectric permittivity model, the resultant Vth(T) and K11(T) models, and the conventional four-parameter refractive index model, the temperature-dependent electro-optic properties of an LC device can be analytically modelled over the whole nematic phase temperature regime, which cannot be provided using only the refractive index model. In addition, our investigation into four types of NLCs according to different molecular substitutions showed that the analytic models and their extracted parameters can provide better chemical insight into designing and synthesizing new types of NLCs by varying their additional polar substituents or terminal tails, especially when considering their temperature-dependent physical properties.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Technology Innovation Industrial Program funded by the Ministry of Trade, Industry & Energy (MI, Korea) [10052667, Development of high sensitive (<30 mJ cm−2) R/G/B color photo-rewritable 3D holographic materials and 1 fps speed frame switching technology]. This work was also partially supported by LG Display Co., Ltd.
References
-
P. G. de Gennes, The Physics of Liquid Crystal, Clarendon Press, Oxford, 1974 Search PubMed.
-
S. Chandrasekhar, Liquid Crystals, Cambridge University Press, Cambridge, 1977 Search PubMed.
-
S. T. Wu and D. K. Yang, Reflective Liquid Crystal Displays, Wiley, New York, 2001 Search PubMed.
- D.-J. Lee, G.-Y. Shim, J.-C. Choi, J.-S. Park, J.-H. Lee, J.-H. Baek, H. C. Choi, Y. M. Ha, A. Ranjkesh and H.-R. Kim, Opt. Express, 2015, 23, 34055–34070 CrossRef PubMed.
-
E. Stupp and M. Brennesholtz, Projection Display, John Wiley & Sons, New York, 1999 Search PubMed.
-
I. C. Khoo, Liquid crystals: physical properties and nonlinear optical phenomena, John Wiley & Sons, New York, 2007 Search PubMed.
-
R. H. Chen, Liquid crystal displays: fundamental physics and technology, John Wiley & Sons, 2011 Search PubMed.
-
D. K. Yang, Fundamentals of liquid crystal devices, John Wiley & Sons, New York, 2014 Search PubMed.
- J. Li, S. Gauza and S. T. Wu, J. Appl. Phys., 2004, 96, 19–24 CrossRef.
- M. S. Zakerhamidi, Z. Ebrahimi, H. Tajalli, A. Ghanadzadeh, M. Moghadam and A. Ranjkesh, J. Mol. Liq., 2010, 157, 119–124 CrossRef.
- A. Ranjkesh, J.-C. Choi, J.-S. Park, M.-K. Park, S. Kiani, M. S. Zakerhamidi and H.-R. Kim, J. Mol. Liq., 2017, 230, 280–289 CrossRef.
- M. F. Vuks, Opt. Spectrosc., 1966, 20, 361–364 Search PubMed.
- T. Devi, B. Choudhury, A. Bhattacharjee and R. Dabrowski, Opto-Electron. Rev., 2014, 22, 24–30 Search PubMed.
- M. K. Das, A. Pramanik, B. Das and R. Dąbrowski, J. Phys. D: Appl. Phys., 2012, 45, 415304 CrossRef.
- M. S. Zakerhamidi and H. Rahimzadeh, J. Mol. Liq., 2012, 172, 41–45 CrossRef.
- G. P. Srivastava and Y. P. Varshni, Physica, 1956, 22, 584–586 CrossRef.
-
T. Hanai, N. Koizumi and R. Gotoh, Bulletin of the Institute for Chemical Research, Kyoto University, 1961, vol. 39, pp. 195–201 Search PubMed.
- M. Heng, S. Rui-Zhi, L. Zhen-Xin and L. Yu-Fang, Chin. Phys. B, 2008, 17, 255–258 CrossRef.
- H. Ma, X. Fu, H. Okada and H. Onnagawa, Liq. Cryst., 2009, 36, 835–838 CrossRef.
- H. Ma, J. Xu, H. Okada, H. Onnagawa, S. Sugimori and K. Toriyama, Curr. Appl. Phys., 2013, 13, 814–818 CrossRef.
- D. Bhattacharjee, P. R. Alapati and A. Bhattacharjee, J. Mol. Liq., 2016, 224, 507–514 CrossRef.
- H. Ma, H. Okada, S. Sugimori, H. Onnagawa and K. Toriyama, Jpn. J. Appl. Phys., 2004, 43, 6234–6238 CrossRef.
- H. Ishikawa, A. Toda, H. Okada and H. Onnagawa, Liq. Cryst., 1997, 22, 743–747 CrossRef.
- T. Nishi, A. Matsubara, H. Okada, H. Onnagawa, S. Sugimori and K. Miyashita, Jpn. J. Appl. Phys., 1995, 34, 236–237 CrossRef.
- J. Czub, R. Dąbrowski, J. Dziaduszek and S. Urban, Liq. Cryst., 2009, 36, 521–529 CrossRef.
- P. Dasgupta, A. Pramanik, M. K. Das and B. Das, Liq. Cryst., 2015, 42, 1083–1094 CrossRef.
- Y. Arakawa and H. Tsuji, Phase Transitions, 2016, 1–8 Search PubMed.
- A. G. Gilani, A. Ranjkesh and M. S. Beevers, J. Solution Chem., 2009, 38, 557–570 CrossRef.
- D. Sinha, S. Haldar and P. K. Mandal, Phase Transitions, 2016, 1–11 Search PubMed.
- S. S. Sastry, T. V. Kumari, S. S. Begum and V. V. Rao, Liq. Cryst., 2011, 38, 277–285 CrossRef.
- I. Haller, Prog. Solid State Chem., 1975, 10, 103–118 CrossRef.
- M. K. Das, P. C. Barman and S. K. Sarkar, Liq. Cryst., 2016, 43, 1268–1275 CrossRef.
- S. K. Sarkar and M. K. Das, Phase Transitions, 2016, 89, 910–921 CrossRef.
- S. Yildiz, H. Özbek, C. Glorieux and J. Thoen, Liq. Cryst., 2007, 34, 611–620 CrossRef.
- A. Kumar, Liq. Cryst., 2013, 40, 1422–1426 CrossRef.
- D. M. Latha, V. G. K. M. Pisipati, P. Pardhasaradhi, P. V. D. Prasad and G. P. Rani, Liq. Cryst., 2012, 39, 1113–1116 CrossRef.
- T. N. Soorya, S. Gupta, A. Kumar, S. Jain, V. P. Arora and B. Bahadur, Indian J. Pure Appl. Phys., 2006, 44, 524–531 Search PubMed.
- S. J. Rzoska, J. Ziolo, W. Sułkowski, J. Jadżyn and G. Czechowski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 052701 CrossRef PubMed.
- L. Mistura, J. Chem. Phys., 1973, 59, 4563–4564 CrossRef.
- J. Thoen and G. Menu, Mol. Cryst. Liq. Cryst., 1983, 97, 163–176 CrossRef.
- P. Cusmin, M. R. de La Fuente, J. Salud, M. A. Pérez-Jubindo, S. Diez-Berart and D. O. López, J. Phys. Chem. B, 2007, 111, 8974–8984 CrossRef PubMed.
- N. Sebastián, M. R. De La Fuente, D. O. López, M. A. Pérez-Jubindo, J. Salud, S. Diez-Berart and M. B. Ros, J. Phys. Chem. B, 2011, 115, 9766–9775 CrossRef PubMed.
- HyperChem™, Release 7.51, Hypercube, Inc., CS MOPAC Pro™, 1996–1999, Cambridge Soft Corporation, 2002.
- M. Schadt, J. Chem. Phys., 1972, 56, 1494–1497 CrossRef.
-
W. H. Jeu, Physical properties of liquid crystalline materials, CRC Press, Gordon and Breach, London, 1980 Search PubMed.
-
B. Bahadur, Liquid crystals: applications and uses, World Scientific, 1990, vol. 1 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: For comparison with the six-parameter dielectric model derived in this work, the fitting results using the four-parameter-based dielectric model are provided. The fitting results, obtained from the four-parameter dielectric permittivity model, of Vth(T) and K11(T) are presented for comparison with the results from the six-parameter dielectric model. Using the six-parameter dielectric model, the fitting results for different sets of nematic liquid crystals are presented. See DOI: 10.1039/c8cp01577e |
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Mohammad
Moghadam
a,
Mohammad
Moghadam
 b,
Jun-Chan
Choi
b,
Jun-Chan
Choi
 a,
Byeonggon
Kim
a,
Byeonggon
Kim
 a,
JeongHoon
Ko
a,
JeongHoon
Ko
 ac,
Mohammad Sadegh
Zakerhamidi
ac,
Mohammad Sadegh
Zakerhamidi
 d and
Hak-Rin
Kim
d and
Hak-Rin
Kim
 *a
*a

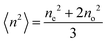



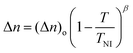
 and (Δn) from eqn (5) and (6) into eqn (3) and (4), the four-parameter refractive index models for ne(T) and no(T) are obtained:11,15
and (Δn) from eqn (5) and (6) into eqn (3) and (4), the four-parameter refractive index models for ne(T) and no(T) are obtained:11,15

 and Δn for an NLC.
and Δn for an NLC.



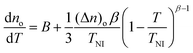
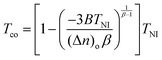













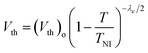
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vth as a function of ln(1 − T/TNI). By extrapolating the intercept value in the linear plot to T = 0 K, the value of (Vth)o can be determined, providing (Vth)o = π((K11)o/εo(Δε)o)1/2.
Vth as a function of ln(1 − T/TNI). By extrapolating the intercept value in the linear plot to T = 0 K, the value of (Vth)o can be determined, providing (Vth)o = π((K11)o/εo(Δε)o)1/2.