Structural evolution and phase transition of uniaxially stretched poly(butylene adipate-co-butylene terephthalate) films as revealed by in situ synchrotron radiation small and wide angle X-ray scattering†
Lifu
Li
a,
Youxin
Ji
ab,
Qianlei
Zhang
a,
Haoyuan
Zhao
a,
Sarmad
Ali
a,
Pinzhang
Chen
a,
Zhijie
Xia
a and
Wei
Chen
 *a
*a
aNational Synchrotron Radiation Lab and CAS Key Laboratory of Soft Matter Chemistry, Anhui Provincial Engineering Laboratory of Advanced Functional Polymer Film, University of Science and Technology of China, Hefei, China. E-mail: wc003@ustc.edu.cn
bSchool of Materials Science and Engineering, National Engineering Research Center for Advanced Polymer Processing Technology, Key Laboratory of Materials Processing and Mold (Zhengzhou University), Ministry of Education, Zhengzhou University, Zhengzhou, 450001, China
First published on 6th November 2018
Abstract
Poly(butylene adipate-co-butylene terephthalate) (PBAT) films under uniaxial stretching at room temperature were characterized by in situ synchrotron radiation wide-angle X-ray scattering (WAXS) and small-angle X-ray scattering (SAXS). Based on the macroscopic stress–strain curve and the microscopic structural information obtained by SAXS/WAXS, three regions are defined. In region I, the molecular chain of the amorphous region undergoes elastic deformation, namely affine deformation. After the yielding point (region II), the oriented amorphous chain starts to crystallize into the metastable β-crystal. In region III, where the strain-hardening happens, the transition from α-crystal to β-crystal occurs through a solid–solid transition mechanism. Therefore, the β-crystal is found to be formed through two different pathways during stretching. Meanwhile, it can be observed that the change in transmittance and phase transition are almost synchronous. This is attributed to the similarity of the refractive index of both the amorphous and crystalline regions after stretching. The relationship between the PBAT phase transition and its optical properties is revealed on the microscopic scale and could provide theoretical guidance for the preparation of agricultural films with higher transmittance.
Introduction
With the increasing concern of plastic pollution in the environment, there is a great demand to develop biodegradable polymeric materials with the comparable properties of petroleum-based polyolefins. Among them, polyesters stand out as one of the most promising environment-friendly polymers. However, as compared with widely used polyolefins, i.e. polyethylene (PE) and iso-tactic polypropylene (i-PP), polyesters, such as poly(lactide) (PLA) and poly butylene terephthalate (PBT) suffer from serious problems including poor processability and poor mechanical properties.1–5 The further fabrication of polyesters is necessary to solve these weaknesses. One efficient strategy is to incorporate rigid (high melting temperature Tm and high glass transition temperature Tg) and soft components (low Tm and Tg) to prepare polyester copolymers. For instance, poly(butylene adipate-co-butylene terephthalate) (PBAT) as shown in Scheme 1, the copolymer of aliphatic (adipic acid) and aromatic acids (terephthalic acid) with Tg ∼ 31 °C and Tm ∼ 125 °C, exhibits the combination of the good processability of poly(butylene adipate) (PBA, Tg ∼ −50 °C and Tm ∼ 60 °C) and the high thermal stability of PBT (Tg ∼ 23 °C and Tm ∼ 230 °C). And the commercially available PBAT product (Ecoflex, BASF) is reported to behave like low-density PE (LDPE).6–13Before addressing the crystal structure and phase transition of PBAT, it is necessary to know the polymeric crystal structure of pure PBA and PBT.14–17 PBA has two crystalline structures, namely α- and β-crystals. The α-crystal is monoclinic with unit cell parameters of a = 6.73 Å, b = 7.94 Å, c = 14.20 Å, and β = 45.5°, and can be obtained at a crystallization temperature of Tc > 31 °C, whereas the β-crystal is obtained at Tc < 29 °C with orthorhombic unit cell parameters of a = 5.06 Å, b = 7.35 Å, and c = 14.67 Å.18 The biodegradability of PBA is highly related to the crystal form: the degradation rate of PBA in the α-crystal form is much faster than that of the β-crystal. PBT also has two types of crystal forms: α- and β-crystals.19,20 Both are triclinic and the unit cell parameters are a = 4.83 Å, b = 5.94 Å, c = 11.59 Å, α = 99.7°, β = 115.2° and γ = 110.8° for the α-crystal and a = 4.95 Å, b = 5.67 Å, c = 12.95 Å, α = 101.7°, β = 121.8° and γ = 99.9° for the β-crystal. Yokouchi et al.19 first observed the coexistence of the α-crystal and β-crystal in stretched PBT samples. The β-crystal tends to exist under stretching conditions. Reversible transformation occurs from the β-crystal to the α-crystal under the conditions of relaxation. Tashiro et al.20 monitored the elongation and relaxation process at room temperature by using infrared spectroscopy technology. It was found that the molar ratio of the β-crystal increases with the increase in the stress.
Butylene adipate (BA) and butylene terephthalate (BT) units are reported to be randomly distributed along the PBAT chain.21 As a result, the crystal size, even though obtained under quiescent conditions, is quite small, i.e. ∼100 nm, which is different from that of polyester homopolymers. Debates related to the crystallization of PBAT are mostly related to the presence or absence of the BA unit in the crystalline region. Kazuhiro Kuwabara et al.22 first attempted to characterize the crystal structure of PBAT. It was found that the crystalline region of PBAT is composed of BT units and almost all the BA units only exist in the non-crystalline regions. The supporting evidence mostly comes from the 1D wide-angle X-ray scattering (WAXS) patterns which show that PBAT has a similar pattern to PBT compared to PBA, and the solid-state NMR results which show that the single spin–lattice relaxation time T1 of the BA unit in PBAT is close to that of the amorphous component of PBA. However, Emily Cranston et al.23 showed that the BA unit is also incorporated in the crystalline region through the rearrangement of the backbone conformation rather than being completely excluded. The double exponential decay of the T1 of the methylene groups next to the carbonyl of BA is determined which represents two different components. Meanwhile, due to the comparable size of the BA and BT monomer units, the molecular rearrangement of BA could well be adjusted to be similar to that of BT in the crystalline region. As a result, the WAXS patterns of PBAT are almost the same as those of PBT. Moreover, X. Q. Shi et al. also studied the crystal structure and properties of the PBAT fibers.24 And they also showed the crystal structure of the PBAT fibers formed by mixed-crystallization of BT and BA units, and the mixed crystallization promoted the formation of a well-developed PBT-like crystal structure. Meanwhile, they confirmed that the crystal structure of the PBAT fibers undergoes PBT-like reversible crystal form transitions, but the α-crystal to β-crystal transition was found to occur in a higher strain region compared with that in PBT. Besides numerous investigations of PBAT, however, few reports related to the in situ characterization of PBAT films during stretching have been reported. The macroscopic properties, i.e. mechanical and optical properties, are closely related to the microscopic parameters. And the in situ study of PBAT films during deformation could help us to better understand the processing–structure–property relationships of PBAT in order to prepare high-quality PBAT films.
In this work, the uniaxial extension of PBAT obtained from blown films was in situ investigated with the assistance of high time resolution synchrotron radiation small- and wide-angle X-ray scattering (SAXS/WAXS) techniques. A detailed evolution of the structural parameters, including orientation, crystallinity (Xc), crystallite size and lamellar thickness, was obtained in association with the stress–strain curve. The origin of the yielding and onset of strain hardening were unveiled. Moreover, the transmittance of PBAT films is highly related to the external applied force, and even under stretching at room temperature, the transmittance would significantly change. Such optical property changes can also be explained through microscopic structural evolution.
Experimental section
Materials
The PBAT resins used in this work are Ecoflex® F Blend C1200 (The PBAT was kindly supplied by BASF Hongrui Biological Technology Co., Ltd, China) with 44 mol% butylene terephthalate (BT) content. The molecular weight (Mw), molecular weight distribution (Mw/Mn), glass temperature (Tg), crystallization temperature (Tc), and melting temperature (Tm) are 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, 2.25, −28 °C, 96 °C and 121 °C, respectively.
000 g mol−1, 2.25, −28 °C, 96 °C and 121 °C, respectively.
Sample preparation
PBAT blown films, of which the take up ratio (TUR) is 5 and the blow up ratio (BUR) is 2 with a thickness of 160 μm, were prepared by using a home-made blown film machine.25–27 For the convenience of characterization, the PBAT films were cut into small stripe-like samples with lengths and widths of 140 mm and 60 mm for the ex situ experiment and 30 mm and 15 mm for the in situ experiment, respectively. PBAT films with a Cauchy strain ε of 50%, 100%, 150%, 200%, 250%, 300% and 350% were obtained using a universal tensile testing machine to test the transmittance and haze.Characterization
The in situ experiments were carried out at the BL16B1 of the Shanghai Synchrotron Radiation Facility (SSRF).28 The X-ray wavelength λ is 0.124 nm and a Pilatus 300 K detector (487 × 619 pixels with a pixel size of 172 μm) was employed to collect the time-resolved two dimensional (2D) scattering patterns for the WAXS measurements. A Rayonix SX-165 CCD detector (2048 × 2048 pixels with a pixel size of 80 μm) was used to collect the 2D SAXS patterns. A home-made stretcher was used to draw the PBAT films.29 The stretching rate was 0.025 mm s−1. The experiments were conducted with WAXS and SAXS technologies with a sample to detector distance of 62 mm and 2187 mm, respectively. The exposure time of WAXS and SAXS was 15 s and 5 s, respectively. The ex situ experiments were carried out at the National Synchrotron Radiation Laboratory (NSRL) in Hefei. The X-ray wavelength λ is 0.154 nm and a Mar345 detector (3000 × 3000 pixels with a pixel size of 150 μm) was employed to collect the 2D scattering patterns for the WAXS measurements. The exposure time was 20 min. The haze and transmittance (%) were measured by using a spherical haze meter (SGW-820 haze meter) with an accuracy of 1% and 0.5% for transmittance and haze, respectively.Data analysis
The one dimensional (1D) WAXS and SAXS profiles can be obtained by using the fit2D software. Both SAXS and WAXS patterns are corrected for background scattering resulting from air and the sample holder. The 2D SAXS patterns are integrated azimuthally to obtain the 1D scattering profiles as a function ofq = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ θ/λ | (1) |
| L = 2π/qmax | (2) |
The lamellar thickness Lc and spacing distance between two neighboring lamellas La are calculated by a correlation function obtained from the equation as follows:30
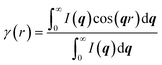 | (3) |
The correlation function is the Fourier transform of the Lorentz corrected SAXS profile. The 2D WAXD patterns are integrated to obtain the 1D scattering profiles as a function of 2θ. Multi-peak fitting is performed on the 1D scattering profiles in order to get the crystallinity Xc of the samples:31
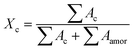 | (4) |
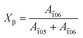 | (5) |
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 05) plane is the characteristic peak of the α-crystal and the (
05) plane is the characteristic peak of the α-crystal and the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 06) plane belongs to the β-crystal.24 The orientation factors are calculated by Hermans' equation:32
06) plane belongs to the β-crystal.24 The orientation factors are calculated by Hermans' equation:32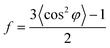 | (6) |
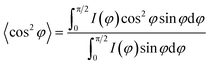 | (7) |
Combined with the thickness at different strains, a formula is used to correct the transmittance to make sure the influence of the thickness of the film on the transmittance is excluded.
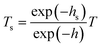 | (8) |
The density of the crystalline phase and amorphous phase can be calculated by the following formula:
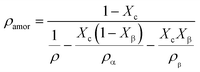 | (9) |
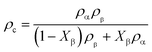 | (10) |
Results
Stress–strain curve of PBAT during uniaxial stretching
Fig. 1 shows the stress–strain curve of the PBAT film at room temperature and the corresponding 2D WAXS and SAXS patterns. The transition point of the curve can be determined by deriving the stress–strain curve. In the initial stage of stretching, the derivative keeps dropping. When the strain reaches ca. 20.5%, there is almost no change in the derivative, which is defined as the yield point of the material (εy). As the strain continues to increase, a plateau region appears. Strain hardening occurs after passing through the plateau zone before breaking. Since the signal-to-noise ratio is relatively small, the turning point of the appearance of the strain hardening region cannot be determined by the first derivative curve. Instead, the turning point is determined through the intersection of two straight lines representing the plateau and the strain-hardening regions, respectively, as shown in Fig. 1. The onset strain (εh) for the strain hardening is thus determined to be 97%. Compared with PBT (yield stress is 7.5 MPa and yield strain is 16% at 25 °C), the yield stress and yield strain of PBAT significantly increased. This should be attributed to the coexistence of the soft (BA) and hard (BT) segments in PBAT.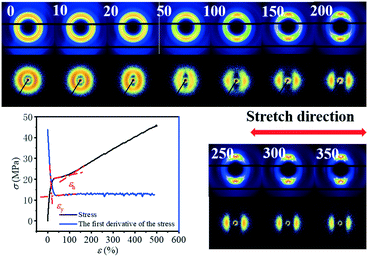 | ||
| Fig. 1 Stress–strain curve of the uniaxially stretched PBAT film and the corresponding 2D WAXS and SAXS patterns. | ||
The selected 2D SAXS and WAXS patterns of the PBAT film under different strains are shown in Fig. 1. The number in the upper left represents the engineering strain. An isotropic diffraction ring is observed in the 2D SAXS pattern at the very beginning, together with three distinct diffraction rings in the 2D WAXS pattern. This suggests that the initial PBAT blown film is crystallized, and the orientation of the crystal is isotropic. Such an isotropic pattern remains almost intact for 2D WAXS patterns beyond the yield point (εy = 20.5%), while a slight shrinking of the 2D SAXS pattern along the meridian direction is observed. The origin of such a phenomenon should be attributed to the elastic deformation of the amorphous component while the crystallite remains almost intact. Further increasing the strain leads to concentration of the WAXS signal along the equator, while the SAXS signal is concentrated along the meridian. And once the PBAT film is extended close to the onset strain of the strain hardening region, three equator streaks are observed in the WAXS pattern, whereas two separated crescentic streaks are observed in the corresponding SAXS patterns (ε = 100%). This indicates that the lamellar structure is aligned along the stretching direction. Within the strain hardening region, the WAXD signal is highly concentrated along the meridian direction and two weaker points can be observed in the direction of the equator. Meanwhile, the crescentic streaks in the SAXS pattern gradually separate more clearly with the increment of strain, while the corresponding intensity becomes weaker. The decreasing SAXS intensity shows that the lamellar structure of the PBAT film is gradually destroyed without a clear boundary between the amorphous and crystalline domains. Further quantitative description of the evolution of the long period will be discussed in following section.
SAXS results
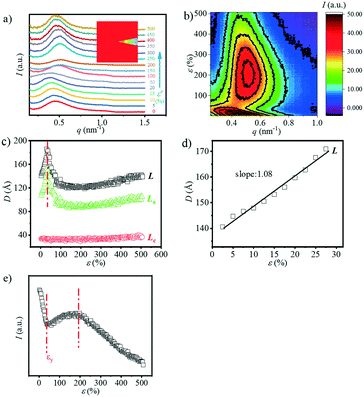
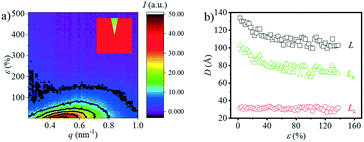
The typical integrated 1D SAXS profiles obtained from the 2D SAXS images and corresponding contour plots along the meridian direction as a function strain are shown in Fig. 2a and b. The meridian intensities are obtained by integration in the azimuthal angular range of −10° ≤ φ ≤ 10° as shown in the legend of Fig. 2a. The direction of stretching is in the meridian direction. From the 1D SAXS profiles, it is obvious that at the early stage of strain, the peak position shifts towards the small angle, suggesting an increment of the long period. However, when the strain reaches about 50%, this peak starts to shift towards a larger one. And it begins to shift slightly towards the small angle again when the strain increases up to ca. 200%. A more clear evolution of the position of this peak can be observed from the contour plots where two different signal intensities appear during the stretching process.The long period L, crystalline lamellar thickness Lc and amorphous thickness La were calculated based on eqn (2) and (3) and such domain sizes are summarized in Fig. 2c. In the early stages of the strain, the L shows an upward trend from 141.0 Å to 186.0 Å. The maximum value is reached when the strain increases up to 32.5%, and afterwards, the L begins to decline. When the strain is beyond 200%, there is a slight increase in the L. A similar phenomenon can be observed with the La, which increases to the maximum value of 152.1 Å (ε = 32.5%) at the very beginning, and then decreases dramatically to the minimum value of 86.4 Å (ε = 200%), following the increasing tendency before breaking. As the strain increases, however, the Lc hardly changes at the beginning and exhibits a slight increase when strain hardening occurs (ε = 100%). The sudden change in the L can be used to determine whether there is a transition from the α-crystal to the β-crystal when drawing the pure PBT.20,33 Meanwhile, the initial slope between long period L and the strain ε is close to 1.00 (Å/%) (Fig. 2d), which is similar to that of PBT with an α-crystal. This suggests that the affine deformation of PBAT films exists within ε < 32.5%. However, different from pure PBT, which still follows affine deformation after phase transition, the abrupt decrement of L shows that the PBAT films no longer elongate affinely. The origin of such a phenomenon will be addressed in the discussion part.
Note that the corresponding strain is 32.5% when the L reaches the maximum value, which is about 10% larger than the εy. This is because the calculated L depends on the two different SAXS signals. In other words, when the second signal appears, the corresponding strain is smaller than the strain when the L reaches the maximum value. Besides the long spacing distance, another important information is the SAXS intensity evolution during stretching, which could provide evidence for the phase transition. The integrated intensity with a q range of 0.15–0.8 nm−1, which covers both α- and β-crystals especially the transition regions, is shown in Fig. 2e. Two apparent turning points, i.e. ε = 37.5% and 192.5%, respectively, can be captured from the curve, which corresponds to two different structural changes. As compared with the long spacing distance evolution (Fig. 2c), the intensity evolution can distinguish the structural change, especially in the high strain region, i.e. ε = 192.5%.
Besides the overall long period evolution with the increment of strain, another interesting phenomenon is the rearrangement of the crystalline domain during stretching. The reorientation of the crystallite can be quantitatively observed through the SAXS curves along the equatorial direction. Fig. 3a shows the 1D SAXS integration curves along the equatorial direction. The equatorial intensities are obtained by integration in the azimuthal angular range of −10° ≤ φ ≤ 10° as shown in the legend of Fig. 3a. The peak position shifts toward the large angle as the strain increases, suggesting the shrinking of the spacing distance along the equatorial direction. When the strain reaches ca. 150%, the peak disappears. Fig. 3b shows the change in the L, La, and Lc along the equatorial direction. Similar to the evolution of the overall Lc (Fig. 2c), the Lc along the meridian direction has almost no change while the L and La decrease continuously. When the strain reaches about 140%, it is almost impossible to calculate these three parameters, which should be attributed the reorientation of the crystallite along the stretch direction (SD) with minor density contrast along the equator.
 | ||
| Fig. 3 a) The contour plots along the equatorial direction vs. strain; b) the long period (L), lamellae thickness (Lc) and the distance between the lamella (La) as a function of strain. | ||
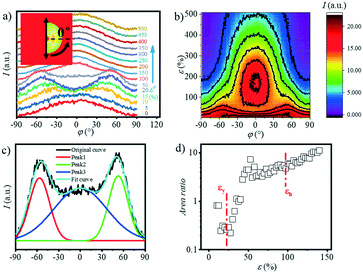
In addition to the long period obtained in both the meridian and equatorial directions, another interesting phenomenon is the four-spot SAXS pattern obtained during stretching (Fig. 1). The 2D SAXS patterns are integrated ranging from q = 0.15 to q = 0.8 nm−1 as a function of the azimuthal angle φ as shown in Fig. 4(a and b), where φ = 0° is defined as the position parallel to the direction of the meridian. With the strain increasing to 10%, two obvious peaks appear gradually at φ = ca. 35° and 135°. As the strain continues to increase, the peaks in both directions gradually disappear and finally, a strong single peak appears centred in the meridian direction. The appearance of the four-spot pattern suggests the formation of the staggered roof structure of the lamellae, which has been widely studied previously.34–36 The appearance of such a four-spot SAXS pattern in PBAT may be attributed to the flexible BA unit in the crystalline domain. As mentioned above, the BA and BT units are reported to be distributed randomly along the PBAT chain, and the BA unit is proven to be included in the crystalline region. The BA unit conformation is a metastable state, which would be deformed under external stress, forming a “staggered roof” structure.
Quantitative description of the peak evolution can be obtained through multi-peak deconvolution as shown in Fig. 4d. Three Gaussian peaks are used to fit the curve. The peaks on both sides are named peak1 and peak2, and the middle peak is named peak3 (Fig. 4c). The area ratio is defined as the following and the result is displayed in Fig. 4c:
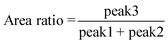 | (11) |
The area ratio decreases at first as the strain increases and gradually increases when the strain reaches εy. This illustrates that when the strain is beyond 10% but does not reach εy, a large number of lamellas are inclined in the meridian direction.
WAXS results
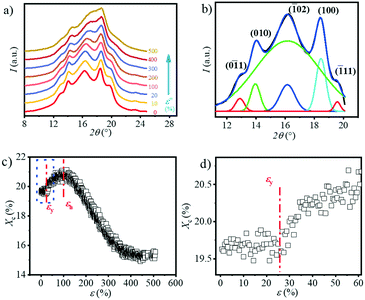
The 1D WAXS integral curves under different tensile strains are shown in Fig. 5a. Five distinct peaks can be observed in the 1D WAXS pattern of the original sample, which are assigned to the (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1), (010), (
1), (010), (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02), (100) and (
02), (100) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11) planes, respectively.37 With the increase in strain, the intensity of the diffraction peaks of the (0
11) planes, respectively.37 With the increase in strain, the intensity of the diffraction peaks of the (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (
1) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11) planes gradually decrease but do not completely disappear before breaking. The peak position of the (
11) planes gradually decrease but do not completely disappear before breaking. The peak position of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) plane gradually shifts to the larger angle. And the peak boundary of the (
02) plane gradually shifts to the larger angle. And the peak boundary of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) and (100) planes becomes blurred. The crystallinity Xc as a function of strain calculated based on eqn (4) is summarized in Fig. 5c. As shown in Fig. 5d, the crystallinity remains almost constant with a value of 19.6% before yielding (ε < 20.5%). When the strain reaches εy, the crystallinity begins to increase and reach the maximum value of ca. 21.5% at εh. The crystallinity starts to drop at εh until it exceeds the extension range of the stretcher. It is worth noting that in the final stage of stretching, the calculated crystallinity is inaccurate because the peaks of the two crystal planes overlap with each other. Similar phenomena can be observed in the stretching of PBT.38
02) and (100) planes becomes blurred. The crystallinity Xc as a function of strain calculated based on eqn (4) is summarized in Fig. 5c. As shown in Fig. 5d, the crystallinity remains almost constant with a value of 19.6% before yielding (ε < 20.5%). When the strain reaches εy, the crystallinity begins to increase and reach the maximum value of ca. 21.5% at εh. The crystallinity starts to drop at εh until it exceeds the extension range of the stretcher. It is worth noting that in the final stage of stretching, the calculated crystallinity is inaccurate because the peaks of the two crystal planes overlap with each other. Similar phenomena can be observed in the stretching of PBT.38
In order to explore the trend of the orientation during the stretching process, the scattering pattern of the (100) plane is integrated. The 1D azimuthal integral curves are shown in Fig. 6a. One broad peak appears at the very beginning, representing the isotropic orientation of the initial sample as discussed above. Accompanying the stretching increase, the peak width decreases gradually, and one sharp single peak appears with ε > ca. 100%. The quantitative description of the orientation ratio f is calculated based on eqn (6) and (7) as summarized in Fig. 6b. The f increases almost linearly with the increment of strain at the very beginning, and reaches the turning point at a strain of ε = 100%, which is close to the onset strain εh of strain hardening. The orientation ratio increases with a slower rate in the strain hardening region as compared with that beyond εh.
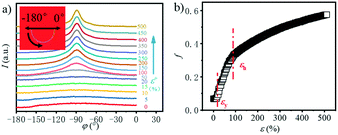 | ||
| Fig. 6 a) Azimuthal integration of the (100) reflection under different tensile strains; b) the evolution of the orientation parameter f with the increase in the strain. | ||
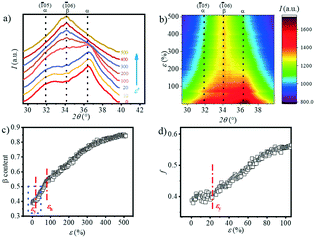
The transition of the α- to β-crystal exists for PBAT during the stretching process.24 In order to quantitatively analyze the α-crystal and β-crystal content changes in the stretching process, the 1D integration WAXS curves and contour plots ranging from 29.5° to 39.5° are displayed in Fig. 7a and b. The initial sample has two very distinct peaks at 31.8° and 36.3° and a weak peak at 34.2°. The appearance of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 05) (31.8°) and (
05) (31.8°) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 06) (34.2°) crystal planes indicates that the α-crystal and β-crystal coexist at the very beginning. The contour plots (Fig. 7b) show that as the strain increases, the two peaks corresponding to the α-crystal gradually disappear and instead the intensity of the peak located at ca. 34.2° is enhanced gradually, which suggests the increment of the β-crystal content. It illustrates that stretching promotes the phase transition from the α-crystal to the β-crystal. The relative content of the β-crystal Xβ is obtained through multi-peak deconvolution as summarized in Fig. 7c. Admittedly, such three peaks cannot fully reflect the real content of the β-crystal, since the WAXS diffraction patterns of the α-crystal and β-crystal overlap with each other. The Xβ shown in Fig. 7c is the relative ratio between these two crystals. It can be seen that at the initial stage of stretching, the Xβ remains almost constant (ε < εy). With the increment of strain, there is a rapid increase in the Xβ until ca. 55%, when the strain is close to εh. This shows the formation of a new β-crystal. Afterwards, the increasing trend of the Xβ slows down. And the maximum value of Xβ reaches 85% before breaking.
06) (34.2°) crystal planes indicates that the α-crystal and β-crystal coexist at the very beginning. The contour plots (Fig. 7b) show that as the strain increases, the two peaks corresponding to the α-crystal gradually disappear and instead the intensity of the peak located at ca. 34.2° is enhanced gradually, which suggests the increment of the β-crystal content. It illustrates that stretching promotes the phase transition from the α-crystal to the β-crystal. The relative content of the β-crystal Xβ is obtained through multi-peak deconvolution as summarized in Fig. 7c. Admittedly, such three peaks cannot fully reflect the real content of the β-crystal, since the WAXS diffraction patterns of the α-crystal and β-crystal overlap with each other. The Xβ shown in Fig. 7c is the relative ratio between these two crystals. It can be seen that at the initial stage of stretching, the Xβ remains almost constant (ε < εy). With the increment of strain, there is a rapid increase in the Xβ until ca. 55%, when the strain is close to εh. This shows the formation of a new β-crystal. Afterwards, the increasing trend of the Xβ slows down. And the maximum value of Xβ reaches 85% before breaking.
Optical properties of the stretched PBAT film
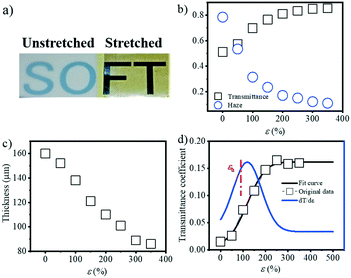
PBAT, as an environment friendly biopolymer, has great potential application in agriculture, such as films. One critical property of agriculture films is their optical properties, i.e. transmissivity and reflectivity. As a result, it's necessary to characterize the optical properties of the PBAT film during stretching, and check the influence of the evolution of the internal structure on its optical properties. Fig. 8a shows the actual image of the transmittance change before and after film stretching. Since the blown film is double-layered, the unstretched film in the figure is selected from half of the double film, and the stretched film is stretched by the two layers together. That is to say, the thickness of the unstretched film is smaller than the thickness of the film after stretching. The transmittance and haze as a function of strain were ex situ characterized as shown in Fig. 8b. The transmittance decreases with the increment of strain, while the corresponding haze is increased. Note that the film thickness decreased during extension (Fig. 8c) from the initial ca. 160 μm to the final ca. 80 μm, and it's necessary to correct the obtained transmittance and haze by the thickness. Based on eqn (8), the corrected transmittance coefficient can be calculated as shown in Fig. 8d. A gradual increment, rather than an abrupt one, in the transmittance coefficient can be obtained with a final plateau value of ca. 0.15. This result clearly indicates that the change in the optical properties of the PBAT film is not only caused by the thickness of the films but also related to the change in the internal structure of the film. Fitting the corrected transmittance curve and seeking its first derivative. A noticeable inflection point is found at a strain of 116.9%, which is close to εh.Discussion
Based on the structural information obtained from SAXS/WAXS, the structural evolution of PBAT during the uniaxial stretching process can be generally divided into three regions, namely region I, II and III as shown in Fig. 9. In region I, the affine deformation of the amorphous region dominates. The straightening of the molecular chain in the amorphous region leads to the increase in L and a decrease in electron density. At the yield point, the crystalline lamellar structure starts to deform into a “staggered-roof” structure, where fragmentation of the original crystal happens. Further increasing the strain leads to the formation of the metastable PBAT β-crystal, which mainly originates from the oriented amorphous component (region II) as evidenced by the increase in the Xβ and Xc. In region III, where the strain hardening happens, the initial α-crystal starts to transform into the β-crystal through solid–solid transition, which would be clarified in following section.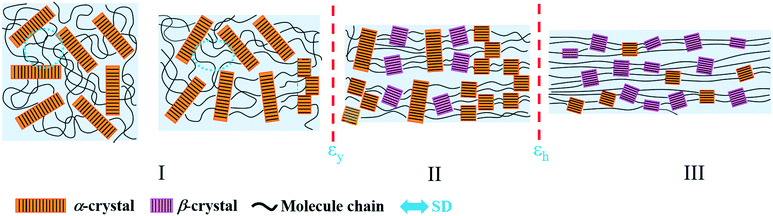 | ||
| Fig. 9 Schematic illustration of the structural evolution of the PBAT films during uniaxial stretching (25 °C). | ||
Generation mechanism of the β-crystal
The β-crystal of PBAT during uniaxial stretching is formed through two different pathways: crystallization from the oriented amorphous domain in region II, and phase transition from the α-crystal (region III). In region II, stretch induced crystallization (SIC) happens. Since the La decreases dramatically (Fig. 2c) and Xc (Fig. 5c) increases significantly, new crystals should be formed within the oriented amorphous region. Meanwhile, there is a significant increment of the total integral intensity (electron density difference) (Fig. 2e) and number of β-crystals (Fig. 8c) after the yield point, which suggests that such a newly formed crystal should be dominated by the β-crystal, leading to the decrease in the L. In other words, the metastable β-crystal is a kinetics favored phase and could be first transformed from the oriented chain in the amorphous domain rather than the α-crystal.In region III, the β-crystal fraction continuously increases (Fig. 8c), while the overall crystallinity Xc decreases (Fig. 5c). However, it should be noted that the total integral intensity of the 1D SAXS profiles in the meridian direction is still increasing (Fig. 2e). Meanwhile, the La is almost no longer changed, indicating that it is difficult to form new lamellae in the amorphous region as in region II. This suggests that the α-crystal starts to transform into the β-crystal within the strain-hardening region (region III).
Two mechanisms related to this phase transition are possible: one is the solid–solid phase transition, or the small-block sliding mechanism,39–42 and the other is the melting–recrystallization.42,43 Strobl et al.44–48 proposed that at first, a block slip mechanism within the crystalline lamellae happens, followed by stress-induced fragmentation and recrystallization after the yield strain. Flory et al.49,50 asserted that melting and recrystallization occur simultaneously during the stretching of the polymer. One characteristic of the melting–recrystallization process is the change in the lamellar thickness Lc: apparent increment of the Lc is possible to be observed during stretching, while that of the solid–solid phase transition remains almost constant. For PBAT, Lc remains almost unchanged throughout the whole stretching process (Fig. 2c).
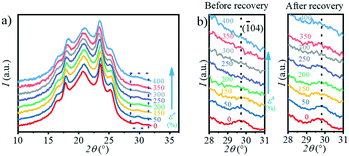
Moreover, during the recovery process, the reversible transition from the β-crystal to the α-crystal occurs. In the ex situ experiment, the PBAT films were first stretched to a certain strain and fixed with a clamp to prevent them from retracting, and characterized by WAXS. The clamp was then removed, at which point the films were retracted and the WAXS test was performed again. The 1D WAXS profiles after recovery at different strains can be obtained by ex situ WAXS as shown in Fig. 10a, and the enlarged area representing the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 04) crystal plane (α-crystal) is shown in Fig. 10b. Interestingly, it can be seen from Fig. 10b that the intensity of the (
04) crystal plane (α-crystal) is shown in Fig. 10b. Interestingly, it can be seen from Fig. 10b that the intensity of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 04) crystal plane (α-crystal) gradually decreases during stretching, and disappears when the strain is >250%. However, once released after the strain reaches 400%, this peak starts to appear again even if it is not obvious due to the small signal-to-noise ratio. Meanwhile, it can be seen that when the stress is released under a different strain, the area of the peak corresponding to the (
04) crystal plane (α-crystal) gradually decreases during stretching, and disappears when the strain is >250%. However, once released after the strain reaches 400%, this peak starts to appear again even if it is not obvious due to the small signal-to-noise ratio. Meanwhile, it can be seen that when the stress is released under a different strain, the area of the peak corresponding to the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 04) crystal plane (α-crystal) on the one-dimensional integral curve is different. The larger the strain, the smaller the peak area. This indicates that there is a transition from the α-crystal to the β-crystal during stretching, and part of the β-crystal is converted to the α-crystal when stress is released. The β-crystal exhibits a higher c value as compared with the α-crystal. The transition between these two crystals is a kind of elastic deformation of the crystalline domain, which is similar to the transition in PBT.24,31,33,51 The major difference is that the transition happens at a ε of ∼10% for PBT, while it happens at ∼20.5% for PBAT in the current study. This should be attributed to the incorporation of a BA unit in the crystalline domain, whose aliphatic chain is relatively flexible and tends to deform at large strains. Moreover, the Tg of PBAT is ≃31 °C while that of PBT is ∼23 °C. During the stretching at room temperature, the molecular mobility of PBAT is faster than that of PBT, resulting in phase transition at a large strain.
04) crystal plane (α-crystal) on the one-dimensional integral curve is different. The larger the strain, the smaller the peak area. This indicates that there is a transition from the α-crystal to the β-crystal during stretching, and part of the β-crystal is converted to the α-crystal when stress is released. The β-crystal exhibits a higher c value as compared with the α-crystal. The transition between these two crystals is a kind of elastic deformation of the crystalline domain, which is similar to the transition in PBT.24,31,33,51 The major difference is that the transition happens at a ε of ∼10% for PBT, while it happens at ∼20.5% for PBAT in the current study. This should be attributed to the incorporation of a BA unit in the crystalline domain, whose aliphatic chain is relatively flexible and tends to deform at large strains. Moreover, the Tg of PBAT is ≃31 °C while that of PBT is ∼23 °C. During the stretching at room temperature, the molecular mobility of PBAT is faster than that of PBT, resulting in phase transition at a large strain.
In summary, in the process of stretching, it is easy to form the β-crystal from the α-crystal by solid–solid phase transformation rather than melting-recrystallization at room temperature. Such a phenomenon, where the metastable phase can be formed under stretching conditions, while it transforms into a more thermal stable phase under release, widely exists in polymer systems with polymorphism. For instance, for poly(L-lactide) (PLLA), the metastable β-crystal formed under large strains is able to transform into the α-crystal.52,53 It is worth noting that this phase transition in PBAT could be assigned to a first-order phase transition similar to those in PBT and PBS systems, which requires further investigation.54,55
Relationship between the structural evolution and optical properties of PBAT
Based on the change in transmittance as shown in Fig. 8, the turning point (ε = ca. 116.9%) can be observed, which corresponds to the phase transition from the α- to β-crystal. The transmittance of the material is determined by the refractive index of each phase in the multiphase component, which is strongly related to the density of the material.56 In order to clarify the change in the optical properties during the PBAT stretching process, the density of the crystalline phase and amorphous phase can be calculated by eqn (9) and (10). The ρα and ρβ of PBT are used instead of those of PBAT as mentioned in the reported literature.19 The change in density with the increase in strain is shown in Fig. 11. As the strain increases, the ρc changes from 1.36 g cm−3 to 1.30 g cm−3, while the ρamor changes from 1.23 g cm−3 to 1.25 g cm−3. The different between the ρc and ρamor (Δρ) changes from 0.12 g cm−3 to 0.05 g cm−3. It indicates that the increase in strain during the stretching process promotes the phase transition and leads to the increase in transmittance.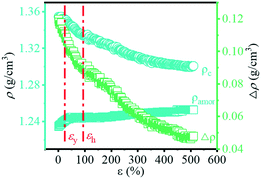 | ||
| Fig. 11 Evolution of the density of the amorphous (ρamor) and crystalline (ρc) components together with their difference (Δρ) with the increase in strain. | ||
Conclusions
The structure evolution of the PBAT films during uniaxial stretching at room temperature was investigated by a combination of SAXS and WAXS. The whole structural evolution process of PBAT films can be generally divided into three different regions. In region I, the affine deformation of the amorphous component dominates. Beyond the yield point, which is the boundary between regions I and II, the metastable β-crystal starts to appear, which originated from the oriented amorphous component. Meanwhile, the transmittance starts to decrease within this region, which is mainly attributed to the decrease in the density between the crystalline and amorphous components. Region III represents the strain-hardening region, where the stable α-crystal begins to transform into the metastable β-crystal through the solid–solid phase transition. Therefore, two different pathways for the formation of the β-crystal were found during the PBAT stretching process. As a main application for the PBAT material, the optical properties of its blown film plays an important role, and current work unveils the origin of the transmittance evolution during the stretching process. This information could provide a useful hint for the application and optimization of PBAT films.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Key Research and Development Program of China (2016YFB0302500) and the National Natural Science Foundation of China (51703217 and 51633009). The authors acknowledge the staff at the BL16B1 of the Shanghai Synchrotron Radiation Facility (SSRF) for their kind help on the in situ WAXS/SAXS tests.Notes and references
- L. B. Li and W. H. de Jeu, Macromolecules, 2004, 37, 5646–5652 CrossRef CAS.
- Z. Kulinski and E. Piorkowska, Polymer, 2005, 46, 10290–10300 CrossRef CAS.
- K. P. Cui, L. P. Meng, N. Tian, W. Q. Zhou, Y. P. Liu, Z. Wang, J. He and L. B. Li, Macromolecules, 2012, 45, 5477–5486 CrossRef CAS.
- J. Zhu, J. Cai, W. Xie, P.-H. Chen, M. Gazzano, M. Scandola and R. A. Gross, Macromolecules, 2013, 46, 796–804 CrossRef CAS.
- K. P. Cui, L. P. Meng, Y. X. Ji, J. Li, S. S. Zhu, X. Y. Li, N. Tian, D. Liu and L. B. Li, Macromolecules, 2014, 47, 677–686 CrossRef CAS.
- L. C. Arruda, M. Magaton, R. E. S. Bretas and M. M. Ueki, Polym. Test., 2015, 43, 27–37 CrossRef CAS.
- E. J. Dil, P. J. Carreau and B. D. Favis, Polymer, 2015, 68, 202–212 CrossRef CAS.
- A. A. Shah, S. Kato, N. Shintani, N. R. Kamini and T. Nakajima-Kambe, Appl. Microbiol. Biotechnol., 2014, 98, 3437–3447 CrossRef CAS.
- L. Jiang, M. P. Wolcott and J. W. Zhang, Biomacromolecules, 2006, 7, 199–207 CrossRef CAS.
- S. Y. Gu, K. Zhang, J. Ren and H. Zhan, Carbohydr. Polym., 2008, 74, 79–85 CrossRef CAS.
- F. Signori, M. B. Coltelli and S. Bronco, Polym. Degrad. Stab., 2009, 94, 74–82 CrossRef CAS.
- M. Kumar, S. Mohanty, S. K. Nayak and M. R. Parvaiz, Bioresour. Technol., 2010, 101, 8406–8415 CrossRef CAS.
- Y. X. Weng, Y. J. Jin, Q. Y. Meng, L. Wang, M. Zhang and Y. Z. Wang, Polym. Test., 2013, 32, 918–926 CrossRef CAS.
- W. Zhang, J. Li, Y. Shang, H. Li, S. Jiang and L. An, CrystEngComm, 2017, 19, 6858–6868 RSC.
- Z. Li, D. Ma, X. Cheng, X. Luo and G. Zhang, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 634–644 CrossRef CAS.
- Y. Zhao and Z. Qiu, CrystEngComm, 2011, 13, 7129–7134 RSC.
- A. Prasannan, T.-L. Bich-Tram, D.-Y. Hsu, P.-D. Hong and G.-R. Pan, CrystEngComm, 2013, 15, 5119–5126 RSC.
- Z. Gan, H. Abe and Y. Doi, Macromol. Chem. Phys., 2002, 203, 2369–2374 CrossRef CAS.
- M. Yokouchi, Y. Sakakibara, Y. Chatani, H. Tadokoro, T. Tanaka and K. Yoda, Macromolecules, 1976, 9, 266–273 CrossRef CAS.
- K. Tashiro, Y. Nakai, M. Kobayashi and H. Tadokoro, Macromolecules, 1980, 13, 137–145 CrossRef CAS.
- U. Witt, R. J. Müller and W. D. Deckwer, Macromol. Chem. Phys., 1996, 197, 1525–1535 CrossRef CAS.
- K. Kuwabara, Z. H. Gan, T. Nakamura, H. Abe and Y. Doi, Biomacromolecules, 2002, 3, 390–396 CrossRef CAS.
- E. Cranston, J. Kawada, S. Raymond, F. G. Morin and R. H. Marchessault, Biomacromolecules, 2003, 4, 995–999 CrossRef CAS PubMed.
- X. Q. Shi, H. Ito and T. Kikutani, Polymer, 2005, 46, 11442–11450 CrossRef CAS.
- Q. Zhang, L. Li, F. Su, Y. Ji, S. Ali, H. Zhao, L. Meng and L. Li, Macromolecules, 2018, 51(11), 4350–4362 CrossRef CAS.
- R. Zhang, Y.-X. Ji, Q.-L. Zhang, J.-Z. Ju, A. Sarmad, L.-F. Li, H.-Y. Zhao and L.-B. Li, Chin. J. Polym. Sci., 2017, 35, 1508–1516 CrossRef CAS.
- H. Zhao, Q. Zhang, S. Ali, L. Li, F. Lv, Y. Ji, F. Su, L. Meng and L. Li, J. Polym. Sci., Part B: Polym. Phys., 2018, 56(20), 1404–1412 CrossRef CAS.
- J. Zeng, F. Bian, J. Wang, X. Li, Y. Wang, F. Tian and P. Zhou, J. Synchrotron Radiat., 2017, 24, 509–520 CrossRef CAS.
- L. Meng, J. Li, K. Cui, X. Chen, Y. Lin, J. Xu and L. Li, Rev. Sci. Instrum., 2013, 84, 115104 CrossRef.
- W. Ruland, Colloid Polym. Sci., 1977, 255, 417–427 CrossRef CAS.
- B. S. Hsiao, Z. G. Wang, F. J. Yeh, Y. Gao and K. C. Sheth, Polymer, 1999, 40, 3515–3523 CrossRef CAS.
- H. Klug and L. Alexander, X-Ray Diffraction Procedures, John Wiley and Sons, New York, 1954 Search PubMed.
- A. A. Apostolov, S. Fakirov, M. Stamm, R. D. Patil and J. E. Mark, Macromolecules, 2000, 33, 6856–6860 CrossRef CAS.
- W. Wilke, M. Bratrich, B. Heise and G. Peichel, Polym. Adv. Technol., 1992, 3, 179–190 CrossRef CAS.
- R. Androsch, N. Stribeck, T. Lüpke and S. Funari, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 1919–1930 CrossRef CAS.
- A. Romo-Uribe, A. Manzur and R. Olayo, J. Mater. Res., 2012, 27, 1351–1359 CrossRef CAS.
- R. Al-Itry, K. Lamnawar, A. Maazouz, N. Billon and C. Combeaud, Eur. Polym. J., 2015, 68, 288–301 CrossRef CAS.
- W. Y. Zhang, J. Q. Li, H. F. Li, S. C. Jiang and L. J. An, Polymer, 2018, 143, 309–315 CrossRef CAS.
- R. Seguela and F. Rietsch, J. Mater. Sci. Lett., 1990, 9, 46–47 CrossRef CAS.
- M. F. Butler, A. M. Donald and A. J. Ryan, Polymer, 1997, 38, 5521–5538 CrossRef CAS.
- Z. Bartczak and E. Lezak, Polymer, 2005, 46, 6050–6063 CrossRef CAS.
- H. H. Song, A. S. Argon and R. E. Cohen, Macromolecules, 1990, 23, 870–876 CrossRef CAS.
- M. A. Kennedy, A. J. Peacock and L. Mandelkern, Macromolecules, 1994, 27, 5297–5310 CrossRef CAS.
- R. Hiss, S. Hobeika, C. Lynn and G. Strobl, Macromolecules, 1999, 32, 4390–4403 CrossRef CAS.
- Y. Men and G. Strobl, Macromolecules, 2003, 36, 1889–1898 CrossRef CAS.
- K. Hong, A. Rastogi and G. Strobl, Macromolecules, 2004, 37, 10165–10173 CrossRef CAS.
- K. Hong and G. Strobl, Macromolecules, 2006, 39, 268–273 CrossRef CAS.
- A. Peterlin, J. Mater. Sci., 1971, 6, 490–508 CrossRef CAS.
- P. J. Flory and D. Y. Yoon, Nature, 1978, 272, 226–229 CrossRef CAS.
- W. Wu, G. D. Wignall and L. Mandelkern, Polymer, 1992, 33, 4137–4140 CrossRef CAS.
- J. P. Runt, X. Zhang, D. M. Miley, K. P. Gallagher and A. Zhang, Macromolecules, 1992, 25, 3902–3905 CrossRef CAS.
- L. Cartier, T. Okihara, Y. Ikada, H. Tsuji, J. Puiggali and B. Lotz, Polymer, 2000, 41, 8909–8919 CrossRef CAS.
- B. Eling, S. Gogolewski and A. Pennings, Polymer, 1982, 23, 1587–1593 CrossRef CAS.
- G. Liu, L. Zheng, X. Zhang, C. Li, S. Jiang and D. Wang, Macromolecules, 2012, 45, 5487–5493 CrossRef CAS.
- Y. Ichikawa, J. Washiyama, Y. Moteki, K. Noguchi and K. Okuyama, Polym. J., 1995, 27, 1230 CrossRef CAS.
- Y. Liu and P. H. Daum, J. Aerosol Sci., 2008, 39, 974–986 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ce01734d |
| This journal is © The Royal Society of Chemistry 2019 |