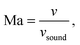Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Passive and active colloidal chemotaxis in a microfluidic channel: mesoscopic and stochastic models
Laurens
Deprez
 and
Pierre
de Buyl
and
Pierre
de Buyl
 *
*
Instituut voor Theoretische Fysica, KU Leuven, 3001 Leuven, Belgium. E-mail: pierre.debuyl@kuleuven.be
First published on 26th April 2017
Abstract
Chemotaxis is the response of a particle to a gradient in the chemical composition of the environment. While it was originally observed for biological organisms, it is of great interest in the context of synthetic active particles such as nanomotors. Experimental demonstration of chemotaxis for chemically-powered colloidal nanomotors was reported in the literature in the context of chemo-attraction in a still fluid or in a microfluidic channel where the gradient is sustained by a specific inlet geometry. In this work, we use mesoscopic particle-based simulations of the colloid and solvent to demonstrate chemotaxis in a microfluidic channel. On the basis of this particle-based model, we evaluate the chemical concentration profiles in the presence of passive or chemically active colloids, compute the chemotactic force acting upon them and propose a stochastic model that rationalises our findings on colloidal chemotaxis. Our model is also able to explain the results of an earlier simulation work that uses a simpler geometry and to extend its interpretation.
1 Introduction
Nanomotors are nano- to micro-meter sized machines that use a local (internal or found in the close environment) source of energy to move or perform work. The catalytic conversion of a chemical fuel on catalytically coated colloids was used with success for different types of motors (metallic rods,1 polystyrene2 and silica3 Janus particles, dimers4). Chemically powered nanomotors represent very promising devices for the execution of tasks such as sensing or cargo delivery in nano- to micro-meter scaled environments.5–7 Understanding the response of nanomotors to chemical concentration gradients, chemotaxis, is critical to engineer these possible applications.The experimental characterisation of chemotactic motion can proceed either via chemical sources that supply the environment with fuel, at specific “target” locations, or via a flow that allows the sustainment of the gradient. The first idea was used by Hong et al. to demonstrate the occurrence of chemotaxis for rod nanomotors.8 The second strategy was used by Baraban et al. in ref. 9 where the authors studied experimentally the chemotactic motion of chemically powered nanomotors in a microfluidic channel and observed a lateral deviation of the nanomotors when the fuel is input asymmetrically at the inlet of the cell. The successful modeling and understanding of colloidal chemotaxis is also relevant for biological systems, with the traditional example being the chemotactic behaviour of bacteria.10 The focus on biological chemotaxis has been put forward by Sengupta et al. who also used a microfluidic channel to observe the enhanced migration of enzymes across a microfluidic channel in the presence of a substrate gradient.11 More recently, the sorting of enzymes on the basis of their chemotactic response has been demonstrated in ref. 12.
Numerical simulations of chemotaxis can either assume an expression for a “chemotactic force” or reproduce the chemotactic process itself, using a direct simulation of the solvent. This article starts with the latter approach using Molecular Dynamics simulation with an explicit solvent in which several chemical species are represented. We then formulate a continuous picture for the solvent concentration field and use it to build a stochastic model that captures the chemotactic behaviour and its connection to our simulation parameters.
The literature on particle-based modeling of chemotaxis for nanomotors is rather scarce. Chen et al.13 considered a simplified system in which a constant chemical gradient is imposed by the boundaries of the simulation cell. In this work, we seek to imitate the experimental setup of Baraban et al.9 and to improve the theoretical understanding of this experimentally relevant configuration for chemically powered nanomotors, albeit using a simpler dimer-type nanomotor instead of the Janus and tubular microjet motors in the experiment. Our computational experiments build gradually by starting with a non-catalytic spherical colloid, then adding a catalytic property to the spherical colloid and finally using the dimer nanomotor. We come back to the results of Chen et al.13 and extend their conclusions.
In Section 2, we review the mesoscopic simulation model. The simulational implementation of the experiment of ref. 9 is laid out in Section 3. The continuous representation of the fluid's diffusion profile, including in the situation where chemical reactions occur on the surface of the colloid, is given in Section 4. There, we also compute the chemical gradient induced forces on the colloids. The stochastic model for the colloids is presented in Section 5. We give the results for both modeling strategies in Section 6 and conclude in Section 7. In Appendix A, we provide full information on how to access the numerical code to reproduce our findings.
2 Simulation model
The solvent consists of point particles with mass mi, position ri and velocity vi. There is no force acting between solvent particles, their interaction is instead modeled via cell-wise collisions at fixed time intervals τ using the Multiparticle Collision Dynamics (MPCD) collision rule introduced by Malevanets and Kapral.14,15 MPCD has been used successfully to investigate the dynamics of colloids in microfluidic channels by Prohm et al., in the context of inertial focusing,16 or by Nikoubashman et al. to study the flow of colloids in the presence of obstacles,17 for instance.The evolution of fluid particles, in the presence of forces due to colloids or to the flow-inducing field, is resolved numerically using the velocity Verlet algorithm18,19
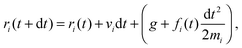 | (1) |
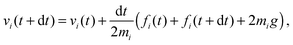 | (2) |
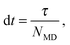 | (3) |
At fixed time intervals τ, the fluid particles are sorted in a lattice of cubic cells of side a, whose origin is shifted randomly to ensure Galilean invariance,20 and their velocities are collided cell-wise according to
| vi′ = vξ + Ωξ(vi − vξ) | (4) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 around a randomly chosen axis and vξ is the centre-of-mass velocity of the cell. The transport properties of a MPCD fluid can be computed analytically, see ref. 21, 22 and references therein. The simulation parameters are given in Table 1.
3 around a randomly chosen axis and vξ is the centre-of-mass velocity of the cell. The transport properties of a MPCD fluid can be computed analytically, see ref. 21, 22 and references therein. The simulation parameters are given in Table 1.
| Parameter | Symbol | Value |
|---|---|---|
| Number density | n | 10 |
| Solvent particle mass | m | 1 |
| MPCD fluid density | ρ | 10 |
| Cell size | a | 1 |
| MPCD time step | τ | 0.5 |
| MD steps per MPCD step | N MD | 50 |
| Cell dimensions | L x , Ly, Lz | 90, 60, 15 |
| Buffer length | L buffer | 20 |
| Temperature | k B T | 1/3 |
| Acceleration | g | 0.001 |
| MPCD collision angle | Θ | 2.6 |
| Reaction probability | p | 1 |
| Colloid radius | σ | 3 |
| Unit interaction energy | ε A | 1 |
One technique to obtain a Poiseuille flow is to impose a constant acceleration field in the simulation cell,23 in combination with periodic boundary conditions in the direction of the flow (x) and stick boundary conditions in the direction transverse to the flow (z). In ref. 19 and 24, this technique was applied to MPCD fluids. In the y direction we use specular boundary conditions for the fluid, so that the flow velocity profile vx(z) bears no dependence on y. We implement stick boundary conditions for the flow in the z direction with a combination of bounce-back collisions and ghost particles at the boundary MPCD cells.25 The ghost particles also set the temperature at the wall. In this work the walls also provide a sufficient thermostatting action to compensate for the flow-induced heating and no bulk thermostatting is used. We have verified that the temperature of the fluid remains stable after a transient period at a value that is about 3% in excess of the temperature set at the walls.
The colloids evolve according to the velocity Verlet algorithm, similarly to the solvent particles, but do not participate in the collisions and are not subject to acceleration field g. In the case of dimer nanomotors, the distance between the two spheres is held constant using the RATTLE algorithm.26
The coupling with solvent particles is done via the shifted and truncated Lennard-Jones 12-6 potential of the form
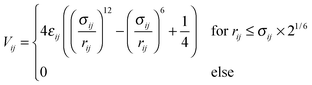 | (5) |
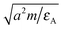 . As the interaction between all colloids and solvent particles of species A is equal, the first subscript to εκ,A is dropped in the following.
. As the interaction between all colloids and solvent particles of species A is equal, the first subscript to εκ,A is dropped in the following.
Confinement of the colloids in the z direction is obtained by a purely repulsive Lennard-Jones 9-3 potential of the form
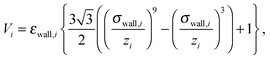 | (6) |
MPCD fluids are well suited to describe chemical reactions influenced by catalytic surfaces27 or in the bulk.28 At the surface of a catalytic colloid C, the reaction
| A + C → B + C | (7) |
All simulations were performed using the open-source RMPCDMD software.29,30
3 Cell design
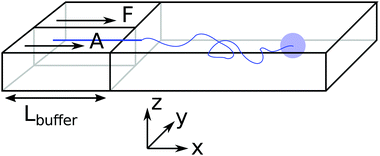
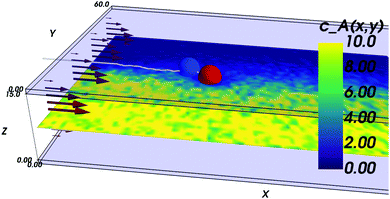
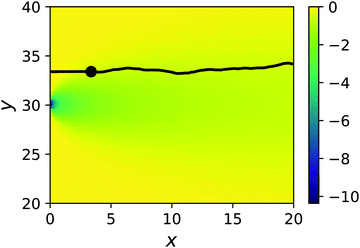
The inspiration for the design of the microfluidic cell comes from the experimental work on the chemotaxis of nanomotors by Baraban et al.9 There, a channel is fed with fluid at a fixed flow rate via three inlets. As only an inlet contains a chemical species of interest, i.e. the fuel for the nanomotors, the lateral distribution of species is inhomogeneous. The effect of the resulting gradient is a chemotactic behaviour that is observed by monitoring the deviation angle of the nanomotors with respect to a straight line motion.To reproduce the experimental features in a simulation, we have setup a thin channel with a forced flow in the program chemotactic_cell of the RMPCDMD software that is illustrated in Fig. 1. A simulation snapshot in Fig. 2 shows the Poiseuille flow, the concentration field for the fluid species A and the trajectory of a dimer nanomotor. To avoid reproducing the inlet channels at a large computational cost, we assign the solvent species to be either A (the fuel) or F (a neutral fluid species) arbitrarily, depending on the lateral position of the particles. The total number of particles in the simulation is constant and particles are not created or destroyed but “recycled” when they re-enter the simulation cell due to the periodic nature of the x boundary. The region of the cell where the forced attribution of species is applied is called the buffer and is located in the region 0 < x < Lbuffer. In the following text of the paper, the trajectories from the mesoscopic simulations are shifted in x by −Lbuffer to match the coordinate system of the stochastic model.
Although the simulations are three dimensional, the motion of the colloids is limited around the centre of the cell in the z-direction by the confining walls.
The flow between two plates is of the Poiseuille type with maximal velocity vflow and average velocity vav = 2/3 vflow. We report the characteristic numbers of the flow in Table 2. For the work of Baraban et al.,9 we use the values found in the article for the flow rate (140 μL per hour), the width (200 μm per inlet, there are three inlets) and temperature (300 K). The height of the channel was confirmed by email to be 30 μm. For the properties of water, we use reference data from the NIST31 (retrieved January 11, 2017: density ρwater = 996.56 kg m−3, and viscosity ηwater = 8.54 × 10−4 Pa s) and take the diffusion coefficient Dexp = 2 × 10−9 m2 s−1 that is a reasonable approximation for both water32 and hydrogen peroxide.33 For the MPCD fluid properties, we refer to the review by Kapral.22 The viscosity is
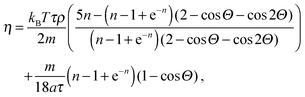 | (8) |
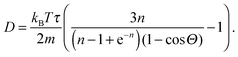 | (9) |
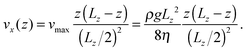 | (10) |
| Number | Simulation | Experiment |
|---|---|---|
| Width (Ly) | 60 | 600 μm |
| Height (Lz) | 15 | 30 μm |
| Average flow velocity vav | 0.063 | 2.16 mm s−1 |
| Maximum flow velocity vmax | 0.095 | 3.24 mm s−1 |
| Pe | 14 | 32 |
| Re | 0.48 | 0.076 |
We have aimed for a similar fluid regime with respect to the experiment, that is a high Péclet number (Pe) flow, as our estimate for the concentration profile relies on Pe ≫ 1 (see Section 4 and ref. 34). A value as high as for the experiment could not be obtained, but the important feature is that the transport by the flow dominates the one by diffusion in the x direction. The Reynolds number Re should remain moderate for the laminar regime to hold.
The Péclet, Reynolds, and Mach numbers for the flow are computed as
| Pe = Lzvav/D, |
| Re = vflowLz/η, |
where
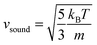 is the speed of sound.16 The maximum Mach number is obtained for the maximum velocity of the flow
is the speed of sound.16 The maximum Mach number is obtained for the maximum velocity of the flow 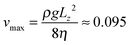 and is Ma ≈ 0.13.
and is Ma ≈ 0.13.
Besides the geometry of the cell, the simulation protocol differs slightly from its experimental counterpart. The colloid moves on a track at fixed 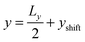 and
and 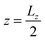 . This restriction is lifted when the x position of the colloid (centre of mass) has passed Lbuffer plus its own radius. This allows for a systematic comparison of the chemotactic drift across repeated runs without suffering from possible disturbance from the resetting of particles in the inlets. The shift yshift in the y direction ensures that solvent particles in the interaction range of the colloid are only of species F and not influenced to a change of species in the buffer region.
. This restriction is lifted when the x position of the colloid (centre of mass) has passed Lbuffer plus its own radius. This allows for a systematic comparison of the chemotactic drift across repeated runs without suffering from possible disturbance from the resetting of particles in the inlets. The shift yshift in the y direction ensures that solvent particles in the interaction range of the colloid are only of species F and not influenced to a change of species in the buffer region.
4 Density profiles and surface interaction
In this section, we compute the stationary concentration field cα(r) for the different chemical species in the cell and the resulting chemotactic force on the colloids.We approximate the evolution of cα(r) by a 1D diffusion equation where the spatial direction of the flow is proportional to time, i.e. x = vflowt, and the diffusion process acts in the transverse direction y. This approximation has been tested experimentally in ref. 34 and is only valid close to z = Lz/2. Close to the boundaries z = 0 and z = Lz of the cell, a different transport regime is taking place. Here, we neglect the variations in the z direction for the computation of the concentration cα(r) in the absence of catalytic particles.
Fixing z = Lz/2 and identifying the time and the x coordinate results in
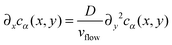 | (11) |
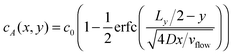 | (12) |
| cF(x,y) = c0 − cA(x,y) | (13) |
| cB(x,y) = 0 | (14) |
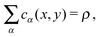 | (15) |
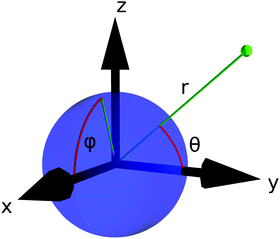
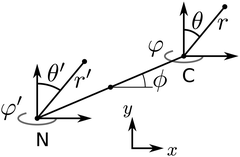
In the remainder of this section, we use coordinates centered on the colloid. The spherical coordinates are defined by the following relations
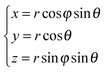 | (16) |
The presence of a catalytic colloid is taken into account in eqn (11) by a radiation boundary condition (RBC) on the surface of the colloid, at radius R. The boundary condition is applied at the limit of the interaction region, i.e. R = 21/6σ, where the continuum diffusive picture breaks down and where the chemical reactions are triggered. The RBC identifies the flux of chemicals with the consumption of the catalytic reaction, at the surface of the colloid. It was developed by Collins and Kimball35 and rederived later by other authors.36,37 The RBC at radius R in the absence of external gradient, for the species A, is
| RkD∂rcA = k0cA, | (17) |
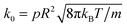 is the chemical rate.38p is the reaction probability defined in Section 2 and m is the mass of a fluid particle.
is the chemical rate.38p is the reaction probability defined in Section 2 and m is the mass of a fluid particle.
4.1 Surface interaction
Following the work of Rückner and Kapral,27 we sum the interaction potential Vκ,α between a colloid of species κ and the fluid particles of species α over the interfacial region to obtain the potential energy. Differentiation with respect to the colloid's coordinate gives the force on the colloid: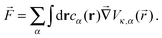 | (18) |
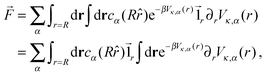 | (19) |
![[1 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0031_20d1.gif) r is the unit vector pointing in the radial direction. Integrating by parts yields
r is the unit vector pointing in the radial direction. Integrating by parts yields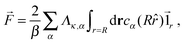 | (20) |
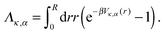 | (21) |
4.2 Single passive colloid
For a single passive colloid of type N, we use the solution (12)–(14) together with eqn (20).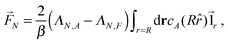 | (22) |
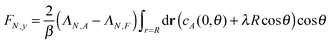 | (23) |
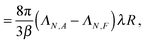 | (24) |
4.3 Single active colloid
To take into account the catalytic activity of a colloid, the diffusion eqn (11) is solved with the radiation boundary condition (RBC). Eqn (17) expresses the flux that originates from the chemical activity of the colloid, which is the only contribution to the flux in the situation where the RBC was derived. The total radial flux is the sum of the reaction-induced flux from eqn (17) and of the diffusive flux†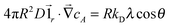 .
.RkD∂rcA = k0cA + RkDλ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (25) |
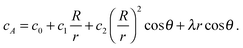 | (26) |
 | (27) |
It is important to mention that (i) in the absence of a gradient, the coefficients in eqn (27) lead to the standard solution of a spherical sink and (ii) in the absence of chemical activity, the solution (12) is recovered to linear order.
To obtain the solution for cB, we observe that the reactive flux of A particles absorbed at the surface of the sphere equals that of B particles, except that the currents flow in opposite directions. The solution to the diffusion equation with these opposite flows on the surface is
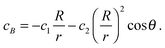 | (28) |
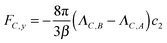 | (29) |
4.4 Dimer nanomotor
A dimer nanomotor is made of two spheres linked rigidly, with distance d between their centre of masses. One (C) is catalytic and acts as a sink for A-species solvent particles and a source of B-species solvent particles, creating locally a gradient centered on C.For the dimer nanomotor, the concentration fields depend on the presence of the catalytic sphere of the motor in the same way as for the single active sphere and we reuse eqn (27) and (29). The force must be evaluated also on the non-catalytic sphere N where the spherical symmetry does not hold. We evaluate this expression numerically as
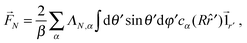 | (30) |
The forces on C and N are summed to obtain the centre-of-mass (com) force:
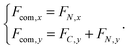 | (31) |
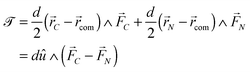 | (32) |
The motion of the dimer is studied via its centre-of-mass position in the x–y plane and its inclination ϕ with respect to the x axis.
5 Langevin dynamics for the colloids
For the spheres, the evolution of x and y (here, coordinates in the laboratory frame of reference) is given by the overdamped Langevin equations.39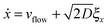 | (33) |
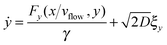 | (34) |
For the dimer, we use the following Langevin equations for the centre of mass and orientation
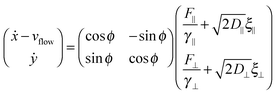 | (35) |
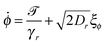 | (36) |
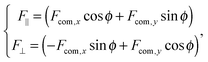 | (37) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is the torque defined in eqn (32). The rotation operations in eqn (36) and (37) are due to the difference in friction parallel and transverse to the axis of the dimer.
is the torque defined in eqn (32). The rotation operations in eqn (36) and (37) are due to the difference in friction parallel and transverse to the axis of the dimer.
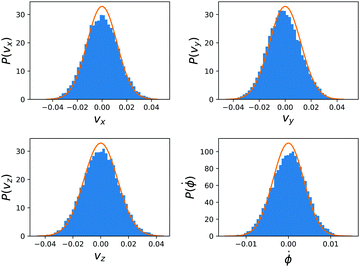
The diffusion coefficients for the dimers are obtained by performing equilibrium simulations in a cell of dimension ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) = (32, 32, 15) and with no chemical reaction, all other simulation parameters are taken equal. The cartesian and angular velocity distributions for the dimer are shown in Fig. 5.
= (32, 32, 15) and with no chemical reaction, all other simulation parameters are taken equal. The cartesian and angular velocity distributions for the dimer are shown in Fig. 5.
The dimer is an anisotropic colloid with axial symmetry. Accordingly, we compute separately the diffusion coefficient parallel (∥) and transverse (⊥) to its axis as
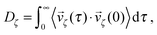 | (38) |
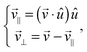 | (39) |
![[1 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0031_20d1.gif) x. The results of these simulations are D∥ =2.0 × 10−3 and D⊥ = 1.5 × 10−3. The rotational motion is characterised in the same fashion, using the velocity autocorrelation of angle ϕ: 〈
x. The results of these simulations are D∥ =2.0 × 10−3 and D⊥ = 1.5 × 10−3. The rotational motion is characterised in the same fashion, using the velocity autocorrelation of angle ϕ: 〈![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) (τ)
(τ)![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) (0)〉 with the result Dr = 1.4 × 10−4. We determine the friction coefficient using the fluctuation–dissipation relation
(0)〉 with the result Dr = 1.4 × 10−4. We determine the friction coefficient using the fluctuation–dissipation relation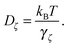 | (40) |
6 Results
6.1 Passive sphere
Here, we place a single sphere at the entry of the cell, in the upper y inlet surrounded by solvent particles of species F. When εA ≠ εN,F, the y component of the force due to the chemical gradient is non-zero.A typical trajectory for the passive sphere is represented in the x–y plane in Fig. 6. The main component is a displacement to the right under the influence of the flow, to which thermal fluctuations are superimposed. For this trajectory, εN,F = εA so there is no chemotactic behaviour.
Upon changing εN,F, a lateral force is exerted on the colloid due to the combination of the asymmetry of cA and cF with respect to the colloid and of the difference in surface interaction between the colloid and the A and F solvent species. This situation is one of the passive diffusiophoresis.
The results for passive spheres are summarised in Fig. 7 for all chosen values of εN,F. For the central panel εN,F = εA = 1, the sphere moves in x down the flow (i.e. from left to right in the figure) and undergoes diffusive motion in y. For εN,F < εA, we have ΛN,A − ΛN,F < 0 and we expect from eqn (24) a lateral force whose sign is opposite to gradient λ. As cA(x,y) decreases for increasing y, λ < 0 and the chemotactic force is upward, as confirmed by the panels εN,F = 0.25 and εN,F = 0.50. Conversely, for εN,F > εA, the chemotactic drift is negative. This is shown for εN,F = 2 and εN,F = 4 in Fig. 7.
Fig. 7 reports the results for both the mesoscopic model and the stochastic model. Given the fluctuating nature of the colloid dynamics, we have repeated the simulations 16 times and denote by a shaded area one standard deviation below and above the average results. We observe that the average trajectories are similar and also that the spread of trajectories is similar.
This first result on passive chemotaxis provides here the simplest context for the experimental setup and allows a possible calibration of the quantity ΛN,A − ΛN,F without any dependence on reaction rates.
6.2 Active sphere
We now turn to the chemotactic behaviour of an active sphere. The injection setup is the same as that for the passive sphere but now εC,F = εA and the mechanism that creates a systematic lateral motion for the passive sphere, that is proportional to ΛC,A − ΛC,F, is effectively zero.What occurs, instead, is that the local gradient in cA generates an asymmetric distribution also for cB that, together with a nonzero value for ΛC,B − ΛC,A, creates an original combination of passive and active diffusiophoresis. Using eqn (29) and observing that c2 > 0 (as λ < 0 everywhere in the simulation), we expect a downward chemotaxis for ΛC,B − ΛC,A < 0 (i.e. εC,B < εA) and an upward chemotaxis for ΛC,B − ΛC,A < 0 (i.e. εC,B > εA). We explore the effect of changing εC,B in Fig. 8 that confirms this direction for the chemotaxis of the active colloid. As for the passive sphere, the comparison between the mesoscopic and the stochastic models is positive.
 | ||
| Fig. 8 Ensemble trajectories for the active sphere simulations. Organisation as in Fig. 7. | ||
Even though the situation of the active sphere is simpler than the experiments on nanomotors of ref. 9, it already contains a complex ingredient: the chemotactic force is entirely caused by the self-generated concentration field around the colloid. Thanks to the derivations in Section 4, we understand how the asymmetry of the imposed concentration fields of A and F lead to an asymmetry in the concentration of B that gives rise to chemotaxis.
6.3 Dimer nanomotor
For the dimer nanomotor, we track in the simulations the centre-of-mass position![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) com and the orientation ϕ. The release from the injection track occurs here as soon as both spheres have exited the buffer region and the initial orientation is ϕ = 0.
com and the orientation ϕ. The release from the injection track occurs here as soon as both spheres have exited the buffer region and the initial orientation is ϕ = 0.
We have chosen, for the simulation parameters, that εC,α = εN,α, for all solvent species α. This is at variance with simulations of the prototypical dimer nanomotor4,13,27,40 where εC,A = εC,B = εA ≠ εN,B. Preliminary tests showed that in this situation the trajectories are pathological in the sense that there was no “gentle” deviation of the orientation ϕ and that no systematic tendency could be found. For nanomotors in a bulk environment with no a priori gradient in the chemical concentrations, this choice would be irrelevant.
Both the lateral deviation in the x–y trajectories and the angular deviation for ϕ are reported in Fig. 9 and 10 and are consistent between the mesoscopic simulations and the stochastic model. This confirms the adequateness of the combined force-torque evolution given by eqn (35) and (36) as both the directions in y and in ϕ are reproduced. The origin of the lateral deviation can be understood as coming not only from the redirection of the self-propelling force, that is oriented along the dimer axis, but also from the net lateral force on the centre of mass whose direction we can infer from eqn (27), (29) and (31). To our knowledge, this is the first time that the continuum force computation of ref. 27 is extended to compute the lateral force on a nanomotor and the resulting torque on the dimer nanomotor.
 | ||
| Fig. 9 Ensemble trajectories for the dimer nanomotor simulations. The centre-of-mass position is used. Organisation as in Fig. 7. | ||
 | ||
| Fig. 10 Ensemble trajectories of the dimer nanomotor simulations. Here, the orientation ϕ with respect to the x axis is shown. Organisation as in Fig. 7. | ||
6.4 Comparison to earlier simulation work
Aside from the geometric considerations that are specific to the microchannel, the stochastic model that we have designed can accommodate other situations. We use it to test, in a qualitative sense, the observations of ref. 13: we re-use the diffusion coefficients that we have obtained with our cell geometry and fluid parameters but change the type of gradient and the interaction type of the motor to match those of the earlier paper, which we call the “constant gradient” model. In ref. 13, Chen et al. designed a cell in which the gradient of the chemical species A and F is constant,‡i.e.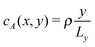 and
and 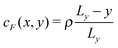 in the absence of chemical reaction, and the interaction parameters ε between the C sphere and both solvent species are identical, εC,A = εC,F = εC,B, so that there is no chemical gradient force on the C sphere (explicitly, ΛC,A = ΛC,B = ΛC,F).
in the absence of chemical reaction, and the interaction parameters ε between the C sphere and both solvent species are identical, εC,A = εC,F = εC,B, so that there is no chemical gradient force on the C sphere (explicitly, ΛC,A = ΛC,B = ΛC,F).
The main findings of Chen et al. are
• The average orientation of the nanomotor is toward y = 0, even though by a small amount (see the inset of Fig. 4(c) of ref. 13).
• The average trajectory of the nanomotor is toward y = Ly (see Fig. 7(a) of ref. 13).
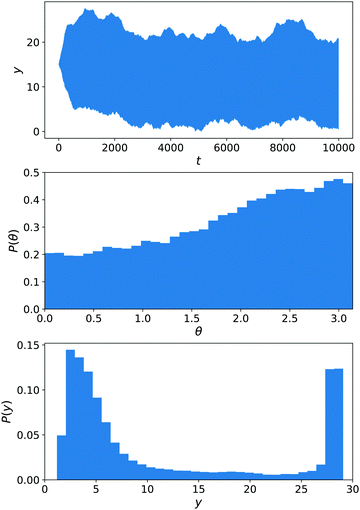
We will show here that these results depend strongly on the choice of parameters for the interaction between the colloid surfaces and the solvent via three observations: the distribution of trajectories y(t), the distribution of angles P(θ), and the distribution of position P(y).
We have performed stochastic simulations with εκ,A = εκ,F = εC,α = 1 (for all solvent species α and colloid species κ) and εN,B = 0.25, Ly = 30, Lz = 15. A harmonic wall with spring constant kwall = 10 prevents the exit of the colloid and is turned on for y < 2 or y > Ły − 2. The nanomotors were started in the x direction, as in ref. 13, to avoid an a priori bias. The results are displayed in Fig. 11. The distribution of y(t) trajectories in the upper panel shows a large spread, from which we cannot conclude a dominant chemotactic behaviour. Examining P(y), we see however that there is an average accumulation of particles close to y = 0. The angular distribution P(θ) does show a bias toward y = 0 (equivalently θ = π), as in ref. 13.
Until now, there was no chemically-induced force on the C sphere. To assess the importance of this choice, we perform another set of simulations εC,B = εN,B that are shown in Fig. 12. This parametrisation is the one used for our main results of Sections 6.1–6.3. From eqn (29)–(32), we know that the torque on the nanomotor will be influenced by this choice. This is reflected in the angular distribution P(θ) in Fig. 12 that now displays a strong orientation toward θ = 0 (i.e. the nanomotor is oriented toward y = Ly). As a result, there is no competition between a downward-facing nanomotor and the greater velocity for upward-facing nanomotor orientation that is observed in ref. 13 and the distribution of y(t) trajectories is narrow, showing a strong chemotactic behaviour. This is confirmed by the distribution of positions P(y).
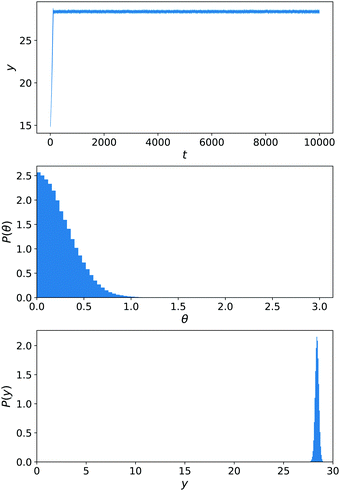 | ||
| Fig. 12 Simulations of the constant-gradient setup with εN,B = 0.25 and εC,B = 0.25. Averages are performed over 20 realisations for 2.5 × 104 < t < 10 × 104. Panels as in Fig. 11. | ||
To conclude this comparison, we have observed competing effects of orientation and propulsion, leading to different chemotactic behaviours. The distribution of angles, for instance, depends strongly on the parameters chosen for the colloid–fluid interaction: for the interaction choice of Chen et al., εC,A = εC,F = εC,B, we also find an average orientation toward y = 0, but for the other choice that we used the average orientation is toward y = Ly. The overall chemotactic behaviour will however also depend on the diffusive and propulsive properties of the dimer.
Although further research on the experimental characterisation of the surface properties of the nanomotors is needed, our stochastic model provides an interesting tool to relate these properties to the effective chemotactic behaviour of nanomotors.
7 Conclusions
We have proposed a particle-based simulation setup, based on Multiparticle Collision Dynamics and Molecular Dynamics, to study the chemotactic motion of passive and active colloids. The concentration field that drives this motion is sustained by the flowing input of the cell, via two inlets, as is done in the experiment described in ref. 9.We then constructed an approximate solution for the chemical concentration profile in the microfluidic channel in the presence of an active colloid and built a stochastic model with a microscopic expression for the systematic force. This model provides a sound basis for the microscopic origin of chemotaxis, i.e. it explains why the colloids move towards higher or lower values of the coordinate y. Upon extending this model to a two-sphere dimer nanomotor, we also gain an understanding of why the nanomotor changes its orientation via a systematic torque. We have thus improved on the formal understanding of the chemotactic motion in the microfluidic channel.
Our stochastic model, adapted to the setup with a constant concentration gradient by Chen et al. reproduces the observation that the nanomotor tends to orient opposite to the gradient. While Chen et al. observed a net positive chemotaxis, this is not the case in the present work. The reason is that the interplay between orientation and propulsion depends on the geometry of the motor and on the choice of parameters. This reasoning is supported by changing the surface interaction also for the C bead, resulting in a cooperation of orientation and propulsion leading to positive chemotaxis. The specific change in εC,B, that is not used in the simulation literature but introduced here in Section 6.3, allowed us to probe a regime of well-defined positive chemotaxis and demonstrates that the class of simulation models introduced by Rückner and Kapral27 possesses a very rich phenomenology.
It is interesting to note that our stochastic model requires only the input of the surface interaction parameters Λκ,α and of the diffusion coefficients of the dimer. In principle, it could be extended to other forms of the interaction potential or rely on a characterisation of Λκ,α that does not reveal the full functional form of this potential, and also to other motor geometries. While we have chosen ΛN,α = ΛC,α for all solvent species α for this first investigation of the model, there is room for possible qualitative changes with other choices, as we have witnessed for the constant gradient configuration.
The overall speed of the motor, as it was the case in earlier simulation studies for dimer nanomotors, only depends on ΛN,A − ΛN,B.27 The torque, on the other hand, depends also on ΛC,A − ΛC,B. A difference in these quantities, and thus in the surface properties of both sides of the nanomotor, could be revealed in a controlled manner in experiments and this reinforces the importance of the microfluidic channel configuration for chemotactic studies.
The present work can be extended to other types of motors, notably the Janus nanomotors that are used in ref. 9 and for which colloidal assemblies have already been used in mesoscopic simulations.41 This line of research is promising to test in silico the behaviour of different motor geometries. Using models suitable for the chemo-mechanics of enzymes, at a mesoscopic level,42–44 could provide very fruitful advances for understanding the recent works on enzyme chemotaxis,11,12 especially given the fact that multiple inlet microfluidic devices originate from studies on bacterial chemotaxis45 and have been used for the enzyme studies.11,12
Appendix
A Computational reproducibility
In this appendix, we review how the present work can be reproduced. The software and parameter files are all available publicly under open-source licences. We have prepared supplementary material that contains the relevant parameter files for the mesoscopic simulations and the code for data analysis and archived them with Zenodo,§ available as ref. 46.All mesoscopic simulations are performed using the open-source software package RMPCDMD29,30 for the simulations of passive and active colloids, developed by the authors with Mu-Jie Huang and Peter Colberg. The output of RMPCDMD consists of H5MD47 files that contain the full trajectory for the colloids, the thermodynamic observables and the correlation functions (velocity autocorrelation functions and mean-squared displacement).
All stochastic simulations are performed using Python, NumPy and Cython in a Jupyter¶ notebook. The analysis of both types of simulations and the execution of the stochastic model simulations are done in the notebook colloidal_chemotaxis.ipynb, except for the constant gradient model that is implemented in a separate Cython module stochastic_nanomotor.pyx and driver program run_cg_nm.py. The equilibrium simulations for the dimer are analysed in the notebook diffusion.ipynb.
The references for the software are the following: NumPy48 is used for all numerical work in the analysis of the mesoscopic model and overall for the stochastic model, SciPy49 is used for computing the erf function and for numerical integration, matplotlib50 to generate the figures, Mayavi51 for Fig. 2, h5py52 to read simulation data, Cython53 to accelerate the nanomotor stochastic simulations, gfortran54 to build the RMPCDMD code.
Acknowledgements
The authors thank Raymond Kapral for interesting discussions and Samuel Sanchez for communicating the height of the cell in ref. 9. PdB is a postdoctoral fellow of the Research Foundation-Flanders (FWO).References
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. S. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424–13431 CrossRef CAS PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 48102 CrossRef PubMed.
- H. Ke, S. Ye, R. L. Carroll and K. Showalter, J. Phys. Chem. A, 2010, 114, 5462–5467 CrossRef CAS PubMed.
- L. F. Valadares, Y.-G. Tao, N. S. Zacharia, V. Kitaev, F. Galembeck, R. Kapral and G. A. Ozin, Small, 2010, 6, 565–572 CrossRef CAS PubMed.
- R. Kapral, J. Chem. Phys., 2013, 138, 020901 CrossRef PubMed.
- J. Wang, Nanomachines, Wiley-VCH, Weinheim, Germany, 2013 Search PubMed.
- S. Ebbens, Curr. Opin. Colloid Interface Sci., 2016, 21, 14–23 CrossRef CAS.
- Y. Hong, N. M. K. Blackman, N. D. Kopp, A. Sen and D. Velegol, Phys. Rev. Lett., 2007, 99, 178103 CrossRef PubMed.
- L. Baraban, S. M. Harazim, S. Sanchez and O. G. Schmidt, Angew. Chem., Int. Ed., 2013, 52, 5552–5556 CrossRef CAS PubMed.
- H. C. Berg, Annu. Rev. Biophys. Bioeng., 1975, 4, 119–136 CrossRef CAS PubMed.
- S. Sengupta, K. K. Dey, H. S. Muddana, T. Tabouillot, M. E. Ibele, P. J. Butler and A. Sen, J. Am. Chem. Soc., 2013, 135, 1406–1414 CrossRef CAS PubMed.
- K. K. Dey, S. Das, M. F. Poyton, S. Sengupta, P. J. Butler, P. S. Cremer and A. Sen, ACS Nano, 2014, 8, 11941–11949 CrossRef CAS PubMed.
- J.-X. Chen, Y.-G. Chen and Y.-Q. Ma, Soft Matter, 2016, 12, 1876–1883 RSC.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605 CrossRef CAS.
- A. Malevanets and R. Kapral, J. Chem. Phys., 2000, 112, 7260 CrossRef CAS.
- C. Prohm, M. Gierlak and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 80 CrossRef CAS PubMed.
- A. Nikoubashman, C. N. Likos and G. Kahl, Soft Matter, 2013, 9, 2603–2613 RSC.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed.
- J. K. Whitmer and E. Luijten, J. Phys.: Condens. Matter, 2010, 22, 104106 CrossRef PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 20201 CrossRef CAS PubMed.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Adv. Polym. Sci., 2008, 221, 1–87 Search PubMed.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89 CrossRef CAS.
- J. Koplik, J. R. Banavar and J. F. Willemsen, Phys. Rev. Lett., 1988, 60, 1282–1285 CrossRef PubMed.
- E. Allahyarov and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 36702 CrossRef CAS PubMed.
- A. Lamura, G. Gompper, T. Ihle and D. M. Kroll, EPL, 2001, 56, 319 CrossRef CAS.
- H. C. Andersen, J. Comput. Phys., 1983, 52, 24 CrossRef CAS.
- G. Rückner and R. Kapral, Phys. Rev. Lett., 2007, 98, 150603 CrossRef PubMed.
- K. Rohlf, S. Fraser and R. Kapral, Comput. Phys. Commun., 2008, 179, 132 CrossRef CAS.
- P. de Buyl, M.-J. Huang and L. Deprez, J. Open Res. Softw., 2017, 5, 3 CrossRef.
- P. de Buyl, P. H. Colberg, L. Deprez and M.-J. Huang, RMPCDMD, 2016, https://doi.org/10.5281/zenodo.198599, Software release 1.0 Search PubMed.
- M. M. E. W. Lemmon and D. Friend, NIST Chemistry WebBook, National Institute of Standards and Technology, Gaithersburg MD, USA, 2016 Search PubMed.
- J. H. Wang, J. Phys. Chem., 1965, 69, 4412 CrossRef CAS.
- D. M. H. Kern, J. Am. Chem. Soc., 1954, 76, 4208–4214 CrossRef CAS.
- R. F. Ismagilov, A. D. Stroock, P. J. A. Kenis, G. Whitesides and H. A. Stone, Appl. Phys. Lett., 2000, 76, 2376–2378 CrossRef CAS.
- F. C. Collins and G. E. Kimball, J. Coll. Sci., Imp. Univ. Tokyo, 1949, 4, 425–437 CAS.
- M. Schell and R. Kapral, J. Chem. Phys., 1981, 75, 915–920 CrossRef CAS.
- D. T. Gillespie, J. Chem. Phys., 2009, 131, 164109 CrossRef PubMed.
- K. Tucci and R. Kapral, J. Chem. Phys., 2004, 120, 8262 CrossRef CAS PubMed.
- J. K. Dhont, An Introduction to Dynamics of Colloids, Elsevier, Amsterdam, The Netherlands, 1996, vol. 2 Search PubMed.
- Y.-G. Tao and R. Kapral, J. Chem. Phys., 2008, 128, 4518 Search PubMed.
- P. de Buyl and R. Kapral, Nanoscale, 2013, 5, 1337–1344 RSC.
- A. Cressman, Y. Togashi, A. S. Mikhailov and R. Kapral, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 050901(R) CrossRef PubMed.
- C. Echeverria, Y. Togashi, A. S. Mikhailov and R. Kapral, Phys. Chem. Chem. Phys., 2011, 13, 10527–10537 RSC.
- Y. Togashi and A. S. Mikhailov, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 8697–8702 CrossRef CAS PubMed.
- H. Mao, P. S. Cremer and M. D. Manson, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5449–5454 CrossRef CAS PubMed.
- P. de Buyl and L. Deprez, Colloidal chemotaxis companion, 2017, https://doi.org/10.5281/zenodo.344036.
- P. de Buyl, P. H. Colberg and F. Höfling, Comput. Phys. Commun., 2014, 185, 1546–1553 CrossRef CAS.
- S. van der Walt, S. Colbert and G. Varoquaux, Comput. Sci. Eng., 2011, 13, 22–30 CrossRef.
- E. Jones, T. Oliphant and P. Peterson, et al., SciPy: Open source scientific tools for Python, 2001, http://www.scipy.org/ Search PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 CrossRef.
- P. Ramachandran and G. Varoquaux, Comput. Sci. Eng., 2011, 13, 40–51 CrossRef.
- A. Collette, Python and HDF5, O'Reilly, 2013 Search PubMed.
- S. Behnel, R. Bradshaw, C. Citro, L. Dalcin, D. Seljebotn and K. Smith, Comput. Sci. Eng., 2011, 13, 31–39 CrossRef.
- The GNU Fortran Compiler (4.9.2), http://https://gcc.gnu.org/onlinedocs/gcc-4.9.2/gfortran/index.html.
Footnotes |
| † The flux is multiplied by the surface of the sphere 4πR2 as this is how the RBC is expressed in the literature. |
| ‡ For clarity, we reuse the species labels and orientation of the gradient used in the present work. This should be kept in mind when comparing with the work of Chen et al. where the gradient is along x and the species are labelled F for the fuel (here, A), S for the inert fluid (here, F) and P for the reaction product (here, B). |
| § http://https://zenodo.org/ |
| ¶ http://jupyter.org/ |
| This journal is © The Royal Society of Chemistry 2017 |