 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ordering block copolymers with structured electrodes
Ulrich
Welling
 and
Marcus
Müller
and
Marcus
Müller
 *
*
Institut für Theoretische Physik, Georg-August-Universität, 37077 Göttingen, Germany. E-mail: mmueller@theorie.physik.uni-goettingen.de
First published on 2nd December 2016
Abstract
We study the kinetics of alignment and registration of block copolymers in an inhomogeneous electric field by computer simulations of a soft, coarse-grained model. The two blocks of the symmetric diblock copolymers are characterized by different dielectric constants. First, we demonstrate that a combination of graphoepitaxy and a homogeneous electric field extends the maximal distance between the topographical guiding patterns that result in defect-free ordering compared to graphoepitaxy alone. In a second study, the electric field in the thin block copolymer film is fabricated by spatially structured electrodes on an isolating substrate arranged in a one-dimensional periodic array; no additional topographical guiding patterns are applied. The dielectrophoretic effect induces long-range orientational order of the lamellae and, additionally, registers the lamellar structure with the electrodes due to the field inhomogeneities at the edges of the structured electrodes. Thus, orientational and translational order is established by the inhomogeneous electric field. The simulations identify a process protocol of time-dependent electric potentials that suppresses defect formation by initially forming a sandwich-like structure and subsequently reorienting these lying into standing lamellae that are registered with the structure of the electrodes. This process-directed self-assembly results in large defect-free arrays of aligned and registered lamellae using electrodes with a saw-tooth period of 4 lamellar periodicities, L0, and a spacing of 10L0.
1 Introduction
Directed self-assembly (DSA) of block copolymer (BCP) materials is considered as a promising strategy for extending the capabilities of lithographic methods to the sub-10 nm range. The amphiphilic architecture of BCPs prevents macroscopic phase separation and, instead, the thermodynamically incompatible components spontaneously form periodic nanostructures.1,2 Chemical or topographic guiding patterns direct this self-assembly into technologically useful structures like lines and spaces. In the former situation – chemoepitaxy3,4 – one employs a chemical stripe pattern, whose periodicity is commensurate bulk lamellar period, L0 of the symmetric BCP to direct the self-assembly.5 In the latter strategy – graphoepitaxy6–10 – topographic trenches on the substrate are used to align and register the BCP morphology. Much current scientific effort focuses on optimizing copolymer materials and guiding strategies to obtain dense, defect-free structures over large areas and in registration with outer boundaries.11–14,17–21 In both cases, chemoepitaxy and graphoepitaxy, the characteristic length scale of the guiding pattern is restricted to a small integer multiple, n = 3–6, of the BCP periodicity, L0. This density multiplication factor, n, is dictated by the finite range, ξ, over which the edges of the guiding pattern – boundaries between chemical stripes or walls of trenches – influence the kinetics of structure formation in the BCP material.In contrast to these short-range, chemical or topographic guiding fields, shear flow14–16,22–31 or electric fields32–48 are well known for controlling the orientation of the BCP morphology over large scales. By virtue of the long-range character of shear or electric fields, pervading the entire sample volume, the field-generating sheared boundaries or electrodes can be many L0 spaced apart. Unfortunately, however, homogeneous long-range fields typically do not give rise to registration of the morphology with outer boundaries.
Here we explore the opportunities that electric-field effects with or without combination of graphoepitaxy offer for aligning and registering the BCP morphology. In the next section, Section 2, we describe our soft, coarse-grained model of BCPs in an inhomogeneous electric field. In Section 3 we demonstrate that the combination of graphoepitaxy and electric-field effect allows the fabrication of defect-free, registered lines-and-spaces structures in wide trenches. Section 4 discusses how an inhomogeneous electric field aligns and registers the BCP morphology and, in Section 5, we extend this strategy to electrodes that are structured with a larger period than L0 by judiciously choosing an assembly protocol. A brief summary and outlook conclude our manuscript.
2 Soft, coarse-grained model and simulation techniques
We employ a highly coarse-grained model for dense BCP melts. n block copolymers are confined into a thin film with dimensions Lx × Ly × Lz. The top and bottom surface of the film, representing the supporting substrate and vacuum, are represented as impenetrable hard walls that exert no preference for any block, A or B. Periodic boundary conditions are applied in the two lateral directions, x and y.Each linear chain molecule is represented by N = 32 coarse-grained interaction centers (beads), which are connected by harmonic springs.49,50
 | (1) |
The non-bonded interactions, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) nb, consist of a soft segment repulsion, characterized by the inverse isothermal compressibility κN, the repulsion of unlike blocks, parameterized by the Flory–Huggins parameter χN, and the energy of the electric field,
nb, consist of a soft segment repulsion, characterized by the inverse isothermal compressibility κN, the repulsion of unlike blocks, parameterized by the Flory–Huggins parameter χN, and the energy of the electric field, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) el.
el.
 | (2) |
 is the invariant degree of polymerization. In our simulations we use
is the invariant degree of polymerization. In our simulations we use 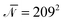 , which corresponds to a typical value of a BCP melt.
, which corresponds to a typical value of a BCP melt.
The first term restrains fluctuations of the total density and in accord with previous studies we set κN = 50. The second term describes the repulsive interaction between unlike segment species, A and B, giving rise to microphase separation. In the following we use the incompatibilities, χN = 18 and χN = 25. Calculations of the minimum free-energy path using self-consistent field theory51 demonstrate that the free-energy barrier of the annihilation of tight dislocation pairs in lamellar copolymer films vanishes at around χN = 18 whereas defects are metastable at χN = 25. The inverse compressibility κN ≈ 2χN is chosen to allow density fluctuations on the same energy scale as those resulting from the repulsion of unlike segments; the value suffices to suppress density fluctuations on the length scale of a small fraction of the polymer size, Re0.
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) A(r) represents the normalized, microscopic density of A segments at position r and it is related to the particle coordinates via
A(r) represents the normalized, microscopic density of A segments at position r and it is related to the particle coordinates via
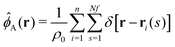 | (3) |
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) B(r). Expressing
B(r). Expressing ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) A and
A and ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) B through the particle coordinates the non-bonded Hamiltonian is a function of the configuration, {ri(s)}, suitable for particle-based computer simulations. In order to regularize the δ-function in eqn (3), we compute the densities and other spatially dependent quantities on a collocation grid by assigning a particle to the nearest grid point. The spacing of the collocation grid, ΔL, is commensurate with the natural period of the copolymer, so that L0 = 12ΔL. This discretization is sufficiently fine to spatially resolve the internal AB interfaces between block copolymer domains in our soft, coarse-grained model, and it is sufficiently coarse for the quasi-instantaneous field approximation that is invoked by the single-chain-in-mean-field algorithm be accurate.49 For the incompatibilities used in this manuscript, the bulk lamellar spacing, as estimated from the isotropy of the bonded single-chain stress, is L0 = 1.558Re0 and L0 = 1.677Re0, respectively, in the absence of an electric field.
B through the particle coordinates the non-bonded Hamiltonian is a function of the configuration, {ri(s)}, suitable for particle-based computer simulations. In order to regularize the δ-function in eqn (3), we compute the densities and other spatially dependent quantities on a collocation grid by assigning a particle to the nearest grid point. The spacing of the collocation grid, ΔL, is commensurate with the natural period of the copolymer, so that L0 = 12ΔL. This discretization is sufficiently fine to spatially resolve the internal AB interfaces between block copolymer domains in our soft, coarse-grained model, and it is sufficiently coarse for the quasi-instantaneous field approximation that is invoked by the single-chain-in-mean-field algorithm be accurate.49 For the incompatibilities used in this manuscript, the bulk lamellar spacing, as estimated from the isotropy of the bonded single-chain stress, is L0 = 1.558Re0 and L0 = 1.677Re0, respectively, in the absence of an electric field.
The electric energy, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) el, is calculated from the solution of the electric field, E = −∇ψ
el, is calculated from the solution of the electric field, E = −∇ψ
 | (4) |
| ∇[ε(r)∇ψ(r)] = 0 | (5) |
 | (6) |
The statistical mechanics of this model is studied by Single-Chain-in-Mean-Field (SCMF) simulations49,53,54 that exploit the separation between the strong bonded and weak non-bonded forces by temporarily substituting the weak non-bonded interactions by fields, wA(r) and wB(r), acting on A and B segments, respectively. The segment positions are updated by Smart Monte-Carlo moves using the force of the strong bonded interaction to propose a trial displacement.55,56 These local random displacements give rise to Rouse-like dynamics.57 The chain relaxation time, τ, characterizes the time that the center of mass of a macromolecule requires to diffuse its end-to-end distance  and it takes the value τ = Re2/D = 9711 Monte Carlo-steps in a disordered state, χN = 0. The slight difference between the end-to-end distance, Re, in a melt and the value, Re0, of non-interacting chain molecules arises from the soft repulsions of strength κ, restraining density fluctuations.
and it takes the value τ = Re2/D = 9711 Monte Carlo-steps in a disordered state, χN = 0. The slight difference between the end-to-end distance, Re, in a melt and the value, Re0, of non-interacting chain molecules arises from the soft repulsions of strength κ, restraining density fluctuations.
In the present study, the fields, wA(r) and wB(r), also include the electrostatic interactions.48 After each Monte-Carlo step, during which each particle has had the chance to be moved once on average, the quasi-instantaneous fields are re-calculated from the particle-densities according to48,49
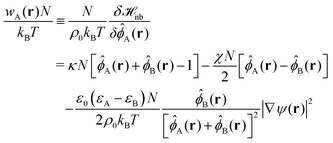 | (7) |
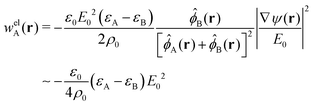 | (8) |
 attracts the component with the larger dielectric constant to regions of high field strength.
attracts the component with the larger dielectric constant to regions of high field strength.
The typical strength of non-bonded interactions is wχA ∼ kBTχ. Thus, we estimate the relative strength of the effect of the electric field by
 | (9) |
This relation motivates the definition of a normalized electric potential,  . In our simulations, this dimensionless parameter,
. In our simulations, this dimensionless parameter, ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) , adopts values in the range 0 ≤ |
, adopts values in the range 0 ≤ |![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) | ≤ 70, and the corresponding homogeneous electric field typically is in the range
| ≤ 70, and the corresponding homogeneous electric field typically is in the range 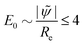 . For the systems with strong inhomogeneities, however, the electric field can be locally larger.
. For the systems with strong inhomogeneities, however, the electric field can be locally larger.
3 Combining graphoepitaxy with a homogeneous electric field
First, we consider the combination of graphoepitaxy and electric-field effect. The BCP system is confined into a trench with neutral walls in z-direction, which represent the substrate and the free surface of the BCP film. The film thickness, Lz = 0.66L0, is chosen as to frustrate lying structures. The side walls at x = 0 and x = Lx = 11L0 attract the A component with a potential | (10) |
In the absence of an electric field, this set-up corresponds to graphoepitaxy in a trench with preferential side walls. The side walls break the translational symmetry along the x-direction and direct the formation of a half-lamella of the preferred component, A, at the two side walls. This topographic guiding field aims at registering and aligning the lamellae across the entire x-direction as the system is quenched from the disordered state, χN = 0, to the microphase-separated state at incompatibility χN = 25. The snapshots in Fig. 1 reveal, however, that only 2 additional, registered and aligned, lamellar domains are formed in the course of structure formation, whereas defects occur in the middle between the two guiding side walls. This observation in our simulation study is consistent with graphoepitaxy experiments where the ordering influence of a preferential side wall often is insufficient to fabricate defect-free lamellar structures in a wide trench.6,8,58
To quantify the degree of smectic order, we monitor the largest eigenvalue, S2, of the tensor defined by dyadic product of the single-chain end-to-end vector. The value S2,max = 1/2 indicates perfect alignment of the end-to-end vector Re of each chain in the same direction. The time evolution of this order parameter, S2(t), is presented in the right panel of Fig. 1. Within a relaxation time, τ, after the quench from the disordered phase, microphase-separated domains are formed and the order parameter increases up to about 10τ. Subsequent changes of the morphology are protracted and no defect-free order is established within 15τ. Presumably the system has reached a metastable state and thermally activated processes are required to annihilate the remaining defects at χN = 25.51,59
In order to enhance graphoepitaxy we apply a homogeneous orthogonal electric field along the y-direction. To reduce the computational effort of solving the electric field, the boundary values of ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) at the preferential walls in the x-direction, x = 0L0 and x = 11L0, and at the neutral walls in z-direction are set to the homogeneous solution of the electric field in a plate capacitor. This approach follows the strategy applied for the simulation of copolymers in cylindrical slabs.48 The potential applied to the electrodes is ±16
at the preferential walls in the x-direction, x = 0L0 and x = 11L0, and at the neutral walls in z-direction are set to the homogeneous solution of the electric field in a plate capacitor. This approach follows the strategy applied for the simulation of copolymers in cylindrical slabs.48 The potential applied to the electrodes is ±16![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) , corresponding to an electric field of 2.9
, corresponding to an electric field of 2.9![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) /L0. The simulations start from the disordered state, χN = 0, and are quenched below the order–disorder transition, χN = 25. Simultaneously the electric field is switched on and the nearly homogeneous electric field along the y-direction creates a torque on the AB domain interfaces, leading to an alignment of the interfaces parallel to the electric field.
/L0. The simulations start from the disordered state, χN = 0, and are quenched below the order–disorder transition, χN = 25. Simultaneously the electric field is switched on and the nearly homogeneous electric field along the y-direction creates a torque on the AB domain interfaces, leading to an alignment of the interfaces parallel to the electric field.
The right panel of Fig. 1 presents snapshots of the time evolution and the order parameter for this combination of topographic and electric guiding fields. This combination results in defect-free assembly in a wide trench, Lx = 11L0, and also accelerates the ordering kinetics. In fact, the defect-free state is established at t = 12.5τ suggesting that electric field significantly contributes to defect removal by lowering the barriers for the annihilation of misaligned defect structures. The time dependence of the order parameter with a field above the critical ordering strength is rather continuous, suggesting that the barriers encountered in the course of structure formations do not significantly exceed the thermal energy scale, kBT. This first example illustrates that the combination of two orthogonal fields – the topographic side walls that locally register the A lamellae and the long-range electric field that dictates the overall orientation of the smectic structure – can significantly extend the process window of defect-free graphoepitaxy towards wider trenches and accelerated ordering kinetics.
4 Film on top of a patterned electrode
In this section we explore if an inhomogeneous field is able to register the lamellae to a specified position in addition to its orientation effect. To this end, we consider two parallel, structured electrodes that are buried inside the insulating substrate, εs = 2, directly below the BCP film, i.e. the bottom surface of the BCP film is flat and the electrodes do not provide any topographic cues that direct the structure formation. The two electrodes are spaced a distance Lx/2 = 15L0 apart. A description of solving the Laplace equation, eqn (5), in this thin-film geometry is provided in the Appendix.The system geometry and the electric potential are presented in Fig. 2. In the middle of the film between the two parallel electrodes, the field is approximately homogeneous and the concomitant torque tends to align the normals of the lamellae parallel to the yz plane. The geometric confinement into a thin film breaks this yz degeneracy because the chosen film thickness, Lz = 3L0/4, maximally frustrates lying lamellar structures (with normals in the z-direction). Thus the combination of homogeneous electric field and film thickness favors the formation of standing lamellae with normals along the y-direction in the middle between the electrodes, i.e., the orientational symmetry is broken.
The electrode structure is periodic along the y-direction, matching the domain spacing, L0, of the BCP. As shown in Fig. 2, there is a pronounced local enhancement of the electric field at the edges of the structured electrodes. The high value of the local field strength gives rise to a dielectrophoretic force that attracts the component, B, with the larger dielectric constant. Thus, the enhancement of the magnitude of the electric field acts similar to a substrate preference in chemoepitaxy – the strength of this attraction being tunable by the applied voltage between the electrodes.
Therefore the structure of the electrodes breaks the translational invariance along the y-direction. Since the periodicity of the electrodes and of the concomitant local enhancement of the field magnitude along the y-direction coincides with lamellar spacing, L0, of the block copolymer, we expect that the lamellar structure will locally register with the edges of the electrodes.
The ordering pathway is presented in Fig. 3; it can be divided in three stages that we discuss in turn:
(i) BAB-sandwich structure
The simulation starts in the disordered state and, at time t = 0, the incompatibility is increased to χN = 25 and a field (of strength 4![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) /L0 in the middle between the electrodes) is applied. In the very initial stage, 0 ≤ t ≤ 0.1τ, the electric field gives rise to a fast process, during which the copolymer forms a BAB sandwich structure. The component, B, of higher dielectric constant segregates towards the bottom and the top of the thin film, whereas the low-ε component, A, is enriched at the center of the film, z ≈ Lz/2. This initial, fast ordering process is caused by two effects: first, the kinked edges of the structured electrode give rise to strong field inhomogeneities that attract one component of the copolymer. An additional, weaker effect occurs on the top surface of the film, particularly in the vicinity of the electrodes. In this region, the component of the field, Ez, perpendicular to the surface passes from the copolymer material with an average dielectric constant of 3.5 into vacuum 1, giving rise to a field inhomogeneity. In the simulation, this surface effect only affects the top discretization layer of width, ΔL. Although our soft, coarse-grained model cannot faithfully represent the sharp density profile of a polymer film in coexistence with its vapor phase,50,60 also in an experimental polymer film, the continuously changing density at the free surface will give rise to a variation of the dielectric constant at the free surface and a concomitant dielectrophoretic force. Adjusting the applied potentials, one will be able to attract the copolymer material with the higher dielectric constant to the film surfaces in an experimental setup.
/L0 in the middle between the electrodes) is applied. In the very initial stage, 0 ≤ t ≤ 0.1τ, the electric field gives rise to a fast process, during which the copolymer forms a BAB sandwich structure. The component, B, of higher dielectric constant segregates towards the bottom and the top of the thin film, whereas the low-ε component, A, is enriched at the center of the film, z ≈ Lz/2. This initial, fast ordering process is caused by two effects: first, the kinked edges of the structured electrode give rise to strong field inhomogeneities that attract one component of the copolymer. An additional, weaker effect occurs on the top surface of the film, particularly in the vicinity of the electrodes. In this region, the component of the field, Ez, perpendicular to the surface passes from the copolymer material with an average dielectric constant of 3.5 into vacuum 1, giving rise to a field inhomogeneity. In the simulation, this surface effect only affects the top discretization layer of width, ΔL. Although our soft, coarse-grained model cannot faithfully represent the sharp density profile of a polymer film in coexistence with its vapor phase,50,60 also in an experimental polymer film, the continuously changing density at the free surface will give rise to a variation of the dielectric constant at the free surface and a concomitant dielectrophoretic force. Adjusting the applied potentials, one will be able to attract the copolymer material with the higher dielectric constant to the film surfaces in an experimental setup.
(ii) Standing, aligned and registered lamellae between electrodes
The film thickness, Lz = 3L0/4 highly frustrates this initial BAB sandwich structure. Thus, starting from the vicinity of the electrodes, this initial structure begins to reorient into standing lamellae for t > 2τ. These standing lamellae are registered with the edges of the structured electrodes due to the dielectrophoretic force in the inhomogeneous field. These registered standing lamellae propagate away from the electrodes along the x-direction, replacing the initial, frustrated BAB sandwich morphology. The orientation of these standing lamellae is stabilized by the homogeneous electric field in the middle between the two electrodes and the geometric confinement into a thin film. The two, registered and aligned, lamellar grains that emerge from each electrode merge in the middle between the electrodes, forming a defect-free, registered and aligned, lamellar structure around t = 15τ, except in the region on top of the electrodes.Right on top of the electrodes, the high field strength stabilizes a lying AB structure, where the high-ε component, B, is attracted to the high-field region at the substrate whereas the low-ε component, A, segregates to the free surface of the film. This lying AB structure differs from the initial BAB sandwich structure in the middle between the electrodes, but it is also frustrated by the thickness constraint. Thus, at this high voltage, a grain boundary between a lying AB structure on top of the electrodes and a defect-free, registered and aligned, lamellar domain between the electrodes is formed.†
(iii) Fusion of the standing, registered and aligned lamellae on top of the electrodes
The high field strength on top of the electrodes stabilizes the lying AB structure against standing lamellae that do not suffer from the film-thickness frustration. Therefore, we gradually reduce the field strength to slowly allow the adjacent, standing lamellae in the middle between the electrodes to invade the top of the electrodes, while still maintaining the positional registration to the edges of the electrodes. Some residual voltage, however, is required to maintain the positional registration of the lamellae at the edges of the electrodes and allow a defect-free fusion of the standing lamellae from the left and the right sides. We have verified that a sudden and complete removal of the electric field is likely to result in defects during the fusion of the standing lamellar domains on top of the electrodes. At the final stage of the simulation, the lamellae are all fully oriented and aligned to the electrode edges, as shown in Fig. 4. This figure demonstrates that the high-ε B-lamellae perfectly align with the edges of the structured electrodes.We emphasize that the temporal control of the external thermodynamic condition – here, the electric potential between the electrodes – during the three stages, encompassing the formation of the initial BAB sandwich structure, the reorientation into standing and registered lamellae between the electrodes, and the removal of the two grain boundaries at the electrodes, is critical. We refer to this strategy as process-directed self-assembly. The initial high electric field is required to align the lamellae in the middle of the film leads to parallel lamellae on top of the electrodes. If the electric field were switched off after the initial alignment step, the lamellae on top of the electrodes would have a high probability to misconnect, introducing defects on the electrodes. Instead, the electric field at the end of the process needs to register the lamellae, but also allow the lamellae to stand on top of the electrode. This synergistic, temporal interplay of field inhomogeneities, which are caused by the electrode edges and break the translational symmetry, and the homogeneous field between the electrodes and geometric confinement, which breaks the orientation symmetry, is the pivoting element of our strategy for simultaneous registration and alignment.
5 Structure multiplication
Although the distance between the electrodes is large, one limitation of the example in the previous section is that the individual electrodes are structured on the same length scale, L0, as the domain spacing of the BCP material. Similar to density multiplication in chemoepitaxy applications,5 where chemical guiding patterns are spaced a small integer multiple, n, of the lamellar spacing apart, defect-free ordering does not require the registering of every lamella, and this structure multiplication is very attractive for fabricating suitable electrodes that direct the structure formation of the BCP material.In order to illustrate structure multiplication, we choose a saw-tooth shape with an angle that is smaller than π/4 and a periodicity of 4L0 along the y-direction as the electrode geometry. The two electrodes are spaced Lx/2 = 10L0 apart along the x-direction. The spatial inhomogeneities of the electric field of this type of electrode are shown in Fig. 5. The field is strongest at the edges of the electrodes. Although the field enhancement is smaller than for the previous electrode shape, we will demonstrate that it still suffices to register the BCP structure.
The ordering pathway, depicted in the top panel of Fig. 6, is similar to the registration and alignment mechanism of the electrode with a finer structure. Fig. 7 presents the details of the initial kinetics of structure formation. Again, in the very early stage, t = 0.01τ, the inhomogeneities of the electric field at the electrodes acts like a preferential field that attracts the component, B, with the higher dielectric constant. This preference directs the spinodal microphase separation of the unstable, disordered structure at χN = 18. The spinodal ordering process leads to the formation a BAB-sandwich structure on top of the electrodes and, to a weaker extent, also in the region between the electrodes.
 | ||
| Fig. 6 The ordering process on top of a saw-tooth patterned electrode. (top) The images show a view at the system from the side at various times as indicated in the key. The strength of the electric field is denoted on the right. After the initial ordering process, which is presented in Fig. 7, the applied field is reduced, resulting in a defect-free, aligned and registered structure at t = 10τ. (bottom) Bottom view of the final structure at t = 10τ. The electrodes are shown in blue. Only the domain with the higher dielectric constant is depicted as teal stripes, the second domain is made invisible for clarity. Additional equipotential surfaces are depicted to indicate the strength of the electric field in the film. The high-ε domains register with the edges of the electrodes, where the electric field is strong. | ||
In the following, t < 0.1τ, this BAB-sandwich structure extends away from the electrodes and pervades the entire film. Whereas the homogeneous electric field in the middle between the electrodes does not exert a torque on the dielectric interfaces, the structure is highly frustrated because its natural thickness L0 is significantly larger than the film thickness 3L0/4.
Thus, starting on top of the electrodes, the structure rearranges. The high field on top of the electrodes does not permit standing lamellae and the BAB-sandwich transforms to a lying AB structure. Between the electrodes, however, the electric field mainly points in the x-direction and thus favors lamellar normals in the yz-plane. Standing lamellae, with normal vectors along the y-direction, conform with the orientation effect of the electric field and do not suffer any frustration from the constraint film thickness. Thus aligned and standing lamellae form between the electrodes. Since the transformation from the BAB-sandwich structure to the aligned, standing lamellae begins from the vicinity of the electrodes, the field inhomogeneities register the positions of the domains. Because the periodicity of the electrodes along the y-direction is 4L0, the registration is a bit more complex as on every side of the electrode only every fourth lamella is registered onto an edge, and the outward edge at the other side of the electrode has a shift of 2L0. This leads to the registration of every second lamellae on one of the sides of the electrode. Thus, similar to the finely structured electrodes, at t = τ the structure consists of a periodic arrangement to two types of grains: (i) a lying AB structure on top of the electrodes and (ii) registered, aligned and standing lamellae between the electrodes.
Gradually reducing the voltage between the electrodes, the grain of lying AB lamellae, which is frustrated by the film-thickness constraint, shrinks and the standing lamellae expand and merge in turn, until a defect-free, aligned structure is formed across the entire film as demonstrated in the bottom panel of Fig. 6. The registration to the edges has some freedom because the angle of the kinks of this type of electrode is low.
This example of structure multiplication with sparse electrodes that are structured with the periodicity of 4L0 and are a distance 10L0 apart also demonstrates that the strategy is rather robust and does not depend, e.g., on the fine details of the edges of the electrodes.
6 Conclusions
Using Single-Chain-in-Mean-Field simulations of a soft, coarse-grained model we have investigated the structure formation of lamella-forming diblock copolymers with dielectric contrast in an inhomogeneous electric field between structured electrodes. The electric field between the electrodes pervades the entire film and dictates the overall orientation of the block copolymer structure. This long-range character of the electric field distinguishes the guiding field from chemo- or graphoepitaxy. The structure of the electrodes gives rise to local field inhomogeneities and the concomitant dielectrophoretic forces register the position of the lamellar structure. Tailoring the time-dependence of the voltage, we have identified a pathway where a sandwich structure is initially formed at the electrodes, avoiding the formation of defects in the film between the electrodes. Subsequently, this structure is replaced by registered standing lamellae. This study illustrates (i) the ability of inhomogeneous electric fields to dictate both, orientational order and translational registration, and (ii) the benefits of tailoring the time-dependence of the field strength to direct the structure formation and avoid defect formation in the initial stages. This study was performed solely using DC fields. An interesting additional option is to investigate the effect of alternating current (AC) fields. Within our coarse-grained model, we expect that the main results of this paper also apply for AC fields, if one replaces the local permittivity ε(r) by its frequency-dependent version. We note that in our coarse-grained model, microscopic degrees of freedom of the segments are integrated out and, therefore, the response is limited to low frequencies. In cases that the frequency of the AC field is in the same order as the chain relaxation time, however, new pathways of defect removal may emerge. We hope that these simulations will inspire experimental studies.Appendix: solving the Laplace equation in a thin film
Since the electric potential, ψ(r), is computed during the update of the quasi-instantaneous fields after every Monte-Carlo step, the numerical strategy of solving the electrostatic Laplace equation, eqn (5), is critical. Due to the long-range character of the electric field, ψ extends below the BCP film into the substrate and far above into the vacuum. We consider the problem for a periodic unit of the electrodes in lateral directions, x and y, and impose a constant electric potential, ψ = 0, on an xy-plane at z = ±30L0 far above and below the substrate surface.The electric field of two flat, structured electrodes of non-circular cross section at z = 0 between two constant potential surfaces at z = ±30L0 is solved numerically by a finite-difference scheme.48Fig. 8 demonstrates the procedure for two saw-tooth electrodes that are spaced 10L0 apart in x direction. The far-field resembles that of two parallel wires and the structure formation in the BCP film has only a negligible influence. Therefore we pre-compute the electric field in a large system, Lz = 60L0 in the initial configuration of a disordered structure, extract the potential ψ on the xy-planes at z− = − 0.5L0 and z+ = Lz + 0.5L0 above and below the BCP thin film, and use these potential values, ψ0(x,y,z−) and ψ0(x,y,z+), as time-independent boundary conditions for the subsequent simulation. This strategy significantly reduces the computational domain, in which ψ has to be calculated in each Monte-Carlo step. This introduces a small error as the electrostatic field for an ordered lamellar system deviates from that of a homogeneous mixture. We calculated the difference of the field (∇ψ)2 at the boundary region for both cases and found that the maximal error, which is found on top of the electrodes has a magnitude of 4% compared to the field of a corresponding plate capacitor with the same distance and potential. The error drops below 1% at a distance of 1L0 to the electrodes. For comparison the field on the bottom of the polymer film is similar to the one of the corresponding plate capacitor, with an increasing perpendicular field component at higher distance to the bottom.
The simulation cell comprises more than a single lateral unit cell that is used to determine the boundary conditions. The boundary values, ψ0, are periodically continued and the electric potential is computed in the domain Lx × Ly × [z−:z+]. An iterative approach of using the electrostatic potential of the preceding step as a starting guess is employed that reduces the effort of keeping the electrostatic solution up to date to a couple of conjugate gradient steps of the order 10, and thus the computational extra costs due to the electrostatic interaction are equal to the costs of a Monte-Carlo sweep for the polymer system.
Acknowledgements
It is a great pleasure to thank Yoav Tsori for stimulating discussions and collaborations. Financial support by the German Science Foundation Mu1674/11 and the European Union FP7 under Grant agreement No. 619793 CoLiSA.MMP (Computational Lithography for Directed Self-Assembly: Materials, Models, and Processes) as well as generous access to supercomputers at the GWDG Göttingen, the HLRN Hannover/Berlin, and the John von Neumann Center for Computing (NIC), Jülich, Germany, are gratefully acknowledged.References
- L. Leibler, Macromolecules, 1980, 13, 1602–1617 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS.
- S. O. Kim, H. H. Solak, M. P. Stoykovich, N. J. Ferrier, J. J. de Pablo and P. F. Nealey, Nature, 2003, 424, 411–414 CrossRef CAS PubMed.
- M. P. Stoykovich, M. Müller, S. O. Kim, H. H. Solak, E. W. Edwards, J. J. de Pablo and P. F. Nealey, Science, 2005, 308, 1442–1446 CrossRef CAS PubMed.
- R. Ruiz, H. M. Kang, F. A. Detcheverry, E. Dobisz, D. S. Kercher, T. R. Albrecht, J. J. de Pablo and P. F. Nealey, Science, 2008, 321, 936–939 CrossRef CAS PubMed.
- R. A. Segalman, H. Yokoyama and E. J. Kramer, Adv. Mater., 2001, 13, 1152–1155 CrossRef CAS.
- J. Y. Cheng, A. M. Mayes and C. A. Ross, Nat. Mater., 2004, 3, 823–828 CrossRef CAS PubMed.
- R. Ruiz, R. L. Sandstrom and C. T. Black, Adv. Mater., 2007, 19, 587–591 CrossRef CAS.
- I. Bita, J. K. W. Yang, Y. S. Jung, C. A. Ross, E. L. Thomas and K. K. Berggren, Science, 2008, 321, 939–943 CrossRef CAS PubMed.
- A. K. G. Tavakkoli, K. W. Gotrik, A. F. Hannon, A. Alexander-Katz, C. A. Ross and K. K. Berggren, Science, 2012, 336, 1294–1298 CrossRef PubMed.
- S. B. Darling, Prog. Polym. Sci., 2007, 32, 1152–1204 CrossRef CAS.
- I. W. Hamley, Prog. Polym. Sci., 2009, 34, 1161–1210 CrossRef CAS.
- H. C. Kim, S. M. Park and W. D. Hinsberg, Chem. Rev., 2010, 110, 146–177 CrossRef CAS PubMed.
- A. P. Marencic, D. H. Adamson, P. M. Chaikin and R. A. Register, Phys. Rev. E, 2010, 81, 011503 CrossRef PubMed.
- A. V. M. Zvelindovsky, B. A. C. van Vlimmeren, G. J. A. Sevink, N. M. Maurits and J. G. E. M. Fraaije, J. Chem. Phys., 1998, 109, 8751 CrossRef CAS.
- A. V. M. Zvelindovsky and G. J. A. Sevink, Europhys. Lett., 2003, 3, 370–376 CrossRef.
- D. J. C. Herr, J. Mater. Res., 2011, 26, 122–139 CrossRef CAS.
- K. Koo, H. Ahn, S. W. Kim, D. Y. Ryu and T. P. Russell, Soft Matter, 2013, 9, 9059–9071 RSC.
- H. Hu, M. Gopinadhan and C. O. Osuji, Soft Matter, 2014, 10, 3867–3889 RSC.
- W. H. Li and M. Müller, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 187–216 CrossRef CAS PubMed.
- W. H. Li and M. Müller, Prog. Polym. Sci., 2016, 54-55, 47–75 CrossRef CAS.
- Z. R. Chen, J. A. Kornfield, S. D. Smith, J. T. Grothaus and M. M. Satkowski, Science, 1997, 277, 1248–1253 CrossRef CAS.
- S. R. Ren, I. W. Hamley, P. I. C. Teixeira and P. D. Olmsted, Phys. Rev. E, 2001, 63, 041503 CrossRef CAS PubMed.
- D. E. Angelescu, J. H. Waller, D. H. Adamson, P. Deshpande, S. Y. Chou, R. A. Register and P. M. Chaikin, Adv. Mater., 2004, 16, 1736–1740 CrossRef CAS.
- D. E. Angelescu, J. H. Waller, R. A. Register and P. M. Chaikin, Adv. Mater., 2005, 17, 1878–1881 CrossRef CAS.
- K. F. Luo and Y. L. Yang, Polymer, 2004, 19, 6745–6751 CrossRef.
- G. Arya, J. Rottler, A. Z. Panagiotopoulos, D. J. Srolovitz and P. M. Chaikin, Langmuir, 2005, 21, 11518–11527 CrossRef CAS PubMed.
- M. W. Wu, R. A. Register and P. M. Chaikin, Phys. Rev. E, 2006, 74, 040801 CrossRef PubMed.
- J. Rottler and D. J. Srolovitz, Phys. Rev. Lett., 2007, 98, 175503 CrossRef.
- A. P. Marencic, M. W. Wu, R. A. Register and P. M. Chaikin, Macromolecules, 2007, 40, 7299–7305 CrossRef CAS.
- S. Pujari, M. A. Keaton, P. M. Chaikin and R. A. Register, Soft Matter, 2012, 8, 5358–5363 RSC.
- K. Amundson, E. Helfand, X. Quan, S. D. Hudson and S. D. Smith, Macromolecules, 1994, 27, 6559–6570 CrossRef CAS.
- T. L. Morkved, M. Lu, A. M. Urbas, E. E. Ehrichs, H. M. Jaeger, P. Mansky and T. P. Russell, Science, 1996, 273, 931–933 CAS.
- B. Ashok, M. Muthukumar and T. P. Russell, J. Chem. Phys., 2001, 115, 1559 CrossRef CAS.
- A. Böker, H. Elbs, H. Hänsel, A. Knoll, S. Ludwigs, H. Zettl, V. Urban, V. Abetz, A. H. E. Müller and G. Krausch, Phys. Rev. Lett., 2002, 89, 135502 CrossRef PubMed.
- A. V. Kyrylyuk, A. V. Zvelindovsky, G. J. A. Sevink and J. G. E. M. Fraaije, Macromolecules, 2002, 35, 1473–1476 CrossRef CAS.
- T. Thurn-Albrecht, J. DeRouchey, T. P. Russell and R. Kolb, Macromolecules, 2002, 35, 8106–8110 CrossRef CAS.
- A. Böker, H. Elbs, H. Hänsel, A. Knoll, S. Ludwigs, H. Zettl, A. Zvelindovsky, G. Sevink, V. Urban, V. Abetz, A. Müller and G. Krausch, Macromolecules, 2003, 36, 8078–8087 CrossRef.
- Y. Tsori and D. Andelman, Macromolecules, 2002, 35, 5161–5170 CrossRef CAS.
- Y. Tsori, F. Tournilhac and L. Leibler, Macromolecules, 2003, 36, 5873–5877 CrossRef CAS.
- M. W. Matsen, Macromolecules, 2006, 39, 5512–5520 CrossRef CAS.
- M. W. Matsen, Phys. Rev. Lett., 2005, 95, 258302 CrossRef CAS PubMed.
- M. W. Matsen, Soft Matter, 2006, 2, 1048–1056 RSC.
- Y. Tsori, D. Andelman, C.-Y. Lin and M. Schick, Macromolecules, 2006, 39, 289–293 CrossRef CAS.
- K. Schmidt, H. G. Schoberth, F. Schubert, H. Hänsel, F. Fischer, T. Weiss, G. Sevink, A. Zvelindovsky, A. Böker and G. Krausch, Soft Matter, 2007, 3, 448–453 RSC.
- Y. Tsori, Macromolecules, 2007, 40, 1698–1702 CrossRef CAS.
- Y. Tsori, Rev. Mod. Phys., 2009, 81, 1471 CrossRef.
- U. Welling, M. Müller, H. Shalev and Y. Tsori, Macromolecules, 2014, 47, 1850–1864 CrossRef CAS.
- K. C. Daoulas and M. Müller, J. Chem. Phys., 2006, 125, 184904 CrossRef PubMed.
- M. H. Müser and M. Müller, J. Chem. Phys., 2015, 142, 174105 CrossRef PubMed.
- W. H. Li, P. F. Nealey, J. J. de Pablo and M. Müller, Phys. Rev. Lett., 2014, 113, 168301 CrossRef PubMed.
- C. Harper, Modern Plastics Handbook, McGraw-Hill, 2000 Search PubMed.
- K. C. Daoulas, M. Müller, J. J. de Pablo, P. F. Nealey and G. D. Smith, Soft Matter, 2006, 2, 573–583 RSC.
- M. Müller, J. Stat. Phys., 2011, 145, 967–1016 CrossRef.
- P. J. Rossky, J. D. Doll and H. L. Friedman, J. Chem. Phys., 1978, 69, 4628–4633 CrossRef CAS.
- M. Müller and K. C. Daoulas, J. Chem. Phys., 2008, 129, 164906 CrossRef PubMed.
- P. E. Rouse, J. Chem. Phys., 1953, 21, 1272–1280 CrossRef CAS.
- H. Jung, S. Woo, S. Park, S. Lee, M. Kang, Y. Choe, J. G. Son, D. Y. Ryu, J. Huh and J. Bang, Soft Matter, 2015, 11, 4242–4250 RSC.
- S. M. Hur, V. Thapar, A. Ramirez-Hernandez, G. S. Khaira, T. Segal-Perez, P. A. Ricon-Delgalilio, W. Li, M. Müller, P. F. Nealey and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14144 CrossRef CAS PubMed.
- M. Müller, B. Steinmüller, K. C. Daoulas, A. Ramirez-Hernandez and J. J. de Pablo, Phys. Chem. Chem. Phys., 2011, 13, 10491–10502 RSC.
- D. Duque, K. Katsov and M. Schick, J. Chem. Phys., 2002, 117, 10315–10320 CrossRef CAS.
Footnote |
| † We note that, in addition to the effect of the electric field, this orientation of the two lamellar domains at the grain boundary is preferred over the alternate configuration of lying AB domains on the electrodes and standing lamellae with normals along the x direction.61 |
| This journal is © The Royal Society of Chemistry 2017 |







