Influence of specific intermolecular interactions on the thermal and dielectric properties of bulk polymers: atomistic molecular dynamics simulations of Nylon 6

Abstract

Specific intermolecular interactions, in particular H-bonding, have a strong influence on the structural, thermal and relaxation characteristics of polymers. We report here the results of molecular dynamics simulations of Nylon 6 which provides an excellent example for the investigation of such an influence. To demonstrate the effect of proper accounting for H-bonding on bulk polymer properties, the AMBER99sb force field is used with two different parametrization approaches leading to two different sets of partial atomic charges. The simulations allowed the study of the thermal and dielectric properties in a wide range of temperatures and cooling rates. The feasibility of the use of the three methods for the estimation of the glass transition temperature not only from the temperature dependence of structural characteristics such as density, but also by using the electrostatic energy and dielectric constant is demonstrated. The values of glass transition temperatures obtained at different cooling rates are practically the same for the three methods. By proper accounting for partial charges in the simulations, a reasonable agreement between the results of our simulations and experimental data for the density, thermal expansion coefficient, static dielectric constant and activation energy of γ and β relaxations is obtained demonstrating the validity of the modeling approach reported.

---

I. Introduction

In order to develop new materials and compounds with designed new properties, it is essential that these properties can be predicted before preparation, processing, and characterization. The main goal of computational materials science is an accurate prediction of the properties of new materials before their development and production. Molecular dynamics simulations using atomistic force fields to describe molecular-level interactions are useful tools for this goal. This approach is of particular importance in the field of polymer/filler nanocomposites, where the material properties depend on its structure at the nano-scale level. However, before predicting the properties of nanocomposites based on a new polymer, it is necessary to reproduce correctly the properties of the polymer matrix.

The importance of accounting accurately for the electrostatic interactions for evaluating the thermal properties of polymers with highly polar groups from computer simulations has been already reported.¹ This is also true for polymers with specific intermolecular interactions, for example, for polyamides with H-bonding between chains providing good mechanical and thermal properties.² Polyamides are very important engineering thermoplastics due to their high strength at elevated temperatures and toughness at low temperatures, combined with other important properties, such as stiffness, wear and abrasion resistance. The most common application of polyamides in the engineering industry is in textile fibres and in the replacement of traditional metals taking advantage of their great elasticity.³ Deforming under load they are able to return to their original shape up to 75 times faster than other materials. Nylon 6 is the most common type of polyamide accounting for 60% of the global production of this polymeric family and providing an excellent example for proper accounting for H-bonding in computer simulations of polymers.

Few molecular dynamic (MD) simulations of crystalline Nylon 6 have been already reported.^8,9 However, simulations of amorphous Nylon 6 providing a wide analysis of its properties are absent. The modelling of nanocomposite materials with the Nylon 6 matrix has extensively been reported. In particular, the influence of the addition of silica nanoparticles,⁹ carbon nanotubes,^10,11 graphene nanosheets¹² and clay¹³ on the properties of the Nylon 6 matrix was studied. However, the major drawback of these studies is the short equilibration time in the creation of the starting system and in the analysis of the temperature dependence of the various characteristics studied. For this reason, only a qualitative correspondence has been obtained between the modelling results and experimental data. Moreover, none of the previous works have addressed the properties of pure amorphous Nylon 6. This paper reports the study of the structural, thermal and relaxation characteristics of polyamide Nylon 6 by using atomistic molecular dynamics simulations. To our knowledge, the present study is the first one in which the importance of the proper consideration of specific intermolecular interactions like hydrogen bonding is demonstrated in order to provide a realistic assessment of the thermal and dielectric properties of bulk Nylon 6. Moreover, the temperature dependence of the structural and dielectric characteristics of this polymer was investigated in a wide temperature range and cooling rates.

The paper is organized as follows. The simulation method, force field, models and procedures are described in Section II. Section III is devoted to the discussion of the simulation results and the structural characteristics of individual polymer molecules and compounds in the condensed state. Moreover, thermophysical properties such as the glass transition temperature estimated from temperature dependence of the density, electrostatic energy and reciprocal value of the dielectric constant, as well as the relaxation processes evaluated in terms of the time decay of the dipole moment autocorrelation functions are also calculated and reported. The main conclusions are presented in Section IV.

II. Method, force field, model, and simulation procedure

Method and force field

The simulations were performed by the atomistic MD approach using the GROMACS 5.0.7 package.¹⁴ To maintain a constant temperature and pressure in the system, the Berendsen thermostat and barostat with temporal constants τ_T = 0.2 ps and τ_p = 0.1 ps, were used, respectively. Long-distance Coulomb interactions were calculated via the particle mesh Ewald approach.^15,16 The cut-off distance (r_c) for the PME electrostatics was chosen to be 1.0 nm. We performed preliminary simulations for cut-offs from 0.8 nm up to 1.5 nm which demonstrated that the correction of the electrostatic energy by changing r_c from 1.0 nm to 1.5 nm does not exceed the computation error (which is about 0.7%), but the time required for the calculations almost doubles. On the other hand, a comparison of the results obtained at r_c = 1.0 nm and 0.8 nm showed a reduction of the calculation time but a more significant underestimation of the electrostatic energy. The bond length was limited by the LINCS algorithm.¹⁷

The inter-atomic potentials of the force field AMBER99sb⁴ were used. AMBER is a family of force fields for MD simulations of biomolecules such as peptides, proteins, and nucleic acids. The choice of the ff99sb parameter set was dictated by the fact that it gives a better description of the hydrogen bonds (in comparison with other AMBER parameter sets) and allows for a better balance of secondary structure elements as evidenced by the improved distribution of backbone dihedrals. However, it should be noted that generally hydrogen bonds are not well described by various force fields and, on average, they are weaker than those suggested by experimental data.⁵ In the AMBER99sb force field, H-bond interactions are taken into account through electrostatic interactions. The use of the partial atomic charges calculated by the ab initio HF/6-31G* (RESP) and semi-empirical AM1-BCC⁶ is allowed. The AM1-BCC method quickly and efficiently generates high-quality atomic charges for use in condensed-phase simulations because it combines the speed of a semi-empirical calculation with the efficiency of the BCI (bond charge increment) approach. It was demonstrated that AM1-BCC yields charge sets of quality comparable to HF/6-31G* RESP-derived charges for the compounds with conjugated bonds and with cyclic fragments.⁷ However, the efficiency of the AM1-BCC approach for aliphatic polyamides has not been yet reported. In the present study, the effects of H-bonding on the structural and thermal characteristics of Nylon 6 are studied using two sets of partial atomic charges (HF/6-31G* (RESP) and AM1-BCC). Moreover, the correspondence of the simulated results with experimental data is examined.

Simulation model and procedure

The procedure for creating equilibrium samples of the polymer melt was similar to the procedure reported previously for polyimides.^1,18 The cubic cell for simulated systems contains 27 polyamide chains with polymerization degree n = 30. To obtain statistically significant results in the study of the thermal properties of the simulated samples of Nylon 6, simulations were carried out during 1 μs that allowed using a proper distribution of starting configurations for the cooling procedure. Five starting configurations (at 300, 400, 500, 600, and 700 ns) were selected for each system. Gradual cooling with cooling rates of 1.5 × 10¹³ K min⁻¹ (10 K/40 ps), 1.5 × 10¹² K min⁻¹ (10 K/400 ps) and 1.5 × 10¹¹ K min⁻¹ (10 K/4 ns) was performed for each of the configurations. The simulation with the lowest cooling rate (1.5 × 10¹⁰ K min⁻¹ (10 K/40 ns)) was applied only to the configurations of the systems with atomic charges obtained by the HF/6-31G* (RESP) calculations.

III. Results and discussion

Characteristics of individual molecules and simulated systems in melt

Two sets of partial atomic charges for Nylon 6. The partial atomic charges were calculated for an oligomeric molecule consisting of three monomer units. The values of the partial charges obtained for the atoms of the central monomer (Table 1) were used to simulate the polymer molecules of Nylon 6. The values of the partial charges of terminal monomers of the oligomeric molecule obtained from ab initio calculations were used for terminal monomers of polymers in MD simulations. The charges on the atoms of the methylene (–CH₂–) groups calculated by ab initio HF/6-31G* (RESP) and semi-empirical AM1-BCC methods differ slightly. The main differences concern the amide groups forming hydrogen bonds in the system. The H-bond energy must be higher in the case of the HF/6-31G* (RESP) calculated charges because in this case the values of the partial charges on the atoms of amide groups are significantly higher (Table 1).

Table 1 Values of the partial atomic charges of amide groups

	N	H	C	O
HF/6-31G* (RESP)	−0.55	0.29	0.67	−0.6
AM1-BCC	−0.32	0.15	0.21	−0.28

---

Structural characteristics of the polymer molecule and sample density. The estimation of the mean square displacements (MSD) of the centers of mass of individual chains at 600 K (in the molten state), reported in Fig. 1, shows that in the system with the AM1-BCC partial atomic charges, a chain is shifted by a distance comparable to its own size already after the first 10 ns of the simulation. In the system with the HF/6-31G* (RESP) charges such a displacement occurs after a time interval one order of magnitude slower, namely, after ∼100 ns of the simulation. In order to obtain correct values of the dimensions of a single molecule (end-to-end distance, radius of gyration and persistence length) as well as of the density of the simulated system, the averaging of the characteristics considered was carried out in the range 300–1000 ns at 600 K. The comparison of the polymer chain average characteristics for the systems obtained with the two sets of partial atomic charges, reported in Table 2, shows that their values are weakly dependent on the differences in the values of the partial atomic charges calculated by HF/6-31G* (RESP) and AM1-BCC methods. For example, the persistence lengths for both systems are very close to each other and to the experimentally reported value (0.54 nm).¹⁹ At the same time, the differences in the densities are more significant. The comparison of the densities for the two systems simulated in the melts at 545 K (corresponding to the temperature of the experimental melt density of 970 kg m^−3 20) shows that the density of the system with the HF/6-31G* (RESP) charges is much closer to the experimental value. It is necessary to point out that even for the system with HF/6-31G* (RESP) charges, the density in the molten state approaches its equilibrium value very fast (it takes about 400 ps). Thus, our equilibration during 4 ns, and even longer for 40 ns (upon cooling from 600 K down to 545 K with steps 10 and 5 degrees) was long enough to obtain the equilibrium density values.

Fig. 1 Time dependence of the mean square displacements (MSD) of the center of mass for the molecules with the AM1-BCC (black line) and HF/6-31G* (RESP) (red line) partial atomic charges. The time of the displacement of an individual chain by a distance comparable to its own dimension is evidenced.

Table 2 Density of the melt (ρ) and average chain characteristics: persistence length (l_p), end-to-end distance (h), and radius of gyration (R_g)

	l p, nm	h, nm	R g, nm	ρ, kg m^−3 at 545 K
AM1-BCC	0.53	5.6	2.26	876
HF/6-31G*	0.56	5.9	2.35	943

---

Thermal characteristics

Glass transition temperature and coefficient of thermal expansion. The glass transition temperature was determined from the density dependence (ρ(T)) curves (Fig. 2a and b) as follows. The linear fit was applied to the ρ(T)-curves in the high-temperature domain (T > T_g) and in the low temperature domain (T < T_g). The intersection of the two straight lines defines the glass transition temperature.^1,18

Fig. 2 Dependence of the density (a and b) and the electrostatic energy (c) on temperature for the systems with the partial atomic charges of Nylon-6 calculated by AM1-BCC ((a) and inset in (c)) and HF/6-31G* (RESP) (b and c).

The analysis of the curves for the density dependence for different systems and different cooling rates showed a strong difference in the position of the transition region (from melt to glass) for the systems with the values of the partial charges on the atoms calculated by the AM1-BCC and HF/6-31G* (RESP) methods (Fig. 2a and b, respectively). Moreover, there is a clear correlation between the changes in the electrostatic interaction energy in these systems and the changes in their density (see Fig. 2a–c).

This behavior is caused by the differences in the values of the partial atomic charges of the amide groups (Table 1). In the case of the charges calculated by HF/6-31G* (RESP), their values are higher, providing a larger contribution of the electrostatic interactions to the total energy of the system at the transition from the molten to the glassy state.

Since the main contribution to the intermolecular interactions in Nylon 6 is provided by H-bonds and in the AMBER99sb force field these interactions are taken into account through electrostatic interactions, the above conclusion is confirmed by comparing the pair radial distribution function (RDF) (g(r)) for the atoms involved in the hydrogen bond formation (Fig. 3a) and potentials of the mean force (A(r)) for them (Fig. 3b), designed for the systems in the glassy state (at 300 K). The pair distribution function was calculated through the following equation:

where ρ_B is the average density of type B atoms around atoms A, N_A and N_B are the number of A and B atoms, respectively, r_ij is the distance between two atoms A and B, and δ is the Kronecker delta function. The potential of the mean force (PMF) was calculated from g(r) as:

A(r) = −k_BT·ln(g(r)) + B, (2)

where k_B is the Boltzmann constant, T is the temperature, and B is a constant that can be neglected, because we are interested only in the change in free energy.

Fig. 3 (a) g(r) for atoms involved in the formation of hydrogen bonds (O and H in amide groups). (b) PMF designed for systems with the HF/6-31G* (RESP) (red curve) and AM1-BCC (black curve) atomic charges in the glassy state. (c) Number of H-bonds (per amide group) as a function of temperature in the systems with the HF/6-31G* (RESP) atomic charges at different cooling rates and in the system with the AM1-BCC charges at γ = 1.5 × 10¹⁰ K min⁻¹.

The much higher maximum of the pair distribution function for atoms involved in the formation of hydrogen bonds and the shift of the maximum position to shorter distances can be seen for the system with the HF/6-31G* (RESP) partial atomic charges in Fig. 3a. This is evidence of the much stronger attractive forces in this system (Fig. 3b). The differences in the H-bond energy for the simulated systems are also manifested in the amount of hydrogen bonds per amide group in each simulated system (Fig. 3c). The H-bond is considered to be formed if the distance between the oxygen atom of the –CO group and the hydrogen atom of the –NH group does not exceed 0.3 nm and the H–N–O angle does not exceed 30°.²¹ Although the temperature dependence of the number of H-bonds per amide group (for the HF/6-31G* (RESP) charges) is very similar to the dependence of density, the intersection points of the two straight lines obtained by the linear fit of the high-temperature domain and the low temperature domain of these curves lie in the region of temperatures that are lower than T_g defined from the ρ(T) and E_el(T) curves. This is understandable, since the H-bonding energy is only for a part of the electrostatic energy.

Since the cooling rate in the MD simulations is several orders of magnitude higher than that in a real experiment, the glass transition temperature measured in the modeling must be higher than the experimental value.²² As reported in Table 3, the T_g values determined at different cooling rates for the system with the HF/6-31G* (RESP) partial atomic charges are in the range of temperatures which are significantly higher than the experimental data. In fact, dry Nylon-6 with the molecular mass of the polymer chains similar to the simulated systems has a glass transition temperature of 310 K.^23,24 At the same time, for the systems with the partial charges calculated by AM1-BCC, the values of the glass transition temperature (at different cooling rates) are in the same interval as the experimental values, and even below (Table 3).

Table 3 Simulated values of the glass transition temperature obtained from density dependence ρ(T)

Nylon 6	10 K/40 ps	10 K/400 ps	10 K/4 ns	10 K/40 ns
AM1-BCC	338 ± 3 K	316 ± 4 K	<290 K	—
HF/6-31G* RESP	427 ± 15 K	413 ± 11 K	401 ± 8 K	387 ± 1 K

---

The slower a liquid is cooled, the longer the time available for configurational sampling at each temperature, and hence the colder it can become before falling out of the liquid-state equilibrium. Consequently, T_g increases with the cooling rate.²²

When comparing the simulation results with experimental data, it should be considered, of course, that in our simulations we are dealing with fully amorphous samples. In fact, additional peaks which would indicate the formation of any order are absent in the RDF curve. Nylon 6 is a semi-crystalline polymer, and in experimental studies samples with different crystallinity were investigated. The formation of crystalline regions in a sample obviously results in a reduction of the amorphous fraction and a restriction of the chain mobility in the amorphous regions by crystallites, that in turn, leads to an increasingly higher T_g with crystallinity development. Experimental data reported in the scientific literature regard samples with crystallinity values below 35%. In particular, the T_g for amorphous samples is 310 K and reaches a limiting value of about 316 K at 5–10% crystallinity.²⁵

It is well known that the glass transition temperature depends on the cooling rate (γ) logarithmically:^26,27

where A and B are polymer-dependent constants, γ is the cooling rate, and T₀ is the glass transition temperature at an infinitely slow cooling rate (i.e. close to experimental conditions). We choose T₀ = 310 K from the experimental data¹⁸ taking into account the molecular mass of the polymer chains in the simulated systems. The results for the charges calculated by HF/6-31G* (RESP) are summarized in Fig. 4a.

Fig. 4 (a) T_g of the simulated system with HF/6-31G* (RESP) atomic charges as a function of cooling rate (black stars) and its approximation by eqn (3) (red line) with the following set of parameters: A = 1.9 × 10⁻²⁰ min K⁻¹, B = 768 K and T₀ = 310 K. (b) Experimental temperature dependence of the coefficient of thermal expansion (CTE) of Nylon 6 (black line) and the dependence for the systems with partial charges HF/6-31G* (RESP) (green curve) and with partial charges AM1-BCC (red curve).

It is known that the glass transition temperature obtained from MD simulations is not suitable for the verification of computational models against experimental data since extremely high CPU resources are required.¹⁸ However, our results suggest that the use of the AMBER99sb force field with HF/6-31G* (RESP) charges gives significantly more reasonable results than those obtained with the AM1-BCC atomic charges.

Measuring the coefficient of thermal expansion (CTE) of the polymer provides an additional way for verifying computational models.²⁸ The CTE, β, was calculated from the temperature dependence of the polymer sample density via the following finite difference relation:

where ρ₁ and ρ₂ are density values for a polymer sample calculated at temperatures T₁ and T₂, respectively.

Fig. 4b shows the temperature dependence of the CTE obtained for the two simulated systems in comparison with the experimental data obtained for Nylon 6 in a wide temperature interval.^29,30 Our calculations over-estimate the experimental CTE in both cases but it can be seen that the CTE values for the system with the partial charges HF/6-31G* (RESP) are closer to the experimental data.

Thus, for the system with the HF/6-31G* (RESP) partial atomic charges both characteristics (T_g and CTE) are more realistic. For this reason, the systems with the HF/6-31G* (RESP) partial atomic charges were used to calculate the dielectric characteristics and to study the relaxation processes of Nylon 6.

In this section, we reported the T_g values estimated from temperature dependence of structural characteristics such as density and electrostatic energy. It is also possible to estimate T_g by monitoring the temperature dependence of relaxation times.³¹ However, this method is less accurate due to the limited range of relaxation times that can be addressed in computer simulations. For this reason, we did not estimate T_g by using the relaxation times deduced, for example, from the diffusion of chain fragments²⁷ and in the next section, we also estimated T_g by using structural characteristics such as the dielectric constant.

Dielectric characteristics and dielectric relaxation

Dipole moment of the amide group. The value of the dipole moment of amide groups with the HF/6-31G* (RESP) partial atomic charges is ≈3.97 D. It is statistically larger than the experimental gas-phase dipole of ≈3.73 D obtained for the low molecular weight compound N-methylacetamide (NMA),³² as it must be due to the magnitude of the dipole moment of the system in the gas phase determined only by the intrinsic dipole moments of the molecules. On the other hand, it is lower than the approximate value of 5.2 D predicted using electronic structure calculations for NMA in aqueous solution.³³ This is understandable because in aqueous solution the H-bonding of NMA molecules with water molecules produces changes in the electronic structure (in comparison with isolated NMA molecules) leading, in particular, to a redistribution of the partial atomic charges in amide groups. Although the polyamide molecules also form hydrogen bonds, the mutual influence of the amide groups on their electronic structure is undoubtedly weaker than the effect of water molecules. Unfortunately, the experimental data that would allow us to compare these effects are missing. Moreover, the significant additional contribution provided by fluctuating atomic charges due to a strong polarization (following the interaction of molecules with water) opposite to the above-mentioned quantum chemical calculations is not treated in our model. The use of polarizable force fields³⁴ can provide a better agreement with experimental data but this would significantly increase the computational cost that comes with polarizability.

Static dielectric constant. The static dielectric constant ε was calculated by applying the software provided by the GROMACS package¹⁴ according to the following equation:³⁵where M is the total dipole moment, ε₀ is the vacuum permittivity, V is the volume of the system, k_B is the Boltzmann constant and T is the temperature.

The temperature dependence of the simulated dielectric constant is shown in Fig. 5 in comparison with the experimental data from ref. 36. The rotation of the polar groups is not possible below T_g and the permittivity is low, with a big increase around T_g. At higher temperatures the increased thermal vibrations cause the permittivity to drop again (in our simulations this can be seen at the slowest cooling rate).

Fig. 5 (a) Changes in the dielectric constant (ε) with temperature. The simulation results are shown in comparison with the experimental data in the inset.³⁶ (b) Plot 1/(ε − 1) vs. temperature.

The value of the dielectric constant depends on the cooling rate. In our simulations with the HF/6-31G* partial atomic charges and at the equilibration during 40 ns at each temperature the static dielectric constant is underestimated in comparison with the experimental values. But, for example, the additional equilibration at 340 K during 200 ns results in an increase in ε, from 2.48 up to 4.1, which is much closer to the experimental value (see the inset in Fig. 5a).

The dependence of the static dielectric constant on the cooling rate is even more pronounced than that for density (Fig. 2). It has been reported that the polymer glass transition temperature can be estimated from the temperature dependence of the inverse value of the dielectric permittivity.³⁷ Moreover, it was experimentally assessed that for many polymer systems exhibiting the dependence of the reciprocal dielectric permittivity on temperature there are at least two regions which correspond to the system being in glassy and rubbery states, respectively. As seen in Fig. 5b, there is a change in the character of the temperature dependence of (1/(ε − 1)) at a certain critical temperature (as for polymer density). The values of this temperature at different cooling rates are very close to those obtained from the ρ(T) dependence.

Relaxation processes in Nylon 6. In a real experiment, T_g is considered as the temperature of the onset of large scale motion of polymer chain segments. Polymer chain mobility is greatly decreased below T_g; however, some local motions may still be activated, corresponding to subglassy, or secondary, relaxation processes. At temperatures above T_g, polymer chains have greater mobility and larger segments of the polymer chains are able to re-orient; therefore, they are able to achieve their equilibrium conformations.

The main relaxation processes in Nylon 6 (Fig. 6) are related to (i) the movement of extended CH₂ sequences of the backbone with involvement of amide groups (the α relaxation), (ii) localized motions involving several monomer units, but influenced by hydrogen bonded amide groups (the β relaxation) (iii) the γ relaxation associated with the dynamics of single monomer units and corresponding to the vibrational motions of the methylene groups in the chains.^38,39

Fig. 6 Schematic representation of α, β, and γ relaxations in Nylon 6.

The cooling rate expresses how much time is spent at each new temperature, and if the cooling process is faster than the relaxation time of a certain process the polymer segment will not be able to relax. According to the experimental data reported for Nylon 6,^36,38,39 the α process relaxation time is tens of microseconds, the β process relaxation time in melt is about 1 ns and reaches ∼10 μs at the glass transition, but the relaxation time of the γ process is changed from about 100 ps in melt up to 100 ns in glassy state. Thus, from our simulation data (even for those obtained at the slowest cooling rate) we can reliably identify only the γ relaxation process.

The relaxation processes in the simulated Nylon 6 systems were evaluated for the case of the lowest cooling rate (10 grad/40 ns (1.5 × 10¹⁰ K min⁻¹)) in terms of the time decay of dipole moment autocorrelation functions (DACF). The DACF are given as:

here, M(r) is the dipole moment of the system at time t.

The time decays of the DACF at different temperatures are reported in Fig. 7.

Fig. 7 The time decays of the DACF at different temperatures from 600 K to 300 K through each 20 K (in color representation from red to black).

We applied two approaches to analyse the DACF. The DACF can be represented as the sum of multiple decaying exponential terms or the Kohlrausch–Williams–Watts (KWW) functions,^40,41 stretched functions:

where τ is the apparent relaxation time, β is a stretching exponent parameter, and A is an amplitude. We represented the autocorrelation functions twice: by using a single relaxation process (eqn (7)) and by using a sum of two processes:

ACF(t) = A₁f₁(t) + A₂f₂(t), (8)

By using the apparent relaxation times and stretching parameters obtained at different temperatures, the mean relaxation times were calculated according to:The corresponding relaxation frequencies, obtained by representing DACF with a single relaxation process and as a sum of two processes, are presented in Fig. 8 together with the weight contributions (A₁ and A₂) of each of the two exponents (eqn (8)).

Fig. 8 (a) Relaxation frequencies at different temperatures obtained by representing DACF using a single relaxation process (green color) and a sum of two processes (shown by black and red colors). (b) Weight contributions of each of the two exponents (A₁ – red color and A₂ – black color) into DACF.

It can be seen that the frequencies obtained when representing DACF by two relaxation processes in the high temperature region (from 600 K to 450 K) show a distinct linear dependence on temperature which means the manifestation of a certain relaxation process. However, the frequencies obtained when representing DACF by one relaxation process at lower temperatures show a distinct linear dependence on temperature.

Moreover, in order to identify the particular relaxation processes we applied the CONTIN approach,⁴² which gives the relaxation time density function (RTDF) from the autocorrelation function, as it is the Laplace transform of the RTDF. Obtaining these functions is not a straightforward process because there are essentially infinite solutions to the problem. After analyzing the relaxation time density functions (Fig. 9a and b) obtained by using the CONTIN procedure, the most physically feasible solutions were selected (Fig. 9c).

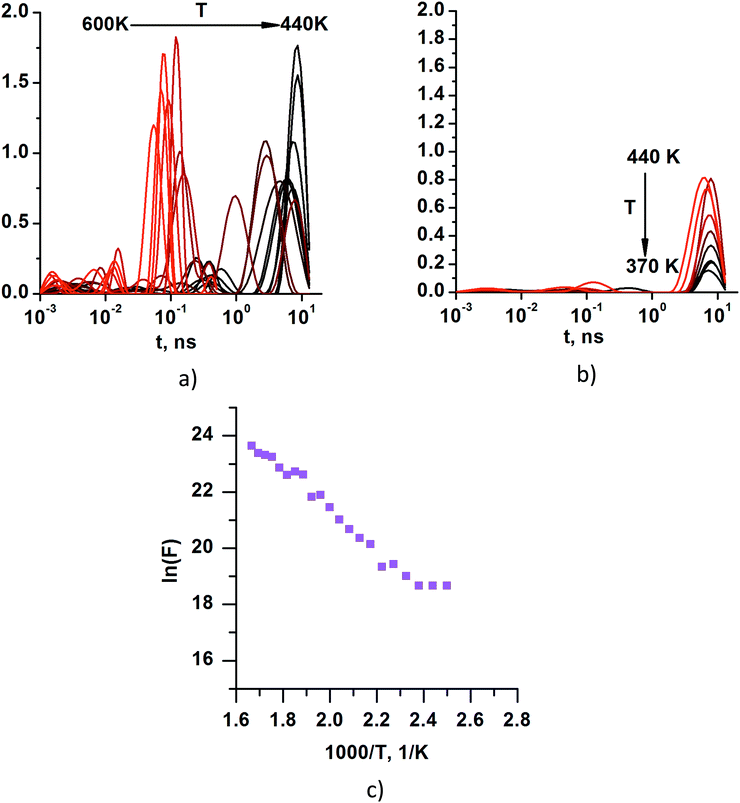Fig. 9 Relaxation time density functions at temperatures (a) 600 K 440 K and (b) 440 K 370 K. (c) Frequencies corresponding to the most intensive peaks of the relaxation time density functions.

It is important to note that the DACF curves that do not decay below 0.8, namely, the curves at temperatures of 360 K and lower (Fig. 7) cannot provide reliable relaxation times with any kind of fit. Thus, we have performed the final analysis for the results obtained at temperatures higher than 360 K. Summarizing, it can be concluded that the temperature dependence of the frequencies of the most pronounced relaxation process in the KWW analysis (obtained by using the fitting of DACF with the sum of two stretched exponents) and in the CONTIN analysis is very close (Fig. 10a). The computed exponential results and experimental data of the relaxation processes³⁸ (which were identified as γ relaxation) represented as a function of the inverse of the temperature demonstrates a linear approximation with very similar slopes (Fig. 10b, lines 2 and 3). The estimated value of the activation energy (where K_B is the Boltzmann constant) of the relaxation process in our simulations is ∼0.517 eV and it is very close to the activation energy of the experimentally identified γ relaxation process of ∼0.477 eV.³⁸

Fig. 10 (a) Temperature dependence of the frequencies of the most intensive relaxation processes obtained from the KWW analysis by using the fitting of DACF with the sum of two stretched exponents (red and black symbols) and from CONTIN (magenta symbols). (b) Linear fitting of the two-exponential and CONTIN data (1), single-exponential data (2) and experimental data (3).

The linear fitting of the CONTIN and of the two-exponential data (line 1 in Fig. 10b) gives higher slopes than the single-exponential data and correspondingly a higher activation energy of about 0.655 eV was obtained which is close to the experimental value attributed to the β relaxation process (0.62 eV).³⁸

IV. Conclusions

With the aim to show the effect of a proper consideration of specific intermolecular interactions like hydrogen bonding on the realistic assessment of the thermal and dielectric properties of bulk polymers, MD simulations of the aliphatic polyamide Nylon 6 in a wide temperature range were performed with the use of the AMBER99sb force field. Two sets of the partial atomic charges (AM1-BCC and HF/6-31G* (RESP)), acceptable for use in the AMBER99sb force field, were examined. In this work, we have employed three different estimations of the glass transition temperature from the temperature dependence of structural characteristics such as density, electrostatic energy and dielectric constant (inverse value). It was observed that using HF/6-31G* (RESP) partial atomic charges leads to reasonable results for the calculation of density, glass transition temperature and coefficient of thermal expansion of Nylon 6 samples. Moreover, the study of the dielectric properties demonstrated a good agreement between the values of the static dielectric constant estimated from our simulations with the HF/6-31G* (RESP) atomic charges and the experimental one.

The relaxation processes in the simulated system of Nylon 6 were evaluated in terms of the time decay of dipole moment autocorrelation functions (DACF). The DACF were analysed by using KWW functions and the CONTIN approach. Because the simulations were executed at relatively slow cooling rates (1.5 × 10¹⁰), two secondary relaxation processes were identified: not only the γ relaxation associated with the dynamics of single monomer units, but also the β relaxation which usually relates to the motions involving several monomer units influenced by hydrogen bonded amide groups. Comparison of the obtained results and the experimental data demonstrated very close values of the activation energies of the relaxation processes observed in our simulations and experimentally identified as γ and β relaxation processes.

Thus, the reasonable agreement between our simulations and experiments suggests that the AMBER 99sb force field with the HF-6-31g* (RESP) partial atomic charges provides an adequate representation of the bulk structure and dynamics of Nylon 6. Armed with this agreement, we will continue our research by studying composites of Nylon 6 with different fillers. Moreover, we are sure that the AMBER 99sb force field with the partial atomic charges calculated in the present study for Nylon 6 by using the HF-6-31g* (RESP) approach can be applied for any aliphatic Nylon. This conclusion is based on the fact that these Nylons differ in terms of the length of the –(CH₂)_n– sequences between amide groups from n = 4 in Nylon 6,6 to n = 11 in Nylon 12. These sequence length changes (in comparison with Nylon 6) cannot have any significant impact on the electron density distribution in amide groups.

Acknowledgements

The calculations were performed using the resources of the Lomonosov supercomputer at Moscow State University and Center of collective use “Complex of modeling and data research mega-class facilities” NRC “Kurchatov Institute” (unique identifier RFMEFI62114X0006). This study was supported by the Russian Ministry of Education and Science within State Contract 14.Z50.31.0002 (megagrant).

References

1. S. V. Lyulin, A. A. Gurtovenko, S. V. Larin, V. M. Nazarychev and A. V. Lyulin, Macromolecules, 2013, 46(15), 6357–6363.
2. Fibrous and Composite Materials for Civil Engineering Applications, ed. R. Fangueiro, Elsevier, Cambridge, 1st edn, 2011.
3. Dudley's Handbook of Practical Gear Design and Manufacture, ed. S. P. Radzevich, CRC Press, Miami, 2nd edn, 2012.
4. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerl, Proteins, 2006, 65, 712–725.
5. O. F. Lange, D. Spoel and B. L. Groo, Biophys. J., 2010, 99, 647–655.
6. A. Jakalian, D. B. Jack and C. I. Bally, J. Comput. Chem., 2002, 23, 1623–1641.
7. A. Jakalian, B. L. Bush, D. B. Jack and C. I. Bally, J. Comput. Chem., 2000, 21, 132–146.
8. Y. Li and W. A. Goddard, Macromolecules, 2002, 35, 8440–8455.
9. J. Yang, H. Shin, H. Kim and H. K. Lee, Appl. Phys. Lett., 2014, 104, 101901.
10. N. Tahreen and A. K. M. Masud, International Journal of Manufacturing, Materials, and Mechanical Engineering, 2013, 3, 62–73.
11. J.-S. Yang, C. L. Yang, M.-S. Wang, B.-D. Chen and X. Guang, RSC Adv., 2012, 2, 2836–2841.
12. Y.-F. Mo, C.-L. Yang, Y.-F. Xing, M.-S. Wang and X. G. Ma, e-Polym., 2014, 14, 169–176.
13. D. R. Katti, K. S. Katti, M. Raviprasad and C. Gu, J. Nanomater., 2012, 341056,  DOI:10.1155/2012/341056.
14. M. J. Abraham, T. Murtola, R. Schulz, S. Ráll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
15. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
16. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
17. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
18. S. V. Lyulin, S. V. Larin, A. A. Gurtovenko, N. V. Lukasheva, V. E. Yudin, V. M. Svetlichnyi and A. V. Lyulin, Polym. Sci., Ser. A, 2012, 54, 631–643.
19. Introduction to Nanofiber Materials, ed. F. K. Ko and Y. Wan, Cambridge University Press, Cambridge, 2014.
20. T. D. Fornes and D. R. Paul, Polímeros: Ciência e Tecnologia, 2003, 13, 212–217.
21. M. Petukhov, G. Rychkov, L. Firsov and L. Serrando, Protein Sci., 2004, 13, 2120–2129.
22. S. V. Lyulin, S. V. Larin, A. A. Gurtovenko, V. M. Nazarychev, S. G. Falkovich, V. E. Yudin, V. M. Svetlichnyi, I. V. Gofman and A. V. Lyulin, Soft Matter, 2014, 10, 1224–1232.
23. Thermal Characterization of Polymeric Materials, ed. A. Turi, Academic Pr, New York, 1st edn, 1981.
24. E. Mukouyama and A. Takegawa, High-molecular chemistry (Jap.), 1956, 136(13), 323–330.
25. Y. P. Khanna, W. P. Kuhn and W. J. Sichina, Macromolecules, 1996, 28, 2644–2646.
26. J. Buchholz, W. Paul, F. Varnik and K. Binder, Chem. Phys., 2002, 117, 7364–7373.
27. A. V. Lyulin, N. K. Balabaev and M. A. J. Michels, Macromolecules, 2002, 35, 9595–9604.
28. V. M. Nazarychev, S. V. Larin, A. V. Yakimansky, N. V. Lukasheva, A. A. Gurtovenko, I. V. Gofman, V. E. Yudin, V. M. Svetlichnyi, J. M. Kenny and S. V. Lyulin, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 912–923.
29. I. Perepechko, Low Temperature Properties of Polymers, MIR Publishers, Moscow, 1980.
30. Comprehensive Nanoscience and Technology, ed. D. Andrews, G. Scholes and G. Wiederrecht, Elsevier, 2010, vol. 5.
31. R. C. Baljon, M. H. M. Van Weert, R. B. DeGraaff and R. Khare, Macromolecules, 2005, 38, 2391–2399.
32. CRC Handbook of Chemistry and Physics, ed. R. C. Weast, CRC Press, Boca Raton, 67th edn, 1968.
33. J. Gao and X. Xia, Science, 1992, 258, 631–639.
34. Ch. M. Baker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 241–254.
35. O. Gereben and L. Pusztai, Chem. Phys. Lett., 2011, 507, 80–83.
36. E. Laredo, M. Grimau, F. Sánchez and A. Bello, Macromolecules, 2003, 36, 9840–9850.
37. E. N. Lushin and R. A. Castro, St. Petersburg State Polytechnical University Journal, Physics and Mathematics, 2013, 182, 90–92.
38. N. Noda, Y.-H. Lee, A. J. Bur, V. M. Prabhu, C. R. Snyder, S. C. Roth and M. McBrearty, Polymer, 2005, 46, 7201–7217.
39. M. Turky, A. M. Ghoneim, A. Kyritsis, K. Raftopoulos and M. A. Moussa, J. Appl. Polym. Sci., 2011, 122, 2039–2046.
40. G. Williams and D. C. Watts, Trans. Faraday Soc., 1970, 66, 80–85.
41. C. P. Lindsey and G. D. Patterson, J. Chem. Phys., 1980, 73(7), 3348–3357.
42. S. W. Provencher, Comput. Phys. Commun., 1982, 27(3), 229–242.

---