Large scale energy storage using multistage osmotic processes: approaching high efficiency and energy density†
Devesh
Bharadwaj
 * and
Henning
Struchtrup
* and
Henning
Struchtrup
Dept. of Mechanical Engineering, University of Victoria, Victoria, BC, Canada. E-mail: devesh@uvic.ca; struchtr@uvic.ca
First published on 14th February 2017
Abstract
With the increase in ocean levels due to global warming, there is a desperate need for clean and renewable energy at this time, more than ever before. Although the economic front of technologies, such as wind and solar power, has shown improvement, the fact remains that these energy sources are intermittently available in nature. This calls for a reliable energy storage technology that can bridge the gap between the supply and demand of electricity, leading us to a world driven by clean and renewable energy. Here, we propose a process for storing electrical energy using engineered osmosis. To store electrical energy, a salty solution is separated into brine and fresh water streams using modified reverse osmosis. When there is a demand for electricity, the chemical potential is converted back into electrical work by mixing the solutions using a modified version of pressure retarded osmosis. With modelling and simulations, we demonstrate that the proposed process can achieve round trip efficiencies of 50–60% and energy densities equivalent to that of a 500 m high pumped-hydro plant. The results demonstrate a promising process to store electrical energy, which, unlike pumped-hydro, is unconstrained by geography.
1 Introduction
Anthropogenic carbon emissions are creating irreversible changes to our climate. Ocean levels are expected to increase at a rate of 0.2–0.6 meters per degree of global warming.1 This increase is expected to affect many coastal areas worldwide.2 Along with changes to ocean levels, warming is linked to rainfall, as it can adversely affect water supply for humans and other ecosystems.3 Long-term rainfall shortages have already been observed in some American and African regions.3–8 The root cause of climate change is undoubtedly linked with the increase in carbon emissions. In order to mitigate carbon emissions, we have to replace our fossil fuel based energy infrastructure with renewable and clean energy sources.There has been an increase in R&D towards clean energy technologies which has induced a growth in the renewable energy industry and improved the economics of such technologies. However, the fact remains that the majority of renewable energy sources are only available intermittently in nature. This intermittent behaviour does not allow a grid to be fully dependent on a renewable energy source. For instance, the majority of solar power plants provide clean energy in the day but rely on natural gas power plants at night.
Electrical energy storage alone cannot possibly solve the climate problem, but it presents a solution to the intermittent nature of renewable energies. Moreover, energy storage has other high-value applications, including improving the power quality and reliability of the grid.9,10 The concept of electrical energy storage is to store energy when available in abundance and recover it when availability is scarce. The concept of storage is simple; however, the technology behind such a process has numerous complications. Furthermore, such a technology has to be efficient, dense and environmentally benign.
There is a battery of choices among energy storage technologies. The leading energy storage technology is pumped hydro, which currently accounts for 99% of the world's grid energy storage.10 A pumped hydro system needs a gravitational potential to move water up and down. Therefore, it requires a hilly region that has two reservoirs at different heights. Pumped hydro is a mature technology and it has the capability to store electricity with high round trip efficiencies of approximately 70–85%. On the down side, it is geographically constrained, has a long lead time (10 years) and due to restricted construction sites, possesses several environmental issues.11,12
This paper presents a technology that stores electrical energy in the form of chemical potential (difference in concentration), instead of gravitational potential (difference in height). Osmotic energy storage (OES) is a process that utilizes a modified version of reverse osmosis (RO) and pressure retarded osmosis (PRO) to create and recover this chemical potential.
RO is a mature technology and has been commercialized for use in desalination in most parts of the world. The RO process is a state of the art technology when it comes to separating salt from water. It has advanced in operation and can desalinate seawater at only a 25% higher energy consumption rate than the possible practical minimum threshold constrained by the laws of thermodynamics for a single stage RO process (for comparison, in 1970, RO processes had a 90% higher energy consumption than the theoretical minimum for a single stage RO process).13 On the contrary, although PRO was recognized half a century ago,14 the limitations and the innovations required to make PRO viable did not unfold until recently.15–19 Consequently, there evolved multiple technologies from this early concept, which ultimately utilize a concentration difference to generate or recover useful work, such as low grade osmotic heat engines20,21 that can be used to generate electrical work from geothermal energy or waste heat and several other technologies that use PRO to reduce the energy consumption in desalination.22–24 Osmotic energy storage (OES) is similar to these technologies in that it relies on creating and utilizing a salinity gradient.
McGinnis and Mandell have previously done a detailed investigation on energy storage systems that create and exploit salinity gradients.25 In their patent they discuss the majority of the possible technologies that can be used for separation, such as conventional RO, electrodialysis, nanofiltration and distillation. Consequently, they discuss the use of conventional PRO and reverse-electrodialysis for energy recovery. Their patent presents some theoretical case studies where they claim efficiencies of 75–85%, when their system can utilize abundant waste heat. If proven economical, such a design enabling the use of waste heat can be attractive in multiple scenarios; however using conventional RO and PRO in scenarios where only electrical energy is available (and required to store) will constrain the energy storage system to low round trip efficiencies and low energy densities. As recently (2016) shown by He and Wang, an energy storage system using single stage RO and PRO exhibits an inverse relationship between energy density and round trip efficiency. In the scenario where irreversibilities in the turbomachinery were ignored, a maximum cycle efficiency of 54.98% was reported with an energy density of 0.389 kW h m−3 (i.e., m3 of total solution used), alternatively when the system was optimized for a high energy density of 0.678 kW h m−3, the round trip efficiencies faced penalties and dropped down to 41.13%. When the losses due to inefficiencies in turbomachinery were added, the system efficiency dropped from 54.98% to 42.55%.26 He and Wang mention that system performance can be improved by multistage RO and PRO, which we discuss in detail in this paper.
The combination of electrodialysis and reverse-electrodialysis for separation and mixing has also been investigated by Kingsbury et al. as a means of storing and recovering useful work from the chemical potential. The so-called ‘concentration battery’ was experimentally tested and it was capable of storing and recovering energy with round trip efficiencies in the range of 21–34%.27 Egmond et al. recently (2017) investigated the efficiencies of concentration gradient flow batteries at elevated temperatures that also implement electrodialysis and reverse electrodialysis. The study reported a charging (electrodialysis-separation stage) efficiency of 58% and discharging (reverse electrodialysis-mixing stage) efficiency of 72%, yielding a possible 42% round trip efficiency.28
In this paper we discuss the design of an osmotic energy storage (OES) technology and show the importance of modified multistage processes for a practical energy storage system. We mathematically model the OES system and then simulate its performance with off-the-shelf components. We optimize the system for a particular number of stages and also study the effect of its performance with different component efficiencies. Overall, the proposed system enables energy storage on a large scale with unconstrained geographical requirements, supplementing the possibility of smooth integration of renewable energy sources into the grid.
2 Working principle of osmotic energy storage
The OES process stores and recovers energy by creating and then utilizing a concentration gradient. At the time of storage, electrical work is consumed to separate a salty water (sw) stream into brine (br) and fresh water (fw). Doing so converts the electrical work from renewable energy sources that needs to be stored as a chemical potential. This potential is stored in the form of br and fw filled reservoirs/tanks. Unlike storing heat, which has losses associated with time, OES can store energy indefinitely without any major losses associated with time. When there is a demand for electricity, the chemical potential can be converted back into electrical work by mixing the br and fw streams, with appropriate technology, as discussed later.The appropriate process of separation and mixing depends on the type of salt solution used and the type of energy needed to be stored. The OES process described in this paper is focused towards storing energy available in the form of electrical work. For the purpose of understanding the OES system, we consider a NaCl salt solution, which is analogous to seawater composition. Furthermore, when it comes to seawater desalination, reverse osmosis (RO) is broadly used to separate fresh water and salt. RO requires electrical work for separation, whereas the other common process of desalination, i.e. distillation, requires thermal energy. RO is inherently more efficient than distillation. Hence, for this and other reasons explained later, we choose RO as our separation technology. The obvious drawback is that RO only allows direct storage of electrical energy; therefore, for a scenario where thermal energy is needed to be stored, a distillation process can be used instead of RO. There has been some work focusing on a thermal-membrane based osmotic energy storage system.25,29 A system that solely relies on distillation as a means of separation is a clever design for places with abundant waste heat, but might not be economical or efficient when electrical energy is the only source. In this paper we focus on a system that solely uses electrical energy via a multistage version of RO for separation, which is crucial to achieve practical round trip efficiencies (discussed in detail later in this section). Using RO, a salty water (sw) stream is separated into brine (br) and fresh water (fw) streams, which can be stored in reservoirs/tanks indefinitely. The two solutions stored have a large concentration difference, thermodynamically speaking, a chemical potential is created.
When there is a demand for electricity, the chemical potential can be utilized to produce electrical work. The common processes that can utilize such a chemical potential are reverse electrodialysis (RED) and pressure retarded osmosis (PRO). The PRO process has been proven to be more efficient in energy recovery and shows better performance when used to mix concentrated brines, compared to RED.30 Hence, PRO is chosen to utilize the chemical potential by mixing br and fw streams.
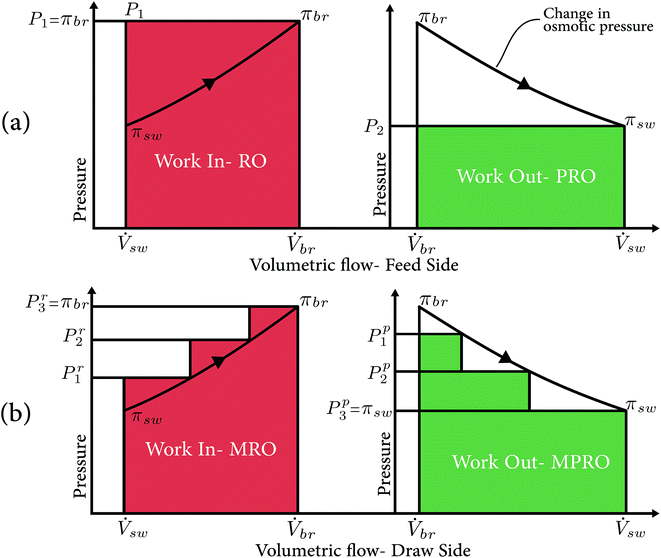
To achieve high round trip efficiency, the OES system needs to consume as little energy as possible for separation (RO) and recover as much as possible while mixing (PRO). For this reason, we study the working of RO and PRO, to better understand and decipher the losses in the design of the processes. We assume an ideal membrane for this particular explanation and we focus on the irreversibilities in the process design. Fig. 1(a) shows the schematics of P–V diagrams for both RO and PRO processes. The horizontal axis shows the volumetric flow of the pressurized stream in the membrane module, while the vertical axis shows the pressure of this stream.
In RO (Fig. 1(a)-left), the salty water (sw) stream enters the membrane module at an osmotic pressure, πsw, with a volumetric flow rate, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) sw. The fresh water (fw) flux across the RO membrane is proportional to the driving force, which is the difference of the hydraulic and osmotic pressure across the membrane,31
sw. The fresh water (fw) flux across the RO membrane is proportional to the driving force, which is the difference of the hydraulic and osmotic pressure across the membrane,31
| Jw = Aw(ΔP − Δπ), | (1) |
Ẇsep = PrΔ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) | (2) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) is the difference of volumetric flows between the entering sw stream and the exiting br stream, and Pr is its hydraulic pressure.
is the difference of volumetric flows between the entering sw stream and the exiting br stream, and Pr is its hydraulic pressure.
The fw crossing the membrane makes the sw stream more salty, increasing its osmotic pressure as it travels down the membrane module. The osmotic pressure curve in Fig. 1 shows the osmotic pressure of the sw stream increasing from πsw to πbr. Ideally, we want to follow the osmotic pressure curve and apply a hydraulic pressure slightly above it, so fw can pass. However, the mechanical constraints do not allow a gradient pressure across the membrane module; hence the hydraulic pressure equal to the osmotic pressure of the exiting br is applied. Hence, the minimum possible power for separation in this case is Ẇsep = πbrΔ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) .
.
The process principle is similar, but in reverse for PRO, where the theoretical maximum work that can be recovered is the area under the osmotic pressure curve. Ideally, we would follow this curve and apply hydraulic pressure slightly less than that of the curve and allow fw to enter, but, just like RO, we cannot have a gradient of pressure across the membrane module. Instead a hydraulic pressure equal to that of the exiting sw stream is applied. The maximum mixing power achievable in this scenario is Ẇmix = πswΔ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) . The PRO schematics shown in Fig. 1, assume an ideal membrane with perfect salt rejection, and that the feed water is deionized water and has no salt. In the case of real membranes and presence of salt on the feed water side, the curves would have to account for the chemical potential loss, as discussed by Lin, Straub, and Elimelech in ref. 32.
. The PRO schematics shown in Fig. 1, assume an ideal membrane with perfect salt rejection, and that the feed water is deionized water and has no salt. In the case of real membranes and presence of salt on the feed water side, the curves would have to account for the chemical potential loss, as discussed by Lin, Straub, and Elimelech in ref. 32.
The round trip efficiency of the system, ηs, is the ratio of the work (power consumed to separate the sw stream) required in separation to the work recovered in mixing, defined as
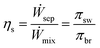 | (3) |
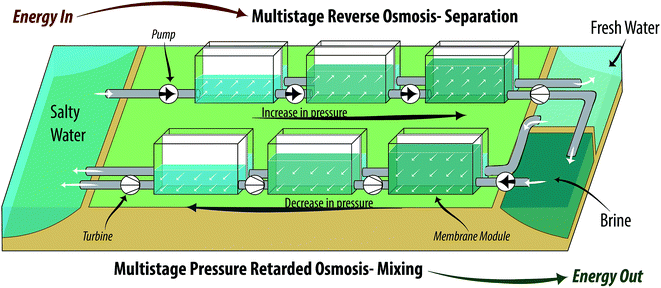 | ||
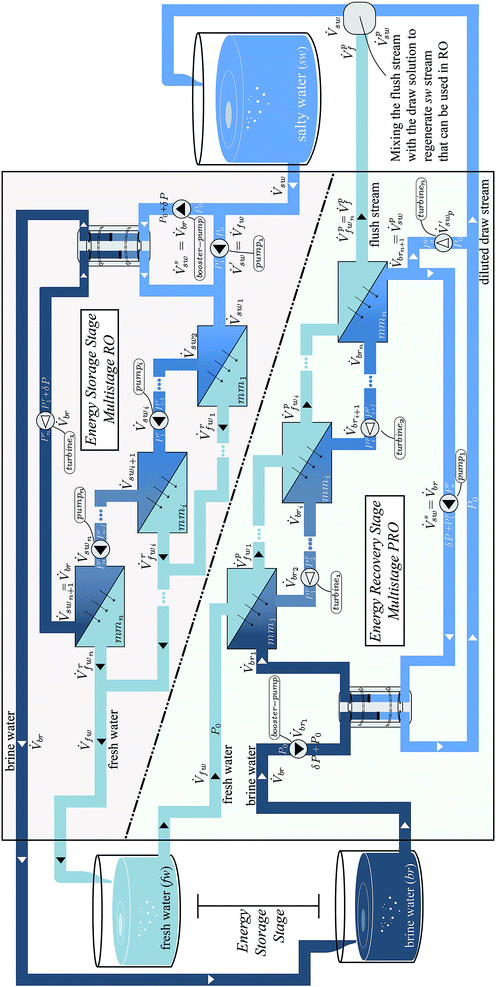
| Fig. 2 Simplified process diagram of a three-stage OES system, with 3 stage RO – separation (top) and 3 stage PRO – mixing (bottom). The change of heights for the liquids represents the change of hydraulic pressures, whereas the change in color represents the change in concentration (darker color – more salt). For a detailed OES process diagram see Fig. 3. | ||
Looking back at eqn (3), one might say that higher round trip efficiencies can be reached by recovering less fresh water, which in an ideal scenario is true (as 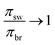 ). But in a realistic scenario, low recovery ratios do not give high round trip efficiencies and also operating at such low recovery ratios means operating at extremely low energy densities (see Section 6).
). But in a realistic scenario, low recovery ratios do not give high round trip efficiencies and also operating at such low recovery ratios means operating at extremely low energy densities (see Section 6).
3 Storing energy: multistage reverse osmosis (MRO)
OES taps unused electrical work and stores it as chemical potential in the form of a concentration difference. The concentration difference is created by separating a seawater (sw) stream into brine (br) and fresh water (fw) streams, using Reverse Osmosis (RO). As discussed in the previous section, the conventional RO process has inherent operational irreversibilities, and hence a modified multistage RO process is used in OES to split the sw stream.In this section, we show how the multistage RO process is designed to reduce entropy generation. The OES process introduced in this paper is modelled mathematically and then simulated with data for real off-the-shelf component properties. The model uses some variables to account for membrane performance, which we explain here, as they are key to understanding the working of OES. The model accounts for losses in the membrane module and the mechanical components. The pressure loss in the pipes and membrane modules is ignored, due to its insignificance.
Fig. 3-top shows an n-stage RO process. The process has n membrane modules (mm), where the pressure of the salty water (sw) stream entering the first membrane module (mm1) is Pr1. The hydraulic pressure of the sw stream is increased incrementally from the first to the last membrane module (mm1 to mmn), using pumps. The exiting brine (br) stream from the nth membrane module is at a pressure of Prn.
A pressure exchanger is used to exchange the pressure of the brine (br) stream (exiting the last membrane module) with the salty water (sw) stream entering the first membrane module at Pr1. In a single stage RO process, the pressure of the exiting brine stream is equal to that of the entering salty water stream, and hence PEX placement is trivial. In a multistage RO process the pressures are different in each membrane module, and hence the pressure of the brine stream has to be dropped from Prn to (Pr1 + δP), using a turbine. δP is the pressure loss in the PEX, and hence this must be added to the stream by a booster pump before it enters the PEX, to accommodate the loss. The benefits provided by the PEX in comparison to a pump–turbine pair and the reason behind the specific positioning of the PEX will be explained in detail in Section 5.1.
The salty water (sw) stream enters the RO part of the OES system, at a volumetric flow of ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) sw and at environmental pressure P0. As the PEX requires equal volumetric flow on both sides, the sw stream is split into
sw and at environmental pressure P0. As the PEX requires equal volumetric flow on both sides, the sw stream is split into ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw and
′′sw and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′sw, where
′sw, where ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw is equal to the volumetric flow of the brine (br) solution and
′′sw is equal to the volumetric flow of the brine (br) solution and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′sw is equal to the volumetric flow of the fresh water (fw) stream. The
′sw is equal to the volumetric flow of the fresh water (fw) stream. The ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw stream is pressurized in a booster pump to overcome the pressure loss δP, before it is sent to the PEX, to exchange pressure between the br stream. The other
′′sw stream is pressurized in a booster pump to overcome the pressure loss δP, before it is sent to the PEX, to exchange pressure between the br stream. The other ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′sw stream is pressurized using a high pressure pump to Pr1 and is then mixed back with the
′sw stream is pressurized using a high pressure pump to Pr1 and is then mixed back with the ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw stream to make
′′sw stream to make ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) sw1.
sw1.
After being pressurized, the salty water (sw) stream ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) sw1 enters the first membrane module (mm1) where some of the fresh water (fw) crosses the membrane as
sw1 enters the first membrane module (mm1) where some of the fresh water (fw) crosses the membrane as 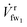 . The volumetric flow of the fw crossing the membrane is controlled by the hydraulic pressure ΔPr1 across the membrane module, which we explain for the ith membrane module (mmi) using the membrane effectiveness factor (see ESI Section 1†).
. The volumetric flow of the fw crossing the membrane is controlled by the hydraulic pressure ΔPr1 across the membrane module, which we explain for the ith membrane module (mmi) using the membrane effectiveness factor (see ESI Section 1†).
We define a fw recovery ratio for a membrane module mmi which describes how much fw is recovered from the sw stream entering the membrane module. All of the membrane modules have their own separate fw recovery ratio X. We describe this ratio and other properties for the ith membrane module (mmi). The fw recovery ratio for mmi is defined as
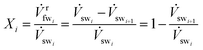 | (4) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) swi;
swi; 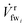 is the fw stream permeating mmi, and
is the fw stream permeating mmi, and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) swi+1 is the resulting saltier sw stream leaving mmi on the retentate side. The fw recovery ratio for RO is defined such that the X value for any RO membrane module is always less than or equal to 1. An X value close to 0 indicates that no fw crosses the membrane layer; on the other hand, an X value close to 1 indicates 100% of the fw is recovered from the sw stream.
swi+1 is the resulting saltier sw stream leaving mmi on the retentate side. The fw recovery ratio for RO is defined such that the X value for any RO membrane module is always less than or equal to 1. An X value close to 0 indicates that no fw crosses the membrane layer; on the other hand, an X value close to 1 indicates 100% of the fw is recovered from the sw stream.
The multistage RO process as shown in Fig. 3 (top) has n membrane modules operating at increasing pressures, where each membrane module gradually increases the salinity of the retentate stream. For the sake of understanding, these saltier retentate streams are referred to with a subscript ‘sw’ and with an incremental numbering. The retentate stream exiting the last membrane module is the resulting br stream. In the same fashion, the fw stream's subscripts are numbered with respect to the membrane module they are permeating from.
OES is designed as a closed loop system; the streams separated in RO, i.e. the resulting fw and br streams on the left of Fig. 3, are used again in PRO, and no external salt or water is required. While optimizing such a system, it is important to constrict the water flow accordingly (optimization parameters are discussed later in Sections 5 and 6). The authors found that using the fw recovery ratio X for modelling and optimization was more straightforward, compared to using hydraulic pressures, which leads to implicit equations and makes flow management complicated. The hydraulic pressure is the actual parameter used in an RO plant for operations; it is directly related to the fw recovery ratio X (ESI Section 1†) and can be easily found after the optimized X values are known. We take this reverse approach as it is easier to work with different X values. For the PRO model, we use the same approach, see Section 4.
We also define a net fw recovery ratio A which gives the relative amount of the fw that has been recovered in total from the sw stream,
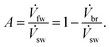 | (5) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) sw is the net volumetric flow of sw entering the RO stage of the OES system;
sw is the net volumetric flow of sw entering the RO stage of the OES system; ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) fw is the net volumetric flow of fw exiting the RO system and
fw is the net volumetric flow of fw exiting the RO system and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) br is the net volumetric flow of br separated in RO.
br is the net volumetric flow of br separated in RO.
It is key to note that the fw recovery ratio X is different from the net fw recovery ratio A. A tells us how much of the sw is split into br and fw, in total. On the other hand Xi tells us how much fw is recovered for that particular membrane module mmi (see Fig. 3).
In the later sections we study how choosing different A values can affect OES performance, where for each case, Xi for a membrane module mmi is optimized in a way that whatever the number of stages we choose to have in RO, each membrane module will recover fw, in a combination that consumes the least power possible. For instance, if 50% (A = 0.5) of the fw is required to be recovered from the sw stream, then the n membrane modules will individually recover a percentage of that 50%. It is not necessary that each of the n membrane modules will recover 1/nth of the fw; the individual X ratios depend on optimization, which outputs a combination of X ratios that would require the lowest work possible. Alternatively, if we understand this with the P–V schematics (Fig. 1), we can imagine reducing the red area in the 3-stage RO graph. There is an optimum pressure combination for Pr1, Pr2 and Pr3 (recovery ratios explicitly dictate the hydraulic pressures, ESI Section 1†) where the red area would be minimum, that is when the required work for achieving 50% fw recovery (i.e. A = 0.5) would be the least.
Ideally in RO separation, the fw stream, as the name suggests, is desired to have no salt. However, with current membranes this is not possible, as some of the salt from the sw side diffuses into the fw side. It is important to minimize any salt crossover in RO, as the resulting streams are used in the energy recovery stage (PRO). The losses associated with this crossflow are discussed in Section 5.2.
The power required for separation for an n stage RO process, as shown in Fig. 3, can be estimated by finding the work consumed and recovered in the components used as
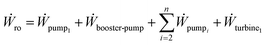 | (6) |
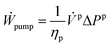 | (7) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) p is the volumetric flow of the stream pressurized in the pump, and ΔPp is the pressure difference of the stream before and after being pressurized. The work recovered in a turbine is given by
p is the volumetric flow of the stream pressurized in the pump, and ΔPp is the pressure difference of the stream before and after being pressurized. The work recovered in a turbine is given byẆturbine = ηt![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) tΔPt tΔPt | (8) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) t is the volumetric flow of the stream being depressurized, and ΔPt is the pressure difference of the stream before and after being depressurized.
t is the volumetric flow of the stream being depressurized, and ΔPt is the pressure difference of the stream before and after being depressurized.
We insert the pump and turbine work equations, eqn (7) and (8) in eqn (6), and use eqn (4) and (5), to simplify the work requirement,
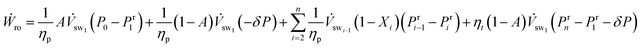 | (9) |
Once all stream properties and hydraulic pressures are solved in terms of the known variables, we optimize the minimum work required for separation, for a particular set of system parameters and component properties. The variable that is used for optimization is the Xi ratio for each mmi. The Xi values correspond to the hydraulic pressures required in that particular membrane module. The hydraulic pressure Pri for the ith membrane module (mmi) is described with all the known variables and the optimizing variable Xi, as shown in ESI Section 1,†eqn (9).
The system parameters include salty water properties, number of stages, n, fresh water recovery ratio, A, and other factors that can be altered; we study the effects of such alterations on energy density and round trip efficiency in Section 6. Component properties include membrane module effectiveness (i.e., ηmm = 0.90, see Section 5.2), pump efficiency (i.e., ηp = 0.95 (ref. 34)), turbine efficiency (i.e., ηt = 0.95 (ref. 35)) and PEX's pressure loss (i.e., δP = 0.5 bar (ref. 36)). The component properties are kept constant when optimizing the system energy density and round trip efficiency, as discussed in Section 6. However, the component properties are varied when their influence on the OES system is studied in Section 5.
Similar modelling is done for PRO as described next.
4 Recovering energy: multistage pressure retarded osmosis (MPRO)
When there is a demand for electricity, the chemical potential is converted back into electrical work by mixing the brine (br) and fresh water (fw) streams using PRO. The br and fw streams were a result of separation from the RO stage. This section presents the mathematical model for multistage PRO. As discussed before, the model accounts for losses in the membrane module and the mechanical components. The pressure loss in the pipes and membrane modules is ignored in this model, due to its insignificance when compared with other losses.Fig. 3-bottom shows an n-stage PRO process, with n membrane modules (mm), where the pressure of the brine (br) stream entering the first membrane module (mm1) is Pp1 (superscript ‘p’ is used to denote PRO, to separate this pressure variable from that of RO). The hydraulic pressure of the br stream is decreased gradually from the first to the last membrane module, according to the osmotic pressure of the br stream, using turbines, hence producing work. The exiting salty water (sw) stream from the nth membrane module (mmn) is at a pressure of Ppn bar. The hydraulic pressures are set after optimization and the method of finding them will become clear in this section.
As labelled in Fig. 3-bottom, a pressure exchanger (PEX) is equipped to exchange the pressure of the ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw stream exiting the nth membrane module (mmn) with that of the brine (br) stream
′′sw stream exiting the nth membrane module (mmn) with that of the brine (br) stream ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) br1, which is entering the first membrane module at Pp1. In a single stage PRO process, the pressure of the exiting salty water (sw) stream is equal to that of the entering br stream, and hence PEX placement is trivial. In multistage PRO, the pressures are different in each membrane module, and hence the pressure of the sw stream is increased from Ppn to (Pp1 + δP), using a pump, where δP is the pressure loss in the PEX, and hence must be added to the stream before it enters the PEX, to accommodate the loss. The benefits provided by the PEX in comparison to a pump–turbine pair and the reason behind the specific positioning of the PEX will be explained in Section 5.1.
br1, which is entering the first membrane module at Pp1. In a single stage PRO process, the pressure of the exiting salty water (sw) stream is equal to that of the entering br stream, and hence PEX placement is trivial. In multistage PRO, the pressures are different in each membrane module, and hence the pressure of the sw stream is increased from Ppn to (Pp1 + δP), using a pump, where δP is the pressure loss in the PEX, and hence must be added to the stream before it enters the PEX, to accommodate the loss. The benefits provided by the PEX in comparison to a pump–turbine pair and the reason behind the specific positioning of the PEX will be explained in Section 5.1.
The brine (br) and fresh water (fw) streams enter the PRO part of the OES system at volumetric flows of ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) br and
br and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) fw, respectively; both streams enter at environmental pressure P0. As the PEX requires equal volumetric flow on each side, the sw stream is split into
fw, respectively; both streams enter at environmental pressure P0. As the PEX requires equal volumetric flow on each side, the sw stream is split into ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw and
′′sw and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′sw,p, where
′sw,p, where ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw is equal to the volumetric flow of the br solution and
′′sw is equal to the volumetric flow of the br solution and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′sw,p is equal to the volumetric flow of the remainder. The
′sw,p is equal to the volumetric flow of the remainder. The ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw stream is pressurized in a pump to match the pressure required in the first membrane module and to overcome the PEX pressure loss δP, before it is sent to the PEX, to exchange pressure between the br stream
′′sw stream is pressurized in a pump to match the pressure required in the first membrane module and to overcome the PEX pressure loss δP, before it is sent to the PEX, to exchange pressure between the br stream ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) br1. The pressure of the other
br1. The pressure of the other ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′sw,p stream is dropped using a turbine to P0 bar and is then mixed back with that of the
′sw,p stream is dropped using a turbine to P0 bar and is then mixed back with that of the ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ′′sw stream, to make
′′sw stream, to make ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) sw.
sw.
After being pressurized to Pp1, the brine (br) stream ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) br1 enters the first membrane module (mmi) on the draw side, along with the fresh water (fw) stream (which is at environmental pressure P0) on the feed side. The osmotic pressure difference between the streams causes some of the fresh water (fw) from the feed side to cross the membrane layer and dilute the br stream. The amount of fw water crossing the membrane is controlled by the hydraulic pressure difference ΔPp1 between the two streams, as defined in ESI Section 2.†
br1 enters the first membrane module (mmi) on the draw side, along with the fresh water (fw) stream (which is at environmental pressure P0) on the feed side. The osmotic pressure difference between the streams causes some of the fresh water (fw) from the feed side to cross the membrane layer and dilute the br stream. The amount of fw water crossing the membrane is controlled by the hydraulic pressure difference ΔPp1 between the two streams, as defined in ESI Section 2.†
We define a fresh water (fw) mixing ratio Yi for the ith membrane module (mm1) which describes how much fw is mixed with the brine (br) stream entering the membrane module. All of the membrane modules have their own separate fw mixing ratio Yi. The fw mixing ratio for mmi is defined as
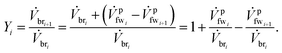 | (10) |
Further we can describe the outgoing brine and fresh water streams in terms of the incoming streams as
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) bri+1 = Yi bri+1 = Yi![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) bri bri | (11) |
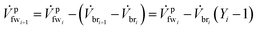 | (12) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) bri;
bri; 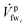 is the fw stream entering mmi on the feed side;
is the fw stream entering mmi on the feed side; ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) bri is the diluted br stream exiting mmi on the draw side and
bri is the diluted br stream exiting mmi on the draw side and 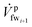 is the left over fw stream exiting mmi on the feed side. The fw mixing ratio for PRO is defined such that Yi for any PRO membrane is always larger or equal to 1. A Yi value close to 1 indicates that no fw crosses the membrane layer; on the other hand, a higher Yi value, for instance Yi = 2 would indicate that the amount of fw mixed results in twice the amount of the br stream.
is the left over fw stream exiting mmi on the feed side. The fw mixing ratio for PRO is defined such that Yi for any PRO membrane is always larger or equal to 1. A Yi value close to 1 indicates that no fw crosses the membrane layer; on the other hand, a higher Yi value, for instance Yi = 2 would indicate that the amount of fw mixed results in twice the amount of the br stream.
The multistage PRO process as shown in Fig. 3 has n membrane modules where each membrane module gradually decreases the salinity of the draw stream. For the sake of understanding, these diluted draw streams are referred to with a subscript ‘br’, with an incremental numbering. In the same fashion, the fw streams are numbered with respect to the membrane module they are permeating from. The diluted brine (br) stream exiting the last membrane module is the resulting swp stream, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) swp. Note that this stream has a lower volumetric flow than that of the salty water (sw) stream used in RO. The reason for this is that the membrane module is unable to take up all the fresh water from the feed side. Ideally, by the end of the PRO process, we want all of the fw to be mixed with the br stream, so that all the useful work can be recovered. However, for the nth membrane module (mmn) the quantity of fw mixed with the br stream depends on the uptake capacity of the membrane module.
swp. Note that this stream has a lower volumetric flow than that of the salty water (sw) stream used in RO. The reason for this is that the membrane module is unable to take up all the fresh water from the feed side. Ideally, by the end of the PRO process, we want all of the fw to be mixed with the br stream, so that all the useful work can be recovered. However, for the nth membrane module (mmn) the quantity of fw mixed with the br stream depends on the uptake capacity of the membrane module.
The loss due to the lack of uptake is felt significantly in the last membrane module, as the freshwater (fw) stream entering the last membrane module (mmn) has built up a high salt concentration from the reverse salt flux (explained later in this section) in the previous membrane modules. In terms of recovering energy, it is not useful to draw water from this fw stream 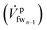 which is at relatively high osmotic pressure. Consequently, the leftover stream, which the membrane is unable to uptake, leaves the last membrane module (mmn) as the flush stream (
which is at relatively high osmotic pressure. Consequently, the leftover stream, which the membrane is unable to uptake, leaves the last membrane module (mmn) as the flush stream (![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) pf), on the feed side. We define the membrane uptake ratio ϕ such that the flush and the incoming streams are related, as
pf), on the feed side. We define the membrane uptake ratio ϕ such that the flush and the incoming streams are related, as
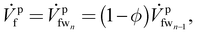 | (13) |
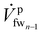 is the feed stream entering the last membrane module (mmn) and
is the feed stream entering the last membrane module (mmn) and 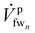 is the feed stream exiting the last membrane module, which is also referred to as the flush stream
is the feed stream exiting the last membrane module, which is also referred to as the flush stream ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) pf. A ϕ value equal to 1 indicates that all fw is drawn to the br side, which indicates the least entropy generation. In the same way, if ϕ is equal to 0, none of the fw crosses the membrane and all of it exits as the flush stream. The uptake ratio is implicitly accounted for by the membrane effectiveness factor. The uptake ratio depends on how well the membrane can draw the feed water stream when operating with lower water flows on the feed side. As shown in the OES process diagram (Fig. 3) the flush stream is mixed, irreversibly, with the draw stream from the last membrane module to make the sw stream that can be used again in RO, as
pf. A ϕ value equal to 1 indicates that all fw is drawn to the br side, which indicates the least entropy generation. In the same way, if ϕ is equal to 0, none of the fw crosses the membrane and all of it exits as the flush stream. The uptake ratio is implicitly accounted for by the membrane effectiveness factor. The uptake ratio depends on how well the membrane can draw the feed water stream when operating with lower water flows on the feed side. As shown in the OES process diagram (Fig. 3) the flush stream is mixed, irreversibly, with the draw stream from the last membrane module to make the sw stream that can be used again in RO, as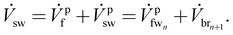 | (14) |
OES is designed as a closed loop system: the streams mixed in PRO are used again in RO and no external salt or water is required. As discussed in the previous section, while optimizing such a system, it is important to constrict the water flow according to the closed-loop constraints (optimization parameters are discussed later in Section 5). The authors found that using the fw mixing ratio Yi for modelling and optimization was more straightforward than using hydraulic pressures which lead to implicit equations and make flow management complicated. The hydraulic pressure is the actual parameter used in a PRO plant for operations; it is directly related to the fw mixing ratio Yi (ESI Section 2†) and can be easily found after the optimized Y values are known. Similar to what was done in the RO model, we take this reverse approach as it is easier to work with different Y values.
Ideally, in PRO mixing, the fresh water (fw) stream, as the name suggests, is desired to have no salt. However, with current membranes this is not possible, some of the salt from the salty water (sw) side diffuses into the fw side. The reverse salt diffusion increases the osmotic pressure of the fw stream and consequently decreases the osmotic pressure of the sw stream. This reduces the amount of energy retrievable from the streams, and hence it is key to reduce the reverse salt diffusion in the membrane module. The losses associated with this crossflow are discussed in Section 5.2.
The power recovered in an n stage PRO process as shown in Fig. 3 is estimated by finding the work consumed and recovered in the components used as
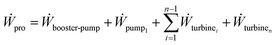 | (15) |
With work for the pumps and turbines given by eqn. (7) and (17), and with eqn (10) and (11), the work eqn (15) becomes
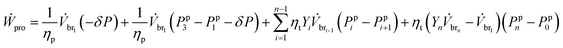 | (16) |
Once all stream properties and hydraulic pressures are solved in terms of the known variables, we optimize the maximum work recoverable while mixing, for a particular set of system parameters and component properties. The variable that is used for optimization is the Yi ratio for each mmi. The Yi value corresponds to the hydraulic pressures required in that particular membrane module. The hydraulic pressure Ppi for mmi is described with all the known variables and the optimizing variable Yi, as shown in ESI Section 2.†
The system parameters include salty water properties, number of stages, n, fresh water recovery ratio, A, and other factors that can be altered; we study the effects of such alterations on energy density and round trip efficiency in Section 6. Component properties include membrane module effectiveness (i.e., ηmm = 0.90, see Section 5.2), pump efficiency (i.e., ηp = 0.95 (ref. 34)), turbine efficiency (i.e., ηt = 0.95 (ref. 35)) and PEX's pressure loss (i.e., δP = 0.5 bar (ref. 36)). The component properties are kept constant when optimizing the system energy density and round trip efficiency, as discussed in Section 6. However, the component properties are varied when their influence on the OES system is studied in Section 5.
5 Influence of different components on OES performance
The OES system comprising RO and PRO is designed by assembling different components, where each component has a specific task. In this section we will study how these components can affect the OES system's overall performance.We can define various parameters to study OES performance; however from a thermodynamic standpoint, round trip efficiency and energy density are the obvious choices, since they are key to study and compare OES performance with other energy storage technologies.
Round trip efficiency, ηs, is defined as the ratio of the power generated while mixing in PRO, to the amount of power consumed to separate the solutions in RO,
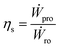 | (17) |
Energy density, ε, is defined as the amount of energy that can be stored in the OES system per m3 of salty water (sw) stored; in other words, the amount of energy that is recovered in the PRO process per m3 of sw, i.e. the power produced per m3 of sw, integrated over time for the whole PRO cycle,
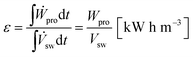 | (18) |
The influence of the components on OES performance is studied in the next few subsections. The first subsection focuses on the mechanical devices and the second section focuses on the membrane modules. Both sections discuss how the OES performance can be improved by identifying where losses occur.
5.1 Mechanical devices
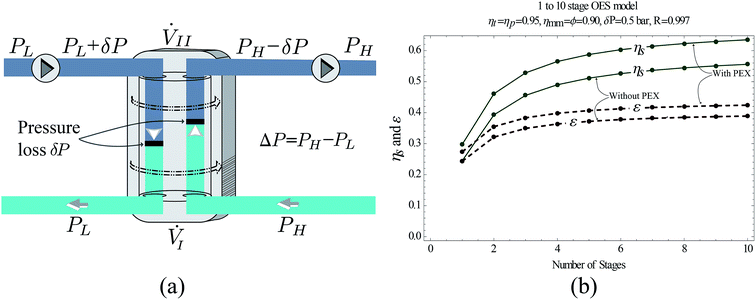
All the components used in OES (pumps, turbines, etc.) have irreversibilities which contribute to the overall losses in the OES system. Incorporating higher efficiency components improves OES performance. However, current off-the-shelf pumps and turbines have efficiencies of 85–95%,34,35 and there are quite a few of these components required in the multi-stage OES process, and hence the losses add up.To improve performance, we replace some of the lower efficiency pressure transfer mechanisms, i.e., pump–turbine pairs, with pressure exchangers (PEX). Unlike a single stage membrane process, in an n-stage system we have to drop and increase the pressure n times on the feed and draw sides in RO and PRO, respectively. This requires multiple pump–turbine pairs, which decreases the system's performance. Our previous research on MPRO plants showed that having a pressure exchanger (PEX) replace a pump–turbine (P–T) combination can increase the system's performance.33 A feed and a booster pump are required to compensate for pressure losses in the PEX. Due to the constant pressure loss in a PEX, such an arrangement is beneficial only when there is a requirement for exchanging pressure between two streams that have a sufficiently large pressure difference. The loss factor of a pressure exchanger (shown in Fig. 4(a)) is defined as33
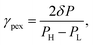 | (19) |
To improve the OES process performance, the pump–turbine (P–T) pairs are replaced with pressure exchangers (PEXs), as shown in Fig. 3. The placement of the pressure exchanger (PEX) is key, and hence, only the pump–turbine pairs which had more losses than the alternative (PEX) were replaced. Such a scenario is mathematically modelled in the previous sections.
Using the work equations defined in eqn (9) and (16), and the performance parameters described in eqn (17) and (18), we simulate the performance of the OES system – with and without pressure exchangers – by varying the number of stages, n, from 1 to 10. The simulation considers current off-the-shelf pumps, turbines and a PEX with a pressure loss of δP = 05 bar. The graph shown in Fig. 4(b) shows the simulation results, where an OES system equipped with pressure exchangers exhibits ∼20% higher round trip efficiency than an OES system without PEX, and the benefit in performance is significant. From a thermodynamic standpoint, it is clear that having pressure exchangers in the appropriate configurations reduces entropy generation in the system and improves OES performance.
5.2 Membrane modules
The key component in the OES system is the membrane module. The membrane module with its semipermeable properties allows for controlled separation and mixing, which is the basis of OES working.RO desalination has more than half a century of industrial operational experience. The RO industry is mature and much older than PRO. Consequently, there has been extensive work to produce robust membranes which have made RO desalination profitable; however, there is still ample room for improvement towards salt rejection, water permeability and anti-fouling properties.37,38 OES is modelled and simulated with current off-the-shelf RO membranes and similar to RO desalination, and there are multiple prospects of the membrane that can be modified to directly improve OES performance, which we discuss later through Fig. 5.
Fouling and concentration polarization are some of the major issues faced in river-seawater PRO.39 A closed loop system like ours uses clean solutions which assists in addressing the issue of fouling and improving membrane performance for both PRO and RO, in that respect.29,40 The other irreversibility in the membranes is the undesired salt flow, which, on the contrary, has a greater negative effect on a closed loop system.41 Reverse salt diffusion in OES results in a salty fresh water (fw) stream out of RO, which is used again in PRO (as it is a closed loop). The salt in fw limits the available chemical potential that can be recovered in PRO, and hence drastically affects OES performance. However, more R&D towards membranes with higher salt rejection capabilities, thinner support layers, higher water permeability coefficients and increased anti-fouling properties can and will directly improve OES performance (see Fig. 5).30,39
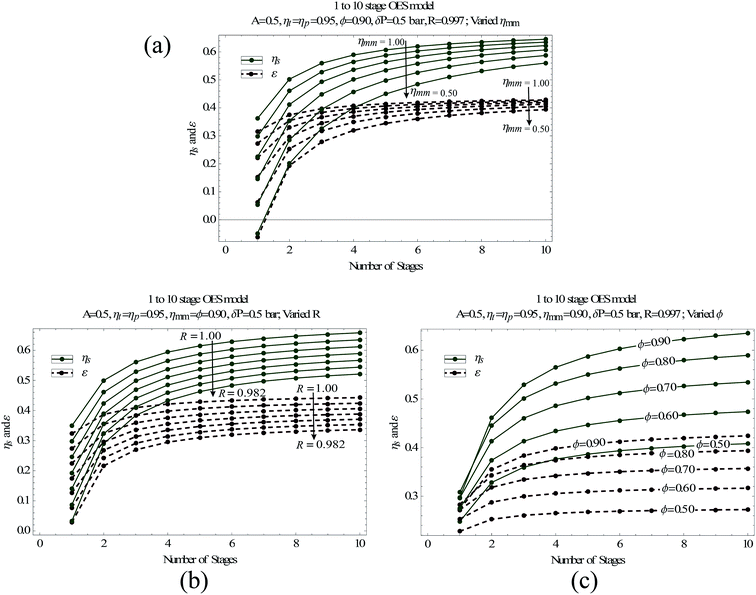
To find out how the membrane properties affect OES performance, we analyze the system's round trip efficiency and energy density over a range of membrane performance values – i.e. different membrane uptake values (ϕ), salt rejection coefficients (R) and membrane module effectiveness factors (ηmm). The simulation results are presented in Fig. 5.
Fig. 5(a) shows the effect of different membrane effectiveness factors, ηmm, on OES performance. This factor is a parameter that accounts for the majority of the losses inside a membrane module, and it is explained in detail in the ESI (available with this paper) Sections 1 and 2,† for RO and PRO, respectively. In a few words, a membrane with a higher membrane effectiveness indicates that the difference in the osmotic pressure of the streams exiting a membrane module is relatively close to the hydraulic pressure difference between the streams. A perfect membrane module with a 100% effectiveness factor, i.e. ηmm = 1, would have the exiting stream's osmotic pressure difference equal to the hydraulic pressure difference between them. Alternatively, a fully irreversible membrane module (ηmm = 0) would show no change in the osmotic pressure of the streams on either side of the membrane. It is important to understand that the effectiveness of a membrane module depends on the operating conditions, and there is no single value of effectiveness that can describe a module.33 One may intentionally desire to operate a membrane module at lower effectiveness factors, by using short membranes, so that the water flux across the whole membrane area is maximized, as a lower ηmm value indicates a relatively larger difference in osmotic and hydraulic pressures between the exiting streams (hence a larger driving force, eqn (1)), which would have been minimized if the ηmm value was closer to 1. However, this would mean that some of the chemical potential is lost, which can be acceptable in the case of river-ocean PRO, as the target might be to optimize membrane power density. But in a closed loop system like ours, such chemical potential loss can cause major penalties in round trip efficiency and power density, as discussed in this paper, using the flush stream. From Sindey Loeb's analysis for PRO in ref. 42, one can conclude a value of ηmm ≈ 0.83. This was achieved, while targeting high membrane power density, instead one could achieve higher membrane effectiveness by changing the volumetric flows and hydraulic pressures. We assume a membrane effectiveness of 90% (i.e., ηmm = 0.90) for simulations in the next section. Achieving an ηmm value of 0.90 is possible; however that might reduce membrane power density and hence require more membrane area to generate an equivalent amount of energy. In the case of mixing brine with fresh water [via PRO], such a shift towards high membrane effectiveness may be acceptable as optimum power densities of 13–22 W m−2 are achievable,24,43 and hence there is plenty of room for sacrificing power density, while still being above the 5 W m−2 mark.44
As the membrane effectiveness factor considers the difference in osmotic pressure between the entering and exiting streams on the draw and feed side, it implicitly accounts for the entropy generated due to reverse salt flux and the lack of water uptake in PRO. To explicitly calculate and understand how these properties individually affect OES performance, we simulate the effect of the salt rejection coefficient R (ESI Sections 1 & 2†) and the membrane uptake ratio ϕ (eqn (13)) in Fig. 5(b) and (c).
Each of the parameters reflects a particular membrane performance capability, theoretically ranging from 0% (completely incapable) to 100% (perfect capability). Obviously, OES's overall performance varies with membrane performance; as indicated in Fig. 5, all three membrane performance parameters affect both energy density, ε and round trip efficiency, ηs.
The simulation results, apart from having the potential to achieve high ε and ηs values, also show the extent of membrane irreversibilities an OES system can sustain without sacrificing energy density and round trip efficiency. Low membrane effectiveness (ηmm) corresponds to high concentration polarization in the membrane and having such membranes in the OES system would decrease the round trip efficiency and energy density of the system. However, due to the multistage configuration, an OES system with membranes performing at a 60% effectiveness factor can still provide a round trip efficiency of ∼40% with 3 stages, instead of only ∼5% with a single stage. Note that in this case, for both 3 stage and single stage OES, an equal amount of fresh water is separated and mixed. Having multiple stages does not correspond to a relatively higher membrane area; this in fact corresponds to using a smaller membrane area for the same task, as in a multistage process the membrane is operated at optimum hydraulic pressures, see Section 2 and refer to ref. 33 for a more detailed explanation.
The losses due to low ϕ and R values directly decrease the chemical potential and may not be possible to mitigate by modifying the process design. A lower R value increases the fresh water (fw) stream's osmotic pressure, which increases the work needed for separation and decreases the work obtainable in PRO. This loss can only be mitigated by improving the salt rejection coefficient. Currently, commercial thin-film composite membranes operate with around 99.6 to 99.8% salt rejection.13,45 We assume a salt rejection of 99.7% (i.e., R = 0.997) for simulations in the next section.
At first glance, one might say that the graphs in Fig. 5 show an improvement in OES performance with higher number of stages, for constant R (and ϕ) values. This is true; however, the improvement in OES performance does not directly indicate that the irreversibilities caused by reverse salt flux (and the lack of water uptake) are being reduced with higher number of stages. It is actually the decrease in other reducible irreversibilities, as explained in Section 2, that improves OES performance (see Fig. 1).
It is also key to note that due to reverse salt flux, approaching water uptake (ϕ) values close to 100% is not possible, as salt accumulation (due to reverse salt flux) and loss of water (due to water flux from the feed to draw side) create a high osmotic pressure on the feed side, which on its own constricts water cross-flow, as explained by eqn (1). Hence, the reverse salt flux in a way restricts the membrane from reaching high water uptake values (ϕ), regardless of the membrane's hydrophilic properties. To conclude, reaching ϕ values close to 1 is important to utilize all the chemical potential, but is impossible to achieve without having higher salt rejection properties in both RO and PRO stage membranes.
Overall, to achieve high round trip efficiency and high energy density, we need to have membranes which can benefit from closed loop operation and operate with high salt rejection (R) and high membrane effectiveness (ηmm) values. In the next section we optimize the OES process and discover that high pressure resistance is another key property required for improved performance.
6 Varying plant parameters for improved performance
So far we have analyzed the n-stage OES system which recovers 50% of the fresh water (fw) from a salty water (sw) stream, i.e., at an osmotic pressure of πsw = 30 bar. This operational process is similar to the standard seawater desalination process. OES is a closed loop system and depending on what gives the desired optimum performance, several sw concentrations and fw recovery ratios can be applied. We now study the three basic parameters that can be altered directly to improve OES's energy density, ε, and round trip efficiency, ηs. They are:(1) Number of stages, n.
(2) Fresh water (fw) recovery ratio, A.
(3) Osmotic pressure (alternatively, the salt concentration) of the salty water stream, πsw.
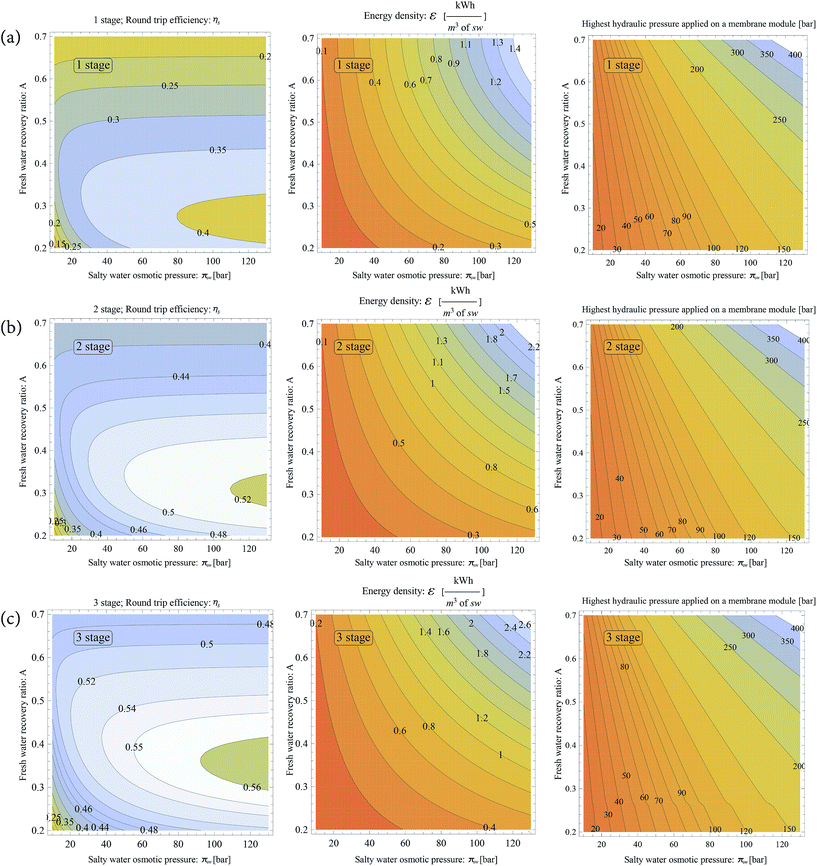
By now it is clear that having a higher number of stages improves the round trip efficiency and energy density of the system. To understand how different A and πsw values affect system performance, we simulate three different OES systems for n = 1, 2 and 3 (the process diagram for n stage OES is shown in Fig. 3) in Fig. 6(a)–(c) respectively. The effect on ηs and ε is studied, when A and πsw values are varied for each n value, as shown in Fig. 6-left and centre columns, respectively. Along with the performance graphs, we have recorded and presented the highest hydraulic pressure applied to a membrane module for that particular A, πsw and n value, as shown in Fig. 6-right column. The highest hydraulic pressure in the OES process occurs in the RO stage, in the n-th stage; this pressure is shown in Fig. 6, right column.
The behaviour of ηs and ε with varying A and πsw values has a similar trend for 1, 2 and 3 stage OES systems; however the performance and magnitude are better at higher stages. We choose to study the behaviour for a 3 stage OES system as it presents promising results. The reasoning behind the trend and behaviour is consistent for all three OES systems with different n values.
The graphs (Fig. 6(c)-left and centre) hint at a relationship between A and πsw, complementing each other. A higher πsw value gives higher energy density and efficiency (as shown in Fig. 6(c)-left and centre columns). However, the problem is that higher osmotic pressure calls for even higher hydraulic pressures for separation. A membrane module can only withstand certain hydraulic pressures without fracturing its structure. This is where a lower fw recovery ratio, A, can reduce the hydraulic pressure required for separation, as less fw is squeezed out at lower A values. At the same time, low A values give high efficiency as shown in Fig. 6(c)-left. Ideally, having high osmotic pressures and lower recovery ratios allows the OES system to perform with high efficiencies, while still operating at reasonably low hydraulic pressures.
Membrane modules in a typical seawater RO desalination plant operate at pressures of 50–60 bars. Reaching higher pressures might not be possible. To achieve high energy density, we need to operate at higher hydraulic pressures. In a recent study, in which operating pressures of 100 to 175 bars were tested on off-the-shelf RO membranes, the membranes exhibited excellent rejection rates of up to 99.62% (when operating at 172 bar). On the contrary, the water permeability of the membrane modules was shown to drastically drop at such high pressures.46 This means that due to lower water flux, more membrane area (at the 3rd RO stage) would be required to accomplish the same separation task when operating at such high pressures. Although still far from commercial application, nanoporous graphene membranes have shown the possibility of extremely high water permeability and salt rejection, as well as the possibility of operating at extremely high pressures (1000–5000 bar), without fracturing the graphene monolayers.47–49
High round trip efficiencies of ∼55% can be achieved when the hydraulic pressure in the 3rd stage RO membrane is only 80 bar. However, if the goal is to achieve high energy density, one can achieve so by operating at high fresh water recovery ratios (A). At a maximum hydraulic pressure close to 175 bar, both high energy density (∼1.2 kW h m−3) and high round trip efficiencies (∼55%) can be achieved. Note, both energy densities and round trip efficiencies increase with higher n values, but with added capital costs.
It is straightforward to cut-off the impractical regions on the graph by considering what pressures a membrane module cannot sustain. However, choosing between high ηs, ε and n can be complicated. Many factors affect the optimization goals of an energy storage plant, such as economics, location of the plant, space availability, charge duration, etc. This paper is focused on introducing the concept and technology of storing energy through a multistage osmotic process; detailed optimization that incorporates these factors is beyond the scope of this paper.
To have a better understanding of the scale for energy density, we can take an example of an energy storage plant built by BC hydro in Field, BC, Canada. The plant was built to improve the reliability and response times to outages which are abundant in this remote location.50 This energy storage plant is capable of storing up to 6 MW h of electricity. If an OES system was built to provide a similar electrical demand, it would have to hold 5000 m3 (for reference – an olympic swimming pool holds around 2500 m3 to 3750 m3 of water) of total solution (i.e., water and salt) at an energy density of 1.2 kw h m−3. Such an amount of liquid storage is not unheard of in the water storage industry, where standard sized tanks for potable water and brine storage can range from 75 m3 to 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 m3.51 However, this is at the lower end of the spectrum for energy storage densities, where battery technologies have energy storage densities ranging from 50–500 kW h m−3 and fuel cells have energy densities of 500–3000 kW h m−3.11 Depending on the available space and economics, storing a large amount of liquid might or might not be an issue. In the case of the 6 MW h energy storage plant in Field, BC, being a remote location there is a lot of available land currently unused. On the contrary, if we consider another storage facility in Toronto, Canada,52 where the city required small and compact energy storage units that can provide 0.25 MW h of electricity storage in an urban setting, OES would not be well suited.
700 m3.51 However, this is at the lower end of the spectrum for energy storage densities, where battery technologies have energy storage densities ranging from 50–500 kW h m−3 and fuel cells have energy densities of 500–3000 kW h m−3.11 Depending on the available space and economics, storing a large amount of liquid might or might not be an issue. In the case of the 6 MW h energy storage plant in Field, BC, being a remote location there is a lot of available land currently unused. On the contrary, if we consider another storage facility in Toronto, Canada,52 where the city required small and compact energy storage units that can provide 0.25 MW h of electricity storage in an urban setting, OES would not be well suited.
At the larger end, i.e. a GW h scale of energy storage, which is currently dominated by pumped hydro, an OES plant would require storing atleast 106 m3 of liquid. Pumped hydro (PH) has comparable energy density to OES;11 however PH takes advantage of giant open reservoirs. In this paper we have discussed how OES can benefit from a closed loop system; having open brine and fresh water reservoirs like PH would give away that advantage. Every cycle may require some type of pretreatment that would consume energy and with evaporation more water might be required regularly. Although, without an economical and feasibility study, we cannot say that storing 1000 million litres of water in enclosed tanks might be impractical (there are a few examples of tank farms storing oil at similar amounts), but it is safe to say that such a size for energy storage [using OES] would require a lot of land and cause additional losses in the system.
7 Conclusion
The results presented in this paper demonstrate that an osmotic energy storage system can be viable for storing electrical energy. Previous studies on storing energy using osmosis have shown a competing relationship between round trip efficiency and energy density. With multistage operation we have shown that both energy density and round trip efficiency can together be improved. The OES system has shown that it can approach practical efficiencies of 50–60% or higher, using the modified RO and PRO approach. The simulations were done assuming co-current flow in PRO for simple explanations; a counter-current flow configuration would, however, have higher round trip efficiencies, energy densities and operate at higher membrane power densities.53OES itself has the potential to incorporate a thermolytic solution and operate as a hybrid RO-distillation set-up for separation. When waste heat is available, such a hybrid system can achieve higher round trip efficiency by separating some of the salty water (sw) solution, while mitigating the losses caused by reverse salt flux.
The OES process showed that it could approach realistic energy densities close to 1.2 kW h m−3, which is approximately equal to that of a 500 meter high pumped hydro energy storage system (i.e. operating at 80% efficiency). A pumped hydro process is known to perform at 10–20% higher efficiency than OES; however, it is geographically constrained. An OES system on the other hand can be constructed in any type of geography and would occupy storage space similar to a 500 meter high pumped hydro plant that would have been restricted to hilly regions.
The OES system is operated in a fashion that it has the potential to store energy for long durations and operate at variable power capacities. The OES system has been shown to perform better when it operates under its peak capacity. This is better explained with an example. Let us assume a 4 MW peak capacity OES plant, operated with 4 arrays of 3-stage PRO processes, at a 1 MW capacity each. In a scenario where the demand for electricity is at half the peak capacity, the OES system can transform from 4 arrays (with 3 stages in each array) to a double array with a 6 stage PRO process in each array. Such a shift and complete utilization of components increase the plant's round trip efficiency and energy density.
Ideally, the OES system would operate with membrane modules that can be used for both RO and PRO. Having such a compact system would clean the membrane when the water flux is in the opposite direction, save space, and possibly decrease capital costs. There has been some work towards surface modification of thin film composite membranes with polydopamine that enables using RO membranes for PRO in a certain pressure range.54 However, to realize the realistic feasibility of the OES system, further work needs to be done to develop commercial membranes. Membranes that can either work as both RO/PRO membranes, or, themselves (separately) offer higher water permeability and salt rejection, while operating at high hydraulic pressures.
References
- G. A. Meehl, et al., Global climate projections, Climate Change 2007: The Physical Science Basis, ed. S. Solomon, et al., Cambridge Univ Press, Cambridge, UK, NewYork, 2007, pp. 747–845 Search PubMed.
- R. J. Nicholls, et al., Coastal systems and low lying areas, Climate Change 2007: Impacts, Adaptation, and Vulnerability, ed. M. L. Parry, et al., Cambridge Univ Press, Cambridge, UK, 2007, pp. 315–357 Search PubMed.
- S. Solomon, G.-K. Plattner, R. Knutti and P. Friedlingstein, Irreversible climate change due to carbon dioxide emissions, PNAS, 2009, 106(6), 1704–1709 CrossRef CAS PubMed.
- K. E. Trenberth, et al., Observations: surface and atmospheric climate change, Climate Change 2007: the Physical Science Basis, ed. S. Solomon, et al., Cambridge Univ Press, Cambridge, UK, 2007, pp. 747–845 Search PubMed.
- R. Seager, et al., Model projections of an imminent transition to a more arid climate in southwestern North America, Science, 2007, 316, 1181–1184 CrossRef CAS PubMed.
- X. Zhang, et al., Detection of human influence on twentieth-century precipitation trends, Nature, 2007, 448, 461–465 CrossRef CAS PubMed.
- X. Gao and F. Giorgi, Increased aridity in the Mediterranean region under greenhouse gas forcing estimated from high resolution simulations with a regional climate model, Global Planet. Change, 2008, 62, 195–209 CrossRef.
- E. J. Burke, S. J. Brown and N. Christidis, Modelling the recent evolution of global drought and projections for the 21st century with the Hadley Centre climate model, Journal of Hydrometeorology, 2006, 7, 1113–1125 CrossRef.
- D. Rastler, Electric Energy Storage Technology Options: A White Paper Primer on Applications, Costs, and Benefits, EPRI, Palo Alto, CA, 2010, p. 1020676 Search PubMed.
- B. Dunn, H. Kamath and J.-M. Tarascon, Electrical Energy Storage for the Grid: A Battery of Choices, Science, 2011, 334(6058), 928–935 CrossRef CAS PubMed.
- H. Chen, T. N. Cong, W. Yang, C. Tan, Y. Li and Y. Ding, Progress in electrical energy storage system: A critical review, Prog. Nat. Sci., 2009, 19(3), 291–312 CrossRef CAS.
- I. Hadjipaschalis, A. Poullikkas and V. Efthimiou, Overview of current and future energy storage technologies for electric power applications, Renewable Sustainable Energy Rev., 2009, 13(6–7), 1513–1522 CrossRef.
- M. Elimelech and W. A. Phillip, The Future of Seawater Desalination: Energy, Technology, and the Environment, Science, 2011, 333(6043), 712–717 CrossRef CAS PubMed.
- R. E. Pattle, Production of Electric Power by mixing Fresh and Salt Water in the Hydroelectric Pile, Nature, 1954, 174(4431), 660 CrossRef CAS.
- A. Achilli and A. E. Childress, Pressure retarded osmosis: From the vision of Sidney Loeb to the first prototype installation—Review, Desalination, 2010, 261(3), 205–211 CrossRef CAS.
- N. Y. Yip, D. Brogioli, H. V. M. Hamelers and K. Nijmeijer, Salinity Gradients for Sustainable Energy: Primer, Progress, and Prospects, Environ. Sci. Technol., 2016, 50(22), 12072–12094 CrossRef CAS PubMed.
- A. P. Straub, A. Deshmukh and M. Elimelech, Pressure-retarded osmosis for power generation from salinity gradients: is it viable?, Energy Environ. Sci., 2016, 9(1), 31–48 CAS.
- K. K. Reimund, J. R. McCutcheon and A. D. Wilson, Thermodynamic analysis of energy density in pressure retarded osmosis: The impact of solution volumes and costs, J. Membr. Sci., 2015, 487, 240–248 CrossRef CAS.
- L. D. Banchik, M. H. Sharqawy and V. J. H. Lienhard, Limits of power production due to finite membrane area in pressure retarded osmosis, J. Membr. Sci., 2014, 468, 81–89 CrossRef CAS.
- R. L. McGinnis, J. R. McCutcheon and M. Elimelech, A novel ammonia–carbon dioxide osmotic heat engine for power generation, J. Membr. Sci., 2007, 305(1–2), 13–19 CrossRef CAS.
- E. Shaulsky, C. Boo, S. Lin and M. Elimelech, Membrane-Based Osmotic Heat Engine with Organic Solvent for Enhanced Power Generation from Low-Grade Heat, Environ. Sci. Technol., 2015, 49(9), 5820–5827 CrossRef CAS PubMed.
- G. Han, J. Zuo, C. Wan and T.-S. Chung, Hybrid pressure retarded osmosis-membrane distillation (PRO-MD) process for osmotic power and clean water generation, Environ. Sci.: Water Res. Technol., 2015, 1(4), 507–515 CAS.
- J. Kim, M. Park, S. A. Snyder and J. H. Kim, Reverse osmosis (RO) and pressure retarded osmosis (PRO) hybrid processes: Model-based scenario study, Desalination, 2013, 322, 121–130 CrossRef CAS.
- H. Sakai, T. Ueyama, M. Irie, K. Matsuyama, A. Tanioka and K. Saito, et al., Energy recovery by PRO in sea water desalination plant, Desalination, 2016, 389, 52–57 CrossRef CAS.
- R. McGinnis and A. Mandell, Utility scale osmotic grid storage, US8795525 B2, 2014, available from: http://www.google.com/patents/US8795525.
- W. He and J. Wang, Feasibility study of energy storage by concentrating/desalinating water: Concentrated Water Energy Storage, Appl. Energy, 2017, 185(1), 872–884 CrossRef CAS.
- R. S. Kingsbury, K. Chu and O. Coronell, Energy storage by reversible electrodialysis: The concentration battery, J. Membr. Sci., 2015, 495, 502–516 CrossRef CAS.
- W. J. van Egmond, U. K. Starke, M. Saakes, C. J. N. Buisman and H. V. M. Hamelers, Energy efficiency of a concentration gradient flow battery at elevated temperatures, J. Power Sources, 2017, 340, 71–79 CrossRef CAS.
- D. D. Anastasio, J. T. Arena, E. A. Cole and J. R. McCutcheon, Impact of temperature on power density in closed-loop pressure retarded osmosis for grid storage, J. Membr. Sci., 2015, 479, 240–245 CrossRef CAS.
- J. W. Post, J. Veerman, H. V. M. Hamelers, G. J. W. Euverink, S. J. Metz and K. Nymeijer, et al., Salinity-gradient power: Evaluation of pressure-retarded osmosis and reverse electrodialysis, J. Membr. Sci., 2007, 288(1–2), 218–230 CrossRef CAS.
- J. R. Mccutcheon and M. Elimelech, Modeling water flux in forward osmosis: Implications for improved membrane design, AIChE J., 2007, 53(7), 1736–1744 CrossRef CAS.
- S. Lin, A. P. Straub and M. Elimelech, Thermodynamic limits of extractable energy by pressure retarded osmosis, Energy Environ. Sci., 2014, 7(8), 2706–2714 CAS.
- D. Bharadwaj, T. M. Fyles and H. Struchtrup, Multistage Pressure-Retarded Osmosis, J. Non-Equilib. Thermodyn., 2016, 41(4), 327–347 CAS.
- T. M. Hunt, T. Hunt, N. D. Vaughan and N. Vaughan, The Hydraulic Handbook, Elsevier, 1996. p. 788 Search PubMed.
- J. L. Gordon, Hydraulic turbine efficiency, Can. J. Civ. Eng., 2001, 28(2), 238–253 CrossRef.
- Rodney B. Clemente, V. P, Technical Service & Aftermarket, Energy Recovery PX Device, Personal Communication.
- L. F. Greenlee, D. F. Lawler, B. D. Freeman, B. Marrot and P. Moulin, Reverse osmosis desalination: Water sources, technology, and today's challenges, Water Res., 2009, 43(9), 2317–2348 CrossRef CAS PubMed.
- K. P. Lee, T. C. Arnot and D. Mattia, A review of reverse osmosis membrane materials for desalination—Development to date and future potential, J. Membr. Sci., 2011, 370(1–2), 1–22 CrossRef CAS.
- T. Thorsen and T. Holt, The potential for power production from salinity gradients by pressure retarded osmosis, J. Membr. Sci., 2009, 335(1–2), 103–110 CrossRef CAS.
- J. R. McCutcheon, R. L. McGinnis and M. Elimelech, A novel ammonia—carbon dioxide forward (direct) osmosis desalination process, Desalination, 2005, 174(1), 1–11 CrossRef CAS.
- A. Achilli, T. Y. Cath and A. E. Childress, Power generation with pressure retarded osmosis: An experimental and theoretical investigation, J. Membr. Sci., 2009, 343(1–2), 42–52 CrossRef CAS.
- S. Loeb, Energy production at the Dead Sea by pressure-retarded osmosis: challenge or chimera?, Desalination, 1998, 120(3), 247–262 CrossRef CAS.
- K. L. Hickenbottom, J. Vanneste, M. Elimelech and T. Y. Cath, Assessing the current state of commercially available membranes and spacers for energy production with pressure retarded osmosis, Desalination, 2016, 389, 108–118 CrossRef CAS.
- S. E. Skilhagen, Osmotic power—a new, renewable energy source, Desalin. Water Treat., 2010, 15(1–3), 271–278 CrossRef.
- M. Busch and W. E. Mickols, Reducing energy consumption in seawater desalination, Desalination, 2004, 165, 299–312 CrossRef CAS.
- R. K. McGovern, M. C. Dillon and V. J. H. Lienhard, The effect of very high hydraulic pressure on the permeability and salt rejection of reverse osmosis membranes, IDA World Congress on Desalination and Water Reuse, 2015 Search PubMed.
- D. Cohen-Tanugi and J. C. Grossman, Water Desalination across Nanoporous Graphene, Nano Lett., 2012, 12(7), 3602–3608 CrossRef CAS PubMed.
- S. Jun, T. Tashi and H. S. Park, Size Dependence of the Nonlinear Elastic Softening of Nanoscale Graphene Monolayers under Plane-Strain Bulge Tests: A Molecular Dynamics Study, J. Nanomater., 2010, 2011, e380286 Search PubMed.
- J. S. Bunch, S. S. Verbridge, J. S. Alden, A. M. van der Zande, J. M. Parpia and H. G. Craighead, et al., Impermeable atomic membranes from graphene sheets, Nano Lett., 2008, 8(8), 2458–2462 CrossRef CAS PubMed.
- Field Battery Energy Storage Project, 2016, available from: https://www.bchydro.com/energy-in-bc/projects/field-battery.html.
- Above Ground Water Storage Tanks Manufacturer | CST Industries, 2016, available from: https://www.cstindustries.com/applications/above-ground-water-storage-tanks-manufacturer.
- Community Energy Storage | Toronto Hydro Electric System, 2016, available from: http://www.torontohydro.com/sites/electricsystem/gridinvestment/powerup/pages/communityenergystorage.aspx.
- A. P. Straub, S. Lin and M. Elimelech, Module-Scale Analysis of Pressure Retarded Osmosis: Performance Limitations and Implications for Full-Scale Operation, Environ. Sci. Technol., 2014, 48(20), 12435–12444 CrossRef CAS PubMed.
- J. T. Arena, B. McCloskey, B. D. Freeman and J. R. McCutcheon, Surface modification of thin film composite membrane support layers with polydopamine: Enabling use of reverse osmosis membranes in pressure retarded osmosis, J. Membr. Sci., 2011, 375(1–2), 55–62 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6se00013d |
| This journal is © The Royal Society of Chemistry 2017 |