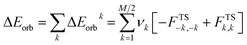Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical investigation on donor–acceptor interaction between a carbonyl compound and an N,N′-dioxide–Sc(III) complex†
Zhishan Su ,
Weiying He,
Junming Wang,
Yini Zuo and
Changwei Hu
,
Weiying He,
Junming Wang,
Yini Zuo and
Changwei Hu *
*
Key Laboratory of Green Chemistry and Technology, Ministry of Education, College of Chemistry, Sichuan University, Chengdu, Sichuan 610064, P. R. China. E-mail: changweihu@scu.edu.cn
First published on 12th December 2017
Abstract
Herein, metal–ligand bonding features in a chelation N,N′-dioxide–Sc(III) complex have been addressed using the DFT method at the M06/6-31+G** Level. The donor–acceptor interaction between the carbonyl substrate and Sc(III)-based catalyst is analyzed in detail by the activation strain model (ASM), energy decomposition analysis (EDA), and natural orbital for chemical valence (NOCV) calculations. The orbital interaction is the major contributor to N,N′-dioxide–[Sc(OTf)]2+ bonding, whereas the electrostatic interaction plays a more important role than orbital interaction in the activation of a carbonyl compound in hexacoordinate N,N′-dioxide–Sc(III) complexes. The substituents in the amide group of the N,N′-dioxide ligand (L) affect the electrostatic energy as well as the orbital energy between the CH2O and Sc(III)-based catalyst by adjusting the Lewis acidity of the metal centre. The complex with ortho-diisopropylphenyl groups in the ligand exhibits a higher reactivity towards CH2O. Compared to OiPr, the counter ion OTf in the Sc(III)-complex enhances the Lewis acidity of the metal centre and facilitates the activation of CH2O by promoting electron density flow from CH2O to the metal fragment. The high catalytic performance of the N,N′-dioxide–Sc(III) complex towards PhCHO and chalcone is attributed to their good nucleophilicity that results in a more stabilizing electrostatic and orbital interaction between the N,N′-dioxide–[Sc(OTf)]2+ complex and carbonyl substrate.
Introduction
The C2-symmetric N,N′-dioxide (L) developed by Feng's group is a class of conformationally flexible ligands, which can be synthesized from cheap optically pure amino acids.1 The experimental investigations indicate that these ligands can act as neutral tetradentate ligands to bind a wide variety of metal ions; this results in the formation of effective and versatile chiral metal-complex catalysts for asymmetric catalysis.1a,b After coordination at the metal centre, the chelating ligand is able to impose a relatively rigid environment, tuning the electron richness of metal centre and, in turn, the reactivity of the coordination complex.2 In the catalytic processes involving N,N′-dioxide–metal complexes, the carbonyl compound is one of the most popular substrates since it can coordinate towards the metal centre in a monodentate or bidentate fashion (if possible) via oxygen atoms to form reacting species. When only one coordinating O atom is available in a carbonyl compound, another ligand, solvent or counter anion can occupy the remaining coordination site to construct an octahedral intermediate for subsequent conversion. The experimental observations and theoretical investigations indicate that the activity and selectivity of a chiral N,N′-dioxide–metal catalyst towards a carbonyl substrate depend closely on the inherent properties (such as Lewis acidity, ionic radius or coordination sphere properties) of the central metal ion as well as ligand structures (amide substituent or the amino acid backbone).3The classical Dewar–Chatt–Duncanson model is generally employed to understand the metal–ligand interaction in organometallic chemistry.4,5 For transition metal-based systems, bonding is attributed to a synergic process of ligand → metal electron donation and metal → ligand back-donation.6 Many useful schemes, including charge decomposition analysis (CDA),7–10 atoms in molecule (AIM),11 block localized wave function energy decomposition (BLW-ED),12 interaction-energy partition analysis,13 lever electronic parameters,14 and molecular electrostatic potential (MEP),15 have been developed to describe this donor–acceptor interaction in metallic complexes. In addition, the results obtained from spectroscopic measurement, such as infrared stretching frequencies (e.g. Tolman electronic parameter (TEP))7,14a–c and NMR chemical shifts,16 can be used as indicators to evaluate the electronic donation of the ligand, or monitor structural as well as energetic changes in complexes with different ligands. Clot and co-workers calculated the vibrational frequency of CO in [Ni(CO)3L] complexes (L = P-donor ligands) by the B3PW91 method.17 The better the donor ability of phosphine (R3P) in the [Ni(CO)3R3P] complex, the lower the ν(CO) vibration becomes as a result of back-donation from metal d orbitals into the low-lying antibonding πCO* orbital.14a,17 The activation strain model (ASM)18–20 or distortion/interaction model21–23 combined with energy decomposition analysis (EDA)24 provides a quantitative tool to understand the physical factors controlling the bonding energy or activation barrier in reactions. Recently, as a useful approach, a combination of the extended transition state (ETS)13,25 scheme with the natural orbitals for the chemical valence (NOCV)26 method (namely ETS-NOCV scheme) is introduced to metallic complexes as well as organic molecules, offering a compact picture of chemical bond formation and its different components, as well as donor–acceptor properties in the molecular complex.2,27–29 In the combined ETS-NOCV scheme, the orbital interaction energy (ΔEorb) between reacting fragments is expressed in terms of NOCV eigenvalues (νk) as
Understanding the properties of the metal–ligand chemical bond is important for rationalizing and predicting the catalytic performance of N,N′-dioxide–metal complexes and developing new catalysts. To date, only few studies have been reported on the electronic properties of a chelating multidentate ligand as compared to those on mono or bidentate phosphines.14b,30,31 The ranking of the donor ability of the chiral N,N′-dioxide ligand featuring four coordinating end groups still remains a challenge. In our previous calculations,3a,b we studied the influence of the chiral backbone, linkage, and the substituent of aniline in the N,N′-dioxide–Mg(II) catalyst on its reactivity towards a dicarbonyl compound (isatin) and the corresponding chiral inductivity in asymmetric carbonyl–ene reaction. Herein, we changed the substituent of amide in the ligand in the N,N′-dioxide–Sc(III) catalysts to investigate the catalytic behaviour of these catalysts towards three mono-carbonyl compounds (formaldehyde, benzaldehyde, and chalcone) via analysis of the donor–acceptor interaction (Scheme 1). Furthermore, the influence of the counterion from two scandium reagents (Sc(OTf)3 and Sc(OiPr)3) on substrate–catalyst interaction (catalytic abilities) has been explored by the DFT method.
Computational details
Geometry optimization and frequency calculations are performed via density functionary theory (DFT) using the Gaussian 09 program package.32 The M06 hybrid functional33 is adopted, in conjugation with the 6-31+G** basis set.34 Natural bond orbital (NBO)35 analysis is employed to obtain further insight into the electronic properties of the system at the same theoretical level. The results of the activation strain model (ASM) on hexacoordinate chiral N,N′-dioxide–Sc(III) complexes are shown in Tables S1–S3,† in which the reaction energy ΔEr between metal-based fragment and ligand or carbonyl substrate in the complexes is decomposed into two chemical meaningful components: the distortion energy (ΔEstrain) and interaction energy (ΔEint), by Gaussian 09. To understand the factors influencing the donor–acceptor interaction, ΔEint is further decomposed into electrostatic interaction (ΔVelstat), Pauli repulsion (ΔEPauli), and orbital interaction (ΔEoi) (i.e., ΔEint = ΔVelstat + ΔEPauli + ΔEoi) by energy decomposition analysis (EDA). EDA and ETS-NOCV calculations are performed by single-point calculation based on the optimized geometries obtained by Gaussian 09 using the Amsterdam density functional (ADF) program36 at the M06/TZP level. We selected ScCl3 and Sc(OTf)3 compounds as models to examine the multi-reference character of scandium compounds at the CCSD/6-31+G**//M06/6-31+G** level using the Gaussian 09 program. The corresponding T1 diagnostics are predicted to be 0.016 for ScCl3 and 0.018 for Sc(OTf)3, which are smaller than the criteria 0.02, as suggested by Lee and Taylor.37Results and discussion
Donor–acceptor interaction between the ligand and [Sc(OTf)]2+ species
Herein, we studied three Sc(III)-complexes (L–[Sc(OTf)]2+) formed by the coordination of N,N′-dioxide ligand (L1–L3) to [Sc(OTf)]2+ in the gas phase. The corresponding complexes are denoted as L1–Sc(III)–OTf, L2–Sc(III)–OTf, and L3–Sc(III)–OTf for convenience. The coordination processes are exothermic by −275.8 to −290.8 kcal mol−1. As shown in Fig. S1,† the main structural parameters of these three complexes are similar, with the average distances between the four O-donors in the ligands to the Sc cation of 2.066–2.075 Å. NBO analysis indicates that the charge transfer (CT) from ligand to the [Sc(OTf)]2+ moiety exhibits the following trend: L1–Sc(III)–OTf (0.942) > L2–Sc(III)–OTf (0.923) > L3–Sc(III)–OTf (0.913). As a result, the natural population analysis (NPA) of charge accumulated on the Sc(III) centre in L3–Sc(III)–OTf (1.629) is slightly larger than those of L1–Sc(III)–OTf (1.600) and L2–Sc(III)–OTf (1.622). As shown in Table 1, the bonding energy (ΔEBE) for L1–Sc(III)–OTf with an aliphatic cyclohexyl group is higher than those of the complexes containing aromatic substituent ligands (L2 and L3). These results indicate that there exists a strong interaction between L1 and [Sc(OTf)]2+ fragment.| Complex | Chargea | CTb | ΔEPauli | ΔVelstat | ΔEoi | ΔEσorb (1) | ΔEσorb (2) | ΔEBEc |
|---|---|---|---|---|---|---|---|---|
| a NPA charge accumulated on Sc(III) ion in the hexacoordinate complexes.b Charge transfer (CT) from the ligand (L1–L3) to the [Sc(OTf)]2+ fragment.c Bonding energy (BE) between the ligand and the [Sc(OTf)]2+ fragment obtained by ADF calculation. | ||||||||
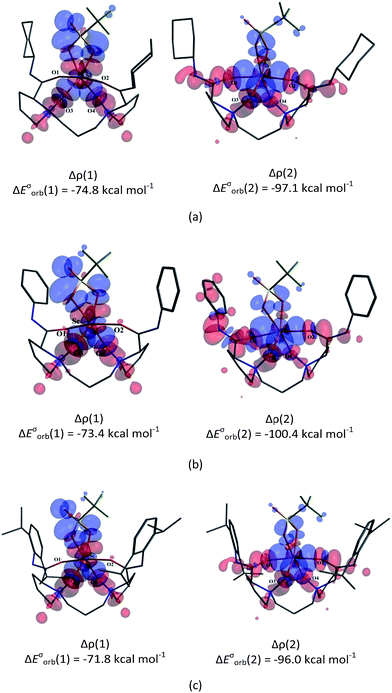
| L1–Sc(III)–OTf | 1.600 | 0.942 | 165.0 | −284.4 | −283.8 | −74.8 | −97.1 | −403.2 |
| L2–Sc(III)–OTf | 1.622 | 0.923 | 163.8 | −272.1 | −284.0 | −73.4 | −100.4 | −392.3 |
| L3–Sc(III)–OTf | 1.629 | 0.913 | 165.3 | −273.1 | −292.7 | −71.8 | −96.0 | −400.6 |
EDA analysis suggests that the electrostatic and orbital interactions are the main contributors for ligand–[Sc(OTf)]2+ interactions in these three complexes. For L1–Sc(III)–OTf, the electron-donating cyclohexyl group enhances the electrostatic interaction between L1 and [Sc(OTf)]2+ fragments (ΔVelstat = −284.4 kcal mol−1), contributing to a more stabilizing interaction energy. For L2–Sc(III)–OTf and L3–Sc(III)–OTf, the ΔVelstat are comparable (−272.1 vs. −273.1 kcal mol−1). Although introduction of ortho-iPr groups into L3 slightly increases the destabilizing ΔEPauli (165.3 kcal mol−1) in L3–Sc(III)–OTf, the more stabilizing orbital interaction (ΔEoi = 292.7 kcal mol−1) compensates for this unfavourable Pauli repulsion. Consequently, the ΔEBE for L3–Sc(III)–OTf is 8.3 kcal mol−1, more stable than that for L2–Sc(III)–OTf.
To quantify the electron-transfer process between ligand and [Sc(OTf)]2+ moieties in these complexes, we visualized the deformation density (Δρ), and the corresponding orbital energies are shown in Fig. 1. Δρ (1) represents the σ-donation from the N-oxide units of the ligand to the unoccupied dx2−y2 orbital of the Sc(III) centre, with ΔEσorb (1) of −71.8 to −74.8 kcal mol−1. For Δρ (2), the electronic density accumulation appears in the coordination region between four O-donors and metal-fragments, thus indicating an electron flow from the ligand to the metal ion to strengthen O–Sc bonding. Interestingly, these effects also weaken the interaction between the counter OTf ion and metal centre, accompanying electronic density flow back from Sc(III) ion to OTf anion. This cooperation effect of coordination units in the chiral N,N′-dioxide–metal complex has also been observed in our previous study.3a
Effect of ligand in the Sc(III)-complex on the activation of CH2O
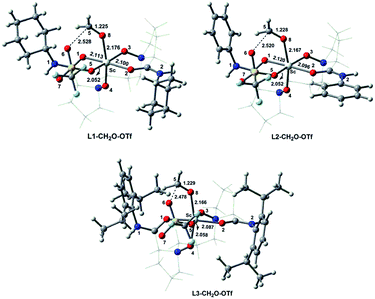
The hexacoordinate complexes (L1–CH2O–OTf, L2–CH2O–OTf, and L3–CH2O–OTf) formed by coordinating formaldehyde (CH2O) to an L–[Sc(OTf)]2+ complex were then investigated. Herein, the counter OTf anion occupies one coordinating site to stabilize the corresponding octahedral geometries (Fig. 2). Compared to free CH2O, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds in these complexes are lengthened by 0.021–0.026 Å. Moreover, the corresponding Wiberg bond indices (WBI) decrease from 1.912 to 1.635–1.654. These results suggest that the C
O bonds in these complexes are lengthened by 0.021–0.026 Å. Moreover, the corresponding Wiberg bond indices (WBI) decrease from 1.912 to 1.635–1.654. These results suggest that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds of CH2O in Lm–CH2O–OTf (m = 1–3) are significantly weakened. The NBO analysis indicates that the charge transfer (CT) occurs from CH2O to a catalyst accompanying the coordination process; this leads to electronic density re-distribution in the CH2O moiety. Consequently, the C
O bonds of CH2O in Lm–CH2O–OTf (m = 1–3) are significantly weakened. The NBO analysis indicates that the charge transfer (CT) occurs from CH2O to a catalyst accompanying the coordination process; this leads to electronic density re-distribution in the CH2O moiety. Consequently, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond becomes more polarized with an increase in dipole moment (from 2.533 Debye in free CH2O to 2.660–2.644 Debye). Accordingly, the C
O bond becomes more polarized with an increase in dipole moment (from 2.533 Debye in free CH2O to 2.660–2.644 Debye). Accordingly, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration frequency (νC
O stretching vibration frequency (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, cm−1) red-shifts from 1864 cm−1 in free CH2O to 1747–1765 cm−1 in the complexes. For L3–CH2O–OTf, the WBI of C
O, cm−1) red-shifts from 1864 cm−1 in free CH2O to 1747–1765 cm−1 in the complexes. For L3–CH2O–OTf, the WBI of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is smaller than those of L1–CH2O–OTf and L2–CH2O–OTf. Moreover, the more negative charge accumulates on the O8 atom (−0.652 vs. −0.621 for L1–CH2O–OTf and −0.630 for L2–CH2O–OTf), which is consistent with the stronger polarity character of the C
O bond is smaller than those of L1–CH2O–OTf and L2–CH2O–OTf. Moreover, the more negative charge accumulates on the O8 atom (−0.652 vs. −0.621 for L1–CH2O–OTf and −0.630 for L2–CH2O–OTf), which is consistent with the stronger polarity character of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and lower νC
O bond and lower νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (1765 cm−1) in the CH2O moiety. These results indicate that the catalyst with the L3 ligand exhibits slightly superior reactivity towards the CH2O substrate.
O (1765 cm−1) in the CH2O moiety. These results indicate that the catalyst with the L3 ligand exhibits slightly superior reactivity towards the CH2O substrate.
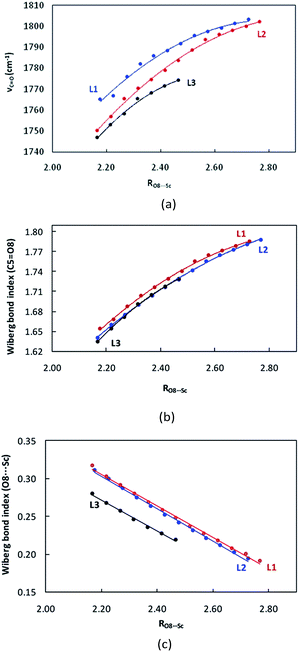
Starting from the optimized structures of the three complexes, we performed the relaxed potential energy surface (PES) scan by increasing the distance between CH2O and Sc(III) centre (RO8⋯Sc, Å) by 0.05 Å at the M06/6-31+G** level. The variation of abovementioned electronic descriptors are shown in Tables S1–S3.† As shown in Fig. 3a and b, νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and the corresponding WBI for the C5
O and the corresponding WBI for the C5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 bond exhibit an increasing tendency with RO8⋯Sc. The corresponding correlation equations are shown in Table 2, with R2 of 0.991–0.997 and 0.999. Although the WBI of the C
O8 bond exhibit an increasing tendency with RO8⋯Sc. The corresponding correlation equations are shown in Table 2, with R2 of 0.991–0.997 and 0.999. Although the WBI of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of the CH2O moiety in L1–CH2O–OTf and L2–CH2O–OTf is comparable (1.654 vs. 1.640), the C
O bond of the CH2O moiety in L1–CH2O–OTf and L2–CH2O–OTf is comparable (1.654 vs. 1.640), the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in L2–CH2O–OTf becomes remarkably less polarized upon lengthening the O8⋯Sc distance. As a result, a steeper variation of νC
O bond in L2–CH2O–OTf becomes remarkably less polarized upon lengthening the O8⋯Sc distance. As a result, a steeper variation of νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is observed for L2–CH2O–OTf (Fig. 3a). Different from νC
O is observed for L2–CH2O–OTf (Fig. 3a). Different from νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, the WBI of O8⋯Sc interaction decreases linearly as the distance between CH2O and catalyst increases (Fig. 3b). Good linear correlations are observed for the three complexes, with an R2 of 0.995–0.997 (Table 3).
O, the WBI of O8⋯Sc interaction decreases linearly as the distance between CH2O and catalyst increases (Fig. 3b). Good linear correlations are observed for the three complexes, with an R2 of 0.995–0.997 (Table 3).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (cm−1), Wiberg bond index (WBI) of C
O (cm−1), Wiberg bond index (WBI) of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the CH2O moiety, the O8⋯Sc interaction as well as ΔEint (kcal mol−1) with O8⋯Sc distance (RO8⋯Sc Å) for L1–CH2O–OTf, L2–CH2O–OTf, and L3–CH2O–OTf complexes
O bond in the CH2O moiety, the O8⋯Sc interaction as well as ΔEint (kcal mol−1) with O8⋯Sc distance (RO8⋯Sc Å) for L1–CH2O–OTf, L2–CH2O–OTf, and L3–CH2O–OTf complexes
| Ligand | Na | Equations | R2 |
|---|---|---|---|
| a Number of data points employed in the correlation. | |||
| L1 | 12 | νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = −96.9 × (RO8⋯Sc)2 + 544.9 × (RO8⋯Sc) + 1037.4 O = −96.9 × (RO8⋯Sc)2 + 544.9 × (RO8⋯Sc) + 1037.4 |
0.991 |
WBIC5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 = −0.227 × (RO8⋯Sc)2 + 1.357 × (RO8⋯Sc) − 0.224 O8 = −0.227 × (RO8⋯Sc)2 + 1.357 × (RO8⋯Sc) − 0.224 |
0.999 | ||
| WBIO8⋯Sc = −0.214 × (RO8⋯Sc) + 0.774 | 0.997 | ||
| ΔEint = 11.6 × (RO8⋯Sc)2 − 34.4 × (RO8⋯Sc) −19.6 | 0.997 | ||
| L2 | 13 | νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = −91.5 × (RO8⋯Sc)2 + 537.3 × (RO8⋯Sc) + 1015.0 O = −91.5 × (RO8⋯Sc)2 + 537.3 × (RO8⋯Sc) + 1015.0 |
0.997 |
WBIC5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 = −0.170 × (RO8⋯Sc)2 + 1.085 × (RO8⋯Sc) + 0.091 O8 = −0.170 × (RO8⋯Sc)2 + 1.085 × (RO8⋯Sc) + 0.091 |
0.999 | ||
| WBIO8⋯Sc = −0.212 × (RO8⋯Sc) + 0.770 | 0.997 | ||
| ΔEint = 9.2 × (RO8⋯Sc)2 − 21.6 × (RO8⋯Sc) − 39.4 | 0.998 | ||
| L3 | 7 | νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = −161.7 × (RO8⋯Sc)2 + 841.1 × (RO8⋯Sc) + 683.4 O = −161.7 × (RO8⋯Sc)2 + 841.1 × (RO8⋯Sc) + 683.4 |
0.995 |
WBIC5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 = −0.355 × (RO8⋯Sc)2 + 1.958 × (RO8⋯Sc) − 0.942 O8 = −0.355 × (RO8⋯Sc)2 + 1.958 × (RO8⋯Sc) − 0.942 |
0.999 | ||
| WBIO8⋯Sc = −0.204 × (RO8⋯Sc) + 0.720 | 0.995 | ||
| ΔEint = 21.7 × (RO8⋯Sc)2 − 80.0 × (RO8⋯Sc) + 27.5 | 0.999 | ||
| Ligand | Substituent | Counterion | Carbonyl substrate | ΔEinta | ΔEstrain | ΔEr | ΔEPauli | ΔVelstat | ΔEoi | ΔEorb (1) | ΔEorb (2) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CAT | Carbonyl substrate | Sum | |||||||||||
| a Interaction energies obtained by ADF are shown in bracket. | |||||||||||||
| L1 | Cyclohexyl | OTf | CH2O | −39.0(−37.0) | 14.4 | 0.7 | 15.0 | −24.0 | 37.1 | −43.6 | −30.5 | −31.5 | −15.6 |
| L2 | Ph | OTf | CH2O | −42.4(−40.8) | 15.0 | 0.8 | 15.8 | −26.6 | 39.6 | −46.6 | −33.8 | −34.5 | −16.8 |
| L3 | 2,6-iPr | OTf | CH2O | −43.6(−41.1) | 19.1 | 0.8 | 20.0 | −23.6 | 40.1 | −47.3 | −33.9 | −34.1 | −18.2 |
| L3 | 2,6-iPr | OiPr | CH2O | −32.6(−30.9) | 2.3 | 0.3 | 2.6 | −30.0 | 22.3 | −34.3 | −18.9 | −25.7 | −3.3 |
| L3 | 2,6-iPr | OTf | PhCHO | −56.4(−53.1) | 20.0 | 2.0 | 22.0 | −34.4 | 42.7 | −56.8 | −39.0 | −34.4 | −21.6 |
| L3 | 2,6-iPr | OTf | Chalcone | −71.7(−67.0) | 21.7 | 4.6 | 26.3 | −45.4 | 47.7 | −65.7 | −49.0 | −33.5 | −27.0 |
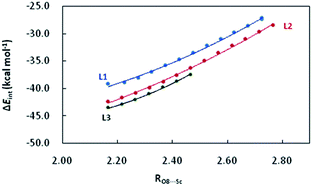
Activation strain model (ASM) analysis indicates that the interaction energy term ΔEint makes a major contributions to the CH2O–L–[Sc(OTf)]2+ interaction in the three abovementioned complexes as compared to the deformation energy ΔEstrain. Furthermore, the deformation energies of the metal-fragment (ΔEstrain(CAT)) are significantly more destabilizing than that of the CH2O fragment (ΔEstrain(CH2O)). Similarly, there also exist good correlations between RO8⋯Sc and ΔEint, with the coefficient of 0.997–0.999 (Fig. 4). Compared to that in L1–CH2O–OTf and L2–CH2O–OTf, ΔEint in L3–CH2O–OTf is clearly more stabilizing at any given point along the O8⋯Sc distance; this indicates the stronger donor–acceptor interaction between CH2O and L3–[Sc(OTf)]2+ moiety, as well as Lewis acidity of Sc(III) ion in L3–CH2O–OTf. These results are in good agreement with a larger electron-deficient character for the Sc(III) centre in L3–CH2O–OTf (NPA charge accumulated on Sc(III) cation is 1.647). Although the ortho-iPr groups in ligand L3 increase the Pauli repulsion between CH2O and Sc-fragment (ΔEPauli = 40.1 kcal mol−1), the more stabilizing energies (electrostatic interaction ΔVelstat and orbital interaction ΔEoi) compensates for this destabilizing steric repulsion; this leads to a more stabilizing ΔEint (−41.1 kcal mol−1). Compared to the case of L3–Sc(III)–OTf, the orbital interaction ΔEoi between the CH2O-fragment and Sc(III)-fragment is smaller than electrostatic energy ΔVelstat by 13.4 kcal mol−1 (−33.9 vs. −47.3 kcal mol−1) in L3–CH2O–OTf. Therefore, the electrostatic interaction is the major driving force to form L3–CH2O–OTf by interaction between CH2O and L3–[Sc(OTf)]2+ moiety.
For L1, the electron-donating cyclohexyl groups in the amide units enhance the electronic density transfer from the ligand to the Sc(III) center in the L1–CH2O–OTf complex; this decreases the Lewis acidity of metal ion (ΔEint = −37.0 kcal mol−1). As expected, both ΔVelstat and ΔEoi are less stabilizing than those in L3–CH2O–OTf by 3.7 and 3.4 kcal mol−1, respectively. With respect to L2, the phenyl group on the right brachial amide tends to be placed in the same plane to the carbonyl of amines in L2–CH2O–OTf. A good conjugate effect between the phenyl group and carbonyl of amines compensates for the electronic-deficient character of Sc(III) cation in L2–CH2O–OTf by strengthening the electron density transfer from ligand to metal, decreasing the stabilizing attracting term (ΔVelstat and ΔEoi) between CH2O-fragment and Sc(III)-fragment by 1.5 kcal mol−1. As a result, the ΔEint of L2–CH2O–OTf is less stabilizing than that of L3–CH2O–OTf (−40.8 vs. −41.1 kcal mol−1).
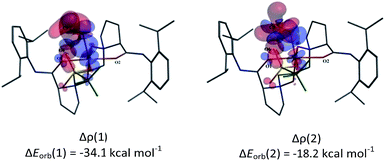
We visualized the deformation density associated with the orbital interaction between CH2O and the Sc(III)-based fragments in the three complexes. The two dominating components of deformation density, Δρ (1) and Δρ (2), with the corresponding energy values are presented in Fig. 5 and S3.† As shown in Fig. 5, the accumulation of electron density appears in the region between the O8 atom and the scandium centre in L3–CH2O–OTf; this indicates electrons flowing from σ-donor O lone electron pair of CH2O to unoccupied d orbital of Sc(III) ion to form the Sc–O bond. Simultaneously, the depletion of electron density on π double C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of CH2O suggests the weakening of π bonds in CH2O. With respect to the second NOCV-based deformation density contribution Δρ (2), it presents 36% of the interfragment orbital interaction, accompanying the weakening of C–H as well as C
O bond of CH2O suggests the weakening of π bonds in CH2O. With respect to the second NOCV-based deformation density contribution Δρ (2), it presents 36% of the interfragment orbital interaction, accompanying the weakening of C–H as well as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds in CH2O. In addition, the slight electronic density accumulation between the O6 atom of OTf anion and the C8 atom of CH2O stabilizes the hexacoordinate complexes, further favouring the activation of CH2O. Similar results are obtained for L1–CH2O–OTf and L2–CH2O–OTf, as shown in Fig. S3 in the ESI.†
O bonds in CH2O. In addition, the slight electronic density accumulation between the O6 atom of OTf anion and the C8 atom of CH2O stabilizes the hexacoordinate complexes, further favouring the activation of CH2O. Similar results are obtained for L1–CH2O–OTf and L2–CH2O–OTf, as shown in Fig. S3 in the ESI.†
As shown in Table S4 and Fig. S4 in the ESI,† CDA analysis indicates that the main molecular orbital involving the donor–acceptor interaction and electronic density transfer between CH2O and L3–Sc(III) in the L3–CH2O–OTf complex is the occupied HOMO-146 orbital. It is constructed from the HOFO-5 of CH2O fragment and LUFO-2, LUFO-3, and LUFO-6 orbitals of the L3–Sc(III) fragment. The HOFO-5 is the hybridized orbital of σ(CH2) and s atomic orbital of CH2O. The total contribution of LUFO orbitals in the L3–Sc(III) fragment is smaller than that of the HOFO-5 of CH2O moiety by 53.2% (66.4% vs. 13.2%). Interestingly, the contribution of the unoccupied orbital in the Sc(III)-based fragment decreases in the order of L3 > L2 > L1, which is in good agreement with electron density transfer from CH2O to catalysts. Thus, the combination of stronger electrostatic interactions and the more stabilizing orbital interaction contributes to the superior reactivity of L3–[Sc(OTf)]2+ towards CH2O.
Effect of counterion on the activation of CH2O
To understand the effect of counterion in the catalyst on Lewis acidity of the metal ion as well as the activation of carbonyl, we replaced the OTf anion in L3–CH2O–OTf with iso-propoxy ion (OiPr). The corresponding optimized geometries of the hexacoordinate complexes L3–CH2O–OiPr are shown Fig. 6. Compared to those for L3–CH2O–OTf, the O8⋯Sc distances are longer by 0.094 Å for L3–CH2O–OiPr. Furthermore, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length of CH2O follows the order L3–CH2O–OTf > L3–CH2O–OiPr. This result indicates that CH2O becomes less weakened in L3–CH2O–OiPr. The O5–Sc distance in L3–CH2O–OiPr is shorter significantly than those of L3–CH2O–OTf (1.862 Å vs. 2.058 Å); this indicates a stronger interaction between OiPr and Sc(III) centre. This result could be attributed to the stronger basicity of OiPr anion than that of OTf anion. Suffering large steric repulsion from OiPr, tetradentate N,N-dioxide ligand moves slightly far away from the metal centre. Accordingly, the average O–Sc distance in ligand in L3–CH2O–OiPr is as long as 2.131 Å. This effect also weakens the coordinate interaction of CH2O to Sc(III) ion; this leads to the less stabilizing ΔVelstat (−34.3 kcal mol−1) and ΔEoi (−18.9 kcal mol−1). NBO analysis indicate that the energy level of LUMO orbitals in two complexes has the order of L3–CH2O–OiPr > L3–CH2O–OTf. Accordingly, the electrophilic indices ω of complexes are 9.4 eV for L3–Sc(III)–OTf and 8.1 eV for L3–Sc(III)–OiPr. Similar to the case of L3–CH2O–OTf, the ΔVelstat is still a major contributor in L3–CH2O–OiPr, which is also confirmed by AIM analysis (Fig. 6). The positive Laplacian of electronic density ∇2ρ at (3, −1) bonding critical points (a and b) is observed between CH2O or OiPr ion to metal centre, which is similar to that of L3–CH2O–OTf in Fig. S5.† Furthermore, ΔEint exhibits the following order L3–CH2O–OTf > L3–CH2O–OiPr, which is in good agreement with the abovementioned results of electrophilic indices. The inferior reactivity of the catalyst with Sc(OiPr)3 as a precursor was also observed in the experiments.3d Therefore, the counter ion could adjust the electrophilicity of the Sc(III)-complex by affecting ΔVelstat and ΔEoi. The Lewis acidity of Sc(III) ion in L3–CH2O–OTf is stronger than that of L3–CH2O–OiPr, consequently, exhibiting high reactivity towards the nucleophilic CH2O substrate.
O bond length of CH2O follows the order L3–CH2O–OTf > L3–CH2O–OiPr. This result indicates that CH2O becomes less weakened in L3–CH2O–OiPr. The O5–Sc distance in L3–CH2O–OiPr is shorter significantly than those of L3–CH2O–OTf (1.862 Å vs. 2.058 Å); this indicates a stronger interaction between OiPr and Sc(III) centre. This result could be attributed to the stronger basicity of OiPr anion than that of OTf anion. Suffering large steric repulsion from OiPr, tetradentate N,N-dioxide ligand moves slightly far away from the metal centre. Accordingly, the average O–Sc distance in ligand in L3–CH2O–OiPr is as long as 2.131 Å. This effect also weakens the coordinate interaction of CH2O to Sc(III) ion; this leads to the less stabilizing ΔVelstat (−34.3 kcal mol−1) and ΔEoi (−18.9 kcal mol−1). NBO analysis indicate that the energy level of LUMO orbitals in two complexes has the order of L3–CH2O–OiPr > L3–CH2O–OTf. Accordingly, the electrophilic indices ω of complexes are 9.4 eV for L3–Sc(III)–OTf and 8.1 eV for L3–Sc(III)–OiPr. Similar to the case of L3–CH2O–OTf, the ΔVelstat is still a major contributor in L3–CH2O–OiPr, which is also confirmed by AIM analysis (Fig. 6). The positive Laplacian of electronic density ∇2ρ at (3, −1) bonding critical points (a and b) is observed between CH2O or OiPr ion to metal centre, which is similar to that of L3–CH2O–OTf in Fig. S5.† Furthermore, ΔEint exhibits the following order L3–CH2O–OTf > L3–CH2O–OiPr, which is in good agreement with the abovementioned results of electrophilic indices. The inferior reactivity of the catalyst with Sc(OiPr)3 as a precursor was also observed in the experiments.3d Therefore, the counter ion could adjust the electrophilicity of the Sc(III)-complex by affecting ΔVelstat and ΔEoi. The Lewis acidity of Sc(III) ion in L3–CH2O–OTf is stronger than that of L3–CH2O–OiPr, consequently, exhibiting high reactivity towards the nucleophilic CH2O substrate.
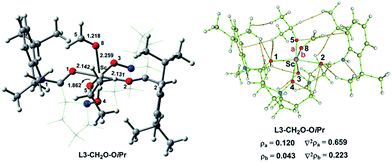 | ||
| Fig. 6 Optimized geometry and AIM analysis of hexacoordinate L3–CH2O–OiPr. Selected bond lengths are in Å. The chiral backbone in the ligand is shown in grey colour for clarity. | ||
Variation of the carbonyl substrate
We used two more carbonyl substrates (PhCHO and chalcone) to further evaluate the reactivity of L3–[Sc(OTf)]2+. The optimized geometries for the hexacoordinate complexes L3–PhCHO–OTf and L3–chalcone–OTf are shown in Fig. 7. As shown in Table S5,† NBO analysis indicates that more negative charges accumulated on the O atom of free PhCHO or chalcone substrates because of electron delocalization of the adjacent phenyl ring (−0.561 and −0.597 vs. −0.533 in CH2O). Consequently, the nucleophilicity of PhCHO and chalcone is significantly enhanced to 2.02 and 2.81 eV, respectively, as compared to that of CH2O (1.73 eV). This effect favours the coordination interaction between PhCHO or chalcone and Sc(III) centre, with shorter O8⋯Sc distances of 2.114 Å for L3–PhCHO–OTf and 2.058 Å for L3–chalcone–OTf, respectively. EDA analysis indicates that the interaction energies ΔEint between carbonyl substrates and scandium-based fragment are −53.1 kcal mol−1 for L3–PhCHO–OTf and −67.0 kcal mol−1 for L3–chalcone–OTf, which are more stabilizing than that of L3–CH2O–OTf (−41.1 kcal mol−1, Table S3†). Furthermore, the NOCV deformation density as well as the corresponding energy ΔEσorb = ΔEorb (1) + ΔEorb (2) for L3–PhCHO–OTf and L3–chalcone–OTf complexes are higher than that of L3–CH2O–OTf (56.0 and 60.5 kcal mol−1 vs. 52.3 kcal mol−1). These results indicate that L3–[Sc(OTf)]2+ exhibits higher reactivity for PhCHO and chalcone substrates as compared to that for CH2O. Contrary to PhCHO, the chalcone with a more significant π-conjugated structure tends to coordinate to L3–[Sc(OTf)]2+, with most stabilizing ΔVelstat (−65.7 kcal mol−1) and ΔEoi (−49.0 kcal mol−1) for carbonyl–Sc(III)–fragment interaction. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds of PhCHO and chalcone in these complexes are lengthened by 0.039 and 0.044 Å, with ΔνC
O bonds of PhCHO and chalcone in these complexes are lengthened by 0.039 and 0.044 Å, with ΔνC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O of 149.3 and 200.5 cm−1, respectively, indicating that C
O of 149.3 and 200.5 cm−1, respectively, indicating that C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds are activated significantly in L3–PhCH2O–OTf and L3–chalcone–OTf. These results are in good agreement with the excellent reactivity of chiral N,N′-dioxide–Sc(III) catalysts for the transformation of chalcone or PhCHO substrates in organometallic catalysis.1a,b
O bonds are activated significantly in L3–PhCH2O–OTf and L3–chalcone–OTf. These results are in good agreement with the excellent reactivity of chiral N,N′-dioxide–Sc(III) catalysts for the transformation of chalcone or PhCHO substrates in organometallic catalysis.1a,b
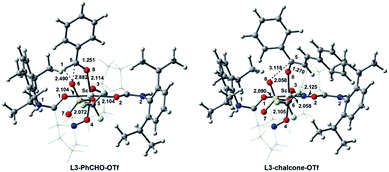 | ||
| Fig. 7 Optimized geometries of the hexacoordinate complexes L3–PhCHO–OTf and L3–chalcone–OTf. Selected bond lengths are in Å. The chiral backbone in ligands is shown in grey colour for clarity. | ||
Conclusions
Theoretical investigation on donor–acceptor interaction between a ligand and carbonyl compound with a metal ion in N,N′-dioxide–Sc(III) complex is performed using the DFT method. The effect of the substituent of the ligand and counter ion on Lewis acidity as well as the reactivity of the Sc(III)-complex towards carbonyl compound is studied. These calculations reveal the following conclusions:(1) The orbital attraction is the major contributor to the interaction between the chiral N,N′-dioxide ligand and Sc(III)-based fragment in the L–[Sc(OTf)]2+ complex. The ligand with the cyclohexyl group in amide exhibits a stronger coordination ability towards the Sc(III) centre as compared to the ligands with an aromatic ring.
(2) The electrostatic interaction is the major driving force to form a hexacoordinate complex by interaction between CH2O and L3–[Sc(OTf)]2+ moiety. Variation of amide moiety in substituents of the ligands adjusts electrostatic energy as well as orbital energy between CH2O and L–[Sc(OTf)]2+ fragment in hexacoordinate complexes, affecting the activation of carbonyl compound. The combination of stronger ΔVelstat and more stabilizing ΔEoi contributes to the high catalytic performance of complex with a 2,6-diisopropylphenyl group towards CH2O.
(3) The counter anion in the complex tunes the energy level of the LUMO orbital of N,N′-dioxide–Sc(III) complex; this affects the electrophilicity of the L–Sc(III)-complex towards the carbonyl substrate. The Lewis acidity of the metal ion in the complex could be adjusted by changing Pauli repulsion, electrostatic, as well as orbital interaction between the carbonyl compound and metal centre.
(4) PhCHO and chalcone with high nucleophilicity exhibit excellent reactivity in the presence of L–[Sc(OTf)]2+ complex; this may be related to more stabilizing electrostatic and orbital interaction. The activation process accompanies with more significantly electron density transfer from a carbonyl compound to a Sc-based fragment.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the National Natural Science Foundation of China (No. 21290182, 21321061 and 21572141), 111 Project (B17030) and the Program for New Century Excellent Talents in the University of China (No. NCET-13-0390) for providing the financial support. We thank Prof. X. M. Feng and Prof. X. H. Liu for helpful discussions.Notes and references
- (a) X. H. Liu, L. L. Lin and X. M. Feng, Acc. Chem. Res., 2011, 44, 574 CrossRef CAS PubMed; (b) X. H. Liu, L. L. Lin and X. M. Feng, Org. Chem. Front., 2014, 1, 298 RSC; (c) K. Shen, X. H. Liu, L. L. Lin and X. M. Feng, Chem. Sci., 2012, 3, 327 RSC; (d) X. H. Liu, H. F. Zheng, Y. Xia, L. L. Lin and X. M. Feng, Acc. Chem. Res., 2017, 50, 2621 CrossRef CAS PubMed.
- M. Fusè, I. Rimoldi, E. Cesarotti, S. Rampino and V. Barone, Phys. Chem. Chem. Phys., 2017, 19, 9028 RSC.
- (a) J. M. Wang, Z. S. Su, N. Yang and C. W. Hu, J. Org. Chem., 2016, 81, 6444 CrossRef CAS PubMed; (b) J. M. Wang, Y. N. Zuo, C. W. Hu and Z. S. Su, Catal. Sci. Technol., 2017, 7, 2183 RSC; (c) Y. N. Zuo, Z. S. Su, J. M. Wang and C. W. Hu, Catal. Today, 2017, 298, 130–137 CrossRef CAS; (d) Q. Zhang, X. Xiao, L. L. Lin, X. H. Liu and X. M. Feng, Org. Biomol. Chem., 2011, 9, 5748 RSC; (e) Y. Y. Chu, X. H. Liu, W. Li, X. L. Hu, L. L. Lin and X. M. Feng, Chem. Sci., 2012, 3, 1996 RSC; (f) M. S. Xie, X. H. Liu, Y. Zhu, X. H. Zhao, Y. Xia, L. Lin and X. M. Feng, Chem.–Eur. J., 2011, 17, 13800 CrossRef CAS PubMed.
- M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, 18, C71–C79 Search PubMed.
- J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 3, 2939 RSC.
- M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576 CrossRef CAS.
- G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717 CrossRef CAS PubMed.
- S. Dapprich and G. Frenking, J. Phys. Chem., 1995, 99, 9352 CrossRef CAS.
- A. W. Ehlers, S. Dapprich, S. F. Vyboishchikov and G. Frenking, Organometallics, 1996, 15, 105 CrossRef CAS.
- G. Frenking, K. Wichmann, N. Fröhlich, J. Grobe, W. Golla, D. Le Van, B. Krebs and M. Läge, Organometallics, 2002, 21, 2921 CrossRef CAS.
- V. Tognetti, L. Joubert, P. Cortona and C. Adamo, J. Phys. Chem. A, 2009, 113, 12322 CrossRef CAS PubMed.
- Y. Mo, J. Gao and S. D. Peyerimhoff, J. Chem. Phys., 2000, 112, 5530 CrossRef CAS.
- T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755 CrossRef CAS.
- (a) C. A. Tolman, Chem. Rev., 1977, 77, 313 CrossRef CAS; (b) N. Fey, Dalton Trans., 2010, 39, 296 RSC; (c) S. L. Mukerjee, S. P. Nolan, C. D. Hoff and R. L. Delavega, Inorg. Chem., 1988, 27, 81 CrossRef CAS; (d) N. Fey, A. G. Orpen and J. N. Harvey, Coord. Chem. Rev., 2009, 253, 704 CrossRef CAS.
- (a) C. H. Suresh and N. Koga, Inorg. Chem., 2002, 41, 1573 CrossRef CAS PubMed; (b) O. Kühl, Coord. Chem. Rev., 2005, 249, 693 CrossRef; (c) D. J. Nelson and S. P. Nolan, Chem. Soc. Rev., 2013, 42, 6723 RSC.
- (a) F. Cheng, A. L. Hector, W. Levason, G. Reid, M. Webster and W. Zhang, Inorg. Chem., 2010, 49, 752 CrossRef CAS PubMed; (b) Q. Teng and H. V. Huynh, Inorg. Chem., 2014, 53, 10964 CrossRef CAS PubMed; (c) H. V. Huynh, Y. Han, R. Jothibasu and J. A. Yang, Organometallics, 2009, 28, 5395 CrossRef CAS; (d) K. Verlinden, H. Buhl, W. Frank and C. Ganter, Eur. J. Inorg. Chem., 2015, 2416 CrossRef CAS.
- L. Perrin, E. Clot, O. Eisenstein, J. Loch and R. H. Crabtree, Inorg. Chem., 2001, 40, 5806 CrossRef CAS PubMed.
- W. J. van Zeist, R. Visser and F. M. Bickelhaupt, Chem.–Eur. J., 2009, 15, 6112 CrossRef CAS PubMed.
- I. Fernandez and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953 RSC.
- I. Fernandez, Phys. Chem. Chem. Phys., 2014, 16, 7662 RSC.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646 CrossRef CAS PubMed.
- X. Hong, Y. Liang, A. K. Griffith, T. H. Lambert and K. N. Houk, Chem. Sci., 2014, 5, 471 RSC.
- Y. F. Yang, Y. Liang, F. Liu and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 1660 CrossRef CAS PubMed.
- M. von Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1 CrossRef CAS.
- (a) A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933 CrossRef CAS PubMed; (b) A. Michalak, M. Mitoraj and T. Ziegler, J. Mol. Model., 2008, 14, 681 CrossRef PubMed.
- (a) M. Mitoraj, M. Parafiniuk, M. Srebro, M. Handzlik, A. Buczek and A. Michalak, J. Mol. Model., 2011, 17, 2337 CrossRef CAS PubMed; (b) M. Mitoraj, J. Phys. Chem. A, 2011, 115, 14708 CrossRef CAS PubMed; (c) R. Kurczab, M. Mitoraj, A. Michalak and T. Ziegler, J. Phys. Chem. A, 2010, 114, 8581 CrossRef CAS PubMed; (d) G. A. Ardizzoia, M. Bea, S. Brenna and B. Therrien, Eur. J. Inorg. Chem., 2016, 3829 CrossRef CAS.
- M. Hamdaoui, M. Ney, V. Sarda, L. Karmazin, C. Ailly, N. Ieffert, S. Dohm, A. Hansen, S. Grimme and J. P. Djukic, Organometallics, 2016, 35, 2207 CrossRef CAS.
- M. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962 CrossRef CAS PubMed.
- Y. Canac and C. Lepetit, Inorg. Chem., 2017, 56, 667 CrossRef CAS PubMed.
- C. Flener Lovitt, G. Frenk and G. S. Girolami, Organometallics, 2012, 31, 4122 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Akatsuji, M. Aricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed.
- (a) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294 CrossRef CAS; (b) V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- E. J. Baerends, T. Ziegler, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. vanFaassen, L. Fan, T. H. Fischer, C. F. Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. V. D. Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. V. Kessel, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. V. Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodríguez, P. Ros, P. R. T. Schipper, H. V. Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Swart, D. Swerhone, G. T. Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF2016, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- (a) W. Y. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460 CrossRef CAS PubMed; (b) T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Quantum Chem. Symp., 1989, S23, 199 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of all stationary points and energies; selected geometric and electronic parameters as well as results of for ETS-NOCV analysis Sc(III)-complexes. See DOI: 10.1039/c7ra12258f |
| This journal is © The Royal Society of Chemistry 2017 |