Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sol–gel synthesis of Sr1−xYbxF2+x nanoparticles dispersible in acrylates†
L. Schmidt,
St. Mahn and
E. Kemnitz *
*
Humboldt-Universität zu Berlin, Department of Chemistry, Brook-Taylor-Straße 2, 12489 Berlin, Germany. E-mail: erhard.kemnitz@chemie.hu-berlin.de
First published on 13th December 2017
Abstract
A new approach to prepare nanoparticles in SrF2-YbF3 systems via the fluorolytic sol–gel synthesis is presented. A series of Sr1−xYbxF2+x (0.12 < x < 0.62) nanoparticles of nonstoichiometric fluorite phases obeying Vegard's law throughout the homogeneity area have been successfully prepared at room temperature. For all Yb concentrations XRD patterns show the formation of cubic phases. For higher Yb concentration (>50 mol%) crystallite sizes decrease abruptly in comparison to lower Yb concentrations (<50 mol%) as detected by XRD. The obtained sols are highly transparent. The investigations by DLS and TEM revealed the presence of monodisperse sol particles with sizes in the lower nm range (∼5 nm). The nanoparticles are characterized by a wide range of homogeneity (up to approx. 60 mol% Yb) and show promise of a wide range of applicability in the areas of medicine, dentistry and optics.
At present, there is great interest in luminescent lanthanide doped nanoparticles for efficient frequency conversion from infrared (IR) to visible (VIS) radiation. Particularly because a visible source pumped by a near infrared (NIR) laser is useful for high-capacity data storage optical devices.1 This process can be obtained by upconversion mechanisms.2 Upconversion nanoparticles emit detectable photons of higher energy in the short wavelength range upon irradiation with near-infrared (NIR) light. Several infrared photons can be absorbed by the material doped with rare earth ions (RE) in order to populate more energetic levels. The use of long lifetime and real ladder-like energy levels of trivalent lanthanide ions embedded in an appropriate inorganic host lattice can produce higher energy luminescence. In recent years, the application of rare earth doped alkaline earth metal fluoride nanoparticles (MF2:RE, M = Ca, Sr, Ba) has attracted the interest of researchers for the possibility of using them as optical labels in medical diagnostics and imaging.2 In order to be successfully employed in in vivo studies, however, the nanoparticles must be efficiently dispersible in physiological solutions.3 In many cases this is a challenging task, as nanoparticles in water have a higher tendency to agglomerate to a larger size and precipitate out of solution. The stability of colloidal dispersed particles depends on the relative magnitude of the forces of attraction and the forces of repulsion. A method to enhance the stabilization of nanoparticles and prevent the formation of precipitates that enhance the sedimentation is the functionalization of particles with hydrophilic capping agents in order to reduce attractive forces between particle surfaces. The most popular methods described in the literature to prepare upconversion nanoparticles are the thermolysis strategy and the hydro(solvo)thermal synthesis with the assistance of surfactants.2,4 In some cases, hydrophilic ligands such as citric acid,3 ethylenediaminetetraacetic acid (EDTA) and (poly)acrylic acid5 are used providing good water solubility. Therefore only very few reports exist in the literature on upconverting nanoparticles directly dispersible in water solution.
Since rare earth doped particles (MF2:RE) are known to emit VIS light under near infrared (NIR) excitation by an upconversion process, they are of great interest in light-curable polymers commonly used in restorative dentistry.6 Usually, light-curing dental filling materials consist of a dimethacrylate monomer, inorganic fillers and a photo-initiator. A blue visible light (420–470 nm) is required for initiating the polymerization process.7 However, despite their widespread application, polymerization shrinkage and a partly incomplete curing is a drawback of these materials. The curing in deep cavities is limited by the penetration depth of the blue light in the tooth structure and the composite itself. Since dental composites also contain a large amount of inorganic fillers (up to 50 vol%) transmittance of VIS, is scattered strongly resulting in shallow curing depths. For this reason, the multilayered technique for the restoration of deep cavities is required. This in turn often requires the destruction of healthy tooth structures. An efficient polymerization by deeply penetrating NIR light can be achieved by embedding upconversion nanoparticles in the monomer matrix.6,7 Furthermore, by using nanoscopic fluorides of alkaline earth metals and rare earth metals as fillers one can improve the cariostatic properties of dental composites and at the same time to provide an increase in X-ray efficiency of such materials. Therefore, nanoparticles of Sr1−xYbxF2+x solid-solutions in SrF2-YbF3 systems are promising materials in terms of dental applications due to their anticariogenic effect, the ability to provide radiopacity to the dental material as well as, doped with Er3+, to improve the polymerization of dental composites. Solid solutions and Sr1−xYbxF2+x nonstoichiometric fluorite phases have been known for decades.8–12 However, the syntheses were carried out at high temperatures resulting in single crystals which allows a thoroughly investigation of the materials. With continuously increasing interest in nanomaterials many synthetic strategies were developed to prepare nanoscopic particles of solid solutions according the requirements for the desired materials.13–17 A challenge represents the synthesis of monodisperse nanoparticles with particle sizes in the lower nanometer range, which are important for further processing.
In this study we present an elegant and easy approach to synthesize Sr1−xYbxF2+x solid-solution nanoparticles homogeneously dispersed in water, which makes them suitable for medical applications. A series of solid solution nanoparticles with various mean crystallite sizes were successfully prepared by the fluorolytic sol–gel route.18,19 X-ray powder diffraction (XRD), dynamic light scattering (DLS) and transmission electron microscopy (TEM) were used to characterize the particles according to their particle size, crystallite size as well as to study the ageing process and crystallite size dependency with increasing ytterbium concentration. The fluorolytic sol–gel synthesis was carried out dissolving acetates of Sr and Yb in water and adding non-aqueous methanolic HF solution (full experimental procedure is available in the ESI†). However, it has to be noted, that by using aqueous HF immediate sedimentation was observed. Apparently, by using alcoholic HF solution we influence the kinetics of fluorolysis and formation of particles and therefore their stability. Furthermore, the formed nanoparticles show a lower solubility in alcoholic solutions as compared to aqueous solutions which has an impact on their solubility product during the formation. The XRD pattern (Fig. 1) of Sr1−xYbxF2+x phases prepared via the fluorolytic sol–gel synthesis show significant reflections which can be clearly assigned to the crystallographic planes of cubic SrF2. There is a slight shift in the XRD peaks towards higher angles. This shift is believed to result from the incorporation of Yb ions into the SrF2 lattice, and the smaller ionic radius of Yb3+ (0.985 Å) as compared to that of Sr2+ (1.26 Å).20 The incorporation of the smaller cation leads to smaller lattice constants as compared to the pure SrF2, which causes the shift to higher angles.17 A series of Sr1−xYbxF2+x nanoparticles with different Yb concentrations (0.12 < x < 0.62) was prepared and characterized by XRD. The results calculated from XRD patterns concerning lattice constants, crystallite sizes and Yb concentrations are given in Table 1. The calculation of the lattice constant a of the crystallographic unit cell in the cubic system for each sample was carried out using the Bragg equation:
| A = a0 + kx |
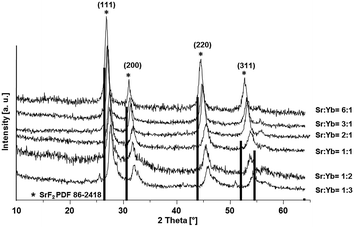 | ||
| Fig. 1 XRD patterns of Sr1−xYbxF2+x (0.12 < x < 0.62) phases obtained via the fluorolytic sol–gel synthesis. | ||
Sr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Yb Yb |
Yb concentration in Sr1−xYbxF2+x th. exp. | Lattice constant a [Å] | Crystallite size [nm] | |
|---|---|---|---|---|
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14% | 12% | 5.753 | 10 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
16% | 17% | 5.737 | 9 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
20% | 15% | 5.744 | 10 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
25% | 21% | 5.726 | 10 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
33% | 31% | 5.694 | 10 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
50% | 51% | 5.630 | 7 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
— | 53% | 5.625 | 6 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
— | 62% | 5.595 | — |
It can also be observed from Fig. 1 that there is a slight shift in the XRD peak position towards higher angles with increase in Yb concentration, resulting in change in the lattice constant. Broad diffraction peaks in the patterns are in agreement with the characteristics of nanosized materials. Fig. 2 shows the lattice constant a as a function of different Yb concentrations. Lattice constants decrease with increase in the Yb concentration perfectly obeying Vegard's law.22 Moreover, this also reflects that Yb3+ ions were substituted in the SrF2 lattice without changing the symmetry of the cubic structure.
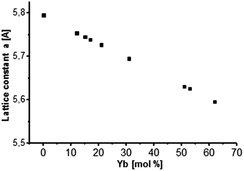 | ||
| Fig. 2 Lattice constant a as a function of Yb concentration incorporated into the cubic SrF2 lattice. A behavior according to Vegard's law is indicated. | ||
Crystallite sizes of the obtained samples were estimated from the full width at half maximum (FWHM) of the most distinct XRD reflections (111), (220) and (311) using the Scherrer equation.23 Here, we found that for samples with Yb concentrations of <50 mol% the calculated mean crystallite size is approx. 10 nm. For samples with Yb concentrations of >50 mol% the mean crystallite size decreases abruptly to approx. 6 nm indicating the formation of smaller primary particles with increasing Yb concentration in the sample.
A transparent sol was obtained at Sr-to-Yb molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
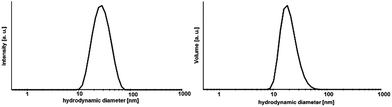
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The determination of the hydrodynamic particle diameter by means of DLS (Fig. 3) shows for the 0.2 M sol with a dynamic viscosity of 1.1 mPa s a monodisperse particle size distribution with a maximum at about 30 nm. Since DLS only provides hydrodynamic diameters and the crystallite sizes according the Scherrer equation give only estimated values TEM was used in order to determine and to provide additional information with respect to the particle size, shape and morphology as well as to prove the crystallinity of the particles. Fig. 4 shows the high resolution TEM image (HRTEM) of a TEM grid dip-coated into a 0.2 M transparent Sr1−xYbxF2+x (x = 0.53) sol. It shows a certain degree of agglomeration of several primary particles. Lattice plane distances can be clearly recognized proving the crystallinity of the particles. The measured lattice plane distances are consistent with the calculated lattice spacings for the nonstoichiometric phase Sr1−xYbxF2+x with x = 0.53 confirming the formation of this phase. From the evaluation of an isolated particle the average particle size can be estimated to be ∼5 nm. The formation of core–shell structured particles can be excluded as no amorphous shells or a difference by material contrast of isolated particles can be observed by TEM. The same sample was then treated at 300 °C in order to remove residual organic and investigated by TEM, subsequently. It seems that the particles have been undergoing a homogenization process at higher temperatures. In the HRTEM image large particles can be seen having the same orientation as well as an amorphous shell. The measured lattice space distances are in good agreement with the calculated lattice plane distances leading to the conclusion that the expected compound is formed. Overall, TEM revealed the presence of agglomerates with sizes of approx. 30 nm, consisting of smaller (∼5 nm) and larger primary particles (∼10 nm). To gain more information about the amorphous layer, STEM (scanning TEM) was used. The image of the particles in the STEM mode (Fig. S1, ESI†) shows the agglomeration of these larger units. The sample is very well structured. The element distribution was determined using EDXS in selected regions of the sample. A homogeneous distribution of the elements Sr, Yb and F was detected. The amorphous region of the sample consists exclusively of carbon and oxygen. No other elements were detected in this area. Since both carbon and oxygen are also detected in the crystalline region, it can be concluded that the sample still contains residual organics, which was supplied either during the synthesis or could not be removed in the course of preparation of the TEM grid. Therefore, the formation of core–shell particles cannot be assigned. However, utilizing TEM in combination with XRD and DLS, the formation of non-stoichiometric phase of the composition Sr1−xYbxF2+x (x = 0.53) as a highly transparent aqueous sol with particle sizes in the lower nanometer range was proven. Samples with different Yb concentrations are of nanocrystalline character but are obtained as nanopowders.
2. The determination of the hydrodynamic particle diameter by means of DLS (Fig. 3) shows for the 0.2 M sol with a dynamic viscosity of 1.1 mPa s a monodisperse particle size distribution with a maximum at about 30 nm. Since DLS only provides hydrodynamic diameters and the crystallite sizes according the Scherrer equation give only estimated values TEM was used in order to determine and to provide additional information with respect to the particle size, shape and morphology as well as to prove the crystallinity of the particles. Fig. 4 shows the high resolution TEM image (HRTEM) of a TEM grid dip-coated into a 0.2 M transparent Sr1−xYbxF2+x (x = 0.53) sol. It shows a certain degree of agglomeration of several primary particles. Lattice plane distances can be clearly recognized proving the crystallinity of the particles. The measured lattice plane distances are consistent with the calculated lattice spacings for the nonstoichiometric phase Sr1−xYbxF2+x with x = 0.53 confirming the formation of this phase. From the evaluation of an isolated particle the average particle size can be estimated to be ∼5 nm. The formation of core–shell structured particles can be excluded as no amorphous shells or a difference by material contrast of isolated particles can be observed by TEM. The same sample was then treated at 300 °C in order to remove residual organic and investigated by TEM, subsequently. It seems that the particles have been undergoing a homogenization process at higher temperatures. In the HRTEM image large particles can be seen having the same orientation as well as an amorphous shell. The measured lattice space distances are in good agreement with the calculated lattice plane distances leading to the conclusion that the expected compound is formed. Overall, TEM revealed the presence of agglomerates with sizes of approx. 30 nm, consisting of smaller (∼5 nm) and larger primary particles (∼10 nm). To gain more information about the amorphous layer, STEM (scanning TEM) was used. The image of the particles in the STEM mode (Fig. S1, ESI†) shows the agglomeration of these larger units. The sample is very well structured. The element distribution was determined using EDXS in selected regions of the sample. A homogeneous distribution of the elements Sr, Yb and F was detected. The amorphous region of the sample consists exclusively of carbon and oxygen. No other elements were detected in this area. Since both carbon and oxygen are also detected in the crystalline region, it can be concluded that the sample still contains residual organics, which was supplied either during the synthesis or could not be removed in the course of preparation of the TEM grid. Therefore, the formation of core–shell particles cannot be assigned. However, utilizing TEM in combination with XRD and DLS, the formation of non-stoichiometric phase of the composition Sr1−xYbxF2+x (x = 0.53) as a highly transparent aqueous sol with particle sizes in the lower nanometer range was proven. Samples with different Yb concentrations are of nanocrystalline character but are obtained as nanopowders.
 | ||
| Fig. 4 HRTEM image of Sr1−xYbxF2+x (x = 0.53) nanoparticles obtained after (i) dip-coating the TEM grid into a 0.2 M sol and (ii) after calcining the particles at 300 °C. | ||
Furthermore, the ageing process of the sol was studied. The 0.2 M sol is highly stable over a period of at least two years and shows neither an increase in turbidity nor signs of ageing resulting in sedimentation or gelation. However, this sol is characterized by a high transparency. It also does not show any changes in the dynamic viscosity and size distribution of the hydrodynamic particle diameters. The 2 years aged sol has a monodisperse particle size distribution with a maximum at about 30 nm and a viscosity of 1.11 mPa s. Comparing the XRD patterns (Fig. 5) of xerogels obtained from 1 week old and 2 years old sol, the diffraction patterns remain unchanged in terms of reflection positions and reflection peak broadening of Sr1−xYbxF2+x (x = 0.53). Therefore, one can conclude that Ostwald ripening does not occur within a period of 2 years although the nanoparticles are present in the aqueous system. This could be explained suggesting the formation of sol particles with a very low solubility and uniform particle size. Ostwald ripening is the growth of the large particles on expense of the small ones. Small-sized particles are being dissolved and re-deposit on the surface of larger particles, reaching more stable thermodynamic state. So the driving force is the minimization of the surface energy. The risk of Ostwald ripening increases if nanoparticles have relatively high aqueous solubility. However, here, it seems not to be the case as the nanoparticles do not show an increase in crystallite size even after 2 years. On the one hand, Ostwald ripening requires to occur a certain solubility of nanoparticles in the solvent, on the other hand it requires a difference in particle size and therefore in solubility. However, DLS shows a very monodisperse size distribution leading to the conclusion that particles of similar hydrodynamic diameters are present. Therefore, Oswald ripening plays a minor role in the ageing process of the sols. Merely recrystallization of the unreacted anhydrous ytterbium acetate to ytterbium acetate tetrahydrate is observed. Since both acetates are water-soluble, this process does not influence the transparency and stability of the sol. Nanoparticles have an extremely large surface area per unit volume of the particles. Because of the large surface area, nanoparticles tend to adsorb substances, such as water molecules and ions, from the surrounding water. The surface of a nanoparticle tends to acquire an electrostatic charge due to the ionization of surface groups and the adsorption of ions from the surrounding solution. The sol particles remain dispersed and stabilized in water for long periods of time (2 years) as a result of the electrostatic forces of the sol particle surfaces themselves. As no additives were added during the synthesis, the obtained sol particles are compatible with water solution.
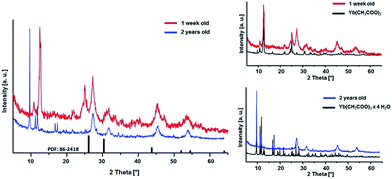 | ||
| Fig. 5 XRD patterns of Sr1−xYbxF2+x (x = 0.53) xerogels obtained from sols of different ageing time. | ||
As demonstrated by XRD patterns of the as-prepared Sr1−xYbxF2+x samples shown in Fig. 1, all the diffraction peaks of the cubic SrF2 lattice are shifted towards higher angles, due to the increasing concentration of Yb in the SrF2 lattice. The cubic lattice constant decreases with increasing Yb content. In contrast, the samples treated at 700 °C show reflections of the nonstoichiometric phases with almost identical reflection positions. It can also be observed from Fig. S2 (ESI†) that there is a shift in the diffraction peak position towards smaller angles as compared to Fig. 1, indicating a decrease in the Yb concentration in the solid solutions. That results in change in the lattice constant. The calculated lattice constants support this result (see Table 2). The lattice constants of samples calcined at 700 °C show a nearly constant value for a as compared to the lattice constants of uncalcined samples which follow Vegard's law. Particularly Sr1−xYbxF2+x phases with higher Yb contents (>20 mol%) show a significant difference in lattice constants at different temperatures. At the same time, XRD analysis shows the coexistence of Yb2O3 and YbOF at 700 °C as shown in Fig. S2 (ESI†).
Sr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Yb Yb |
Yb concentration in Sr1−xYbxF2+x | Lattice constant a [Å] | Lattice constant a [Å] 700 °C | Yb concentration in Sr1−xYbxF2+x at 700 °C |
|---|---|---|---|---|
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
12% | 5.753 | 5.794 | 10% |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
17% | 5.737 | 5.762 | 8% |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
15% | 5.744 | 5.767 | 8% |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
21% | 5.726 | 5.766 | 7% |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
31% | 5.694 | 5.771 | 6% |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
51% | 5.630 | 5.775 | 14% |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
53% | 5.625 | 5.747 | 8% |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
62% | 5.595 | 5.787 | 19% |
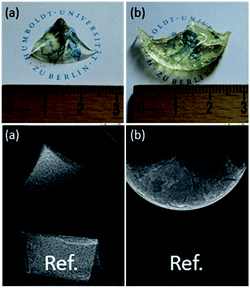
It has to be noted that the synthesis of composite materials where Sr1−xYbxF2+x nanoparticles are homogeneously dispersed in an organic polymer matrix is rather challenging. The initial solvent to prepare transparent Sr1−xYbxF2+x sols and nanoparticles is water. The problem is that hydrophobic resins such as Bis-GMA and TEGDMA commonly used in dental filling materials have poor water solubility. Therefore they are not miscible with water. By mixing transparent Sr1−xYbxF2+x sols with hydrophobic resins, upon mixing, they separate into two immiscible phases. Also, starting from nanoscopic Sr1−xYbxF2+x solid particles only turbid materials are obtained indicating inhomogeneous dispersion of the particles. This is, obviously larger agglomerates of nanoparticles in the organic matrix are formed. This problem can be overcome by replacing water during the synthesis or in the matrix with polar organic solvents such as ethanol or by modifying the nanoparticles formed with suitable complexing agents thus making them compatible to the organic monomers. Additionally, the hydrophilicity of the resins can be improved adding hydrophilic monomers, such as HEMA. A post modification of the particle surface by polyacrylic acid is also an elegant option to redisperse these particles in dimethacrylates. As seen in Fig. 6, after polymerization we obtained transparent plastics. Radiological experiments proved an increased radiopacity of the plastic with at least 6 wt% of particles inside (Fig. 6b), in comparison to the same reference.
Conclusions
In summary, we present the synthesis of SrF2-YbF3 nanoparticles via the fluorolytic sol–gel synthesis. The obtained particles are solid solutions of YbF3 in the cubic lattice of SrF2, which can be described as nonstoichiometric Sr1−xYbxF2+x phases with Vegard behavior. The formation was confirmed by XRD and TEM analysis. The cubic lattice constant decreases with increasing Yb content. After thermal treatment of the solid solutions at 700 °C, however, an increase in the lattice constant is observed which is accompanied by the formation of a SrF2 phase with lower ytterbium concentrations and the formation of YbOF phases. Smaller crystallite sizes (<6 nm) are stabilized with higher ytterbium concentrations in the SrF2 lattice. Highly transparent monodisperse sols of Sr1−xYbxF2+x (x = 0.53) in water solution with hydrodynamic diameters of ∼30 nm and crystallite sizes of ∼6 nm are stable over a period of at least 2 years without facing loss of visual transparency and viscosity. The nanoparticles are characterized by a wide range of homogeneity (up to approx. 60 mol% Yb). Without further preparation steps, the as-prepared Sr1−xYbxF2+x (x = 0.53) particles are homogeneously dispersible in water solution and therefore show promise of a wide range of applicability in the areas of medicine, dentistry and optics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Holm Kirmse (Department of Physics) for TEM measurements. The financial support by DFG (Deutsche Forschungsgemeinschaft) in the framework of the graduate school GRK 1582 (“Fluorine as a key element”) is gratefully acknowledged.Notes and references
- P. P. Fedorov, A. a. Luginina, S. V. Kuznetsov and V. V. Osiko, J. Fluorine Chem., 2011, 132, 1012–1039 CrossRef CAS.
- G. Chen, H. Qiu, P. N. Prasad and X. Chen, Chem. Rev., 2014, 114, 5161–5214 CrossRef CAS PubMed.
- M. Pedroni, F. Piccinelli, T. Passuello, S. Polizzi, J. Ueda, P. Haro-Gonzalez, L. M. Maestro, D. Jaque, J. Garcia-Sole, M. Bettinelli and A. Speghini, Cryst. Growth Des., 2013, 13, 4906–4913 CAS.
- Y.-P. Du, X. Sun, Y.-W. Zhang, Z.-G. Yan, L.-D. Sun and C.-H. Yan, Cryst. Growth Des., 2009, 9, 2013–2019 CAS.
- H. Qiu, G. Chen, R. Fan, L. Yang, C. Liu, S. Hao, M. J. Sailor, H. Ågren, C. Yang and P. N. Prasad, Nanoscale, 2014, 6, 753–757 RSC.
- A. Stepuk, D. Mohn, R. N. Grass, M. Zehnder, K. W. Krämer, F. Pellé, A. Ferrier and W. J. Stark, Dent. Mater., 2012, 28, 304–311 CrossRef CAS PubMed.
- M. Uo, E. Kudo, A. Okada, K. Soga and Y. Kogo, J. Photopolym. Sci. Technol., 2009, 22, 551–554 CrossRef CAS.
- B. P. Sobolev, K. B. Seiranian, L. S. Garashina and P. P. Fedorov, J. Solid State Chem., 1979, 28, 51–58 CrossRef CAS.
- B. P. Sobolev and K. B. Seiranian, J. Solid State Chem., 1981, 39, 337–344 CrossRef CAS.
- B. P. Sobolev, D. N. Karimov, S. N. Sul’yanov and Z. I. Zhmurova, Crystallogr. Rep., 2009, 54, 122–130 CrossRef CAS.
- V. a. Chernyshev, a. E. Nikiforov and a. D. Nazemnikh, J. Phys.: Conf. Ser., 2011, 324, 012025 CrossRef.
- V. a. Chernyshev, a. E. Nikiforov, V. P. Volodin and G. S. Slepukhin, Phys. Solid State, 2010, 52, 1874–1879 CrossRef CAS.
- J. Chen and J. X. Zhao, Sensors, 2012, 12, 2414–2435 CrossRef CAS PubMed.
- L. G. Jacobsohn, C. J. Kucera, T. L. James, K. B. Sprinkle, J. R. DiMaio, B. Kokuoz, B. Yazgan-Kukouz, T. a. DeVol and J. Ballato, Materials, 2010, 3, 2053–2068 CrossRef CAS.
- J. Sun, J. Xian and H. Du, Appl. Surf. Sci., 2011, 257, 3592–3595 CrossRef CAS.
- S. V. Kuznetsov, I. V. Yarotskaya, P. P. Fedorov, V. V. Voronov, S. V. Lavrishchev, T. T. Basiev and V. V. Osiko, Russ. J. Inorg. Chem., 2007, 52, 315–320 CrossRef.
- J. Sun, J. Xian, X. Zhang and H. Du, J. Rare Earths, 2011, 29, 32–38 CrossRef CAS.
- E. Kemnitz, U. Gross, S. Rüdiger and C. S. Shekar, Angew. Chem., Int. Ed. Engl., 2003, 42, 4251–4254 CrossRef CAS PubMed.
- S. Rüdiger and E. Kemnitz, Dalton Trans., 2008, 9226, 1117–1127 RSC.
- R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767 CrossRef.
- X. Qiao, X. Fan, M. Wang and X. Zhang, J. Phys. D: Appl. Phys., 2009, 42, 055103 CrossRef.
- L. Vegard, Zeitschrift für Physik, 1921, 5, 17–26 CrossRef CAS.
- A. L. Patterson, Phys. Rev., 1939, 56, 978–982 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental procedures, STEM image and hypermap of the elements, XRD pattern after treatment at 700 °C. See DOI: 10.1039/c7ra12210a |
| This journal is © The Royal Society of Chemistry 2017 |