Peculiar electronic, strong in-plane and out-of-plane second harmonic generation and piezoelectric properties of atom-thick α-M₂X₃ (M = Ga, In; X = S, Se): role of spontaneous electric dipole orientations

Abstract

Second harmonic generation (SHG) and piezoelectric properties of two-dimensional (2D) materials are sparking great interest. However, out-of-plane SHG in 2D materials has been rarely reported; the theoretical out-of-plane piezoelectric response in atom-thick 2D materials is very limited at the present stage. α-M₂X₃ monolayers exhibit out-of-plane spontaneous polarizations, promising out-of-plane SHG and piezoelectricity. Here, we perform first-principles calculations of the electronic, SHG and piezoelectric properties of single- and few-layer α-M₂X₃. Results indicate the bandgaps of α-M₂X₃ monolayers are in the visible range, and become much narrower as the layer number goes up. Furthermore, the narrower bandgaps are broadened by more than 1.00 eV by switching the electric dipole orientation in few-layer α-M₂X₃. α-M₂X₃ monolayers exhibit superior in-plane and out-of-plane SHG properties; in particular, their out-of-plane SHG coefficients are comparable with those of GaAs crystals. Furthermore, the out-of-plane SHG coefficients can be effectively tuned by switching the electric dipole orientation in α-M₂X₃ few-layers. α-M₂X₃ monolayers exhibit superior in-plane and considerable out-of-plane piezoelectricity, and the latter is significantly enhanced in bilayer α-M₂X₃ because of the built-in electric field originating from the parallel electric dipoles. Our work will stimulate research on the ultrathin 2D photo detection, SHG and piezoelectric devices.

---

1. Introduction

Second harmonic generation (SHG) and piezoelectric properties caused by noncentrosymmetry in two-dimensional (2D) atom-thick materials are sparking great interest. For instance, 2D MoS₂,^1,2 GaSe,^3,4 SiC,⁵ BN⁶ and GeC⁷ nanosheets display fascinating prospects in ultrathin SHG devices. However, these 2D materials only exhibit in-plane SHG properties as they embody out-of-plane centrosymmetric characters, i.e. out-of-plane SHG has not been discovered in these 2D materials. On the other hand, monolayer BN,⁸ MoS₂,⁹ GaSe,¹⁰ GaSSe,¹¹ buckled hexagonal compounds¹² and doped graphene,¹³ have a wide range of applications including in mechanical stress sensors, actuators and energy harvesting devices¹⁴ since they are piezoelectric. Even though a recent calculation has found strong out-of-plane piezoelectricity in multilayer MoSTe¹⁵ and a recent experiment has shown that out-of-plane piezoelectricity occurs in multilayer (10 nm-thick) α-In₂Se₃ flakes,¹⁶ the obtained out-of-plane piezoelectricity in atom-thick 2D materials such as monolayers^11–13 and bilayers is very limited. This makes it impossible to fabricate effective ultrathin 2D piezoelectric devices allowing out-of-plane mechanical–electrical energy conversions.

On the other hand, 2D nanosheets exfoliated from α- and β-In₂Se₃ bulk crystals are attracting great attention in the aspects of the thermal conductivity, phase transformation,^17,18 photo-responsibility,^19,20 sensitivity,²¹ dielectric²² and optical properties.²³ The electric field perpendicular to α- and β-In₂Se₃ monolayers induce a semiconductor to metal transition.²⁴ Remarkably, the class of α-M₂X₃ ferroelectric monolayers exhibit in-plane and out-of-plane reversible spontaneous polarizations,²⁵ promising in-plane and out-of-plane SHG and piezoelectric responses. Indeed, out-of-plane SHG has been recently discovered in monolayer α-In₂Se₃; however the features and magnitude of the SHG coefficients are still unknown.¹⁶ Moreover, monolayer multiferroics exhibit very small out-of-plane SHG coefficients χ⁽²⁾_zzy and χ⁽²⁾_zyz.²⁶ This simulates us to explore the SHG and piezoelectricity of α-M₂X₃ monolayers using first-principles calculations, expecting to find strong out-of-plane SHG and piezoelectricity.

Experiments indicate that the physical properties of In₂Se₃ multilayer nanosheets, such as optical bandgap²³ and thermal conductivity,¹⁷ show a strong layer-dependent behavior. These remind us to study the correlation between the layer thickness and the electronic, piezoelectric and SHG properties of atomic-thick M₂X₃ nanosheets. It should be noted that the nanosheet in our theoretical calculations is much thinner than that in previous experiments.^17,23 Moreover, the van der Waals heterostructure of α-In₂Se₃/WSe₂ shows a significant bandgap reduction when switching the electric dipole orientation of the In₂Se₃ layer. In essence, switching the electric orientation is changing stacking sequences. It has been shown SHG of few-layer GaSe nanosheets²⁷ and piezoelectricity of multilayer MoSTe¹⁵ can be effectively tuned by using various stacking sequences. Therefore, it is meaningful to explore how the electric dipole orientation affects the electronic, piezoelectric and SHG properties of few-layer M₂X₃.

2. Calculation models and details

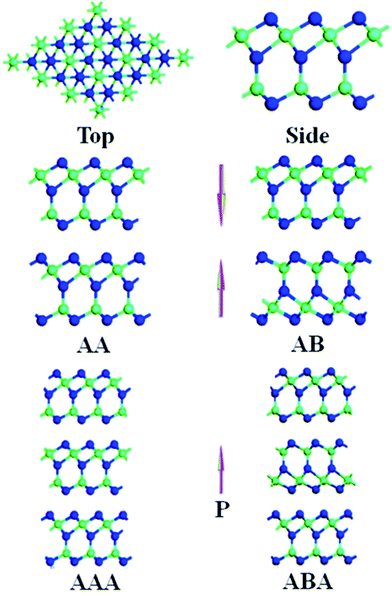
Single- and few-layer β-M₂X₃ nanosheets are centrosymmetric, their piezoelectricity and SHG vanish. We thereby study the electronic, piezoelectric and SHG properties of monolayer α-M₂X₃ (M = Ga, In; X = S, Se), and their top and side views are displayed in Fig. 1. To study the layer-dependent behavior, the bilayer and trilayer exfoliated from α-Ga₂S₃ and α-In₂Se₃ bulk crystals are considered, which are respectively named as AA and AAA stacking. Furthermore, to investigate the effect of the electric dipole orientation, bilayer AB is achieved by switching the electric dipole orientation of the bottom layer in AA, while trilayer ABA is attained by switching the electric dipole orientation of the middle layer in AAA.

Fig. 1 Schematics of top and side views of monolayer α-M₂X₃. The green atoms denote M (M = Ga, In) atoms, while the blue atoms denote X (X = S, Se) atoms. This figure represents bilayer AB is achieved by switching the electric dipole orientation of the bottom α-M₂X₃ layer in bilayer AA, and trilayer ABA is obtained by switching the electric dipole orientation of the middle α-M₂X₃ layer in trilayer AAA.

All calculations are on the basis of the density functional theory (DFT) using the projector-augmented wave (PAW)²⁸ method as implemented in the Vienna Ab initio Simulation Package (VASP).^29–32 The generalized gradient approximation (GGA) parameterized by Perdew, Burke, and Ernzerhof (PBE)³³ with van der Waals (vdW) correction proposed by Crimme (DFT-D2)³⁴ is employed. The single electron wave functions are expanded with a large wave cutoff energy of 500 eV. To minimize the periodic interaction along the z axis, the vacuum spacing between adjacent nanosheets is set to be at least 20 Å. A gamma-centered k-point grid of 11 × 11 × 1 is used to optimize geometry structures, and the convergence criteria for electronic and ionic relaxations are respectively set as 10⁻⁷ and 10⁻³ eV Å⁻¹. A k-point grid of 31 × 31 × 1 is used to calculate piezoelectric coefficients of monolayers and few-layers. The more dense k-point grid of 60 × 60 × 1 is used to obtain SHG coefficients of monolayers, while the k-point of 45 × 45 × 1 is applied for few-layers.

3. Results and discussions

3.1. Structural properties

As shown in Fig. 1, α-M₂X₃ monolayers are five atoms thick, with atoms arranged in the sequence of X–M–X–M–X in the direction perpendicular to the layers. Table 1 summarizes the calculated in-plane constant a and effective thickness h of α-M₂X₃ monolayers. As the α-M₂X₃ bulk crystal contains three basic layers, the theoretical h of α-M₂X₃ monolayers is simply taken as 1/3 of the lattice constant c of optimized bulk crystals. The calculated h are larger than that of monolayer MX₂ (M = Mo, W; X = S, Se)³⁵ and GaX (X = S, Se, Te),²⁷ indicating a stronger SHG intensity in α-M₂X₃ monolayers than that in MoX₂ and GaX monolayers as the SHG intensity shows a quadratic dependence on the thickness, according to the dipole theory.⁴ It is very convenient to identify layer numbers of α-M₂X₃ nanosheets using the effective thickness value in further experiments, which will accelerate explorations of their properties.

Table 1 Calculated in-plane constants a (Å), effective thicknesses h (Å), PBE bandgaps E^PBE_g (eV), HSE06 bandgaps E^HSE06_g (eV), minimum direct energy gaps E^HSE06_min (eV) and SHG coefficients χ⁽²⁾(0) (pm V⁻¹) of monolayer α-M₂X₃ (M = Ga, In; X = S, Se), few-layer α-Ga₂S₃ and α-In₂Se₃

		a	h	E^PBEg	E^HSE06g	E^HSE06min	χ^(2)xxy(0)	χ^(2)zxx(0)	χ^(2)zzz(0)
α-Ga2S3	ML	3.59	8.94	1.79(I)	2.95(I)	3.25(G)	25.4	23.8	162.6
	AA	3.59	17.88	0.65(I)	1.80(I)	2.05(G)	23.0	27.4	184.2
	AB	3.59	17.88	1.64(I)	2.80(I)	3.04(G)	25.0	−0.3	0.8
	ABA	3.59	26.82	1.52(I)	2.64(I)	2.81(G)	24.2	6.4	47.6
α-Ga2Se3	ML	3.77	9.40	1.06(I)	2.04(I)	2.30(G)	34.6	26.2	208.0
α-In2S3	ML	3.83	9.18	1.29(I)	2.30(I)	2.36(G)	30.6	36.6	207.6
α-In2Se3	ML	3.99	9.68	0.88(I)	1.80(I)	1.83(G)	42.2	41.8	252.6
	AB	3.99	19.36	0.57(I)	1.45(I)	1.46(G)	44.0	−1.80	−0.02
	ABA	4.00	29.04	0.45(I)	1.25(I)	1.26(G)	48.2	8.2	61.4

---

Similar to previous calculations,³⁶ the formation energies of single- and few-layer α-M₂X₃ nanosheets are defined as E_f = E/N − E_ref/N_ref, where E and E_ref are respectively the energies of nanosheets and corresponding bulk crystals. N and N_ref are the numbers of atoms in the respective unit cells. The calculated formation energies of monolayer α-M₂X₃, few-layer α-Ga₂S₃ and α-In₂Se₃ are shown in Fig. 2. The formation energies of α-M₂X₃ monolayers are comparable or even smaller than that of monolayer MoS₂. The formation energies of monolayer, bilayer AA, and trilayer AAA α-Ga₂S₃ (α-In₂Se₃) decrease as their layer numbers increase, suggesting it is more likely to successfully obtain α-Ga₂S₃ (α-In₂Se₃) nanosheets with larger layer numbers. Indeed, trilayer AAA α-In₂Se₃, i.e. 3.1 nm-thick α-In₂Se₃ nanosheets have been synthesized using mechanical exfoliation.²³ Moreover, the formation energy of α-Ga₂S₃ nanosheets is to some extent smaller than that of corresponding α-In₂Se₃ nanosheets, indicating it is more likely to obtain α-Ga₂S₃ nanosheets. Furthermore, the difference of the formation energy can be negligible for AA (AAA) and AB (ABA), ensuring the feasibility to achieve AB (ABA) by switching the electric dipole orientation in AA (AAA) from the standpoint of energetics.

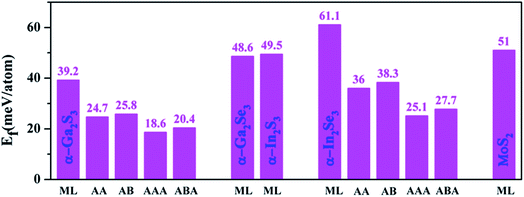Fig. 2 Calculated formation energies of monolayer α-M₂X₃, few-layer α-Ga₂S₃ and α-In₂Se₃. The formation energy of the synthesized MoS₂ monolayer is shown for comparison.

3.2. Electronic properties

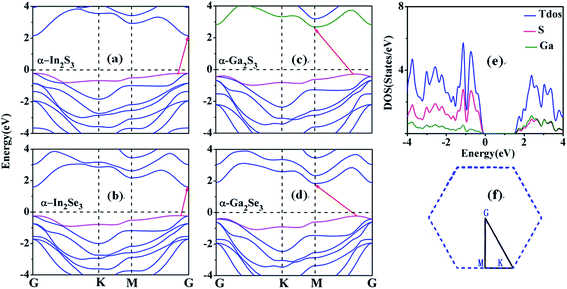
In contrast to the previous bandgap calculation using the HSE06 functional with 25% exact exchange,²⁵ we calculated the band structure of single-layer α-M₂X₃ using 30% EE, cf. ESI (SI-1†). The calculated band structures are displayed in Fig. 3. α-M₂X₃ monolayers are indirect bandgap semiconductors with their valence band maximum (VBM) located between the M (0.0, 0.5, 0.0) and gamma (0.0, 0.0, 0.0) points. The conduction band minimum (CBM) is located at the M point for monolayer α-Ga₂S₃ and α-Ga₂Se₃, while for single-layer α-In₂S₃ and α-In₂Se₃ it is located at the gamma point. The top valence band of α-M₂X₃ monolayers is relatively flat, resulting in a high density of electronic states in the top valence band region as shown in Fig. 3(e), which is the origin of large SHG coefficients.⁷

Fig. 3 Calculated band structure of (a) α-In₂S₃, (b) α-In₂Se₃, (c) α-Ga₂S₃ and (d) α-Ga₂Se₃ using HSE06 incorporating 30% EE. (e) Total and partial density of states of monolayer α-Ga₂S₃ calculated using PBE. (f) The high symmetry k-point path in the Brillouin Zone is chosen as: gamma (0, 0, 0) → k (−1/3, 2/3, 0) → M (0, 1/2, 0) → gamma (0, 0, 0), and gamma is abbreviated as G.

Table 1 summarizes the PBE and HSE06 bandgaps of α-M₂X₃ monolayers. The PBE bandgap of 0.88 eV for monolayer α-In₂Se₃ gets very close to the calculated bandgap of 0.82 eV using PBE + SOC,²⁴ suggesting spin-orbital coupling (SOC) does not significantly modify the electronic property. The HSE06 bandgap of 1.80 eV for single-layer α-In₂Se₃ gets close to the calculated bandgap of 1.92 eV using the GW approximation,²⁴ but slightly larger than the bandgap of 1.45 eV calculated using HSE06 with 25% exact exchange.²⁵ The energy gaps of each monolayer at the gamma point are close to their respective indirect bandgaps, which is more evident for α-In₂S₃ and α-In₂Se₃ monolayers. It is expected the interband optical transition at the gamma point improves optical responses of α-M₂X₃ monolayers because no phonons are required for this optical transition to proceed. Additionally, the HSE06 bandgaps of α-M₂X₃ monolayers are large enough to avoid current leakages, and thereby they are promising in piezoelectric devices.

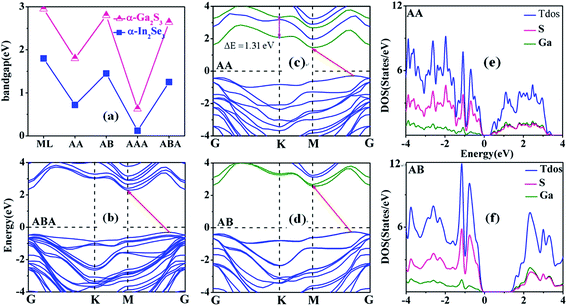
Fig. 4 displays the band structures of bilayer AA and AB, and trilayer ABA α-Ga₂S₃ calculated using HSE06. If there were no interlayer interaction, the band structure of bilayer AA α-Ga₂S₃ should be identical to that of monolayer α-Ga₂S₃. Nevertheless, the bands from different α-Ga₂S₃ layers in AA are pronouncedly splitted. Comparisons of Fig. 3(c) and 4(c) show the bottom valence bands from various α-Ga₂S₃ layers in AA are splitted by as large as 1.31 eV. Resultantly, the bandgap of AA significantly gets reduced by 1.15 eV in comparison with that of monolayer α-Ga₂S₃ as Table 1 shows, and that of trilayer AAA α-Ga₂S₃ further decreases as shown in Fig. 4(a). In brief, we find the bandgap of few-layer α-Ga₂S₃ nanosheets becomes much narrower as their layer number increases. This bandgap reduction is also pronounced for few-layer α-In₂Se₃ nanosheets. Fig. 4(a) indicates the bandgap of trilayer AAA α-In₂Se₃ nearly vanishes. Similarly, optical absorption spectra show the bandgap decreases from 2.80 eV to 1.45 eV as the layer thickness increases from 3.1 nm to 20.1 nm.²³ Considering the effective thickness of monolayer α-In₂Se₃ is ∼1 nm, the optical bandgap of 1.45 eV for α-In₂Se₃ nanosheets with ∼20 layers gets close to our theoretical value of 1.48 eV for α-In₂Se₃ bulk crystals. Nevertheless, the experimental bandgap of 2.8 eV for 3.1 nm-thick (trilayer) α-In₂Se₃ nanosheets significantly varies from the zero bandgap of trilayer AAA α-In₂Se₃. Moreover, PBE calculations also find the bandgap of bilayer AA and trilayer AAA α-In₂Se₃ is closed.²⁵ It seems further bandgap measurements of few-layer α-In₂Se₃ are emergently needed to interpret the huge divergence between experimental and theoretical bandgaps. On the other hand, we note the band splitting in non-ferroelectric MoS₂ nanosheets is not so pronounced.³⁵ Single-layer MoS₂ embodies out-of-plane centrosymmetric characters and in-plane non-centrosymmetric characters. Therefore, the pronounced band splitting in few-layer α-Ga₂S₃ (α-In₂Se₃) nanosheets is caused by the built-in electric field originated from the parallel out-of-plane electric polarizations (dipoles) of α-Ga₂S₃ (α-In₂Se₃) layers (cf. ESI-3†). This is further affirmed by semiconducting α-In₂Se₃ monolayers becoming metallic when an electric filed perpendicular is applied.²⁴

Fig. 4 (a) Bandgap variation of monolayer (ML), bilayer AA and AB, trilayer AAA and ABA α-Ga₂S₃ (α-In₂Se₃) nanosheets. Calculated Band structure of bilayer (c) AA and (d) AB, and (b) trilayer ABA α-Ga₂S₃ calculated using HSE06. Total and partial density of states (DOS) of bilayer (e) AA and (f) AB α-Ga₂S₃ calculated using PBE.

The band splitting of bilayer AB α-Ga₂S₃ is not pronounced, and accordingly the bandgap difference between monolayer and bilayer AB α-Ga₂S₃ is very small. This is because the built-in electric field significantly decreases as the out-of-plane electric polarizations (dipoles) of α-Ga₂S₃ layers are antiparallelly aligned (cf. ESI-3†). Furthermore, the band splitting in Fig. 4(b) is minor in ABA α-Ga₂S₃ as expected. The divergence of electronic properties between AA and AB α-Ga₂S₃ is further emphasized in Fig. 4(e) and (f). The peaks in the conduction band region of bilayer AB α-Ga₂S₃ look similar to that of monolayer α-Ga₂S₃. Nevertheless, the peaks in AA α-Ga₂S₃ are significantly splitted, particularly for the peaks between −3 and −2 eV. Briefly, the bandgap in AA α-Ga₂S₃ is broadened by 1.00 eV in AB α-Ga₂S₃, which is very advantageous for applications as photodetectors since one can select the sensing photon energy window by switching electric dipole orientation. Additionally, the zero bandgap in AAA α-In₂Se₃ is opened in ABA α-In₂Se₃, indicating the semiconducting nature can be achieved by switching the electric dipole orientation.

3.3. SHG properties

The length-gauge formulism at the independent-particle level derived by Aversa and Sipe³⁷ and rearranged by Rashkeev et al.³⁸ is used to calculate second-harmonic generation (SHG) coefficients (cf. ESI-2†), and its details are displayed in a previous work.³⁹ Similar to previous works,^7,27 the energy differences between HSE06 and PBE bandgaps are used for scissors corrections to reduce the errors caused by neglected many-body effects;^40–42 the effective unit cell volume is applied to reduce underestimations caused by the large vacuum spacing. For α-M₂X₃ monolayers and few-layers, the effective volume is obtained by multiplying the area of in-plane unit cell and the effective thickness.

Because single- and few-layer α-M₂X₃ belong to C_3v symmetry, they have eleven static SHG coefficients and only three of them are independent dictated by Kleiman's symmetry: χ⁽²⁾_yyy(0) = −χ⁽²⁾_yxx(0) = −χ⁽²⁾_xxy(0) = −χ⁽²⁾_xyx(0), χ⁽²⁾_zzz(0) and χ⁽²⁾_zxx(0) = χ⁽²⁾_zyy(0) = χ⁽²⁾_yyz(0) = χ⁽²⁾_yzy(0) = χ⁽²⁾_xzx(0) = χ⁽²⁾_xxz(0). The static χ⁽²⁾_xxy(0), χ⁽²⁾_zxx(0) and χ⁽²⁾_zzz(0) are summarized in Table 1. The static χ⁽²⁾_xxy(0) describes the in-plane SHG phenomenon, which has been discovered in previous experiments of MoS₂,² GaSe⁴ and BN⁴³ monolayers. Even though the static χ⁽²⁾_xxy(0) of α-M₂X₃ monolayers is much smaller than that of MoS₂ (ref. 35) and GaSe²⁷ monolayers, it is still comparable with χ⁽²⁾_zxy(0) of 28.2 pm V⁻¹ for an archetypical nonlinear optical crystal AgGaS₂,⁴⁴ ensuring α-M₂X₃ monolayers can be used as in-plane two-dimensional SHG devices. More importantly, α-M₂X₃ monolayers have additional SHG components χ⁽²⁾_zzz(0) and χ⁽²⁾_zxx(0) compared with MoS₂ and GaSe monolayers. Especially, the calculated χ⁽²⁾_zzz(0) of α-M₂X₃ monolayers are comparable or even larger than the static SHG coefficient of 173.2 pm V⁻¹ for GaAs crystals.⁴⁵ Therefore, α-M₂X₃ monolayers are of great importance in ultrathin two-dimensional devices allowing strong out-of-plane SHG occurs.

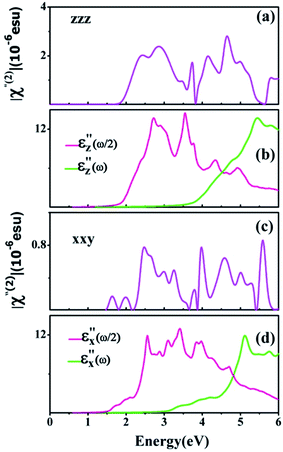
Fig. 5 represents the calculated real and imaginary parts of SHG coefficients χ⁽²⁾_zzz(−2ω,ω,ω), χ⁽²⁾_zxx(−2ω,ω,ω) and χ⁽²⁾_xxy(−2ω,ω,ω) of α-M₂X₃ monolayers. The χ⁽²⁾_zzz(−2ω,ω,ω) and χ⁽²⁾_xxy(−2ω,ω,ω) components are significant in the entire range of optical energy. The χ⁽²⁾_zzz(−2ω,ω,ω) component is several times larger than χ⁽²⁾_xxy(−2ω,ω,ω) and χ⁽²⁾_zxx(−2ω,ω,ω). For χ⁽²⁾_zxx(−2ω,ω,ω), the electric field of both incoming and outgoing photons is parallel to the z axis, and thereby the electric depolarization vanishes. To analyze the prominent features in SHG spectra, the absolute values of imaginary part of χ⁽²⁾_zzz(−2ω,ω,ω) and χ⁽²⁾_xxy(−2ω,ω,ω) for monolayer α-Ga₂S₃ are plotted in Fig. 6 and compared with the absorptive part of corresponding dielectric function ε′′. The first prominent peak between 1.7 and 3.8 eV in the χ⁽²⁾_zzz(−2ω,ω,ω) spectrum is caused by double-photon resonances (cf. Fig. 6(a) and (b)). In contrast, the double-peak structure between 3.8 and 5.6 eV in χ⁽²⁾_zzz(−2ω,ω,ω) comes from single- and double-photon resonances. These single- and double-photon resonances only involve optical transitions for the electric filed vector E⃑ parallel to the z axis (E⃑‖z). Fig. 6 further suggests the first prominent peak between 2.2 and 3.6 eV in the χ⁽²⁾_xxy(−2ω,ω,ω) spectrum is caused by double-photon resonances with E⃑‖x (cf. Fig. 6(c) and (d)), while the peak between 3.9 and 5.4 eV in χ⁽²⁾_xxy(−2ω,ω,ω) comes from both single- and double-photon resonances with E⃑‖x.

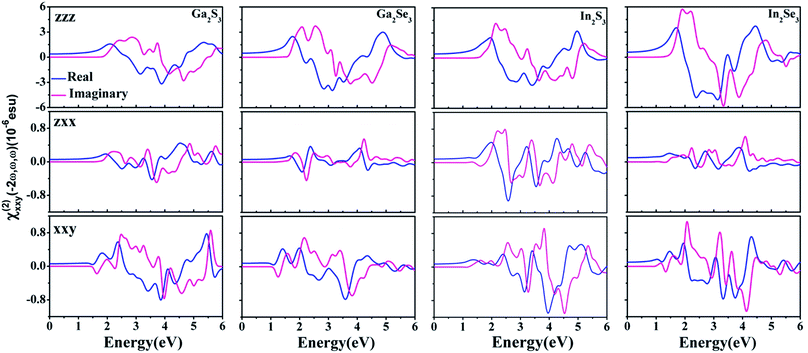Fig. 5 Calculated real and imaginary parts of SHG coefficients χ⁽²⁾_zzz(−2ω,ω,ω), χ⁽²⁾_zxx(−2ω,ω,ω) and χ⁽²⁾_xxy(−2ω,ω,ω) of monolayer α-M₂X₃.

Fig. 6 (a) Absolute value of the imaginary part of χ⁽²⁾_zzz(−2ω,ω,ω), (b) imaginary part of the dielectric function ε′′_z as a function of ω/2 and ω, (c) absolute value of the imaginary part of χ⁽²⁾_xxy(−2ω,ω,ω), and (d) imaginary part of the dielectric function ε′′_x as a function of ω/2 and ω of monolayer α-Ga₂S₃.

As shown in Table 1, the HSE06 bandgaps of few-layer α-Ga₂S₃ are in the visible range. In contrast, the HSE06 bandgaps of few-layer α-In₂Se₃ and AAA α-Ga₂S₃ are much narrower, which promises low laser damage thresholds. Therefore, we focus on SHG properties of bilayer AA and AB, and ABA α-Ga₂S₃, and their real and imaginary parts of χ⁽²⁾_zzz(−2ω,ω,ω), χ⁽²⁾_zxx(−2ω,ω,ω) and χ⁽²⁾_xxy(−2ω,ω,ω) are displayed in Fig. 7. The line shape of the three SHG spectra of AA α-Ga₂S₃ is very similar to that of monolayer α-Ga₂S₃, and the SHG spectra of AA are significantly redshifted in comparison with that of monolayer α-Ga₂S₃ because of the sizable bandgap reduction. Moreover, the calculated χ⁽²⁾_zzz(0), χ⁽²⁾_zxx(0) and χ⁽²⁾_xxy(0) of AA α-Ga₂S₃ are very close to those of monolayer α-Ga₂S₃, respectively. These suggest that optical transitions occur within each α-Ga₂S₃ layer, namely the SHG property of each α-Ga₂S₃ layer is not modified by the built-in electric field of the neighboring α-Ga₂S₃ layer. According to the electric dipole theory, the SHG intensity shows a quadratic dependence on the SHG coefficient and the layer thickness,⁴ and thereby the non-resonant SHG intensity in bilayer AA is about four times that in monolayers.

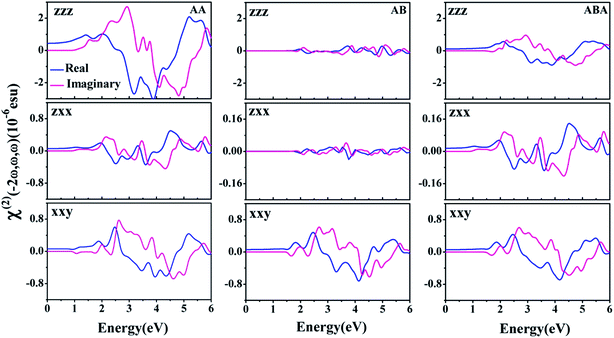Fig. 7 Calculated real and imaginary parts of SHG coefficients χ⁽²⁾_zzz(−2ω,ω,ω), χ⁽²⁾_zxx(−2ω,ω,ω) and χ⁽²⁾_xxy(−2ω,ω,ω) of bilayer AA, AB, and trilayer ABA α-Ga₂S₃.

The redshift of χ⁽²⁾_xxy(−2ω,ω,ω) for AB α-Ga₂S₃ is negligible as the bandgap difference of monolayers and AB is small. χ⁽²⁾_zzz(−2ω,ω,ω) and χ⁽²⁾_zxx(−2ω,ω,ω) of AB α-Ga₂S₃ nearly vanishes, which is further corroborated by its vanishing static χ⁽²⁾_zzz(0) and χ⁽²⁾_zxx(0). The electric dipole in the z(x) direction of the top and bottom α-Ga₂S₃ layers in bilayer AB points oppositely, and accordingly their contribution to the static χ⁽²⁾_zzz(0)(χ⁽²⁾_zxx(0)) cancels each other. The electric dipole in the z direction is the out-of-plane electric dipole, while the electric dipole in the x direction is the in-plane electric dipole. The χ⁽²⁾_zzz(−2ω,ω,ω) component of trilayer ABA α-Ga₂S₃ is 1/3 that of monolayer α-Ga₂S₃ as the contribution of the middle and bottom layers to χ⁽²⁾_zzz(−2ω,ω,ω) in trilayer ABA cancels each other. Therefore, we propose that one can effectively tune the out-of-plane SHG coefficient by switching the electric dipole orientation in 2D nanosheets. Additionally, we summarize χ⁽²⁾(0) of AB and ABA α-In₂Se₃ in Table 1, which indicates the obtained optical rules are valid for other α-M₂X₃ nanosheets. The SHG property of few-layer α-In₂Se₃ in recent experiments could be obtained by analogy.¹⁶

3.4. Piezoelectric properties

To obtain piezoelectric strain coefficients d_ij which measure mechanical–electrical energy conversion ratios, we calculate elastic constants C_ij and piezoelectric stress coefficients e_ij using density functional perturbation theory (DFPT).⁴⁶ The clamped-ion elastic and piezoelectric coefficients are obtained from purely electronic contributions, while the relaxed-ion coefficients are obtained from the sum of electronic and ionic contributions. The relaxed-ion elastic and piezoelectric coefficients are physically meaningful and can be directly compared with experimental results. As shown in Table 2, single- and few-layer α-M₂X₃ have three independent elastic constants: C₁₁, C₁₂ and C₆₆. The calculated clamped-ion and relaxed-ion elastic constants follow the correlation of C₆₆ ≈ (C₁₁ − C₁₂)/2. The relaxed-ion elastic constants fulfil the Born criteria of stability of 2D hexagonal structures,^47–49 i.e. C₁₁ > 0 and C₁₁–C₁₂ > 0, ensuing these monolayers and few-layers are mechanically stable. The calculated relaxed-ion Young's moduli (Y = (C₁₁² − C₁₂²)/C₁₁) of single-layer α-M₂X₃ are smaller than that of graphene (341 N m⁻¹) and monolayer BN (275.9 N m⁻¹),⁵⁰ and comparable with that of monolayer TMDCs.⁵¹ Therefore, α-M₂X₃ monolayers are much softer than graphene and monolayer BN, and their stiffness is comparable with that of monolayer TMDCs. Moreover, the calculated Young's moduli of bilayer (trilayer) α-Ga₂S₃ are about two (three) times that of monolayer α-Ga₂S₃. This is because, of the same strain, the force needed for bilayers (trilayers) is two (three) times that of monolayers.

Table 2 Theoretical elastic constants C_ij and Yang moduli Y (N m⁻¹) in both clamped- and relaxed-ion cases of monolayer α-M₂X₃ and few-layer α-Ga₂S₃

		Clamped-ion				Relaxed-ion
		C11	C12	C66	Y	C11	C12	C66	Y
α-Ga2S3	ML	146.7	48.6	48.9	130.5	115.5	45.0	35.1	104.3
	AA	293.3	97.6	97.6	261.0	228.2	83.3	72.4	197.7
	AB	292.3	96.2	97.6	260.6	224.3	85.4	69.3	191.7
	ABA	439.2	145.8	146.7	390.7	348.7	134.5	106.6	296.8
	AB
	ab
α-Ga2Se3	ML	120.9	39.9	40.2	107.7	91.8	42.0	24.6	72.5
α-In2S3	ML	117.0	43.2	36.6	101.0	75.6	36.6	19.2	57.8
α-In2Se3	ML	96.3	35.1	30.6	83.5	68.4	24.0	21.9	59.9

---

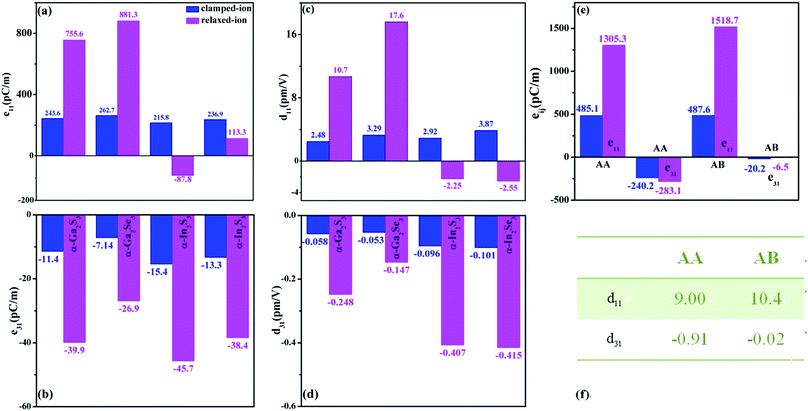
Single- and few-layer α-M₂X₃ have two independent piezoelectric stress coefficients e₁₁ and e₃₁ dictated by C_3v symmetry. The piezoelectric strain coefficients d₁₁ and d₃₁, which respectively measure the mechanical–electrical energy conversion ratios in x and z directions, are expressed as d₁₁ = e₁₁/(C₁₁ − C₁₂) and d₃₁ = e₃₁/(C₁₁ + C₁₂).¹² The relaxed-ion e₁₁ values of monolayer α-Ga₂S₃ and α-Ga₂Se₃ in Fig. 8(a) are even larger than that of monolayer 2H-CrTe₂, which has the largest e₁₁ of 654 pC m⁻¹ among TMDCs.¹² The relaxed-ion d₁₁ values of single-layer α-Ga₂Se₃ and α-In₂Se₃ in Fig. 8(c) are comparable with the maximum d₁₁ of 13.45 pm V⁻¹ for monolayer TMDCs, and larger than the maximum d₁₁ of 8.47 pm V⁻¹ for Janus group-III chalcogenide monolayers.¹¹ The relaxed-ion d₁₁ values of α-In₂S₃ and α-In₂S₃ monolayers are comparable with the maximum d₁₁ of 2.30 pm V⁻¹ for group-III chalcogenides.¹⁰ Therefore, α-M₂X₃ monolayers are promising in ultrathin piezoelectric sensors and nano-generators. Fig. 8(a) and (c) further suggest the electronic and ionic polarizations of α-Ga₂S₃ and α-Ga₂Se₃ monolayers both positively contribute to relaxed-ion piezoelectric coefficients e₁₁ and d₁₁, resulting in significant in-plane piezoelectricity. In contrast, the electronic and ionic polarizations of α-In₂S₃ and α-In₂Se₃ monolayers oppositely contribute to relaxed-ion e₁₁ and d₁₁, resulting in smaller in-plane piezoelectricity. Our calculation also generates relaxed-ion e₁₁ and d₁₁ are respectively 369 pC m⁻¹ and 3.72 pm V⁻¹ for monolayer MoS₂, in good agreement with previous theoretical values of 364 pC m⁻¹ and 3.73 pm V⁻¹,⁸ indicating our theoretical results are numerically reliable.

Fig. 8 Piezoelectric coefficients (a) e₁₁, (b) e₃₁, (c) d₁₁ and (d) d₃₁ of monolayer α-M₂X₃ in clamped- and relaxed-ion cases. (e) Clamped- and relaxed-ion e₁₁ and e₃₁ of bilayer AA and AB α-Ga₂S₃. (f) Relaxed-ion d₁₁ and d₃₁ (pm V⁻¹) of AA and AB α-Ga₂S₃.

Fig. 8(b) and (d) suggest α-M₂X₃ monolayers have nonzero out-of-plane piezoelectric coefficients e₃₁ and d₃₁. The electronic and ionic polarizations of all α-M₂X₃ monolayers both negatively contribute to e₃₁ and d₃₁. The d₃₁ values of α-M₂X₃ monolayers are comparable with the maximum d₃₁ of 0.46 pm V⁻¹ for monolayer Janus group-III chalcogenides¹¹ and the maximum d₃₁ of 0.658 pm V⁻¹ for bucked hexagonal compounds.¹² However, the bucked hexagonal compounds are energetically metastable. In contrast, α-M₂X₃ monolayers are energetically, dynamically²⁵ and mechanically stable, ensuing they are experimentally feasible.

The calculated piezoelectric coefficients e₁₁ and e₃₁ of AA and AB α-Ga₂S₃ are summarized in Fig. 8(e), while their d₁₁ and d₃₁ coefficients are displayed in Fig. 8(f). Comparisons of Fig. 8(a) and (e) show the clamped-ion (relaxed-ion) e₁₁ of AB α-Ga₂S₃ is exactly twice that of monolayer α-Ga₂S₃. This is because, of the same strain, the change of polarization charges in the x direction of bilayer AB α-Ga₂S₃ is twice that of monolayer α-Ga₂S₃. Therefore, the piezoelectric effect occurs within each α-Ga₂S₃ layer in AB, namely the piezoelectricity of each α-Ga₂S₃ layer is not modified by the built-in electric field of the neighboring α-Ga₂S₃ layer. This is further affirmed by the relaxed-ion d₁₁ of 10.4 pm V⁻¹ for AB α-Ga₂S₃ being very close to that (10.7 pm V⁻¹) for monolayer α-Ga₂S₃. The relaxed-ion d₃₁ of bilayer AB nearly vanishes since the piezoelectric contribution to d₃₁ of each α-Ga₂S₃ layer cancels each other.

Fig. 8(a) and (e) further suggest the clamped-ion e₁₁ of 485.1 pC m⁻¹ for bilayer AA α-Ga₂S₃ is exactly twice that (243.6 pC m⁻¹) of monolayer α-Ga₂S₃, while the relaxed-ion e₁₁ of 1350.3 pC m⁻¹ for AA α-Ga₂S₃ is to some extent smaller than twice that (755.6 pC m⁻¹) of monolayer α-Ga₂S₃. The clamped-ion e₃₁ of −240.2 pC m⁻¹ for AA α-Ga₂S₃ is much larger than that (−11.4 pC m⁻¹) of monolayer α-Ga₂S₃, namely the clamped-ion e₃₁ of AA α-Ga₂S₃ is much enhanced by the strong built-in electric field originated from the parallel out-of-plane electric polarizations of α-Ga₂S₃ layers. The relaxed-ion d₃₁ of −0.91 pm V⁻¹ for AA α-Ga₂S₃ is accordingly several times larger than that (−0.248 pm V⁻¹) of monolayer α-Ga₂S₃, suggesting AA α-Ga₂S₃ is much more easily polarized than monolayer α-Ga₂S₃. Similarly, the electric dipole (0.165 eÅ) of AA α-In₂Se₃ is much larger than that (0.07 eÅ) of monolayer α-In₂Se₃.²⁵

Briefly, we find AA α-Ga₂S₃ has the largest out-of-plane d₃₁ among all atomic-thick 2D materials up to date. More importantly, the built-in electric field can induce strong out-of-plane piezoelectricity in atomic-thick 2D materials, which is corroborated by a recent calculation which finds large d₃₁ of −1.234 pm V⁻¹ and d₃₃ of −13.517 pm V⁻¹ in multilayer MoSTe.¹⁵ However, the large d₃₃(∂P₃/∂σ₃, P is the electric polarization and σ is the stress) in multilayer MoSTe will vanish in atomic-thick 2D MoSTe such as monolayer¹⁵ and bilayer MoSTe (cf. ESI-4†). This reflects it is very difficult to impose stresses along the z direction for atomic-thick 2D materials since their effective thickness is far smaller than their flake size. For instance, the effective thickness of monolayer MoSSe is about 6.3 Å while its flake size is more than 5 μm.⁵² The effective thickness of monolayer MoSSe is considered as the average of that of MoS₂ and MoSe₂ monolayers.³⁵ In contrast, it is easy to impose stresses along the x direction to achieve large d₃₁(∂P₃/∂σ₁) because of the large size of atomic-thick 2D materials. Therefore, it is more reasonable to induce out-of-plane piezoelectricity by imposing stresses along the x direction within atomic-thick 2D materials. Moreover, the d₃₁ coefficient of −1.234 pm V⁻¹ for multilayer MoSTe decreases to −0.417 pm V⁻¹ of bilayer MoSTe (cf. ESI-4†), being smaller than that of AA Ga₂S₃. The small bandgap of AAA α-Ga₂S₃ is disadvantageous to avoid current leakages. The piezoelectric coefficient d₁₁ of ABA α-Ga₂S₃ should be close to that of monolayer α-Ga₂S₃, while its d₃₁ coefficient is around 1/3 that of monolayer α-Ga₂S₃ since the piezoelectric response occurs within each α-Ga₂S₃ layer.

4. Summaries

We have carried out first-principles calculations of structural, electronic, SHG and piezoelectric properties of single- and few-layer α-M₂X₃ (M = Ga, In; X = S, Se). Firstly, α-M₂X₃ few-layers are energetically favorable and mechanically stable, ensuring bilayer AA and trilayer AAA can be successfully attained by mechanical exfoliation and bilayer AB and trilayer ABA can be achieved by switching the electric dipole orientation. Secondly, the relative flat top valence band of α-M₂X₃ monolayer promises large SHG coefficients, and their large bandgaps are helpful to avoid current leakages in piezoelectric devices. The splitting of energy bands in few-layer AA and AAA is very pronounced because of the built-in electric field originated from the parallel out-of-plane electric dipoles, while in contrast, that of AB and ABA is not pronounced because the built-in electric field significantly diminishes as the out-of-plane electric dipoles are antiparallelly aligned. Therefore, we propose a completely new method, i.e. switching the electric dipole orientation to tune electronic structures and bandgaps, which is very advantageous to tune the sensing photon energy window and achieve the semiconducting nature. Thirdly, the in-plane SHG coefficients of α-M₂X₃ monolayers are comparable with that of AgGaS₂ crystals. More importantly, we find out-of-plane SHG in α-M₂X₃ monolayers and their out-of-plane SHG coefficients are comparable with that of GaAs crystals. Furthermore, SHG occurs within each α-M₂X₃ layers in AA and AB, and accordingly one can achieve an enhanced out-of-plane SHG intensity in AA and eliminate the out-of-plane SHG in AB. Fourthly, the stiffness of α-M₂X₃ monolayers is comparable that with monolayer TMDCs. α-M₂X₃ monolayers exhibit strong in-plane and considerable out-of-plane piezoelectricity. Furthermore, out-of-plane piezoelectricity vanishes in AB α-Ga₂S₃, and it is greatly enhanced in AA α-Ga₂S₃ as the electric dipoles are parallelly aligned. To our knowledge, out-of-plane SHG in 2D materials has been rarely reported, while the out-of-plane piezoelectricity is very limited in ultrathin 2D materials. Here we have presented strong out-of-plane SHG and piezoelectricity in ultrathin 2D materials. In general, our research will stimulate researches on the ultrathin 2D photo detection, SHG and piezoelectric devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by National Nature Science foundation of China (21373099, 21573090), Jilin Province Science and Technology Development Plan (20150101005JC) and the Ministry of Education of China (20130061110020). We also thank professor Yong-Fan Zhang in Fuzhou University for SHG calculation program developing.

References

1. D. Neshev and Y. Kivshar, Science, 2014, 344, 483.
2. X. Yin, Z. Ye, D. A. Chenet, Y. Ye, K. O'Brien, J. C. Hone and X. Zhang, Science, 2014, 344, 488.
3. W. Jie, X. Chen, D. Li, L. Xie, Y. Y. Hui, S. P. Lau, X. Cui and J. Hao, Angew. Chem., Int. Ed., 2015, 54, 1185.
4. X. Zhou, J. Cheng, Y. Zhou, T. Cao, H. Hong, Z. Liao, S. Wu, H. Peng, K. Liu and D. P. Yu, J. Am. Chem. Soc., 2015, 137, 7994.
5. I. J. Wu and G. Y. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035447.
6. G. Y. Guo and J. C. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075416.
7. L. Hu and D. S. Wei, Phys. Chem. Chem. Phys., 2017, 19, 2235.
8. K. A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871.
9. H. Zhu, Y. Wang, J. Xiao, M. Liu, S. Xiong, Z. J. Wong, Z. Ye, Y. Ye, X. Yin and X. Zhang, Nat. Nanotechnol., 2015, 10, 151.
10. W. Li and J. Li, Nano Res., 2015, 8, 3796.
11. Y. Guo, S. Zhou, Y. Bai and J. Zhao, Appl. Phys. Lett., 2017, 110, 163102.
12. M. N. Blonsky, H. L. Zhuang, A. K. Singh and R. G. Hennig, ACS Nano, 2015, 9, 9885.
13. M. T. Ong and E. J. Reed, ACS Nano, 2012, 6, 1387.
14. W. Wu, L. Wang, Y. Li, F. Zhang, L. Lin, S. Niu, D. Chenet, X. Zhang, Y. Hao, T. F. Heinz, J. Hone and Z. L. Wang, Nature, 2014, 514, 470.
15. L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242.
16. Y. Zhou, D. Wu, Y. Zhu, Y. Cho, Q. He, X. Yang, K. Herrera, Z. Chu, Y. Han, M. C. Downer, H. Peng and K. Lai, Nano Lett., 2017, 17, 5508.
17. S. Zhou, X. Tao and Y. Gu, J. Phys. Chem. C, 2016, 120, 4753.
18. X. Tao and Y. Gu, Nano Lett., 2013, 13, 3501.
19. G. Almeida, S. Dogan, G. Bertoni, C. Giannini, R. Gaspari, S. Perissinotto, R. Krahne, S. Ghosh and L. Manna, J. Am. Chem. Soc., 2017, 139, 3005.
20. R. B. Jacobs-Gedrim, M. Shanmugam, N. Jain, C. A. Durcan, M. T. Murphy, T. M. Murray, R. J. Matyi, R. L. Moore and B. Yu, ACS Nano, 2014, 8, 514.
21. W. Feng, W. Zheng, F. Gao, X. Chen, G. Liu, T. Hasan, W. Cao and P. Hu, Chem. Mater., 2016, 28, 4278.
22. D. Wu, A. J. Pak, Y. Liu, Y. Zhou, X. Wu, Y. Zhu, M. Lin, Y. Han, Y. Ren, H. Peng, Y. Tsai, G. S. Hwang and K. Lai, Nano Lett., 2015, 15, 8136.
23. J. Quereda, R. Biele, G. Rubio-Bollinger, N. Agraït, R. D'Agosta and A. Castellanos-Gomez, Adv. Opt. Mater., 2016, 4, 1939.
24. L. Debbichi, O. Eriksson and S. Lebègue, J. Phys. Chem. Lett., 2015, 6, 3098.
25. W. Ding, J. Zhu, Z. Wang, Y. Gao, D. Xiao, Y. Gu, Z. Zhang and W. Zhu, Nat. Commun., 2017, 8, 14956.
26. H. Wang and X. Qian, Nano Lett., 2017, 17, 5027.
27. L. Hu, X. R. Huang and D. S. Wei, Phys. Chem. Chem. Phys., 2017, 19, 11131.
28. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
29. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
30. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
31. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
32. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
34. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
35. C. Y. Wang and G. Y. Guo, J. Phys. Chem. C, 2015, 119, 13268.
36. H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232.
37. C. Aversa and J. E. Sipe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14636.
38. S. N. Rashkeev, W. R. L. Lambrecht and B. Segall, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3905.
39. Z. Fang, J. Lin, R. Liu, P. Liu, Y. Li, X. Huang, K. Ding, L. Ning and Y. Zhang, CrystEngComm, 2014, 16, 10569.
40. M. Grüning and C. Attaccalite, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 081102.
41. H. C. Hsueh, G. Y. Guo and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085404.
42. F. Karlický and M. Otyepka, Ann. Phys., 2014, 526, 408.
43. Y. Li, Y. Rao, K. F. Mak, Y. You, S. Wang, C. R. Dean and T. F. Heinz, Nano Lett., 2013, 13, 3329.
44. L. Bai, Z. Lin, Z. Wang, C. Chen and M. H. Lee, J. Chem. Phys., 2004, 120, 8772.
45. Z. Ma, K. Wu, R. Sa, Q. Li and Y. Zhang, J. Alloys Compd., 2013, 568, 16.
46. X. Wu, D. Vanderbilt and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035105.
47. H. L. Zhuang, M. D. Johannes, M. N. Blonsky and R. G. Hennig, Appl. Phys. Lett., 2014, 104, 022116.
48. M. Born and H. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 1954.
49. F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
50. D. Çakır, F. M. Peeters and C. Sevik, Appl. Phys. Lett., 2014, 104, 203110.
51. M. M. Alyörük, Y. Aierken, D. Çakır, F. M. Peeters and C. Sevik, J. Phys. Chem. C, 2015, 119, 23231.
52. J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra11014f

---