Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-consistent determination of the fictitious temperature in thermally-assisted-occupation density functional theory†
Chih-Ying Lina,
Kerwin Huia,
Jui-Hui Chunga and
Jeng-Da Chai *ab
*ab
aDepartment of Physics, National Taiwan University, Taipei 10617, Taiwan. E-mail: jdchai@phys.ntu.edu.tw
bCenter for Theoretical Sciences and Center for Quantum Science and Engineering, National Taiwan University, Taipei 10617, Taiwan
First published on 30th October 2017
Abstract
We propose a self-consistent scheme for the determination of the fictitious temperature in thermally-assisted-occupation density functional theory (TAO-DFT) [J.-D. Chai, J. Chem. Phys., 2012, 136, 154104], a very efficient electronic structure method for studying nanoscale systems with strong static correlation effects (which are “challenging systems” for traditional electronic structure methods). In comparison with semilocal density functionals in Kohn–Sham density functional theory (KS-DFT), the corresponding semilocal density functionals in TAO-DFT (with the self-consistent fictitious temperature) provide significant improvement for systems with strong static correlation effects (e.g., the dissociation of H2 and N2 and twisted ethylene), and retain very similar performance for systems without strong static correlation effects (e.g., thermochemistry, kinetics, and reaction energies), yielding a much more balanced performance for both types of systems than those in KS-DFT. Besides, a reliably accurate description of noncovalent interactions can be efficiently achieved via the inclusion of dispersion corrections in TAO-DFT. Relative to the previous system-independent fictitious temperature scheme in TAO-DFT, the present self-consistent fictitious temperature scheme in TAO-DFT is generally superior in performance for a very broad range of applications.
I. Introduction
Over the last 20 years, Kohn–Sham density functional theory (KS-DFT)1 has been a very popular electronic structure method for the ground-state properties of large systems, due to its delicate balance between cost and performance.2 However, since the exact exchange–correlation (XC) energy functional Exc[ρ] (i.e., the essential ingredient of KS-DFT) has not been known, density functional approximations (DFAs) for Exc[ρ] have been consecutively developed to extend the applicability of KS-DFT to a wide range of systems.Functionals based on the conventional semilocal DFAs, such as the local density approximation (LDA)3,4 and generalized gradient approximations (GGAs),5–7 are reasonably accurate for properties governed by short-range XC effects, and are computationally efficient for very large systems (for brevity, hereafter we adopt “DFAs” for “the conventional semilocal DFAs”). Nevertheless, the DFA XC functionals in KS-DFT (KS-DFAs) can yield erroneous results in situations where an accurate description of nonlocal XC effects is necessary.8–18 Since the 1990s, numerous efforts have been made by researchers to reduce the qualitative failures of KS-DFAs at affordable computational costs.
In particular, an accurate prediction of the ground-state properties of systems with strong static correlation effects (i.e., multi-reference (MR) systems) has been a very important and challenging subject in KS-DFT.8,14–18 Within the framework of KS-DFT, the conventional DFA,3–7 global hybrid,19,20 range-separated hybrid,21–26 and double-hybrid27 XC functionals can lead to unreliable results for MR systems, due to the inappropriate treatment of static correlation. Fully nonlocal XC functionals, such as those based on the random phase approximation (RPA), can be essential to provide a reasonably accurate description of static correlation. However, these functionals are computationally very demanding, which limits their application only to small systems.2,9,28,29
To address these challenges with minimum computational complexity, Chai has recently developed thermally-assisted-occupation density functional theory (TAO-DFT),16–18 a density functional theory with fractional orbital occupations given by the Fermi–Dirac distribution function (controlled by a fictitious temperature θ), wherein strong static correlation is explicitly described by the entropy contribution (e.g., see eqn (26) of ref. 16). Unlike finite-temperature density functional theory (which is developed for the thermodynamic properties of physical systems at finite temperatures),30 TAO-DFT is developed for the ground-state properties of physical systems at zero temperature (just like KS-DFT). The conventional DFA, global hybrid, and range-separated hybrid XC functionals in KS-DFT can be combined seamlessly with TAO-DFT.16–18 Note also that TAO-DFT has similar computational cost as KS-DFT for single-point energy and analytical nuclear gradient calculations, and reduces to KS-DFT for systems without strong static correlation effects (i.e., single-reference (SR) systems). Accordingly, TAO-DFT provides a much more balanced performance for both SR and MR systems than KS-DFT. Very recently, TAO-DFT has been applied to study the ground-state properties of nanoscale systems (e.g., containing up to a few thousand electrons) with strong static correlation effects,31–35 all of which are very challenging systems for traditional electronic structure methods!
Nevertheless, as the optimal θ in TAO-DFT is closely related to the strength of static correlation,16–18 it should be sufficiently small for SR systems, and can span a wide range of values for MR systems. Therefore, for the DFA functionals in TAO-DFT (TAO-DFAs), it is impossible to adopt a common (system-independent) θ that is optimal for both SR and MR systems. To go beyond the previous TAO-DFAs (with a system-independent θ), in this work, we propose an iterative scheme for the self-consistent determination of θ for TAO-DFAs, yielding very promising performance for a wide variety of SR and MR systems. The rest of this paper is organized as follows. First, we briefly review the formulation of TAO-DFT. Secondly, we define and discuss a number of properties associated with the reference system in TAO-DFT, yielding a stability index in TAO-DFT. Thirdly, we develop a self-consistent scheme for the determination of θ (based on the stability index), and examine the performance of TAO-DFAs (with the self-consistent θ) for various SR and MR systems. Finally, we give our conclusions and future plans.
II. TAO-DFT
A. Self-consistent equations
Consider a physical system of Nα up-spin and Nβ down-spin electrons moving in an external potential vext(r) at zero (physical) temperature. In spin-polarized (spin-unrestricted) TAO-DFT,16,17 one adopts the thermally-assisted-occupation (TAO) reference system, which is an auxiliary system with Nα up-spin and Nβ down-spin noninteracting electrons at the fictitious (reference) temperature θ (measured in energy units), with the corresponding thermal equilibrium density distributions ρs,α(r) and ρs,β(r) exactly equal to the up-spin density ρα(r) and down-spin density ρβ(r), respectively, of the original interacting (physical) system at zero temperature. The resulting self-consistent equations for the σ-spin electrons (σ = α or β) are given by (i runs for the orbital index)
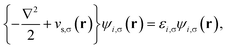 | (1) |
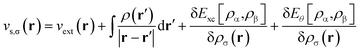 | (2) |
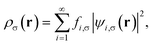 | (3) |
| fi,σ = {1 + exp[(εi,σ − μσ)/θ]}−1, | (4) |
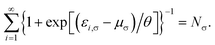 | (5) |
The formulation of spin-polarized TAO-DFT yields the two sets (one for each spin function) of self-consistent equations, eqn (1) to (5), for ρα(r) and ρβ(r), respectively, which are coupled with the ground-state density
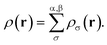 | (6) |
The self-consistent procedure described in ref. 16 may be adopted to obtain the converged {εi,σ}, {fi,σ}, {ψi,σ(r)}, ρα(r), and ρ(r). Subsequently, the noninteracting kinetic free energy
| Asθ[{fi,α,ψi,α},{fi,β,ψi,β}] = Tsθ[{fi,α,ψi,α},{fi,β,ψi,β}] + ESθ[{fi,α},{fi,β}] | (7) |
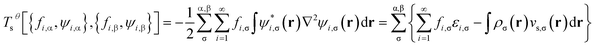 | (8) |
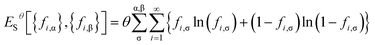 | (9) |
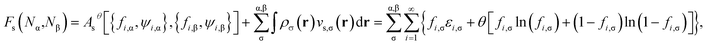 | (10) |
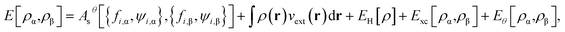 | (11) |
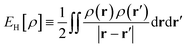 is the Hartree energy. Spin-unpolarized (spin-restricted) TAO-DFT can be formulated by imposing the constraints of ψi,α(r) = ψi,β(r) and fi,α = fi,β to spin-polarized TAO-DFT. Note also that TAO-DFT at θ = 0 is the same as KS-DFT.
is the Hartree energy. Spin-unpolarized (spin-restricted) TAO-DFT can be formulated by imposing the constraints of ψi,α(r) = ψi,β(r) and fi,α = fi,β to spin-polarized TAO-DFT. Note also that TAO-DFT at θ = 0 is the same as KS-DFT.
B. Strong static correlation from the DFA and hybrid functionals in TAO-DFT
As the exact Exc[ρα,ρβ] and Eθ[ρα,ρβ] (i.e., the essential ingredients of spin-polarized TAO-DFT), in terms of the spin densities ρα(r) and ρβ(r), remain unknown, it is necessary to develop DFAs for both Exc[ρα,ρβ] and Eθ[ρα,ρβ] in TAO-DFT (i.e., TAO-DFAs) for practical purposes. Therefore, the accuracy of TAO-DFAs depends on the underlying DFAs and the chosen fictitious temperature θ. Noted that EDFAxc[ρα,ρβ] can be readily obtained from that of KS-DFA, and EDFAθ[ρα,ρβ] can be constructed from AsDFA,θ[ρα,ρβ], which can be expressed in terms of its spin-unpolarized form AsDFA,θ[ρ]:
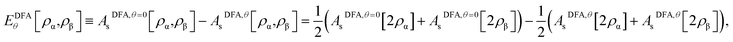 | (12) |
In 2012, Chai developed TAO-LDA (i.e., the first and simplest TAO-DFA),16 adopting the LDA XC functional ELDAxc[ρα,ρβ]3,4 and the LDA θ-dependent energy functional ELDAθ[ρα,ρβ] (given by eqn (12) with AsLDA,θ[ρ], the LDA for Asθ[ρ]39 (also see eqn (37) of ref. 16)) in TAO-DFT. Even at the simplest LDA level, TAO-LDA was shown to provide a reasonably accurate description of static correlation via the entropy contribution ESθ[{fi,α},{fi,β}] (see eqn (9)), when the distribution of TOONs {fi,σ} (related to the chosen θ) is close to the distribution of the natural orbital occupation numbers (NOONs) for an interacting (physical) system.40 This suggests that a θ related to the distribution of NOONs should be adopted for TAO-LDA to adequately describe strong static correlation effects. Nonetheless, for the sake of simplicity, an optimal system-independent θ = 7 mhartree for TAO-LDA was previously defined as the largest θ value for which the performance of TAO-LDA (with this θ) and that of KS-LDA (i.e., the θ = 0 case) remain comparable for SR systems. Consequently, TAO-LDA (with θ = 7 mhartree) was shown to consistently outperform KS-LDA for MR systems (due to the appropriate treatment of static correlation), while performing comparably to KS-LDA for SR systems (i.e., in the absence of strong static correlation effects).
To go beyond TAO-LDA with similar computational complexity, in 2014, Chai also developed TAO-GGAs,17 employing the GGA XC functionals EGGAxc[ρα,ρβ] and the gradient expansion approximation (GEA) θ-dependent energy functional EGEAθ[ρα,ρβ] (given by eqn (12) with AsGEA,θ[ρ], the GEA for Asθ[ρ]39) in TAO-DFT. Since TAO-GGAs should outperform TAO-LDA mainly for properties governed by short-range XC effects,2,9 and the orbital energy gaps of TAO-LDA and TAO-GGAs (i.e., TAO-DFAs) should be similar,10 the optimal θ values for all TAO-DFAs should remain similar. Therefore, the optimal system-independent θ = 7 mhartree can be adopted for all TAO-DFAs. By construction, EGEAθ[ρα,ρβ] should be more accurate than ELDAθ[ρα,ρβ] for the nearly uniform electron gas. However, for a small θ value (i.e., 7 mhartree), their difference was found to be much smaller than the difference between two distinct XC functionals. Therefore, ELDAθ[ρα,ρβ] may also be employed for TAO-GGAs. TAO-DFAs (with θ = 7 mhartree) were indeed shown to consistently outperform the corresponding KS-DFAs (i.e., the θ = 0 cases) for MR systems, while performing comparably to the corresponding KS-DFAs for SR systems. TAO-GGAs were found to be superior to TAO-LDA in performance for a broad range of SR systems. Besides, the inclusion of dispersion corrections in TAO-DFAs was found to yield an efficient and reasonably accurate description of noncovalent interactions.
To provide an improved description of nonlocal exchange effects, in 2017, Chai further developed the global and range-separated hybrid schemes in TAO-DFT,18 incorporating the exact exchange into TAO-DFAs. With a few simple modifications, the conventional global hybrid and range-separated hybrid XC functionals in KS-DFT can be combined seamlessly with TAO-DFT. Similar to TAO-DFAs, a global hybrid functional in TAO-DFT was also shown to provide a reasonably accurate description of static correlation, when the distribution of TOONs {fi,σ} (related to the chosen θ) is close to the distribution of NOONs. Note that a global hybrid functional with a larger fraction of exact exchange yields larger orbital energy gaps,10 and hence requires a larger θ value to retain a similar distribution of TOONs in TAO-DFT. In the system-independent θ scheme, a linear relationship between the optimal θ value and the fraction of exact exchange ax was established for a global hybrid functional in TAO-DFT. Global hybrid functionals in TAO-DFT (with the optimal system-independent θ values) were found to consistently outperform the corresponding global hybrid functionals in KS-DFT (i.e., the θ = 0 cases) for MR systems, while performing comparably to the corresponding global hybrid functionals in KS-DFT for SR systems. Relative to TAO-DFAs, global hybrid functionals in TAO-DFT were shown to be generally superior in performance for a wide range of applications. In addition, the inclusion of dispersion corrections in hybrid TAO-DFT was also found to lead to an efficient and reasonably accurate description of noncovalent interactions.
C. System-independent θ scheme
TAO-DFT with DFA and global hybrid functionals in the aforementioned system-independent θ scheme is conceptually simple, easy to implement, computationally efficient, and reasonably accurate for a wide range of SR and MR systems.16–18 Furthermore, the analytical computation of nuclear gradients is readily available for this scheme, which is crucially important for the efficient optimization of molecular geometries. Therefore, this scheme can be promising for the study of ground states of large SR and MR systems. However, as with all approximate electronic structure methods, some limitations remain. While the DFA and global hybrid functionals in TAO-DFT (with the optimal system-independent θ values) perform comparably to the corresponding DFA and global hybrid functionals in KS-DFT (i.e., the θ = 0 cases) for several SR systems, some results remain noticeably different (e.g., atomization energies and noncovalent interactions),17,18 wherein the smaller θ values should be adopted. On the other hand, the DFA and global hybrid functionals in TAO-DFT (with the optimal system-independent θ values) can provide insufficient amounts of static correlation for some MR systems (e.g., the dissociation of H2 and N2 and twisted ethylene),16–18 wherein the larger θ values should be employed. Accordingly, to improve the performance of the DFA and global hybrid functionals in TAO-DFT for a wide range of SR and MR systems, the optimal θ could be related to the stability (i.e., the SR/MR character) of systems.To improve upon the system-independent θ scheme, in the following sections, we define and discuss various properties associated with the TAO reference system, which are shown to be useful for the definition of a stability index in TAO-DFT. In addition, we express the optimal θ of a system as a function of the stability index, yielding a self-consistent scheme for the determination of optimal θ in TAO-DFT.
III. Various properties of the TAO reference system
Here, we define and discuss various properties associated with the TAO reference system, which can be obtained rather straightforwardly from standard TAO-DFT calculations at essentially no extra computational cost.For a physical system with Nσ σ-spin (σ = α or β) and N![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif)
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) -spin (i.e., opposite-spin) electrons in an external potential vext(r) at zero (physical) temperature, the TAO reference system (i.e., an auxiliary system with Nσ σ-spin and N
-spin (i.e., opposite-spin) electrons in an external potential vext(r) at zero (physical) temperature, the TAO reference system (i.e., an auxiliary system with Nσ σ-spin and N![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif)
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) -spin noninteracting electrons at the fictitious temperature θ) is adopted in spin-polarized TAO-DFT.16,17 As mentioned previously, the Helmholtz free energy of the TAO reference system at the fictitious temperature θ is given by (see eqn (10))
-spin noninteracting electrons at the fictitious temperature θ) is adopted in spin-polarized TAO-DFT.16,17 As mentioned previously, the Helmholtz free energy of the TAO reference system at the fictitious temperature θ is given by (see eqn (10))
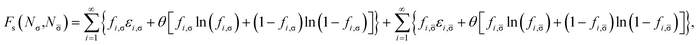 | (13) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) } are the TAO orbital energies (see eqn (1)), and {fi,σ} and {fi,
} are the TAO orbital energies (see eqn (1)), and {fi,σ} and {fi,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) } are the TOONs given by the Fermi–Dirac distribution function (see eqn (4))
} are the TOONs given by the Fermi–Dirac distribution function (see eqn (4))| fi,σ = {1 + exp[(εi,σ − μσ)/θ]}−1, | (14) |
fi,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) = {1 + exp[(εi, = {1 + exp[(εi,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) − μ − μ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) )/θ]}−1, )/θ]}−1,
| (15) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) (see eqn (5)) are the chemical potentials chosen to conserve Nσ and N
(see eqn (5)) are the chemical potentials chosen to conserve Nσ and N![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) , respectively,
, respectively,
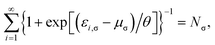 | (16) |
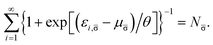 | (17) |
Removing a σ-spin electron from the TAO reference system at fixed vs,σ(r) and vs,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) (r) (i.e., {εi,σ} and {εi,
(r) (i.e., {εi,σ} and {εi,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) } remain unchanged, respectively) yields the Helmholtz free energy
} remain unchanged, respectively) yields the Helmholtz free energy
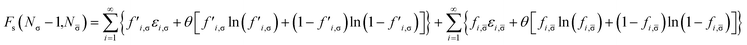 | (18) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif)
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) -spin electrons in the TAO reference system. Here, the σ-spin TOONs {f′i,σ} are rearranged based on the Fermi–Dirac distribution function
-spin electrons in the TAO reference system. Here, the σ-spin TOONs {f′i,σ} are rearranged based on the Fermi–Dirac distribution function| f′i,σ = {1 + exp[(εi,σ − μ′σ)/θ]}−1, | (19) |
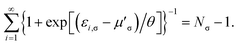 | (20) |
Therefore, the σ-spin ionization potential of the TAO reference system can be defined as
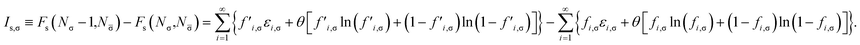 | (21) |
Similarly, adding a σ-spin electron to the TAO reference system at fixed vs,σ(r) and vs,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) (r) (i.e., {εi,σ} and {εi,
(r) (i.e., {εi,σ} and {εi,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) } remain unchanged, respectively) yields the Helmholtz free energy
} remain unchanged, respectively) yields the Helmholtz free energy
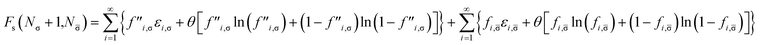 | (22) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif)
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) -spin electrons in the TAO reference system. Here, the σ-spin TOONs {f′′i,σ} are rearranged based on the Fermi–Dirac distribution function
-spin electrons in the TAO reference system. Here, the σ-spin TOONs {f′′i,σ} are rearranged based on the Fermi–Dirac distribution function| f′′i,σ = {1 + exp[(εi,σ − μ′′σ)/θ]}−1, | (23) |
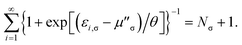 | (24) |
Accordingly, the σ-spin electron affinity of the TAO reference system can be defined as
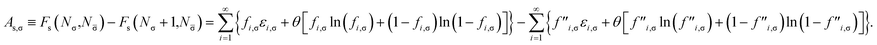 | (25) |
Consequently, the σ-spin TAO gap can be defined as
| ΔTAO,σ ≡ Is,σ − As,σ. | (26) |
At θ = 0, TAO-DFT reduces to KS-DFT, wherein Is,σ = −εNσ,σ (the negative of the orbital energy of the σ-spin HOMO (highest occupied molecular orbital)), As,σ = −εNσ+1,σ (the negative of the orbital energy of the σ-spin LUMO (lowest unoccupied molecular orbital)), and hence ΔTAO,σ = εNσ+1,σ − εNσ,σ (the σ-spin HOMO–LUMO gap).
In addition, the ionization potential of the TAO reference system can be defined as
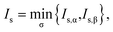 | (27) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) (r). Similarly, the electron affinity of the TAO reference system can be defined as
(r). Similarly, the electron affinity of the TAO reference system can be defined as
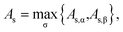 | (28) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) (r). Accordingly, the TAO gap can be defined as
(r). Accordingly, the TAO gap can be defined as
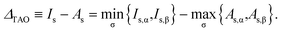 | (29) |
IV. Self-consistent θ scheme for TAO-DFAS
A. Stability index in TAO-DFT: ΔMST
For a spin-unpolarized system with high stability (i.e., low chemical reactivity), the exact NOONs should be very close to either 0 or 1, the optimal θ in TAO-DFT should be vanishingly small, and hence the corresponding TAO gap (ΔTAO), which should be very close to the HOMO–LUMO gap in KS-DFT for this system, should be very large. In KS-DFT, the HOMO–LUMO gap (or a closely related quantity, the global hardness) has been commonly adopted as an important stability index for a spin-unpolarized system.41–47 Accordingly, in TAO-DFT, we adopt the TAO gap as the stability index for a spin-unpolarized system. The larger the TAO gap, the more stable the spin-unpolarized system.For a spin-polarized system, the α-spin TAO gap (ΔTAO,α) and the β-spin TAO gap (ΔTAO,β), which serve as the stability indexes for the α-spin electrons and β-spin electrons, respectively, of the system can be different. Therefore, to have a unique description for the system stability, we adopt the maximum spin TAO gap
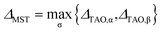 | (30) |
B. Determination of the self-consistent θ
As previously mentioned, the fictitious temperature θ in TAO-DFT should be chosen so that the distribution of TOONs is close to that of NOONs.16,17 In this situation, the strong static correlation effects can be adequately described by the entropy contribution. While the exact NOONs are intractable for large systems (due to the exponential complexity), some common characteristics are summarized as follows. Since SR systems do not have significant amounts of static correlation, the exact NOONs should be close to either 0 or 1, which can be properly simulated by the TOONs in TAO-DFT (with a sufficiently small θ). However, for MR systems, the distribution of NOONs can be diverse (due to the varying strength of static correlation), and hence, the optimal θ in TAO-DFT can span a wide range of values. As shown in ref. 16 and 17, the optimal system-independent θ for TAO-DFAs is about 40 mhartree for the dissociation of H2 and N2, and about 15 mhartree for twisted ethylene. Therefore, for TAO-DFAs, it is impossible to adopt a system-independent θ that is optimal for a wide range of SR and MR systems.To rectify the above situations, it is essential to go beyond the system-independent θ scheme. In the present scheme, we express the fictitious temperature of a spin-polarized system
θ ≡ θ(ΔMST) = θ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) erfc(ΔMST/Δ0) erfc(ΔMST/Δ0)
| (31) |
| θ0 = 40 mhartree | (32) |
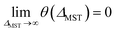 .
.
For a given Δ0, the self-consistent θ of a spin-polarized system can be obtained as follows: (i) choose a trial θ (between 0 and θ0); (ii) with this θ, follow the self-consistent procedure described in ref. 16 to obtain the converged TAO orbital energies {εi,σ} and TOONs {fi,σ}; (ii) determine ΔTAO,σ by eqn (26), ΔMST by eqn (30), and new θ by eqn (31). This process is repeated, until self-consistency is attained.
All calculations are performed with a development version of Q-Chem 4.3.48 Spin-restricted theory is used for singlet states and spin-unrestricted theory for others, unless noted otherwise. For the interaction energies of the weakly bound systems, the counterpoise correction49 is adopted to reduce the basis set superposition error (BSSE). Results are computed using the 6-311++G(3df,3pd) basis set with the fine grid EML(75,302), consisting of 75 Euler–Maclaurin radial grid points and 302 Lebedev angular grid points, unless noted otherwise. The error for each entry is defined as (error = theoretical value − reference value). The notation adopted for characterizing statistical errors is as follows: mean signed errors (MSEs), mean absolute errors (MAEs), root-mean-square (rms) errors, maximum negative errors (Max(−)), and maximum positive errors (Max(+)).
For a system with a non-vanishing ΔMST (e.g., a SR system), θ = 0 for Δ0 = 0 and θ = θ0 as Δ0 → ∞. Therefore, for SR systems, the performance of TAO-DFAs (with a sufficiently small Δ0) in the present scheme should be very similar to that of the corresponding KS-DFAs (i.e., the θ = 0 cases). Accordingly, the numerical investigations described in ref. 16 can be adopted to define the optimal Δ0 value for TAO-DFAs in the present scheme.
In this work, the performance of TAO-LDA (with Δ0 = 5, 10, 15, …, and 100 mhartree) in the present scheme is examined for the SR systems: the reaction energies of the 30 chemical reactions in the NHTBH38/04 and HTBH38/04 sets.50,51 The optimal Δ0 value for TAO-LDA in the present scheme is defined as the largest Δ0 value for which the difference between the rms error of TAO-LDA (with this Δ0) in the present scheme and that of KS-LDA (i.e., the θ = 0 case) is less than 0.1 kcal mol−1 for the 30 reaction energies. On the basis of our numerical investigations (see Fig. 1), the optimal characteristic gap for TAO-LDA is estimated to be
| Δ0 = 70 mhartree. | (33) |
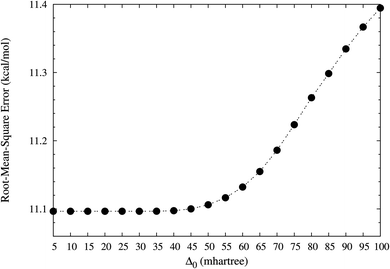 | ||
| Fig. 1 Root-mean-square (rms) errors of the reaction energies of the 30 chemical reactions in the NHTBH38/04 and HTBH38/04 sets,50,51 calculated using TAO-LDA (with various Δ0) in the present self-consistent θ scheme (together with eqn (31) and (32)). The rms error of KS-LDA (i.e., the θ = 0 case) is numerically the same as that of TAO-LDA (with Δ0 = 5 mhartree) in the present scheme for the 30 reaction energies. | ||
In the present self-consistent θ scheme, our preliminary TAO-LDA results show that the converged θ value for each system studied is unique (within the numerical accuracy of our calculations, i.e., 0.01 mhartree), regardless of the choice of initial trial θ values. Therefore, for all the TAO-DFA calculations in this work, we adopt the initial trial θ = 7 mhartree, unless noted otherwise.
As mentioned previously, the orbital energy gaps of TAO-LDA and TAO-GGAs (i.e., TAO-DFAs) should be similar, and hence, the same optimal characteristic gap (given by eqn (33)) can be adopted for all TAO-DFAs in the present scheme. To further confirm this, we examine the performance of TAO-LDA and various TAO-GGAs (with the self-consistent θ given by eqn (31)–(33)) on the 30 reaction energies. For brevity, hereafter the self-consistent θ given by eqn (31)–(33) is denoted as θ*. The results are compared with those obtained from the corresponding KS-DFAs (i.e., the θ = 0 cases) and TAO-DFAs (with the optimal system-independent θ = 7 mhartree).17 For the choice of TAO-GGAs, we adopt TAO-PBE, TAO-BLYP, and TAO-BLYP-D, which are the PBE,5 BLYP,6,7 and BLYP-D (i.e., BLYP with dispersion corrections)12 XC functionals (together with the LDA θ-dependent energy functional ELDAθ) in TAO-DFT.17 At θ = 0, TAO-LDA, TAO-PBE, TAO-BLYP, and TAO-BLYP-D reduce to KS-LDA, KS-PBE, KS-BLYP, and KS-BLYP-D, respectively.
As shown in Table 1, the 30 reaction energies calculated using TAO-LDA, TAO-PBE, TAO-BLYP, and TAO-BLYP-D (with θ*) are indeed very similar to those calculated using KS-LDA, KS-PBE, KS-BLYP, and KS-BLYP-D, respectively (see Table S1 in ESI†). By contrast, the results obtained with TAO-DFAs (with θ = 7 mhartree) are only qualitatively similar to those obtained with the corresponding KS-DFAs (i.e., the θ = 0 cases).17
| θ* | θ = 0 mhartree | θ = 7 mhartree | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LDA | PBE | BLYP | BLYP-D | LDA | PBE | BLYP | BLYP-D | LDA | PBE | BLYP | BLYP-D | |
| MSE | −0.55 | 0.85 | 0.56 | 0.50 | −0.41 | 1.08 | 0.80 | 0.74 | −1.32 | 0.23 | −0.12 | −0.20 |
| MAE | 8.63 | 4.57 | 3.37 | 3.19 | 8.51 | 4.39 | 3.23 | 3.02 | 7.09 | 3.97 | 3.80 | 3.67 |
| rms | 11.19 | 6.39 | 4.47 | 4.31 | 11.10 | 6.24 | 4.37 | 4.20 | 9.38 | 5.97 | 4.95 | 4.89 |
| Max(−) | −18.31 | −8.12 | −7.24 | −7.28 | −18.31 | −7.86 | −7.24 | −7.28 | −15.92 | −8.89 | −11.24 | −11.71 |
| Max(+) | 35.68 | 22.59 | 11.96 | 12.03 | 35.68 | 22.59 | 11.96 | 12.03 | 30.50 | 21.60 | 10.65 | 10.73 |
C. Results and discussion for the test sets
For a comprehensive comparison, we assess the performance of TAO-LDA, TAO-PBE, TAO-BLYP, and TAO-BLYP-D (with the θ* and system-independent θ values) on various test sets, including both SR and MR systems.• The 223 atomization energies (AEs) of the G3/99 set,52–54
• The 40 ionization potentials (IPs), 25 electron affinities (EAs), and 8 proton affinities (PAs) of the G2-1 set,55
• The 76 barrier heights (BHs) of the NHTBH38/04 and HTBH38/04 sets,50,51
• The 22 noncovalent interactions of the S22 set.56
Since these systems do not possess much static correlation, the exact NOONs should be close to either 0 or 1, and hence can be properly simulated by the TOONs of TAO-DFAs (with a sufficiently small θ).
Table 2 summarizes the statistical errors of TAO-LDA, TAO-PBE, TAO-BLYP, and TAO-BLYP-D (with various θ values) for the ωB97 training set (see Tables S2 to S4 in ESI†). While the results obtained from TAO-DFAs (with the optimal system-independent θ = 7 mhartree)17 are qualitatively similar to those obtained from the corresponding KS-DFAs (i.e., the θ = 0 cases), some results remain noticeably different (e.g., the AEs of the G3/99 set), showing the limitations of TAO-DFAs (with θ = 7 mhartree). By contrast, TAO-DFAs (with θ*) perform very similarly to the corresponding KS-DFAs for the entire ωB97 training set! Therefore, it can be anticipated that the accuracy of KS-DFAs can essentially be transferred to that of the corresponding TAO-DFAs (with θ*) for a wide range of SR systems, revealing the significance of the present scheme. Relative to TAO-LDA, TAO-GGAs provide enormous improvement for the AEs of the G3/99 set, the EAs and PAs of the G2-1 set, and the BHs of the NHTBH38/04 and HTBH38/04 sets, due to the improved treatment of short-range XC effects. For the IPs of the G2-1 set, TAO-GGAs perform slightly better than TAO-LDA. For the noncovalent interactions of the S22 set, KS-BLYP-D and TAO-BLYP-D (i.e., the dispersion-corrected functionals13 in KS-DFT and TAO-DFT, respectively) are reliably accurate, while all the other functionals perform poorly.
| System | Error | θ* | θ = 0 mhartree | θ = 7 mhartree | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LDA | PBE | BLYP | BLYP-D | LDA | PBE | BLYP | BLYP-D | LDA | PBE | BLYP | BLYP-D | ||
| G3/99 (223) | MSE | 120.47 | 20.75 | −4.74 | −0.98 | 120.60 | 20.90 | −4.59 | −0.83 | 95.02 | 7.91 | −16.24 | −12.27 |
| MAE | 120.54 | 21.48 | 9.84 | 7.04 | 120.60 | 21.51 | 9.76 | 7.03 | 95.04 | 11.41 | 19.01 | 15.33 | |
| rms | 142.37 | 26.15 | 12.99 | 9.15 | 142.51 | 26.30 | 12.96 | 9.17 | 114.19 | 15.07 | 24.24 | 19.35 | |
| IP (40) | MSE | 3.38 | 0.19 | −1.38 | −1.38 | 3.42 | 0.03 | −1.50 | −1.50 | 1.79 | −1.08 | −2.61 | −2.61 |
| MAE | 5.56 | 3.44 | 4.31 | 4.31 | 5.54 | 3.46 | 4.43 | 4.44 | 6.18 | 4.86 | 6.10 | 6.10 | |
| rms | 6.69 | 4.32 | 5.16 | 5.17 | 6.66 | 4.35 | 5.28 | 5.29 | 7.63 | 6.00 | 7.40 | 7.40 | |
| EA (25) | MSE | 6.13 | 1.19 | −0.06 | −0.07 | 6.45 | 1.72 | 0.36 | 0.36 | 4.20 | 0.22 | −1.08 | −1.07 |
| MAE | 6.13 | 2.82 | 2.83 | 2.83 | 6.45 | 2.42 | 2.57 | 2.57 | 5.49 | 2.88 | 4.38 | 4.40 | |
| rms | 7.02 | 3.51 | 3.46 | 3.48 | 7.29 | 3.06 | 3.17 | 3.17 | 6.45 | 3.44 | 5.44 | 5.47 | |
| PA (8) | MSE | −5.91 | −0.83 | −1.47 | −1.09 | −5.91 | −0.83 | −1.47 | −1.09 | −5.66 | −0.58 | −1.22 | −0.84 |
| MAE | 5.91 | 1.60 | 1.58 | 1.55 | 5.91 | 1.60 | 1.58 | 1.55 | 5.66 | 1.47 | 1.50 | 1.55 | |
| rms | 6.40 | 1.91 | 2.10 | 1.98 | 6.40 | 1.91 | 2.10 | 1.98 | 6.16 | 1.80 | 1.94 | 1.86 | |
| NHTBH (38) | MSE | −12.50 | −8.71 | −8.89 | −9.53 | −12.41 | −8.52 | −8.69 | −9.32 | −11.93 | −8.38 | −8.52 | −9.15 |
| MAE | 12.71 | 8.81 | 8.93 | 9.55 | 12.62 | 8.62 | 8.72 | 9.35 | 12.15 | 8.49 | 8.56 | 9.19 | |
| rms | 16.16 | 10.75 | 10.42 | 10.98 | 16.13 | 10.61 | 10.27 | 10.83 | 15.09 | 10.28 | 9.90 | 10.46 | |
| HTBH (38) | MSE | −17.90 | −9.67 | −7.84 | −8.89 | −17.90 | −9.67 | −7.84 | −8.89 | −16.34 | −9.20 | −7.25 | −8.33 |
| MAE | 17.90 | 9.67 | 7.84 | 8.89 | 17.90 | 9.67 | 7.84 | 8.89 | 16.34 | 9.20 | 7.29 | 8.34 | |
| rms | 18.92 | 10.37 | 8.66 | 9.52 | 18.92 | 10.37 | 8.66 | 9.52 | 17.06 | 9.87 | 8.24 | 9.17 | |
| S22 (22) | MSE | −1.95 | 2.78 | 5.07 | 0.24 | −1.97 | 2.77 | 5.05 | 0.23 | −2.30 | 2.44 | 4.70 | −0.12 |
| MAE | 2.07 | 2.78 | 5.07 | 0.34 | 2.08 | 2.77 | 5.05 | 0.33 | 2.33 | 2.44 | 4.70 | 0.28 | |
| rms | 3.17 | 3.90 | 6.33 | 0.45 | 3.18 | 3.89 | 6.31 | 0.45 | 3.40 | 3.57 | 5.95 | 0.37 | |
| Total (394) | MSE | 65.75 | 10.20 | −4.19 | −2.49 | 65.86 | 10.33 | −4.07 | −2.37 | 51.26 | 2.81 | −10.81 | −8.99 |
| MAE | 72.36 | 14.65 | 8.12 | 6.43 | 72.41 | 14.63 | 8.05 | 6.40 | 57.76 | 9.01 | 13.48 | 11.31 | |
| rms | 107.43 | 20.30 | 10.91 | 8.44 | 107.53 | 20.40 | 10.88 | 8.44 | 86.26 | 12.38 | 18.92 | 15.43 | |
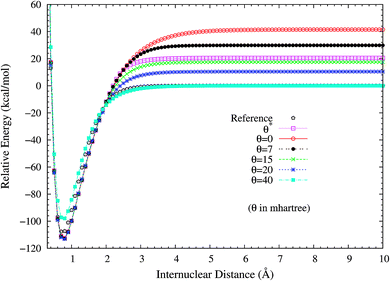
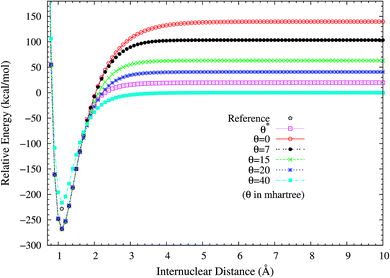
To investigate the performance of the present scheme for the SCE problems, the potential energy curves (in relative energy) for the ground state of H2 are calculated using spin-restricted TAO-LDA with various θ values (see Fig. 2), where the zeros of energy are set at the respective spin-unrestricted dissociation limits. The reference curve is obtained from the coupled-cluster theory with iterative singles and doubles (CCSD),57 which is equivalent to the exact full configuration interaction (FCI) method for any two-electron system.58 Near the equilibrium bond length of H2, where the SR character is dominant, TAO-LDA (with θ*) performs very similarly to KS-LDA (i.e., the θ = 0 case), matching reasonably well with the exact CCSD curve. Nevertheless, it has a noticeable SCE at the dissociation limit, where the MR character is significant. By contrast, while spin-restricted TAO-LDA (with θ = 40 mhartree) performs less satisfactorily at the equilibrium geometry, it can dissociate H2 correctly (i.e., possessing a vanishingly small SCE) to the respective spin-unrestricted dissociation limit.
To assess if this is relevant to the distribution of TOONs, we plot the occupation numbers of the 1σg orbital for the ground state of H2 as a function of the internuclear distance R, calculated using spin-restricted TAO-LDA with various θ values (see Fig. 3), where the reference data are the FCI NOONs (1.9643 at R = 0.741 Å (the equilibrium bond length), 1.5162 at R = 2.117 Å, and 1.0000 at R = 7.938 Å).58 As can be seen easily, the 1σg orbital occupation numbers of spin-restricted TAO-LDA (with θ = 40 mhartree) match reasonably well with the FCI NOONs, which is closely related to the vanishingly small SCE of TAO-LDA (with this θ). Similar results are also found for TAO-PBE, TAO-BLYP, and TAO-BLYP-D (see Fig. S1 and S2 in ESI†). Accordingly, in TAO-DFT, it is indeed essential to adopt a θ that is related to the distribution of NOONs.
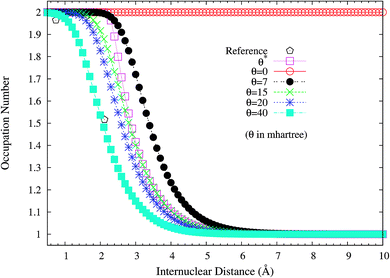 | ||
| Fig. 3 Occupation numbers of the 1σg orbital for the ground state of H2 as a function of the internuclear distance R, calculated using spin-restricted TAO-LDA with the θ* and system-independent θ values. The θ = 0 case corresponds to spin-restricted KS-LDA. The reference data are the FCI NOONs.58 | ||
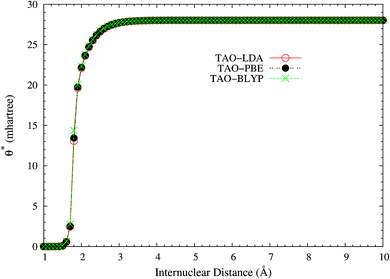
Here, we plot the θ* values for the ground state of H2 as a function of the internuclear distance R, calculated using spin-restricted TAO-LDA, TAO-PBE, and TAO-BLYP/TAO-BLYP-D in the present scheme. As shown in Fig. 4, the θ* values of spin-restricted TAO-DFAs are vanishingly small near the equilibrium bond length of H2 (i.e., in the absence of strong static correlation effects), and approach some constant values (about 15.5 mhartree) at the respective dissociation limits (i.e., in the presence of strong static correlation effects).
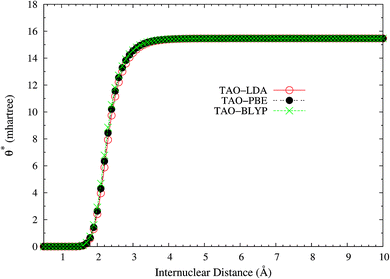 | ||
| Fig. 4 The θ* values for the ground state of H2 as a function of the internuclear distance R, calculated using spin-restricted TAO-LDA, TAO-PBE, and TAO-BLYP/TAO-BLYP-D in the present scheme. | ||
It is noteworthy that similar results are also found for N2 dissociation (a triple-bond breaking system), where experimental results are also presented for comparison.59,60 As shown in Fig. 5, spin-restricted TAO-LDA (with θ = 40 mhartree) can dissociate N2 properly (leading to a vanishingly small SCE) to the respective spin-unrestricted dissociation limit, which is highly correlated with the fact that the occupation numbers of the 3σg (see Fig. 6) and 1πux (see Fig. 7) orbitals for the ground state of N2 as functions of the internuclear distance R, calculated using TAO-LDA (with this θ), agree reasonably well with the corresponding NOONs of MR configuration interaction (MRCI) method (i.e., the reference data).61 Nevertheless, spin-restricted TAO-LDA (with θ = 40 mhartree) performs less satisfactorily near the equilibrium bond length of N2, where the SR character is pronounced. By contrast, TAO-LDA (with θ*) performs very similarly to KS-LDA (i.e., the θ = 0 case) near the equilibrium geometry, and performs reasonably well (yielding a small SCE) at the dissociation limit. Similar results are also found for TAO-PBE, TAO-BLYP, and TAO-BLYP-D (see Fig. S3 to S5 in ESI†). Unsurprisingly, the θ* values (see Fig. 8) of spin-restricted TAO-DFAs are vanishingly small near the equilibrium bond length of N2, and approach some constant values (about 28.0 mhartree) at the respective dissociation limits. This highlights the importance of the present scheme in TAO-DFT.
 | ||
| Fig. 5 Potential energy curves (in relative energy) for the ground state of N2, calculated using spin-restricted TAO-LDA with the θ* and system-independent θ values. The θ = 0 case corresponds to spin-restricted KS-LDA. The reference data (−228.3 (kcal mol−1) at R = 1.098 Å (i.e., the equilibrium bond length)) are the experimental results.59,60 The zeros of energy are set at the respective spin-unrestricted dissociation limits. | ||
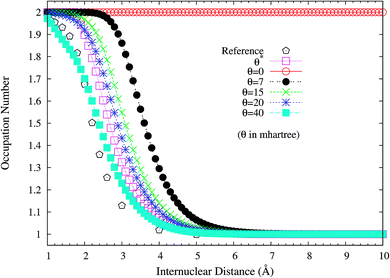 | ||
| Fig. 6 Occupation numbers of the 3σg orbital for the ground state of N2 as a function of the internuclear distance R, calculated using spin-restricted TAO-LDA with the θ* and system-independent θ values. The θ = 0 case corresponds to spin-restricted KS-LDA. The reference data are the NOONs of the MRCI method.61 | ||
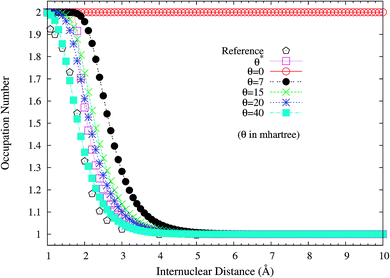 | ||
| Fig. 7 Occupation numbers of the 1πux orbital for the ground state of N2 as a function of the internuclear distance R, calculated using spin-restricted TAO-LDA with the θ* and system-independent θ values. The θ = 0 case corresponds to spin-restricted KS-LDA. The reference data are the NOONs of the MRCI method.61 | ||
To assess how spin-restricted TAO-DFT improves upon these problems, we plot the torsion potential energy curves (in relative energy) for the ground state of twisted ethylene as a function of the HCCH torsion angle, calculated using spin-restricted TAO-LDA with various θ values (see Fig. 9), where the zeros of energy are set at the respective minimum energies. The experimental geometry of ethylene (RCC = 1.339 Å, RCH = 1.086 Å, and ∠HCH = 117.6°)62 is adopted in the calculations. On the basis of the spin-restricted TAO-LDA results, the unphysical cusp can be removed with θ* or a system-independent θ larger than or equal to 7 mhartree. Besides, an accurate torsion barrier can be obtained from TAO-LDA (with θ = 15 mhartree), when compared with the torsion barrier obtained from the complete-active-space second-order perturbation theory (CASPT2), that is, 65.2 (kcal mol−1).63 While TAO-LDA (with θ*) consistently outperforms KS-LDA (i.e., the θ = 0 case) and TAO-LDA (with θ = 7 mhartree), the predicted torsion barrier remains a bit too high.
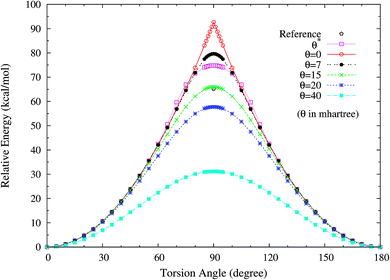 | ||
| Fig. 9 Torsion potential energy curves (in relative energy) for the ground state of twisted ethylene as a function of the HCCH torsion angle, calculated using spin-restricted TAO-LDA with the θ* and system-independent θ values. The θ = 0 case corresponds to spin-restricted KS-LDA. The reference data are the CASPT2 results.63 The zeros of energy are set at the respective minimum energies. | ||
To examine if this is also relevant to the distribution of TOONs, we plot the occupation numbers of the π(1b2) orbital for the ground state of twisted ethylene as a function of the HCCH torsion angle, calculated using spin-restricted TAO-LDA with various θ values. As shown in Fig. 10, the π(1b2) orbital occupation numbers of spin-restricted TAO-LDA (with θ = 15 mhartree) match reasonably well with the half-projected NOONs of complete-active-space self-consistent field (CASSCF) method (i.e., the reference data),64 which is closely related to the accurate torsion potential energy curve obtained from TAO-LDA (with this θ). Similar results are also found for TAO-PBE, TAO-BLYP, and TAO-BLYP-D (see Fig. S6 and S7 in ESI†). Again, this emphasizes the importance of adopting a θ related to the distribution of NOONs in TAO-DFT.
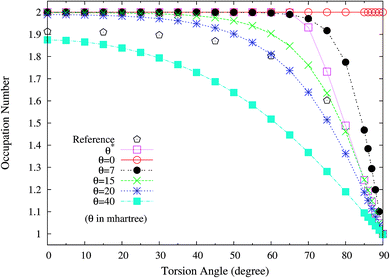 | ||
| Fig. 10 Occupation numbers of the π(1b2) orbital for the ground state of twisted ethylene as a function of the HCCH torsion angle, calculated using spin-restricted TAO-LDA with the θ* and system-independent θ values. The θ = 0 case corresponds to spin-restricted KS-LDA. The reference data are the half-projected NOONs of the CASSCF method (HPNO-CAS).64 | ||
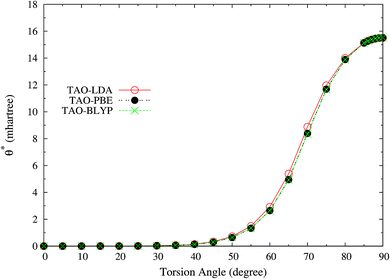
Here, we plot the θ* values for the ground state of twisted ethylene as a function of the HCCH torsion angle, calculated using spin-restricted TAO-LDA, TAO-PBE, and TAO-BLYP/TAO-BLYP-D in the present scheme. As shown in Fig. 11, the θ* values of spin-restricted TAO-DFAs are vanishingly small near the equilibrium geometry of ethylene (i.e., in the absence of strong static correlation effects), and reach the respective maximum values (about 15.5 mhartree) as the HCCH torsion angle is 90° (i.e., in the presence of strong static correlation effects).
V. Conclusions
In summary, we have developed an iterative scheme for the self-consistent determination of the fictitious temperature θ in TAO-DFT. In particular, TAO-DFAs (with the self-consistent fictitious temperature, i.e., θ*) have been shown to greatly improve upon the corresponding KS-DFAs (i.e., the θ = 0 cases) and TAO-DFAs (with the optimal system-independent θ = 7 mhartree) for MR systems (e.g., the dissociation of H2 and N2 and twisted ethylene), while performing very similarly to the corresponding KS-DFAs for SR systems (e.g., thermochemistry, kinetics, and reaction energies). It is expected that the accuracy of KS-DFAs could essentially be transferred to that of the corresponding TAO-DFAs (with θ*) for a wide range of SR systems. Therefore, TAO-DFAs (with θ*) can treat both SR and MR systems at the nanoscale in a much more balanced way than the corresponding KS-DFAs, revealing the importance of the present scheme! Besides, an approach combining TAO-DFAs and dispersion corrections has been shown to yield an efficient and reasonably accurate description of noncovalent interactions. Relative to TAO-LDA, TAO-GGAs are generally superior in performance for a broad range of applications, such as thermochemistry, kinetics, and reaction energies.In addition, as the orbital energy gaps of TAO-LDA and TAO-GGAs are similar, the self-consistent fictitious temperature in TAO-DFT is, essentially, DFA insensitive (e.g., see Fig. 4, 8 and 11). Therefore, for computational efficiency, it is possible to design an algorithm that can obtain the self-consistent fictitious temperature with TAO-LDA, and then adopt this value to calculate properties with a more sophisticated TAO-DFA.
Despite some progress, there remains room for improvement in the present scheme. By construction, TAO-DFAs (with θ*) can perform better than the corresponding TAO-DFAs (with θ = 7 mhartree)17 for a wide range of SR and MR systems. However, the former are computationally more expensive than the latter for single-point energy and geometry optimization calculations. For the efficient optimization of molecular geometries, the development of analytical nuclear gradients for TAO-DFAs (with θ*) will be essential, which can greatly enhance their applicability to large systems with strong static correlation effects. In addition, different stability indexes (see eqn (30)) and different types of functions (see eqn (31)) may also be adopted for the representation of θ in TAO-DFT, which may further improve the accuracy of the present scheme for general applications. We plan to pursue some of these issues in the near future.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Ministry of Science and Technology of Taiwan (Grant No. MOST104-2628-M-002-011-MY3), National Taiwan University (Grant No. NTU-CCP-106R891706; NTU-CDP-105R7818), the Center for Quantum Science and Engineering at NTU (Grant No. NTU-ERP-106R8700-2), and the National Center for Theoretical Sciences of Taiwan.References
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- S. Kümmel and L. Kronik, Rev. Mod. Phys., 2008, 80, 3–60 CrossRef.
- P. A. M. Dirac, Proc. Cambridge Philos. Soc., 1930, 26, 376–385 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, L. A. Constantin, J. Sun and G. I. Csonka, J. Chem. Theory Comput., 2009, 5, 902–908 CrossRef CAS PubMed.
- C.-W. Tsai, Y.-C. Su, G.-D. Li and J.-D. Chai, Phys. Chem. Chem. Phys., 2013, 15, 8352–8361 RSC.
- J. F. Dobson, et al., Aust. J. Chem., 2001, 54, 513–527 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, J. Chem. Phys., 2008, 129, 121104 CrossRef PubMed.
- G. Gryn'ova, M. L. Coote and C. Corminboeuf, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 440–459 CrossRef PubMed.
- J.-D. Chai, J. Chem. Phys., 2012, 136, 154104 CrossRef PubMed.
- J.-D. Chai, J. Chem. Phys., 2014, 140, 18A521 CrossRef PubMed.
- J.-D. Chai, J. Chem. Phys., 2017, 146, 044102 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. Savin, in Recent Developments and Applications of Modern Density Functional Theory, ed. J. M. Seminario, Elsevier, Amsterdam, 1996, pp. 327–357 Search PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263–272 CrossRef CAS PubMed.
- C.-W. Wang, K. Hui and J.-D. Chai, J. Chem. Phys., 2016, 145, 204101 CrossRef PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- D. Peng, S. N. Steinmann, H. van Aggelen and W. Yang, J. Chem. Phys., 2013, 139, 104112 CrossRef PubMed.
- H. van Aggelen, Y. Yang and W. Yang, Phys. Rev. A, 2013, 88, 030501(R) CrossRef.
- N. D. Mermin, Phys. Rev., 1965, 137, A1441–A1443 CrossRef.
- C.-S. Wu and J.-D. Chai, J. Chem. Theory Comput., 2015, 11, 2003–2011 CrossRef CAS PubMed.
- C.-N. Yeh and J.-D. Chai, Sci. Rep., 2016, 6, 30562 CrossRef CAS PubMed.
- S. Seenithurai and J.-D. Chai, Sci. Rep., 2016, 6, 33081 CrossRef CAS PubMed.
- C.-S. Wu, P.-Y. Lee and J.-D. Chai, Sci. Rep., 2016, 6, 37249 CrossRef PubMed.
- S. Seenithurai and J.-D. Chai, Sci. Rep., 2017, 7, 4966 CrossRef PubMed.
- U. von Barth and L. Hedin, J. Phys. C: Solid State Phys., 1972, 5, 1629–1642 CrossRef CAS.
- P. W. Ayers and W. Yang, J. Chem. Phys., 2006, 124, 224108 CrossRef PubMed.
- G. L. Oliver and J. P. Perdew, Phys. Rev. A, 1979, 20, 397–403 CrossRef CAS.
- F. Perrot, Phys. Rev. A, 1979, 20, 586–594 CrossRef CAS.
- P.-O. Löwdin and H. Shull, Phys. Rev., 1956, 101, 1730–1739 CrossRef.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. G. Pearson, J. Org. Chem., 1989, 54, 1423–1430 CrossRef CAS.
- Z. Zhou and R. G. Parr, J. Am. Chem. Soc., 1990, 112, 5720–5724 CrossRef CAS.
- J.-i. Aihara, J. Phys. Chem. A, 1999, 103, 7487–7495 CrossRef CAS.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS PubMed.
- M. Franco-Pérez, J. L. Gázquez, P. W. Ayers and A. Vela, J. Chem. Phys., 2015, 143, 154103 CrossRef PubMed.
- M. Franco-Pérez, P. W. Ayers, J. L. Gázquez and A. Vela, Phys. Chem. Chem. Phys., 2017, 19, 13687–13695 RSC.
- Y. Shao, et al., Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- Y. Zhao, B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 2715–2719 CrossRef CAS.
- Y. Zhao, N. González-García and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 2012–2018 CrossRef CAS PubMed.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern, K. Raghavachari and J. A. Pople, J. Chem. Phys., 1998, 109, 42–55 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 2000, 112, 7374–7383 CrossRef CAS.
- J. A. Pople, M. Head-Gordon, D. J. Fox, K. Raghavachari and L. A. Curtiss, J. Chem. Phys., 1989, 90, 5622–5629 CrossRef CAS.
- P. Jurečka, J. Šponer, J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- T. Helgaker, P. Jørgensen, and J. Olsen, Molecular Electronic-Structure Theory, Wiley, New York, 2000 Search PubMed.
- K. P. Huber and G. Herzberg, in Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979, p. 412 Search PubMed.
- D. Sundholm, P. Pyykko and L. Laaksonen, Mol. Phys., 1985, 56, 1411–1418 CrossRef CAS.
- M. S. Gordon, et al., J. Chem. Phys., 1999, 110, 4199–4207 CrossRef CAS.
- G. Herzberg, Molecular Spectra and Molecular Structure: Electronic Spectra and Electronic Structure of Polyatomic Molecules, Van Nostrand, New York, 1966 Search PubMed.
- X. Lopez, M. Piris, J. M. Matxain, F. Ruipérez and J. M. Ugalde, ChemPhysChem, 2011, 12, 1673–1676 CrossRef CAS PubMed.
- R. G. A. Bone and P. Pulay, Int. J. Quantum Chem., 1992, 45, 133–166 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra10241k |
| This journal is © The Royal Society of Chemistry 2017 |