Engineered ridge and micropillar array detectors to quantify the directional migration of fibroblasts

Abstract

Cell migrations on substrates are important in diverse processes such as wound healing, embryogenesis, and pathologies like cancer metastasis. An understanding of the cellular mechanobiology during migration requires development of suitable engineering platforms to better represent the anisotropic in vivo cellular environment and measure traction forces due to cell adhesion. We fabricated a custom elastomeric micropillar array detector (mPAD), comprised of alternate ridge and pillar topographical features, using a lithographic fabrication method that creates an anisotropic microenvironment and also permits the measurement of traction forces. We used the finite element method to compare predictions of calculated tractions for pillar geometries with different aspect ratios using linear and nonlinear constitutive models. These simulations showed the importance of pillar aspect ratios and constitutive models in computing resulting tractions. We cultured 3T3 fibroblasts on the engineered mPAD and characterized cellular migrations over a three hour period. Our results show highly elongated cellular and nuclear morphologies on the mPAD substrates as compared to cells cultured on control elastomeric substrates. Cells on mPADs demonstrated persistent directional motion along ridges as compared to random movements on control substrates. These results showed the importance of substrate anisotropy in the alignment of fibroblasts on mPAD. We also measured differences in the cellular tractions along the length of the cell on mPAD substrates. Engineered mPADs are hence useful in directing cellular motions and in delineating mechanobiological processes during adhesion and migration.

---

Introduction

Cell motility is important in several biological processes including embryogenesis, wound healing, immune response, and metastasis.¹ Biochemical and mechanical cues are exquisitely integrated and regulated within cells to produce adhesions and migrations. The overall migration occurs in distinct steps which begins with protrusions of the membrane at the leading cell edge, signalling and generation of traction forces at the cell-matrix adhesions, displacement of the bulk cell body, and finally, cellular detachment at the rear end.² Individual cells cultured on isotropic 2D surfaces are well spread and migrate in random directions. In contrast, engineered surfaces, created using micropatterning, permit manipulation and control of the substrate stiffness, topographic features, and anisotropy.^3–7 To explore the effects of geometric patterning on cells, Parker and colleagues used micro-contact printing to create adhesive islands of different sizes and shapes and measured tractions for individually constrained cells.⁸ They showed that traction forces were highest in sharp corners where cellular processes were also directed. Cell polarizations due to asymmetric patterning induce changes in the mechanical stresses across transmembrane receptors to activate signal transduction pathways; these cause protrusions in the cytoskeleton to define the leading migration direction.⁹

Migration of cells is characterized by directional persistence and is regulated by molecular pathways that mediate differences in tractions between the leading and retracting ends of a migrating cell.¹⁰ Pathak and Kumar showed that human glioma cells constrained within wide channels are less polarized and hence similar to that of isotropic cell spreading on unconfined substrates.¹¹ Cells present in narrow channels however demonstrated highly polarized traction forces that were affected by matrix stiffness and confinement. Other studies demonstrated that fibroblasts confined within narrow channels developed lower tractions and had lower migration speeds as compared to cells in wide channels.⁴ Cellular confinement within channels is however not representative of the in vivo three dimensional tissue milieu of cells which consists of adherent polarized cells located in an organized and anisotropic extracellular matrix. To explore the role of substrate anisotropy in cell tractions and migrations, Tymchenko and co-workers designed a silicon substrate with surface topographical cues, created using photolithography and deep reactive ion etching, to obtain an array of vertical pillars between solid ridges.¹² They characterized the migration and contact guidance of endothelial and fibroblast cells on the engineered substrates. Contact guidance is a characteristic phenomenon in which cells can adjust their migration behaviours based on the substrate topography.^13,14 They showed that endothelial cells alone oriented and migrated in the direction of ridges. In contrast, fibroblasts did not align, elongate, or migrate along the ridges to exhibit contact guidance.¹² Dissecting the spatio-temporal events leading to the creation of front-rear polarity and quantifying cellular tractions during cell migration warrants the development of suitable engineering platforms with soft deformable micropillars to measure tractions and the presence of ridges to aid in cellular alignment.

In this study, we fabricated a poly dimethyl siloxane (PDMS) micropillar array detector (mPAD) comprised of micropillars and ridges using a facile fabrication technique and characterized the traction forces exerted by individual adherent cells. Our fabrication approach eliminates the use of deep reactive ion etching that is sometimes associated with undesirable features such as presence of scallop-like notches and frustum shaped pillars. We also investigated the migration behavior of fibroblasts on mPAD substrates and quantified the resultant forces exerted by cells using deflections of microfabricated pillars as reported in several earlier studies.^15,16 The micropillar displacements were converted to cellular traction forces using beam behaviour under pure bending.¹⁷ Euler–Bernoulli, Timoshenko beam equations and non-linear constitutive models, including the Arruda–Boyce and neo-Hookean models, implemented within a finite element framework were used to compare the traction results from these different models. Such comparisons are essential to compute tractions for pillars that undergo large deformations due to cell adhesions and have different aspect ratios which do not permit the use of standard bending models, with linear elastic assumptions, for non-slender beams. Contrary to earlier reports,¹² we demonstrate that topographical cues on the engineered mPAD substrates influence fibroblasts morphologies and result in persistent cellular migrations in the direction of the ridges. Cell morphologies have oriented features similar to the anisotropic in vivo cellular milieu without constraining effects produced within channels.^11,18 Engineered substrates coupled with force measurement are useful in characterizing the differences in signalling pathways in migratory cells and in the developmental patterning of tissues.

Materials and methods

Fabrication and characterization of mPAD substrates

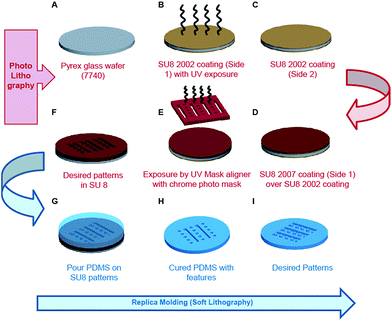
The schematic details of process flow during fabrication of mPAD's are illustrated in Fig. 1. The process begins with heating fresh X2 Pyrex glass wafer 7740 at 100 °C for 10 minutes to remove the surface moisture followed by a cooling step (Fig. 1A). SU8 2002 (Microchem, Newton, MA) was next spin coated at 3000 rpm for 30 seconds and the wafer soft baked by heating it at 65 °C and 95 °C for 2 minutes each. The soft bake was accompanied by UV exposure using a mask aligner (MIDAS), without a photomask, and a post exposure bake at 65 °C and 95 °C. The wafer was finally hard baked at 120 °C for about 10 minutes to obtain photoresist coating on a single side (side 1) of the glass wafer (Fig. 1B). The opposite side (side 2) was next coated with SU8 2002 for 30 seconds at 3000 rpm, the wafer soft baked at 65 °C and 95 °C for 3 minutes each, and hard baked at 120 °C for about 10 minutes (Fig. 1C). SU8 2007 (Microchem, Newton, MA) was spin coated on side 1 at 1600 rpm for 30 seconds and the assembly soft baked at 65 °C for 3 minutes and at 95 °C for 6 minutes (Fig. 1D). Exposure was carried out in two steps using a chrome mask to obtain desired patterns. Each exposure step lasted for ten seconds, with a three second interval between steps, and was followed with post exposure bake (65 °C and 95 °C for five minutes each) and a hard baking step (120 °C for about ten minutes; Fig. 1E). The photolithography process was completed by developing the wafer until the optimal desired patterns in SU8 were obtained (Fig. 1F). The photoresist pattern served as a master for fabricating PDMS mPAD substrates through a replica moulding process using a 10 : 1 base to curing agent of a silicone elastomer mixture (Sylgard® 184, Dow Corning). The elastomeric mixture was degassed to remove air bubbles, poured over SU8 patterns, and cured overnight at 80 °C in a convection oven (Fig. 1G). Cured PDMS patterns were peeled and treated overnight with trichloro (1H,1H,2H,2H-perfluorooctyl) silane vapour under vacuum (Fig. 1H). Freshly prepared PDMS was poured over silanized patterns, cured overnight in a convection oven at 80 °C and gently peeled to obtain the desired elastomeric mPAD for this study (Fig. 1J). PDMS coated coverslips, mixed in a 10 : 1 ratio, were used as controls to compare differences in the cell migrations with engineered mPAD.

Fig. 1 Schematic details of the process flow adopted for fabricating the mPAD are illustrated. (A–F) Photolithography steps for generating SU8 patterns. (G–I) Soft lithography steps for generating the final PDMS based mPAD.

Scanning electron microscopy (Quanta 200 ESEM, FEI, and The Netherlands) was performed on the elastomeric mPAD's, mounted on double sided carbon tape (Electron Microscopy Sciences, USA) and stuck on an aluminium stub, to visualize the patterns. Specimens were transferred from the desiccator to a sputter coater (Bal-Tec SCD 500, Liechtenstein) that was purged thrice with argon, the samples coated with gold, and imaged using accelerating voltages between 5 and 20 kV.

Finite element models to calculate traction forces using micropillar bending

Micropillars were modelled as cantilevers with circular cross sections using a commercial solver (ABAQUS CAE). We used three different geometries to model the pillars in this study: first, an aspect ratio of 1 : 3 to represent mPAD's fabricated in our study and second, 1 : 5 aspect ratio which is commonly reported in many earlier works.^19,20 Finally, we used an ideal slender beam of 1 : 10 aspect ratio to compare numerical results with analytically obtained values from Euler–Bernoulli and Timoshenko models for all pillar geometries in this study. The pillar length was taken to be constant and boundary conditions were applied by assuming fixed nodes at the base. The top surface was pinned to the centroid of a circle to which shear loads were incrementally applied from 0 to 50 nN for the mPAD's with aspect ratios of 1 : 3 and 1 : 5. In contrast, we used a force range 0–30 nN for the highly slender 1 : 10 pillars. All cylindrical pillars were modelled as a hyperelastic solid and were meshed using hybrid quadratic hexagonal and swept wedge elements. Results are reported from geometries with 435577 nodes and 107520 elements which were obtained following mesh refinement. Because linear and nonlinear models are reported in the literature to model the bending of PDMS pillars, we also assessed the applicability of neo-Hookean and Arruda–Boyce constitutive models using the finite element framework and assumed the pillars to be incompressible over the deformation range.

Substrate functionalization and cell culture studies

The mPAD surfaces were oxidized in a plasma cleaner (PDC-32G, Harrick Plasma, USA) for 2 minutes under low frequency followed by 5 minute treatment under high frequency to increase the surface hydrophilicity. Fibronectin (50 μg ml⁻¹; Sigma Aldrich F2006) coated coverslips were next transferred to the activated mPAD regions to permit cell adhesion to the micropillar tops and that of the ridges. The mPAD substrate was sterilized using graded alcohol treatment and coated with 5μg ml⁻¹ DiI (molecular probes) at 37 °C for 1 hour to allow visualization of the top surface of the pillar. The substrate was immersed in 0.2% F-127 pluronic acid at room temperature for 1 hour to restrict cell adhesion to the top of the micropillars and ridges. Mouse embryonic fibroblasts (NIH/3T3) were cultured in T25 flasks in a tissue culture incubator at 37 °C, 100% humidity, and 5% CO₂ in DMEM supplemented with 10% FBS. Sterilized mPAD's were placed in 35 mm tissue culture dishes, seeded with ∼2 × 10⁵ cells ml⁻¹, and placed on a live cell microscope stage with an incubator and heat controller. The fibroblasts were allowed to attach and equilibrate for about 2–3 hours and imaged over 3 hours (10× phase objective; NA 0.30; 1 frame/5 min) to characterize migration behaviours. At the end of migration, cells were fixed with 4% formaldehyde in PBS and permeabilized with 0.1% Triton X-100 in PBS for immunofluorescence studies. Filamentous actin was visualized using rhodamine-conjugated phalloidin (molecular probes) to stain the actin networks red; DAPI was used to visualize the nucleus in blue. Confocal images were collected using Leica DMI-6000B microscope (63× Oil immersion objective, NA 1.40).

Analysis of cell migration and traction force microscopy

Stacks of 8-bit grayscale bright field time-lapse sequences, acquired every 5 minutes over the three hour period, were analysed using NIH Image J (version 1.46r) to quantify the cell centroids during migrations. Cell and nuclear areas were also measured for cells on control PDMS coated coverslips (n = 18) and mPAD's (n = 15). Confocal images (63× oil immersion objective, NA 1.40) were obtained at 0.1 μm increment/step size in a direction perpendicular to the mPAD surface. The mPAD's were cultured with fibroblasts, a Z-stack images of DiI stained pillars were visualized using 561 nm filter, and the images deconvolved using in-built software. Two images were selected at each desired location that contained the cell of interest on the micropillars. The first image corresponded to the top of the micropillars and the second was located towards the micropillar base (see figure below). Uncompressed images were exported into MATLAB (v8.2 2013a; The Math Works, Natick, MA) and a custom written algorithm was used to quantify the micropillar deflections using the cross sectional areas of their base and top from a defined region of interest. Specifically, the boundary of the micropillar cross-sectional area was manually marked in each image using the intensity values of the associated pixels. Centroids corresponding to the bounded regions were identified in the base and top images for each micropillar. A comparison of the misalignment in the centroid positions of the top image with respect to the base yielded the deflection for a given micropillar. The deflections were converted to forces using a neo-Hookean model. A global colour map for displacements and forces was constructed for each cell based on these results.

Results and discussion

There are five main implications from our study: first, we fabricated PDMS ridge-pillar patterns using replica molding that have not been reported earlier to the best of our knowledge. Second, we demonstrated fibroblast cytoskeleton and nucleus alignment along the ridges on the ridge-pillar patterned substrates. Third, we used micropillar displacements caused by fibroblast cell interactions with the substrates during migration as inputs to calculate the tractions using inverse methods implemented using a finite element approach. We used the Euler–Bernoulli and Timoshenko beam theory with the inclusion of two different nonlinear material models to compute the resulting tractions. Comparisons between the predictions from different models clearly showed dependence of the calculated tractions on the pillar aspect ratio and the choice of linear/nonlinear material models to describe the micropillar properties. Fourth, the ridge-pillar micropatterned substrates permitted persistent directional migration in fibroblasts over a 3 hour duration. Finally, we show variations in cellular tractions along the length of the polarized cell.

Microfabrication of ridge-pillar mPAD detectors

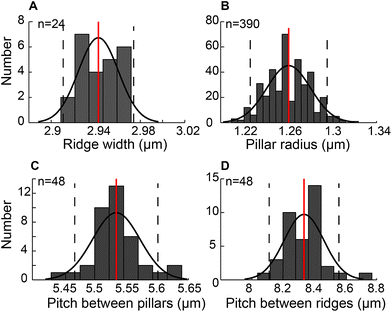
The engineered mPAD's were fabricated using a two-step replica moulding process to produce alternate rows of pillars and ridges. Fig. 2 shows a bright field image and the accompanying scanning electron micrograph (SEM) of the mPAD. The latter was used to quantify various parameters which are essential in the measurement of forces and in assessing repeatability of the pattern. We characterized the ridge width, pillar radius, pitch between pillars in the direction of the ridges, and the pitch between ridges using image processing software. Histograms for each of these parameters with the corresponding fits were obtained based on a normal distribution assumption (Fig. 3).

Fig. 2 (A) Bright field images of mPAD substrate. (B) The corresponding SEM was used to quantify various topological features. (C) SEM with tilt shows heights of the pillars and ridges.

Fig. 3 Histograms with mean and one standard deviation are plotted for the mPAD to show normal distributions for (A) distribution of ridge widths (B) micropillar radius (C) pitch between pillars measured along the ridge direction, and (D) pitch between the ridges.

The patterns had ridge widths of 2.94 ± 0.02 μm measured over 19 200 μm² area (n = 24). We also obtained an average micropillar radius of 1.26 ± 0.02 μm (n = 390) and spacing between pillars of 5.50 ± 0.21 μm (n = 48) measured within 60 × 40 μm². The pitch between pillar-ridge-pillar patterns was 8.33 ± 0.12 μm (n = 48) over the same area. We calculated the aspect ratio, measured as the ratio of the diameter to pillar height, to be 1 : 3 in our study based on 6 μm height for the patterns.

PDMS micropillar detectors have been routinely used to characterize cell–substrate interactions and traction forces exerted by cells on substrates.^15,21 In most studies, the pillar diameters range from 0.75–3 μm with aspect ratios varying from about 1 : 0.53 to 8.^16,17,20,22 Pitch values, ranging from 0.8 μm²³ to 12 μm,²⁴ have been reported in traction force microscopy experiments. A high pillar density simulates a substrate continuum and prevents the influence of pillars in cell locomotion. In contrast, sparse pillar density permits large deflections that are useful in measuring cellular tractions. We quantified the influence of substrate anisotropy on the adhesion and migration of fibroblasts using the pillar-ridge mPAD substrates. Micropillars placed between the ridges were used to quantify the cellular traction forces. Our studies show clear alignment of fibroblasts along micro-patterned ridges (Fig. 4B) in contrast to the relatively rounded cellular morphology on control PDMS substrates without the presence of patterns (Fig. 4A).

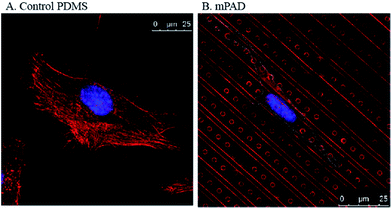Fig. 4 Confocal images of fibroblasts stained using DAPI for the nucleus and rhodamine phalloidin for the actin are shown for (A) control PDMS coated cover slips and (B) mPAD arrays.

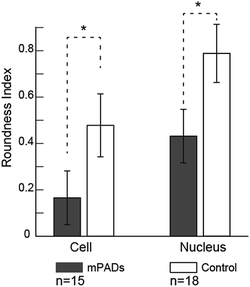
We also note differences in the cell cytoskeleton and nuclear areas of cultured cells on the mPAD. Nuclei and cells on mPAD's were elongated in the direction of the ridges as compared to cells on control PDMS substrates. The roundness index for cytoskeleton and nucleus (Fig. 5) shows significant deviation for cells on mPAD's as compared to control substrates. Presence of ridges in the mPAD patterns makes them anisotropic and influences cell morphologies as compared to control surfaces. Tan and co-workers were among the earliest to fabricate micropillars with oval cross sections; they showed the effects of the mechanical anisotropy due to engineered substrates on cell behavior.¹⁵ The elliptical pillars in their study required 8 times more force to deflect along the long axis than those along the short axis.

Fig. 5 Comparisons in the cell spread and nuclear areas on control and mPAD's show the effect of the engineered substrate in aligning the cell to make it highly elongated as compared to the control PDMS substrate. Statistically significant differences are indicated (p < 0.05).

More recently, Saez et al. used microfabrication to develop oval shaped pillars with stiffness four times in the major direction as compared to minor one to assess the effects of substrate anisotropy and rigidity on cell migrations.¹⁹ Teixeira and coworkers report the use of multiple parallel grooved-ridged surfaces to characterize morphological features, such as elongation and alignment, for human corneal epithelial cells.²⁵ The cytoskeleton and nucleus aligned on the grooved substrates as compared to control surfaces that did not have any topographical features. Distortions of the nucleus may alter cellular transcription which influences cell adhesion and migration. Few studies however reported differences in the traction forces or the directional persistence of fibroblasts on topographical surfaces due to cellular alignment to the best of our knowledge.

Traction forces due to micropillar deflections

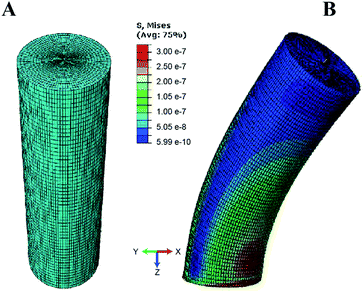
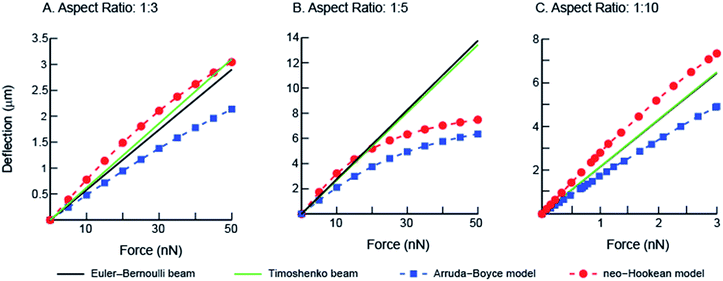
To quantify the traction forces exerted by the elastomeric micro-pillars, we obtained the positions of the deflected pillars using confocal imaging at the end of individual fibroblast migrations. We characterized deflections and von Mises stress distributions for the micropillars simulated under shear loading for three different aspect ratios (1 : 3, 1 : 5 and 1 : 10) using the numerical finite element method (Fig. 6). Differences in the results between the linear elastic Euler–Bernoulli theory, Timoshenko beam theory and nonlinear material models for the three micropillar geometries with different aspect ratios are plotted below (Fig. 7 A–C). Because the 1 : 10 aspect ratio pillars are highly compliant, a different scale was used to clearly show differences between the models as compared to Fig. 7A and B. These graphs show few differences for the Euler–Bernoulli and Timoshenko models for pillars with aspect ratios of 1 : 5 and 1 : 10. Our results show marginal increase in the stiffness of the 1 : 3 aspect ratio pillars which were used in the experimental studies that may be better described using the Timoshenko model. The effects of nonlinear material models to describe the elastic properties of the beams are also apparent in these figures which have not been reported earlier. The neo-Hookean model has been successful in describing the properties of elastomeric materials at smaller deformations but is inexact in capturing the stiffening behavior at large deformations.²⁶ In contrast, the 8-chain Arruda–Boyce model is better at describing the stress–strain response over a large deformation region due to stiffening effects of elastomers.²⁶ Differences between linear and nonlinear material models are apparent even at small deformations.

Fig. 6 Shear loading of the micropillar was simulated using finite element scheme based on neo-Hookean material model. (A) An aspect ratio of 1 : 3 was used for the meshed pillar geometry (B) von-Mises stresses are shown for the micropillar during deflection.

Fig. 7 Comparisons from simulations corresponding to Euler–Bernoulli and Timoshenko beam theories for linear elastic, neo-Hookean, and Arruda–Boyce models are shown for (A) 1 : 3 aspect ratio micropillars from this study (B) 1 : 5 aspect ratio commonly reported in literature, and (C) 1 : 10 ideal slender beam.

Short elastomeric pillars, with aspect ratios ranging from 1 : 0.53 to 1 : 8.0 have been widely used to report traction forces by adherent cells.^16,17,20,22 These studies however used the same form of the strain energy function to calculate forces, based on Euler–Bernoulli beam bending with linear elastic material model, for micropillars with different aspect ratios. Schoen and colleagues used 2–9 aspect ratio (pillar length to the diameter) scaled pillars, fabricated using PDMS, and estimated their bending stiffness using a micromanipulator with an attached MEMS force sensor.²⁷ Using these results they suggested the inclusion of a correction factor to account for the substrate warping and shear components during micropillar bending. The reported tractions were ∼40% higher as compared to cases where warping was not included in the calculations.²⁷ Lin et al. showed that the total displacement of a soft elastomeric micropillar during bending using indentation with probes included a component associated with the penetration of the probe into PDMS (34%) and that due to the underlying substrate deformation (11%). The displacement components in the study were obtained by fitting the experimental bending data of a scaled 1 : 2 aspect ratio PDMS pillar model with finite element simulations.²⁸ More recently, Khare et al. used colored PDMS micropillars of 1 : 3 aspect ratio which were similar to those in our study, and performed experiments on scaled models of the pillars.²⁹ They fit these data to a non-linear Yeoh model and reported tractions due to micropillars. The nonlinear response of PDMS micropillars under bending is highlighted in their data. We used a neo-Hookean nonlinear material model for PDMS micropillars based on their experimentally measured constitutive properties using planar biaxial tests.²⁶ Comparisons between results from the different constitutive models in our study show that the choice of material model and beam theory are both crucial factors in reporting the tractions exerted by cells. Because deflections reported in the literature lie within a narrow deformation range of the stress–strain curve, we used results from the neo-Hookean model in calculations of tractions using micropillars in our study.

Role of ridges in directing persistent migrations in fibroblasts

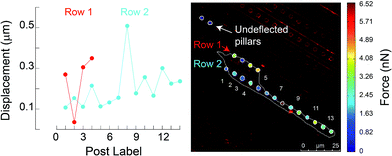
To characterize effects of ridges in the mPAD on cell migrations, we measured the centroid for each fibroblast (n = 29) at five minute intervals over the three hour duration using the bright field images (ESI Movie 1;† Fig. 8). These data show that cells were oriented and migrated unidirectionally along the ridges on the engineered mPAD surfaces throughout the migration duration; cells were however not constrained to move in these directions (Fig. 8). Direction reversals were clearly observed in some of these cells. Mechanobiology has been studied extensively on patterned surfaces. Cell migrations on continuous substrates are modulated through mechanical signals, such as substrate stiffness or topographic cues.^25,30–32 Substrate stiffness influences cell–substrate interactions and consequently the cellular tractions and migrations.^33,34 Engineered substrate topography is a useful method to create desired cellular adhesions to substrates.^2,12,25 Reports on single-cell migration confine cell movements using either 2D microfluidic channels or chemo attractants that are created using patterning of differential areas through protein modulators and inhibitors.^11,35,36 Few studies have however quantified the role of substrate anisotropies in cell migration which are essential in several physiological processes. Earlier studies used grooved surfaces to demonstrate contact guidance in single cells but did not report any traction forces.^11,25 Tymchenko and co-workers used microfabricated pillar-ridge combinations in silicon wafers to characterize migrations of endothelial and fibroblast cells.¹² They showed that endothelial cells alone (n = 5) aligned in the direction of the ridges; there was neither contact guidance for the rounded fibroblasts cells in their studies (n = 19) on the engineered substrates nor persistence of directional migration. Results from our study however show that topographic cues aid fibroblast alignment, elongation, and migration along the ridges on the mPAD substrates without the constraining effects on cellular motions within channels which are previously reported in cell migrations.⁶ We used the micropillar deflections to quantify the traction forces of the cells after migration (n = 14). Traction maps were constructed to explore spatial variations for the fibroblasts on the mPAD and are shown for a representative cell on the mPAD (Fig. 9A and B). Maximum tractions for each cell varied from 2.19 to 31.5 nN; these variations may be on account of selecting cells at different stages in migration in this study. Earlier studies have characterized cell morphologies on mPAD and demonstrated that the centre of the leading edge protrusions is a site of high actin-filament density which aids in the formation of lamellipodia and filopodia at the leading edge.^19,37 Quantifying the front-rear polarization in cells using the ridge-pillar mPAD's and the corresponding changes in tractions along the length of a polarized cell allows us to explore the role of the cytoskeleton and the nucleus in mechanotransduction during migration. Experiments using such engineering platforms are also attractive to explore the role of signalling molecules in individual cells during migration.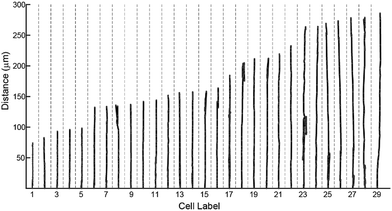

Fig. 8 Migration trajectories of fibroblasts along the substrate ridges (n = 29) measured over a 3 hour period are plotted. Reversals of cell directions are clearly visible in some of the cells.

Fig. 9 (A) Micropillar displacements are shown for the adherent cell on the mPAD. (B) Contour plot of the traction forces was calculated using a neo-Hookean model. Control pillars which were used to calculate zero tractions are also highlighted.

Conclusions

Mechanical cues exerted by cells on substrates during adhesion and migration are important in several biological processes. Various platforms have been developed to measure forces exerted by cells on substrates. We fabricated an engineered mPAD, comprised of alternating ridges and pillars, and quantified the displacements exerted by cells during adhesion and migration. Our results show that the cell cytoskeleton and nuclear morphology on the mPAD's are highly elongated as compared to control PDMS substrates that lack ridges. The anisotropic engineered substrate hence aids in aligning the fibroblasts and in their directional unconstrained motion that has not been reported earlier. Micropillars are useful in quantifying the traction forces and are based on measured beam deflections by fibroblasts cultured on the substrates. We converted the deflections into forces using a finite element model based on neo-Hookean constitutive model. Differences in the measured forces arise due to the aspect ratio of the micropillars and the assumed material model used to define the constitutive properties of the pillar material. The mPAD device may also be used in future studies to characterize the role of specific markers in cell alignment and migration.

Conflicts of interest

No conflicts of interest.

Acknowledgements

We are grateful to Prof. Pramod Pullarkat (Raman Research Institute, Bangalore) for the NIH 3T3 cells used in this study. NG acknowledges Department of Science and Technology for the Ramanujan fellowship and research grant that supported part of this work and to the Department of Biotechnology (Bioengineering and Biodesign) for project support. Thanks to Mr Ankur Kulkarni (IISc) for help with confocal imaging and the staff at the CeNSE facility at IISc where part of this work was carried out. The International Collaborative R&D Program (N0000894) by MOTIE is acknowledged by DWL.

Notes and references

1. D. A. Lauffenburger and A. F. Horwitz, Cell, 1996, 84, 359–369.
2. X. Jiang, D. A. Bruzewicz, A. P. Wong, P. Matthieu and G. M. Whitesides, Proc. Natl. Acad. Sci., 2005, 102, 975–978.
3. M. Ghibaudo, J. M. D. Meglio, P. Hersen and B. Ladoux, Lab Chip, 2011, 11, 805–812.
4. P. S. Raman, C. D. Paul, K. M. Stroka and K. Konstantopoulos, Lab Chip, 2013, 13, 4599–4607.
5. H. Sunami, I. Yokota and Y. Igarashi, Biomater. Sci., 2014, 2, 399–409.
6. J. Hong, S. Lee, S. Park and J. Lee, J. Micromech. Microeng., 2015, 25, 045012.
7. S. Lee, J. Hong and J. Lee, Soft Matter, 2016, 12, 2325–2333.
8. K. K. Parker, A. L. Brock, C. Brangwynne, R. J. Mannix, N. Wang, E. Ostuni, N. A. Geisse, J. C. Adams, G. M. Whitesides and D. E. Ingber, FASEB J., 2002, 16, 1195–1204.
9. F. Pouthas, P. Girard, V. Lecaudey, T. B. Ly, D. Gilmour, C. Bolin, R. Pepperkok and E. G. Reynauld, J. Cell Sci., 2008, 121, 2406–2414.
10. U. Theisen, E. Straube and A. Straube, Dev. Cell, 2012, 23, 1153–1166.
11. A. Pathak and S. Kumar, Proc. Natl. Acad. Sci., 2012, 109, 10334–10339.
12. N. Tymchenko, J. Wallentin, S. Petronis, L. M. Bjursten, B. Kasemo and J. Gold, Biophys. J., 2007, 93, 335–345.
13. M. J. Dalby, M. O. Riehle, S. J. Yarwood, C. D. Wilkinson and A. S. Curtis, Exp. Cell Res., 2003, 284, 274–282.
14. X. F. Walboomers, H. J. Croes, L. A. Ginsel and J. A. Jansen, J. Biomed. Mater. Res., 1999, 47, 204–212.
15. J. L. Tan, J. Tien, D. M. Pirone, D. S. Gray, K. Bhadriraju and C. S. Chen, Proc. Natl. Acad. Sci., 2003, 100, 1484–1489.
16. M. T. Yang, N. J. Sniadecki and C. S. Chen, Adv. Mater., 2007, 19, 3119–3123.
17. J. Fu, Y.-K. Wang, M. T. Yang, R. A. Desai, X. Yu, Z. Liu and C. S. Chen, Nat. Methods, 2010, 7(9), 733–736.
18. W. R. Legant, J. S. Miller, B. L. Blakely, D. M. Cohen, G. M. Genin and C. S. Chen, Nat. Methods, 2010, 7, 969–971.
19. A. Saez, E. Anon, M. Ghibaudo, O. du Roure, J.-M. Di Meglio, P. Hersen, P. Silberzan, A. Buguin and B. Ladoux, J. Phys.: Condens. Matter, 2010, 22, 194119.
20. C. A. Lemmon, N. J. Sniadecki, S. A. Ruiz, J. L. Tan, L. H. Romer and C. S. Chen, Mech. Chem. Biosyst., 2005, 2, 1–16.
21. S. Petronis, J. Gold and B. Kasemo, J. Micromech. Microeng., 2003, 13, 900–913.
22. M. T. Yang, J. Fu, Y. K. Wang, R. A. Desai and C. S. Chen, Nat. Protoc., 2011, 6, 187–213.
23. M. A. Bucaro, Y. Vasquez, B. D. Hatton and J. Aizenberg, ACS Nano, 2012, 6, 6222–6230.
24. M. Ghibaudo, J. M. di Meglio, P. Hersen and B. Ladoux, Lab Chip, 2011, 11, 805–812.
25. A. I. Teixeira, G. A. Brams, P. J. Bertics, C. J. Murphy and P. F. Nealey, J. Cell Sci., 2003, 116, 1881–1892.
26. A. R. Babu and N. Gundiah, Exp. Mech., 2014, 54, 1177–1187.
27. I. Schoen, W. Hu, E. Klotzsch and V. Vogel, Nano Lett., 2010, 10, 1823–1830.
28. I. K. Lin, K. S. Ou, Y. M. Liao, Y. Liu, K. S. Chen and X. Zhang, J. Microelectromech. Syst., 2009, 18(5), 1087–1099.
29. S. M. Khare, A. Awasthi, V. Venkataraman and S. P. Koushika, Biomicrofluidics, 2015, 9, 014111.
30. C. M. Lo, H. B. Wang, M. Dembo and Y. L. Wang, Biophys. J., 2000, 79, 144–152.
31. D. E. Discher, P. A. Janmey and Y. L. Wang, Science, 2005, 310, 1139–1143.
32. M. Nikkah, F. Edalat, S. Manoucheri and A. Khademhosseini, Biomaterials, 2012, 33, 5230–5246.
33. J. Fu, Y. K. Wang, M. T. Yang, R. A. Desai, X. Yu, Z. Liu and C. S. Chen, Nat. Methods, 2010, 7, 733–736.
34. M. F. Fournier, R. Sauser, D. Ambrosi, J. J. Meister and A. B. Verkhovsky, J. Cell Biol., 2010, 188, 287–297.
35. V. Vogel and M. Sheetz, Nat. Rev. Mol. Cell Biol., 2006, 7, 265–275.
36. K. Saha, A. J. Keung, E. F. Irwin, Y. Li, L. Little, D. V. Schaffer and K. E. Healey, Biophys. J., 2008, 95, 4426–4438.
37. O. du Roure, C. Dequidt, A. Richert, R. H. Austin, A. Buguin, P. Chavrier, P. Silberzan and B. Ladoux, Proc. SPIE Int. Soc. Opt. Eng, 2004, 5345, 26–34.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary movie 1: migration of 3T3 fibroblasts on the mPAD are shown over a 3 hour period (1 frame/5 minutes). The cell outline and the centroid are marked to show the directional and persistent migration of cells on mPAD's. See DOI: 10.1039/c7ra09068d

---