Control of interface interactions between natural rubber and solid surfaces through charge effects: an AFM study in force spectroscopic mode

Abstract

This work presents a detailed investigation of interface interactions between natural rubber (NR) particles and solid surfaces in aqueous medium at high ionic strength (0.1 M) using AFM in fast force spectroscopy mode. In this study, an original method for fixing the NR on the substrate was developed. This avoided the usual perturbations common in standard immobilization techniques. We proved that the adhesion process of the NR is monitored by slight changes in the surface charge state of the contacting solid surfaces made of silicon oxide or silicon nitride. The results were interpreted using Dynamic Force Spectroscopy theory, with the introduction of a supplementary term describing the electrostatic energy. Furthermore, these experiments revealed that adhesion between NR and tip was time dependent in a cumulative process. In addition, an increase of the adhesion between NR and AFM tip with the size of the rubber particles was measured. This was related to the higher concentration in lipids versus proteins for larger NR particles. These results are of great importance both for practical applications in solution-based industrial processes and to the fundamental knowledge of adhesion process involved for biopolymers or living cells.

---

1. Introduction

Adhesion of biocompounds at a surface is a subject of intensive research because of its widespread application in the fields of biomedicine, biomaterials and biotechnology. Adhesion is driven by the interfacial mixing of several biocompounds, for example, proteins, lipids, polysaccharides or any biopolymers. An example is natural rubber latex extracted from the sap of the rubber tree Hevea brasiliensis. This is a stable dispersion of colloidal particles, named natural rubber (NR) particles, which constitutes the major source of rubber material used in hygienic and medical sectors or in the tire industry. NRs are composed of a polyisoprene core surrounded by a shell layer (SL) of mixed lipids and proteins. Here “lipid” is the generic term for a mixture of lipids, phospholipids, free fatty acids, or fatty acids associated with phospholipids.¹ The suspension of NR particles is composed of a bimodal distribution of small (SRP) and large (LRP) particles with diameters of 100–200 nm and 500–1000 nm, respectively.^2–4 The SL has a typical thickness of ∼3–20 nm (ref. 1) but its fine structure is still in debate as several models have been proposed.^1,5–7 NR particles have a global negative surface charge, regardless of whether the lipid polar headgroups are protruding or the proteins facing the bulk electrolyte solution.^1,8 Recent studies demonstrate that inhomogeneities in the superficial layer composition are due to the size of the particles. This concerns both the lipid content, which is higher in LRPs than in SRPs, and the nature and organization of the proteins, themselves.³

The attachment of these biocompounds to a hard surface depends on the physicochemical characteristics of both facing interfaces and of the surrounding fluid. This is an important matter especially for industrial concerns. For instance, latex in its NR form is rarely used in pristine state; it is now common practice to incorporate various micro- or nano-particles. These “fillers” enhance selected properties such as elasticity or durability.³ Another important example in industry is the use of latex for water-based pressure sensitive adhesives (PSAs) for packaging applications such as latex-based acrylic adhesive.^9,10 The adhesion properties, like the one called “tack”, reflect the incomplete contact at the interface between adhesive and adherent. At low contact pressure and for short dwell times, the contact is highly dependent on the bonding process, even at the molecular level. The tack of a polymer is a non-fundamental material property¹¹ but is of importance for the optimum adhesive formulation. It is highly influenced by (i) the viscoelastic properties of the bulk material, (ii) the surface and interfacial tensions of adhesive and adherent, with consequences on the wetting properties of the adherent by the adhesive.¹¹ It must be noted that interfacial tensions may depend on the electrical state of the interface. Indeed, an electrostatic term can be introduced in the expression of the thermodynamic work of adhesion,¹² which has been proved empirically to be proportional to the experimental maximum energy of adhesion.^11,13 In general, the approach and adhesion of biocompounds to a surface are governed by several forces: electrostatics,¹⁴ van der Waals,¹⁵ hydrophobic,¹⁶ hydration,¹⁷ hydrogen bonding,^18,19 specific chemical interactions and steric forces.^15,20 Experimental results underline the major role of a combination of the electrostatic and hydrophobic forces,^18,19 solution ionic strength (IS) and pH.^21–29 The stability and interfacial interactions of colloidal nanoparticles can be well described to a first approximation by the DLVO theory.^30,31 Two forces are involved: the attractive van der Waals and repulsive electrical double layer forces.³² The strength and range of the van der Waals force are determined by the dielectric properties of the interacting surface and the media. For the electrical double-layer force, both the range and magnitude are highly dependent on the concentration and type of ions present in the aqueous medium. The strength of the double-layer force is determined by the surface charge density and the surface potential, while its range,³³ defined by the Debye length, is determined by the ionic strength since the surface charge is screened by mobile counter-ions in the aqueous medium.

An important debate concerning the adhesion of biomolecules stems from the properties of this electrostatic double-layer.³⁴ Many studies of the electrostatic interactions have led to contrasting conclusions. For instance, the adsorption of various proteins, was studied as a function of an externally imposed potential through a superficial indium tin oxide (ITO) layer deposited on a substrate.³⁵ The authors concluded that electrostatic interactions play a minor role in the process of protein adhesion on hydrophilic surfaces.³⁵ However, other studies arrived at the opposite conclusion: the electrostatic double-layer force was significant in the interaction of proteins with the surface.^36–39 The adsorption of bovine serum albumin (BSA) onto carbon electrodes⁴⁰ was shown to be enhanced when the applied potential was increased. This phenomenon was attributed to a polarization effect within the structure of the incoming protein molecules in the vicinity of the electrode surface.⁴¹ Numerical models have also been developed. By taking into account the combined role of interfacial ion distribution, charge regulation of amino acids in the proximity of the surface, the electroneutrality and mass balance,³⁴ a detailed understanding of the importance of how surface charge may affect the adsorption behavior was proposed. This model was successfully used on two model proteins (lysozyme and R-lactalbumin).³⁵ Simulation^42,43 of the adsorption of model peptides on self-assembled monolayer surfaces revealed that strong electrostatic interactions lead to entropy driven binding of peptides on a charged surface. A change in their structure reduced the configurational entropy. It was also shown⁴⁴ that a weak electrical potential applied to a conductive polymer grafted with a amphiphilic molecule could induce the preferential adsorption of proteins by switching the apparent surface of contact between a hydrophobic or hydrophilic state.

Most of the work on the adhesion properties of lipids has taken the path of arranging amphipathic lipid molecules into bilayers separated by an aqueous phase: either spherical bilayers, called liposomes, or planar bilayers. Some molecular dynamics simulations^45,46 of the adhesive forces between the lipid molecules in liposomes estimate that the minimal force required to pull the lipid molecule out of the membrane is a few hundred pN. The interplay of electrostatic interactions or hydrogen bonding on a silicon nitride AFM tip covered or not with polyelectrolyte multilayers has been studied by several authors.^19,47,48 The force required by the tip to break through the bilayer has been measured, as an indication of the overall membrane stability^49,50 and to quantify the destabilizing effect of toxic agents on the membrane (disease-related peptides, etc.).^51,52 It was shown that different factors, notably the temperature or the ions present in the aqueous buffer, can disturb the molecular interactions and the packing of lipids in the bilayers.⁵³

Other parameters involved in the adhesion of biopolymers are also important. As mentioned before, one is the contact time.¹⁸ Experiments using an AFM tip in interaction with either proteins or bacteria have revealed that the adhesion increased as the residence time of the AFM tip increased during tip retraction.^54–57 The surface chemistry and wettability⁵⁸ also influence the time dependent conformational changes in adsorbed proteins and mediate the adsorption kinetics and binding strengths,^59–61 as well as subsequent protein activity.^62,63 It was speculated^18,58 that conformational changes might arise from a two-step model. The first step, on the order of seconds to minutes, involves the rearrangement of amino acids at the protein surface. The second, taking much longer, relates to the more hypothetical rearrangement of the internal amino acids from the protein core towards the protein surface. It must be mentioned too that adhesion may increase with loading force^18,64 during AFM tip approach. This could causing a conformational change of the biomolecule during its contact with the solid.⁵⁸ In general, AFM experiments have so far shown that the adhesive forces between biomolecules and AFM probes increased with the loading rate and, in most cases, a linear relationship was observed between adhesion and the logarithm of the loading rate.^53,65–75 These experimental results have been interpreted using the theory of Dynamic Force Spectroscopy (DFS).^{65–67,71–73,76} This theory considers the weak non-covalent interactions governing structural cohesion and mediating mutual interactions between biocolloids, living cells, bacteria or solid surfaces. The irreversible bond cleavage at the origin of the rupture of adhesion can be interpreted using classical kinetic theory. Rupture obeys a first-order law where the dissociation rate (the “off-rate”), ν_m, is time dependent.⁷⁷ When pulled apart with a force ramp, the dissociation kinetics are transformed into a dynamic spectrum of the bond cleavage force as a function of the amplitude of the loading rate.⁷² The application of force lowers the energy barriers by the mechanical potential, E_m, and leads to an exponential amplification of the dissociation kinetics, so that the off rate ν(t) ≈ ν_m exp(E_m/k_BT). For a single barrier, this peak in the force distribution shifts to higher force in proportion to log_e (loading rate) according to a linear law.⁷² Despite the fact that experiments are more likely to measure multiple bonds, it was demonstrated that the multi-bond force spectrum can take the same mathematical form as the single-bond model in standard conditions⁷⁶ as verified in a number of experimental systems.^68–75,78

In this paper we present a study of the adhesive interaction of NR particles with the mineral solid surfaces of silicon oxide and silicon nitride in aqueous medium at high ionic strength (0.1 M) in order to (i) drastically decrease electrostatic long range interactions that would prevent coagulation processes between rubber particles with same charges as those used in industrial methods and (ii) focus on short-range interactions. An original method was implemented using the AFM in force spectroscopy mode to apply a fast loading rate (≈3 × 10⁶ pN s⁻¹). The filler surface (i.e. the mineral solid) and its interaction with NR were closely mimicked by the AFM tip surface allowing a precise quantification of these adhesive interactions. This AFM observation of nano-sized NR particles could be achieved only if their adhesion to the substrate was sufficient to withstand the lateral forces exerted by the AFM tip and avoid being swept away from the substrate. Regardless of the size of the NR, they could be fixed to the substrate using a method developed to avoid the traditional mechanical trapping or chemical gluing techniques.^21,79–81 By comparing the interactions between NR and the tip, we show that the adhesion process can be monitored through the slight changes in surface charge state. This effect is found to be the reason of the self-immobilization of the NR on the substrate. These results were interpreted using DFS theory with the inclusion of a supplementary term to describe the electrostatic energy. In addition, we showed that the adhesion values between the NR surface layer (SL) and tip are time dependent in agreement with the adhesion force history dependence evidenced by Marshall et al.⁷³ In addition, an increase of the adhesion between NR and AFM tip with the size of the rubber particles was measured. This is related to the higher concentration in lipids versus proteins for larger NR particles.^3,82

2. Experimental

2.1. Preparation of NR samples

Concentrated HA-latex (60 wt%) was purchased from Trang Latex Co. Ltd., Thailand. This solution was diluted in high purity water (Milli-Q, Millipore) to obtain a final concentration of ∼1.8 × 10⁻² wt%. Magnesium sulfate salts (MgSO₄) were added to this solution to obtain 100 mM ionic strength (IS) solution. In parallel a pure MgSO₄ solution with a 100 mM IS was prepared.

We used borosilicate glass slides as a substrate. The slides were either as bought or covered with a thin layer of indium-tin-oxide (ITO, from Neyco, Vacuum and Materials, Vanves, France). These slides were cleaned by rubbing the surface with cotton, dipped in a pre-mixed fine powder of calcium carbonate suspended in 2–4% commercial basic detergent solution. They were then carefully rinsed with Milli-Q water. The sample was covered with a 500 μL drop of the diluted NR solution for 2 hours and further rinsed by tilting it and gently running a stream (∼1 mL) of the 0.1 M IS MgSO₄ solution to remove any non-adhered NR particles. This rinsing operation was performed 3 times. The slide was directly mounted on the liquid cell chamber (Electrochemistry Cell, “EC_Cell”, Nanowizard 3, JPK Instruments AG, Berlin, Germany) used for the AFM experiments and 600 μL of the 0.1 M IS MgSO₄ solution was poured in to maintain the aqueous environment.

The pH of the solution was verified to be constant and equal to 7.4 ± 0.1. This assures a macroscopic constant negative electrical surface state of NR throughout the experiments and checked by electrophoretic mobility measurements.¹

2.2. AFM experiments

AFM studies were performed using a Nanowizard 3 AFM head (JPK Instruments AG, Germany) coupled to a commercial inverted microscope (Axio Observer Z1, Carl Zeiss, Germany). We used two types of AFM cantilevers with nominal stiffness value in the range of 0.03 N m⁻¹, a full tip cone angle around 40° and tip height larger than 3 μm. For the first type, cantilever and tip are made from bulk n-type silicon covered with a native silicon dioxide layer (HQ:CSC38 AFM probe, MikroMasch, Nanoworld AG), named in the following “SiO₂ tip”. The other, “Si₃N₄ tip”, is characterized by a silicon nitride tip (MSCT AFM probe, Bruker AFM Probes). For each cantilever, the sensitivity of the system deflection was measured by performing force spectroscopy (approach/retract curves) in air on a clean glass surface. For the spring constant calibration, the cantilever was retracted ∼500 μm away from the substrate and thermal oscillations were measured in air for a few seconds. The resulting frequency curve was then fitted using the JPK software to generate the correct spring constant value. A typical resonance frequency in air was 10 kHz. AFM data were acquired using a high-speed force spectroscopy mode (Quantitative Imaging mode, JPK). In this mode, a complete force curve (approach and retract) was acquired at each pixel of the (128 × 128 pixels²) images, regardless of the lateral scan size. This minimizes the lateral interactions^83,84 between tip and NR particles. For all the results presented here, the approach and retraction speeds at every pixel were constant (100 μm s⁻¹). The height extension of the AFM cantilever was fixed at 1 μm. The digitization rate for every approach and retract curve was higher than 50 kHz. The set-point force (maximum applied force during the tip approach) was chosen to fulfill two conditions: (i) reducing lateral interactions by minimizing the vertical force to avoid sweeping away of the NR particle by AFM tip; (ii) obtaining stable and reproducible approach/retract curves. Thus the typical optimal set-up forces were 1.5 nN for silicon dioxide tip and 2 nN for the silicon nitride tip. Each AFM image was scanned line by line, starting from the bottom of the image to its top. For each line, the pixels were scanned successively from left to right. All the experiments were performed at a constant temperature of 24.0 ± 1.0 °C.

First a coarse scan was made to check the localization of both SRP and LRP particles on the substrate. The lateral scan size is (10 μm)² unless other specified. To obtain more details of individual SRP or LRP, three successive AFM images were systematically performed. A wide scan – named Im#1 – with a lateral scan size of (1.5 μm)² was made, followed by a second image (Im#2) to investigate the summit of the NR of interest using a much smaller scan size of (50 nm)². In these conditions, the contact between the AFM and the NR particle took place through the tip apex. This ensured that the contact area was kept constant for all NRs and greatly reduced an edge effect where the tip edge interacts with the sides of the NR when off-center. Using this procedure, reliable information on the relative variation of adhesion – a surface property – could be obtained from measuring just the vertical force of detachment from the substrate in all experiments made with the same tip. This particular scan size of (50 nm)² was chosen as it is of the same order of magnitude as the typical contact area of the AFM tip with a standard radius of curvature of few tens of nanometers. In this way, the area of the contact zone could be considered to be constant during the acquisition of Im#2. Therefore, from the acquired AFM data, the time evolution of the adhesion properties at a specific point of the sample could be deduced. A third scan (Im#3) with a (1.5 μm)² scan size was then made at the same position as in image#1 in order to (i) confirm that the particle had not detached, been displaced, or deteriorated during the first two scans and (ii) check for possible contamination of the AFM tip. This last point was controlled by following the evolution of the AFM adhesion signal on other regions of the substrate away from NR particles for the duration of the experiments on the same day with the same cantilever and sample. This adhesion signal was found to be constant (see Fig. SI1†), establishing that no contamination of the AFM apex occurred whatever the type of cantilever, the size of NR, the type of retract curve and the applied voltage. Typical values for the adhesion signal, away from the NR particles, varied between 0.10 nN and 0.45 nN depending on the local shape (and contacting area) of the AFM tip.

To obtain reliable values for the adhesion characterizing the contact between the tip and NR particle from the images Im#1 and Im#3, we chose the points near the top of the NR particle. At these points only the apex of the tip was in interaction with the NR so that the contact area could be considered to be constant in all experiments independent of the diameter or exact shape of the NR. Thus, reliable values and the variability for the adhesion between tip and NR were obtained by the normal adhesive force as measured from the retract curves and normalized to a constant contact area. We proceeded as follows: first we checked the height signal in order to detect the summit of the studied NR. In Fig. SI2A† (black line) or SI2B† (grey line), the time variation was plotted versus the pixel time. The pixel time is the cumulated time spent by the tip at a given position on the surface through all successive approach and retract steps. Then the upper envelope of the raw AFM height signal was plotted as the orange curves in Fig. SI2.† The time scale then gives the equivalent position of the NR's summit and its height. From the determination of this position, a reliable value for the adhesion near the summit of the NR was obtained from the equivalent adhesion plots. These may vary as a function of the operating conditions of voltage and tip structure. In the case of Im#3, the part of this envelope curve corresponding to the small zone ((50 nm)²) investigated in “Im#2” was excluded from the calculation of the mean signal. This will induce a higher error bar in case of the smallest NR particles with diameter less than 200 nm, since this zone carries more weight than for a bigger NR.

In the following, the AFM images presented show the raw data with no filtering, flattening or smoothing operation during acquisition unless specified. Mathematical treatment of the AFM data to extract physical parameters (such as adhesion, stiffness, etc.) was performed by custom Matlab (MathWorks, Natick, USA) programs or by using OriginPro software (OriginLab Corporation, Northampton, USA).

2.3. Electrical measurements

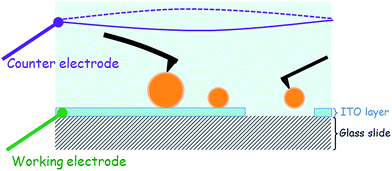
For the ITO-covered substrate, a voltage may be applied or measured by connecting the two electrodes of the EC_Cell. The working electrode was the ITO layer, while the other, the counter electrode, was made of a 0.6 mm diameter platinum wire in the shape of a 15 mm ring. This Pt ring was immersed into the aqueous medium at a distance of ≈8 mm from the working electrode as shown in the schematic in Fig. 1. The electrical signals were applied to these electrodes or the signals measured using a potentiostat (Modulab, Solartron analytical, Ametek Advanced Measurement Technology, USA).

Fig. 1 Schematic of the AFM liquid cell chamber.

3. Results

3.1. Adhesion of NR onto the substrate

3.1.1. Borosilicate substrate. Fig. 2 shows that both SRP and LRP adhered to a borosilicate substrate as they could be imaged by AFM in a large scan (20 μm)² using a SiO₂ AFM tip with a set-point force slightly less than 1 nN. However, from time to time some NR particles were detached from the substrate as seen in Fig. 2B (white square). The probability of NRs detachment during AFM scanning was greatly enhanced for scans with smaller lateral size (2 μm)² (Fig. 3). The NR particles were swept away at the positions marked by the yellow arrows. Attempts were made to minimize this spurious effect without any success. It is noticeable that the detachment of the NR always occurred when the AFM tip had passed beyond the summit of the NR. This can be explained by considering the geometry of the AFM scan (Fig. 3B and C). The cantilever is tilted by ten degrees with respect with the plane of the substrate. In this configuration, two effects combine to increase the net lateral component of the interaction force from position “1” to “2”, i.e. parallel to the surface of the sample. Firstly, the effective area of contact between the tip and the NR increases (Fig. 3C: yellow line) and second, a higher angle (α) of tip contact surface (Fig. 3C). From the typical value of the vertical component of the repulsive force, F₀ ≈ 1 nN, exerted by the tip on the NR (measured by the flexion of the AFM cantilever) and geometrical considerations of the 10° cantilever tilt angle and half of the tip cone angle of 20°, the lateral forces exerted by both back and forth sides of the tip were calculated. The difference between them gave an estimation of the adhesion force of 0.33 ± 0.05 nN between NR and substrate under maximum bonding stress in shear conditions. As adhesion rupture in both shear and tensile conditions are connected to the breaking of bonds at the interface, it is very likely that this value for adhesion in shear mode is a good estimate of that in tensile mode. The tensile mode is measured in a subsequent experiments described below. It should be noted that both the tip and substrate surfaces in contact with the NR are made from similar silica materials; therefore, we anticipate similar probabilities for the NR attachment to both silica surfaces. This could explain why NR were easily detached under these experimental conditions and followed by spurious attachment to the edge of the tip, which creates a “phantom” image (the small sphere at the right and down side of the main NR particle) in Fig. 3A and B. Note also that this detachment and attachment to the tip's edge occurred during the second smallest scan of (2 μm)². It must be emphasized that this spurious state of adhesion of NR particles to the edge of the AFM tip did not contaminate the AFM's apex. Indeed, in the control measurement, the adhesion signal on the bare substrate was constant over time showing the same type of behavior as in Fig. SI1.†

Fig. 2 Typical AFM height images in the case of a borosilicate substrate (SiO₂ tip): two large scans (scan size (20 μm)²) were done. In the second image (B) some NR is missing as evidenced in the white squares.

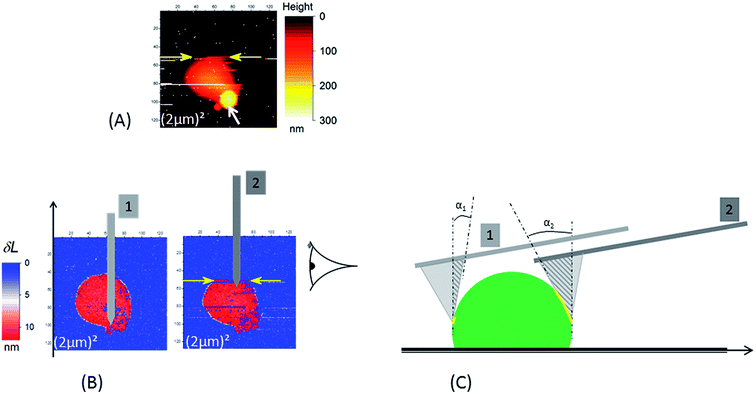Fig. 3 In the case of a borosilicate substrate the occurrence of the sweeping away of NR (see Fig. 2) during AFM scan is enhanced when scan size decreases: in (A) the NR particle is swept away at the scan line indicated by the yellow arrows (the acquisition of the AFM data is done from the bottom to the top of the image). This image was the second scan – with a (2 μm)² scan size – after those in Fig. 2; the first one is shown in (3B.1). Around 6 minutes separate two consecutive AFM images. The white arrow in (A) indicates the position of the “phantom” image (see main text for explanation). (B and C) Illustration of the origin of the increase of detachment probability between the “ascending” (position of the cantilever no. 1) and “descending” (position of the cantilever no. 2); two effects due to the tilt angle (10°) of the AFM cantilever versus the sample surface are present: (i) increase of contact area (yellow line) between the active edge (the dark gray triangle) of AFM tip and the NR particle; (ii) horizontal component of force exerted by the cantilever. The AFM images in (B) are δL signals as defined in the main text for the two successive small scans ((2 μm)²). The schematic in (C) is the right side view of NR particle in (B). In (C) NR and tip are not drawn at the same magnification.

Despite the low and intermittent adhesion of NR on the borosilicate substrate, information on adhesion between the SiO₂ AFM tip and the NR were obtained by studying retract curves at every pixel of the AFM data. A typical example is plotted in Fig. 4A and B. After adhesion rupture (magenta star in Fig. 4B), the cantilever underwent slightly damped oscillations (maximum amplitude 0.65 ± 0.05 nN) with a frequency of 2.561 ± 0.009 kHz as deduced from fast Fourier transform (black curve in Fig. 4C). This frequency corresponds to that deduced from the thermal vibration spectrum of the cantilever in liquid, measured at a distance of 500 μm away from the substrate (grey curve in Fig. 4C). After the damping of the oscillations generated by this adhesion rupture, the force reached an asymptotic value. This null-force level is ≈500 nm distance from the retract point corresponding to the maximum repulsive force as shown by the horizontal red line in Fig. 4A and B. The adhesion – Y_adh – was referenced to this level (Fig. 4B).

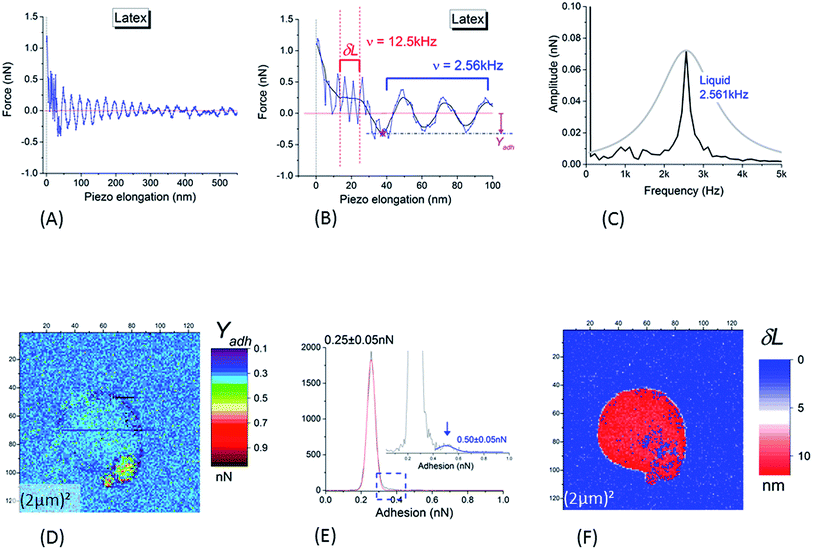Fig. 4 (A and B) Typical retract curve for points corresponding to NR particles (substrate and tip in silica); (B) is a magnification of (A) at low piezo elongation (blue curve: raw data; black curve: smoothed signal). The horizontal red line is the null-force level, the asymptotic value of the force after the damping of the oscillations generated by the rupture of adhesion (marked by the magenta star in (B)). Adhesion – Y_adh – is referenced to the null-force level (B). After the rupture of adhesion, the cantilever is enduring slightly damped oscillations the frequency of which is equal to 2.561 ± 0.009 kHz as deduced from fast Fourier transform ((C), black curve). This frequency corresponds to that deduced from the thermal vibration spectrum of the cantilever in liquid, as measured at a distance of 500 μm from of the substrate and shown in (C) (grey curve). Oscillations at higher frequency (12.50 ± 0.05 kHz) are present in the piezo elongation domain before the zone of free oscillations in liquid: this domain is visible between the two vertical dashed lines plotted in (B). This high valued frequency corresponds to that (12.490 ± 0.005 kHz) deduced from the measurement of the thermal vibrations of the cantilever in air (at a distance of 500 μm from the substrate). (D) Adhesion image corresponding to height image in Fig. 3B. (E) Histogram of (D); the insert is a magnification of it around the right edge of the main peak. In (F) is plotted the width (δL) of the superficial layer as defined in main text (Section 3.1.1).

Another interesting feature is visible in Fig. 4B where a magnification of the retract curves along the piezo elongation's axis reveals the presence of higher frequency oscillations (12.50 ± 0.05 kHz) in the piezo elongation domain before reaching the zone of free oscillations in liquid (between the red vertical dashed lines). This high frequency was near to that of the thermal vibrations of the cantilever in air at a distance of 500 μm from the substrate. Such a significant decrease in resonance frequency of thermal oscillations from a cantilever oscillating in air to one in aqueous medium is usually interpreted⁸⁵ by the existence of a boundary layer of liquid in contact with the cantilever, acting as an added inertial mass to the cantilever. This means that the slip speed of this layer is null at the cantilever/fluid interface. We showed here that the frequency of oscillations in the small range along the piezo-displacement axis, near the deeper part of the core–shell structure of the NR investigated by the AFM tip, was of the same order of magnitude as in air. We hypothesized that within this small range, the cantilever plunged into a superficial hydrophobic layer of NR where the condition of a null slippery speed of the interface layer was no longer valid. The width, δL, of this zone with high frequency oscillations (Fig. 4B) corresponds to the thickness of the surface layer surrounding the harder NR core which was probed in the almost linear regime near the force set-point. An example of δL image is plotted in Fig. 4F. From this, we deduce that the mean value of the SL thickness was equal to 11 ± 3 nm. This value is in good agreement with other direct AFM measurements,⁸⁶ and is slightly higher than that obtained with non-local measurements.^30,87,88

The adhesion image (Fig. 4D) shows that the adhesion (in tensile stress) between SiO₂ tip and borosilicate substrate was small: a value of 0.25 ± 0.05 nN was obtained from the main peak in histogram in Fig. 4E. It is worth noting that the large NR particle could not be distinguished from the bare SiO₂ substrate in this image. The values of the adhesion are very similar; between the NR particle and the SiO₂ tip, we obtain 0.25 ± 0.05 nN in tensile mode or 0.33 ± 0.05 nN in shear stress mode on the silicate substrate. This implies that NR particle will adhere to the SiO₂ substrate or tip with similar probabilities. A slightly higher contrast in adhesion is noted for the small satellite at the bottom-right edge of the main sphere, clearly evidenced by the small but detectable peak at the right side of the main peak in the histogram of the Fig. 4E. This peak is centered on 0.50 ± 0.05 nN. This value is probably related to adhesion between two neighboring NRs through their SL; the main NR sphere on the substrate, and the NR adhering to the edge of the tip from a previous scan.

3.1.2. ITO substrate. It must be mentioned first of all that ITO substrates conditioned in the same way as for SiO₂ slides, i.e. without connection to the potentiostat, gave similar results. The attachment of NR on the substrate is incomplete with randomly spurious detachment occurring randomly. However, by applying an electric voltage, we could immobilize irreversibly the NRs onto the ITO substrate. To achieve this, the two electrodes of the EC_Cell (the ITO layer and platinum wire: see Fig. 1) were connected to the potentiostat and a voltage applied at the end of the NR adhesion step. Control experiments were performed to check this. First, the electrochemical status of the solution was verified by acquiring cyclic voltammogram curves (current–voltage I(V)) in the narrow potential window inside which the voltage would be applied in the last step (Fig. SI3A†). This enabled us to check that no spurious electrochemical effect occurred either to the solution or NR particles during subsequent electrical procedures. Fig. SI3B† displays a typical I(V) curve with a quasi-linear behavior over this range of voltage showing that no active redox couple was present (no faradic current is present). The offset between the upper and lower quasi-linear curves corresponds to the direction of the voltage ramp (up and down at a rate of 10 mV s⁻¹). This stems from the capacitive effect of the diffuse layer. The measured capacitance of 10 ± 2 μF accords with the calculated value from a simple model of a capacitor¹² by taking the Debye thickness of the diffuse layer of ≈1 nm for a aqueous ionic solution with a ionic strength of 0.1 M as the distance between electrodes. In a second step, we measured the intrinsic natural potential difference between the counter and working electrodes also known as the spontaneous potential or open-circuit potential (OCP). At this stage no current flowed through the potentiostat and the solid electric connections. As illustrated in Fig. SI3C,† this OCP decreased according to an exponential law with a time constant in the range of 450 ± 50 s before reaching a steady state characterized by an OCP value of −270 ± 30 mV. This time range corresponds to the charging time related to diffusion of ions in the aqueous solution of a resistor/capacitor circuit constituted by the MgSO₄ solution between the electrodes. Indeed, by assuming a diffusion coefficient for ions of D ≈ 1.10⁻⁹ m² s⁻¹ and a limiting conductivity for MgSO₄ solution of Λ_MgSO4 = 150 S cm² mol⁻¹, we found a diffusion length of the order of magnitude of 700 μm, the typical distance between the two electrodes. In these experiments, this step took 45 minutes.

After these controls, the potential of the ITO layer (working electrode) was changed linearly with time from the OCP value to the chosen voltage and then maintained constant for the experiments. AFM data acquisition was started 5 minutes later when stationary regime was reached (time constant 2.0 ± 0.2 s). The value of this constant voltage was chosen (i) to impede NR detachment from the substrate during the AFM scans and (ii) to be in the linear regime (non-faradic evolutions) of the voltammogram in Fig. SI3B.† This demonstrated that the application of a positive voltage enabled successful AFM imaging and the tip/NR adhesion properties to be studied without any detachment of NR particles regardless of their size, AFM tip and applied voltage. This is described in more detail in the next section.

3.2. Adhesion properties between NR and AFM tip

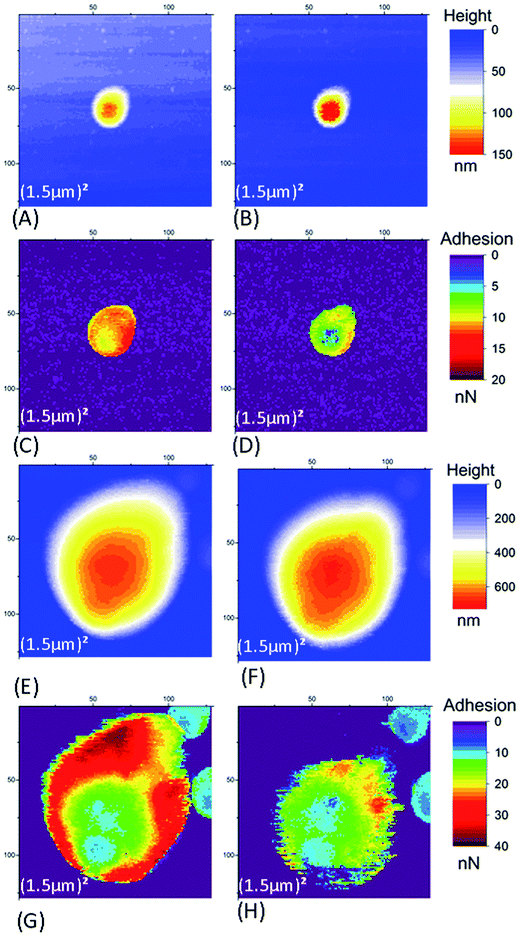
Fig. SI4† presents three different types of retract curves that were observed for NR particles adhering to the ITO substrate, independent of the nature of the AFM tip (SiO₂ or Si₃N₄) and the applied voltage. The first one, type I in Fig. SI4A,† is characterized by a low adhesion of only a few tenths of nN. This type of retract curve was systematically observed on the bare part of the substrate (i.e. away from the NR particles). Note that this was the only type of retract curve observed on the borosilicate substrate, whether for different tips, on top of or away from the NR particles. In contrast, the type II and III curves were only observed for pixels on the NR particles. These curves indicate a much larger adhesion in the range of few tens of nN. The type II curve differs from type III by the quasi-instantaneous return to state of null force. In Fig. SI4C,† type III adhesion curves possess two or more plateaus after the main adhesion rupture point. In contrast to what was observed with SiO₂ substrates (Section 3.1.1) we noticed an evolution of the measured AFM signals on the NR particles between successive scans, independent of the tip and the applied voltage. We will discuss these variations first in the AFM images of a large scan zone (Im#1 and Im#3). Then we will focus our interest on the small (50 nm)² images (Im#2).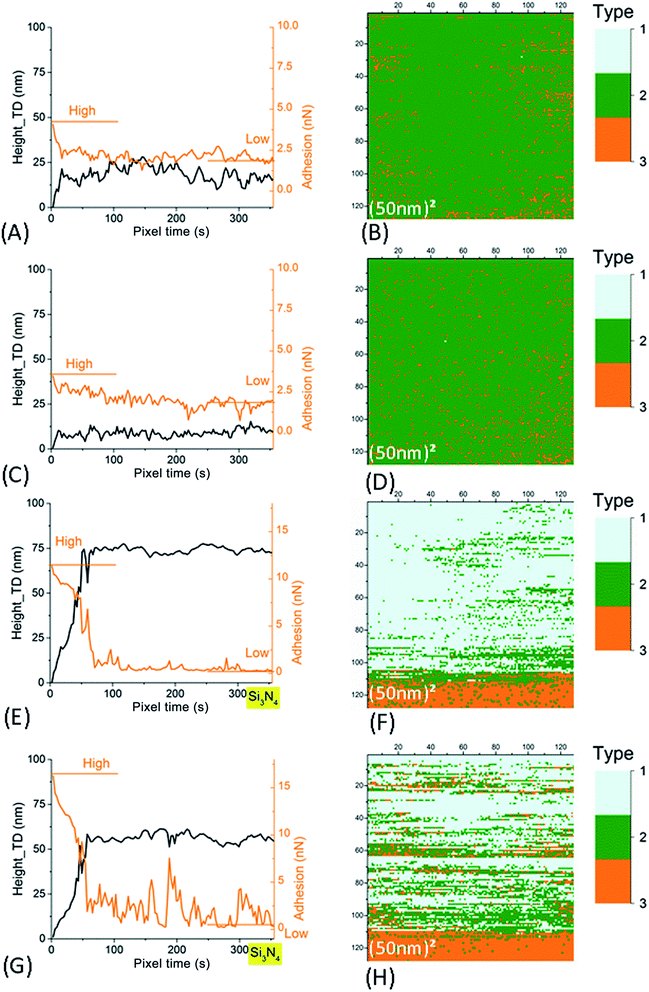

3.2.1. Large scan images (Im#1 and Im#3). Typical AFM height and adhesion images, obtained at zero applied voltage for both SRP and LRP, are shown in Fig. 5 and SI5† for the two tips, Si₃N₄ and SiO₂, respectively. All the data for these two types of tips are summarized in Fig. 6. The first observation is that tip/NR adhesion, of a few tens of nN, is one order of magnitude higher for a Si₃N₄ tip than for a SiO₂ tip and increases with the size of the NR particle. Moreover, it is worth noting that the tip/NR adhesion is systematically lower for image #3 than for image #1 and the absolute value of the difference between them increases with the size of the rubber particles (Fig. SI6†). This last effect is correlated with a slight increase in both the height and stiffness of the NR particles (Fig. SI6†). These effects have much higher amplitudes with Si₃N₄ tips than SiO₂ ones. Besides, similar experiments made with a voltage of +50 mV applied to the ITO substrate revealed a noticeable decrease of tip/NR adhesion for all tips and NR dimensions (Fig. 6). Turning our attention to the adhesion signal, we observe that the adhesion signal on the NR decreases from Im#1 to Im#3, showing that these AFM signals are time dependent. In order to understand the phenomenon better, we will look more closely at the data obtained during Im#2 scanning.

Fig. 5 Case of Si₃N₄ tip and a 0 mV voltage applied to the ITO substrate, large scan images (1.5 μm)² – Im#1 and Im#3, of small (A–D) and large (E–H) NR particles. The left and right columns are AFM data for Im#1 and Im#3 respectively. Images (A, B, E and F) are height data and images (C, D, G and H) are for adhesion.

Fig. 6 Variation of the adhesion signal for the complete set of three successive images, Im#1–3, versus the height (as measured in Im#1) of the NR particles for SiO₂ tip (A and C) and Si₃N₄ tip (B and D) at different voltages (0 mV for (A and B) and +50 mV for (C and D)). The blue vertical lines along the Y axes in images (B and D) represent the adhesion scale for SiO₂ tip as plotted in (A and C).

3.2.2. Small scan images (Im#2). In Im#2, the contact between the tip and the sample can be considered as quasi punctual, so the time spent by the tip at the quasi-same location is proportional to the pixel number in the AFM scan. This time is called the “pixel time“. The time evolution of the two AFM signals (adhesion in orange and height in black) is plotted in Fig. 7 for both tips and for SRP and LRP particles. A detailed explanation for the data treatment is given in Fig. SI7.† In the right column of Fig. 7, the AFM images corresponding to the type of the retract curve are also plotted. One remarkable feature is that adhesion is time dependent with a transition from a high adhesion state to a low one regardless of the tip. This effect is enhanced for Si₃N₄ tips (Fig. 7, left column). The state of low adhesion is close to the AFM detection threshold (≤1 nN) for all applied voltages used. The adhesion value for the high-adhesion state in Im#2 is lower than that measured for Im#1. This holds for both types of tip, the voltage applied to the substrate and the size of the NR. In addition to the decrease in adhesion, a slight increase of the NR particle height is observed. Furthermore, changes in the applied voltage induce a noticeable decrease of tip/NR adhesion independent of the tip or the NR dimensions that reaches the AFM detection threshold at +50 mV. The complete set of results for the three types of images (Im#1 to Im#3) is plotted in Fig. 6.

Fig. 7 Left column: time evolution of AFM signals in Im#2 (scan size of the associated image: (50 nm)²). The smoothened height signal (black line) after correction of this residual thermal drift (as explained in Fig. SI7B†) and adhesion signals (orange line) are plotted. Right column: (50 nm)² AFM images for signal characterizing the type of retract curve (see main text and Fig. SI4† for more explanation). (A–D) For SiO₂ tip. (E–H) For Si₃N₄ tip. Data in (A, B, E and F) are for small NR particles (SRP). Data in (C, D, G and H) are for large NR particles (LRP).

4. Discussion

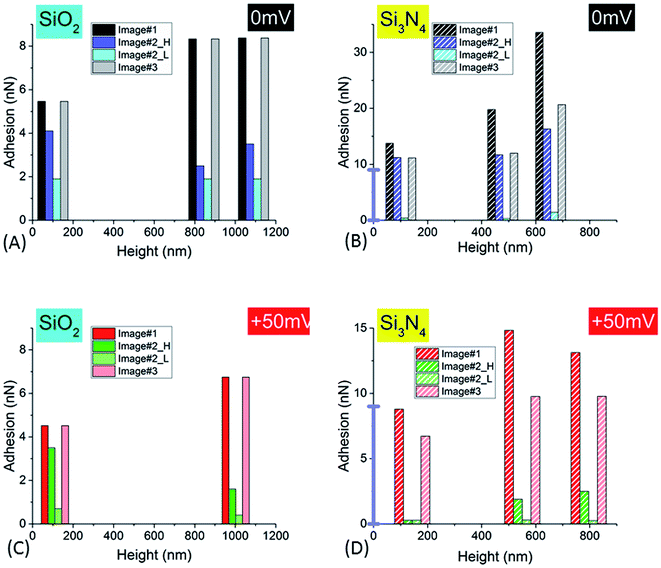
Thanks to the development of this original method for immobilizing the NR on a solid surface, whatever their size, we were able to study adhesion properties between NRs and AFM tips in well controlled conditions. We found that adhesive properties of NRs depend highly on their surface charge state. Tip/NR adhesion was shown to be much higher with Si₃N₄ tip than for SiO₂ tip, two materials with different surface charge properties as it will be detailed below. In addition, an increase in the voltage applied at the ITO substrate induced a noticeable decrease of tip/NR adhesion whatever the tip or the NR's size. Another important experimental feature is that the tip/NR adhesion properties were shown to be dependent on the contact time between NR and tip. This dependency varied according to the nature of AFM tip, it was more pronounced in the case of Si₃N₄.

4.1. Influence of NR size

We found that the adhesion between the AFM tip and NR and its relative variation between Im#1 and Im#3 increased with the size of the particles in case of Si₃N₄ tips (Fig. SI6†). This could be due to the higher concentration in lipids for larger NR particles^3,82 and the related enhanced electrostatic interactions between the tip and the polar lipidic heads protruding from the SL.¹ However, we cannot exclude the role of the proteins present in the SL,^2,4,8 in agreement with the model of a proteinaceous layer anchored at the NR core surrounded by lipidic polymers.¹

When measuring the NR's stiffness, the SL and the NR core can be considered to be two springs in series. Thus, due to the low SL thickness, the NR stiffness mainly reflects the properties of the polyisoprene core of the nanoparticle so that NRs, whatever their size, have stiffness values around 70 mN m⁻¹. However, the stiffness measured for LRP is slightly higher than for SRP, which might be related to the different lipo-protein shell composition of the NR: a higher lipid concentration for LRP when compared to SRP associated to a different protein content and organization.⁸

4.2. Influence of the electrostatic state of contacting surfaces

We first proved that adhesion of NR particles on ITO planar surfaces was high enough to permit their AFM examination. This was obtained by applying a null or positive voltage to the ITO layer (measured versus the reference electrode). It must be emphasized that this higher adhesion to ITO substrate compared to silica cannot be attributed to a roughness effect since RMS roughness of these two surfaces have similar values of few nanometers over an AFM scanned area of (10 μm)². We attribute this effect to enhanced electrostatic interactions between negatively charged NRs^1,3,82 and the positively charged ITO layer at the pH used in this study (pH = 7.4 ± 0.1). The isoelectric point, IEP, of ITO in OCP condition lies between 3.5 and 6.⁸⁹

For immobilized NR particles, the experiments detailed here revealed that adhesion between AFM tip and NR depends on (i) the voltage applied to the substrate (whatever the tip) and (ii) the nature of the AFM tip through its electric state of charge. The electrical influence of the substrate polarization onto the tip/NR adhesion is probably not due to a direct effect of the applied voltage to the ITO layer as there is an ionic screening of surface charges. The Debye length of ∼1 nm is indeed much smaller than the typical height of NR (a few hundreds of nanometers) for the 0.1 M ionic strength of the aqueous solution. It can be more reasonably explained by a direct electrical resistive connection through the NR's thin surface layer. As the IEP of SiO₂ of between 2 and 3 (ref. 90 and 91) is significantly lower than that of Si₃N₄ (between 3.5 and 6 (ref. 92)), the surface state of charge is different for both tips leading to a modification of the adhesion properties between the tip and NR. We can thus conclude that the electrical state of both surfaces is an important parameter for their adhesive properties even in the case of high ionic strength solutions for which long-range electrostatic interactions (the double-layer force in the context of the DLVO theory) are screened over a nanometric range. We indeed did not observe any electrostatic effect during the approach curve when the tip/NR distance was as small as the jump-to-contact point. This electrostatic effect at short range could be explained by the presence of ion-bridging forces.^33,93,94

4.3. Time dependency of NR/solid surface adhesive properties

NR/solid surface adhesive properties are time-dependent as strongly revealed in the case of Si₃N₄ tip. Indeed, the value of adhesion varies with the cumulated time spent by the tip at a given position as clearly evidenced for small AFM scan areas (Im#2; scan size (50 nm)²) for which the contact can be considered as quasi punctual. However this decrease of adhesion is also systematically observed in Im#3 when compared to Im#1 for zones not investigated during the small size scan in Im#2: the amplitude of this variation is nevertheless lower than that occurring during Im#2. This can be explained, as for Im#2, by the fact that the distance separating two successive pixels, for Im#1 and Im#3 – around 12 nm – is smaller than the mean tip radius of ∼30–50 nm: each zone of the NR is thus probed by the AFM tip during around six AFM approaches. Such an effect was also observed for SiO₂ tip but with smaller variations. As short-range electrostatic interactions were proved to be dominant in the experiments reported here, it is worth noting that the relevant time is the contact time between the two facing electric double layers. It is estimated from the duration spent by the tip in the repulsive regime during both its approach and retract movements: it is roughly equal to ≈2 ms per pixel, a value ten times lower than the total time spent by the tip at every pixel, the so-called pixel time.

From these observations it can be concluded that the AFM signals depend on the total (i.e. cumulated) contact time, τ, between the two facing double layers during the probation of the minimum investigated area surface ((30–50 nm)²) by the AFM tip, in its successive approach and retract movements. The variation of NR/tip adhesion versus the total contact time, τ, is plotted in Fig. 8.

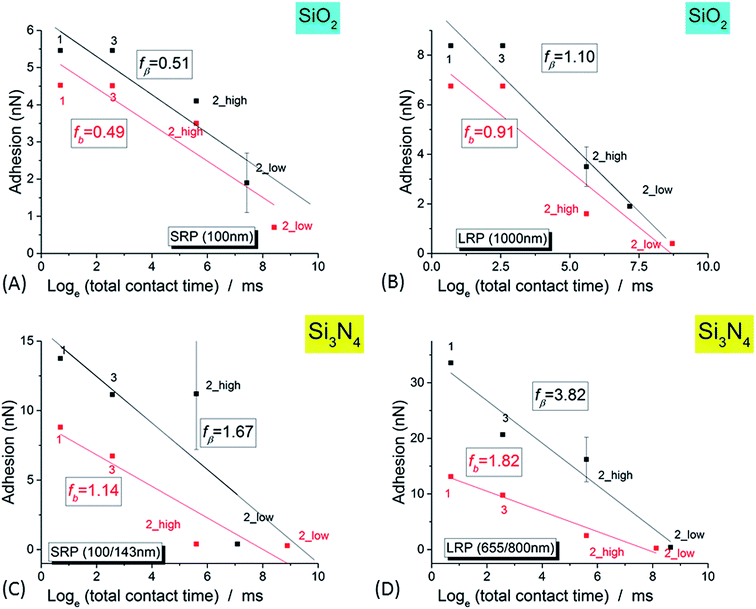Fig. 8 Variation of the adhesion signal (for the complete set of three successive images, Im#1–3, versus the logarithm of the total contact time, as defined in the main text, for SiO₂ tip (A and B) and Si₃N₄ tip (C and D), for small NR (SRP; (A and C)) and large NR (LRP; (B and D)) particles. For Im#2, the low and high levels of adhesion are plotted. The black (respectively red) markers correspond to 0 mV and +50 mV voltages, respectively. The lines are the best linear fits according to eqn (1) (see main text).

4.4. Interpretation within the framework of the theory of dynamic strength of molecular adhesion bonds

For biological matter like that implied in latex compounds, molecular linkages to external surfaces, via their superficial layer, arise mainly from weak noncovalent interactions. It was predicted and observed that these bonds will fail under any level of pulling force if this force be held for sufficient time. Thus, when tested with force probe method as such AFM^21,95,96 or ultrasensitive transducer constituted by a cell-size membrane capsule pressurized by micropipette suction,⁴⁶ strength of adhesion at interfaces was proved to have time-dependent properties.⁶⁶ Bond strength was indeed shown to be depending on loading rate as the bond survival time diminished with increasing loading rate.⁶⁶ Dissociation under force of weak noncovalent chemical bonds stands far from equilibrium kinetics. In this case, rupture strengths for weak biochemical bonds are not constant but instead depend on the rate of force application and duration of loading.⁶⁵ Contrary to the case of condensed liquids, the thermal impulses that drive dissociation are not dissipated rapidly by viscous coupling to the environment.⁶⁵ Application of force in all mechanical experiments occurs over a time scale much longer than relaxation times for thermal impulses (typically <10⁻¹² s (ref. 65)). In standard experiments mechanical loading rate ranges from 1 to 10⁶ pN s⁻¹.⁶⁶ In the experiments presented here it was constant and equal to 3 × 10⁶ pN s⁻¹.

An increased rate of bond dissociation under external force⁶⁵ was first emphasized by Bell⁷⁷ using a phenomenological model for the off rate, which is an extension of transition state theory for reactions in gases introduced by Eyring and others.^97,98 In the theory of Dynamic Force Spectroscopy analysis developed by Evans et al.,^65–67 dissociation under force is assumed to be sufficiently slow so that there are many thermal impulses per force escape. The external force is considered as stationary over the time scale of these excitations.⁶⁵ The likelihood of detachment of a single bond under force is assumed to be a first-order kinetic process along a single thermodynamic pathway for dissociation, leading to an exponentially decaying function of time.^65,66,71,72 However, due to the high rate of thermal excitations, the probability of bond survival is no longer a simple exponentially decaying function of time but is characterized by a time-dependent rate of dissociation, the off-rate, ν_m and has to be integrated over successive small time steps. Evans et al. thus deduced that the probability of failure is the product of this off-rate – that increases in time – and a likelihood of bond survival that decreases with time. This can thus exhibit a maximum at a specific time or, equivalently, a force as the loading rate is a constant. Adhesion, as directly related to bond strength, is defined from the force corresponding to the peak of the rupture force distribution. Its value increases with the rate of loading⁶⁵ as the energy landscape along a reaction pathway in unbonding is modified by the external force.^65,77 This supplemental mechanical energy lowers energy barriers, decreases the likelihood of bond survival, and speeds up dissociation.⁶⁶ Lowering the barrier by the mechanical potential, E_m, leads thus to an amplification of the dissociation kinetics.^65,99

The bond strength, f*, measured in our experiments as the adhesion during the retract of the tip from the substrate, is usually plotted versus the logarithm of the mechanical loading rate, r. With further theoretical arguments detailed in ESI† it is possible to prove the following relation between f* and the effective contact time of double layers, τ, as defined above:

f* = −f_β log_e(τ) + [c + log_e(Δf₀)] (1)

As shown in Fig. 8 the experimental data presented in this paper are well fitted by such a logarithmic relationship – eqn (1) – confirming the validity of the theory of molecular adhesion bond of Evans and coworkers for the adhesion of the AFM tip and the surface layer of the latex nanoparticles. However we measured a value for the slope f_β in the range of few nanonewtons, ten to hundred times higher than in the case of the biotin/streptavidin example where only a pure mechanical ramping was applied.⁶⁶ To explain that discrepancy, we hypothesize that this higher value is stemming from the electrostatic influence of the double layers of both the AFM tip and the SL. We thus postulate that an electrostatic term has to be added to the only mechanical one, E_m, in the initial theory in order to explain our experimental results within the framework of the Dynamic Force Spectroscopy theory:

E = E_m + E_e (2)

A rough calculation of the order of magnitude for the electrostatic energy stocked in this process could bring a further justification of that idea. Charge density of the latex particles is indeed known to be in the range of 0.1 C m⁻².⁸² From that, by supposing a typical area of contact between the AFM tip and the NR's SL of (30 nm)², the electrostatic energy, E_e, is estimated to be in the range of 5 × 10⁻¹⁸ J if a voltage variation of ∼50 mV, the order of magnitude of what was used in our experiments, is considered. From that, the calculated ratio between electrostatic and mechanical energies is proved to be in good agreement with the value of ratio between the respective f_β values.

The relative positioning of the electrical levels associated to both tips and substrates – as plotted in Fig. 9A – may be estimated thanks to the following remarks: (i) IEPs for Si₃N₄ and ITO (in the OCP configuration) and, consequently, their related surface potentials are in the same order of value (see above), (ii) from the value of potential for ITO in OCP, the voltages corresponding to ITO polarization states at 0 mV and +50 mV versus the platinum reference electrode can be placed in this diagram and (iii) the potential for SiO₂ tip is lower than that of Si₃N₄ accordingly to their respective IEP. It is now possible to plot a rough estimation of the variation of f_β versus these relative values of voltage, δV, for the different cases of tips and substrates we studied in this paper (Fig. 9B). These experimental points can be roughly fitted by parabolic profiles (full lines in Fig. 9B). This can be explained by the fact that the f_β coefficient is, as mentioned above, proportional to the energy related to the process of electrically activated rupture due to this voltage difference δV. The value of this energy can be estimated through that of a condenser, the electrodes of which would be the tip and the substrate – which leads to a variation in (δV)². This observation enforces our interpretation of the adhesion phenomena between the AFM tip and the NR's particles by an electrical activated process.

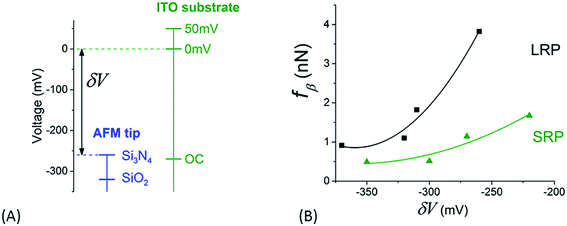Fig. 9 (A) Relative positioning of surface voltages for both tip and sample as explained in the main text. (B) Variation of the slope, f_β, of the fits in Fig. 8 versus the difference of surface potential, δV, as determined from graph in (A).

The Dynamic Force Spectroscopy theory was thus successively applied to these experiments studying the variation of adhesion properties versus the so-called effective contact time. This time was defined as the sum of interacting times due to probation by the AFM tip of the minimum investigated area surface ((30–50 nm)² as estimated from the mean diameter of its apex) in its successive approach and retract curves. This cumulative-like effect might be explained by a similar argument as that developed in ref. 73 suggesting that the off-rate could depend also on the entire history of force application rather than the only instantaneous value of force.

In spite of its simplicity, the model based on the crucial role of the electrostatic interactions between biopolymers (modelized by the NR particles) and surfaces such as that of the AFM tip or the substrate with varied electrical surface properties permits a reasonable interpretation of the experimental results presented here in the context of the Dynamic Force Spectroscopy theory. This electrostatic effect was proved to cause an enhancement of the effect of the mechanical ramping on the dynamic spectrum of bond strengths as studied by the AFM experiments we conducted in a fast loading regime.

Such electrostatic effects on the time evolution of the adhesion properties of biological surfaces such as the lipid/protein superficial layer of latex nanoparticles have not been observed²¹ before, probably for the two following reasons: (i) the probing force was increased at a lower rate, likely hampering the observation of such transitions; (ii) the used AFM tips were in such an electrostatic state that the transition to the lowest adhesion state had already occurred at the very beginning of the AFM experiments²¹ and thus could not be detected despite the fact that similar silicon nitride probes (MSCT cantilevers, Bruker AFM Probes) were used. These cantilevers were indeed pre-conditioned in quite different conditions:²¹ in an initial procedure they were treated by UV and ozone during 15 min.²¹ This cleaning procedure is indeed known to be a strong oxidizing treatment so that the Si₃N₄ surface layer was very likely oxidized in a silica one thus modifying its electrical state.^92,100 This fact could very likely explain that the AFM tip with this silica overlayer²¹ leads to type II retract curves as with the SiO₂ probe we used and not type III as with our native Si₃N₄ tips. This confirms the fact that the adhesion data are highly dependent on the electrical state, mainly stemming from the redox properties of the solid surface contacting the biocompound.

5. Conclusion

In this paper, we studied the surface interactions of NR particles with three types of solid surfaces (silicon oxide, silicon nitride and ITO) in aqueous medium at high ionic strength (0.1 M, MgSO₄). We performed an AFM investigation in force spectroscopy mode in the fast loading rate regime (≈3 × 10⁶ pN s⁻¹). An easy method was found to prevent the NR on the substrate from being swept away by the AFM tip. Through the comparison of interactions between NR and either the tip or the substrate, we prove that the adhesion process can be monitored by slight changes in the surface charge state.

These results were interpreted using Dynamic Force Spectroscopy (DFS)^{65–67,71–73,76} theory where a term to describe the electrostatic energy is added to the classical mechanical potential of the DFS theory. This was applied in our experiments by fitting variation of adhesion versus the effective contact time. This contact time was defined as the sum of all interaction periods of the minimum surface area investigated by the AFM tip apex in its successive approach and retract curves. This cumulative-like effect could be explained by a similar argument to that developed in ref. 73, which suggests that the off-rate could depend on the entire history of the applied force rather than the instantaneous value of force. Through these results, we emphasized the crucial role of the electrostatic interactions on the adhesion properties between biopolymers and solids with a variety of surface electrical properties. The electrostatic effect caused an enhancement of the mechanical ramping effect on the dynamic spectrum of bond strengths in the AFM experiments performed in fast loading regime. These results are of importance both for practical applications in solution-based industrial processes and to the fundamental knowledge of adhesion processes involving biopolymers or living cells.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank ANRT for CIFRE funding (2011/1324). PS acknowledges the French Institute of the French Embassy in India for the Researcher Fellowship of the Charpak internship program. This work was partly supported by the program “Investissements d’Avenir du LabEx PALM (ANR-10-LABX-0039-PALM). We express our gratitude to Dr Andrew Mayne (ISMO, Orsay) for his English revision of the manuscript.

References

1. C. N. Rochette, J. J. Crassous, M. Drechsler, F. Gaboriaud, M. Eloy, B. de Gaudemaris and J. F. L. Duval, Langmuir, 2013, 29, 14655–14665.
2. K. Berthelot, S. Lecomte, Y. Estevez and F. Peruch, Biochimie, 2014, 106, 1–9.
3. A. J. Chan, K. Steenkeste, M. Eloy, D. Brosson, F. Gaboriaud and M.-P. Fontaine-Aupart, Rubber Chem. Technol., 2015, 88, 248–257.
4. K. Berthelot, S. Lecomte, Y. Estevez, B. Coulary-Salin and F. Peruch, Biochim. Biophys. Acta, Proteins Proteomics, 2014, 1844, 473–485.
5. J. Sansatsadeekul, J. Sakdapipanich and P. Rojruthai, J. Biosci. Bioeng., 2011, 111, 628–634.
6. K. Nawamawat, J. T. Sakdapipanich, C. C. Ho, Y. Ma, J. Song and J. G. Vancso, Colloids Surf., A, 2011, 390, 157–166.
7. Y. Tanaka, S. Kawahara and J. Tangpakdee, KGK, Kautsch. Gummi Kunstst., 1997, 50, 6–11.
8. K. Berthelot, S. Lecomte, Y. Estevez, V. Zhendre, S. Henry, J. Thévenot, E. J. Dufourc, I. D. Alves and F. Peruch, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 287–299.
9. S. Ren and M. A. Dubé, Int. J. Adhes. Adhes., 2017, 75, 132–138.
10. C. Tan, T. Tirri and C.-E. Wilen, Int. J. Adhes. Adhes., 2016, 66, 104–113.
11. A. Zosel, Colloid Polym. Sci., 1985, 263, 541–553.
12. A. J. Bard and L. R. Faulkner, Electrochemical methods: fundamentals and applications, ed. A. J. Bard and L. R. Faulkner, Wiley, New York, 2nd edn, 2001, p. c1980.
13. A. E. O'Connor and N. Willenbacher, Int. J. Adhes. Adhes., 2004, 24, 335–346.
14. L. M. Mosley, K. A. Hunter and W. A. Ducker, Environ. Sci. Technol., 2003, 37, 3303–3308.
15. A. T. Poortinga, R. Bos, W. Norde and H. J. Busscher, Surf. Sci. Rep., 2002, 47, 1–32.
16. M. B. Salerno, B. E. Logan and D. Velegol, Langmuir, 2004, 20, 10625–10629.
17. J. J. Valle-Delgado, J. A. Molina-Bolívar, F. Galisteo-González, M. J. Gálvez-Ruiz, A. Feiler and M. W. Rutland, J. Phys. Chem. B, 2004, 108, 5365–5371.
18. L.-C. Xu, V. Vadillo-Rodriguez and B. E. Logan, Langmuir, 2005, 21, 7491–7500.
19. E. Diamanti, L. Cuellar, D. Gregurec, S. E. Moya and E. Donath, Langmuir, 2015, 31, 8623–8632.
20. M. Fletcher, Bacterial adhesion: molecular and ecological diversity, Wiley-Liss, New York, 1996.
21. F. Gaboriaud, B. de Gaudemaris, T. Rousseau, S. Derclaye and Y. F. Dufrêne, Soft Matter, 2012, 8, 2724–2729.
22. N. I. Abu-Lail and T. A. Camesano, Biomacromolecules, 2003, 4, 1000–1012.
23. A. Zita and M. Hermansson, Appl. Environ. Microbiol., 1994, 60, 3041–3048.
24. P. A. Deshpande and D. R. Shonnard, Water Resour. Res., 1999, 35, 1619–1627.
25. H. H. M. Rijnaarts, W. Norde, J. Lyklema and A. J. B. Zehnder, Colloids Surf., B, 1999, 14, 179–195.
26. L.-C. Xu and B. E. Logan, Environ. Sci. Technol., 2005, 39, 3592–3600.
27. F. Ahimou, F. A. Denis, A. Touhami and Y. F. Dufrêne, Langmuir, 2002, 18, 9937–9941.
28. S. B. Sadr Ghayeni, P. J. Beatson, R. P. Schneider and A. G. Fane, J. Membr. Sci., 1998, 138, 29–42.
29. D. G. Jewett, T. A. Hilbert, B. E. Logan, R. G. Arnold and R. C. Bales, Water Res., 1995, 29, 1673–1680.
30. B. V. Derjaguin and L. D. Landau, Acta Physicochim. URSS, 1941, 14, 633–662.
31. E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948.
32. K. Kendall, Molecular Adhesion and Its Applications, The Sticky Universe, Kluwer Academic Publishers, 2001.
33. X. Liu, K. L. Feilberg, W. Yan, E. H. Stenby and E. Thormann, Langmuir, 2017, 33, 4426–4434.
34. R. A. Hartvig, M. van de Weert, J. Østergaard, L. Jorgensen and H. Jensen, Langmuir, 2011, 27, 2634–2643.
35. M. A. Bos, Z. Shervani, A. C. I. Anusiem, M. Giesbers, W. Norde and J. M. Kleijn, Colloids Surf., B, 1994, 3, 91–100.
36. W. Norde and J. Lyklema, J. Biomater. Sci., Polym. Ed., 1991, 2, 183–202.
37. G. V. Lubarsky, M. M. Browne, S. A. Mitchell, M. R. Davidson and R. H. Bradley, Colloids Surf., B, 2005, 44, 56–63.
38. T. Goda and Y. Miyahara, Langmuir, 2012, 28, 14730–14738.
39. B.-H. Chiou, Y.-T. Tsai and C. M. Wang, Langmuir, 2014, 30, 1550–1556.
40. T. E. Benavidez and C. D. Garcia, Langmuir, 2013, 29, 14154–14162.
41. T. E. Benavidez, D. Torrente, M. Marucho and C. D. Garcia, Langmuir, 2015, 31, 2455–2462.
42. K. G. Sprenger and J. Pfaendtner, Langmuir, 2016, 32, 5690–5701.
43. M. Deighan and J. Pfaendtner, Langmuir, 2013, 29, 7999–8009.
44. J. Liao, Y. Zhu, Z. Zhou, J. Chen, G. Tan, C. Ning and C. Mao, Angew. Chem., Int. Ed., 2014, 53, 13068–13072.
45. S.-J. Marrink, O. Berger, P. Tieleman and F. Jähnig, Biophys. J., 1998, 74, 931–943.
46. E. Evans, K. Ritchie and R. Merkel, Biophys. J., 1995, 68, 2580–2587.
47. C. Satriano, G. Lupo, C. Motta, C. D. Anfuso, P. Di Pietro and B. Kasemo, Colloids Surf., B, 2017, 149, 48–55.
48. J. Kurniawan, J. Ventrici, G. Kittleson and T. L. Kuhl, Langmuir, 2017, 33, 382–387.
49. S. Künneke, D. Krüger and A. Janshoff, Biophys. J., 2004, 86, 1545–1553.
50. S. J. Attwood, Y. Choi and Z. Leonenko, Int. J. Mol. Sci., 2013, 14, 3514–3539.
51. S. Kotova, C. Vijayasarathy, E. K. Dimitriadis, L. Ikonomou, H. Jaffe and P. A. Sieving, Biochemistry, 2010, 49, 7023–7032.
52. S. Seghezza, S. Dante, A. Diaspro and C. Canale, J. Mol. Recognit., 2015, 28, 742–750.
53. D. Augustyńska, K. Burda, M. Jemioła-Rzemińska and K. Strzałka, Chem.-Biol. Interact., 2016, 256, 236–248.
54. J. Hemmerlé, S. M. Altmann, M. Maaloum, J. K. H. Hörber, L. Heinrich, J.-C. Voegel and P. Schaaf, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 6705–6710.
55. V. Vadillo-Rodriguez, H. J. Busscher, W. Norde, J. de Vries and H. C. van der Mei, J. Colloid Interface Sci., 2004, 278, 251–254.
56. M. Mondon, S. Berger and C. Ziegler, Anal. Bioanal. Chem., 2003, 375, 849–855.
57. J. K. Stuart and V. Hlady, Langmuir, 1995, 11, 1368–1374.
58. L.-C. Xu and C. A. Siedlecki, Biomaterials, 2007, 28, 3273–3283.
59. C. C. Dupont-Gillain, C. M. J. Fauroux, D. C. J. Gardner and G. J. Leggett, J. Biomed. Mater. Res., Part A, 2003, 67, 548–558.
60. F. Fang, J. Satulovsky and I. Szleifer, Biophys. J., 2005, 89, 1516–1533.
61. M. Agashe, V. Raut, S. J. Stuart and R. A. Latour, Langmuir, 2005, 21, 1103–1117.
62. Y. Wu, F. I. Simonovsky, B. D. Ratner and T. A. Horbett, J. Biomed. Mater. Res., Part A, 2005, 74, 722–738.
63. D. M. Hylton, S. W. Shalaby and R. A. Latour, J. Biomed. Mater. Res., Part A, 2005, 73, 349–358.
64. L. Dorogin, A. Tiwari, C. Rotella, P. Mangiagalli and B. N. J. Persson, Phys. Rev. Lett., 2017, 118, 238001.
65. E. Evans and K. Ritchie, Biophys. J., 1997, 72, 1541–1555.
66. R. Merkel, P. Nassoy, A. Leung, K. Ritchie and E. Evans, Nature, 1999, 397, 50–53.
67. E. Evans, D. Berk and A. Leung, Biophys. J., 1991, 59, 838–848.
68. J. Fritz, A. G. Katopodis, F. Kolbinger and D. Anselmetti, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 12283–12288.
69. W. Hanley, O. McCarty, S. Jadhav, Y. Tseng, D. Wirtz and K. Konstantopoulos, J. Biol. Chem., 2003, 278, 10556–10561.
70. W. D. Hanley, D. Wirtz and K. Konstantopoulos, J. Cell Sci., 2004, 117, 2503–2511.
71. E. Evans, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128.
72. E. Evans and P. Williams, in Physics of Bio-Molecules and Cells, ed. H. Flyvberg, F. Julicher, P. Ormos and F. David, EDP Sciences, Springer-Verlag, Paris, 2002, pp. 145–185.
73. B. T. Marshall, K. K. Sarangapani, J. Lou, R. P. McEver and C. Zhu, Biophys. J., 2005, 88, 1458–1466.
74. D. Alsteens, M. Pfreundschuh, C. Zhang, P. M. Spoerri, S. R. Coughlin, B. K. Kobilka and D. J. Müller, Nat. Methods, 2015, 12, 845–851.
75. D. Alsteens, R. Newton, R. Schubert, D. Martinez-Martin, M. Delguste, B. Roska and D. J. Müller, Nat. Nanotechnol., 2017, 12, 177–183.
76. R. W. Friddle, A. Noy and J. J. D. Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13573–13578.
77. G. I. Bell, Science, 1978, 200, 618–627.
78. L.-C. Xu and C. A. Siedlecki, Langmuir, 2009, 25, 3675–3681.
79. D. Alsteens, A. Beaussart, S. El-Kirat-Chatel, R. M. A. Sullan and Y. F. Dufrene, PLoS Pathog., 2013, 9, e1003516.
80. D. J. Müller and Y. F. Dufrêne, Trends Cell Biol., 2011, 21, 461–469.
81. C. Formosa-Dague, C. Feuillie, A. Beaussart, S. Derclaye, S. Kucharíková, I. Lasa, P. Van Dijck and Y. F. Dufrêne, ACS Nano, 2016, 10, 3443–3452.
82. A. J. Chan, K. Steenkeste, A. Canette, M. Eloy, D. Brosson, F. Gaboriaud and M.-P. Fontaine-Aupart, Langmuir, 2015, 31, 12437–12446.
83. S. Dhahri, M. Ramonda and C. Marlière, PLoS One, 2013, 8, e61663.
84. C. Marlière and S. Dhahri, Nanoscale, 2015, 7, 8843–8857.
85. R. Garcia and R. Perez, Surf. Sci. Rep., 2002, 47, 197–301.
86. C. Marlière, et al., Submitted..
87. W. G. Wren, Rubber Chem. Technol., 1942, 15, 107–114.
88. D. J. Siler, M. Goodrich-Tanrikulu, K. Cornish, A. E. Stafford and T. A. Mckeon, Plant Physiol. Biochem., 1997, 35, 881–889.
89. C. Goebbert, R. Nonninger, M. A. Aegerter and H. Schmidt, Thin Solid Films, 1999, 351, 79–84.
90. G. A. Parks, Chem. Rev., 1965, 65, 177–198.
91. M. Kosmulski, in Surface Charging and Points of Zero Charge, ed. M. Kosmulski, Crc Press-Taylor & Francis Group, Boca Raton, 2009, pp. 1–101.
92. I. Sokolov, Q. K. Ong, H. Shodiev, N. Chechik, D. James and M. Oliver, J. Colloid Interface Sci., 2006, 300, 475–481.
93. R. M. Pashley, J. Colloid Interface Sci., 1984, 102, 23–35.
94. K. Besteman, M. A. G. Zevenbergen, H. A. Heering and S. G. Lemay, Phys. Rev. Lett., 2004, 93, 170802.
95. G. U. Lee, D. A. Kidwell and R. J. Colton, Langmuir, 1994, 10, 354–357.
96. E. L. Florin, V. T. Moy and H. E. Gaub, Science, 1994, 264, 415–417.
97. H. Eyring, J. Chem. Phys., 1935, 3, 107–115.
98. P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341.
99. E. Evans, in Handbook of Biological Physics, ed. R. Lipowsky and E. Sackmann, North-Holland, 1995, vol. 1, pp. 723–754.
100. B. V. Zhmud, A. Meurk and L. Bergström, J. Colloid Interface Sci., 1998, 207, 332–343.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra08589c

---