Prismatic morphology of an ADP crystal grown in a defined crystallographic direction

Abstract

Herein, ammonium dihydrogen phosphate (NH₄H₂PO₄, ADP) crystals were grown in a defined crystallographic direction (θ = 90°, Φ = 45°) in an aqueous solution using the point seed rapid growth method. Ex situ atomic microscopy (AFM) measurements were implemented to observe the prismatic growth micro-morphology of ADP and Cr³⁺-doped ADP in the defined crystallographic direction. It was found that with the increasing supersaturation, the growth morphology changed in turn to elementary steps, macro steps, and 2D nuclei. Moreover, the differences between ADP and Cr³⁺-doped ADP grown in the defined crystallographic direction have been discussed. The influence of Cr³⁺ on the growth of ADP crystals has been explored.

---

Introduction

The ammonium dihydrogen phosphate (NH₄H₂PO₄, ADP) crystal has various applications as a piezo-electric material and as a monochromator for X-ray fluorescence analysis;^1–5 it is a typical isomorph of potassium dihydrogen phosphate (KDP) crystal, which is the only optical material used in inertial confinement fusion (ICF) engineering.⁶ Growth parameters, such as supersaturation, have significant influence on the crystal growth morphology,⁷ and the growth mechanism of the crystal faces is especially dependent on the parameter of supersaturation.⁸ Both macro steps and 2D nucleation occur during the growth of ADP in the Z direction, as has been reported by many researchers.^9–16 Xu Dongli and Xue Dongfeng et al. researched the chemical bonding of ADP and predicted that the natural shape of ADP was a tetragonal bipyramid;^17,18 moreover, the theoretical growth and equilibrium forms of ADP were studied.^19,20

Currently, the application of DKDP/KDP crystals is deterred by the bottleneck of their low laser damage threshold (LDT);²¹ moreover, the LDT of ADP crystals is higher than that of the KDP/DKDP crystals.¹⁵ Furthermore, non-critical phase matching (NCPM) performed on type-I crystals (θ = 90°, Φ = 45°), namely type-I (ooe) noncritical phase matching in the direction 90° to the crystal Z axis (θ = 90°) and 45° to the crystal X axis (Φ = 45°), has greater angular acceptance and avoids phase mismatch caused by dispersion in the crystal to achieve more efficient and more stable output power.^22,23 In addition, the sizes in the [100] and [001] directions of crystals grown in Z-seed slices are smaller; moreover, because of the distribution of chemical bonds in the ADP crystal,²⁴ the aspect ratio [Z/X] of ADP is very small; this leads to low utilization of the ADP crystal. Therefore, ADP crystals have been grown in a defined crystallographic direction (θ = 90°, Φ = 45°) by our research group. This method can improve the morphology of the ADP crystal by ensuring the growth in the direction of fourth harmonic generation to the greatest extent, by which we can obtain crystals of ample size and enhance their utilization rate; additionally, this method may improve the growth sections and homogeneity of the ADP crystals.

In this study, ADP crystals were grown in a defined crystallographic direction (θ = 90°, Φ = 45°, which is the direction of NCPM) in an aqueous solution using the point seed rapid growth method.^25,26 Ex situ atomic microscopy (AFM) measurements were implemented to observe the prismatic growth micro-morphology of ADP. Moreover, Cr³⁺ was added to the growth solution to study the effects of Cr³⁺ on this growth direction as Cr³⁺ is a common impurity ion. Furthermore, prismatic morphology of the chromium-doped ADP crystals grown in the defined crystallographic direction was obtained. The differences between ADP and Cr³⁺-doped ADP in the defined crystallographic direction have also been discussed.

Experimental

The small ADP crystals grown in the defined crystallographic direction in our experiments were prepared using the point seed rapid growth method with the decreasing temperature.^27,28 Moreover, seed crystal slices were obtained from the as-grown crystals in the direction of (θ = 90°, Φ = 45°), as shown in Fig. 1. Additionally, the initial growth temperature was about 50 °C. The supersaturation σ was created by decreasing the temperature of the solution, which could be calculated by^6,27

σ = (C₀ − C_e)/C_e (1)

where C₀ and C_e are the actual and equilibrium concentrations given in mass fractions. Thus, crystals suitable for surface microtopography, as shown in Fig. 2, could be obtained after a two-day growth process. The crystals were quickly withdrawn from the solution and dipped once or twice in a mixed solution of alcohol and propyl alcohol, which had the same temperature as the crystals and growth solution. Then, the mixed solution was removed with a piece of silk cloth. Ex situ atomic microscopy (AFM) measurements were conducted using a Bruker Dimension Icon scanning probe microscope (SPM) system in the ScanAsyst mode with standard SiN cantilevers^15,28 to observe the prismatic growth micro-morphologies of ADP and Cr³⁺-doped ADP. Professional software associated with AFM was used to measure the step heights and widths in the AFM images.

Fig. 1 The seed crystal slices in the direction of θ = 90°, Φ = 45°.

Fig. 2 Crystals suitable for surface microtopography (the yellow numbers represent the different σ values and the scale plate).

Results and discussion

Prismatic growth micro-morphology of the ADP crystals

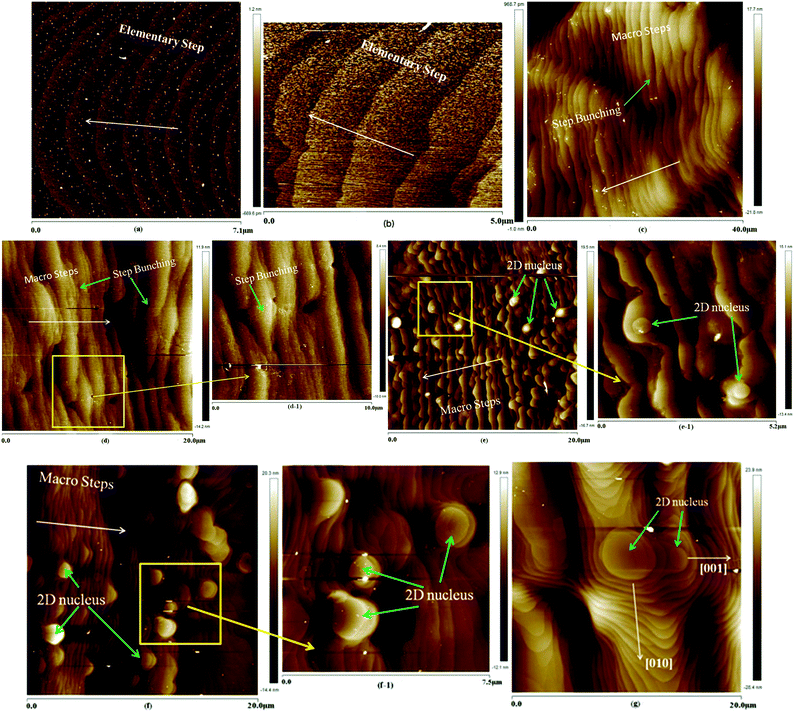
The prismatic, namely (100) face, growth micro-morphologies of ADP at different supersaturations are shown in Fig. 3.

Fig. 3 The (100) face growth micro-morphologies of ADP at different supersaturations. (a) σ = 0.6%; (b) σ = 0.8%; (c) σ = 1.0%; (d) σ = 1.2%; (d-1) partial enlarged view of (d); (e) σ = 1.4%; (e-1) partial enlarged view of (e); (f) σ = 1.8%; (f-1) partial enlarged view of (f); (g) σ = 2.2% (the white arrows indicate the direction of step movement).

Fig. 3(a) shows the surface microtopography at a supersaturation of 0.6%; the average step height of the steps was measured to be about 0.366 nm, equal to half of the length of unit cell a or b (7.502 Å (ref. 6)). This can be named as the elementary step. Thus, it can be seen that only the spiral growth mechanism is observed, and the direction of the step bending points to the dislocation source. Additionally, the steps are equidistant and regular, showing a steady initial growth stage of the ADP crystal, and correspond well with the growth theory.²⁹ It is illustrated in Fig. 3(b) that at a supersaturation of 0.8%, the height of the elementary step is about 0.490 nm, which is approximately equal to half of the length of the unit cell. At the edges of the elementary steps, some ridges and dents emerge; this occurs because the growth units prefer to be absorbed into the edges of the steps, forming ridges, or because the fluctuations impede the absorption of the growth units, forming dents with small fluctuations of the growth conditions. In Fig. 3(c), at a supersaturation of 1.0%, the average height of the step is 4.61 nm, which is equivalent to six times the length of a. This shows that the crystal surface is covered by macro steps, which are the result of a process called step bunching; the macro steps increase in height and terrace width with distance from the top of the hillock and integrate multiple micro steps. The shape of the macro steps is approximately regular; this indicates that the macro steps develop and step forward as a whole, rather than by respective growth of elementary steps. When the supersaturation increases to 1.2%, the process of step bunching continues, and the macro steps become larger, as shown in Fig. 3(d). In addition, the average height of the steps is about 12.3 nm, which is equal to 17 times the length of a. A partial magnified image of Fig. 3(d) is shown in Fig. 3(d-1); this image clearly illustrates the topography of the macro steps and the process of step bunching. The macro steps are neither straight nor strictly parallel, but have more complicated shapes; this indicates that the crystal surface may be influenced not only by supersaturation but also by other factors. At a supersaturation of 1.4%, as shown in Fig. 3(e), the process of step bunching still occurs; the average height of the macro steps is about 20.8 nm, equal to 28 times the length of the unit cell. However, some islands without any signs of dislocation outcrop appear on the terraces between two steps, and their average radius is about 230 nm, much greater than the radius of the critical nucleus at this supersaturation. These islands are called 2D nuclei and are much more visible in Fig. 3(e-1), particularly in the magnified image shown in Fig. 3(e). When the supersaturation is increased to 1.8%, the radius of the 2D nuclei increases to about 1.107 μm, and the height of the macro steps is about 23.1 nm, as clearly shown in Fig. 3(f) and (f-1); moreover, the quantity of 2D nuclei obviously increases. The 2D nucleation mechanism is dominant in the crystal growth process.

Fig. 3(g) illustrates the (100) face growth micro-morphology at σ = 2.2%; it can be seen that the radius of the 2D nuclei increases to about 4.21 μm; this indicates that the 2D nuclei grow and step forward via step growth. The growth velocity of the 2D nuclei is anisotropic, as shown in Fig. 3(g). The velocity in the [001] direction is obviously smaller than that in the [010] direction, and this phenomenon is in good accordance with the chemical bond distribution shown in ref. 15. The chemical bond strengths of the α and β bond chains are stronger than that of the γ bond chain;¹⁵ this leads to a low aspect ratio of the ADP crystals.

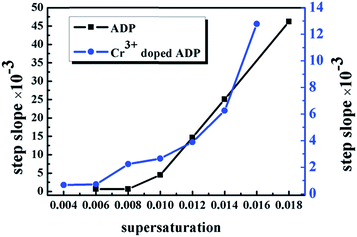
The relationship between the supersaturation and the step heights of the ADP crystals in the defined crystallographic direction is shown in Fig. 6. Thus, we can know that (1) the height of the elementary step is about half the height of the unit cell; (2) the growth steps are all elementary steps when σ ≤ 0.8%, and this indicates that the process of crystal growth is stable, with few fluctuations influencing the crystal growth; (3) under the condition of σ ≤ 1.2%, only the spiral step growth mechanism exists in the aqueous solution. Moreover, the elementary steps develop into macro steps, which integrate multiple micro steps via step bunching with the increasing supersaturation; (4) islands, namely 2D nuclei, without any signs of dislocation outcrop appear on the terraces between two steps when σ > 1.2%; thus, the spiral step growth mechanism and 2D nucleation mechanism coexist during the process of crystal growth. When the supersaturation is increased by decreasing the temperature, the 2D nucleation mechanism, whose velocity is anisotropic, will be dominant until the crystal growth is complete.

By comparing our results with those reported in ref. 15, in which (100) face growth morphologies have been obtained for ADP crystals grown in the Z direction at different supersaturations, we can determine the differences and similarities between the prismatic growth morphologies of the ADP crystals in the Z direction and the defined direction.

Similarities: (1) the variation trends of both growth mechanisms are the same, namely changing from the spiral step growth mechanism to the coexistence of spiral step growth and 2D nucleation mechanisms and then to a dominant 2D nucleation mechanism. (2) The exposed faces of the crystals during the growth processes are the same; in both cases, the faces are (100) and (101).

Differences: (1) when σ = 0.6%, 2D nuclei appear on the surface of ADP grown in the Z direction, whereas, this occurs for ADP grown in the defined direction at σ = 1.4%. This phenomenon indicates that the growth rate of the prismatic face of ADP in the defined direction is smaller than that in the Z direction. Therefore, the aspect ratio of ADP in the defined direction is larger. (2) The growth rates of the (100) and (101) faces are different in the two directions.

Prismatic growth micro-morphology of Cr³⁺-doped ADP

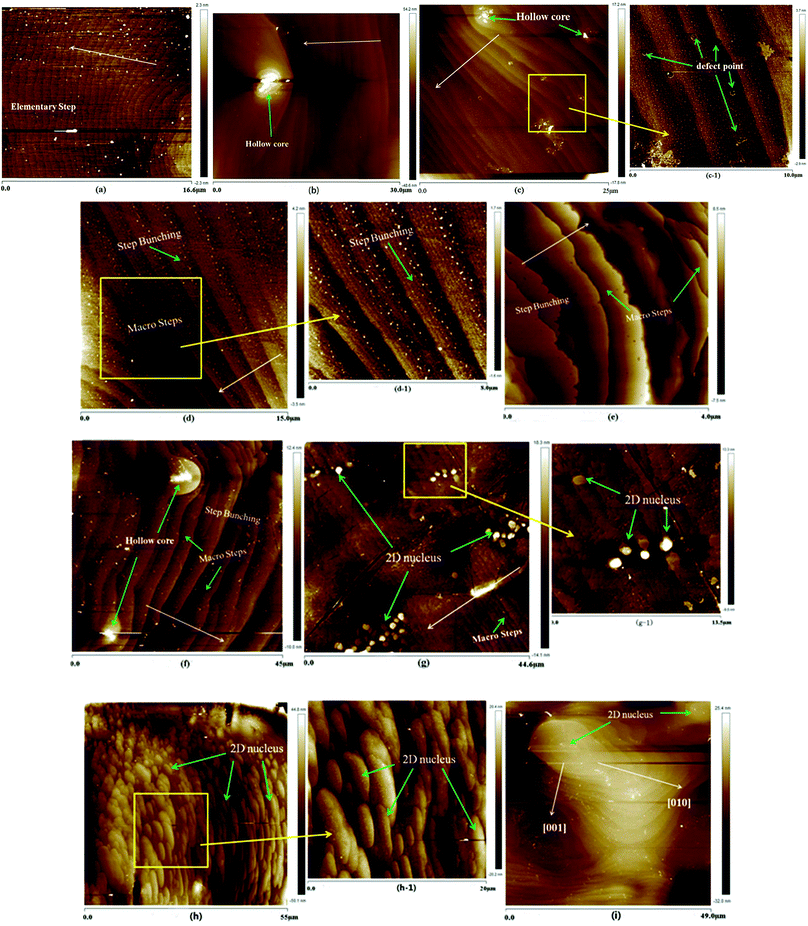
Crystals suitable for AFM measurements were doped with 3 ppm Cr³⁺; the concentration of Cr³⁺ doped was chosen based on our early growth experiments. The prismatic, namely (100) face, growth micro-morphologies of Cr³⁺-doped ADP at different supersaturations are shown in Fig. 4.

Fig. 4 The (100) face growth micro-morphologies of Cr³⁺-doped ADP at different supersaturations. (a) σ = 0.4%; (b) σ = 0.6%; (c) σ = 0.8%; (c-1) partial enlarged view of (c); (d) σ = 1.0%; (d-1) partial enlarged view of (d); (e) σ = 1.2%; (f) σ = 1.4%; (f-1) partial enlarged view of (f); (g) σ = 1.6%; (g-1) partial enlarged view of (g); (h) σ = 1.8%; (h-1) partial enlarged view of (h); and (i) σ = 2.0% (the white arrows indicate the direction of step movement).

The (100) face growth morphology of the ADP crystal at a supersaturation of 0.4% is shown in Fig. 4(a); the height of the elementary step is about 0.347 nm, which is half the height of the unit cell. These steps are formed during the initial growth process of ADP and are regular and approximately parallel to each other; they originate from the spiral core produced by screw dislocations. And in the spiral growth mechanism, the equidistant elementary-height steps propagate from the outcrop of the dislocation source of maximum activity.¹¹ In Fig. 4(b), there is a visible hollow core (the core is covered by residual solution after emerging from the growth solution, and the residual solution recrystallizes into small grains). The hollow core is located in the direction of the step propagation and may play a pinning role. As the step free energy exceeds the critical value of the pinning energy, the steps will break through the fence of stoppers and continue to spread out with equidistant heights. The average height of the steps, as shown in Fig. 4(b), is 0.713 nm, equal to the height of the unit cell. Therefore, the impurity, namely Cr³⁺, in our experiments may play a role in pinning.

In Fig. 4(c), step bunching appears, and the macro steps integrate multiple elementary steps to 1.88 nm. Some circular points among the steps can be seen in the partial enlarged view of Fig. 4(c); these are believed to be defect points caused by the doped impurities. It is believed that this is why inclusions readily appear in the Cr³⁺-doped ADP, as shown in Fig. 5. As the σ increases to 1.0%, as shown in Fig. 4(d), step bunching continues with a height of 2.37 nm, far less than the height of the steps of the ADP crystals. As the supersaturation increases to 1.2%, as shown in Fig. 4(e), the step bunching continues; the average height of the macro steps is about 3.5 nm. In Fig. 4(f), at a supersaturation of 1.4%, a hollow core is observed; this proves that the impurity ion Cr³⁺ plays an important role in the formation of defects. When σ increases to 1.6%, as shown in Fig. 4(g), some 2D islands without any signs of dislocation outcrop appear on the terraces between two steps; their average radius is about 700 nm, much greater than the radius of the critical nucleus at this supersaturation.⁶ The quantity and radii of the 2D islands increase rapidly, and the islands are distributed regularly and in good proportion, as shown in Fig. 4(h); this indicates that the 2D nucleation mechanism is dominant. In Fig. 4(i), it can be seen that the two-dimensional islands continue to increase with an anisotropic growth velocity. The velocity in the [001] direction is obviously smaller than that in the [010] direction, same as the case with non-Cr³⁺-doped ADP.

Fig. 5 Cr³⁺-doped ADP crystal (there are many inclusions in the crystal).

The overall relationship between the supersaturation and the step height of Cr³⁺-doped ADP crystals in the defined crystallographic direction is shown in Fig. 6. Therefore, as σ ≤ 1.4%, the spiral step growth mechanism controls the crystal growth. In the initial process, elementary steps originate from the outcrop of the dislocation source of maximum activity; moreover, the steps are bending and moving towards one another at the front edge. The impurities are pinned on the steps of the (100) face and form hollow cores, which may lead to the appearance of defects or inclusions. Then, macro steps occur via coalescence of multiple micro steps. When σ > 0.014, two-dimensional islands appear with an anisotropic growth velocity, i.e. the velocity in the [001] direction is obviously smaller than that in the [010] direction. Moreover, as σ increases, 2D nuclei form and the 2D nucleation mechanism becomes dominant.

Fig. 6 Relationships between supersaturation and the step heights of ADP and Cr³⁺-doped ADP crystals.

Comparative analysis of the prismatic morphologies of ADP and Cr³⁺-doped ADP

As is known, the normal growth rate R in the spiral growth mechanism on the prismatic face of crystals depends on the steepness P of the dislocation hillock and the tangential growth rate V of the dislocation step:^6,29,30

R = PV (2)

V = bβσ (3)

where β = β₀ exp(−E_A/kT) is the kinetic coefficient of the step. E_A is the barrier for activation of the initial stage of growth, k is the Boltzmann constant, and T is the temperature. According to ref. 6, b and β₀ are considered to be constants because they are connected with the densities and characteristic dimensions of the structural elements. Therefore, V depends only on the supersaturation σ and the temperature T, and it can be considered that V for all prismatic faces with the same simple and growth indices are the same.

The steepness P of a hillock from an isotropic spiral is determined by the structure of the dislocation. Moreover, the steepness is given by:^6,30,31

where m is the number of unit steps in the Burgers vector of the dislocation, h is the height of an elementary step, r_c is the radius of a critical nucleus, and 2L is the length of the perimeter of dislocations. Furthermore, r_c can be given by^6,30,31

r_c = Ωγ/kTσ (5)

where γ is the free energy of the step edge per unit length per unit step height, and Ω is the molecular volume in the solid. In addition, the parameters used to calculate the dependence of steepness on supersaturation are listed in Table 1. The r_c values at the supersaturations where the 2D nuclei only started to appear (1.2% (undoped) and 1.4% (doped)) can also be calculated by the formula (5).^32,33

Table 1 The parameters used to calculate the dependence of steepness on supersaturation (the subscript 1 represents the ADP crystals and 2 indicates Cr³⁺-doped ADP)

h1(not Cr^3+ doped) (nm)	h2(Cr^3+ doped) (nm)	γ^6 (mJ m^−2)	Ω^6 (cm^3 mol^−1)	k (J K^−1)
0.366	0.347	20	9.68 × 10^−23	1.38 × 10^−23

---

Therefore, the radius of a critical nucleus r_c of ADP in the defined crystallographic direction at different supersaturations can be calculated as shown in Table 2.

Table 2 The radii of the critical nucleus r_c of ADP crystal and Cr³⁺-doped ADP crystal

Σ (%)	0.4	0.6	0.8	1.0	1.2	1.4	1.6	1.8
rc (nm)	7.01	4.68	3.51	2.81	2.34	2.0	1.75	1.56

---

The actual experimental curves of the steepness P of the prismatic faces of the ADP crystals are shown in Fig. 7. Speculating that m in the formula (4) equals 1–3 and according to (4) and (5), the 2L values of the ADP and Cr³⁺-doped ADP crystals can be calculated, as shown in Table 2.

Fig. 7 The steepness P of the prismatic faces of the ADP crystals (the black curve represents ADP and the blue curve indicates Cr³⁺-doped ADP).

As shown in Table 3, for the ADP and Cr³⁺-doped ADP crystals, the maximum value of σ, which meets the condition 2L ≥ 0, increases as m increases. This indicates that as σ increases, the number of layers of the dislocation source will increase. Moreover, as m is constant, 2L₁ increases initially and then decreases; however, 2L₂ shows a decreasing trend with the increasing σ. Furthermore, 2L₁ is larger than 2L₂ at the same value of m at low supersaturation (σ ≤ 0.8%) when the step heights are very low; as the macro steps propagate after σ = 1.0%, Cr³⁺ obviously decreases the overlay layers of the elementary steps and decreases the growth velocity of the (100) face. Therefore, it appears that Cr³⁺ can impede the length of the perimeter of dislocations and the size of the dislocation cores. This leads to a smaller height of the steps for Cr³⁺-doped ADP; thus, the growth velocity R decreases at the same supersaturation and temperature. At the same supersaturation in both Cr³⁺-doped ADP and undoped ADP crystals, the steps of spiral dislocation or 2D nuclei can expand in height and terrace width with time. Moreover, according to the formulas (2)–(4) and fitting of the two curves in Fig. 7, σ increases dynamically with step growth and consumption of the solute; this leads to an increase in the growth velocity R in both Cr³⁺-doped ADP and undoped ADP crystals.

Table 3 2L values of ADP crystal and Cr³⁺-doped ADP crystal when m equals 1–3 (the negative values at some supersaturation concentrations indicate that 2L at these values of m cannot be obtained and m should increase)

Σ (%)	0.4	0.6	0.8	1.0	1.2	1.4	1.6	1.8
2L1 (m = 1) (nm)	—	475.9	496.4	28.3	−19.5	−23.4	—	−21.7
2L1 (m = 2) (nm)	—	1040.7	1059.5	110.0	5.4	−8.8	—	−13.8
2L1 (m = 3) (nm)	—	1605.5	1622.5	191.7	30.3	5.8	—	0.9
2L2 (m = 1) (nm)	413.1	426.6	97.4	98.2	49.6	20.6	−0.98	—
2L2 (m = 2) (nm)	959.3	942.1	261.6	222.8	143.7	79.1	27.7	—
2L2 (m = 3) (nm)	1505.6	1457.6	425.7	360.9	237.8	137.7	52.7	—

---

Conclusions

In this study, ADP crystals were grown in an aqueous solution in a defined crystallographic direction (θ = 90°, Φ = 45°, which is the direction of non-critical phase matching fourth harmonic generation) using the point seed rapid growth method. Ex situ atomic microscopy (AFM) measurements were implemented to observe the prismatic growth micro-morphology of ADP. Moreover, the prismatic morphology of chromium-doped ADP crystal grown in the defined crystallographic direction was determined. For the ADP without Cr³⁺ doping, under the condition of σ ≤ 1.2%, only the spiral step growth mechanism occurred in an aqueous solution. In addition, when σ > 1.2%, the spiral step growth mechanism and 2D nucleation mechanism coexisted in the process of crystal growth. With regard to Cr³⁺-doped ADP, when σ ≤ 1.4%, the spiral step growth mechanism controlled the crystal growth. Moreover, two-dimensional islands appeared with an anisotropic growth velocity when σ > 0.014. With the increasing σ, the 2D nuclei grow, and the 2D nucleation mechanism becomes dominant. The influence of Cr³⁺ on the growth of ADP crystals in the defined crystallographic direction has been explored and discussed. For the ADP and Cr³⁺-doped ADP crystals, the maximum value of σ, which meets with the condition 2L ≥ 0, increases as m increases. This indicates that the larger the σ, the more the layers of the dislocation source. Moreover, as m is constant, 2L₁ increases initially and then decreases; however, 2L₂ shows a decreasing trend with the increasing σ. Furthermore, 2L₁ is larger than 2L₂ at the same value of m at low supersaturation (σ ≤ 0.8%) when the step heights are very low; as the macro steps propagate after σ = 1.0%, Cr³⁺ can obviously decrease the overlay layers of the elementary steps and slow the growth velocity of the (100) face. Therefore, this indicates that Cr³⁺ can impede the length of the perimeter of dislocations and the size of the dislocation cores. This leads to a smaller step height in Cr³⁺-doped ADP; thus, the growth velocity R decreases at the same supersaturation and temperature.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support was provided by the National Natural Science Foundation of China (Grants No. 51323002 and 51402173) and the Ministry of Education (Grant No. 625010360).

References

1. K. Srinivasan, A. Cantoni and G. Bocelli, Compositional dependence of morphology and lattice parameters during growth of K1-x(NH4)xH2PO4 mixed crystals, Cryst. Res. Technol., 2010, 45(7), 737–746.
2. Y. Asakuma, Q. Li, H. M. Ang, M. Tade, K. Maeda and K. Fukui, A study of growth mechanism of KDP and ADP by means of quantum chemistry, Appl. Surf. Sci., 2008, 254(15), 4524–4530.
3. R. Ananda Kumari, Growth and characterization of NLO crystal, Indian J. Pure Appl. Phys., 2009, 47, 369–371.
4. P. Rajesh, K. Boopathi and P. Ramasamy, Investigations on the solubility, growth, structural, optical, mechanical, dielectric and SHG behaviour of ammonium acetate doped ammonium dihydrogen phosphate crystals, J. Cryst. Growth, 2011, 318, 751–756.
5. R. Kripal, S. Shukla and P. Dwivedi, EPR and optical studies of Cu2+ doped ammonium dihydrogen phosphate single crystals, Phys. B, 2012, 407, 656–663.
6. L. N. Rashkovich, KDP-family single crystal, Published under the Adam Hilger imprint by IOP Publishing Ltd, 1991.
7. R. J. Davey and J. W. Mullin, The effect of supersaturation on growth features on the {100} faces of ammonium dihydrogen phosphate crystals, J. Cryst. Growth, 1975, 29(1), 45–48.
8. H. Takubo, S. Kume and M. Koizumi, Relationships between supersaturation, solution velocity, crystal habit and growth rate in crystallization of NH4H2PO4, J. Cryst. Growth, 1984, 67(2), 217–226.
9. W. J. P. Van Enckevort, R. Janssen-van Rosmalen and W. H. van der Linden, Evidence for spiral growth on the pyramidal faces of KDP and ADP single crystals, J. Cryst. Growth, 1980, 49(3), 502–514.
10. M. Aguiló, Crystal morphology of ADP (NH4H2PO4): a qualitative approach, J. Cryst. Growth, 1984, 69, 527–536.
11. L. N. Rashkovich and B. Yu Shekunov, Morphology of growing vicinal surface: prismatic faces of ADP and KDP crystals in solutions, J. Cryst. Growth, 1990, 100(1–2), 133–144.
12. D. Xu, D. Xue and H. Ratajczak, Morphology and structure studies of KDP and ADP crystallites in the water and ethanol solutions, J. Mol. Struct., 2005, 740, 37–45.
13. J. Yu, M. Li and X. Wang, {100} surface topography under 2D nucleation growth of ADP crystals: ex situ investigation by atomic force microscopy, Gongneng Cailiao, 2008, 39, 1034–1036.
14. Y. Jiang-Tao, L. Ming-Wei and W. Xiao-Ding, Advance process and dynamic topographic changes of ADP crystals phase interface observed by in situ atomic force microscopy, J. Eng. Thermophys., 2008, 29(5), 721–725.
15. Y. Lian and L. Zhu, et al., The rapid growth of ADP single crystal, CrystEngComm, 2016, 18, 7530–7536.
16. E. Vlieg, The role of surface and interface structure in crystal growth, Prog. Cryst. Growth Charact. Mater., 2016, 62, 203–211.
17. D. Xu and D. Xue, Chemical bond and microscopic growth habit of ADP crystals, Rengong Jingti Xuebao, 2005, 34, 823–827.
18. D. Xue and H. Ratajczak, J. Mol. Struct.: THEOCHEM, 2005, 716, 207–210.
19. M. Aguiló and C. F. Woensdregt, Theoretical growth and equilibrium forms of ADP (NH4H2PO4), J. Cryst. Growth, 1987, 83(4), 549–559.
20. Asakuma, Q. Li, H. Ming Ang, M. Tade, K. Maeda and K. Fukui, A study of growth mechanism of KDP and ADP crystals by means of quantum chemistry, Appl. Surf. Sci., 2008, 254, 4524–4530.
21. C. M. Miller, E. I. Moses and C. R. Wuest, The National Ignition Facility, Opt. Eng., 2004, 43(12), 2841–2853.
22. S. Ji, et al., Room temperature, high-efficiency, noncritical phase-matching fourth harmonic generation in partially deuterated ADP crystal, Opt. Lett., 2013, 38, 1679–1681.
23. S. Ji, S. Zhang, M. Xu, B. Liu, L. Zhu, L. Zhang, X. Xu, Z. Wang and X. Sun, Non-critical phase-matching conditions for fourth harmonic generation of DKDP crystal, Opt. Mater. Express, 2012, 6(2), 735–739.
24. X. Ren, C. Sun, K. Li, D. Xu and D. Xue, Chemical Bonding and Single Crystal Growth of ADP Crystals, Mater. Focus, 2013, 2(4), 309–315.
25. X. Feng and L. Zhu, et al., Growth and highly efficient third harmonic generation of ammonium dihydrogen phosphate crystals, RSC Adv., 2016, 6, 33983–33989.
26. M. Xu, Z. Wang, B. Wang, B. Liu, X. Sun and X. Xu, Study on optical property of rapid growth KDP and DKDP crystals, Chin. Opt. Lett., 2012, 10, S11602.
27. F. Liu, Z. Lisong, G. Yu and X. Sun, Effect of pH value on the growth morphology of KH2PO4 crystal grown in defined crystallographic direction, Cryst. Res. Technol., 2015, 50(2), 164–170.
28. F. Liu, et al., Effect of supersaturation on hillock of directional Growth of KDP crystals, Sci. Rep., 2014, 4, 6886.
29. B. Ranguelov, P. Müller, J.-J. Metois and S. Stoyanov, Step density waves on growing vicinal crystal surfaces – Theory and experiment, J. Cryst. Growth, 2017, 457, 184–187.
30. J. J. De Yoreo, T. A. Land, L. N. Rashkovich, T. A. Onischenko, J. D. Lee, O. V. Monovskii and N. P. Zaitseva, The effect of dislocation cores on growth hillock vicinality and normal growth rates of KDP {101} surfaces, J. Cryst. Growth, 1997, 182, 442–460.
31. J. J. De Yoreo, A. K. Burnham and P. K. Whitman, Developing KH2PO4 and KD2PO4 crystals for the world's most powerful laser, Int. Mater. Rev., 2002, 47(3), 113.
32. G. Arunmozhi, E. M. De Gomes and S. Ganesamoorthy, Growth kinetics of zinc(tris)thiourea sulphate (ZTS) crystal, J. Cryst. Growth, 2014, 388, 22–28.
33. P. Bennema and O. Söhnel, Calculations of interfacial tensions, J. Cryst. Growth, 1990, 102, 841–847.

---