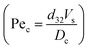Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mass transfer investigation in a horizontal–vertical pulsed packed extraction column†
Sajad Khooshechin ab,
Mohammad Ali Moosaviana,
Jaber Safdari*b and
Mohammad Hassan Mallahb
ab,
Mohammad Ali Moosaviana,
Jaber Safdari*b and
Mohammad Hassan Mallahb
aSchool of Chemical Engineering, Faculty of Engineering, University of Tehran, Tehran, Iran
bMaterial and Nuclear Fuel Research School, Nuclear Science and Technology Research Institute, P.O. Box: 11365-8486, Tehran, Iran. E-mail: Jsafdari@aeoi.org.ir; Fax: +98 21 88221116; Tel: +98 21 88221117
First published on 6th December 2017
Abstract
In this study, hydrodynamic parameters and the mass transfer coefficient were investigated in a pilot version of a horizontal–vertical pulsed packed extraction column using a toluene–acetone–water system. The effects of the operational parameters on the volumetric overall mass transfer coefficient and hydrodynamic parameters away from the flooding point were studied, and it was found that the volumetric overall mass transfer coefficient, mean drop size and disperse phase holdup were significantly affected by the pulse intensity. However, the dispersed and continuous phase flow rates have a weaker effect. On the other hand, by increasing the pulse intensity the mean drop size and volumetric overall mass transfer coefficient were reduced and increased, respectively, in both sections of the column, but the disperse phase holdup displayed different behavior in the horizontal and vertical sections. By increasing the pulse intensity, the disperse phase holdup was first reduced and then increased in the horizontal section; however, an incremental trend was observed in the vertical section. The effect of the dispersed phase flow rate was significant for all the investigated parameters, but weaker. For instance, all the investigated parameters were increased by enhancing the dispersed phase flow rate. In contrast, the continuous phase flow rate has sometimes had no significant effect, for example, on the mean drop size in both sections of the column. Finally, two empirical correlations for the prediction of the volumetric overall mass transfer coefficient based on the continuous phase were derived in terms of the Sherwood number, Reynolds number and other dimensionless numbers. Good agreement between predictions and experiments was found for all operating conditions that were investigated.
1. Introduction
Liquid–liquid extraction is a useful technique used in various separation technologies, for example, in the chemical, biochemical, and petroleum industries, in hydrometallurgy for the purification of metals and in nuclear fuel reprocessing.1–5 Solvent extraction equipment can be classified into mixer-settlers and different types of countercurrent extraction columns. On comparing the performance characteristics of these devices, columns are found to be highly efficient and exhibit low costs in respect of their stage numbers, solvent inventory, settler area, site area and maintenance.6 The efficiency of mass transfer is generally a function of the diffusion constant, degree of turbulence and interfacial area available for mass transfer. Factors that can be changed by liquid–liquid contactors to improve the efficiency of mass transfer include the degree of turbulence imparted to the system and the interfacial area.7 The rate of mass transfer in liquid–liquid extraction can be increased by mechanical agitation such as pulsations imparted to the liquids by an external mechanical or electronic device. Internal mechanical parts are eliminated, leakage is minimized, and the pulsator can be isolated.7–10One form of countercurrent extraction equipment that uses an external mechanical device is the pulsed column. Pulsed columns have been of interest in the field of liquid–liquid extraction because pulsing improves the rate of mass transfer by reducing the drop size.10 Chantry et al. (1955) showed that the column height required to achieve a given degree of extraction is reduced by a factor of three via pulsation. These columns have an obvious advantage over other mechanical contactors when processing corrosive or radioactive solutions because the pulsing unit can be remote from the column. In addition, the absence of moving mechanical parts in such columns facilitates repair and servicing. On the basis of the published literature, pulsed extraction columns can be categorized into the vertical type (sieve plate, packed, and disc and doughnut), the horizontal type (sieve plate and packed) and the horizontal–vertical type (sieve plate and packed), of which the horizontal–vertical pulsed packed column is introduced in this work.
Most reported investigations have dealt with the sieve plate and packing type of vertical structures.9,11,12 However, there are some reasons why horizontal pulsed columns are more desirable than vertical columns, such as their easier maintenance when throughput is high or higher performance in limited areas.13 However, horizontal pulsed columns have a lower production capacity than vertical columns in the same conditions. As both vertical and horizontal columns have their own advantages and disadvantages, it is important to consider the specific process. Regarding the third category, better performance is expected from combining horizontal and vertical columns as a horizontal–vertical structure, in particular when restrictions prevent the use of vertical columns. Akhgar et al.14 and Amani et al.15 have investigated the hydrodynamic parameters of a horizontal–vertical pulsed sieve plate column, but no data are published in the literature regarding the mass transfer performance of this structure, even that of the sieve plate. An investigation of the hydrodynamic parameters, as well as the mass transfer performance, is therefore necessary for this packing type.
In order to design or scale up a pulsed column for a desired extraction process, it is essential to predict the mass transfer behavior using a suitable model. There are many approaches for dealing with mass transfer, e.g., the plug flow model (PFM), axial dispersion model (ADM), drop population balance model (DPBM) and forward mixing model (FM). The first two models (PFM and ADM) are widely used for extraction columns.12 However, the development of the other models has been rather limited owing to the complexity of the problems involved.
In the present work, for the first time the mass transfer performance and hydrodynamic parameters of a horizontal–vertical pulsed packed extraction column were investigated. The volumetric overall mass transfer coefficient was measured using the axial dispersion model to evaluate the performance of the column. The effects of the pulse intensity and the flow rates of the disperse and continuous phases on the hydrodynamic parameters and the volumetric overall mass transfer coefficient were investigated using a toluene–acetone–water system. This is a standard system for evaluating the performance of a liquid–liquid extraction column that has been used by many researchers.9,16–20
2. Experimental
2.1. Liquid–liquid system
Three different liquid–liquid systems have been proposed by the European Federation of Chemical Engineering for evaluating the characteristics of a liquid–liquid extraction column.21 These systems comprise butanol–water, toluene–water and butyl acetate–water, which cover a wide range of interfacial tensions. Acetone can be used as the solute in mass transfer experiments. Among these systems, toluene–acetone–water is commonly used by many investigators for evaluating liquid–liquid extractors, in particular pulsed columns.9,16–20 The liquid–liquid system that was studied in this work was therefore toluene–acetone–water. The direction of mass transfer was from the aqueous to the organic phase (continuous to disperse phase). In all experiments, dilute solutions were investigated with approximately 3.5 wt% acetone in the aqueous phase. Distilled water was used as the continuous phase, and a technical grade of toluene with a purity of at least 99.5 wt% was used as the disperse phase. The physical properties of the liquid–liquid system at the laboratory temperature are listed in Table 1. All experiments were carried out at a temperature of 20 ± 1 °C.| Physical property | Toluene–acetone–water |
|---|---|
| ρc (kg m−3) | 994.5–995.7 |
| ρd (kg m−3) | 864.4–865.2 |
| μc (mPpa s) | 1.059–1.075 |
| μd (mPpa s) | 0.574–0.584 |
| σ (mN m−1) | 27.5–30.1 |
| Dc (nm2 s−1) | 1.09–1.14 |
| Dd (nm2 s−1) | 2.7–2.8 |
2.2. Description of equipment
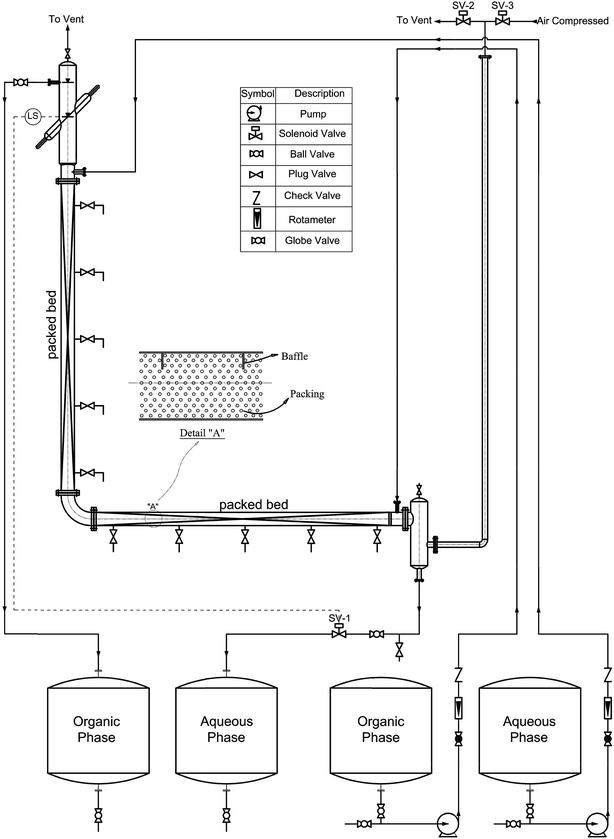
A schematic diagram of the experimental apparatus is shown in Fig. 1. The active part of the column in both horizontal and vertical sections, which was filled with packing to a height of 1.3 m, had an internal diameter of 0.06 m and was made of glass. Ceramic rushing rings with a diameter of 0.63 cm and a porosity of 60% were used as packing. Five pairs of samplers were arranged at equal intervals along the effective zones of the horizontal and vertical sections of the column. The location of the interface of the two phases at the top of the column was automatically controlled by an optical sensor. A solenoid valve that was normally kept closed was positioned in the outlet stream of the continuous phase. This valve received electronic signals from the optical sensor. When the location of the interface was about to change, the optical sensor sent a signal to the solenoid valve and the aqueous phase was allowed to leave the column. The organic phase was allowed to leave the column via an overflow. The contents of the column were pulsed at the desired amplitude and frequency using compressed air that was frequently forced into an air leg joined to the bottom settling zone of the column.2.3. Procedure
Before the experiments were carried out, both phases were saturated, after which the solute was added to the continuous phase to give an acetone concentration of about 3.5 wt%. The amplitude and frequency of the pulsations were next adjusted to the desired values and, after the column had been filled with the continuous phase, the disperse phase was introduced. In the steady-state condition samples were withdrawn from sampling valves installed on the horizontal and vertical sections. After a sample was taken, up to 5 mL of the aqueous phase was immediately separated, and the solute concentration was determined using a UV/vis spectrophotometer analyzer.The drop size was measured during steady-state conditions and determined using a photographic technique. Digital photos were taken using a Nikon D5000 digital camera. The drop size was measured at three positions in the active zones of the column in both horizontal and vertical sections. The drop dimensions were then analyzed by AutoCAD software. More than 1500 drops were selected for each set of experimental conditions at six points in the active zones (three points in each section) to guarantee that the Sauter mean drop diameter that was determined had statistical significance. The Sauter mean diameter d32 was calculated using the following equation:
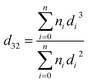 | (1) |
The disperse phase holdup (φ) is defined as the volume fraction of the extraction column that is occupied by the disperse phase:
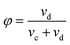 | (2) |
In the present work, three operational parameters, namely, the pulse intensity and the volumetric flow rates of both phases, were examined. Twenty experiments were carried out according to the central composite design method (CCDM), whereby the parameters were systematically varied in 15 experiments with the central data point repeated six times in order to determine the accuracy of the system in question and check the reproducibility of the experiments, which proved to be good. The error of the system was found to be about 4.3%. The intervals of the pulse intensity and the volumetric flow rates of the continuous and disperse phases were set to 1.2–1.6 cm s−1, 1.0–4.0 L h−1, and 1.0–4.0 L h−1, respectively.
The average absolute relative deviation (AARD) was used to compare the predicted results with the experimental data, and is defined as follows:
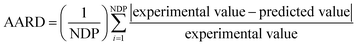 | (3) |
3. Modelling
As mentioned before, there are many different approaches for dealing with mass transfer in liquid–liquid extraction columns. Among these models, the axial dispersion model combines relative ease of implementation with the achievement of relatively accurate results.11 Therefore, this model was selected for the present study.The simplest approach for dealing with mass transfer is based on the ideal assumption that each phase moves in perfect plug flow and all elements of both phases have the same residence time in the column. The column wall and internals cause fluids to flow in all directions, which invalidates the above assumption. To overcome this defect, Danckwerts (1953) for the first time proposed that for each phase all the known and unknown influencing parameters that cause deviations from ideal flow could be amalgamated into one parameter, which is named the axial dispersion coefficient (E), for the flow of each phase.22 On the basis of the axial dispersion model and the mass balance in the column, the equation set for steady-state processes under constant boundary conditions for both phase velocities was established as follows:
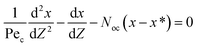 | (4) |
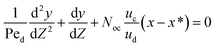 | (5) |
| Z = 0, → x = xin and y = yout | (6) |
| Z = 1, → x = xout and y = yin | (7) |
4. Results and discussion
4.1. Hydrodynamics
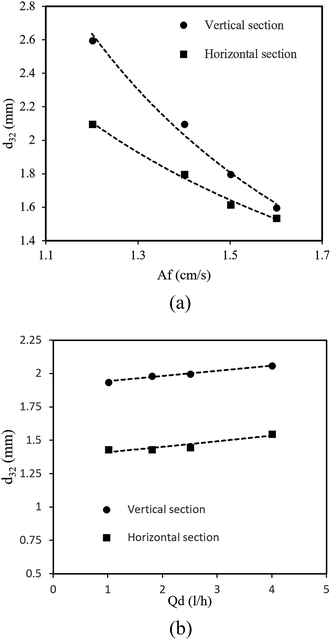
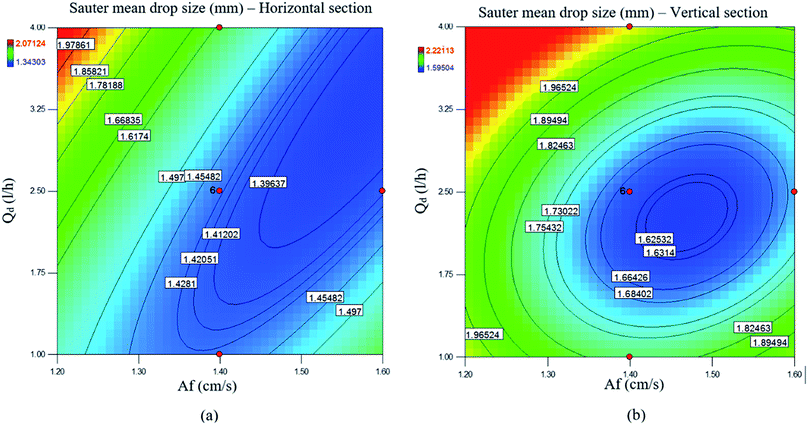
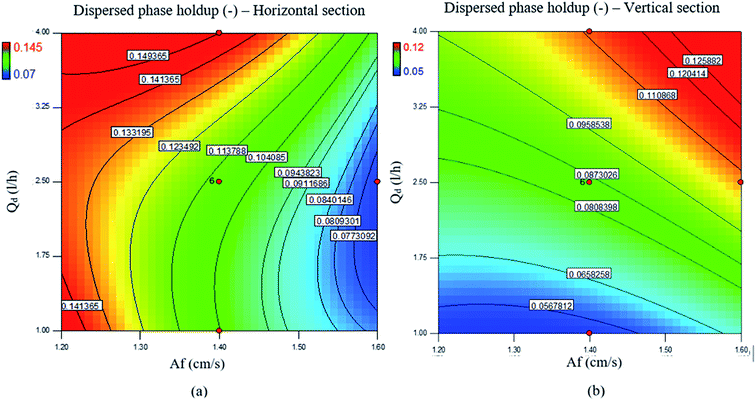
As mentioned in most reference works, a pulsed column can operate in three different flow regimes, i.e., mixer-settler, dispersion and emulsion, which depend on the pulse intensity (Af = amplitude × frequency).10 The mixer-settler regime is characterized by the separation of light and heavy phases into discrete and clear layers during the quiescent period of the pulse cycle. The dispersion regime is the next in sequence and is found upon a further increase in the pulse intensity. This regime is characterized by a non-uniform drop size distribution and no coalescence of drops of the disperse phase. With an increase in the pulse velocity, the drop size decreases and thus an emulsion is formed. All these flow regimes can be observed in the vertical and horizontal types of pulsed sieve plate column. However, on the basis of our knowledge and practical observations, only the dispersion and emulsion regimes are found in a vertical pulsed packed column, in contrast to the horizontal type. Regarding the structure of the pulsed column used in this work, we should determine the transitional pulse intensity required to work in the dispersion regime. This is usually the recommended regime, as it combines high flux and good mass transfer.24 Therefore, as was described above, it was possible to identify visually different flow regimes by applying different pulse velocities. Thus, values of A and f that led to the dispersion regime were selected. After a few tests, the minimum and maximum pulse intensities for working in the dispersion regime were found to be 1.2 and 1.6 cm s−1, respectively. The maximum intensity was chosen to prevent flooding.The experimental results revealed that the volumetric flow rates had a weaker effect than the pulse intensity on the drop size. As seen in Fig. 2b, the mean drop size slightly increased with the increase in the dispersed phase flow rate. The coalescence rate of drops increased owing to the increase in the flow rate of the disperse phase so that the mean drop size increased. Moreover, in this research, a change in the flow rate of the continuous phase had no significant effect on the mean drop size. It should be noted that the dotted lines in the figures are only guides to the eye. As shown above, the mean drop size is mostly affected by the pulse intensity and flow rate of the disperse phase, and contours of the mean drop size upon changes in the pulse intensity and flow rate of the disperse phase are shown in Fig. 3.
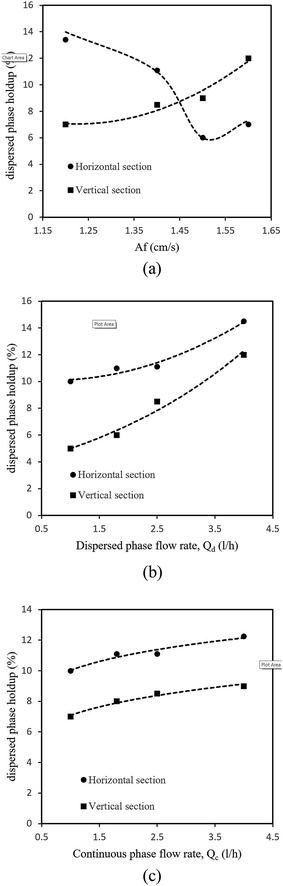
The effects of the flow rates of the disperse and continuous phases on the holdup are shown in Fig. 4b and c. It is clearly observed from these figures that the disperse phase holdup increased upon increasing the flow rate of the disperse phase in both horizontal and vertical sections. However, the flow rate of the continuous phase had a slight effect on the holdup. As with the mean drop size, the disperse phase holdup is also mostly affected by the pulse intensity and flow rate of the disperse phase, and contours of the disperse phase holdup upon changes in the pulse intensity and flow rate of the disperse phase are shown in Fig. 5.
4.2. Mass transfer
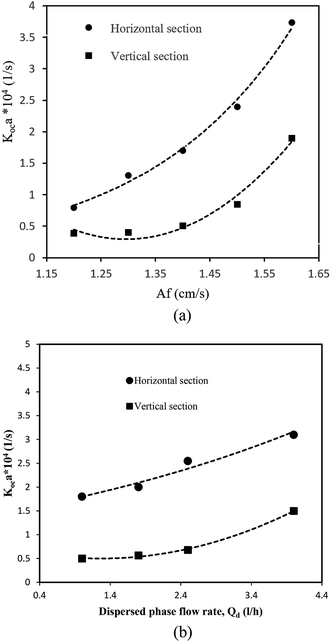
According to work carried out by other investigators,9,12,16 the main operational parameters that affect the mass transfer performance of a column are the pulse intensity and flow rate of the disperse phase. Fig. 6a illustrates the effect of the pulse intensity on the volumetric overall mass transfer coefficient. It is seen from Fig. 6a that the mass transfer performance was improved by increasing the pulse intensity in both horizontal and vertical sections. By increasing the pulse intensity, the degree of turbulence imparted to the system is greatly increased. Furthermore, the specific area available for mass transfer is increased because the drop size is smaller, and therefore the overall mass transfer coefficient is increased. As can be seen from Fig. 6a, the overall mass transfer coefficient was higher in the horizontal section. This may relate to the mass transfer direction. The solvent in this extraction research was the disperse phase. Furthermore, the maximum driving force of mass transfer and hence the maximum performance are found where the solvent is pure, because the solvent enters the horizontal section, which has the maximum driving force, and this section thus has the highest mass transfer coefficient. The effect of the flow rate of the disperse phase on the volumetric overall mass transfer coefficient is shown in Fig. 6b. As can be seen, the volumetric overall mass transfer coefficient was slightly increased by increasing the flow rate of the disperse phase. An increase in the velocity of the disperse phase causes an increase in the disperse phase holdup, as well as the drop size, and it is therefore expected that the interfacial area is not changed, but, as demonstrated by Asadollahzadeh et al.,28 the effect of the disperse phase holdup is more profound and consequently the interfacial area is slightly increased by increasing the velocity of the disperse phase.4.3. Predictive correlation of the overall mass transfer coefficient based on the continuous phase
The development of a new correlation for predicting the overall mass transfer coefficient based on the continuous phase in a horizontal–vertical pulsed packed extraction column is one of the main purposes of the present work. Most correlations that have been proposed for predicting the mass transfer coefficient in an extraction column relate to columns other than pulsed packed columns such as pulsed sieve plate, Kühni, rotating disc and spray columns. However, Torab-mostaedi and Safdari9 proposed semi-empirical correlations for predicting the Sherwood number of the continuous phase in a pulsed packed extraction column. For the mass transfer direction from the continuous to the disperse phase, they presented the following equation for 10 < Re < 150:9| Shoc = −49.76 + 14.8Re0.64 | (8) |
It should be noted that the overall mass transfer coefficient can be expressed as a dimensionless Sherwood number (see the abovementioned correlation) based on the continuous phase, which is defined as follows:
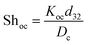 | (9) |
In addition, Safari et al. have investigated the mass transfer performance in a pulsed packed column and proposed the following correlation for predicting the overall mass transfer coefficient:12
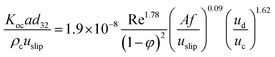 | (10) |
Fig. 7 shows a comparison of the experimental value of the Sherwood number in the horizontal section with those calculated by eqn (8) and (10) in the same experimental conditions. As can be seen, the data predicted by both correlations display remarkable deviations from the experimental values, and furthermore a greater deviation is seen for the vertical section. This deviation is mostly due to the structure used in this study. In addition, experimental data for the overall mass transfer coefficient were compared with those obtained by the correlations that were proposed for other types of extraction column, which are presented in Table S1†.9,12,16,19,29–35 A reliable correlation for predicting the mass transfer coefficient in a horizontal–vertical pulsed packed extraction column is therefore required.
 | ||
| Fig. 7 Comparison of experimental values of the Sherwood number with values calculated using the equations proposed by Torab-mostaedi and Safdari9 and Safari et al.12 for the water–acetone–toluene system. | ||
Consequently, the experimental data for the overall mass transfer coefficient based on the continuous phase are correlated in terms of dimensionless numbers. The significance of each dimensionless number for the overall mass transfer coefficient has been investigated using statistical methods. Finally, the following equations were obtained for predicting the overall mass transfer coefficients in the horizontal and vertical sections, respectively:
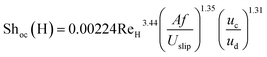 | (11) |
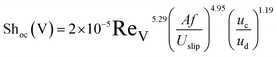 | (12) |
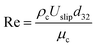 | (13) |
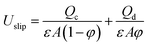 | (14) |
In order to evaluate the overall mass transfer coefficients predicted using eqn (11) and (12), experimental data were compared with those predicted by eqn (11) and (12). The average relative deviations (ARDs) of the values of Shoc(H) and Shoc(V) predicted using eqn (11) and (12) from experimental data were 12.1% and 15.5%, respectively.
A comparison of the experimental data with values calculated by eqn (11) and (12) is illustrated in Fig. 8. It can be seen that most of the predicted values have an error of less than 20%, except at two and three points in the horizontal and vertical sections, respectively. According to Fig. 8, there is good agreement between the experimental and calculated data.
4.4. Axial dispersion coefficients of continuous and disperse phases
The axial dispersion coefficient represents all the known and unknown influencing parameters that cause deviations from plug flow.22 Therefore, a lower axial dispersion coefficient is more favorable, because non-ideal terms reach a minimum and the mass transfer performance can be improved.36 As shown by Amani et al.23 and other investigators, the pulse intensity has the greatest impact on axial dispersion, and the effects of the two other operational parameters are negligible.9,16,23,37 Table 2 shows the effect of the pulse intensity on the axial dispersion coefficients of the continuous and disperse phases. It is seen that the axial dispersion coefficients of both the disperse and the continuous phase increase with the pulse intensity, which is not suitable for mass transfer performance. In contrast, an increase in pulse intensity leads to an increase in the mass transfer coefficient, and it can be concluded that the axial dispersion effect is not dominant. Thus, the overall result of an increase in pulse intensity is an improvement in the mass transfer performance. Another point observed from Table 2 is that the axial dispersion coefficient of the disperse phase is lower than that of the continuous phase in each section.| Af (cm s−1) | Qc (L h−1) | Qd (L h−1) | Koca × 104 (L s−1) | Ec (m2 s−1) | Ed (m2 s−1) | |||
|---|---|---|---|---|---|---|---|---|
| H | V | H | V | H | V | |||
| a H: horizontal section, V: vertical section. | ||||||||
| 1.2 | 2.5 | 2.5 | 0.866 | 0.419 | 7.71 × 10−6 | 5.43 × 10−5 | 4.66 × 10−7 | 6.76 × 10−7 |
| 1.4 | 2.5 | 2.5 | 1.708 | 0.483 | 1.33 × 10−5 | 1.99 × 10−4 | 1.20 × 10−6 | 8.50 × 10−7 |
| 1.5 | 2.5 | 2.5 | 2.191 | 0.815 | 9.67 × 10−5 | 3.36 × 10−4 | 4.92 × 10−6 | 9.38 × 10−7 |
| 1.6 | 2.5 | 2.5 | 3.73 | 1.753 | 8.48 × 10−5 | 5.6 × 10−4 | 7.21 × 10−6 | 5.54 × 10−6 |
5. Conclusions
This paper presents an experimental investigation of the mass transfer performance and hydrodynamic parameters of the toluene–acetone–water system in a pilot version of a horizontal–vertical pulsed packed extraction column. The investigation of mass transfer was performed using the axial dispersion model. The effects of operational variables, such as the flow rates of the disperse and continuous phases and pulse intensity, on the volumetric overall mass transfer coefficients and hydrodynamic parameters were studied. It was found that the pulse intensity is the most important operational parameter. By increasing the pulse intensity the hydrodynamic parameters changed in such a way that the mass transfer coefficient increased. In addition, the mass transfer coefficient was influenced by the flow rate of the disperse phase. Finally, this work has provided two valuable correlations for the prediction of the volumetric overall mass transfer coefficient in a horizontal–vertical pulsed packed extraction column. Good agreement between predictions and experimental data causes these correlations to be recommended for the calculation of mass transfer coefficients and consequently for the final selection of the column height.Conflicts of interest
There are no conflicts to declare.Nomenclature
Greek symbols
| ρ | Density (kg m−3) |
| φ | Disperse phase holdup |
| μ | Viscosity (kg m−1.s) |
| ε | Void fraction |
| σ | Interfacial tension between two phases (N m−1) |
Subscripts/superscripts
| c | Continuous phase or column |
| d | Disperse phase |
| o | Overall value |
| * | Equilibrium value |
| in | Inlet to the column |
| out | Outlet from the column |
References
- X. Sun, H. Luo and S. Dai, Chem. Rev., 2012, 112, 2100–2128 CrossRef CAS PubMed.
- S. Saha, R. Mistri and B. C. Ray, J. Chromatogr. A, 2010, 1217, 307–311 CrossRef CAS PubMed.
- S. Saha, R. Mistri and B. C. Ray, J. Chromatogr. A, 2009, 1216, 3059–3063 CrossRef CAS PubMed.
- D. P. Mantuano, G. Dorella, R. C. A. Elias and M. B. Mansur, J. Power Sources, 2006, 159, 1510–1518 CrossRef CAS.
- H. G. Schutze, W. A. Quebedeaux and H. Lochte, Ind. Eng. Chem., Anal. Ed., 1938, 10, 675–677 CrossRef CAS.
- J. C. Godfrey and M. J. Slater, Liquid–liquid extraction equipment, Wiley Chichester, UK, 1994 Search PubMed.
- S. Khooshechin, J. Safdari, M. A. Moosavian and M. H. Mallah, Int. J. Heat Fluid Flow, 2013, 44, 684–691 CrossRef CAS.
- A. Hussain, T.-B. Liang and M. Slater, Chem. Eng. Res. Des., 1988, 66, 541–554 CAS.
- M. Torab-Mostaedi and J. Safdari, Chem. Eng. Process., 2009, 48, 1321–1326 CrossRef CAS.
- R. Yadav and A. Patwardhan, Chem. Eng. J., 2008, 138, 389–415 CrossRef CAS.
- A. E. Ferreira, S. Agarwal, R. M. Machado, M. L. F. Gameiro, S. M. Santos, M. T. A. Reis, M. R. C. Ismael, M. J. N. Correia and J. M. Carvalho, Hydrometallurgy, 2010, 104, 66–75 CrossRef CAS.
- A. Safari, J. Safdari, H. Abolghasemi, M. Forughi and M. Moghaddam, Chem. Eng. Res. Des., 2012, 90, 193–200 CrossRef CAS.
- A. Melnyk, S. Vijayan and D. Woods, Can. J. Chem. Eng., 1992, 70, 417–425 CrossRef CAS.
- S. Akhgar, J. Safdari, J. Towfighi, P. Amani and M. H. Mallah, RSC Adv., 2017, 7, 2288–2300 RSC.
- P. Amani, J. Safdari, H. Abolghasemi, M. H. Mallah and A. Davari, Int. J. Heat Fluid Flow, 2017, 65, 266–276 Search PubMed.
- M. Asadollahzadeh, A. Hemmati, M. Torab-Mostaedi, M. Shirvani, A. Ghaemi and Z. Mohsenzadeh, Chin. J. Chem. Eng., 2017, 25, 53–61 CrossRef CAS.
- M. Torab-Mostaedi, A. Ghaemi, M. Asadollahzadeh and P. Pejmanzad, Braz. J. Chem. Eng., 2011, 28, 447–456 CrossRef CAS.
- M. Torab-Mostaedi and J. Safdari, Braz. J. Chem. Eng., 2009, 26, 685–694 CrossRef CAS.
- M. Torab-Mostaedi, S. Safdari, M. Moosavian and M. G. Maragheh, Braz. J. Chem. Eng., 2008, 25, 473–481 CrossRef CAS.
- M. Torab-Mostaedi, A. Ghaemi and M. Asadollahzadeh, Can. J. Chem. Eng., 2012, 90, 1570–1578 CrossRef.
- T. Míšek, R. Berger and J. Schröter, EFCE Publ. Ser., 1985, 46, 1 Search PubMed.
- P. Danckwerts, Chem. Eng. Sci., 1953, 2, 1–13 CrossRef CAS.
- P. Amani, J. Safdari, A. Gharib, H. Badakhshan and M. H. Mallah, Prog. Nucl. Energy, 2017, 98, 71–84 CrossRef CAS.
- B. Grinbaum, Solvent Extr. Ion Exch., 2006, 24, 795–822 CrossRef CAS.
- A. Kumar and S. Hartland, Ind. Eng. Chem. Res., 1996, 35, 2682–2695 CrossRef CAS.
- S. Ousmane, M. Isabelle, M.-S. Mario, T. Mamadou and A. Jacques, Chem. Eng. Res. Des., 2011, 89, 60–68 CrossRef CAS.
- G. Angelov and C. Gourdon, Chem. Eng. Res. Des., 2012, 90, 877–883 CrossRef CAS.
- M. Asadollahzadeh, S. Shahhosseini, M. Torab-Mostaedi and A. Ghaemi, Chem. Eng. Res. Des., 2015, 100, 104–112 CrossRef CAS.
- A. Rahbar-Kelishami and H. Bahmanyar, Chem. Eng. Res. Des., 2012, 90, 615–621 CrossRef CAS.
- C.-H. He, Y.-H. Gao, S.-H. Yang and D. W. Edwards, J. Loss Prev. Process Ind., 2004, 17, 195–204 CrossRef.
- A. Kumar and S. Hartland, Chem. Eng. Res. Des., 1999, 77, 372–384 CrossRef CAS.
- A. F. Seibert and J. R. Fair, Ind. Eng. Chem. Res., 1988, 27, 470–481 CrossRef CAS.
- R. Clift, Bubbles, drops, and particles, 1978 Search PubMed.
- M. E. Weber, Ind. Eng. Chem. Fundam., 1975, 14, 365–366 CAS.
- A. Lochiel and P. Calderbank, Chem. Eng. Sci., 1964, 19, 471–484 CrossRef CAS.
- T. C. Lo, M. H. I. Baird and C. Hanson, Handbook of solvent extraction, Wiley, New York, 1983 Search PubMed.
- F. Panahinia, J. Safdari, M. Ghannadi-Maragheh, P. Amani and M. H. Mallah, Sep. Sci. Technol., 2017, 52, 1537–1552 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07999k |
| This journal is © The Royal Society of Chemistry 2017 |