Open Access Article
Open Access ArticleCellulose-derived carbon nanofibers/graphene composite electrodes for powerful compact supercapacitors†
Volodymyr Kuzmenko *ab,
Nan Wanga,
Mazharul Haquea,
Olga Nabokac,
Mattias Flygared,
Krister Svenssond,
Paul Gatenholmbe,
Johan Liua and
Peter Enokssonab
*ab,
Nan Wanga,
Mazharul Haquea,
Olga Nabokac,
Mattias Flygared,
Krister Svenssond,
Paul Gatenholmbe,
Johan Liua and
Peter Enokssonab
aDepartment of Microtechnology and Nanoscience, Chalmers University of Technology, 41296 Gothenburg, Sweden. E-mail: kuzmenko@chalmers.se; Tel: +46 31772 19 91
bWallenberg Wood Science Center, Chalmers University of Technology, 41296 Gothenburg, Sweden
cNational Research Council Canada, 1200 Montreal Rd., Ottawa, ON K1A 0R6, Canada
dDepartment of Physics and Electrical Engineering, Karlstad University, 65188 Karlstad, Sweden
eDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, 41296 Gothenburg, Sweden
First published on 28th September 2017
Abstract
Herein, we demonstrate a unique supercapacitor composite electrode material that is originated from a sustainable cellulosic precursor via simultaneous one-step carbonization/reduction of cellulose/graphene oxide mats at 800 °C. The resulting freestanding material consists of mechanically stable carbon nanofibrous (CNF, fiber diameter 50–500 nm) scaffolds tightly intertwined with highly conductive reduced graphene oxide (rGO) sheets with a thickness of 1–3 nm. The material is mesoporous and has electrical conductivity of 49 S cm−1, attributed to the well-interconnected graphene layers. The electrochemical evaluation of the CNF/graphene composite electrodes in a supercapacitor device shows very promising volumetric values of capacitance, energy and power density (up to 46 F cm−3, 1.46 W h L−1 and 1.09 kW L−1, respectively). Moreover, the composite electrodes retain an impressive 97% of the initial capacitance over 4000 cycles. With these superior properties, the produced composite electrodes should be the “looked-for” components in compact supercapacitors used for increasingly popular portable electronics and hybrid vehicles.
Introduction
Modern society consumes huge amounts of energy, which entails unprecedented scientific attention towards the development of efficient methods of energy harvesting, storage and delivery. The boundaries of energy storage have been tremendously expanded in order to satisfy various evolving applications. As a result, supercapacitors occupied their niche as high-power energy storage devices with long cycle life, low maintenance cost, safe and pollution-free operation and the capability to function at high temperatures.1–3 Distinctive advantages promote an extensive use of supercapacitors in wearable electronics,4,5 uninterruptible power supplies,6 wireless sensors,7 electric hybrid vehicles,8,9 and energy harvesters, for instance, wind turbines,10 solar cells or piezoelectric systems.11 Most of these applications place harsh limitations on available space for energy storage devices, which brought up the need of compact supercapacitors with high volumetric capacitance.12Supercapacitors are mostly based on carbon materials as electrodes,13,14 which is due to their superb intrinsic properties such as high electrical conductivity, mechanical robustness, electrochemical and thermal stability, and the capability to be manufactured in a cost-effective manner from various renewable resources.15–17 However, in order to satisfy volumetric requirements imposed on commercial supercapacitors, carbon materials also need to have sufficiently high bulk density and thickness without considerable weakening of the electrochemical performance.12 The challenge of fitting all these valuable characteristics into one material is rather difficult. That is why carbon composite materials are particularly interesting as they could be designed in a way to combine the beneficial properties of its constituents: high mesoporosity for fast ionic transportation with high packing density for volume-limited portable electronics;18,19 freestanding and robust nature for convenient handling with high electrical conductivity for low charge transfer resistance.20,21
Graphene definitely earned its right to be a constituent in a potentially flawless electrode material. Soon after its first revelation in 2004,22 graphene, for a good reason, was attracting record attention and utilization in seemingly every application in the world,23 including energy storage.24,25 A high specific surface area of a single graphene sheet, i.e. ∼2630 m2 g−1,26 creates many active binding sites for double-layer capacitance. In addition, graphene's planar open atomic structure with high electrical conductivity provides fast access for electrolyte ions to its surface and excellent transfer of electrons to a collector. Furthermore, the high mechanical and chemical stability allows electrochemical durability of graphene in different electrolytes after a large number of charge–discharge cycles.27,28 In theory, single-layer graphene is a perfect electrode material for a supercapacitor; however, the capacitance of multi-layer or bulk graphene, which could be practically produced on a large scale with appropriate thickness, is far from a single-layer graphene.29 This undesirable deviation is explained by agglomeration or stacking of graphene sheets due to the van der Waals attractions,30,31 resulting in hindered ion diffusion to the surface of individual sheets. This is why graphene needs a complementary part in order to prevent sheet aggregation, while retaining the material integrity, ion permeability, and good conductivity between the sheets.32 Carbon nanofibers (CNFs), obtained from electrospun precursors, possess the desired advantages due to their excellent properties: sieve-like nanosized morphology, freestanding nature and well-interconnected porosity.33,34
In this study, we present a sustainable and efficient composite carbon material consisting of CNFs and reduced graphene oxide (rGO). It is fabricated in a creative manner via carbonization of the electrospun fibrous cellulose functionalized with graphene oxide (GO) (Fig. 1). Water-soluble GO has strong affinity to hydrophilic cellulose due to abundant polar surface functionalities from both sides,35–37 which results in homogeneous coverage of cellulosic fibers with GO flakes. This structure remains integral and freestanding after simultaneous one-step carbonization/reduction of cellulose/GO into CNF/rGO at 800 °C. The problem of graphene sheet stacking is diminished due to the following factors: (1) solid-state high temperature reduction, which prevents agglomeration between graphene layers,38 and (2) the nanospacer effect of CNFs that stick in between graphene layers. Dense packing of interpenetrated conductive rGO sheets and CNFs makes this structure suitable for supercapacitors with high volumetric demands in comparison with vast majority of the previously reported carbon electrodes,14 often having either too high resistance2 or too low packing density.39 Moreover, due to the capability of CNFs to act as excellent conductive bridges between rGO sheets, the composite's electrical conductivity is one of the highest among the 3D graphene nanomaterials.40 This exceptional feature leads to the efficient electron transport crucial for high power applications.36
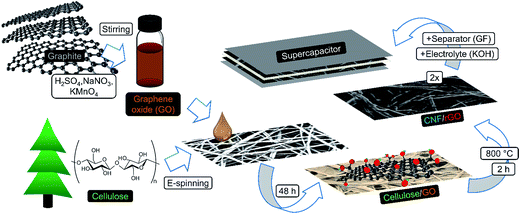 | ||
| Fig. 1 Schematic illustration of the fabrication process of CNF/rGO composite electrodes for a compact supercapacitor. | ||
Another important aspect of this study is its orientation on sustainable/renewable resources, which is vital for the future of energy storage devices.41 Commonly produced graphene is not a sustainable carbon material, and is preferably used only as an additive that enhances the valuable properties of electrode composites.42 On the contrary to nanocarbons derived from fossil fuels, biomass-derived nanocarbons are cost-effective for large-scale applications and cause minimal harm to the environment.43 It becomes even more relevant after the adoption of the Paris Agreement, which makes majority of the world's biggest economies to finally unite their efforts in order to slow down detrimental climate changes through reductions of greenhouse gas emissions.44
Experimental
Preparation of composite electrodes
Cellulosic mats were fabricated through cellulose acetate electrospinning (from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of acetone and dimethylacetamide) with subsequent NaOH-aided deacetylation to cellulose as described in our previous study.16 These mats were embedded into a frame and immersed for 2 days (sides were turned over after 1 day) into a beaker containing graphene oxide (GO) aqueous solution. The beaker was subjected to continuous gentle shaking in order to obtain homogenous adsorption of GO flakes onto the surface of the cellulosic fibers. After the GO treatment, the cellulose/GO mats were dried in a fume hood for 4 h, followed by the careful removal of the frame. Finally, they were carbonized in a tube furnace with nitrogen gas flow in order to obtain a CNF/rGO composite nanomaterial. The temperature was raised with a rate of 5 °C min−1 up to 800 °C and was held for 2 h.
1 mixture of acetone and dimethylacetamide) with subsequent NaOH-aided deacetylation to cellulose as described in our previous study.16 These mats were embedded into a frame and immersed for 2 days (sides were turned over after 1 day) into a beaker containing graphene oxide (GO) aqueous solution. The beaker was subjected to continuous gentle shaking in order to obtain homogenous adsorption of GO flakes onto the surface of the cellulosic fibers. After the GO treatment, the cellulose/GO mats were dried in a fume hood for 4 h, followed by the careful removal of the frame. Finally, they were carbonized in a tube furnace with nitrogen gas flow in order to obtain a CNF/rGO composite nanomaterial. The temperature was raised with a rate of 5 °C min−1 up to 800 °C and was held for 2 h.
In this study, GO solution was prepared via ingeniously modified Hummers method that allows fabrication of GO flakes with very small size that could easily permeate into fibrous cellulosic mats. In a typical experiment, graphite flakes (5 g) with an average diameter of 20 μm, NaNO3 (3.75 g) and concentrated H2SO4 (200 mL) were mixed at 0 °C. KMnO4 (15 g) was slowly added into the mixture within about 1 h, followed by stirring for another 1 h in an ice-water bath. Following this, the ice water bath was replaced by an oil bath, in which the temperature was controlled in the range of 32–40 °C. The mixture was continuously stirred in the oil bath for 2 h. Then, H2SO4 (400 mL, 5 wt%) was added into the reaction container, which was further stirred for 1 h at 98 °C. The reaction was terminated by adding H2O2 (15 mL, 30 wt%) into the above solution when the temperature was lowered to 60 °C. The mixture was precipitated at room temperature, centrifuged and washed with deionized water until the pH value was close to 7. The obtained colloid was dispersed into deionized water (1 L) to obtain a GO solution with a concentration of 5 mg mL−1. The further exfoliation of GO was carried out by using a L5M high-shear laboratory mixer (Silverson Machines) with a maximum handling volume of 12 L. The high-shear mixer significantly reduced the GO size to less than 1 μm due to an intense local shearing rate (104 s−1). The mixing head comprised a four-blade rotor placed within a fixed stator (D rotor-stator = 100 μm). The diameter of the rotor was 32 mm. Following shear mixing, the obtained GO suspension was centrifuged at 6000 rpm for 10 min to remove all the large particles and to deliver a homogenous GO dispersion.
Material characterization
Scanning electron microscopy (SEM, Leo Ultra 55 FEG SEM, Zeiss) was performed in the secondary electron mode at the acceleration voltage of 3 kV to analyze the morphology of the materials. Atomic force microscopy (AFM, Digital Instrument Nanoscope IIIA from Digital Instrument Inc.) was operated in the tapping mode, using 10 nm thin tips under the cantilever (Micro Masch silicon cantilever NSC 15). Transmission electron microscopy (TEM, JEOL JEM 2100) equipped with a LaB6 cathode and a digital CCD camera (SC1000 Orius) was used for making microstructure images at an electron acceleration voltage of 80 kV, which is below the threshold for electron-beam induced damages. Samples for TEM analysis were cut from the prepared composite films (using a pair of scissors) and each sample was sandwiched between two Cu grids (Athene G204, 400 mesh). Selected area electron diffraction pattern (SAED) was performed using low current densities at selected parts of the samples. Thermogravimetric analysis (TGA, Pyris TGA 7, Perkin Elmer) was performed in N2 atmosphere from 105 to 800 °C at a heating rate of 5 °C min−1 to investigate the carbonization process and to determine the rGO content in the final composite. N2 adsorption experiments (TriStar 3000 V6.04 A surface area and pore analyzer) were conducted at 77 K after the samples were degassed under vacuum at 225 °C for 4 h. The surface area was measured using the Brunauer–Emmett–Teller (BET) method, and pore size distribution was calculated by the Barett–Joyner–Halenda (BJH) method using an adsorption isotherm. X-ray photoelectron spectroscopy (XPS, Quantum 2000 scanning ESCA microprobe, Physical Electronics) was carried out using an Al Kα X-ray source (1486.6 eV) and the beam size of 100 μm with an analyzed area of about 400 × 500 μm2 and a depth of 4–5 nm. X-ray diffraction (XRD, Philips X'Pert Materials Research Diffractometer) analysis was performed using Cu Kα radiation (λ = 1.54184 Å) at a scanning rate of 1.5° min−1. Raman spectroscopy (Horiba XploRA spectrometer equipped with an Olympus BX41 microscope) was carried out using a 638 nm laser source. The electrical conductivity of the materials was measured using a four-point probe system (CMT-SR2000N, AIT). The thickness of electrode materials was measured using a digital micrometer (Mitutoyo).Electrochemical setup and measurements
The CNF/rGO composites and pure CNFs were evaluated as electrodes for a supercapacitor using symmetrical two-electrode Swagelok cells. The cells consisted of the following components: the freestanding carbon materials as working electrodes, glass fiber mats (Whatman) as separators, and aqueous solution of KOH (6 M, 99.99%, Sigma) as the electrolyte. The size of the working electrodes and separators was adjusted to a circular area (respective diameters were 10 and 12 mm) to fit current collectors. The electrodes were soaked with the electrolyte solution for 6 h before starting the measurements.Electrochemical measurements (Gamry Reference 3000 potentiostat/galvanostat/ZRA) were performed at ambient conditions. A voltage range of 0–1.0 V was used for cyclic voltammetry (CV) and galvanostatic charge–discharge (GCD) measurements. Electrochemical impedance spectroscopy (EIS) was performed over a frequency range from 100 kHz to 10 mHz. Electrochemical stability experiments were conducted using cyclic charge–discharge (CCD) for 4000 cycles with a current density of 0.9 A cm−3.
The evaluation of the volumetric capacitance Cv (F cm−3) from the CV curves was made at 5 mV s−1 scan rate according to eqn (1); the volumetric energy density Edv (W h L−1) and power density Pdv (W L−1) were estimated from the GCD curves following eqn (2) and (3), respectively.
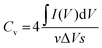 | (1) |
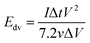 | (2) |
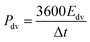 | (3) |
Results and discussion
Morphology and surface properties of composites
SEM and AFM help to reveal the morphological and topographical features of the precursors and the resulting carbon composites. Fibrous cellulosic mats with the thickness of 50–100 μm and fiber diameters in the 0.5–2 μm range were used as robust frameworks for the composite synthesis (Fig. 2A and S1A of the ESI†). These mats were further functionalized with GO, which resulted in composite precursors with desired coverage of cellulosic fibers with GO sheets (Fig. 2B and S1B†). This excellent coverage is achieved due to strong attractive forces such as van der Waals and hydrogen bonding between polar oxygen-containing groups of cellulose and GO.2,35The high temperature treatment of the precursors simultaneously triggered the transformation of fibrous cellulose into CNF (via carbonization) and GO into rGO (via reduction). The ensuing materials, pure CNFs and CNF/rGO composites, are flexible and freestanding mats with 40–60 μm thickness. The pure CNF material consists of randomly oriented nanofibers with diameter in the range of 50–500 nm (Fig. 2C and S1C†). Its morphology is inherited from the cellulosic precursor, and the only difference is the shrinkage of the fibers due to the thermal weight loss.45 In the CNF/rGO composite, CNFs are uniformly interconnected with few-layered graphene sheets that have slightly wrinkled texture (Fig. 2D and S1D†). The wrinkles emerge during rGO preparation46 and may possibly indicate the connection of rGO nanosheets to each other, which is favorable for electron transport.29 Such a strong integration of constituents is also necessary for mechanical and electrochemical stability of carbon electrodes. Moreover, macropores and large voids between the fibers could serve as ion channels, which enhance the quick penetration of electrolyte ions into the electrode material.18,20
TEM images provide a closer look at the microstructure of the CNF/rGO composite. Semi-transparent wrinkled sheets of rGO with a thickness of roughly 1–3 nm (Fig. S2†) are located both on top of CNFs and are also extended between them, thus creating a continuous conductive network with hierarchical dimensions with the exposure of additional surface to the electrolyte (Fig. 2E). Transparency and fairly small thickness of the sheets verify that they are efficiently exfoliated and their stacking is rather minor.47 Interlayer fringes of the graphitic lattice are clearly visible in rGO sheets, oriented parallel to the TEM beam, throughout the composite material (Fig. 2F). Remarkably, SAED pattern of the few-layered rGO component shows a clear hexagonal pattern with rings, which verifies a fairly high crystalline order within the sheets and their incommensurate stacking, typical for turbostratic graphitic structures (Fig. 2F, inset).27
TGA was used to investigate the behavior of the precursors during carbonization and also to estimate the content of both components in the final CNF/rGO composite. The cellulose sample demonstrates the major weight loss occurring in the temperature range of 250–400 °C when depolymerization of cellulose takes place simultaneously with dehydration and release of volatile compounds such as carbon dioxide, methanol, and acetic acid (Fig. 3A).48 This behavior is typical for cellulosic materials.36,49,50 In this study, the weight yield of the carbonizate was only 5.65% at 800 °C. In contrast, TGA curves of the cellulose/GO samples show a completely different decomposition behavior. The weight loss initiates at 150 °C, is slightly steeper in the range of cellulose decomposition and continues smoothly up to 650 °C. The weight yield of the composite is 23.53% at 800 °C. This tremendous increase of the yield for the composite in comparison to the pure CNFs could be partially explained by the presence of rGO, which show the weight yield of 62.88% after thermal reduction. Knowing the initial weight loading of GO, i.e. 31.2%, it is possible to calculate the content of CNF and rGO in the final product. Their respective weight fractions are 16.6% and 83.4%. However, the increase of the composite yield should be likewise attributed to the reported flame-retarding behavior of GO in polymeric composites, which prevents the loose release of volatile products from the degrading polymer.51 This makes it extremely challenging to estimate the actual weight fractions of CNFs and rGO in the composite.
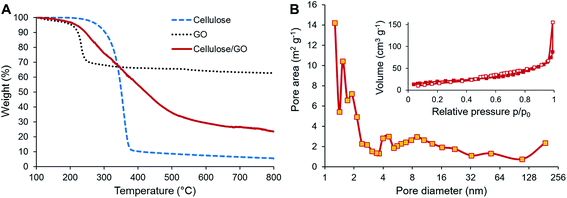 | ||
| Fig. 3 (A) TGA of cellulose and cellulose/GO. (B) Nitrogen adsorption/desorption isotherms (inset) and pore size distribution (main image) of CNF/rGO. | ||
BET analysis of N2 adsorption isotherms was used to determine the specific surface areas of the carbon materials and to explore their pore-filling behavior. Both pure CNF and CNF/rGO composite materials exhibit type-III adsorption–desorption isotherms with a constant rise in the 0.1–0.7 P/P0 range and negligible adsorption volume in the low pressure range (Fig. 3B (inset) demonstrates the isotherms for the CNF/rGO composite), which corresponds to mesoporous carbons with negligible microporosity.27 This could explain the relatively low values of specific surface area of the pure CNF material (45 m2 g−1) and the composite material (143 m2 g−1). However, for good volumetric performance, the large surface area of carbon electrodes is rather disadvantageous as it is inevitably supplemented by high porosity, i.e. low packing density. There is still a great need for mesopores (pores with the diameter range of 2–50 nm) as they provide the necessary transport channels for electrolyte ions that help to utilize the electrode surface more comprehensively and to decrease electrolyte resistance, which directly has a positive influence on power capability.52 Pore size distribution for the CNF/rGO composite material is shown in Fig. 3B. It is vivid that the synthesized composites have hierarchical porosity; in addition, the mesopores with the size of ≈4–30 nm and borderline micropores with the size of ≈2 nm take up a substantial fraction of the total pore area and the average pore diameter is 4.9 nm.
XPS analysis provides useful information about surface elemental composition and functional groups. The results of this analysis show that the surface of all the materials consists of only carbon and oxygen (in addition to non-detected hydrogen). The C1s spectra (Fig. 4A–C) of cellulose, cellulose/GO and CNF/rGO were resolved to four types of carbon atoms which could be assigned to C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (the peak at 284.5 eV) and to oxygen-containing bonds such as C–O (286.3 eV), C
C bonds (the peak at 284.5 eV) and to oxygen-containing bonds such as C–O (286.3 eV), C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (287.7 eV) and O–C
O (287.7 eV) and O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (288.9 eV).53 Cellulose has the highest oxygen content among the three materials (45.5 at%). Its C1s spectrum has intense peak for C–O, fairly strong for C
O (288.9 eV).53 Cellulose has the highest oxygen content among the three materials (45.5 at%). Its C1s spectrum has intense peak for C–O, fairly strong for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and almost negligible for C–C/C
O and almost negligible for C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, which totally complies with the chemical composition of cellulose.54 A large amount of polar oxygenated groups makes the surface of cellulose fibers attractive for hydrophilic GO sheets. Following functionalization, cellulose/GO precursor could be characterized by the retained high oxygen content (34.8 at%) and a significant increase of the peak corresponding to C–C/C
C, which totally complies with the chemical composition of cellulose.54 A large amount of polar oxygenated groups makes the surface of cellulose fibers attractive for hydrophilic GO sheets. Following functionalization, cellulose/GO precursor could be characterized by the retained high oxygen content (34.8 at%) and a significant increase of the peak corresponding to C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, which reveals the presence of oxygenated graphitic sheets. Following high temperature treatment, the ensuing CNF/rGO material has an elemental composition typical for pure carbons, i.e. extremely high carbon content (96.8 at%) with the dominant peak for C–C/C
C bonds, which reveals the presence of oxygenated graphitic sheets. Following high temperature treatment, the ensuing CNF/rGO material has an elemental composition typical for pure carbons, i.e. extremely high carbon content (96.8 at%) with the dominant peak for C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. These results confirm simultaneous carbonization of cellulose and effective thermal reduction of GO.
C bonds. These results confirm simultaneous carbonization of cellulose and effective thermal reduction of GO.
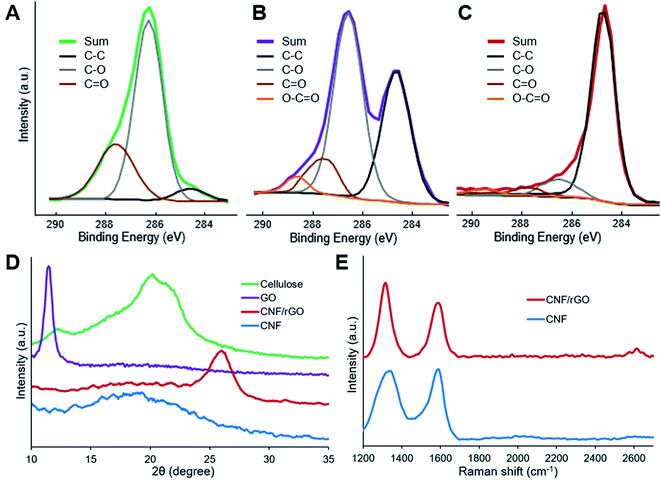 | ||
| Fig. 4 XPS C1s spectra of (A) cellulose, (B) cellulose/GO and (C) CNF/rGO. (D) XRD patterns of cellulose, GO, CNF/rGO and CNF. (E) Raman spectra of CNF and CNF/rGO. | ||
XRD patterns of the precursors and the resulting carbon materials are shown in Fig. 4D. The XRD pattern of cellulose sample reveals three distinctive peaks at 12.1° (101), 20.0° (10–1) and 21.9° (002), which precisely correspond to lattice planes of cellulose II.55 For GO, a strong diffraction peak at 11.6° appears and it should be attributed to the turbostratic structure of GO layers. The interlayer spacing of the GO is approximately 7.65 Å, and it is much larger than 3.34 Å of the (002) lattice plane for graphite. This phenomenon could be easily explained by the incorporation of bulky hydrated oxygen-containing groups between graphite layers during GO preparation,2 which correlates with previously mentioned XPS results. The outcomes of the effective thermal reduction of GO and restoration of π-conjugated system are the emerging broad peak at 26.1° (corresponding to rGO with an interlayer distance of 3.41 Å that is almost equal to graphite)35 and the disappearing peak at 11.6°, whereas carbonization of cellulose results in CNF with relatively amorphous structure demonstrated by a broad peak at 18–20°.16
Raman spectra of both the carbon materials are shown in Fig. 4E. The D-band at 1329 cm−1 and 2D-band at 2614 cm−1 (observed only for the CNF/rGO material) could be assigned to in-plane vibrations of sp2-bonded carbons with structural defects or lattice fringes, while the G-band at 1588 cm−1 – is attributed to sp2-bonded carbons with more ordered crystalline structure.53 Typical carbon spectra once again demonstrate the reduction of GO and cellulose carbonization. The ID/IG ratio for the CNF/rGO composite is 1.40, which is much higher than the reported ratio for graphite. This phenomenon could be explained by the formation of many small graphitic domains, thus more lattice fringes are formed on oxidative exfoliation of graphite and subsequent GO reduction.56
Carbonization of GO-functionalized cellulosic precursors results in the strong fusion between the CNF network and graphene sheets in the final CNF/rGO composite. Well-spread rGO layers act as perfect conductive connectors between CNF current pathways, which are very important for decreasing both internal resistance and contact resistance with collectors. The CNF/rGO composites have electrical conductivity of 49 S cm−1, about 10 times higher value than the pure CNFs (4.2 S cm−1). A freestanding carbon material with such a high electrical conductivity does not require conventionally used conductive fillers and volume-consuming redundant binders. This facilitates the filling of the precious volume of a supercapacitor cell only with an active electrode material, and on doing so the volumetric capacitance and energy density would substantially increase.57
Electrochemical analysis
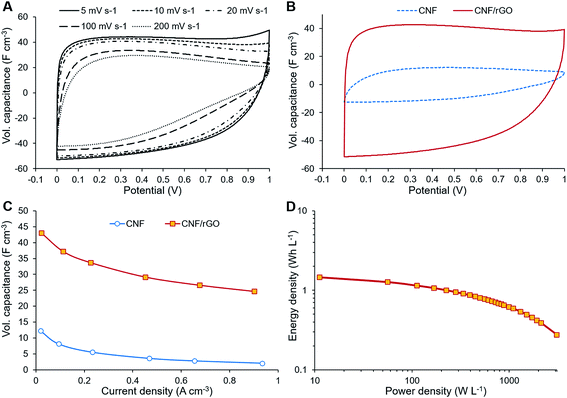
The electrochemical performance of the composite CNF/rGO electrode material was assessed in symmetrical two-electrode Swagelok cells. For comparison, the electrodes made of the pure CNFs were also evaluated. The CV measurements were performed at the voltage range of 0–1 V at different scan rates from 5 to 200 mV s−1. The CV curves in Fig. 5A demonstrate scan rate dependence for the composite electrode. The shape of the curves at lower scan rates between 5 and 20 mV s−1 is moderately rectangular without apparent faradaic peaks, which indicates mostly electrical double layer (EDL) capacitive behavior with a rapid current–voltage response and low resistance of ion transport within the electrode.35 For the higher scan rates such as 100 or 200 mV s−1, the rectangular shape of the CV curves becomes slightly distorted due to the increased resistance of electrolyte ion transport.32The volumetric capacitance of the electrodes was calculated from the integrated area of the curves at 5 mV s−1 scan rate using eqn (1). Fig. 5B displays the CV curves of both CNF/rGO and pure CNF electrodes. It should be mentioned that their thickness of 40–60 μm is comparable to that of commercial electrodes (100–200 μm), which makes these values trustworthy.58 The composite electrodes demonstrate superior volumetric capacitance (46 F cm−3 vs. 12 F cm−3 for the pure CNF). The volumetric capacitance value of the CNF/rGO composite stands fairly high among the reported carbon electrodes and conducting polymer-based electrodes.12,14 Such performance could be explained by three possible factors: (1) relatively high packing density (≈0.45 g cm−3) of the material due to its low porosity;58 moreover, during the device assembly the electrodes become compressed, which increases their packing density even further via the elimination of interfibrous spaces.12 (2) extremely high electrical conductivity due to the absence of a binder material and apparently due to abundant conductive interconnections between rGO sheets and CNFs, which facilitates effective charge transfer throughout the material; (3) reorganization of rGO sheets during intercalation of electrolyte ions, which leads to a higher accessible surface area.59
The electrochemical behavior of the electrode materials was further investigated through GCD measurements. Fig. 5C shows the dependence of the specific capacitance (calculated from GCD measurements) on the current density. At 0.9 A cm−3 the specific capacitance of the composite electrode is about 57% of that at 0.0225 A cm−3, which is due to its fairly large thickness and subsequent inability of the electrolyte ions to diffuse quickly to the inner cavities at a higher current density.59 These GCD results are consistent with the dependence of specific capacitance on the scan rate as shown by the CV measurements. The ions need to be in proximity to the electrode surface for a supercapacitor to maintain high rate capability; however, the non-porous CNFs are unable to keep the ions attached to the surface. On the contrary to CNFs, the rGO component could retain ions between its sheets separated by sub-micrometer distances, thus creating ion-buffering reservoirs and reducing ion diffusion length. These trapped ions have instant access to the electrode surface even at the highest current density.18
GCD measurements were also used to assess energy density and power density of a supercapacitor device with the composite electrode material. These essential characteristics of a supercapacitor were calculated using eqn (2) and (3). At the current density of 0.9 A cm−3, the device has a high volumetric energy density of 0.83 W h L−1 and power density of 445 W L−1. These values are very promising for compact supercapacitors that rely on sustainable materials. The Ragone plot of the CNF/rGO demonstrates a typical energy density/power density inverse proportion (Fig. 5D), with the highest energy density of 1.46 W h L−1 (at the current density of 0.023 A cm−3) and the highest power density of 3076 W L−1 (at the current density of 6.8 A cm−3).
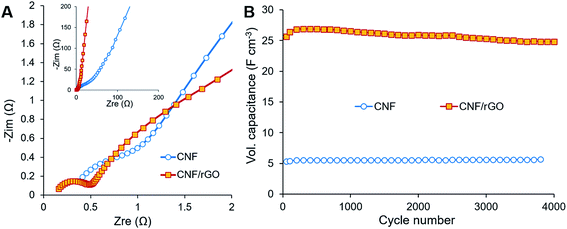
The electrochemical behavior of the electrode materials was further analyzed using EIS. Fig. 6A (main image) shows enlarged Nyquist plots of the electrodes in the high frequency region, where bulk electrolyte solution resistance (Rs) and charge transfer resistance (Rct) are expressed as the initial intercept of the plot with the X-axis and as the semicircle, respectively.2 Though the same electrolyte solution is used for the cells with different electrodes, the first cell containing the CNF/rGO electrode has lower Rs (0.16 Ω) than the cell containing the pure CNF (0.38 Ω). It is due to the fact that Rs is determined not only by the conductivity of the electrolyte, but also by the thickness of its layer.2 Apparently, the electrolyte layer between the rGO sheets is thinner, which is consistent with the hypothesis of ion-buffering reservoirs mentioned previously. Nevertheless, the devices with both the electrode materials are characterized by low Rs and essentially by low Rct particularly for the ones with the CNF/rGO composite electrodes. The very low value of Rct (0.35 Ω) could be attributed to few of the characteristic features of the composite material: (i) its hierarchical meso- and macroporosity, which decreases the interfacial resistance between the electrolyte and the electrode material (ionic resistance), and (ii) its high conductivity and binder-free elastic nature, which decreases the intrinsic resistance and the resistance between the electrode material and the collectors (electronic resistance).40 Fig. 6A (inset) shows Nyquist plots in the medium-low frequency region, including the slope of the 45° portion of the curve known as Warburg impedance.57 The short Warburg region along with good line verticality indicates the composite electrodes' effective pore accessibility for the electrolyte ion diffusion and flawless EDL capacitive behavior.2
The long-time cyclic stability of the supercapacitor device was evaluated in order to show its capability to continuously deliver energy throughout many charge/discharge cycles (Fig. 6B). Over 4000 cycles at the current density of 2 A g−1, the device with the CNF/rGO electrodes retains about 97%, while the device containing the pure CNF electrodes would retain up to 106% of initial capacitance. The latter result is most probably related to etching, i.e. activation of the CNF electrodes at the initial part of the cycling.12 Overall, both devices demonstrated excellent capacitance retention. SEM images recorded after cycling of the composite electrodes confirm their great electrochemical stability of the pure CNFs and their robust combination with the interpenetrating rGO sheets (Fig. S3†).
Conclusions
This study presents a sustainable and efficient CNF/rGO composite electrode material. First, the original synthesis method utilizes the intrinsic hydrophilic properties of cellulose and GO to attach them together and form a composite precursor. In the next step, the simultaneous abilities of cellulose and GO to carbonize and to reduce to rGO, respectively, during high temperature treatment are used to obtain the final composite material. In this material, CNFs act as nanospacers in the interpenetrated CNF/rGO network, which enhances the supercapacitor's excellent volumetric electrochemical performance. Sustainable cellulose-derived constituent makes a great ensemble with value-added graphene material. Most probably, further tuning of composite electrode materials based on biomass-derived nanocarbons and valuable additives is the future of cost-effective large-scale production of energy storage devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Wallenberg Wood Science Center funded by Knut and Alice Wallenberg Foundation, Horizon 2020 SmartMEMPHIS projects (No. 644378) and the Production Area of Advance program, Chalmers University of Technology, Sweden, are greatly acknowledged for their financial support. We also thank Anne Wendel, Anders Mårtensson and Alec Anderson for their help with the XPS and AFM analysis.References
- Q. Liu, J. Yang, R. Wang, H. Wang and S. Ji, Manganese dioxide core–shell nanostructure to achieve excellent cycling stability for asymmetric supercapacitor applications, RSC Adv., 2017, 7, 33635–33641 RSC.
- Q. Zhou, X. Ye, Z. Wan and C. Jia, A three-dimensional flexible supercapacitor with enhanced performance based on lightweight, conductive graphene-cotton fabric electrode, J. Power Sources, 2015, 296, 186–196 CrossRef CAS.
- T. Hibino, K. Kobayashi, M. Nagao and S. Kawasaki, High-temperature supercapacitor with a proton-conducting metal pyrophosphate electrolyte, Sci. Rep., 2015, 5, 7903 CrossRef CAS PubMed.
- K. Jost, D. Stenger, C. R. Perez, J. K. McDonough, K. Lian, Y. Gogotsi and G. Dion, Knitted and screen printed carbon-fiber supercapacitors for applications in wearable electronics, Energy Environ. Sci., 2013, 6, 2698–2705 CAS.
- L. Bao and X. Li, Towards textile energy storage from cotton t-shirts, Adv. Mater., 2012, 24, 3246–3252 CrossRef CAS PubMed.
- A. Lahyani, P. Venet, A. Guermazi and A. Troudi, Battery/supercapacitors combination in uninterruptible power supply (UPS), IEEE Trans. Power Electron., 2013, 28, 1509–1522 CrossRef.
- L. G. H. Staaf, P. Lundgren and P. Enoksson, Present and future supercapacitor carbon electrode materials for improved energy storage used in intelligent wireless sensor systems, Nano Energy, 2014, 9, 128–141 CrossRef CAS.
- R. Kühne, Electric buses – an energy efficient urban transportation means, Energy, 2010, 35, 4510–4513 CrossRef.
- R. J. Miller and P. Simon, Electrochemical capacitors for energy management, Science, 2008, 321, 651–652 CrossRef PubMed.
- D. Pavković, M. Hoić, J. Deur and J. Petrić, Energy storage systems sizing study for a high-altitude wind energy application, Energy, 2014, 76, 91–103 CrossRef.
- L. Yuan, X. Xiao, T. Ding, J. Zhong, X. Zhang, Y. Shen, B. Hu, Y. Huang, J. Zhou and Z. L. Wang, Paper-based supercapacitors for self-powered nanosystems, Angew. Chem., Int. Ed., 2012, 51, 4934–4938 CrossRef CAS PubMed.
- Z. Wang, P. Tammela, P. Zhang, M. Strømme and L. Nyholm, High areal and volumetric capacity sustainable all-polymer paper-based supercapacitors, J. Mater. Chem. A, 2014, 2, 16761–16769 CAS.
- P. Simon and Y. Gogotsi, Materials for electrochemical capacitors, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Carbons and electrolytes for advanced supercapacitors, Adv. Mater., 2014, 26, 2219–2251 CrossRef PubMed.
- L. L. Zhang and X. S. Zhao, Carbon-based materials as supercapacitor electrodes, Chem. Soc. Rev., 2009, 38, 2520–2531 RSC.
- V. Kuzmenko, O. Naboka, P. Gatenholm and P. Enoksson, Ammonium chloride promoted synthesis of carbon nanofibers from electrospun cellulose acetate, Carbon, 2014, 67, 694–703 CrossRef CAS.
- S. Hu and Y.-L. Hsieh, Lignin derived activated carbon particulates as an electric supercapacitor: carbonization and activation on porous structures and microstructures, RSC Adv., 2017, 7, 30459–30468 RSC.
- Y. Li, Z. Li and P. K. Shen, Simultaneous formation of ultrahigh surface area and three-dimensional hierarchical porous graphene-like networks for fast and highly stable supercapacitors, Adv. Mater., 2013, 25, 2474–2480 CrossRef CAS PubMed.
- M. Ghidiu, M. R. Lukatskaya, M. Q. Zhao, Y. Gogotsi and M. W. Barsoum, Conductive two-dimensional titanium carbide ‘clay’ with high volumetric capacitance, Nature, 2014, 516, 78–81 CAS.
- V. Kuzmenko, O. Naboka, M. Haque, H. Staaf, G. Göransson, P. Gatenholm and P. Enoksson, Sustainable carbon nanofibers/nanotubes composites from cellulose as electrodes for supercapacitors, Energy, 2015, 90, 1490–1496 CrossRef CAS.
- Z. Niu, L. Liu, L. Zhang, W. Zhou, X. Chen and S. Xie, Programmable nanocarbon-based architectures for flexible supercapacitors, Adv. Energy Mater., 2015, 5, 1500677 CrossRef.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. S. Novoselov, V. I. Fal′ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, A roadmap for graphene, Nature, 2012, 490, 192–200 CrossRef CAS PubMed.
- C. Hu, L. Song, Z. Zhang, N. Chen, Z. Feng and L. Qu, Tailored graphene systems for unconventional applications in energy conversion and storage devices, Energy Environ. Sci., 2015, 8, 31–54 CAS.
- F. Bonaccorso, L. Colombo, G. Yu, M. Stoller, V. Tozzini, A. C. Ferrari, R. S. Ruoff and V. Pellegrini, Graphene, related two-dimensional crystals, and hybrid systems for energy conversion and storage, Science, 2015, 347, 1246501–1246509 CrossRef PubMed.
- A. Peigney, C. Laurent, E. Flahaut, R. R. Bacsa and A. Rousset, Specific surface area of carbon nanotubes and bundles of carbon nanotubes, Carbon, 2001, 39, 507–514 CrossRef CAS.
- J. Huang, J. Wang, C. Wang, H. Zhang, C. Lu and J. Wang, Hierarchical porous graphene carbon-based supercapacitors, Chem. Mater., 2015, 27, 2107–2113 CrossRef CAS.
- Y. Huang, J. Liang and Y. Chen, An overview of the applications of graphene-based materials in supercapacitors, Small, 2012, 8, 1805–1834 CrossRef CAS PubMed.
- Y. Wang, Y. Wu, Y. Huang, F. Zhang, X. Yang, Y. Ma and Y. Chen, Preventing graphene sheets from restacking for high-capacitance performance, J. Phys. Chem. C, 2011, 115, 23192–23197 CAS.
- S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Graphene-based composite materials, Nature, 2006, 442, 282–286 CrossRef CAS PubMed.
- X. Cao, Z. Yin and H. Zhang, Three-dimensional graphene materials: preparation, structures and application in supercapacitors, Energy Environ. Sci., 2014, 7, 1850–1865 CAS.
- K. Gao, Z. Shao, J. Li, X. Wang, X. Peng, W. Wang and F. Wang, Cellulose nanofiber–graphene all solid-state flexible supercapacitors, J. Mater. Chem. A, 2013, 1, 63–67 CAS.
- V. Kuzmenko, O. Naboka, H. Staaf, M. Haque, G. Göransson, P. Lundgren, P. Gatenholm and P. Enoksson, Capacitive effects of nitrogen doping on cellulose-derived carbon nanofibers, Mater. Chem. Phys., 2015, 160, 59–65 CrossRef CAS.
- W. K. Chee, H. N. Lim, Z. Zainal, I. Harrison, N. M. Huang, Y. Andou, K. F. Chong and A. Pandikumar, Electrospun nanofiber membranes as ultrathin flexible supercapacitors, RSC Adv., 2017, 7, 12033–12040 RSC.
- Q. Zheng, Z. Cai, Z. Ma and S. Gong, Cellulose nanofibril/reduced graphene oxide/carbon nanotube hybrid aerogels for highly flexible and all-solid-state supercapacitors, ACS Appl. Mater. Interfaces, 2015, 7, 3263–3271 CAS.
- Z. Li, J. Liu, K. Jiang and T. Thundat, Carbonized nanocellulose sustainably boosts the performance of activated carbon in ionic liquid supercapacitors, Nano Energy, 2016, 25, 161–169 CrossRef.
- J. Zhang, Y. Cao, J. Feng and P. Wu, Graphene-oxide-sheet-induced gelation of cellulose and promoted mechanical properties of composite aerogels, J. Phys. Chem. C, 2012, 116, 8063–8068 CAS.
- Q. Du, M. Zheng, L. Zhang, Y. Wang, J. Chen, L. Xue, W. Dai, G. Ji and J. Cao, Preparation of functionalized graphene sheets by a low-temperature thermal exfoliation approach and their electrochemical supercapacitive behaviors, Electrochim. Acta, 2010, 55, 3897–3903 CrossRef CAS.
- V. Presser, L. Zhang, J. J. Niu, J. McDonough, C. Perez, H. Fong and Y. Gogotsi, Flexible nano-felts of carbide-derived carbon with ultra-high power handling capability, Adv. Energy Mater., 2011, 1, 423–430 CrossRef CAS.
- S. He and W. Chen, 3D graphene nanomaterials for binder-free supercapacitors: scientific design for enhanced performance, Nanoscale, 2015, 7, 6957–6990 RSC.
- D. Larcher and J.-M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, The role of graphene for electrochemical energy storage, Nat. Mater., 2015, 14, 271–279 CrossRef CAS PubMed.
- M.-M. Titirici, R. J. White, N. Brun, V. L. Budarin, D. S. Su, F. del Monte, J. H. Clark and M. J. MacLachlan, Sustainable carbon materials, Chem. Soc. Rev., 2015, 44, 250–290 RSC.
- UNFCCC, Adoption of the Paris Agreement, FCCC/CP/2015/L.9/Rev.1, 12 Dec 2015 Search PubMed.
- P. Morgan, Carbon fibers and their composites, Taylor & Francis Group, Boca Raton, FL, 2005 Search PubMed.
- T. Rath and P. P. Kundu, Reduced graphene oxide paper based nanocomposite materials for flexible supercapacitors, RSC Adv., 2015, 5, 26666–26674 RSC.
- S. Zhang, Y. Yan, Y. Huo, Y. Yang, J. Feng and Y. Chen, Electrochemically reduced graphene oxide and its capacitance performance, Mater. Chem. Phys., 2014, 148, 903–908 CrossRef CAS.
- F. J. Kilzer and A. Broido, Speculations on the nature of cellulose pyrolysis, Pyrodynamics, 1965, 2, 151–163 CAS.
- W. Ouyang, J. Sun, J. Memon, C. Wang, J. Geng and Y. Huang, Scalable preparation of three-dimensional porous structures of reduced graphene oxide/cellulose composites and their application in supercapacitors, Carbon, 2013, 62, 501–509 CrossRef CAS.
- L. Jiang, G. W. Nelson, S. O. Han, H. Kim, I. N. Sim and J. S. Foord, Natural cellulose materials for supercapacitors, Electrochim. Acta, 2016, 192, 251–258 CrossRef CAS.
- A. L. Higginbotham, J. R. Lomeda, A. B. Morgan and J. M. Tour, Graphite oxide flame-retardant polymer nanocomposites, ACS Appl. Mater. Interfaces, 2009, 1, 2256–2261 CAS.
- A. G. Pandolfo and A. F. Hollenkamp, Carbon properties and their role in supercapacitors, J. Power Sources, 2006, 157, 11–27 CrossRef CAS.
- Y. R. Rhim, D. Zhang, D. H. F. airbrother, K. A. Wepasnick, K. J. Livi and R. J. Bodnar, Changes in electrical and microstructural properties of microcristalline cellulose as function of carbonization temperature, Carbon, 2010, 48, 1012–1024 CrossRef CAS.
- L. S. Johansson and J. M. Campbell, Reproducible XPS on biopolymers: cellulose studies, Surf. Interface Anal., 2004, 36, 1018–1022 CrossRef CAS.
- S. Y. Oh, D. I. Yoo, Y. Shin, H. C. Kim, H. Y. Kim, Y. S. Chung, W. H. Park and J. H. Youk, Crystalline structure analysis of cellulose treated with sodium hydroxide and carbon dioxide by means of x-ray diffraction and FTIR spectroscopy, Carbohydr. Res., 2005, 340, 2376–2391 CrossRef CAS PubMed.
- F. Tuinstra and J. L. Koenig, Raman spectrum of graphite, J. Chem. Phys., 1970, 53, 1126–1130 CrossRef CAS.
- M. D. Stoller, S. Park, Y. Zhu, J. An and R. S. Ruoff, Graphene-based ultracapacitors, Nano Lett., 2008, 8, 3498–3502 CrossRef CAS PubMed.
- Y. Gogotsi and P. Simon, True performance metrics in electrochemical energy storage, Science, 2011, 334, 917–918 CrossRef CAS PubMed.
- S. Ban, X. Jing, H. Zhou, L. Zhang and J. Zhang, Experimental and modeling study on charge storage/transfer mechanism of graphene-based supercapacitors, J. Power Sources, 2014, 268, 604–609 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07533b |
| This journal is © The Royal Society of Chemistry 2017 |