Model creation and electronic structure calculation of amorphous hydrogenated boron carbide: a classical/ab initio hybrid approach

Abstract

Amorphous hydrogenated boron carbide (a-BC:H), grown by plasma enhanced chemical vapor deposition of orthocarborane precursors, is an amorphous molecular solid with strong short range order, no long range order, and unknown medium range order. Determination of the structure of a-BC:H is an essential prerequisite for obtaining predictive control over its fabrication. The aim of this work is to establish an approach for modeling molecular amorphous solids, as well as to create and analyze geometry optimized models of a-BC:H that are consistent with experimental data from the literature. The modeling process combines classical molecular dynamics and ab initio electronic structure methods. Further, general trends were established between the composition and electronic structure properties. The total density of states shows semi-metal behavior with an approach toward semi-conducting behavior with reduced H content. A similar but weaker trend was apparent for B content. Also, the percent contents of both hydrogen and boron were found to be inversely proportional to the dielectric constant. These electronic structure results are in line with other experimental results reported in the literature. The proposed modeling method was found to be suitable and effective for a-BC:H and its applicability to other members of this family of solids is also expected.

---

Introduction

Boron-rich carbides (B_xC) are most commonly known for their high hardness, low density, extreme abrasion resistance, high melting point, and thermal stability, all of which contribute to remarkable performances such as in refractory applications, ballistic armors, as cutting tools, as an abrasive powder, and in coatings.^1–6 Depending on the growth process, they can also exhibit a wide range of chemical and electrical properties, opening up the door to another array of potential applications. For example, thin-film amorphous hydrogenated boron carbide (a-BC:H) grown via plasma-enhanced chemical vapor deposition (PECVD)^7–10 has shown promise as a low-κ dielectric material for ultra-large scale integrated circuit design¹¹ and for direct conversion solid-state neutron detection^12–16 because (upon doping) it is a p-type semiconductor with a high neutron absorption cross section.

Despite the significance of B_xC materials for applications, the relationship between fabrication parameters and the resultant atomic structure is often not well understood, particularly for the non-crystalline varieties. Consequently, very few atomic-scale theoretical studies for this family of disordered solids exist in the literature. In this paper we present a modeling effort that combines classical molecular dynamics and ab initio electronic structure methods to create and analyze geometry optimized models of a-BC:H. The combined classical and ab initio approach is necessary at the present time for two key reasons. First, there are no known classical potentials available for B, C, and H in the icosahedral configurations present. Therefore, some degree of ab initio correction must be applied to—at least—any final structure obtained using approximate classical methods. Second, because a-BC:H has large icosahedral building blocks and it is disordered, a fairly large simulation cell must be used to mitigate any impact of periodicity. Consequently, the number of atoms and the necessary duration of the simulation extends well beyond that which is possible to compute with ab initio methods in a reasonable time period with typical high-performance computing equipment.

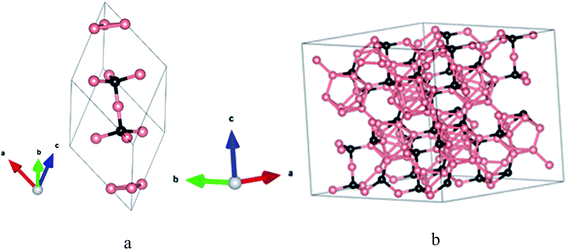
The structures of crystalline elemental boron and boron-carbide offer fundamental guidance regarding the structure of a-BC:H (rigorously represented as a-B_xC:H_y). Elemental boron crystallizes in rhombohedral, tetragonal, or cubic forms depending on the temperature and pressure.¹⁷ For all of these systems, an icosahedron serves as a key structural subunit. For the crystal systems, the constituent atoms are found in a variety of bonding configurations that sometimes include vertex, edge, or face sharing icosahedral structures. In many cases, interstitial boron atoms are present. The range of variation is incredibly diverse. The addition of carbon naturally complicates the matter. Crystalline B_xC tends to crystallize within a network of icosahedral fragments mirroring the structure of α-rhombohedral boron.^6,18,19 The icosahedra are bonded to each other through traditional two-center two-electron covalent bonds at six so-called polar sites. At the same time, the other six boron atoms (at so-called equatorial sites) are bonded to a three-atom chain that runs through the body diagonal.^1,20 A primitive-cell model of B_xC is shown in Fig. 1a.

Fig. 1 (a) B₄C rhombohedral primitive cell; (b) B₄C supercell. With boron pink and carbon black.

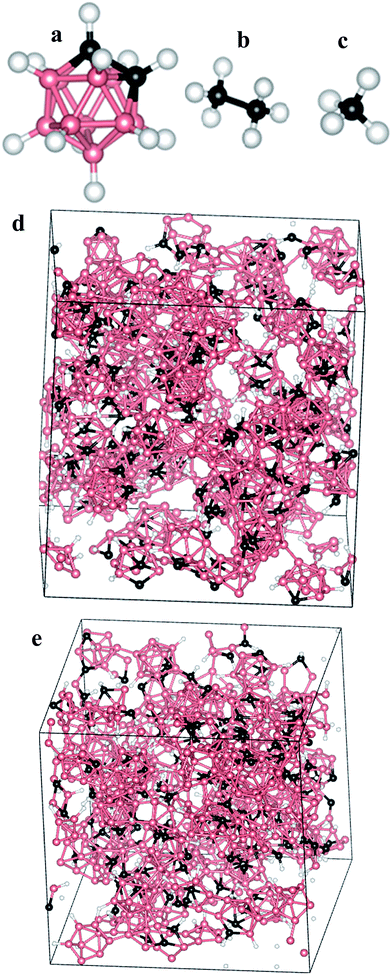
For amorphous boron carbide, the structure is far more complicated and is dependent on the growth method as well as the precursor used.^21,22 Herein, our focus is on modeling the atomic structure of a-BC:H thin-films grown by the PECVD method from orthocarborane (1,2-B₁₀C₂H₁₂) precursor molecules (Fig. 2a).²³ As a consequence of starting from molecular precursors and using a relatively low temperature growth process, the resultant icosahedra-based amorphous thin-films have been found to generally adhere to a set of structural guidelines obtained by using magic angle spinning solid-state NMR spectroscopy (SSNMR).²³ The PECVD grown a-BC:H is expected to have two intraicosahedral carbon atoms per icosahedron, as opposed to just one or none in the case of crystalline B_xC. Furthermore, because the precursor contains H, the inter-icosahedral bonding is primarily covalent in nature and not of the 2-electron 3-center variety that is found in many other crystalline boron-rich solids.²⁴ The variable H content^9,25 will strongly influence the overall density and number of inter-icosahedral bonds by controlling access to the electronically active boron sites.²⁶ Additionally, it was observed that extra-icosahedral hydrocarbon species were formed during the growth process and that these tended to bond with open boron sites permitting cross-links between icosahedra or simply acting as appendages. In either case, the hydrocarbon species would form 5 and 6 member coordinations with the icosahedral boron. One should expect that this difference of structure would lead to dramatically different properties compared to the crystalline B_xC. The variable degree to which each of the above features manifest themselves according to the parameters of the growth process potentially allows for fine-tuning of the ultimate material properties.

Fig. 2 Molecular structure of the initial molecules. (a) B₁₀C₂H₁₂; (b) CH₃CH₃; (c) CH₄; (d) structure of a sample model (d1.7–H23.5–B/C4.8) produced by LAMMPS; (e) structure of the same sample model (d1.7–H23.5–B/C4.8) after VASP relaxation. In all cases: boron: pink, carbon: black, hydrogen: white.

In the next section we introduce the modelling method that we employed along with the methods that we used to subsequently compute and analyze the electronic structure of the models. We then provide results and discussion of the modeling and electronic structure computations. At the end of the paper we summarize our work and draw conclusions that may be used for the development of future efforts.

Methods

Because of the lack of periodicity in amorphous materials, a large simulation box is required to minimize spurious long-range order effects that are introduced by periodic boundary conditions. Another challenge is that the box must also be large enough to allow for statistical sampling of the large number of possible short-range structural variations of the elementary units. In the case of a-BC:H—being a molecular-based amorphous solid rather than a relatively simpler atomic-based amorphous solid—the number of atoms per elementary unit is about twenty compared to the one or two atoms per elementary unit found in more well-studied amorphous solids (e.g. a-C, a-SiO₂, etc.). Therefore, sampling diverse configurations requires a large number of atoms. Compounding the challenge for a-BC:H is the fact that classical potentials are not well-developed for the unusual bonding pattern in the icosahedra, which includes 5- and 6-coordinated B and C atoms.

PECVD-grown samples of a-BC:H^23,27 have demonstrated differences in three key parameters: density, the percentage of H content, and the B/C ratio. Therefore, the same three parameters were systematically varied so as to span a range of densities (g cm⁻³), boron to carbon ratios, and percent hydrogen content to create a series of simulated models. Other growth parameters such as temperature, pressure, etc. were not considered at this time.

Hither, we created a-BC:H models by employing a hybrid method that consisted of classical molecular dynamic (MD) represented by LAMMPS²⁸ and ab initio force relaxation represented by the Vienna ab initio simulation package (VASP).²⁹ We then used the Oorthogonalized linear combination of atomic orbitals (OLCAO)³⁰ method to calculate the electronic structure properties. Each program and the rationale for using it is described subsequently.

LAMMPS

LAMMPS was used to perform a gas phase MD simulation starting from three molecular species (CH₄, CH₃CH₃, B₁₀C₂H₁₂) (Fig. 2a–c) where the number of each species was selected to follow published B/C ratios.²⁷ The outline of the gas phase MD simulation consists of (1) populating a large simulation box with widely distributed molecular precursors designed to satisfy desired B/C ratio; and (2) shrinking the box containing said molecular species to a desired volume, and thus density, dictated by published experimental work.²⁷ During the condensation step we (1) demanded that all B–B, B–C, and C–C bonds remain intact to enforce retention of the molecular species; (2) allowed B–H and C–H bonds to be destroyed allowing molecular precursors to lose H as H₂; (3) allowed exposed B and C atoms to bond with other exposed B and C atoms from other icosahedra or hydrocarbons; and (4) when close to the desired density we cyclically removed free H from the simulation, re-populated dehydrogenated B and C, and allowed the cell size to change until we reached the desired final density. The process of removing free H and repopulating dehydrogenated B or C with H atoms to reach the desired hydrogen content was performed in an iterative cycle.

Solely relying on the explicit interatomic analytic potential forms that are available in LAMMPS cannot ensure that the molecular precursors will retain their structure. Thus, the above approach forces retention of the molecular structures—except for hydrogenation/dehydrogenation processes—but it still allows for inter-molecular bond formation and destruction to occur. During the condensation process, the long-range forces were not the dominant driver of inter-molecular attraction. Instead, the volume-reduction of the simulation cell was used to slowly bring molecular units together. As a result, the non-bonded interatomic potential was mostly irrelevant and could be modeled as a simple Lennard-Jones potential with ε and σ values of (0.066, 3.5), (0.03, 2.5), and (0.066, 3.5) for B bonds, H bonds, and C bonds respectively. With respect to the bonded interatomic potential, the bond coefficients were (5000, 1.7) for B–B; (5000, 1.1) for B,C–H; (5000, 1.6) for B–C; (5000, 1.5) for C–C; and (5000, 0.74) for H–H while the angle coefficients were (500, 60) for all icosahedral C and B bonds; (500, 120) for all icosahedral H bonds, and (500, 109.5) for all external C–H hydrocarbon bonds. The dominant factor in the formation of linkages and the overall network structure was controlled by the introduction of custom modifications to the LAMMPS bond-break/bond-create fix. We introduced code to enforce molecular cohesion with specific bonded-atom rules while allowing for the dynamic creation and destruction of B–B, C–H, B–H, and H–H bonds. The syntax of the modified fixes are shown in the ESI,† with the parameter meanings given in ESI Table 1.†

At the end of the LAMMPS condensation step, the resulting box has the desired solid density, desired H content, and desired B/C ratio. At this point it is important to emphasize that the modeling process described above is not intended to accurately replicate the actual growth process of the a-BC:H thin-films. That process is substantially more complicated because it occurs within an Ar plasma and over time-scales that extend far beyond the capacity of even highly parallelized classical MD methods. The intent of the above modeling process is to introduce an artificial sequence that is still capable of producing a physically sound model of the actual material which could subsequently guide further fabrication processes. Indeed, as will be described below, that mission was largely accomplished, although, as will also be pointed out, there is certainly room for improvement. Fig. 2d shows the structure of a sample model after the full condensation workflow.

VASP

After the classical MD condensation, we used VASP to perform a geometry optimization of the atoms within the final structure to bring the models into their locally lowest energy configuration. The cell shape and volume were kept fixed during the relaxations to maintain the densities of the models. The models were relaxed with high accuracy and a relatively high cut off energy starting at 300 eV for initial relaxations and going up to 700 eV at the final stages. The projector augmented wave method with the Perdew–Burke–Ernzerhof (PAW-PBE)^31,32 pseudopotentials was used. The electronic and ionic convergence criteria was set to 10⁻⁵ eV and 10⁻³ eV Å⁻¹ respectively. Because the models were fairly large (820–1279 atoms) we used only the Γ k-point for Brillouin-zone integration.

OLCAO

The electronic structures of the fully relaxed models were then computed using the OLCAO method specifically to enable easy decomposition of the total density of states (TDOS) into partial (PDOS) components and also because of the accuracy that can be obtained for the higher energy electronic states that are required for computation of the dielectric function. Details regarding the general nature of calculations that may be performed with the OLCAO method are provided in the published literature.³⁰ Specifics associated with the present calculations are as follows: the calculation used the local density approximation (LDA) for the exchange-correlation term via the Wigner interpolation formula. One Γ k-point was used for Brillouin zone integration, a full basis-set was used which included all occupied orbitals plus one further shell of unoccupied orbitals for each element for the DOS calculations, and an extended basis-set with an additional shell of unoccupied orbitals beyond the full basis was used for the optical properties calculation.

We have categorized the selection of our models into seven groups—representing seven different compositions—with three models constructed for each composition. The three models of each composition were compared with each other to test the accountability of our methodology and they were found to be quite consistent. That is, very similar models were generated when starting with the same number of molecules (i.e. B/C ratio) as long as the end-goal parameters (H%, density) were the same. Therefore, we believe that the condensation method is effectively deterministic and reliably reproducible. In total, twenty one models were constructed, however, only seven models (one from each group) were considered for VASP relaxation of the ionic positions (because of the expense of performing many ab initio calculations). Note that, due to the computational expense that would be associated with iterative full-cell relaxation, the ultimate pressures were not computed. We anticipate that some residual stresses must remain in the system but that they will not be significant for the calculation because of the considerable attention that was given to the gentle assembly icosahedral sub-units. Future efforts will be needed to quantify that issue. For convenience, the models will be named henceforth in the following pattern dx–Hy–B/Cz, where x is the density in (g cm⁻³), y is the percentage of H content, and z is the ratio of boron to carbon (number of atoms). Table 1 shows a list of the constructed models with their corresponding parameters (values are rounded to the first decimal place). Fig. 2e shows the structure of a sample model (d1.7–H23.2–B/C4.8) after the VASP relaxation.

Table 1 List of the constructed models with their corresponding parameters

Model number	%H	d (g cm^−3)	B/C	Total number of atoms	Model name
1	11	2.3	4.6	820	d2.3–H11–B/C4.6
2	13.1	1.7	4.8	975	d1.7–H13.1–B/C4.8
3	18.5	1.7	4.8	1039	d1.7–H18.5–B/C4.8
4	16	2.1	4.5	873	d2.1–H16–B/C4.5
5	23.2	1.7	4.8	1103	d1.7–H23.2–B/C4.8
6	29	1.7	4.9	1187	d1.7–H29–B/C4.9
7	33.8	1.7	4.8	1279	d1.7–H33.8–B/C4.8

---

Results and discussion

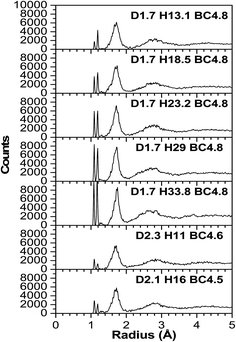
As expected, most of the icosahedra underwent a slight to modest structural distortion during the VASP relaxation because of the influence of other nearby molecules. A few other icosahedra experienced more severe distortion and they lost their icosahedral shape indicating that the influence of neighboring molecules can be significant. Fig. 3–6 illustrate the calculated radial pair distribution function (RPDF), the TDOS, the PDOS, and the complex dielectric function (ε) combined with the energy loss function (ELF).

Fig. 3 The calculated radial pair distribution function (RPDF) of a-BC:H.

Any simulations of amorphous materials at the atomic level should clearly indicate that the models are not affected by periodic boundary conditions. From the RPDFs (Fig. 3), the models clearly correspond to that of an amorphous solid because they are characterized by broad peaks—as opposed to the sharp peaks for a crystalline solid. Also, the RPDFs approach a constant value at 5 Å, indicative of non-periodicity. However, certain aspects of short range order are maintained and expressed by two sharp peaks at 1.1 and 1.2 angstroms (Å) corresponding to the H–C and H–B bonds. The peaks are expected because the material is known to have a strong short range order from the icosahedra. Following that, a third wider and less sharp peak ranges from 1.5 to 1.9 (Å), which is typical for the bond lengths of various boron and carbon neighboring pairs (inter- and intra-icosahedral). Another even smaller and wider peak at 2.2–3.4 (Å) is associated with the second and third (two atoms at the farthest opposite side from each other on a single icosahedron) neighboring atoms. In a perfectly shaped icosahedron with an edge length (a), the distance to the second neighboring atoms is 1.6 × (a), and to the third neighboring atoms is 1.9 × (a), but given that our icosahedra contain two different elements (B and C), it is expected that they are not perfectly shaped since there exist three different bond lengths that correspond to the different B–B, B–C and C–C bonds (represent the icosahedra edges), these distances can be easily calculated by summing up the two covalent radii of the two atoms participating in the bond which gives an edge length (a) varying from 1.38–1.74 (Å), so the distances to the second neighboring atoms ranges from 2.208–2.708 (Å) (multiplying by 1.6). The farthest distance between two atoms in an icosahedron, which is geometrically calculated as 1.9 × (a), with (a) ranges between 1.38 and 1.74 (Å) is a distance of 2.622–3.306 (Å). It can be concluded that the models are largely reasonable and in agreement with the experiment in terms of being amorphous and in terms of being constructed from molecular subunits that are bonded to each other directly and via hydrocarbon linkers. In that sense, the atoms are realistically distributed, and even with the wide range of the atomic densities (not the volumetric mass density) in the models, the RPDF peaks appear at consistent distances which indicate the homogeneity of the models.

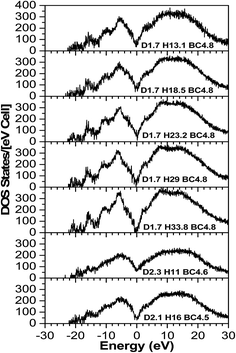
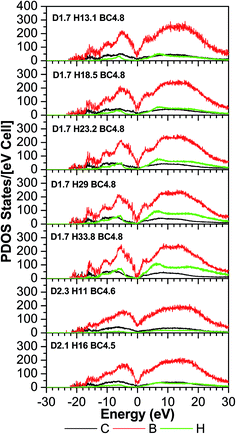
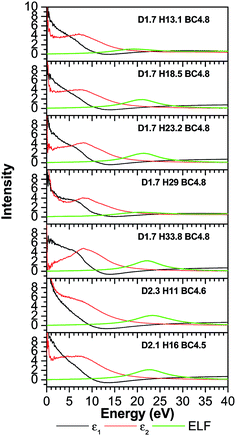
The TDOS (Fig. 4) also corresponds to that of an amorphous solid and—except around zero energy—the overall patterns of the TDOS graphs are similar for all different compositions. For the models where the density and the B/C ratio is fixed (1.7 g cm⁻³ and 4.8 respectively), the correlation between the hydrogen content and the tendency toward a reduced value of the TDOS at the Fermi energy is apparent. As more hydrogen is present in the structure the number of available states at the Fermi energy decreases. This can be explained with the fact that the H is an s-block element—its outermost valence electron is in an s-orbital—while the B and C are p-block—the outermost valence electrons are in a p-orbital—elements and they form sp hybridized molecular orbitals. The energy of a subshell 2p (the case for B and C) is ∼20–30% larger than that of a subshell 1s (the case for H), so the resulting hybridized orbitals are lower in energy compared to when separated. In case of less H content, the dominant bonds are from the B and C, since they are both p-block, the linear atomic orbital combination is an overlap of two subshells with very close energies and the resultant molecular orbital has relatively higher energy. This analogy is consistent with the experimental studies by Nordell et al.²⁷ for films of the same compositions as those studied here. For the models with higher densities (2.1 and 2.3 g cm⁻³), the hydrogen content is very small (16% and 11%). It was experimentally seen that the density is inversely proportional to the H content,²⁷ and the density of states at the Fermi level for the higher density models is higher than that of the one with a comparable H content but more B content (d1.7–H13.1–B/C4.8). Thus, the high density of states around zero energy can be attributed to the relatively small B content. It can be concluded that the compositions at the boron-rich end have an increased likelihood of developing a band gap. This is supported by the partial density of states (PDOS) of the models in Fig. 5. It is apparent that the portion of both the valence and conduction bands near the Fermi energy are dominated by B, and that the H contribution is lesser, even for models with a considerable amount of H content. The dielectric function ε (Fig. 6) is also typical for that of a metalloid for the first few eVs, particularly, the imaginary part (ε₂), which represents the absorption. Its characteristic energy onset of ∼2–4 eV reasonably corresponds to that of a semiconductor. The dielectric constant is seen to be inversely proportional with the H and B content.

Fig. 4 The calculated total density of state (TDOS) of a-BC:H.

Fig. 5 The calculated partial density of state (PDOS) of a-BC:H.

Fig. 6 The calculated dielectric function ε and energy loss function (ELF) of a-BC:H.

Published experimental studies shows that amorphous hydrogenated boron carbide thin-films exhibit a p-type semiconducting behavior.²⁷ However, direct interpretation of our calculations suggest a metalloid or semi-metallic behavior, except for the model d1.7–H33.77–B/C4.8 where it shows a gap between the dominant portions of the valence and conduction bands of ∼0.5 eV, but it is polluted with many gap states such that it is not possible to clearly identify a semi-conducting electronic structure. This semi-metallic behavior is expressed by the overlap between the valence and conduction bands in the TDOS (the E_f in semiconductor lies in a band gap, while in metals the E_f lies in the middle of the conduction band) calculations (Fig. 4), and a non-zero imaginary part ε₂ (absence of an optical bandgap) of the dielectric function (Fig. 6) signifies absorption throughout the whole range of the spectrum. However, this quantitative difference in our calculation is limited to the bandgap. The reasons for this disagreement between the experimental and theoretical results is that the theoretical studies often fail to demonstrate the semiconducting behavior of icosahedra containing boron-rich solids in both crystalline and amorphous form^33–36 because they consider an idealized structure, whereas the real structure contains defects (although our system is amorphous, structural defects such as vacancies and antisites may still exist because they are driven by the valence electron deficiency in the icosahedra). Another reason for this discrepancy is that the OLCAO method is a LDA-DFT based method, and it is a fact that LDA-DFT tend to underestimate the band gap by ∼50%.³⁷ It will give a semi quantitative agreement with experimental results in the case of insulators and semiconductors, but in some cases (e.g. transition metal oxides) it can falsely predict a metal.

Conclusions

We have created a series of models of a-BC:H using a hybrid classical MD and ab initio force relaxation method and then studied their electronic structures. The models had various stoichiometries and special attention was paid to the effect of the hydrogen content. We calculated the total density of state (TDOS) and its partial components (PDOS), the complex dielectric function ε, and the radial pair distribution function (RPDF) for these models. While the models we have created do not fully express the peculiarities of the system such as the structural defects—caused by the electron deficiency, or the existence of different compositions of the icosahedra, B₁₂, B₁₁C, or B₁₀C₂—which are found to be the driving force for the experimentally proven semiconducting behavior of icosahedra containing B_xC, they do deliver a considerable amount of information. The correlation of the composition of the material to its electronic properties has been established. The general trend for the semi-metal character toward semi-conducting character has doubtlessly been confirmed. It was found that the H and B contents are inversely proportional to both the number of the electronic states available around the Fermi energy level, as well as the dielectric constant of the material. The above results are in agreement with the experimental results²⁷ to a large extent. Our modeling methodology was also proven dependable, and it can be generalized to model molecular-based amorphous solids (e.g., polymer derived pre-ceramics).

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562.

References

1. D. Vladislav, R. Sara, A. Haber Richard and M. Chhowalla, Boron Carbide: Structure, Properties, and Stability under Stress, J. Am. Ceram. Soc., 2011, 94(11), 3605–3628.
2. F. Gan, Structure and properties of amorphous thin film for optical data storage, J. Non-Cryst. Solids, 2008, 354(12–13), 1089–1099.
3. T. Hu, L. Steihl, W. Rafaniello, T. Fawcett, D. D. Hawn and J. G. Mashall, et al., Structures and properties of disordered boron carbide coatings generated by magnetron sputtering, Thin Solid Films, 1998, 332(1–2), 80–86.
4. K. Shirai, Electronic structures and mechanical properties of boron and boron-rich crystals (Part I), J. Superhard Mater., 2010, 32(3), 205–225.
5. K. Shirai, Electronic structures and mechanical properties of boron and boron-rich crystals (Part 2), J. Superhard Mater., 2010, 32(5), 336–345.
6. N. Vast, J. Sjakste and E. Betranhandy, Boron carbides from first principles, J. Phys.: Conf. Ser., 2009, 176(1), 012002.
7. D. Byun, B. R. Spady, N. J. Ianno and P. A. Dowben, Comparison of different chemical vapor deposition methodologies for the fabrication of heterojunction boron-carbide diodes, Nanostruct. Mater., 1995, 5(4), 465–471.
8. S.-D. Hwang, K. Yang, P. A. Dowben, A. A. Ahmad, N. J. Ianno and J. Z. Li, et al., Fabrication of n-type nickel doped B5C1+δ homojunction and heterojunction diodes, Appl. Phys. Lett., 1997, 70(8), 1028–1030.
9. D. L. Schulz, A. Lutfurakhmanov, B. Mayo, J. Sandstrom, D. Bunzow and S. B. Qadri, et al., Characterization of a-B5C:H prepared by PECVD of orthocarborane: results of preliminary FTIR and nuclear reaction analysis studies, J. Non-Cryst. Solids, 2008, 354(19–25), 2369–2371.
10. V. K. Alimov, D. B. Bogomolov, M. N. Churaeva, A. E. Gorodetsky, S. L. Kanashenko and A. I. Kanaev, et al., Characterization of a-B/C:H films deposited from different boron containing precursors, J. Nucl. Mater., 1992, 196–198, 670–675.
11. S. W. King, Dielectric Barrier, Etch Stop, and Metal Capping Materials for State of the Art and beyond Metal Interconnects, ECS J. Solid State Sci. Technol., 2015, 4(1), N3029–N3047.
12. B. W. Robertson, S. Adenwalla, A. Harken, P. Welsch, J. I. Brand and P. A. Dowben, et al., A class of boron-rich solid-state neutron detectors, Appl. Phys. Lett., 2002, 80(19), 3644–3646.
13. D. Emin and T. L. Aselage, A proposed boron-carbide-based solid-state neutron detector, J. Appl. Phys., 2005, 97(1), 013529.
14. A. N. Caruso, P. A. Dowben, S. Balkir, N. Schemm, K. Osberg and R. W. Fairchild, et al., The all boron carbide diode neutron detector: comparison with theory, Mater. Sci. Eng., B, 2006, 135(2), 129–133.
15. N. Hong, J. Mullins, K. Foreman and S. Adenwalla, Boron carbide based solid state neutron detectors: the effects of bias and time constant on detection efficiency, J. Phys. D: Appl. Phys., 2010, 43(27), 275101.
16. A. N. Caruso, The physics of solid-state neutron detector materials and geometries, J. Phys.: Condens. Matter, 2010, 22(44), 443201.
17. A. Oganov and V. Solozhenko, Boron: a hunt for superhard polymorphs, J. Superhard Mater., 2009, 31(5), 285–291.
18. R. Lazzari, N. Vast, J. M. Besson, S. Baroni and A. Dal Corso, Atomic Structure and Vibrational Properties of Icosahedral B₄C Boron Carbide, Phys. Rev. Lett., 1999, 83(16), 3230–3233.
19. F. Mauri, N. Vast and C. J. Pickard, Atomic Structure of Icosahedral B4C Boron Carbide from a First Principles Analysis of NMR Spectra, Phys. Rev. Lett., 2001, 87(8), 085506.
20. H. K. Clark and J. L. Hoard, The Crystal Structure of Boron Carbide, J. Am. Chem. Soc., 1943, 65(11), 2115–2119.
21. R. Bao and D. B. Chrisey, Short range order structure of amorphous B₄C boron carbide thin films, J. Mater. Sci., 2011, 46(11), 3952–3959.
22. C. Pallier, J.-M. Leyssale, L. A. Truflandier, A. T. Bui, P. Weisbecker and C. Gervais, et al., Structure of an Amorphous Boron Carbide Film: An Experimental and Computational Approach, Chem. Mater., 2013, 25(13), 2618–2629.
23. M. M. Paquette, W. Li, M. Sky Driver, S. Karki, A. N. Caruso and N. A. Oyler, The local physical structure of amorphous hydrogenated boron carbide: insights from magic angle spinning solid-state NMR spectroscopy, J. Phys.: Condens. Matter, 2011, 23(43), 435002.
24. E. D. Jemmis, M. M. Balakrishnarajan and P. D. Pancharatna, A Unifying Electron-Counting Rule for Macropolyhedral Boranes, Metallaboranes, and Metallocenes, J. Am. Chem. Soc., 2001, 123(18), 4313–4323.
25. R. B. Billa, T. Hofmann, M. Schubert and B. W. Robertson, Annealing effects on the optical properties of semiconducting boron carbide, J. Appl. Phys., 2009, 106(3), 033515.
26. H. C. Longuet-Higgins and M. d. V. Roberts, The Electronic Structure of an Icosahedron of Boron Atoms, Proc. R. Soc. London, Ser. A, 1955, 230(1180), 110–119.
27. B. J. Nordell, S. Karki, T. D. Nguyen, P. Rulis, A. N. Caruso and S. S. Purohit, et al., The influence of hydrogen on the chemical, mechanical, optical/electronic, and electrical transport properties of amorphous hydrogenated boron carbide, J. Appl. Phys., 2015, 118(3), 035703.
28. LAMMPS Molecular Dynamics Simulator [Internet], [cited 2015 Oct 3], http://lammps.sandia.gov/.
29. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169.
30. W.-Y. Ching and P. Rulis, Electronic Structure Methods for Complex Materials: The Orthogonalized Linear Combination of Atomic Orbitals, Oxford University Press, 2012.
31. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979.
32. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775.
33. R. Schmechel and H. Werheit, Structural Defects of Some Icosahedral Boron-Rich Solids and Their Correlation with the Electronic Properties, J. Solid State Chem., 2000, 154(1), 61–67.
34. D. R. Armstrong, J. Bolland, P. G. Perkins, G. Will and A. Kirfel, The nature of the chemical bonding in boron carbide. IV. Electronic band structure of boron carbide, B 13 C 2, and three models of the structure B₁₂C₃, Acta Crystallogr., Sect. B: Struct. Sci., 1983, 39(3), 324–329.
35. D. W. Bullett, Structure and bonding in crystalline boron and B₁₂C₃, J. Phys. C: Solid State Phys., 1982, 15(3), 415.
36. V. I. Ivashchenko, V. I. Shevchenko and P. E. A. Turchi, First-principles study of the atomic and electronic structures of crystalline and amorphous B₄C, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(23), 235208.
37. C. S. Wang and W. E. Pickett, Density-Functional Theory of Excitation Spectra of Semiconductors: Application to Si, Phys. Rev. Lett., 1983, 51(7), 597–600.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra06988j

---