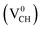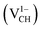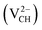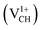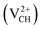Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Li states on a C–H vacancy in graphane: a first-principles study
R. E. Mapasha *a,
M. P. Molepob and
N. Chettyac
*a,
M. P. Molepob and
N. Chettyac
aDepartment of Physics, University of Pretoria, Pretoria 0002, South Africa. E-mail: edwin.mapasha@up.ac.za
bCollege of Graduate Studies, University of South Africa, UNISA, 0003 Pretoria, South Africa
cNational Institute for Theoretical Physics, Johannesburg, 2000, South Africa
First published on 15th August 2017
Abstract
Using a hybrid density functional theory approach, we have studied the effect of the interaction of a Li atom with a C–H pair vacancy defect (VCH) in a graphane monolayer on the thermodynamic stability, structural, magnetic and electronic properties, taking into account the effect of charge doping. We found that a Li atom and charge doping enhanced the thermodynamic stability of a VCH defective graphane monolayer. The Li–VCH system may likely act as a single deep donor, and can readily compensate the acceptor. The effects of Li introduce more occupied states in the band gap, and there exists strong hybridization between the C 2p states and Li 2s states at the vicinity of the Fermi level (EF) responsible for the large magnetic moment noted. The −1 charge doping (Li1−–VCH) further populates the occupied states in the band gap, shifting the EF towards the conduction band minimum. Consequently, the Li1−–VCH system possesses spintronic effects such as half-metallic ferromagnetic character and pronounced magnetism. The +1 charge doping (Li1+–VCH) removes some of the Li induced occupied states, slightly shifting the EF towards the valence band maximum leading to a reduction in the magnetic moment. Our findings give an explanation of the origin of magnetism in a VCH defective graphane system and suggest a possible practical way of controlling it.
Introduction
Graphane,1–3 a fully hydrogenated graphene monolayer,4–8 continues to gain research attention because of its special properties such as high volumetric hydrogen density and a wide direct energy band gap.9–14 Elias et al.2 reported that graphane samples are thermodynamically stable at room temperature. Collectively, this is evidence that a graphane system can be an excellent candidate for energy storage devices and room temperature nano-technological devices.Just like in many real materials, Elias et al.2 reported that graphane samples contain defects. The hydrogen (H) vacancies (VH) in a graphane monolayer are simple defects that one can consider and are the most frequently studied.14–22 Although defects can improve or deteriorate the quality of a material, several density functional theory (DFT) studies14,21,22 have consistently shown that a VH defect introduces magnetism in a graphane monolayer and provides a localized magnetic moment of 1 μB per vacancy. Experimental characterizations revealed the magnetic features in a near fully hydrogenated graphene.23 It was suggested that this magnetism originates from the missing H, when it leaves an unpaired electron in the lone dangling bond connecting the C atom.19 Very recently, Mapasha et al.22 have investigated the effect of charge doping on the electronic properties of the VH vacancy in a graphane monolayer using the DFT method. It was found that charge doping fine tunes the electronic structure of this defective system. Other previous studies reported that the magnetic moment of the VH vacancy can be increased (suppressed) by adsorption of transition metals19 (radicals21). Generally, it was concluded that a VH defect can be used to design spintronic devices.
The other experimentally reported defects in graphane samples are carbon (C) vacancies.2 It was reported that this type of defect occurs unintentionally during the process of hydrogenating graphene. Since every C is bonded to a H atom in the graphane model, when modeling a C vacancy, both atoms have to be removed as a C–H pair (VCH). The intentional creation of a VCH defect can be achieved experimentally using a high-energy ion beam. It was reported that synthesis of a VCH defect should be much easier than that of VH.18 It has been established that the structural reorganization induced by a VCH defect in a graphane monolayer is qualitatively different from that seen in graphene with a C vacancy as emphasized by Pujari et al.24 In the case of graphene, two of the C atoms around the defect reorganize to form a σ bond stabilizing in a pentagon-like defect structure.25,26 On the contrary, there is no σ bond formation amongst the three C atoms surrounding a VCH defect in a graphane monolayer.24 It is of interest to consider charge doping and foreign atom adsorption as possibilities for stabilizing the VCH defect structure.
DFT studies further reported that a VCH defect induces the mid gap states with a permanent magnetic moment of 1 μB in a graphane monolayer.18,24 These magnetic features were experimentally detected by Elias et al.2 during the synthesis of graphane samples. The obtained magnetic moment arises from the dangling bonds on the three C atoms surrounding the VCH vacancy, mainly contributed by the C 2p orbital electronic configuration. To prove this, the C dangling bonds were saturated using H atoms, and the resulting structure stabilized into a non-magnetic character.18,24 Lithium (Li), belonging to the same periodic table group as H, is well known for its H opposing trend when doped on the graphene system.27–32 Inspired by this, it is worth investigating how the interaction of C dangling bonds surrounding a VCH vacancy with a Li atom would affect the induced magnetism as well as the thermodynamic stability. This could be a way of controlling the induced magnetism in a VCH defected graphane which could be essential for technological devices. Although there is no literature on the Li adatom above the VCH vacancy, a few studies of Li on pristine graphane are available.33–37 It has been reported that the single Li adatom prefers to bind with the substrate as opposed to the Li clusters, at zero kelvin.33–36 The Li adatom introduces mid-gap states within the graphane band gap.34–36 The latter was confirmed experimentally using angle resolved photoelectron microscopy.37 It is worthwhile in this study to investigate how the Li adatom binds with the VCH vacancy, and the hybridization between the Li 2s and dangling C 2p orbitals within the band gap.
In semiconductors, defects can exist in multiple charge states due to variation in the electronic chemical potential (Fermi level) from the valence band maximum (VBM) to conduction band minimum (CBM) with respect to the change in the charge doping (addition of electrons or holes).38 Experimentally, the variation in Fermi level occurs by applying an electric field. Through charge state modulation, the defect local structure can be altered and result in the new thermodynamic ground state of the system. Knowledge of the stable charge states of the defect and the Fermi level position where the new charge takes over (thermodynamic transition level), in terms of stability within the band gap of the semiconductor, is essential for nanotechnology device operation. The charge states in the band gap of a semiconductor are usually observed using ab initio methods and experimental techniques such as deep level transient spectroscopy (DLTS) and electron paramagnetic resonance (EPR) when identifying the thermodynamic transition levels.38 It is worthwhile in this study to investigate the local structure and the thermodynamic stability of the VCH vacancy defect without and with Li with different charge states, since this knowledge is still scarce.
It is essential to examine how charge modulation controls the defect induced magnetism, which is the basic requirement for nano-scale spintronic application devices. It is well known that the standard DFT functionals severely underestimate the band gaps of semiconductors, which can easily lead to wrong predictions for transition levels and defect states positions. To avoid this, we use the screened hybrid exchange correlation functional developed by Heyd, Scuseria, and Ernzerhof (HSE06 functional)39,40 that has been proven to accurately predict the correct value of the band gap and defect transition levels in doped semiconductors.41,42
In this paper, we use hybrid DFT to study the thermodynamic stability and structural and magnetic properties of a VCH vacancy considering the effect of charge doping. Furthermore, the interaction of a Li atom with a VCH vacancy is investigated, also considering the effect of charge states. Generally, we report that the defect induced properties in a graphane monolayer critically depend on the charge states. This study provides a way of inducing, increasing and controlling magnetism in a graphane monolayer by creating defects and modulating their charge states, which is a basic requirement for designing nano-electronic devices.
Computational details
Our electronic structure calculations were performed using the DFT approach implemented within the Vienna ab initio simulation packages (VASP) code.43–46 For the description of the exchange–correlation interaction, the Heyd, Scuseria, and Ernzerhof functional (HSE06 functional)39,40 was employed. For the core electron and chemically active valence electron interactions, the projector augmented wave (PAW) method47 was used for the generation of the pseudopotentials. For the plane wave functions expansion, an energy cut-off of 500 eV was set. For the integration of the hexagonal Brillouin zone of a 1 × 1 unit cell, the 10 × 10 × 1 k-mesh generated using the Monkhorst–Pack scheme48 is sufficient to yield accurate results. However, for the large supercell system, a 4 × 4 × 1 k-mesh is suitable for the integration. We employed the Methfessel–Paxton (MP) scheme49 to populate the electronic states in the self-consistent field calculations. Our supercell structures were allowed to relax until the residual atomic forces were reduced to less than 0.01 eV Å−1, using the Hellman–Feynman theorem. During the self-consistent field calculations, the total energy was allowed to converge to within 10−7 eV. The supercell periodic boundary conditions are considered in this study and the interlayer spacing along the z-axis was set to 15 Å to significantly reduce the periodic image interactions.To gain an insight into the stability of a VCH defect at different charge states q within the graphane band gap, the formation energy should be evaluated using the following expression,
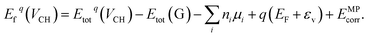 | (1) |
The term Etotq(VCH) is the total energy of a graphane supercell with a VCH defect in a charge state q, and Etot(G) is the total energy of the equivalent pristine graphane supercell. The parameter ni is the number of atoms i (C and H) removed from a graphane supercell. μi refers to the chemical potentials of the reservoir of the removed H and C atoms. The chemical potential of the H atom is obtained from the converged total energy of an isolated H2 molecule placed in a cubic cell of lattice constants a = b = c = 15 Å, whereas that of C is from a fully relaxed graphene monolayer supercell.
The Fermi level EF is an electronic chemical potential of the electron reservoir. The εv variable is usually the energy level valence band maximum (VBM) of a pristine graphane system. To significantly reduce the effects of spurious electrostatic interactions of the periodic images introduced by charge doping on the defects, the Markov–Payne50 correction potential term EMPcorr was included in eqn (1). The detailed description of the EMPcorr term is found in ref. 50. This term should not be ignored to avoid the introduction of errors into the total energy of the system that might affect the accuracy of the formation energy values, although its contribution is very small in this study. To calculate the formation energy of the Li on VCH vacancy defect (Li–VCH) at each nominal charge state q, eqn (1) is modified as follows,
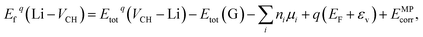 | (2) |
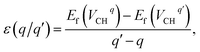 | (3) |
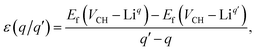 | (4) |
Results and discussion
Pristine graphane properties
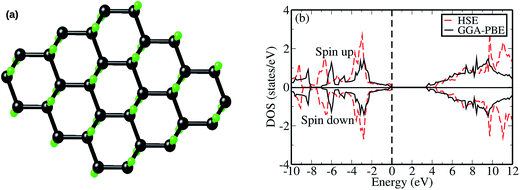
It is important to first report the structural and electronic properties of a pristine graphane monolayer obtained using both the generalized gradient approximation of Perdew, Burke and Ernzerhof (GGA-PBE)51 and hybrid HSE06 functionals. The purpose of this section is to prove that HSE06 functionals can accurately predict the band gap of a pristine graphane system. A previous study demonstrated that graphane can be modeled in different configurations or isomers such as chair-like, boat-like and armchair-like.1 The review article of Sahin et al.14 and references therein summarize other possible graphane isomers. The chair-like configuration was reported to be the most energetically stable as compared to other isomers,1,14 and was also experimentally synthesized.2 Based on this information, all our calculations were performed employing a chair-like model structure.Fig. 1(a) presents a fully optimized chair-like graphane model structure. We report that although both the GGA-PBE and HSE06 functionals give the same structural appearance of graphane, they differ slightly in predicting the structural parameters, as shown in Table 1. The HSE06 and GGA-PBE functionals predict the lattice constant as 2.51 Å and 2.54 Å respectively. These values are in excellent agreement with the previous results shown in Table 1. Comparing the two functionals, it is noted that the HSE06 lattice constant is approximately 1% lower than the GGA-PBE value. The HSE06 and GGA-PBE functionals predict the C–C bond length d(C–C) as 1.52 Å and 1.54 Å respectively. This d(C–C) value is in good agreement with the previous theoretical data presented in Table 1. Generally, the inclusion of some portion of exact Hartree–Fock (HF) exchange in a DFT expression slightly shortens the bond distances in the carbon material systems.40
The spin polarized TDOS plot for a pristine graphane monolayer calculated using both the GGA-PBE and HSE06 functionals is shown in Fig. 1(b). In agreement with the previous study,12 the shape of the HSE06 TDOS is almost identical to that of GGA-PBE for the entire plot, except that the TDOS for HSE06 shows a relatively larger energy band gap. Both functionals predict that a pristine graphane monolayer is a wide band gap semiconductor, where the quantities are shown in Table 1. Based on experimental measurements, Elias et al.2 revealed that graphane possesses insulating features, without reporting the magnitude of the band gap. The GGA-PBE functional predicts a band gap of 3.38 eV. Since it is well known that a GGA-PBE functional is inadequate (underestimates) in predicting the band gaps of semiconductors, the use of the HSE06 functional is able to reduce the underestimation by predicting a value of 4.39 eV. This value is in good agreement with the HSE06 values reported in previous studies.12,52,53 Based on this, we employed the HSE06 functional in the subsequent calculations of a VCH vacancy in a graphane monolayer.
Properties of a VCH defect in a graphane monolayer
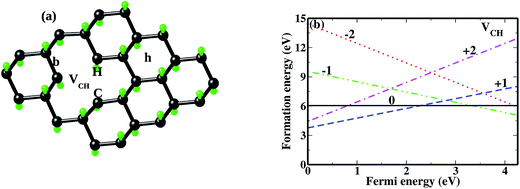
As mentioned earlier, when modeling a C vacancy in graphane, both the C and H atoms have to be removed as a pair (VCH) since every C is bonded to a H atom as shown in Fig. 2(a). This type of defect in a graphane monolayer sample is easily realizable experimentally and can be stable at room temperature for a long time without any characteristic alteration.2 In this section, we studied the thermodynamic stability, structural, electronic and magnetic properties of a VCH defect in a graphane monolayer system. The effects of different VCH defect charge states q = −2, −1, 0, +1, and +2, and the variation in Fermi level (EF) position within the band gap were considered.For the thermodynamic stability analysis, the formation energy Efq(VCH) of a VCH vacancy at each charge state was calculated using eqn (1). Firstly, the total energy of a VCH vacancy was converged as a function of the supercell sizes of 3 × 3, 5 × 5, 7 × 7 and 9 × 9. For each supercell size, the formation energy Efq(VCH) at q = 0 was calculated using eqn (1). The Efq(VCH) values of 5.83 eV, 5.99 eV, 6.02 eV and 6.05 eV, corresponding respectively to 3 × 3, 5 × 5, 7 × 7 and 9 × 9 sizes, were obtained. Although it is clearly noted that convergence starts at 5 × 5, the 7 × 7 supercell has been used for the subsequent calculations. The formation energies Efq(VCH) of a VCH vacancy in the multiple charge states 0 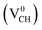 , −1
, −1 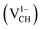 , −2
, −2 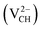 , +1
, +1 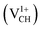 and +2
and +2 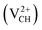 as a function of EF are shown in Fig. 2(b). The values of Efq(VCH) are allowed to vary within the energy band gap (ranging from 0 eV to 4.39 eV).
as a function of EF are shown in Fig. 2(b). The values of Efq(VCH) are allowed to vary within the energy band gap (ranging from 0 eV to 4.39 eV).
The Efq(VCH) of the 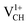 and
and 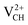 systems decrease when the position of EF approaches the VBM, while those of the
systems decrease when the position of EF approaches the VBM, while those of the 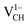 and
and 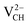 systems decrease when EF shifts up towards the CBM as shown in Fig. 2(b). This indicates that a VCH defect would be likely to act as a source of both acceptor and donor compensation depending on the position of EF. Fig. 2(b) shows that the
systems decrease when EF shifts up towards the CBM as shown in Fig. 2(b). This indicates that a VCH defect would be likely to act as a source of both acceptor and donor compensation depending on the position of EF. Fig. 2(b) shows that the 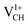 vacancy system has the lowest formation energy from the VBM (EF = 0 eV) to EF = 2.13 eV, followed by the
vacancy system has the lowest formation energy from the VBM (EF = 0 eV) to EF = 2.13 eV, followed by the 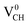 system from EF = 2.13 eV to 3.35 eV, and at the far end of the band gap, the
system from EF = 2.13 eV to 3.35 eV, and at the far end of the band gap, the 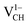 system is most stable from EF = 3.35 eV to the CBM. Since it is noted that only the −1, 0 and +1 charge states are thermodynamically stable within the graphane band gap, the −2 and +2 charge states were excluded in the subsequent calculations. We further calculated the VCH vacancy thermodynamic transition levels ε(q/q′) using eqn (3). The obtained ε(q/q′) values are indicated by the intersection of the two formation energy lines of the charge states q and q′ shown in Fig. 2(b). Our calculations predict the donor (0/+1) and acceptor (−1/0) levels occurring at Ev = +2.13 eV and Ec = −1.04 eV respectively. The position of the donor (0/+1) level reveals that a VCH defect may likely act as a deep donor. More likely, these results suggest that a VCH defect will be too deep to be ionized. If the DLTS spectrum of a VCH defect can be recorded, we suggest that the two peaks corresponding to the (0/+1) and (−1/0) deep levels should be observable at higher temperatures. Since it has been reported that the HSE06 functional is able to correctly mimic experiments in identifying the transition levels in semiconductors,41,42 we expect our calculated values to agree very well with future experimental results.
system is most stable from EF = 3.35 eV to the CBM. Since it is noted that only the −1, 0 and +1 charge states are thermodynamically stable within the graphane band gap, the −2 and +2 charge states were excluded in the subsequent calculations. We further calculated the VCH vacancy thermodynamic transition levels ε(q/q′) using eqn (3). The obtained ε(q/q′) values are indicated by the intersection of the two formation energy lines of the charge states q and q′ shown in Fig. 2(b). Our calculations predict the donor (0/+1) and acceptor (−1/0) levels occurring at Ev = +2.13 eV and Ec = −1.04 eV respectively. The position of the donor (0/+1) level reveals that a VCH defect may likely act as a deep donor. More likely, these results suggest that a VCH defect will be too deep to be ionized. If the DLTS spectrum of a VCH defect can be recorded, we suggest that the two peaks corresponding to the (0/+1) and (−1/0) deep levels should be observable at higher temperatures. Since it has been reported that the HSE06 functional is able to correctly mimic experiments in identifying the transition levels in semiconductors,41,42 we expect our calculated values to agree very well with future experimental results.
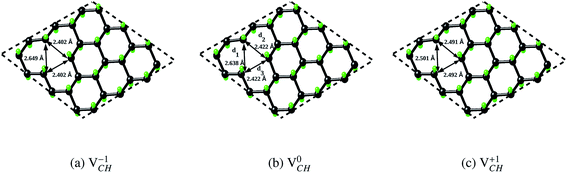
We further examined the dependence of local geometry of a VCH defect on the −1, 0 and +1 charge states. The atomic relaxation of the VCH defect in the multiple charge states is shown in Fig. 3(a) for −1, Fig. 3(b) for 0 and Fig. 3(c) for +1. During relaxation, the three C atoms surrounding the VCH vacancy undergo significant structural distortions, and thus the graphane monolayer threefold symmetry breaks due to the Jahn–Teller effect. These three C atoms surrounding the VCH defect form an asymmetric triangle-like arrangement (shape), as shown in Fig. 3.
In the 0 charge state 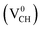 , the three C atoms are slightly displaced away from the VCH vacancy defect after relaxation. As a result, our relaxed C–C dangling bond distances d1, d2 and d3 constructing a triangle-like shape are 2.64 Å, 2.42 Å and 2.42 Å respectively. Our calculated HSE06 values are about 0.10 Å less than the GGA-PBE values reported by Pujari et al.,24 although the trend is the same. The slightly shorter bond distances in our calculations should be attributed to the use of exact short range Hartree–Fock (HF) exchange, that usually underestimates the structure of carbon systems with a very small magnitude.40
, the three C atoms are slightly displaced away from the VCH vacancy defect after relaxation. As a result, our relaxed C–C dangling bond distances d1, d2 and d3 constructing a triangle-like shape are 2.64 Å, 2.42 Å and 2.42 Å respectively. Our calculated HSE06 values are about 0.10 Å less than the GGA-PBE values reported by Pujari et al.,24 although the trend is the same. The slightly shorter bond distances in our calculations should be attributed to the use of exact short range Hartree–Fock (HF) exchange, that usually underestimates the structure of carbon systems with a very small magnitude.40
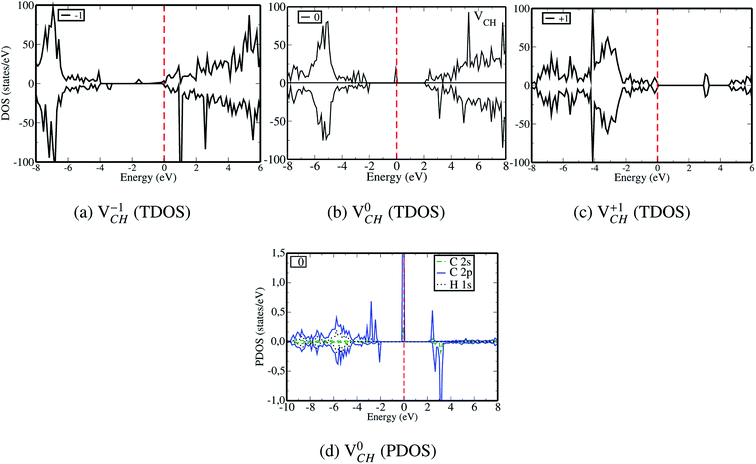
Since creation of a VCH defect in a graphane model structure leaves the three nearest neighbour (adjacent) C atoms surrounding the vacancy, each with a dangling bond, we suggest that the bond distance d1 separates the two carbon atoms of the same electronic spin, whereas d2 and d3 separate those of opposite spins. Thus, the relatively large value of d1 should be attributed to a high Coulomb repulsion of the same spin electrons, as compared to those of the opposite spins (d2 and d3). In order to understand the effect of a VCH defect on the electronic structure of a graphane monolayer, the TDOS were evaluated and presented in Fig. 4. Fig. 4(b) shows the TDOS for a 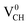 defect. The
defect. The 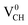 defect induces the spin polarized mid gap states with a sharp peak crossing the EF. Experimental characterization of graphane revealed that the deep defect levels are due to the absence of H23 or C2 occurring during the synthesis. Moreover, these partially occupied mid gap states appear only in the spin-up channel at the EF, revealing a half-metallic character. This spintronic effect is crucial in the developing nanoelectronic field. The fascinating half-metallic nature in a
defect induces the spin polarized mid gap states with a sharp peak crossing the EF. Experimental characterization of graphane revealed that the deep defect levels are due to the absence of H23 or C2 occurring during the synthesis. Moreover, these partially occupied mid gap states appear only in the spin-up channel at the EF, revealing a half-metallic character. This spintronic effect is crucial in the developing nanoelectronic field. The fascinating half-metallic nature in a 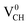 defect system might be attributed to the effect of dangling bonds from the three carbon atoms surrounding the VCH defect. In agreement with previous studies,24 this system is ferromagnetic with an integral magnetic moment of 1.0 μB.
defect system might be attributed to the effect of dangling bonds from the three carbon atoms surrounding the VCH defect. In agreement with previous studies,24 this system is ferromagnetic with an integral magnetic moment of 1.0 μB.
The obtained magnetic moment of 1.0 μB in the three dangling bonds system can be explained as follows; since it is well known that each dangling bond should contribute to 1.0 μB, the dangling bonds on the two C atoms of different electronic spins pair, and thus result in cancellation of their magnetic moment contributions. Consequently, the resulting magnetic moment of 1.0 μB in a 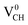 defected graphane mainly arises from the third C atom that has an unpaired electron. To examine the stability of the induced magnetic state, the magnetization energy as the total energy difference between the spin imposed TDOS (spin-polarized) and that of the non-spin imposed TDOS (non-spin polarized) was calculated. Our calculated magnetization energy is −169 meV. The negative sign shows that a
defected graphane mainly arises from the third C atom that has an unpaired electron. To examine the stability of the induced magnetic state, the magnetization energy as the total energy difference between the spin imposed TDOS (spin-polarized) and that of the non-spin imposed TDOS (non-spin polarized) was calculated. Our calculated magnetization energy is −169 meV. The negative sign shows that a 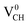 defect is more energetically stable in a spin-polarized state than in a non-spin polarized state, revealing that the ground state of this defective system is magnetic. Our calculated magnetization energy is more than the room temperature thermal energy of 25 meV, indicating that the
defect is more energetically stable in a spin-polarized state than in a non-spin polarized state, revealing that the ground state of this defective system is magnetic. Our calculated magnetization energy is more than the room temperature thermal energy of 25 meV, indicating that the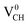 defect-induced magnetism is relatively too strong. We further calculated the partial density of states (PDOS) for a
defect-induced magnetism is relatively too strong. We further calculated the partial density of states (PDOS) for a 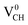 defect system to explore the origin of its magnetism. Fig. 4(d) shows the PDOS for one polarized C atom adjacent to the VCH. The pronounced peak states seen crossing the EF in Fig. 4(d) originate from the C 2p orbital electronic configuration in agreement with Pujari et al.24 The C 2s orbital has a small contribution of about 0.2 states per eV. This reveals that the noted magnetic moment in a
defect system to explore the origin of its magnetism. Fig. 4(d) shows the PDOS for one polarized C atom adjacent to the VCH. The pronounced peak states seen crossing the EF in Fig. 4(d) originate from the C 2p orbital electronic configuration in agreement with Pujari et al.24 The C 2s orbital has a small contribution of about 0.2 states per eV. This reveals that the noted magnetic moment in a 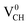 defect predominantly originates from the polarized C 2p orbital, with little contribution from the C 2s orbital. The H atom attached to this polarized C atom site does not have any magnetic influence.
defect predominantly originates from the polarized C 2p orbital, with little contribution from the C 2s orbital. The H atom attached to this polarized C atom site does not have any magnetic influence.
Fig. 3(a) clearly indicates that the bond distances surrounding a VCH defect are sensitive to charge doping. The effect of −1 charge doping 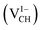 is to expand the distance d1 by the magnitude of 0.02 Å and reduce d2 and d3 by 0.01 Å relative to the values for
is to expand the distance d1 by the magnitude of 0.02 Å and reduce d2 and d3 by 0.01 Å relative to the values for 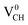 . This indicates that an addition of an electron into this system slightly increases the coulomb repulsion between the two C atoms suggested to have electrons of the same spin. Fig. 4(a) shows that charge doping into a VCH defect does not only affect the geometrical structure but also the electronic properties. An addition of −1 charge state still gives the ground state spin polarized TDOS, but doubles the total magnetic moment (2.0 μB). We also note that the effect of −1 charge doping introduces extra occupied spin-down states within the band gap and also pushes the EF to the CBM position, revealing that a
. This indicates that an addition of an electron into this system slightly increases the coulomb repulsion between the two C atoms suggested to have electrons of the same spin. Fig. 4(a) shows that charge doping into a VCH defect does not only affect the geometrical structure but also the electronic properties. An addition of −1 charge state still gives the ground state spin polarized TDOS, but doubles the total magnetic moment (2.0 μB). We also note that the effect of −1 charge doping introduces extra occupied spin-down states within the band gap and also pushes the EF to the CBM position, revealing that a 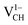 defect is a typical n-type defect. This EF shift completely destroys the half-metallic character (see Fig. 4(a)).
defect is a typical n-type defect. This EF shift completely destroys the half-metallic character (see Fig. 4(a)).
A different scenario is noted when the +1 charge is doped into the system 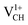 . The distance d1 decreases significantly by the magnitude of 0.14 Å, while d2 and d3 expand by 0.07 Å relative to the values of
. The distance d1 decreases significantly by the magnitude of 0.14 Å, while d2 and d3 expand by 0.07 Å relative to the values of 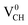 . It is clear that an addition of +1 charge enforces structural reconstruction around the VCH defect, because d1 is almost equal to d2 and d3. This further suggests that the relaxation of a
. It is clear that an addition of +1 charge enforces structural reconstruction around the VCH defect, because d1 is almost equal to d2 and d3. This further suggests that the relaxation of a 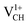 defect is trying to preserve the hexagonal 3-fold symmetry. From the TDOS plot of
defect is trying to preserve the hexagonal 3-fold symmetry. From the TDOS plot of 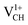 shown in Fig. 4(c), it is noted that the spin-up TDOS and spin-down TDOS are invertibly symmetrical, revealing that the ground state of a
shown in Fig. 4(c), it is noted that the spin-up TDOS and spin-down TDOS are invertibly symmetrical, revealing that the ground state of a 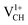 defect is non-spin polarized and has no magnetic moment. As mentioned earlier, creation of a VCH defect leaves its three neighboring C atoms having an unpaired excited electron each. Then, withdrawal of an electron by the addition of a +1 charge leaves two excited electrons. The non-spin polarization ground state in the
defect is non-spin polarized and has no magnetic moment. As mentioned earlier, creation of a VCH defect leaves its three neighboring C atoms having an unpaired excited electron each. Then, withdrawal of an electron by the addition of a +1 charge leaves two excited electrons. The non-spin polarization ground state in the 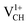 defect confirms that the two polarized electrons pair after structural relaxation. Fig. 4(c) also shows that the EF has been shifted to the top of the VBM, indicating that a
defect confirms that the two polarized electrons pair after structural relaxation. Fig. 4(c) also shows that the EF has been shifted to the top of the VBM, indicating that a 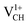 defect has a deficiency of electrons. In conclusion, the electronic structure of a VCH defect in the graphane monolayer can be altered via charge state modulation.
defect has a deficiency of electrons. In conclusion, the electronic structure of a VCH defect in the graphane monolayer can be altered via charge state modulation.
Properties of Li adatom above the VCH vacancy in a graphane monolayer
We further investigated the effects of Li on the induced electronic states localized on the three adjacent C atoms surrounding the VCH defect site, on the same level of accuracy. Firstly, the Li adatom preferred site on a graphane structure was examined from the binding energies (Eb) calculation analysis. Fig. 2(a) presents the possible Li adsorption sites surrounding the VCH defect in a graphane geometry model. The following sites were considered; (1) Li adatom above the center of a hexagon (Li-h), (2) Li adatom above the VCH defect (Li–VCH), (3) Li adatom above the hydrogen atom (Li–H), (4) Li adatom above the carbon atom (Li–C) that is bonded to a H atom on the other side of the layer and (5) Li adatom above the midpoint between the two nearest neighbour carbon atoms also known as a bridge site (Li-b). To find the most energetically favourable site, the binding energy of each Li configuration was calculated using the following expression;| Eb = Etot(VCH + Li) − Etot(VCH) − Etot(Li), | (5) |
| Adsorption site | Eb (eV) | q (e) | Δh (Å) |
|---|---|---|---|
| Li–VCH | 1.72 | 0.87 | 1.54 |
| Li–C | 0.60 | 0.82 | 1.66 |
| Li-h | 0.58 | 0.96 | 1.70 |
| Li–H | −1.19 | 0.19 | 4.19 |
| Li-b | 0.96 | 0.80 | 1.59 |
Table 2 shows that the Li–VCH configuration is the preferred site with the highest binding energy of 1.72 eV, followed by Li-b → Li–C → Li-h → Li–H. The values of Δh follow the binding energy opposing trend of Li–H → Li-h → Li–C → Li-b → Li–VCH. The Li–VCH configuration has the shortest Δh suggesting that the Li adatom is more free to approach the three dangling C atoms surrounding the VCH vacancy. This observation is in consensus with the previous results of a Li adatom above a C vacancy in a graphene monolayer.55,56 To quantify an interaction between Li and the graphane system, the amount of charge transfer q was calculated using the Bader charge analysis.57 Table 2 shows that the sign of the q values is positive, indicating that an amount of charge has been transferred from the foreign atom to the substrate, owing to the low electron affinity of the Li atom (0.62 eV) compared to that of the C atom (1.26 eV). Apart from configuration Li–H with 0.19e, all other configurations possess an average of 0.9e charge transfer.
Since our results revealed that a Li–VCH configuration gives a stable structure, and that the Li atom bonds strongly with the graphane substrate although ionically, we further examined its charge density distribution. Fig. 5(a) and (c) show the iso-surfaces of difference charge density (Δρ) of the VCH vacancy in a graphane monolayer and the Li atom on the VCH vacancy in a graphane monolayer, respectively. Δρ is calculated as the difference between the initial atomic charge density used to start the calculation and the final converged charge density. The red iso-surfaces in Fig. 5 indicate where the electrons would prefer to go during the electronic cycles. Fig. 5(b) is the side view of charge density distribution of the VCH vacancy to show clearly that no charge is accumulated on the C atom but is on the H atom. Fig. 5(a) shows that the charge density distribution of the VCH vacancy in a graphane monolayer is non-uniform, it is mainly localized around the H atoms as well as at the C–C bond center. Since the C–C bonding in a graphane monolayer is covalent, Δρ indicates that the electronic charge densities are minimal at the C atoms (depletion region) but increase towards the center of C–C bonds (accumulation region). We suggest the charge density global minimum region to be at the VCH vacancy. Fig. 5(c) shows that the charge density distribution of the Li–VCH configuration is also non-uniform. It is noted in Fig. 5(c) that there are no charge densities accumulated around the Li atom and C–Li bonds. It has been established earlier in this study that Li donates most of its electronic charge ionically to its three nearest neighbour C atoms, and gains the positive charge which can be interpreted as a depleted region. Hussain et al.35 reported that in a pristine graphane monolayer, most of the Li charge is transferred to six C atoms to which the Li atom is covalently bonded. Fig. 5(c) shows that there is no iso-surface charge density on the three C atoms bonded to the Li atom, but that the charge density is slightly enhanced along the C–C bonds closest to the Li adatom as compared to the other C–C bonds far away. This suggests that the three C atoms bonded to the Li atom can also be regarded as depleted regions because the charge density accumulated from the Li adatom has been further shared with their nearest neighbour C atoms as interpreted from the Δρ plot (Fig. 5(c)).
We further studied the response of the Li–VCH structure on the Li charge state alteration. The effect of Li nominal charge doping q = −1, 0 and +1 on the thermodynamic stability and structural and electronic properties of the Li–VCH structure (denoted as Li1−–VCH, Li0–VCH and Li1+–VCH) was examined. To study the thermodynamic stability, the formation energy Efq(Li–VCH) and charge transition levels ε(q/q′) are calculated using eqn (2) and (4) respectively.
The formation energies for the Li–VCH configuration in its various nominal charge states Li1−–VCH, Li0–VCH and Li1+–VCH as a function of EF are shown in Fig. 6. Calculated at EF = 0 eV, the formation energy for Li0–VCH is 2.42 eV, lower than that of 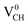 by the magnitude of 3.46 eV, revealing an enhancement of the
by the magnitude of 3.46 eV, revealing an enhancement of the 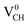 vacancy stability by the Li atom. Furthermore, Fig. 6 shows that the formation energy for Li1+–VCH is the lowest for the entire bottom half of the band gap up to EF = 2.70 eV, indicating that Li–VCH may likely act as a deep donor. At the VBM (EF = 0 eV), its formation energy is negative (−0.25 eV) revealing the spontaneous (exothermic) formation of the Li ion (Li+) in the VCH vacancy system. In the Li1+–VCH configuration, the Li adatom relaxes to a Δh of 1.51 Å from 1.54 Å for Li0–VCH. The lowest formation energy and small Δh suggest that creation of an ion in a Li–VCH configuration further enhances the binding force between a Li atom and the three dangling C atoms adjacent to the VCH vacancy. On the other hand, the formation energy for the Li1−–VCH configuration is 6.49 eV at EF = 0 eV. This value decreases as the value of EF increases across the band gap and becomes most stable from EF = 4.00 eV to the CBM. The Li adatom relaxes to a Δh of 1.86 Å above the VCH revealing a relatively weak binding.
vacancy stability by the Li atom. Furthermore, Fig. 6 shows that the formation energy for Li1+–VCH is the lowest for the entire bottom half of the band gap up to EF = 2.70 eV, indicating that Li–VCH may likely act as a deep donor. At the VBM (EF = 0 eV), its formation energy is negative (−0.25 eV) revealing the spontaneous (exothermic) formation of the Li ion (Li+) in the VCH vacancy system. In the Li1+–VCH configuration, the Li adatom relaxes to a Δh of 1.51 Å from 1.54 Å for Li0–VCH. The lowest formation energy and small Δh suggest that creation of an ion in a Li–VCH configuration further enhances the binding force between a Li atom and the three dangling C atoms adjacent to the VCH vacancy. On the other hand, the formation energy for the Li1−–VCH configuration is 6.49 eV at EF = 0 eV. This value decreases as the value of EF increases across the band gap and becomes most stable from EF = 4.00 eV to the CBM. The Li adatom relaxes to a Δh of 1.86 Å above the VCH revealing a relatively weak binding.
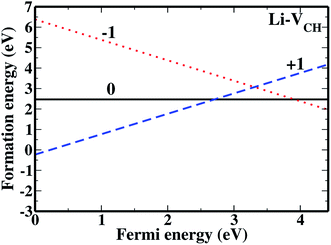 | ||
| Fig. 6 The formation energies for Li1−–VCH, Li0–VCH and Li1+–VCH as a function of EF. The points where the two lines intersect coincide with the thermodynamic transition levels. | ||
The charge transition energy levels for the Li–VCH configurations obtained from eqn (4) are represented by the intersection of the formation energy lines on the graphane band gap shown in Fig. 6. The charge transition energy level values are ε(0/+1) = 2.70 eV relative to the VBM (1.75 eV from the CBM) and ε(0/−1) = 3.98 eV (0.47 eV below the CBM). Comparing Fig. 6 and 2(b), it is noted that the effect of Li is to slightly shift both the donor and acceptor charge transition levels of VCH towards the CBM. Nonetheless, the Li–VCH configuration acts as a deep donor, and does not induce n-type conductivity in the graphane monolayer.
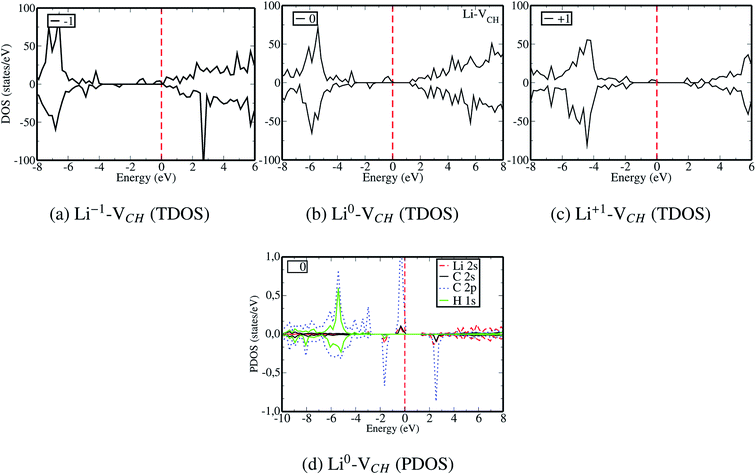
To gain an insight into the electronic properties of the Li–VCH configuration, the TDOS were computed and plotted in Fig. 7. Fig. 7(a)–(c) depict the TDOS for Li1−–VCH, Li0–VCH and Li+–VCH respectively. Firstly, we compared the TDOS for the 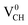 defect depicted in Fig. 4(b) with those of Li0–VCH as shown in Fig. 7(b). The Li introduces the fully occupied states at 0.85 eV above the VBM in the spin-down channel. The
defect depicted in Fig. 4(b) with those of Li0–VCH as shown in Fig. 7(b). The Li introduces the fully occupied states at 0.85 eV above the VBM in the spin-down channel. The 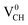 system is half-metallic ferromagnetic (see Fig. 4(b)), but for the Li0–VCH system, the Li atom fills up the VCH partially occupied C 2p states slightly pushing the EF upwards. The fully occupied induced states, only in the majority spin, are noted at the vicinity of the EF. Consequently, the Li0–VCH system is ferromagnetic with an integral magnetic moment of 2.00 μB per supercell, more than that of
system is half-metallic ferromagnetic (see Fig. 4(b)), but for the Li0–VCH system, the Li atom fills up the VCH partially occupied C 2p states slightly pushing the EF upwards. The fully occupied induced states, only in the majority spin, are noted at the vicinity of the EF. Consequently, the Li0–VCH system is ferromagnetic with an integral magnetic moment of 2.00 μB per supercell, more than that of 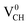 by 1.00 μB. We further examined the origin of the magnetism in a Li0–VCH system using the PDOS shown in Fig. 7(d). The pronounced C 2p states and small contributions of the C 2s states hybridize with the Li 2s states at the vicinity of the EF. Typically, enhancement of the magnetic moment by 1.00 μB should be due to the influence of the Li valence electron and its orbital occupancy (C 2p orbital states) on the C atoms.
by 1.00 μB. We further examined the origin of the magnetism in a Li0–VCH system using the PDOS shown in Fig. 7(d). The pronounced C 2p states and small contributions of the C 2s states hybridize with the Li 2s states at the vicinity of the EF. Typically, enhancement of the magnetic moment by 1.00 μB should be due to the influence of the Li valence electron and its orbital occupancy (C 2p orbital states) on the C atoms.
For the Li1−–VCH configuration, the effect of −1 charge doping is to shift the EF towards the CBM, leaving most of the induced in gap states occupied as shown in Fig. 7(a). As a result, an integral magnetic moment of 3.00 μB per supercell is attainable. An enhancement of the magnetism in a Li1−–VCH configuration indicates that an injected electron does localize on the defects and is not distributed all over the supercell space. The Li1−–VCH configuration is half-metallic ferromagnetic as revealed by the TDOS plot shown in Fig. 7(a), and also possesses the features of an n-type donor system. For the Li+–VCH configuration, creation of the Li ion shifts the EF as well as the corresponding occupied majority spin states by 1.10 eV towards the VBM as shown in Fig. 7(c), revealing the feature of a deep donor system. The effects of +1 charge doping remove the Li induced occupied spin-down states at 0.85 eV above the VBM. As a result, the induced magnetic moment becomes 1.00 μB per supercell. This deviation in magnetism suggests that an ejected electron should originate from the Li 2s orbital states. An understanding of the variation of the induced magnetism due to charge state alteration should be clear when considering an idea of the simple electronic counting from the DOS analysis. It is concluded that VCH defect magnetism can be evolved due to the influence of the Li adsorption as well as its charge state alteration.
Conclusions
We used a hybrid DFT approach (HSE06) to study the interaction of a Li atom with a VCH vacancy defect in a graphane monolayer. Firstly, the effects of a VCH defect in a graphane monolayer were investigated in terms of the stability and structural, magnetic and electronic properties, involving the influence of charge doping. The formation energies plot analysis revealed that only the −1, 0 and +1 charge states are thermodynamically stable within the graphane band gap, and that the VCH vacancy is a single deep donor defect, and may likely compensate the acceptor depending on the position of EF. The local geometry of a VCH defect is very sensitive to the charge doping. Our results suggest that a VCH defect induces half-metallic stable ferromagnetism in a graphane monolayer mainly originating from the C 2p orbital states. The −1 (+1) charge doping doubles (suppresses) the VCH defect induced magnetic moment, and yields a spin polarized n-type (non-spin polarized) system. In conclusion, the electronic structure of a VCH defect in the graphane monolayer can be controlled via charge state modulation.Secondly, a Li adatom was introduced into a VCH defect in the graphane system and also charged. It was found that the Li enhances the thermodynamic stability of a VCH defect. The formation energy as a function of EF plot indicates that the Li–VCH system may likely act as a single deep donor, and is ready to compensate the acceptor. The Li introduces more occupied states in the band gap, and also there is hybridization between the C 2p states and Li 2s states at the vicinity of the EF in the spin-up channel only, leading to enhancement of the magnetism. The −1 charge doping (Li1−–VCH) further populates the occupied states in the band gap shifting the EF towards the CBM. Consequently, the Li1−–VCH system is half-metallic ferromagnetic, and possesses pronounced magnetism. The +1 charge doping (Li1+–VCH) removes some of the Li induced occupied states, slightly shifting the EF towards the VBM leading to a reduction in the magnetic moment. An understanding of the variation of the induced magnetism due to charge state alteration should be clear when considering an idea of the simple electronic counting from the density of states analysis. Our findings give an explanation of the origin of magnetism in a VCH defective graphane system and suggest a possible practical way of controlling it.
Acknowledgements
The authors would like to thank the University of Pretoria, University of South Africa and the National Research Foundation (NRF) for support. We are grateful to Prof. J. Pretorius and Prof. W. Meyer for assisting with the VASP code. REM is grateful to Mr E. Igumbor for fruitful discussions. NC thanks the National Institute for Theoretical Physics (NIThep) for financial support.References
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401 CrossRef.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610 CrossRef CAS PubMed.
- A. Savchenko, Science, 2009, 323, 589 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jungian, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183 CrossRef CAS PubMed.
- P. R. Wallace, Phys. Rev., 1947, 71, 622 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, M. I. Katsnelson, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Nature, 2005, 438, 197 CrossRef CAS PubMed.
- K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim and A. K. Geim, Science, 2007, 315, 1379 CrossRef CAS PubMed.
- O. Leenaerts, H. Peelaers, A. D. Hernandez-Nieves, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195436 CrossRef.
- D. W. Boukhvalov, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035427 CrossRef.
- D. W. Boukhvalov and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085413 CrossRef.
- F. Karlicky, R. Zboril and M. Otyepka, J. Chem. Phys., 2012, 137, 034709 CrossRef PubMed.
- A. Z. Alzahrani and G. P. Srivastava, Appl. Surf. Sci., 2010, 256, 5783 CrossRef CAS.
- H. Sahin, O. Leenaerts, S. K. Singh and F. M. Peeters, WIREs. Comput. Mol. Sci., 2015, 5, 255 CrossRef CAS.
- S. Lebegue, M. Klintenberg, O. Eriksson and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245117 CrossRef.
- P. Chandrachud, B. S. Pujari, S. Haldar, B. Sanyal and D. G. Kanhere, J. Phys.: Condens. Matter, 2010, 22, 465502 CrossRef PubMed.
- H. Sahin, C. Ataca and S. Ciraci, Appl. Phys. Lett., 2009, 95, 222510 CrossRef.
- H. Sahin, C. Ataca and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205417 CrossRef.
- C.-K. Yang, Carbon, 2010, 48, 3901 CrossRef CAS.
- B. Wu and C. Yang, Appl. Phys. Lett., 2012, 2, 012173 Search PubMed.
- J. Berashevich and T. Chakraborty, Nanotechnology, 2010, 21, 355201 CrossRef PubMed.
- R. E. Mapasha, M. P. Molepo and N. Chetty, Phys. E, 2016, 79, 52–58 CrossRef CAS.
- A. Y. S. Eng, H. L. Poh, F. Sanek, M. Marysko, S. Matejkova, Z. Sofer and M. Pumera, ACS Nano, 2013, 7, 5930–5939 CrossRef CAS PubMed.
- B. S. Pujari and D. G. Kanhere, J. Phys. Chem. C, 2009, 113, 21063–21067 CAS.
- V. M. Pereira, J. M. B. L. dos Santos and A. H. C. Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115109 CrossRef.
- A. Zobelli, V. Ivanovskaya, P. Wagner, I. Suarez-Martinez, A. Yaya and C. P. Ewels, Phys. Status Solidi B, 2012, 249, 1521–3951 CrossRef.
- K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430 CrossRef.
- M. Farjam and R. Tabar, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 045417 CrossRef.
- M. Khantha, N. A. Cordero, L. M. Molina, J. A. Alonso and L. A. Girifalco, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125422 CrossRef.
- P. A. Denis, Chem. Phys. Lett., 2010, 492, 251–257 CrossRef CAS.
- C.-K. Yang, Appl. Phys. Lett., 2009, 94, 163115 CrossRef.
- R. E. Mapasha and N. Chetty, Comput. Mater. Sci., 2010, 49, 787 CrossRef CAS.
- M. Khazaei, M. S. Bahramy, N. S. Venkataramanan, H. Mizuseki and Y. Kawazoe, J. Appl. Phys., 2009, 106, 094303 CrossRef.
- T. Hussain, B. Pathak, T. A. Maark, C. M. Araujo, R. H. Scheicher and R. Ahuja, EPL, 2011, 96, 27013 CrossRef.
- T. Hussain, B. Pathak, T. A. Maark, R. Ramzan and R. Ahuja, EPL, 2012, 99, 47004 CrossRef.
- T. Hussain, B. Pathak, A. D. Sarkar and R. Ahuja, Appl. Phys. Lett., 2012, 101, 103907 CrossRef.
- S. Watcharinyanon, L. I. Johansson, A. A. Zakharov and C. Virojanadara, Surf. Sci., 2012, 606, 3 CrossRef.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192 CrossRef CAS PubMed.
- A. Janotti and C. G. Van de Walle, Phys. Status Solidi B, 2011, 248, 799 CrossRef CAS.
- H.-P. Komsa and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075207 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 11169 CrossRef.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616 CrossRef CAS.
- G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Q. Hu, J. H. Zhang, S. Q. Wu and Z. Z. Zhu, Solid State Commun., 2015, 209, 210 Search PubMed.
- M. N. Amini, O. Leenaerts, B. Partoens and D. Lamoen, J. Phys. Chem. C, 2013, 117, 16242–16247 CAS.
- R. C. Andrew, R. E. Mapasha and N. Chetty, J. Chem. Phys., 2013, 138, 244709 CrossRef CAS PubMed.
- K. M. Fair, X. Y. Cui, L. Li, C. C. Shieh, R. K. Zheng and Z. W. Liu, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 014102 CrossRef.
- S. Seenithurai, R. K. Pandyan, S. V. Kumar, C. Saranya and M. Mahendran, Int. J. Hydrogen Energy, 2014, 39, 11016–11026 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules-A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |