Electric field tunable band-gap crossover in black(blue) phosphorus/g-ZnO van der Waals heterostructures

Abstract

Electrically controlled band-gaps and efficient carrier confinement or separation are crucial in the design of nanoscale light-emitting and photoelectric devices. Here, using hybrid density functional calculations, we studied the electronic and optical properties of graphitic zinc oxide (g-ZnO) and phosphorene van der Waals (vdW) heterostructures. We found that although black(blue) phosphorus/g-ZnO shows an intrinsic type-I(type-II) band alignment with a direct(indirect) band-gap, a vertical electric field can induce type-I-to-type-II transition for the black phosphorus/g-ZnO, and the band edges of blue phosphorus/g-ZnO can be electrically modulated to obtain a direct band-gap at the Γ point. Intriguingly, the heterostructures also showed improved visible-UV light adsorption compared with the single-layers. Our findings reveal that g-ZnO can be used not only as a capping layer to protect the electronic characteristics of phosphorene, but also as the active layer to tune the electronic and optical properties of phosphorene, which may promote potential phosphorene-based applications in the future.

---

1 Introduction

Since the successful exfoliation of graphene,^1,2 two-dimensional (2D) materials such as single-layer (1L) transition metal dichalcogenides (TMDs)^3,4 have attracted great attention because of the peculiar physics brought about by them and their potential for the next generation of nanoscale device applications.^3–5 Recently, a new elemental 2D material called black phosphorus (black-p) has been fabricated by several research groups.^6–8 Unlike semimetallic graphene and the typical 1L-TMD MoS₂, which both exhibit low electron carrier mobility^5,9,10 (10–200 cm² V⁻¹ s⁻¹), black-p has many fascinating properties such as a finite direct band-gap (E_g) and high electron mobility (1000 cm² V⁻¹ s⁻¹) at room temperature.^11,12 Very recently the theoretically-predicted blue phosphorus (blue-p),¹³ which is an allotrope of phosphorene, was successfully synthesized.¹⁴ Theoretical calculations indicated that blue-p has a wider E_g and a higher hole mobility (1700 cm² V⁻¹ s⁻¹) than black-p.^15,16

Despite these advantages of phosphorene, black-p and blue-p have poor structural stability at ambient conditions in the presence of water and oxygen molecules.^17–20 Enhanced stability was reported in few-layer black-p flakes, which were passivated by Al₂O₃.^21,22 The multilayer black-p was predicted to demonstrate better stability than its 1L counterpart.²³ In this sense, chemically stable 2D materials can be considered as capping layers to protect phosphorene from ambient degradation.^24,25

Zinc oxide (ZnO) is a key technological material which is well known for its versatile properties and applications in photocatalysts,²⁶ solar cells,²⁷ piezoelectrics,²⁸ etc. Graphitic zinc oxide (g-ZnO) is the 2D form of bulk ZnO.^29–31 Compared with bulk ZnO, little is known about g-ZnO although it has been confirmed experimentally for several years.²⁹ Importantly, previous theoretical and experimental works have shown that g-ZnO is chemically stable.^29–31 Yao et al. found that g-ZnO is a suitable substrate for graphene in real applications.³² A natural question arises: can g-ZnO be used to protect the intrinsic electronic properties of phosphorene? Van der Waals (vdW) heterostructures based on the integration of 2D materials have presented abundant opportunities for applications in light-emitting^33,34 and photoelectric devices.^35,36 In the design of these devices, the electrically controlled E_g and efficient carrier confinement or separation are crucial.^34,35,37 However, the E_g type and band alignment are usually fixed,^38–41 e.g., black-p/MoS₂³⁸ and black-p/blue-p,³⁹ which limits the multifunctionality of the devices. Considering that the heterostructures are often subjected to an electric field (E) when applied to nano-electronic devices, another question arises: can black(blue)-p/g-ZnO vdW heterostructures have electrically tunable electronic properties for the above applications?

2 Computational methods

First-principles calculations were performed using the VASP code^42,43 with the PAW method.⁴⁴ We approximated the exchange–correlation potential with the PBE functional.⁴⁵ A plane-wave cutoff of 750 eV was used throughout. 14 × 2 × 2(16 × 16 × 1) k-point meshes⁴⁶ were used for the black-p(blue-p)/g-ZnO heterostructures. Using these parameters, an energy convergence of less than 0.015 meV per atom was achieved.⁴⁷ The crystal structures were relaxed until the inter-atomic forces were smaller than 0.01 eV Å⁻¹. A vacuum space of 15 Å was used in the direction normal to the layers. The vdW-DF method was used to describe the vdW interactions.⁴⁸ Since the E_g is usually underestimated by DFT, e.g., the PBE calculated E_g of black-p is 0.93 eV while the experimental value is 1.45 eV,⁴⁹ the electronic and optical properties were calculated using the HSE06 hybrid functional.⁵⁰

3 Results and discussion

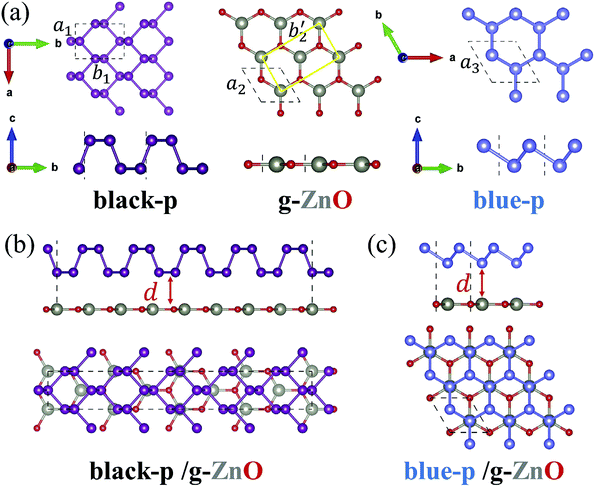
We first obtained the equilibrium structures of black-p, g-ZnO and blue-p. As shown in Fig. 1(a), the calculated lattice constants of black-p, g-ZnO and blue-p were a₁(b₁) = 3.299(4.613) Å, a₂ = 3.289 Å and a₃ = 3.278 Å, respectively, which agreed well with previous theoretical and experimental values.^{14,29–31,39} To construct blue-p/g-ZnO, the lattice constant was set to 3.283 Å so that the maximum lattice mismatch was just 0.16%. For black-p/g-ZnO, we first changed the primitive cell of g-ZnO to a rectangle unit cell with a₂ = 3.289 Å and b′₂ = 5.696 Å, then the heterostructure consisted of a 1 × 5 × 1 primitive cell of black-p and a 1 × 4 × 1 rectangle unit cell of g-ZnO. The lattice constants of black-p/g-ZnO were a = 3.294 Å and b = 22.925 Å and the maximum lattice mismatches were only Δa = 0.15% and Δb = 0.62%. Thus, g-ZnO had well-matched lattice constants with respect to black(blue)-p.

Fig. 1 The top view (upper panel) and side view (lower panel) of (a) the three single layers, (b) black-p/g-ZnO and (c) blue-p/g-ZnO. The dotted lines in (a) denote the primitive cells. The yellow solid lines in (a) denote the rectangle unit cell of g-ZnO. The dotted lines in (b) and (c) denote the heterostructures.

To get the most stable black-p/g-ZnO, we moved the black-p along the armchair direction while the g-ZnO was kept fixed. Meanwhile, the relative displacement between the black-p and g-ZnO along the zigzag direction was considered. Then we relaxed all the possible patterns of heterostructures and obtained the corresponding total energies. For blue-p/g-ZnO there were AA, AB and C patterns.⁵¹ Other typical patterns are provided in the ESI†.⁴⁷ The most stable patterns are shown in Fig. 1(b) and (c). We found that the AB pattern, where the lower P atoms were just above the Zn atoms, was the most stable pattern of the blue-p/g-ZnO, which is similar to the case of h-BN/graphene.⁵¹ In the relaxed structure of isolated g-ZnO, the Zn and O atoms formed a hexagonal plane,³² which could also be seen in the blue-p/g-ZnO. In the black-p/g-ZnO however, the Zn and O atoms had little buckling height (h_Zn–O) along the c direction even when we relaxed the black-p/g-ZnO without fixing the in-plane lattice constants. The maximum h_Zn–O (0.34 Å) we achieved was within the scope of the experimental value,²⁹ where the g-ZnO grown on Ag(111) showed a h_Zn–O of 0.12–0.58 Å. Besides, the average h_Zn–O of the black-p/g-ZnO was just 0.007 Å. The calculated E_gs of the isolated g-ZnO without h_Zn–O and that with h_Zn–O in the black-p/g-ZnO were 3.29 and 3.27 eV, respectively, suggesting that the very small strain and the h_Zn–O have negligible effects on the electronic properties.

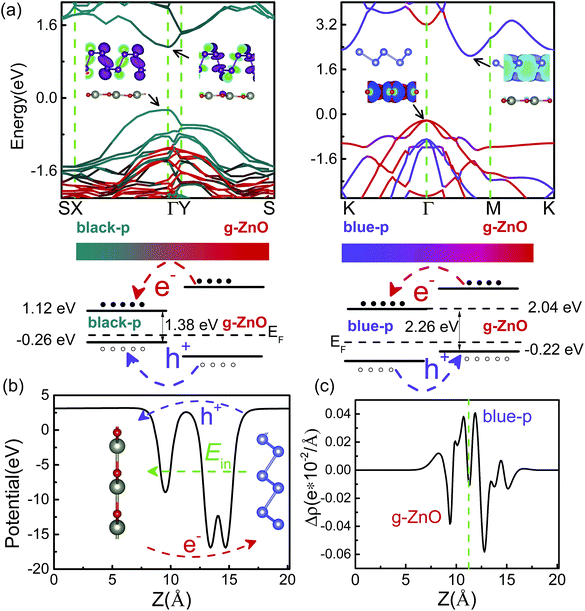
The interlayer distance (d) of the black(blue)-p/g-ZnO was 3.23(3.44) Å. The binding energy (E_b) of the black(blue)-p/g-ZnO, which was calculated by E_b = E[black(blue)-p/g-ZnO] − E[black(blue)-p] − E(g-ZnO), was 34.82(23.55) meV per atom. Note that different strategies in describing the vdW interactions often lead to marked differences in quantifying the E_b(d). The predicted E_b(d) of black-p/g-ZnO was 43.32(3.09), 50.23(2.95) and 52.39(2.79) meV per atom (Å) by optPBE,⁵² optB88 (ref. 52) and DFT+D3,⁵³ respectively. OptPBE, optB88 and DFT+D3 predicted that the E_b(d) of blue-p/g-ZnO was 31.98(3.2), 38.79(3.09) and 40.67(2.86) meV per atom (Å), respectively. Clearly, all the vdW functionals employed here gave qualitatively consistent results about the relative amplitude relation of E_b(d) for the two heterostructures, i.e., the black-p/g-ZnO had a larger (lower) E_b(d) than the blue-p/g-ZnO. Besides, other main conclusions (e.g., the most stable patterns of heterostructures and the electric field induced E_g crossover) were also not affected by the choice of vdW functional. Therefore, in what follows we just show the results using vdW-DF.⁴⁸ The E_b(d) values obtained by other vdW functionals can be used as references for experimental measurements. As shown in Fig. 2(a), the black-p/g-ZnO displayed a direct E_g of 1.38 eV, and both the valence band maximum (VBM) and conduction band minimum (CBM) were located at the Γ point. Whereas blue-p/g-ZnO showed an indirect E_g of 2.26 eV, and the VBM was located at the Γ point while the CBM lay between the Γ and M points. Compared with isolated black(blue)-p (Fig. S3†), the direct(indirect) E_g character of black(blue)-p was kept and the E_g of black/g-ZnO was nearly unchanged, while the E_g of blue/g-ZnO decreased to 2.26 eV. To understand this, the band structures of black-p(blue)/g-ZnO were projected to their components. We can see that both the VBM and CBM of black-p/g-ZnO were contributed by black-p, suggesting the type-I heterostructure. For blue-p/g-ZnO, the VBM was contributed by g-ZnO while the CBM was distributed on blue-p, indicating the type-II heterostructure. From Fig. 2(a) and S3,† we can also see the main energy-band dispersion of isolated blue-p in blue/g-ZnO. Thus, the above results imply that g-ZnO can be used as a potential capping layer to protect the main electronic characters of phosphorene, especially black-p. The band alignments of heterostructures are even more important than the band structures in material and device design. Type-I band alignment of black-p/g-ZnO can facilitate the radiative recombination of holes and electrons, which is desirable in light-emitting applications.³³ Type-II band alignment of blue-p/g-ZnO is one of the key factors for the efficient separation of photogenerated electron–hole pairs, which can increase the carriers’ lifetime and is desired for applications in photodetection and photovoltaics.^35,36 The photogenerated electrons of g-ZnO can be easily transferred to the CB of blue-p while the photogenerated holes of blue-p have the counter movement, i.e., from blue-p to the VBM of g-ZnO. As a result, the energy-wasted electron–hole recombination could be greatly reduced. We can gain further insight from the band decomposed charge densities of VBM(CBM). As shown in the inset of Fig. 2(a), all the charge carriers are confined in the black-p, while the lowest-energy electrons and holes of blue-p/g-ZnO are spatially localized on the blue-p and g-ZnO, respectively. Another key factor which efficiently separates the electrons and holes is the large built-in electric field (E). Thus we plotted the average in-plane electrostatic potential of blue-p/g-ZnO. Fig. 2(b) clearly shows the significant potential difference at the interface region, indicating the large built-in E, which promotes the transition of electrons(holes). The transfer of carriers can also be seen from the differential charge density (eqn S4†). As shown in Fig. 2(c), the negative(positive) values denote the accumulation of electrons(holes) at the blue-p(g-ZnO), indicating that the p-type g-ZnO and n-type blue-p form a type-II p–n heterostructure.

Fig. 2 (a) The band structures of black-p/g-ZnO (left panel) and blue-p/g-ZnO (right panel). The color scales denote the contributions from the single layers. Inset is the band decomposed charge density of VBM(CBM). The isosurface value is 0.001 e⁻ bohr⁻³. Schematics of the band alignments are also shown. (b) The average electrostatic potential and (c) differential charge density of blue-p/g-ZnO along the z direction. E_in is the built-in electric field. The negative(positive) values of Δρ denote the gain(loss) of electrons.

As an efficient photoelectric device, it should absorb as much visible-UV light as possible. Thus we studied the optical absorption by calculating the frequency dependent dielectric function in the independent-particle picture. As shown in Fig. 3, the black-p/g-ZnO exhibited stronger visible-UV light absorption than its components, especially in the energy range of ∼2.12 to 5 eV. The blue-p/g-ZnO showed a wider absorption range and overall stronger visible-UV light absorption in the energy range of ∼2.4 to 4.5 eV. The enhanced optical absorption can be understood from the interlayer coupling and charge transfer in the heterostructures, where the electronic states overlap and the new optical transitions are induced.

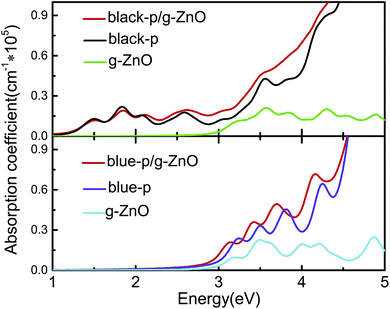Fig. 3 Absorption coefficients of black(blue)-p/g-ZnO and the components. The imaginary parts of the dielectric functions are averaged over all the directions.

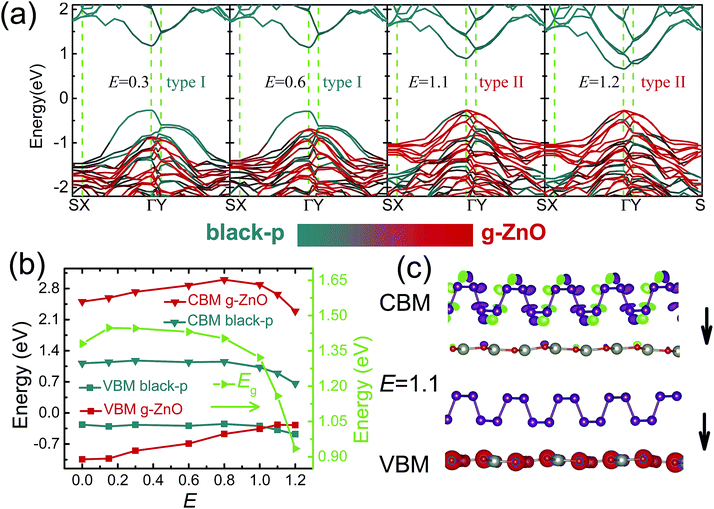
Finally, we will discuss the effect of E on the electronic properties. A positive E from black(blue)-p to g-ZnO is introduced. Table 1 shows the structural information of heterostructures without external E and with E = 1.2 V Å⁻¹. It was found that the relaxed bond lengths and bond angles were hardly affected by the E. Only the interlayer distances had relatively small changes. Besides, the band-gaps of black-p/g-ZnO and blue-p/g-ZnO at E = 1.1 V Å⁻¹ were 1.16 and 1.24 eV, respectively, indicating the character of semiconductors. Therefore, our results show that the structures of the heterostructures were still undamaged in such a strong electric field.^54–57

Table 1 Structural information of heterostructures at E = 0 and E = 1.2 V Å⁻¹. d is the interlayer distance (Å). P–P and Zn–O denote the average bond lengths (Å). P–P–P and Zn–O–Zn are the average bond angles (degrees)

E	d	P–P	Zn–O	P–P–P	Zn–O–Zn
Black-p/g-ZnO
0	3.23	2.26	1.91	103.42	120.04
1.2	3.26	2.25	1.91	103.29	119.78
Blue-p/g-ZnO
0	3.44	2.27	1.9	92.66	120
1.2	3.54	2.27	1.9	92.63	119.49

---

As seen in Fig. 4(a) and (b), the E initially exerted little influence on the E_g of black-p/g-ZnO. This is because both the VBM and CBM of black-p were nearly unchanged at first. In contrast to black-p, the VBM and CBM of g-ZnO linearly increased with E when the E was less than 0.8 V Å⁻¹. Thus the energy difference between the VBM of black-p and the VBM of g-ZnO gradually decreased. The VBM of black-p began to decrease at E = 0.8 V Å⁻¹, while the VBM of g-ZnO continued to increase with E. When the E increased to 1.1 V Å⁻¹, the VBM of g-ZnO became the VBM of the black-p/g-ZnO. This can be clearly seen in Fig. 4(a) (E = 1.1 V Å⁻¹), where g-ZnO played the dominant role for the contributions of VBs around the Fermi level and the VBM was fully occupied by the O-p_x and Zn-d_xy states of g-ZnO. At the same time, the CBM of the black-p/g-ZnO was still contributed by the black-p, thus type-I-to-type-II E_g crossover occurred. From Fig. 4(c) we can see the lowest-energy electrons and holes located at different layers.

Fig. 4 (a) The effect of E on the band structures of black-p/g-ZnO. (b) The evolution of VBM(CBM) of black-p/g-ZnO with E. The Fermi level is set as zero. (c) The band decomposed charge density of VBM(CBM) of black-p/g-ZnO at E = 1.1 V Å⁻¹. The arrows denote the direction of the vertical electric field. The color scales denote the contributions from the single layers. The isosurface value is 0.001 e⁻ bohr⁻³.

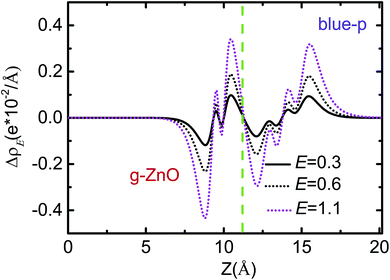
As shown in Fig. 5 and S5,† the E_g of blue-p/g-ZnO linearly decreased with increasing E, showing a giant Stark effect. The indirect gap character and type-II band alignment were not affected by the E at first. However, the CBM of blue-p shifted to the Γ point when the E increased to 1.1 V Å⁻¹, forming the direct E_g. The indirect-to-direct transition of E_g was greatly beneficial to the transition of photogenerated electrons from the VBM of g-ZnO to the CBM of blue-p as the momentum was preserved in this process. When the E increased to 1.2 V Å⁻¹, the E_g sharply reduced to nearly zero (0.08 eV), but the direct E_g character was kept. It was expected that the blue-p/g-ZnO would be a metal when the E increased further. This is different from the case of black-p/g-ZnO, which was still a semiconductor at E = 1.2 V Å⁻¹. Notably, the E_in and E had the same potential direction and the interlayer coupling was enhanced when the external E was introduced, which can be clearly seen in Fig. 6. The enhanced interaction can offer improved carrier separation performance in blue-p/g-ZnO.

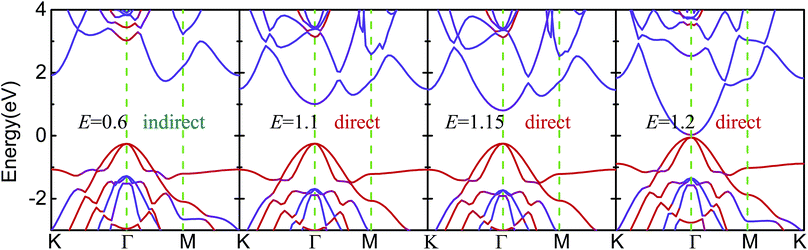Fig. 5 The effect of E on the band structures of blue-p/g-ZnO. The color scales denote the contributions from the single layers. The “direct” and “indirect” denote the types of E_g.

Fig. 6 The effect of E on the differential charge density of blue-p/g-ZnO.

4 Conclusion

In summary, we have theoretically studied the electronic and optical properties of vdW heterostructures black(blue)-p/g-ZnO by means of hybrid density functional calculations. Although the black(blue) phosphorus/g-ZnO is found to show an intrinsic type-I(type-II) band alignment with direct(indirect) band-gap, a vertical electric field can induce a type-I-to-type-II transition for the black phosphorus/g-ZnO and modulate the band edges of blue phosphorus/g-ZnO to get a direct band-gap at the Γ point. Moreover, improved visible-UV light absorption is demonstrated in the heterostructures. Our results indicate that g-ZnO can be used not only as a capping layer to protect the electronic characteristics of phosphorene, but also as an active layer to tune the electronic and optical properties of phosphorene.

Acknowledgements

Wei Zhang thanks Dr Weixiao Ji, Prof. Xianqi Dai and Dr Yaqiang Ma for their help. We acknowledge the support from the Basic Research Project of Central University (LGYB201715), the National Natural Science Foundation of China (11574154) and the open project (201702) of Jiangsu Provincial Key Laboratory for Numerical Simulation of Large Scale Complex Systems.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197.
3. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699.
4. T. Heine, Acc. Chem. Res., 2015, 48, 65.
5. K. S. Novoselov, D. Jiang, T. J. Booth, W. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451.
6. L. K. Li, Y. J. Yu, G. J. Ye, Q. Q. Ge, X. D. Ou, H. Wu, D. L. Feng, X. H. Chen and Y. B. Zhang, Nat. Nanotechnol., 2014, 9, 372.
7. A. Castellanos, et al., 2D Mater., 2014, 1, 025001.
8. H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. F. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033.
9. B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147.
10. M. S. Fuhrer and J. Hone, Nat. Nanotechnol., 2013, 8, 146.
11. S. P. Koenig, R. A. Doganov, H. Schmidt, A. C. Neto and B. Özyilmaz, Appl. Phys. Lett., 2014, 104, 103106.
12. F. Schwierz, Nat. Nanotechnol., 2010, 5, 487.
13. Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 112, 176802.
14. J. L. Zhang, S. T. Zhao, C. Han, Z. Z. Wang, S. Zhong, S. Sun, R. Guo, X. Zhou, C. D. Gu, K. D. Yuan, Z. Y. Li and W. Chen, Nano Lett., 2016, 16, 4903.
15. B. Ghosh, S. Nahas, S. Bhowmick and A. Agarwal, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115433.
16. J. Xiao, M. Q. Long, X. J. Zhang, J. Ouyang, H. Xu and Y. L. Gao, Sci. Rep., 2015, 5, 09961.
17. X. Liu, J. D. Wood, K. S. Chen, E. Cho and M. C. Hersam, J. Phys. Chem. Lett., 2015, 6, 773.
18. J. O. Island, G. A. Steele, H. S. J. van der Zant and A. Castellanos-Gomez, 2D Mater., 2015, 2, 011002.
19. G. X. Wang, W. J. Slough, R. Pandey and S. P. Karna, 2D Mater., 2016, 3, 025011.
20. Y. Zhao, et al., Angew. Chem., Int. Ed., 2016, 55, 5003.
21. J. Na, Y. T. Lee, J. A. Lim, D. K. Hwang, G. T. Kim, W. K. Choi and Y. W. Song, ACS Nano, 2014, 8, 11753.
22. X. Luo, J. C. M. Hwang, H. Liu, Y. Du and P. D. Ye, IEEE Electron Device Lett., 2014, 35, 1314.
23. Y. Q. Cai, G. Zhang and Y. W. Zhang, Sci. Rep., 2014, 4, 6677.
24. Y. Shi, et al., Nano Lett., 2012, 12, 2784.
25. G. R. Berdiyorov, M. Neek-Amal, F. M. Peeters and A. C. T. van Duin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 024107.
26. K. Maeda, T. Takata, M. Hara, N. Saito, Y. Inoue, H. Kobayashi and K. Domen, J. Am. Chem. Soc., 2005, 127, 8286.
27. M. Law, L. E. Greene, J. C. Johnson, R. Saykally and P. Yang, Nat. Mater., 2005, 4, 455.
28. S. J. Chang, T. J. Hsueh, I. C. Chen and B. R. Huang, Nanotechnology, 2008, 19, 175502.
29. C. Tusche, H. L. Meyerheim and J. Kirschner, Phys. Rev. Lett., 2007, 99, 1026102.
30. H. T. Quang, A. Bachmatiuk, A. Dianat, F. Ortmann, J. Zhao, J. H. Warner, J. Eckert, G. Cunniberti and M. H. Rümmeli, ACS Nano, 2015, 9, 11408.
31. J. Lee, D. C. Sorescu and X. Deng, J. Phys. Chem. Lett., 2016, 7, 1335.
32. Q. S. Yao, Y. Z. Liu, R. F. Lu, C. Y. Xiao, K. M. Deng and E. J. Kan, RSC Adv., 2014, 4, 17478.
33. Z. H. Lu, D. J. Lockwood and J. M. Baribeau, Nature, 1995, 378, 258.
34. X. W. Gong, et al., Nat. Photonics, 2016, 10, 253.
35. Z. Wang, H. Yin, C. Jiang, M. Safdar and J. He, Appl. Phys. Lett., 2012, 10, 253109.
36. F. Wang, Z. X. Wang, K. Xu, F. M. Wang, Q. S. Wang, Y. Huang, L. Yin and J. He, Nano Lett., 2015, 15, 7558.
37. J. Kim, et al., Science, 2015, 349, 723.
38. L. Huang, Y. Li, Z. M. Wei and J. B. Li, Sci. Rep., 2015, 5, 16448.
39. L. Huang and J. B. Li, Appl. Phys. Lett., 2016, 108, 083101.
40. W. Y. Yu, Z. L. Zhu, S. L. Zhang, X. L. Cai, X. Wang, C. Y. Niu and W. B. Zhang, Appl. Phys. Lett., 2016, 109, 103104.
41. P. Chen, et al., Nanoscale, 2016, 8, 3254.
42. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
43. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
44. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
46. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
47. See ESI.†.
48. M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, 2D Mater., 2004, 92, 246401.
49. H. Liu, et al., ACS Nano, 2014, 8, 4033.
50. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
51. Y. C. Fan, M. W. Zhao, Z. H. Wang, X. J. Zhang and H. Y. Zhang, Appl. Phys. Lett., 2011, 98, 083103.
52. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
53. S. Grimme, J. Antony, S. Ehrlich and S. Krieg, J. Chem. Phys., 2010, 132, 154104.
54. G. X. Wang, R. Pandey and S. P. Karnab, Nanoscale, 2015, 7, 524.
55. I. Choudhuri, P. Garga and B. Pathak, J. Mater. Chem. C, 2015, 4, 8253.
56. J. Zhou, Q. Wang, Q. Sun, Y. Kawazoe and P. Jena, Phys. Chem. Chem. Phys., 2015, 17, 17182.
57. D. Nafday, M. Kabir and T. Saha-Dasgupta, Phys. Rev. B, 2016, 93, 045433.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra06097a

---