Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Binder free 2D aligned efficient MnO2 micro flowers as stable electrodes for symmetric supercapacitor applications†
Anil A. Kashaleac,
Madagonda M. Vadiyarb,
Sanjay S. Kolekarb,
Bhaskar R. Sathec,
Jia-Yaw Chang *d,
Hom N. Dhakal
*d,
Hom N. Dhakal e and
Anil V. Ghule
e and
Anil V. Ghule *ab
*ab
aDepartment of Nanotechnology, Dr Babasaheb Ambedkar Marathwada University, Aurangabad 431004, Maharashtra, India
bDepartment of Chemistry, Shivaji University, Kolhapur 416004, Maharashtra, India. E-mail: anighule@gmail.com; avg_chem@unishivaji.ac.in
cDepartment of Chemistry, Dr Babasaheb Ambedkar Marathwada University, Aurangabad 431004, Maharashtra, India
dDepartment of Chemical Engineering, National Taiwan University of Science and Technology, Taipei 10607, Taiwan. E-mail: jychang@mail.ntust.edu.tw
eSchool of Engineering, University of Portsmouth, Hampshire PO1 3DJ, UK
First published on 25th July 2017
Abstract
Herein, δ-MnO2 micro-flower thin films are grown directly onto a stainless steel mesh via a simple rotational chemical bath deposition technique. Moreover, the influence of the concentration of precursor ratio of MnSO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMnO4 is investigated and the obtained samples are designated as M1 (KMnO4
KMnO4 is investigated and the obtained samples are designated as M1 (KMnO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MnSO4 = 3
MnSO4 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), M2 (KMnO4
1), M2 (KMnO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MnSO4 = 3
MnSO4 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and M3 (KMnO4
2) and M3 (KMnO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MnSO4 = 3
MnSO4 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3). The concentration of MnSO4 as a starting material has a significant influence on the reaction kinetics, which subsequently alters the morphology and also the electrochemical performance. Among these three electrodes, the M1 electrode exhibits a high specific capacitance of 376 F g−1 at a current density of 5 mA cm−2 and a high specific energy of 52 W h kg−1, which is higher than M2 (specific capacitance 312 F g−1 and specific energy 43 W h kg−1) and M3 (specific capacitance 283 F g−1 and specific energy 39 W h kg−1) electrodes. Due to the interesting performance of the M1 based electrode, the symmetric device is fabricated using two electrodes M1 (3
3). The concentration of MnSO4 as a starting material has a significant influence on the reaction kinetics, which subsequently alters the morphology and also the electrochemical performance. Among these three electrodes, the M1 electrode exhibits a high specific capacitance of 376 F g−1 at a current density of 5 mA cm−2 and a high specific energy of 52 W h kg−1, which is higher than M2 (specific capacitance 312 F g−1 and specific energy 43 W h kg−1) and M3 (specific capacitance 283 F g−1 and specific energy 39 W h kg−1) electrodes. Due to the interesting performance of the M1 based electrode, the symmetric device is fabricated using two electrodes M1 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and represented as SSM/M1//M1/SSM. The device provides a maximum specific capacitance of 87 F g−1 and specific energy density of 32 W h kg−1 at a current density of 5 mA cm−2. In addition, the symmetric device of the M1 electrode also exhibits good cycle stability showing 138% capacitance retention up to 2500 cycles. The enhanced electrochemical performance could be attributed to the direct growth of micro-flowers of MnO2 on a stainless steel mesh, which provides more pathways for easy diffusion of electrolyte ions into the electrode. This study provides new insight and pathways for the development of low-cost and high-performance energy storage devices.
1) and represented as SSM/M1//M1/SSM. The device provides a maximum specific capacitance of 87 F g−1 and specific energy density of 32 W h kg−1 at a current density of 5 mA cm−2. In addition, the symmetric device of the M1 electrode also exhibits good cycle stability showing 138% capacitance retention up to 2500 cycles. The enhanced electrochemical performance could be attributed to the direct growth of micro-flowers of MnO2 on a stainless steel mesh, which provides more pathways for easy diffusion of electrolyte ions into the electrode. This study provides new insight and pathways for the development of low-cost and high-performance energy storage devices.
1. Introduction
Increasing environmental issues and depleting natural energy sources such as coal, gas, and oil have created the need to develop green and sustainable energy sources coupled with energy conversion and energy storage capabilities. In line with this concern, researchers have mostly focused on the development of energy storage devices such as capacitors, accumulators, supercapacitors, and batteries.1–5 Among these energy storage devices, supercapacitors are considered to be a promising alternative taking into consideration their fast charge–discharge rate, long cycle life, and high power density compared to conventional capacitors and batteries.3,6 Based on the charge storage mechanism, supercapacitors are classified into electrical double layer capacitors (EDLCs) and redox supercapacitors (pseudocapacitors).7–10 In EDLCs, the capacitance comes from the charge separation at electrode/electrolyte interfaces7,9 and in the case of pseudocapacitors, the capacitance arises from faradaic reaction at the electrode/electrolyte surface.8,9 Recently, researchers have paid more attention towards pseudocapacitor because of the associated higher energy storage capacity compared to carbon-based electrodes (i.e. EDLCs).3 To date, various transition metal oxides viz. Co3O4,11 MnO2,12 NiO,13,14 RuO2,15 V2O5,16 etc. have been explored in pseudocapacitors as an electrode material. Among these candidates, MnO2 is considered as the most promising electrode material in terms of its low cost, natural abundance, high theoretical capacity (1370 F g−1), high voltage window in aqueous electrolyte and more environment-friendly than other transition metal oxides.17–22 MnO2 naturally occurs in five allotropic forms viz. α, β, γ, δ and λ. Among these, α, β and γ take a one-dimensional structure, while δ and λ forms two and three-dimensional structures, respectively.23,24 These structural differences are responsible for the significant differences in their electrochemical properties. A good capacitor requires structures with enough structural gaps, properly sized tunnels or well-separated layers, facilitating intercalation/de-intercalation for a maximum number of electrolytic ions. Hence, the reported specific capacitance (SC) values for different allotropes of MnO2 are in the order of α = δ > γ > λ > β.24,25 Among α and δ allotropes, δ-MnO2 is preferred for supercapacitor application due to its 2-dimensional layered structure. The interlayer galleries provide high-speed pathways for diffusion of alkali cations or protons during the charge and discharge processes resulting in improved capacitance and rate behavior compared to other polymorphs.26,27 However, δ-MnO2 materials are prepared in both thin film28–34 and powder forms.24,35–38 Among these two forms, the direct growth of δ-MnO2 thin films is preferable, as the composite powder needs to be coated onto a suitable substrate using an appropriate amount of binder and conducting agent. This decreases the electrochemically active surface area and increases the mass of the electrode, resulting in an increase in contact resistance and a decrease in performance.29,39 On the other hand, direct growth of MnO2 film reduces the contact resistance and leads to enhanced electrochemical performance.40The recent reports for direct growth of MnO2 thin films include electrodeposition,41 sol–gel,42 successive ionic layer adsorption and reaction (SILAR),30,43 hydrothermal44 and chemical bath deposition (CBD) methods.45 Among this, CBD is a soft chemical, environmentally friendly and cost-effective method; suitable for large scale production. The shorter deposition times and lower reaction temperature makes this method more charming. Moreover, features of these materials such as morphology, structure, dimensions, and phase can be easily controlled through adjusting preparative parameters such as the reaction temperature, reaction time, concentration of matrix solution, reducing and a complexing agent, etc. Generally, MnO2 thin films are synthesized either using KMnO4 or MnSO4 precursors. However, there are very few reports on the synthesis of the MnO2 thin films using a mixture of KMnO4 and MnSO4 precursors with an appropriately varying ratio. For example, Sarkar et al.28 synthesized MnO2 thin film on stainless steel substrate using a mixture of KMnO4 and MnSO4 precursors and reported the maximum specific capacitance of 360 F g−1 at 0.82 A g−1 current density.
With this motivation, herein this work, we have successfully synthesized δ-MnO2 micro-flowers thin films directly onto the stainless steel mesh (300 meshes) by using modified rotational CBD method. In addition, the influence of KMnO4 and MnSO4 concentration on the formation of an electrode of the micro-flowers of MnO2 is investigated for the first time. Moreover, the electrochemical properties of the individual electrode and symmetric supercapacitor device were explored for their practical application.
2. Experimental
2.1 Materials and chemicals
Stainless steel mesh (SSM) substrate with 300 mesh size was purchased from Micro Mesh India Private Limited. The starting chemicals KMnO4 and MnSO4·H2O were commercially purchased from Sigma Aldrich chemicals. All the chemicals were used as received without further purification.2.2 Synthesis of MnO2 on SSM
In a typical synthesis, the MnO2 thin film is directly grown on SSM by simple rotational chemical bath deposition (CBD) method. Initially, the precursor solutions of aqueous 0.3 M KMnO4 and 0.1 M MnSO4·H2O were prepared separately and mixed together under constant stirring for 5 min. Meanwhile, SSM substrates of 1 cm × 3 cm dimensions were ultrasonically cleaned in successive steps by soaking into a detergent soap solution, distilled water and acetone, subsequently for 30 min each. These pre-cleaned substrates were immersed carefully into the precursor bath solution, which was subsequently heated to a temperature of 70 °C. The immersed substrates were rotated with a gear motor at 55 rpm for 3 h till the formation of brown-black precipitate in the bath solution. In the reaction bath, a heterogeneous reaction occurs and the thin film of MnO2 based solid mass is formed on the SSM substrate. After 3 h, the substrates were taken out, washed with deionized water, dried in air and labeled as M1. For better comparison, similar procedure except for varying the molar ratio of MnSO4 with respect to the KMnO4 (0.3 M) was used to synthesis MnO2 thin films. The films with molar ratio of (KMnO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MnSO4) = (0.3
MnSO4) = (0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2) and (KMnO4
0.2) and (KMnO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MnSO4) = (0.3
MnSO4) = (0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3) were labelled as M2 and M3, respectively. The weight of MnO2 deposited on SSM substrate decreases with increasing concentration of MnSO4, which indicates that the rate of formation of MnO2 increases with increasing concentration of MnSO4. The weights of MnO2 deposited on SSM substrate are 0.9 mg, 0.7 mg, and 0.5 mg for M1, M2, and M3, respectively.
0.3) were labelled as M2 and M3, respectively. The weight of MnO2 deposited on SSM substrate decreases with increasing concentration of MnSO4, which indicates that the rate of formation of MnO2 increases with increasing concentration of MnSO4. The weights of MnO2 deposited on SSM substrate are 0.9 mg, 0.7 mg, and 0.5 mg for M1, M2, and M3, respectively.
2.3 Material characterizations
X-ray diffraction (XRD) (Bruker, D2-Phaser X-ray diffractometer) with CuKα1 (λ = 1.5406 Å) radiation in the range 20–80° and scanning electron microscopy (SEM, JEOL JSM-6360) was used to characterize the crystal structure, phase identification and the morphology of the samples.2.4 Electrochemical measurements
All the electrochemical studies were performed in 1 M Na2SO4 aqueous electrolyte at room temperature using a CHI 608E Electrochemical Analyser. Cyclic voltammetry (CV), galvanostatic charge–discharge (GCD) and electrochemical impedance spectroscopy (EIS) measurements were carried out using the standard three-electrode system with MnO2/SSM, graphite and a saturated Ag/AgCl electrode as the working, counter and a reference electrode, respectively. The CV curves were measured with varying scan rates of 10–100 mV s−1 between the optimized potential window ranges of −0.2 to 0.8 V vs. saturated Ag/AgCl electrode. EIS measurements were performed in the frequency range of 1000 kHz to 1 Hz at an open circuit potential with an ac perturbation of 5 mV. The specific capacitance of the MnO2 based supercapacitor system was calculated from the GCD curves according to the following eqn (1) reported in the literature.2,15,46–49
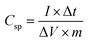 | (1) |
The power density (P, kW kg−1) and energy density (E, W h kg−1) of three-electrode and the two-electrode (symmetric capacitor) configuration are calculated from the galvanostatic charge–discharge curves by using the eqn (2) and (3) reported in the literature.2,46–48
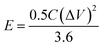 | (2) |
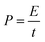 | (3) |
In the fabrication of thin film based symmetric supercapacitor, the as-synthesised two M1/SSM electrodes with dimensions of 1 cm × 1 cm were used as a negative and positive electrode. These two electrodes were separated by a filter paper as a separator and the assembly was soaked into 1 M Na2SO4 solution for about 24 h. The filter paper is used as a membrane (separator) which allows the easy ion transfer process and furthermore it is nontoxic and economic. In addition, the filter paper also has another important advantage i.e. it hinders the contact between the two electrodes. Then, the device was encompassed between a pair of glasses and inserted into a small bottle to avoid leakage of the electrolyte. The values of the specific capacitance, energy density, and power density were normalized based on the total mass of electrode material excluding the mass of SSM. This mass was calculated by using simple weight difference method, wherein, the value for negative electrode (M1/SSM) and also for the positive electrode (M1/SSM) was noted to be 0.9 mg.
3. Results and discussion
The formation of MnO2 micro-flowers takes place with two different reactants involved in the reaction undergoing oxidation and reduction. MnSO4 follows oxidation reaction from Mn2+ to Mn4+, while KMnO4 follows reduction process from Mn7+ to Mn4+ controlling the reaction kinetics which is interesting.24,50,51 The possible reaction mechanism for both oxidation and reduction reaction is as follows;| 3MnSO4 + 2KMnO4 + 2H2O → 5MnO2 + K2SO4 + 2H2SO4 |
3.1 X-ray diffraction (XRD)
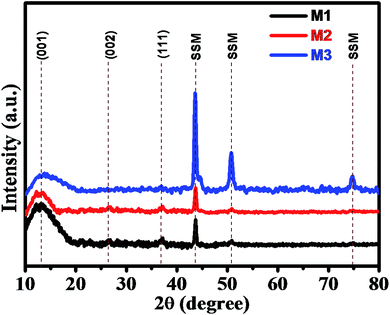
The superimposed X-ray diffraction (XRD) patterns of all three as-deposited thin films (M1, M2, and M3) are shown in Fig. 1 to confirm the phase composition of the product. From the XRD pattern, broad and weak reflection peaks were observed, which indicates that all the three thin films are amorphous in nature. The broader peaks were observed at around 12° 26° and 37°, which correspond to the (001) (002) and (111) planes of MnO2, respectively. These characteristic peaks indicate that the as-deposited synthesized thin films belong to birnessite δ-MnO2 structure. The XRD pattern is in good agreement with the diffraction peaks reported in JCPDS card no. 80-1098.6,52 The peak broadening or poor intensity may be due to the small particle size and distorted structure of the deposited thin films. Apart from these peaks, we observed some extra peaks at 43°, 51° and 75° due to the exposed stainless steel mesh substrate, which was in good agreement with the XRD pattern of bare SSM substrate prior to MnO2 deposition (Fig. S2†). Here, we have again confirmed the δ-MnO2 phase of synthesized thin film by obtaining the XRD spectrum of the precipitated powder as shown in Fig. S1.† In the XRD pattern obtained from the powder, we clearly observe well-defined diffraction peaks and absence of substrate peaks. These diffracted peaks are in good agreement with the standard pattern of birnessite δ-MnO2 phase (JCPDF 80-1098),6,52 exhibiting (001), (002), (111) and (020) planes. The spectrum shows the growth of pure δ-phase of MnO2 with monoclinic amorphous (C2/m space group) δ-MnO2 thin films (JCPDS 80-1098). More significantly, the (001) and (002) peaks in δ-MnO2 correspond to its layered structure.3.2 Scanning electron microscopy (SEM)
The morphology of the synthesized MnO2 thin film electrodes (M1, M2, and M3) was confirmed by using scanning electron microscope (SEM) with different magnification. Fig. 2 presents SEM images of M1, M2 and M3 samples at low and high magnifications. From the figure, it is noted that the synthesized δ-MnO2 shows micro-flowers like morphology. The high-resolution SEM images reveal that the micro-flowers are composed of a bunch of vertically aligned thin nanosheet-like petals. The density of micro-flowers on the electrode surface decreases in the order M1 > M2 > M3, which also confirms the decrease in weight with increasing MnSO4 concentration. This could be due to the increase in the rate of formation of MnO2 material. Furthermore, a decrease in the size of the micro-flower is observed with increasing MnSO4 concentration, which might be due to sufficient time availed for the formation of micro-flowers on SSM substrate. The diameter of the micro-flowers of M1, M2, and M3 samples was found to be ∼0.5, ∼0.25 and ∼0.20 μm, respectively. The increased size of micro-flowers in M1 can be attributed to the lower reaction rate providing sufficient time for growth. The diameter of the M1 micro-flower is larger as compared to M2 and M3 micro-flowers. It means that the length of the nanosheets in M1 micro-flowers is higher, indicating a higher surface area to accumulate a large number of charges and are well developed as compared to M2 and M3. These advantages of M1 are significant for supercapacitor electrode materials demonstrating high specific capacitance and high-rate of charge–discharge capability.3.3 Electrochemical characterization
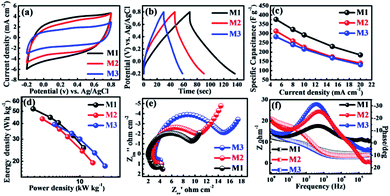
The porous and highly stable micro-flowers electrode samples grown without the aid of binder on the SSM substrate were studied for their supercapacitor performance. All the electrochemical measurements were carried out by constructing a cell with three electrode configuration. 1 M Na2SO4 was used as an electrolyte and scanning was performed within the potential window of −0.2 to 0.8 V (vs. Ag/AgCl). The cyclic voltammograms of all three (M1, M2, and M3) MnO2 thin films were recorded at a scan rate of 10 mV s−1 as shown in Fig. 3a. From the figure, it is observed that all the CV curves were exhibiting slightly distorted rectangular shape indicating the pseudocapacitive behavior of all the samples. In addition, M1 thin film demonstrates the symmetric CV along with the anodic and cathodic direction with the highest area under the CV curve as compared to M2 and M3 thin films, and hence, M1 exhibits highest specific capacitance. The CV studies of all three MnO2 thin films at different scan rates from 10–100 mV s−1 are shown in Fig. S3(a–c).† All MnO2 thin films reveal quasi-rectangular nature suggesting that the electrochemical storage is mostly due to faradic reactions. This could be due to the intercalation/de-intercalation of Na+ cations from the electrolyte into the MnO2 thin film based electrode material leading to the reversible transition of Mn4+ to Mn3+ and vice versa. This is shown in the equation below.53,54| MnO2 + Na+ + e− ↔ MnOONa |
It also shows that with increasing scan rate, the area under the CV curve increases, suggesting that the material has good diffusion control and better rate capability.55
For further support for the capacitive performance of the electrodes, we carried out the galvanostatic charge–discharge (GCD) testing. Accordingly, Fig. 3b shows GCD curves for the all three MnO2 electrodes, measured between optimized potential window from −0.2 to 0.8 V (vs. Ag/AgCl) at a constant current density (5 mA cm−2) in 1 M Na2SO4 electrolyte. Significantly, the M1 thin film samples show best electrochemical performance as compared to M2 and M3 samples. This is due to its higher discharging time and small initial potential drop as compared to the M2 and M3 samples. Additionally, the charge–discharge curves obtained at various current densities (5–20 mA cm−2) are demonstrated in Fig. S3(d–f).† All the GCD curves in the Fig. S3(d–f)† do not demonstrate an ideal triangular shape, which is indicative of pseudocapacitive nature. The specific capacitances of all the electrodes were calculated from the galvanostatic charge–discharge curves and eqn (1). The specific capacitances of M1, M2, and M3 with scan rate from 5–20 mA cm−2 are found to be 376–184, 312–140 and 283–132 F g−1, respectively. Table S1† provides the values of specific capacitance of all three electrodes (M1, M2, and M3) at different current densities. More significantly, the plot of specific capacitance versus current density is shown in Fig. 3c. The M1 sample exhibited significantly enhanced electrochemical performance showing specific capacitance as high as 376 F g−1 at 5 mA cm−2 current density. This is marginally higher as compared to the M2 (301 F g−1) and M3 (110 F g−1) samples at the same current density (5 mA cm−2). It is seen that the highest specific capacitance is obtained for an M1 electrode which might be due to strong interconnections between the bunch of micro-flowers network morphology of the electrode and moreover the size of the nanosheets in micro-flower is larger compared to M2 and M3 micro-flower. Large nanosheets have more surface area (M1) than smaller nanosheets (M2 and M3) as confirmed from the SEM images. The M1 (KMnO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MnSO4 = 3
MnSO4 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) gives the maximum specific capacitance of 376 F g−1 at 5 mA cm−2 current density. This specific capacitance is higher than those reported in the earlier literature (Table 1).
1) gives the maximum specific capacitance of 376 F g−1 at 5 mA cm−2 current density. This specific capacitance is higher than those reported in the earlier literature (Table 1).
| Electrode materials | Current density/scan rate | Electrolyte | Specific capacitance | Ref. |
|---|---|---|---|---|
| δ-MnO2/SS | 6 A g−1 | 0.1 M Na2SO4 | ∼180 F g−1 | 56 |
| PF-RGO-MnO2 | 5 A g−1 | 1 M Na2SO4 | ∼230 F g−1 | 57 |
| G/MnO2 NF | 0.5 A g−1 | 1 M Na2SO4 | 320 F g−1 | 58 |
| δ-MnO2 | 1 A g−1 | 1 M Na2SO4 | 336 F g−1 | 59 |
| GO-DE@MnO2 | 0.5 A g−1 | 1 M Na2SO4 | 152 F g−1 | 60 |
| MnO2NSAs@VCFs | 0.5 A g−1 | 1 M Na2SO4 | 115 F g−1 | 61 |
| MnO2/graphene | 0.5 A g−1 | PVA/H3PO4 | 254 F g−1 | 62 |
| MnO2 | 1 mV s−1 | 0.5 Li2SO4 | 201 F g−1 | 63 |
| δ-MnO2 | 0.5 mA cm−2 | 0.1 M Na2SO4 | 236 F g−1 | 24 |
| MnO2 | 0.82 A g−1 | 0.5 M Na2SO4 | 360 F g−1 | 28 |
| MnO2 | 1 mV s−1 | 1 M Na2SO4 | 310 F g−1 | 31 |
| MnO2 | 5 mV s−1 | 1 M Na2SO4 | 328 F g−1 | 32 |
| MnO2 | 5 mV s−1 | 0.1 M Na2SO4 | 234 F g−1 | 34 |
| δ-MnO2 (M1) | 5 mA cm−2 | 1 M Na2SO4 | 376 F g−1 | This work |
More importantly, the realistic utility of synthesized MnO2 samples is determined by the value of power density (PD) and energy density (ED). The values of energy density and power density are plotted in Ragone plot as shown in Fig. 3d. From the Ragone plot, it is observed that all three MnO2 electrodes provide higher energy density and power density. Among these electrodes, the M1 gives the highest energy density of 52 W h kg−1 with a power density of 2.7 kW kg−1 compared to the other two electrodes M2 and M3 (Table S1†).
To further understand the electrochemical characteristics, the ion transport property within the MnO2 electrode was investigated using electrochemical impedance spectroscopy (EIS). The EIS measurements of all three electrodes were carried out within the frequency range of 1000 kHz to 1 Hz at AC amplitude of 5 mV in 1 M Na2SO4 electrolyte solution. The Fig. 3e presents Nyquist plots of all three electrodes (M1, M2, and M3) of stacked MnO2 nanosheets measured at its open circuit potential with an ac perturbation of 5 mV. All the Nyquist plots consist of semicircle at the high-frequency range and a straight line in the low-frequency zone. The intercept of the initial point of a semicircle with the real axis at the highest frequency represents the equivalent series resistance (ESR), which is composed of the combined series resistance of the electrolyte, electrode, current collectors, and the electrode/current collector contact resistance. The ESR values of M1, M2, and M3 obtained from the intersection of the Nyquist plot at the X-axis are 1.9, 2.7 and 3.0 Ω, respectively. The ESR values increase from M1 to M2 and from M2 to M3 electrode, which means that the M1 has less ESR value than the other two electrodes. The diameter of the semicircle in the high-frequency region is used to determine the charge transfer resistance (Rct) at the interface between the electrode material and electrolyte. The Rct values of M1, M2, and M3 obtained from the diameter of the semicircle are 7.2, 8.3 and 11.8 Ω, respectively. It is apparent that the value of Rct gradually increases from of M1 to M3 as the concentration of MnSO4 increases with respect to KMnO4 concentration. Both the ESR and Rct values of all three electrodes of MnO2 indicate that the M1 shows better electrochemical capacitive behavior than the other two electrodes (M2 and M3). The results obtained for M1 could be attributed to the small diameter of the semicircle (Rct = 7.5 Ω) than that noted for other electrodes owing to easier accessibility and minimal charge transfer resistance due to their porous structure. The line at the low-frequency region, making an angle of 45° to the real axis is called the Warburg line and is a result of the diffusion of electrolyte ions within porous electrodes. The length of the Warburg line is shorter for M1 than the other two electrodes, indicating fast ion diffusion in the porous M1 electrode. Fig. 3f compares the Bode plots of all MnO2 micro-flower electrodes tested in 1 M Na2SO4 to detect the charge transfer resistance (Rct). On the whole, the Bode plots of all three MnO2 electrodes (M1, M2, and M3) in the electrolyte tend to show similar patterns but display different values of Rct + Rs (Fig. 3f) on the Y-axis. These values were used to obtain information on the Rct which provide an index of the electrode's internal resistance in the electrolyte. The Rct of ∼10, ∼12 and ∼17 Ω was deduced for respective micro-flower electrodes indicating that M1 electrodes with lower Rct have more affinity towards the electrochemical reaction at the electrode–electrolyte interface, which is seen as an increase in the overall capacitance value. The phase angle of all three electrodes is less than 32 indicate that all MnO2 based electrode materials exhibit pseudocapacitive nature and is in good agreement with the CV and CD results.
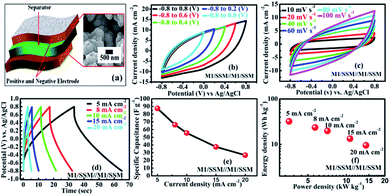
To explore the performance of the cell in the real application, symmetric supercapacitor (SC) device (Fig. 4a) is fabricated using two M1 thin film samples and designated as SSM/M1//M1/SSM with 1 M Na2SO4 as the aqueous electrolyte. The symmetric device has been extended and explored for its electrochemical performance. As shown in the Fig. 4b, the M1 micro-flowers thin films assembled symmetric supercapacitor cell can indeed be operated within varying potential window between −0.8 to 0.8 V to estimate the optimal operating potential window of the cell. Generally, the large operating voltage leads to the electrolysis of water. However, we selected the potential window within −0.8 to 0.8 V as the operating voltage of our supercapacitor device since in our case we observed the same nature of all the CV curves at different voltages and there is no deformation of the CV curve even at a higher voltage window extending within −0.8 to 0.8 V. Also, the CV shape under this condition is more rectangular compared to lower voltage window.
Fig. 4c shows the CV curves at different scan rates (10–100 mV s−1) resulting from the symmetric supercapacitor device within −0.8 to 0.8 V cell voltage. Comparing the CV curves of the single electrodes of M1, M2 and M3 with that of the assembled symmetric supercapacitor, it is observed that the CV curve of the device appears similar in shape to that of the M1 single electrode, but the area under the curve is very less than that of the M1 single electrode, implying a great decrement in their electrochemical performances. However, no obvious distortion in the shape of the CV curves could be found even at a high voltage scan rate of 100 mV s−1, indicating an excellent rate capability.
Furthermore, GCD curves of the assembled symmetric supercapacitor show nearly symmetric triangular shapes at various current densities of 5, 8, 10, 15, and 20 mA cm−2 over the potential window of −0.8 to 0.8 V, as shown in Fig. 4d. It can be seen that the charge and discharge curves are all straight and have fairly symmetric nature, which indicates a rapid current-potential response. The corresponding specific capacitances, derived from the discharge curves are 87.5, 66.2, 55.6, 37.5 and 26.7 F g−1, respectively (shown in Fig. 4e). Based on these data, the energy and powder densities of the SC device were further calculated and shown in Fig. 4f. The power density is found to ascend with current density increase from 5 to 20 mA cm−2. However, the specific capacitance decreased from 87 to 27 F g−1 and the energy density also declined from 32 to 10 W h kg−1 presenting a notable capacity fading of 60%.64
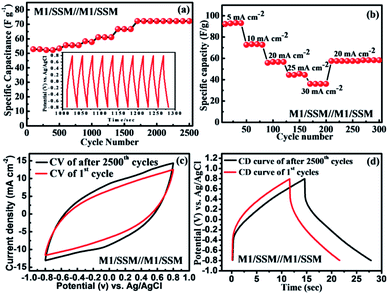
The cycle performance is of great importance for newly fabricated electrochemical supercapacitors based devices. The cycling stability of SSM/M1//M1/SSM cell was recorded by galvanostatic charge–discharge cycling at a current density of 10 mA cm−2 and result is shown in Fig. 5a. Where the cell capacitance does not fade, instead, it gradually increases with the increasing cycles. Their specific capacitance increases from 52 to 72 F g−1 in the initial 1700 cycles and then remains stable up to 2500 cycles. In another word, it shows 138% of initial capacitance after the 2500 cycles, which is attributed to the activation process taking place at the beginning of the CD cycling test. During this process, the electrolyte gradually penetrates into the electrodes, a large number of active points onto the electrode become activated contributing to the increase of the specific capacitance.19,65–67 The device shows improved capacitance retention when compared to the previous reports CFS/MnO2//CFS/MnO2 (ref. 68) (110% capacity retention after 5000 cycles), MnO2@CNTs/Ni-based SSC69 (83.4% capacity retention after 1000 cycles), MGF SSC device70 (91.4% capacity retention after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles) and SSC of MnO2/CNTs composite48 (91.3% capacity retention after 5000 cycles). The main reason for the capacitance loss for manganese oxide-based supercapacitor is reported to be only the dissolution of active materials into electrolyte solution during cycling.71–73 However, in our experiment, the electrolyte remains transparent even after the cycling test, indicating that the majority of the MnO2 is stable and not dissolved. These results suggest that the direct growth of MnO2 on substrates present remarkable electrochemical stability of the electrode. The inset in Fig. 5a is the charge–discharge curve of the SSM/M1//M1/SSM electrode cell in the potential range from −0.8 to 0.8 V at 10 mA cm−2. After charge–discharge cycling for 1000 min, the charge curves are still found to be very symmetric to their corresponding discharge counterparts.
000 cycles) and SSC of MnO2/CNTs composite48 (91.3% capacity retention after 5000 cycles). The main reason for the capacitance loss for manganese oxide-based supercapacitor is reported to be only the dissolution of active materials into electrolyte solution during cycling.71–73 However, in our experiment, the electrolyte remains transparent even after the cycling test, indicating that the majority of the MnO2 is stable and not dissolved. These results suggest that the direct growth of MnO2 on substrates present remarkable electrochemical stability of the electrode. The inset in Fig. 5a is the charge–discharge curve of the SSM/M1//M1/SSM electrode cell in the potential range from −0.8 to 0.8 V at 10 mA cm−2. After charge–discharge cycling for 1000 min, the charge curves are still found to be very symmetric to their corresponding discharge counterparts.
In addition, the rate capability of the same symmetric device (after 2500 cycles) of the MnO2 electrode SSM/M1//M1/SSM at different current densities were calculated to investigate the versatility and stability of the device as shown in Fig. 5b. The symmetric device of MnO2 electrodes was cycled for different current densities of 5, 10, 20, 25, and 30 mA cm−2 successively and the corresponding specific capacitances measured within 4 cycles is found to be 92.3, 73.2, 57.6, 45.4, and 36.1 F g−1, respectively. As shown in Fig. 5b, when the current density is reset to 20 mA cm−2 again, the specific capacitance is recovered to 57.2 F g−1 which is about 99.9% of the specific capacitance of the initial 10 cycles at 20 mA cm−2, suggesting an excellent rate capability and stability of the symmetric device of MnO2 electrodes (SSM/M1//M1/SSM).
Fig. 5c and d shows the electrochemical performance of the symmetric device (SSM/M1//M1/SSM) of MnO2 electrodes before and after 2500 cycles. The CV curves of MnO2 symmetric device shows nearly rectangular shape even after 2500 cycles at the scan rate of 100 mV s−1 (Fig. 5c). The symmetrical CD behavior at a current density of 10 mA cm−2 is shown in Fig. 5d and the performance show consistency with CV curves in Fig. 5c. It is an interesting to note that the capacitance increases steadily during the 2500 cycles, showing a 38% increase after 2500 cycles (Fig. 5a). The CV curves of the device of MnO2 sample after cycling test also show higher capacitance as revealed by the larger CV loop area in Fig. 5c. Similarly, the prolonged charge and discharge periods of the sample indicate an increase in capacitance upon cycling (Fig. 5d). Furthermore, we have compared the Nyquist plot of the device before and after 2500 cycles and the results are shown in Fig. S4.† The Nyquist impedance plot of the device is found to be similar to that observed in the single electrode (M1) of MnO2 (Fig. 3e). However, larger ESR and charge transfer resistance values were noted when compared to the single electrode (M1). The ESR and Rct values of the device were observed to decrease with increasing charge–discharge cycles (2500 cycle). These results were in good agreement showing an increase in capacitance upon cycling due to the decrease in the ESR and Rct values.
Interestingly, the symmetric device shows improved capacitance retention (138% retention over 2500 cycles) which enhanced our curiosity and hence we have studied XRD and SEM after electrochemistry of MnO2 thin films. Fig. 6 presents the XRD patterns and SEM images of the M1 electrode before and after 2500 cycles. From the XRD spectra (Fig. 6a) we observed an increase in crystalline quality along with the observation of one extra peak at ∼17° which is the characteristic peak of α-MnO2 (in XRD of after 2500 cycled, Fig. 6a). This indicates that after 2500 cycles, the thin film forms a composite phase of δ-MnO2 (JCPDS no. 80-1098) and α-MnO2 (JCPDS no. 44-0141). This phase transformation results in a small change in morphology of the MnO2 thin film electrode after 2500 cycles as shown in Fig. 6c. The closed micro-flowers morphology of the electrode transforms into open petals like as well as some rod likes structures. This may be due to the changes in the volume of the structure during charge–discharge cycling, which may be responsible for the formation of cracks in the structure. During the charge–discharge process, ions of electrolytes are intercalated and deintercalated in the structure of the electrode. Definitely, the change in phase (mixed phase) and the open structure efficiently increases the electrode–electrolyte contact area, improving the specific capacitance, which results in excellent cycling performance. Thus, this change in morphology along with the phase transformation can be attributed to the observed increase in supercapacitor performance.
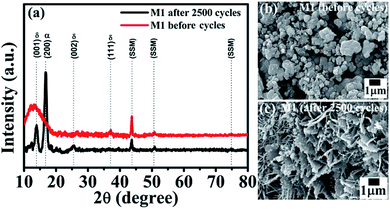 | ||
| Fig. 6 (a) XRD spectra of the M1 electrode of the device before and after 2500 cycles. SEM images of the M1 electrode of the device (b) before and (c) after 2500 cycles. | ||
4. Conclusions
In summary, we have developed binder free MnO2 thin films on SSM substrates via simple and economic rotational chemical bath deposition technique. These MnO2 thin films show micro-flowers like a structured network. The M1 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) thin films demonstrate excellent specific capacitance of 376 F g−1 at 5 mA cm−2 current density. Furthermore, the symmetric device fabricated using two M1 (3
1) thin films demonstrate excellent specific capacitance of 376 F g−1 at 5 mA cm−2 current density. Furthermore, the symmetric device fabricated using two M1 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) electrodes designated as (SSM/M1//M1/SSM) provides a maximum specific capacitance of 87 F g−1 and also delivers an energy density of 32 W h kg−1 at a current density of 5 mA cm−2. The device also exhibits good cycle stability showing 138% capacitance retention up to 2500 cycles. These interesting results are expected to pave ways for a new avenue in the development of low-cost and high-performance devices in the field of supercapacitor and other energy storage devices.
1) electrodes designated as (SSM/M1//M1/SSM) provides a maximum specific capacitance of 87 F g−1 and also delivers an energy density of 32 W h kg−1 at a current density of 5 mA cm−2. The device also exhibits good cycle stability showing 138% capacitance retention up to 2500 cycles. These interesting results are expected to pave ways for a new avenue in the development of low-cost and high-performance devices in the field of supercapacitor and other energy storage devices.
Acknowledgements
AAK is thankful to CSIR, New Delhi for the research fellowship (File no. 09/809(0013)/2012-EMR-I). The authors are thankful to UGC-DAE Consortium for Scientific Research, Indore (Project Ref. No: CSR-I/CRS-48/48) and UGC, New Delhi (F. No. 41-370/2012 (SR)) for the financial support. Financial support by Ministry of Science and Technology, R.O.C. Contract No. 105-2119-M-011-002 is acknowledged.References
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- M. M. Vadiyar, S. C. Bhise, S. S. Kolekar, J.-Y. Chang, K. S. Ghule and A. V. Ghule, J. Mater. Chem. A, 2016, 4, 3504–3512 CAS.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 CAS.
- Q. Yang, Q. Li, Z. Yan, X. Hu, L. Kang, Z. Lei and Z.-H. Liu, Electrochim. Acta, 2014, 129, 237–244 CrossRef CAS.
- G. A. Ferrero, M. Sevilla and A. B. Fuertes, Sustainable Energy Fuels, 2017, 1, 127–137 Search PubMed.
- M. Huang, Y. Zhang, F. Li, Z. Wang, Alamusi, N. Hu, Z. Wen and Q. Liu, Sci. Rep., 2014, 4, 4518 CrossRef PubMed.
- J. Lee, S. Yoon, T. Hyeon, S. M. Oh and K. Bum Kim, Chem. Commun., 1999, 2177–2178, 10.1039/A906872D.
- C. Meng, C. Liu, L. Chen, C. Hu and S. Fan, Nano Lett., 2010, 10, 4025–4031 CrossRef CAS PubMed.
- S. Chen, J. Zhu, X. Wu, Q. Han and X. Wang, ACS Nano, 2010, 4, 2822–2830 CrossRef CAS PubMed.
- M. Huang, F. Li, F. Dong, Y. X. Zhang and L. L. Zhang, J. Mater. Chem. A, 2015, 3, 21380–21423 CAS.
- M. M. Vadiyar, S. S. Kolekar, J.-Y. Chang, A. A. Kashale and A. V. Ghule, Electrochim. Acta, 2016, 222, 1604–1615 CrossRef CAS.
- R. B. Rakhi, B. Ahmed, D. Anjum and H. N. Alshareef, ACS Appl. Mater. Interfaces, 2016, 8, 18806–18814 CAS.
- Y. Han, S. Zhang, N. Shen, D. Li and X. Li, Mater. Lett., 2017, 188, 1–4 CrossRef CAS.
- Q. X. Xia, J. M. Yun, R. S. Mane, L. Li, J. Fu, J. H. Lim and K. H. Kim, Sustainable Energy Fuels, 2017, 1, 529–539 Search PubMed.
- Z. Peng, X. Liu, H. Meng, Z. Li, B. Li, Z. Liu and S. Liu, ACS Appl. Mater. Interfaces, 2017, 9, 4577–4586 Search PubMed.
- Y. Zhang, J. Zheng, Y. Zhao, T. Hu, Z. Gao and C. Meng, Appl. Surf. Sci., 2016, 377, 385–393 CrossRef CAS.
- Z. Wu, L. Li, J. M. Yan and X. B. Zhang, Adv. Sci., 2017, 4, 1600382 CrossRef PubMed.
- J. Song, H. Li, S. Li, H. Zhu, Y. Ge, S. Wang, X. Feng and Y. Liu, New J. Chem., 2017, 14, 3750–3757 RSC.
- W. Li, K. Xu, L. An, F. Jiang, X. Zhou, J. Yang, Z. Chen, R. Zou and J. Hu, J. Mater. Chem. A, 2014, 2, 1443–1447 CAS.
- Z. Song, W. Liu, M. Zhao, Y. Zhang, G. Liu, C. Yu and J. Qiu, J. Alloys Compd., 2013, 560, 151–155 CrossRef CAS.
- H.-Y. Wang, F.-X. Xiao, L. Yu, B. Liu and X. W. Lou, Small, 2014, 10, 3181–3186 CrossRef CAS PubMed.
- W. Li, K. Xu, B. Li, J. Sun, F. Jiang, Z. Yu, R. Zou, Z. Chen and J. Hu, ChemElectroChem, 2014, 1, 1003–1008 CrossRef CAS.
- B. Yin, S. Zhang, H. Jiang, F. Qu and X. Wu, J. Mater. Chem. A, 2015, 3, 5722–5729 CAS.
- S. Devaraj and N. Munichandraiah, J. Phys. Chem. C, 2008, 112, 4406–4417 CAS.
- M. Aghazadeh, M. G. Maragheh, M. R. Ganjali, P. Norouzi and F. Faridbod, Appl. Surf. Sci., 2016, 364, 141–147 CrossRef CAS.
- O. A. Vargas, A. Caballero, L. Hernán and J. Morales, J. Power Sources, 2011, 196, 3350–3354 CrossRef CAS.
- A. A. Radhiyah, M. Izan Izwan, V. Baiju, C. Kwok Feng, I. Jamil and R. Jose, RSC Adv., 2015, 5, 9667–9673 RSC.
- A. Sarkar, A. Kumar Satpati, V. Kumar and S. Kumar, Electrochim. Acta, 2015, 167, 126–131 CrossRef CAS.
- N. R. Chodankar, G. S. Gund, D. P. Dubal and C. D. Lokhande, RSC Adv., 2014, 4, 61503–61513 RSC.
- M. M. Vadiyar, S. S. Kolekar, N. G. Deshpande, J.-Y. Chang, A. A. Kashale and A. V. Ghule, Ionics, 2016, 1–9 Search PubMed.
- Y. Hu, H. Zhu, J. Wang and Z. Chen, J. Alloys Compd., 2011, 509, 10234–10240 CrossRef CAS.
- D. P. Dubal, R. Holze and P. M. Kulal, J. Mater. Sci., 2013, 48, 714–719 CrossRef CAS.
- D. Yan, Z. Guo, G. Zhu, H. Yang, R. Wei, H. Xu and A. Yu, Mater. Lett., 2012, 82, 156–158 CrossRef CAS.
- H. Ashassi-Sorkhabi, E. Asghari and P. La'le Badakhshan, Curr. Appl. Phys., 2014, 14, 187–191 CrossRef.
- Y. Yang and C. Huang, J. Solid State Electrochem., 2010, 14, 1293–1301 CrossRef CAS.
- D. Cui, K. Gao, P. Lu, H. Yang, Y. Liu and D. Xue, Funct. Mater., 2011, 04, 57–60 CrossRef CAS.
- Y. Lv, H. Li, Y. Xie, S. Li, J. Li, Y. Xing and Y. Song, Particuology, 2014, 15, 34–38 CrossRef CAS.
- H. Jiang, T. Sun, C. Li and J. Ma, J. Mater. Chem., 2012, 22, 2751–2756 RSC.
- G. S. Gund, D. P. Dubal, S. S. Shinde and C. D. Lokhande, ACS Appl. Mater. Interfaces, 2014, 6, 3176–3188 CAS.
- J. Zhang, C. Guo, L. Zhang and C. M. Li, Chem. Commun., 2013, 49, 6334–6336 RSC.
- M. K. Dey, P. K. Sahoo and A. K. Satpati, J. Electroanal. Chem., 2017, 788, 175–183 CrossRef CAS.
- S. S. Falahatgar, F. E. Ghodsi, F. Z. Tepehan, G. G. Tepehan, İ. Turhan and S. Pishdadian, J. Non-Cryst. Solids, 2015, 427, 1–9 CrossRef CAS.
- G. S. Gund, D. P. Dubal, N. R. Chodankar, J. Y. Cho, P. Gomez-Romero, C. Park and C. D. Lokhande, Sci. Rep., 2015, 5, 12454 CrossRef PubMed.
- M. Huang, X. L. Zhao, F. Li, L. L. Zhang and Y. X. Zhang, J. Power Sources, 2015, 277, 36–43 CrossRef CAS.
- N. R. Chodankar, D. P. Dubal, G. S. Gund and C. D. Lokhande, J. Energy Chem., 2016, 25, 463–471 CrossRef.
- Z. Su, C. Yang, B. Xie, Z. Lin, Z. Zhang, J. Liu, B. Li, F. Kang and C. P. Wong, Energy Environ. Sci., 2014, 7, 2652–2659 CAS.
- J. Ge, Y. Qu, L. Cao, F. Wang, L. Dou, J. Yu and B. Ding, J. Mater. Chem. A, 2016, 4, 7795–7804 CAS.
- J.-W. Wang, Y. Chen and B.-Z. Chen, J. Alloys Compd., 2016, 688, 184–197 CrossRef CAS.
- D. T. Dam, T. Huang and J.-M. Lee, Sustainable Energy Fuels, 2017, 1, 324–335 Search PubMed.
- S. Devaraj and N. Munichandraiah, J. Electrochem. Soc., 2007, 154, A80–A88 CrossRef CAS.
- Y.-X. Miao, L.-H. Ren, L. Shi and W.-C. Li, RSC Adv., 2015, 5, 62732–62738 RSC.
- R. Chen, J. Yu and W. Xiao, J. Mater. Chem. A, 2013, 1, 11682–11690 CAS.
- H. Li, Y. He, V. Pavlinek, Q. Cheng, P. Saha and C. Li, J. Mater. Chem. A, 2015, 3, 17165–17171 CAS.
- M. Seredych and T. J. Bandosz, J. Mater. Chem., 2012, 22, 23525–23533 RSC.
- P. A. Shinde, N. R. Chodankar, V. C. Lokhande, A. Patil, T. Ji, J. H. Kim and C. D. Lokhande, RSC Adv., 2016, 6, 113442–113451 RSC.
- Y. Hu, J. Wang, X. Jiang, Y. Zheng and Z. Chen, Appl. Surf. Sci., 2013, 271, 193–201 CrossRef CAS.
- H. Su, P. Zhu, L. Zhang, F. Zhou, G. Li, T. Li, Q. Wang, R. Sun and C. Wong, J. Electroanal. Chem., 2017, 786, 28–34 CrossRef CAS.
- Y. Zheng, W. Pann, D. Zhengn and C. Sun, J. Electrochem. Soc., 2016, 163, D230–D238 CrossRef CAS.
- B. Xu, L. Yu, M. Sun, F. Ye, Y. Zhong, G. Cheng, H. Wang and Y. Mai, RSC Adv., 2017, 7, 14910–14916 RSC.
- Z. Q. Wen, M. Li, F. Li, S. J. Zhu, X. Y. Liu, Y. X. Zhang, T. Kumeria, D. Losic, Y. Gao, W. Zhang and S. X. He, Dalton Trans., 2016, 45, 936–942 RSC.
- S. C. Sekhar, G. Nagaraju, S. M. Cha and J. S. Yu, Dalton Trans., 2016, 45, 19322–19328 RSC.
- L. Peng, X. Peng, B. Liu, C. Wu, Y. Xie and G. Yu, Nano Lett., 2013, 13, 2151–2157 CrossRef CAS PubMed.
- Q. Qu, P. Zhang, B. Wang, Y. Chen, S. Tian, Y. Wu and R. Holze, J. Phys. Chem. C, 2009, 113, 14020–14027 CAS.
- F. Ataherian and N.-L. Wu, Electrochem. Commun., 2011, 13, 1264–1267 CrossRef CAS.
- X. Lu, D. Zheng, T. Zhai, Z. Liu, Y. Huang, S. Xie and Y. Tong, Energy Environ. Sci., 2011, 4, 2915–2921 CAS.
- T. Wang, Z. Peng, Y. Wang, J. Tang and G. Zheng, Sci. Rep., 2013, 3, 2693 CrossRef PubMed.
- O. Ghodbane, J.-L. Pascal and F. Favier, ACS Appl. Mater. Interfaces, 2009, 1, 1130–1139 CAS.
- Y. Wen, T. Qin, Z. Wang, X. Jiang, S. Peng, J. Zhang, J. Hou, F. Huang, D. He and G. Cao, J. Alloys Compd., 2017, 699, 126–135 CrossRef CAS.
- P. Sun, H. Yi, T. Peng, Y. Jing, R. Wang, H. Wang and X. Wang, J. Power Sources, 2017, 341, 27–35 CrossRef CAS.
- Z. Li, Y. An, Z. Hu, N. An, Y. Zhang, B. Guo, Z. Zhang, Y. Yang and H. Wu, J. Mater. Chem. A, 2016, 4, 10618–10626 CAS.
- Z. Wang, Q. Qin, W. Xu, J. Yan and Y. Wu, ACS Appl. Mater. Interfaces, 2016, 8, 18078–18088 CAS.
- W. Wei, X. Cui, W. Chen and D. G. Ivey, Electrochim. Acta, 2009, 54, 2271–2275 CrossRef CAS.
- S. C. Pang, M. A. Anderson and T. W. Chapman, J. Electrochem. Soc., 2000, 147, 444–450 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra05655a |
| This journal is © The Royal Society of Chemistry 2017 |