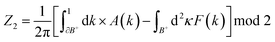Strain induced quantum spin Hall insulator in monolayer β-BiSb from first-principles study

Abstract

Topological insulator (TI) is a peculiar phase of matter exhibiting excellent quantum transport properties with potential applications in lower-power-consuming electronic devices. Searching for inversion-asymmetric quantum spin Hall (QSH) insulators persists as an effect for realizing new topological phenomena. Using first-principles density functional theory calculations, we investigate the geometry, dynamic stability, and electronic structures of monolayer β-BiSb. We find that it presents QSH state under biaxial tensile strain of 14%. The nontrivial topological situation in the strained system is confirmed by the identified band inversion, Z₂ topological invariant (Z₂ = 1), and an explicit presence of the topological edge states. Owning to the asymmetric structure, remarkable Rashba spin splitting is produced in both the valence and conduction bands of the strained system. These results provide an intriguing platform for applications of monolayer β-BiSb in future alternative quantum Hall spintronic devices.

---

1. Introduction

Quantum Hall spintronic devices employ spin instead of charge as an information carrier, by taking advantage of the spin polarized electronic energy state in a less because the SOC is too weak to produce an observable effect under realistic conditions, as the gap opened by the spin–orbit interaction turns out to be on the order of 10⁻³ eV.¹³ Subsequently, quite a few compounds have been found to be 2D TIs, such as the silicene, material.¹ Topological insulators (TIs) are new states germanene, ZrTe₅ monolayers, and chemically modified of quantum matter that have unleashed tremendous interest in fundamental condensed matter physics and material science.^2–4 Two-dimensional (2D) TIs, also called quantum spin Hall (QSH) insulators,^5,6 are emerging as a novel state of quantum matter. Such states are characterized by an insulating bulk, and the edge can support spin-polarized gapless states with a Dirac-cone-like linear energy dispersion, thus providing a platform for potential applications in quantum Hall spintronic devices. The unique fingerprint of TI materials is their gapless boundary state, which is spin-locked due to the protection of the time-reversal symmetry, namely the propagation direction of surface electrons is robustly linked to their spin orientation.^7,8 As a result, all the scatterings of electrons in the presence of nonmagnetic impurities in 2D TIs are totally forbidden, leading to no dissipation transport edge channels.⁹ Furthermore, Majorana Fermions will appear when the material gets in contact with a superconductor.¹⁰ Besides their fundamental physical importance Majorana Fermions may play an important role in topological quantum computation schemes.¹¹ Graphene was the first system proposed to be a QSH insulator through the spin–orbital coupling (SOC) effect.¹² Unfortunately, this proposal is practically use-stanene.^14–20 However, up to now, the only experimental confirmation of 2D TIs was reported in HgTe/CdTe and InAs/GaSb/AlSb quantum well systems in an extreme experimental condition below 10 K.^21–23 Nevertheless, the experimental activity on the QSH effect in HgTe/CdTe and InAs/GaSb quantum wells has remained limited by notorious practical difficulties. Extensive effort has been devoted to search new QSH insulators.^24,25 However, desirable materials preferably with large bulk gaps are still lacking. Therefore, the finding of new 2D TI materials with large bulk gaps is still intriguing and important.

To design 2D TIs for practical utilization, there must possess two essential points of the materials: one is the sizable bulk band gap, and the other, layered structure with van der Waals' (VDW) force between layers. The reason is that a large energy gap in 2D TIs is required to stabilize the boundary current against the influence of thermally activated bulk carriers, and layered structure, easy to get the chemical stability of 2D system. In recent years, the search for 2D TIs has been extended to Bi and Sb single-element materials^26–30 in view of their strong SOC, a precondition which is indispensable for realizing robust topological insulators at high temperature. Interestingly, there exists a bulk BiSb compound (β-BiSb, space group R3̄m, no. 166), which is a natural form of antimonide and bismuth.³¹ Recently, Singh et al. predicted the lowest ground state structure of bulk BiSb with space group of R3m, no. 160.³² Actually, the natural form of β-BiSb crystal has the same layered structure as arsenic and antimony (β-SbAs)³³ with space group of R3̄m, no. 166. S. Zhang et al. have made progress in group VA materials, such as the theoretical prediction of arsenene and antimonene and experimental preparation of antimonene.^34,35 So the theoretical study of the 2D monolayer β-BiSb, which has not been synthesized so far, can not only enhance our understanding of their intrinsic characteristics but also facilitate the applications of the family of 2D VA–VA compound semiconductors.

In the present work, we have provided the electronic and topological properties of monolayer β-BiSb. Firstly, a basic geometry of monolayer β-BiSb was established with honeycomb structure. By means of first-principles density functional theory (DFT) computations, we calculated the cohesive energy and phonon vibrational spectra of monolayer β-BiSb, which confirm the thermodynamic and kinetic stabilities. Then, we investigate the electronic structure of monolayer β-BiSb with PBE, as well as PBE+SOC calculations. Interestingly, a robust SOC in monolayer β-BiSb results in a band-gap reduction of 60 meV. Under biaxial tensile strain, the gap of monolayer β-BiSb can be closed and reopened with a concomitant change of band shapes, which is reminiscent of band inversion known in many topological insulators. Accordingly, the QSH effect in monolayer β-BiSb is robust under biaxial tensile strain of 14%, which is confirmed by the direct calculation of the Z₂ topological invariant and the nontrivial topological edge states. The giant band gap of monolayer β-BiSb and the robust topological properties under tensile strain are attractive features for potential applications of monolayer β-BiSb in quantum Hall spintronic devices.

2. Computational method

Our DFT calculations have been performed using Vienna ab initio simulation package (VASP) code.³⁶ We used the Perdew–Burke–Ernzerhof (PBE)³⁷ exchange–correlation functional for the GGA. The projector augmented wave (PAW) method³⁸ was employed to describe the electron–ion interaction. A vacuum of 20 Å perpendicular to the sheets (along the c axis) was applied to avoid the interaction between layers. A kinetic energy cutoff of 500 eV was used for geometry optimization. The total energy has converged to 10⁻³ eV per atom with respect to the cutoff energy of plane wave and k-points sampling. The geometrical structure is optimized until Hellmann–Feynman residual forces less than 0.01 eV Å⁻¹. The phonon calculations are carried out using the supercell method through the PHONOPY code,^39,40 and the real-space force constants of supercells are calculated in the density-functional perturbation theory (DFPT) as implemented in VASP. Moreover, a more strict energy (10⁻⁸ eV per atom) and force convergence criterion (10⁻⁴ eV Å⁻¹) are used during the vibrational spectra calculations. The convergence of vibrational spectra is also checked with respect to super-cell size and 7 × 7 × 1 supercells are used, and the path of integration in first Brillouin zone is along K(1/3, 2/3, 0.0) → Γ(0.0, 0.0, 0.0) → M(0.0, 0.5, 0.0) → K(1/3, 2/3, 0.0). These over-converged technical parameters used in the calculation can ensure our prediction reliable. The Brillouin-zone sampling is carried out with a 21 × 21 × 1 Monkhorst–Pack⁴¹ grid for 2D sheets. Tetrahedron method was used with a quick projection scheme in the calculations of the density of state (DOS). For the calculations of the band structures, we used Gaussian smearing in combination with a small width of 0.05 eV. Spin–orbital coupling effects are included self-consistently up to second order (LS coupling).³ Since the SOC term is large just close to the core, the corresponding contributions to the Hamiltonian are only evaluated inside the PAW spheres using all-electron partial waves.

3. Results and discussions

The geometrical structure of monolayer β-BiSb is presented in Fig. 1(a). The optimized crystal parameters are a = b = 4.24 Å, along with the bond length d = 2.97 Å and buckled hight h = 1.69 Å. From Fig. 1(a) we can see that the honeycomb structure is almost the same as that of blue phosphorene, which is a newly emerging 2D group-V material with well optoelectronic properties.⁴²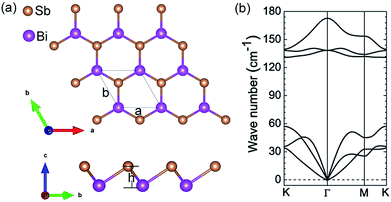

Fig. 1 (a) Top and side views of monolayer β-BiSb. (b) Vibrational phonon spectra of monolayer β-BiSb. No soft modes present in the structure.

To learn the thermodynamic stability of β-BiSb, we calculated the cohesive energy (E_coh), which is defined as the following formula:

E_coh = [E_BiSb − (E_Bi + E_Sb)]/2

E_BiSb is the total energy of monolayer β-BiSb, E_Bi and E_Sb are the energies derived from monolayer Bi and Sb nanosheets, respectively. The calculated E_coh is −2.98 eV per atom, leading to well thermodynamic stability. To further confirm the structural stability of monolayer β-BiSb, we have performed vibrational phonon spectra calculations. As presented in Fig. 1(b), there are no negative frequencies, thus confirming the dynamical stability of monolayer β-BiSb.

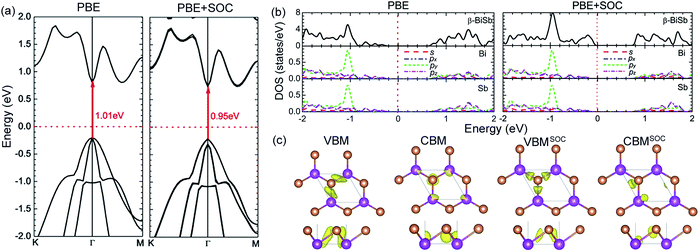
Now we turn to the electronic structure of monolayer β-BiSb. The calculated band structures with PBE method, along with PBE+SOC method are presented in Fig. 2(a). From Fig. 2(a) we can find that the fundamental band gap (E_g) are both direct band gap with 1.01 and 0.95 eV by PBE functional and PBE+SOC, respectively. However, bulk BiSb is known to exhibit with the band gap of an indirect band gap semiconducting nature.⁴³ In monolayer β-BiSb, the conduction band minimum (CBM) shows a parabolic nature near Γ point, indicating the presence of highly mobile light electrons (nearly free-electrons), while the valence band maximum (VBM) indicates the presence of relatively heavy holes near Γ point. Intriguingly, the band gap with PBE+SOC is slightly smaller than that of PBE with 60 meV because of the split of valance band with SOC. The calculated strength of Rashba spin splitting, including the Rashba energy (E_R), the Rashba momentum (k_o), and the Rashba constant (α_R) are E_R = 2.12 meV, k_o = 0.0101 Å⁻¹, α_R = 2E_R/k_o = 0.42 eV Å, which are a little smaller than that of Singh's recent results.⁴⁴

Fig. 2 (a) Band structures of monolayer β-BiSb, which are calculated at PBE level with and without SOC. (b) The partial density of states (PDOS) and (c) the isosurfaces of charge density distribution of VBM and CBM for monolayer β-BiSb calculated at the PBE level with and without SOC. The Fermi level is set as zero and indicated with a dot line.

To further shed light on the underlying bonding mechanism of Bi and Sb atoms in monolayer β-BiSb, we show in Fig. 2(b) the total and partial density of states (PDOS) of monolayer β-BiSb using PBE functional with and without SOC, respectively. As shown in Fig. 2(b), the partial density of states (PDOS) projected onto s and p orbitals of Bi and Sb atoms shows similar pattern and peak positions whether in valence band or conduction band, indicating a strong hybridization of s and p orbitals between Bi and Sb. When SOC is included in the calculations, all electronic states broaden a little. The Bi-p and Sb-p states still dominate the valence band. While the conduction states move towards the low energy region and narrow the energy gap. Meanwhile, CB states also split into two parts distinctly due to degenerated states and destroyed symmetry induced by SOC.

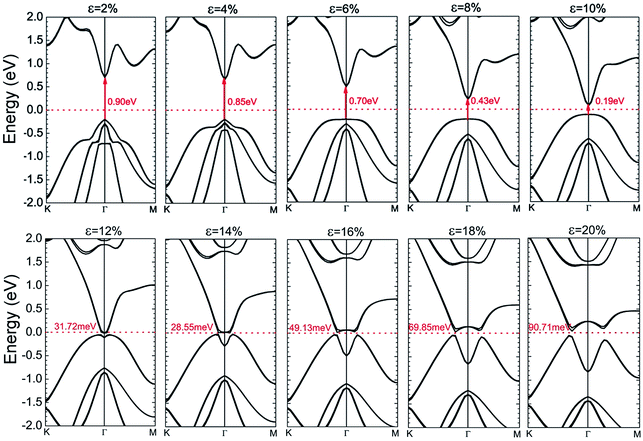
As we know, the character of Frontier states is not only of interest for a microscopic understanding of the conduction channels but also of great concern for the design of optimal contacts.⁴⁵ The charge density corresponds to VBM and CBM with and without SOC are presented in Fig. 2(c), respectively. The VBM and CBM are similar and a typical lone pair electron state are found in these Frontier states, which is similar to those of phosphorene.⁴⁶ For the semiconducting nanosheet, strain engineering is a favorable strategy to induce a switch between a trivial and a nontrivial topological phase in the system. We demonstrate that the Rashba effect in β-BiSb monolayer can be efficiently tuned under biaxial tensile strains, as shown in Fig. 3. We find that there exists direct band gap at Γ point as the tensile strain varying from 2% to 12%, and the band gap decreased gradually with maximum valence band transformed from “Λ shape” to “M shape”. Such a trend eventually leads to the smallest band gap near Γ point when the strain is 14%. On account of the asymmetric structure of β-BiSb, Rashba spin splitting is produced in both the valence and conduction bands in the strained system. Excitingly, the band gap opens again when the strain is larger than 14%. From Fig. 3 we can see that the Rashba energy (E_R) along with the Rashba momentum (k_o) become bigger and bigger with the tensile strains increasing.

Fig. 3 Band structures of monolayer β-BiSb under in-layer biaxial uniform strains (ε = n%, n = 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20) at PBE level with SOC. The band gap is narrow (28.55 meV) at ε = 14%, which is reminiscent of band inversion and characterizes many known TIs. The Fermi level is set as zero and indicated with a dot line.

The characteristic of band gaps closing and reopening associated with the change of band shapes is reminiscent of band inversion, which characterizes many known topological insulators (TIs).^7,14,20 In order to ascertain the topological phase transition in the strained monolayer β-BiSb, we calculated the Z₂ topological invariants. In the presence of time-reversal symmetry, Kramer's theorem dictates that the energy eigenstates must come in pairs. This allows us to enforce the so-called time-reversal constraint on the Bloch functions:

|u_n(−k)〉 = Θ|u_n(k)〉

where |u_n(−k)〉 is the periodic part of the Bloch function, and Θ = e^iπS_y/h̄K is the time reversal operator with the spin operator S_y and the complex conjugation K. Accordingly, we only need to obtain Bloch functions in half of the Brillouin zone, denoted by B⁺, as those in the other half are fixed by above equation. The band topology is characterized by the Z₂ invariant, given by⁴⁷
where 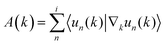is the Berry connection and F(k) = ∇_κ × A(k)|_Z is the Berry curvature; the sum is over occupied bands. A topological insulator is characterized by Z₂ = 1, while ordinary insulators have Z₂ = 0. The nonzero Z₂ invariant is an obstruction to smoothly defining the Bloch functions in B⁺ under the time-reversal constraint. Since inversion symmetry is absent in this system, the Z₂ invariants cannot be determined from the parities of the filled states. To this end, we have used the n-field configuration method.⁴⁸ We find that the Z₂ topological invariant is 0 with the tensile strains of ≤12% and ≥16%, while Z₂ = 1 with the tensile strain of 14%. Actually, atomically thin binary VA–VA compound semiconductors have been found to be flexible in our previous study, and the desirable strains could be achievable in the elastic regime at a low energy penalty.⁴⁹ Consequently, the strained system need relative small stress. Moreover, S. Zhang et al. have found that the Z₂ topological invariant is 1 for atomically thin binary VA–VA compound β-SbAs under the tensile strain of 12%.³³ So the tensile strain of 14% for monolayer β-BiSb is reliable and sensible. These results firmly demonstrate that there is indeed a strain-induced topological phase transition in β-BiSb. Therefore, compared to the case of antimonene, the β-BiSb monolayer is also expected as a potential candidate to achieve the QSH effect.

In order to give a general idea about the energetic stability of the strained systems, the calculated formation energies of the strained systems are −2.22, −2.20, −2.19, −2.19, −2.18, −2.18, −2.16, −2.15, −2.15, −2.14 eV per atom, with the strain from 2% to 20% by interval of 2%, respectively. Meanwhile, we check the dynamical stability of the system under different external strains, we performed the phonon spectra calculations. As shown in Fig. 4, there are no negative frequencies, suggesting dynamical stabilities of monolayer β-BiSb under strains.

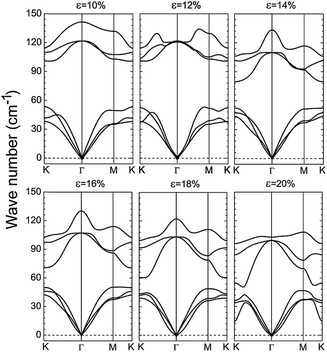Fig. 4 Vibrational phonon spectra of monolayer β-BiSb under in-layer biaxial tensile strain of n% (n = 10, 12, 14, 16, 18, 20). No soft modes present in the structure.

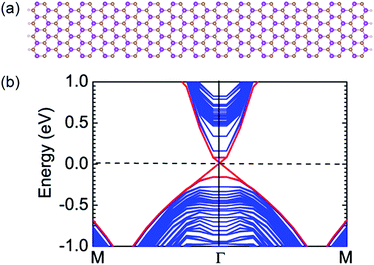
The 2D nontrivial insulating state is often characterized by topologically protected conducting edge states with in the bulk gap.^50–52 Thus, the β-BiSb monolayer under the tensile strain of 14% should hold an odd number of topologically protected Dirac-like edge states connecting the conduction and valence-band edges at Γ high-symmetry points. To further confirm the nontrivial features of β-BiSb monolayer under the tensile strain of 14%, we constructed a zigzag β-BiSb nanoribbon structure, and the edge unsaturated atoms are terminated by hydrogen atoms to eliminate all dangling bonds, as seen in Fig. 5(a). The width of the zigzag β-BiSb nanoribbon adopted here is 100 Å, which is enough to avoid interactions between edge states of the two sides. The band structure of the nanoribbon is shown in Fig. 5(b). The gapless edge states appear and cross linearly at the Γ point, which further confirms the nontrivial topological phase in the β-BiSb monolayer under the tensile strain of 14%. Thus, our results provide a promising strategy for designing 2D VA–VA QSH insulators.

Fig. 5 (a) Atomic structure of monolayer β-BiSb nanoribbon (over 100 Å) with zigzag edges under tensile strain. The dangling bonds in the zigzag nanoribbon edges are terminated by hydrogen atoms. (b) Band structures of the monolayer β-BiSb nanoribbon at ε = 14%. The helical edge states (red lines) can be clearly identified around Γ point. The Fermi level is set to zero, indicated by the horizontal dashed line.

4. Conclusions

In conclusion, a new 2D material, monolayer β-BiSb, has been proposed to exhibit fascinating TI properties under biaxial tensile strain of 14%. We demonstrate its energetic and dynamic stabilities by cohesive energy and phonon spectra, respectively. The band structure calculations indicate a robust SOC in monolayer β-BiSb results in a band-gap reduction of 60 meV. Interestingly, we find that the gap closing and reopening is associated with TI characteristics under biaxial tensile strain. The identified band inversion, Z₂ topological invariant (Z₂ = 1), and an explicit presence of the topological edge states have been used to confirm the nontrivial topological situation in the strained system. Remarkable Rashba spin splitting is produced in both the valence and conduction bands of the strained system because of the asymmetric structure. Therefore, similar to the case of antimonene and bilayer bismuth, the β-BiSb monolayer is also expected as a potential candidate to achieve the QSH effect. We believe that these unexplored 2D group VA–VA semiconductors, as exemplified by β-BiSb monolayer, will lead to a large family of 2D semiconductors with intriguing electronic properties.

Acknowledgements

We thank Dr Yandong Ma for helping to calculate the Z₂ topological invariant, and Dr Shengli Zhang for helpful discussions. This work was supported by the National Natural Science Foundation of China (No. 11504332, 11304288, 21403109 and 21303041), the Natural Science Foundation of Henan Province (No. 162300410254 and 162300410116), Program for Innovative Research Team of Henan Polytechnic University (No. T2016-2), Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase), the Beijing National Laboratory for Molecular Sciences (No. BNLMS20150144), and the Open Project of Key Laboratory of Radio Frequency and Micro-Nano Electronics of Jiangsu Province (LRME201601).

References

1. Z. F. Wang, S. Jin and F. Liu, Spatially separated spin carriers in spin-semiconducting graphene nanoribbons, Phys. Rev. Lett., 2013, 111, 297–398.
2. X. L. Qi and S. C. Zhang, The quantum spin Hall effect and topological insulators, Phys. Today, 2010, 63, 33–38.
3. X. L. Qi and S. C. Zhang, Topological insulators and superconductors, Rev. Mod. Phys., 2010, 83, 175–179.
4. B. Yan and S. C. Zhang, Topological materials, Rep. Prog. Phys., 2012, 75, 96501–96523.
5. J. E. Moore, The birth of topological insulators, Nature, 2010, 464, 194–198.
6. M. Z. Hasan and C. L. Kane, Colloquium: topological insulators, Rev. Mod. Phys., 2010, 82, 3045–3067.
7. H. J. Zhang, C. X. Liu, X. L. Qi, X. Dai, Z. Fang and S. C. Zhang, Topological insulators in Bi₂Se₃, Bi₂Te₃ and Sb₂Te₃ with a single Dirac cone on the surface, Nat. Phys., 2009, 5, 438–442.
8. B. Rasche, A. Isaeva, M. Ruck, S. Borisenko, V. Zabolotnyy, B. Büchner, K. Koepernik, C. Ortix, M. Richtern and J. van den Brink, Stacked topological insulator built from bismuth-based graphene sheet analogues, Nat. Mater., 2013, 12(5), 422–425.
9. B. A. Bernevig and S. C. Zhang, Quantum Spin Hall Effect, Phys. Rev. Lett., 2006, 96, 148–151.
10. L. Fu and C. L. Kane, Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 9, 897–899.
11. M. Cheng, R. M. Lutchyn and S. D. Sarma, Topological protection of Majorana qubits, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 85, 98–102.
12. C. L. Kane and E. J. Mele, Quantum spin Hall effect in graphene, Phys. Rev. Lett., 2005, 95, 226801–226804.
13. Y. Yao, F. Ye, X. L. Qi, S. C. Zhang and Z. Fang, Spin–orbit gap of graphene: first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 041401(R).
14. Y. P. Wang, W. X. Ji, C. W. Zhang, P. Li, F. Li, P. J. Wang, S. S. Li and S. S. Yan, Large-gap quantum spin Hall state in functionalized dumbbell stanene, Appl. Phys. Lett., 2016, 108, 073104.
15. C. C. Liu, H. Jiang and Y. G. Yao, Low-energy effective Hamiltonian involving spin-orbit coupling in silicene and two-dimensional germanium and tin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 4, 4193–4198.
16. H. M. Weng, X. Dai and Z. Fang, Transition-metal pentatelluride ZrTe₅ and HfTe₅: a paradigm for large-gap quantum spin Hall insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 4, 339–345.
17. C. C. Liu, W. X. Feng and Y. G. Yao, Quantum spin Hall effect in silicene and two-dimensional germanium, Phys. Rev. Lett., 2011, 107, 2989–2996.
18. F. C. Chuang, C. H. Hsu, C. Y. Chen, Z. Q. Huang, V. O-zolins, H. Lin and A. Bansil, Tunable topological electronic structures in Sb(111) bilayers: a first-principles study, Appl. Phys. Lett., 2013, 102, 022424.
19. Z. G. Song, C. C. Liu, J. B. Yang, J. Z. Han, B. T. Fu, M. Ye, Y. C. Yang, Q. Niu, J. Lu and Y. G. Yao, Quantum spin Hall insulators and quantum valley Hall insulators of BiX/SbX (X = H, F, Cl and Br) monolayers with a record bulk band gap, NPG Asia Mater., 2014, 6, 147.
20. C. Si, J. W. Liu, Y. Xu, J. Wu, B. L. Gu and W. H. Duan, Functionalized germanene as a prototype of large-gap two-dimensional topological insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 115429–115435.
21. M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L. W. Molenkamp, X. L. Qi and S. C. Zhang, Quantum spin Hall insulator state in HgTe quantum wells, Science, 2007, 318, 766–770.
22. B. A. Bernevig, T. L. Hughes and S. C. Zhang, Quantum spin Hall effect and topological phase transition in HgTe quantum wells, Science, 2007, 314, 1757–1761.
23. I. Knez, C. T. Rettner, S. H. Yang, S. S. P. Parkin, L. J. Du, R. R. Du and G. Sullivan, Observation of edge transport in the disordered regime of topologically insulating InAs/GaSb quantum wells, Phys. Rev. Lett., 2014, 112, 339–345.
24. D. Zhang, W. Lou, M. Miao, S. C. Zhang and K. Chang, Interface-induced topological insulator transition in GaAs/Ge/GaAs quantum wells, Phys. Rev. Lett., 2013, 111, 5514–5518.
25. D. Xiao, W. Zhu, Y. Ran, N. Nagaosa and S. Okamoto, Interface engineering of quantum Hall effects in digital transition metal oxide heterostructures, Nat. Commun., 2011, 2, 1145–1154.
26. S. Murakami, Quantum spin Hall effect and enhanced magnetic response by spin–orbit coupling, Phys. Rev. Lett., 2006, 97, 15299–15309.
27. M. Wada, S. Murakami, F. Freimuth and G. Bihlmayer, Well-localized edge states in two-dimensional topological insulators: ultrathin Bi films, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 83, 812–819.
28. Z. Liu, C. X. Liu, Y. S. Wu, W. H. Duan, F. Liu and J. Wu, Stable nontrivial Z₂ topology in ultrathin Bi(111) films: a first-principles study, Phys. Rev. Lett., 2011, 107, 628–637.
29. Z. Q. Huang, F. C. Chuang, C. H. Hsu, Y. T. Liu, H. R. Chang, H. Lin and A. Bansil, Nontrivial topological electronic structures in a single Bi(111) bilayer on different substrates: a first-principles study, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 938–944.
30. P. F. Zhang, Z. Liu, W. Duan, F. Liu and J. Wu, Topological and electronic transitions in a Sb(111) nanofilm: the interplay between quantum confinement and surface effect, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 151–152.
31. P. Cucka and C. S. Barrett, The crystal structure of Bi and of solid solutions of Pb, Sn, Sb and Te in Bi, Acta Crystallogr., 1962, 15, 865–872.
32. S. Singh, W. Ibarra-Hernández, I. Valencia-Jaime, G. Avendaño-Franco and A. H. Romero, Investigation of novel crystal structures of Bi-Sb binaries predicted using the minima hopping method, Phys. Chem. Chem. Phys., 2016, 18, 29771–29785.
33. S. Zhang, M. Xie, B. Cai, H. Zhang, Y. Ma, Z. Chen, Z. Zhu, Z. Hu and H. Zeng, Semiconductor-topological insulator transition of two-dimensional SbAs induced by biaxial tensile strain, Phys. Rev. B, 2016, 93, 245303–245307.
34. S. Zhang, M. Xie, F. Li, Z. Yan, Y. Li, E. Kan, W. Liu, Z. Chen and H. Zeng, Semiconducting group 15 monolayers: a broad range of band gaps and high carrier mobilities, Angew. Chem., Int. Ed., 2016, 55, 1666.
35. J. Ji, X. Song, J. Liu, Z. Yan, C. Huo, S. Zhang, M. Su, L. Liao, W. Wang, Z. Ni, Y. Hao and H. Zeng, Two-dimensional antimonene single crystals grown by van der Waals epitaxy, Nat. Commun., 2016, 7, 13352.
36. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1998, 80, 3865–3868.
38. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
39. A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl₂-type SiO₂ at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106–134109.
40. A. Togo, see http://www.sourceforge.net/projects/phonopy for phonopy.
41. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
42. L. Y. Zhu, S. S. Wang, S. Guan, Y. Liu, T. T. Zhang, G. B. Chen and S. A. Yang, Blue phosphorene oxide: strain- tunable quantum phase transitions and novel 2D emergent Fermions, Nano Lett., 2016, 16, 6548–6554.
43. S. Singh, A. C. Garcia-Castro, I. Valencia-Jaime, F. Muñoz and A. H. Romero, Prediction and control of spin polarization in a Weyl semimetallic phase of BiSb, Phys. Rev. B, 2016, 94, 161116–161125.
44. S. Singh and A. H. Romero, Giant tunable Rashba splitting in two-dimensional BiSb monolayer and in BiSb/AlN heterostructures, Phys. Rev. B, 2017, 95, 165444–165510.
45. D. Tománek, Interfacing graphene and related 2D materials with the 3D world, J. Phys.: Condens. Matter, 2015, 27, 133203–133215.
46. A. N. Rudenko and M. I. Katsnelson, Quasiparticle band structure and tight-binding model for single- and bilayer black phosphorus, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 3520–3527.
47. L. Fu and C. L. Kane, Time reversal polarization and a Z₂ adiabatic spin pump, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195312–195313.
48. T. Fukui and Y. Hatsugai, Quantum spin Hall effect in three dimensional materials: lattice computation of Z₂ topological invariants and its application to Bi and Sb, J. Phys. Soc. Jpn., 2006, 76, 053702–053705.
49. W. Y. Yu, Z. L. Zhu, C. Y. Niu, X. F. Wang and W. B. Zhang, Atomically thin binary V–V compound semiconductor: a first-principles study, J. Mater. Chem. C, 2016, 4, 6581–6587.
50. L. Y. Li, X. M. Zhang, X. Chen and M. W. Zhao, Giant topological nontrivial band gaps in chloridized gallium bismuthide, Nano Lett., 2015, 15, 1296–1301.
51. Y. D. Ma, L. Z. Kou, A. J. Du and T. Heine, Group 14 element-based non-centrosymmetric quantum spin Hall insulators with large bulk gap, Nano Res., 2015, 8, 3412–3420.
52. L. Z. Kou, Y. D. Ma, B. H. Yan, X. Tan, C. F. Chen and S. C. Smith, Encapsulated silicene: a robust large-gap topological insulator, ACS Appl. Mater. Interfaces, 2015, 7, 19226–19233.

---

Footnote

† PACS numbers: 73.43.-f, 71.70.Ej, 71.70.Fk.

---