Morphology and phase tuning of α- and β-MnO₂ nanocacti evolved at varying modes of acid count for their well-coordinated energy storage and visible-light-driven photocatalytic behaviour

Abstract

A simple hydrothermal method is developed to synthesize two different phases, α and β of MnO₂ nanocacti (comprising nanowires with 1–10 nm diameter self assembled by ultrathin sheets) as well as MnO₂ nanorods (10–40 nm diameter) without any seed or template. Sudden addition of concentrated H₂SO₄ (0.3–0.4 μL) results in the formation of nanocacti while gradual addition (dropwise) of H₂SO₄ solution (0.3–0.4 M) results in nanorods. Besides, the α phase of MnO₂ exists at relatively high acidic strength (4 pH) compared to the β phase, which is consistent at 5 pH. Thus this could be the first report exploring the possibilities of tuning morphology as well as the phase of MnO₂ through simple optimizations in acidic content. We find that polymorphic MnO₂ nanocacti exhibit superior photocatalytic activity and high energy capacity as an anode in Li-ion batteries than polymorphic MnO₂ nanorods. The α phase of MnO₂ performs better than the β phase. α-MnO₂ nanocacti demonstrate high visible light driven photocatalytic activity by degrading >90% of congo red and methyl orange dyes in 40 mg L⁻¹ organic dye aqueous solution with 0.1 g of the as-prepared sample within 25 and 70 min, respectively. We highlight the differences between the photocatalytic activities of different phases, α and β of MnO₂ nanostructures, depending on the charge transport through different dimensions of the same pristine MnO₂. The constant cycling stability of α-MnO₂ nanocacti with capacities as low as 300 mA h g⁻¹ at 1C rate after 50 cycles as an anode makes it a promising material for energy storage applications. We attribute the high electro- and photo-chemical activity for α-MnO₂ nanocacti to their highly mesoporous structure making this one of the highest specific surface areas (271 m² g⁻¹) possibly ever reported for pristine MnO₂.

---

1. Introduction

Semiconductor based metal oxides (such as TiO₂, ZnO, SnO₂, WO₃, CeO₂ (ref. 1–6)) have gained much attention owing to their high stability, non-toxicity and favourable chemical properties. Particularly, manganese oxides (MnO, Mn₂O₃, Mn₃O₄, Mn₅O₈ and MnO₂) are of considerable importance due to their rich polymorphism and structural flexibility with excellent physical and chemical properties.^7,8 Among these, MnO₂ being one of the most stable manganese oxides⁹ has drawn much attention. Multiple valence states of manganese ions favor the existence of manganese dioxide (MnO₂) in many polymorphic forms as α, β, γ, λ and ε depending on the linkage of fundamental MnO₆ octahedron units.^10,11 They are extensively used in a wide range of applications such as energy storage systems,^12–20 fuel cell catalysts,^21–24 water treatment,^25,26 biosensors^27,28 and so on.

In the past few decades MnO₂ are intensively investigated as promising electrode materials for primary lithium batteries, alkaline batteries and electrochemical capacitors.^13,29–34 Feng et al.¹³ have studied the electrochemical behavior of α-MnO₂ crystals with caddice-clew-like and urchin-like morphologies as anodes for Li-ion batteries. Li et al.³⁰ have reported an extremely stable MnO₂ anode incorporated with 3D porous graphene-like networks for lithium-ion batteries. Chen et al.³⁴ have illustrated high specific capacity and excellent cyclic performance of MnO₂ nanorods with the application of CMC binder.

Manganese dioxide (MnO₂) has several merits like low-cost, nontoxic property, ease of synthesis, acid resistance, strong adsorption and oxidation ability, which have made it a promising photocatalyst for oxidative degradation of organic and inorganic contaminants in wastewater.^35–38 Yin et al. have reported an enhanced photocatalytic activity of MnO₂ nanowires by showcasing the complete degradation of congo red dye molecules in 30 min.³⁹ Cao et al.⁴⁰ have demonstrated an excellent catalytic performance of α- and β-MnO₂ nanorods in the Fenton-like reaction. Saravanakumar et al.⁴¹ have reported the Ag nanoparticles anchored on MnO₂ nanowires as an efficient visible light driven photocatalyst. Kalamuei et al.⁴² have evaluated the efficiency of MnO₂ nanoparticles as a photocatalyst for the decolorization of methylene blue.

The chemical properties of manganese oxides mainly depend on their oxidation state, nanostructure and morphology. The synthesis of pristine MnO₂ with various morphologies such as nanosphere,^43,44 nanorod,⁴⁵ nanowire,⁴⁶ nanobelts,⁴⁷ nanoflower,^48,49 nanotube,⁵⁰ pillow-shape,⁵¹ urchin-like,^43,52 hollow nanosphere, hollow nanocube,⁵³ and hollow cone⁵⁴ have been reported. Different chemical methods such as sol–gel templating,⁵⁵ thermal decomposition,⁵⁶ refluxing,⁵⁷ solvent free solid reaction,⁵⁸ electrodeposition,⁵⁹ and hydrothermal techniques^45,46 have been reported to synthesize MnO₂ nanostructures.

In the present work hydrothermal method is followed to synthesize MnO₂ nanostructures due to its simplicity, low cost and effectiveness. We have effectively utilized hydrothermal technique to synthesize two different polymorphs (α and β) of MnO₂ nanocacti as well as nanorods without using any seed, capping agent or template. Tuning in morphology and phase of the as synthesized product was made possible by modifying acidic conditions during synthesis. Variations in photocatalytic activity for degradation of CR (congo red) and MO (methyl orange) dyes and performance as anode material for Li-ion battery with respect to changes in morphology and phase of as synthesized product have been calibrated.

2. Experimental

2.1 Synthesis

A homogeneous solution of 40 mL containing 4 mM KMnO₄ and 6 mM NaNO₂ (2 : 3 molar ratio) was prepared through continuous stirring. Then 0.2 μL of H₂SO₄ was added directly into the solution under continuous stirring using micro-pipette. Prepared solution was sealed inside a Teflon-lined stainless steel autoclave (50 mL) of 80% capacity of total volume. The autoclave was kept in muffle furnace and hydrothermal process was carried out at a temperature of 170 °C for 12 h. Then, it was allowed to cool at room temperature naturally. Next, precipitates were centrifuged and thoroughly washed with de-ionized water and ethanol for several times and were dried in hot air oven at 100 °C for 5 h to obtain final product. Further, it was calcined at 400 °C for 6 h and named as sample S1. Same synthesis process was repeated by changing quantity of H₂SO₄ to 0.3 μL and as prepared sample was named as S2.

In another typical synthesis, 0.3 M H₂SO₄ was prepared in 4 mL of de-ionized water and added drop wise into the solution containing 4 mM KMnO₄ and 6 mM NaNO₂ under continuous stirring to form a homogeneous solution of 40 mL. Further synthesis processes were followed same as before and as prepared sample was named as S3. In further similar experiment, molarity of H₂SO₄ was modified to 0.4 M while keeping other synthesis parameters constant and subsequent obtained product was named as sample S4.

2.2 Photocatalytic experiments

Methyl orange (MO) and congo red (CR) were used as dyes to investigate photocatalytic activities of as prepared samples. 0.1 g of as prepared sample (S1–S4) was suspended in 200 mL of 40 mg L⁻¹ organic dye aqueous solution. Then, the solution was magnetically stirred in dark for 1 h to attain adsorption–desorption equilibrium. The solution was illuminated with visible light source using a 500 W halogen lamp at room temperature. To minimize the heat produced by lamp, a provision of in and out flow of ice cold water was implemented into the solution. Photocatalytic activity of the photocatalyst was analyzed by monitoring dye decolorization for different times at maximum absorption wavelength using UV-vis spectrophotometer. At every 10 min of interval, 3 mL of dye solution was extracted and centrifuged for UV-visible absorption measurement. Same processes were repeated for the CR dye degradation, but samples were extracted at every 5 min of intervals for analysis.

2.3 Photocurrent measurements

Photocurrent measurements were studied using three electrode system with Pt-wire, Ag/AgCl (in saturated KCl) and synthesized material coated on FTO (fluorine doped tin oxide) substrate as counter, reference and working electrode respectively. For making working electrode, firstly 5 mg of as prepared material was thoroughly mixed with 10 mL Triton X-100 using de-ionized water to form a homogenous slurry. Secondly, the slurry was uniformly coated over (0.5 × 0.5 cm²) area of FTO surface via doctor blade. Finally, the electrode was obtained after heating it at 100 °C for 6 h. The photocurrent measurements were carried out on a CHI608E electrochemical workstation with 0.1 M Na₂SO₄ solution as electrolyte. For photon source, 250 W Xe lamp (OSRAM, Germany) was employed.

2.4 Electrode preparation

Anode electrode was prepared by mixing 80 wt% of active material (sample S1–S4) with 10 wt% super P carbon black as conducting material and 10 wt% sodium alginate binder. Resultant mixture was grinded vigorously for 1 h with addition of adequate amount of de-ionized water to form homogeneous slurry. The slurry was uniformly coated on a copper foil of thickness ∼12 μm and dried at 100 °C for 10 h. The foil was then cut in circular form with 10 mm diameter and pressed under 1 ton pressure for 30 seconds using hydraulic press. The lithium foil cropped in circular form with 12 mm diameter was used as counter electrode. Electrolyte was prepared by mixing 1 M LiPF₆ in solution containing 1 : 1 volume ratio of ethylene carbonate (EC) and dimethyl carbonate (DMC). Poly propylene (Celgard-2400) of 14 nm film was used as a separator. Coin cell type lithium ion battery was assembled in argon filled dry glove box (Aero Glove box). Charge/discharge measurements of the coin cell type lithium ion battery were galvanostatically studied using battery cycle tester (BT Lab, BSC 810, France) at 1C rate. The electrochemical impedance spectroscopy (EIS) was measured in frequency range of 400 kHz–0.1 Hz.

2.5 Characterization

Structural analyses were performed by X-ray diffraction (XRD) measurements using PAN analytical X′ Pert Pro diffractometer employing Cu-Kα rays of wavelength 1.5406 Å with a tube current of 30 mA at 40 kV in the 2θ range of 10–80 degree. ‘Quanta 200 FEG FE-SEM’, field emission scanning electron microscope was used for morphological analyses of as prepared samples. Energy-dispersive X-ray spectroscopy technique was performed using ‘Bruker 129 eV’ with ‘Espirit software’ for elemental analyses. ‘HR-TEM, JEM-2010, 200 kV’, high resolution transmission electron microscope was also employed for morphological analysis. For TEM analysis, specimen was prepared by forming a homogenous mixture of powder sample with acetone using an ultrasonicator. Functional group analyses were performed by Fourier transform infrared spectroscopy via KBr pellet technique in range of 400–2000 cm⁻¹ (FTIR) using Perkin Elmer Spectrophotometer. Surface area and porosity measurements were carried out using a Quantachrome Nova-1000 surface analyzer at liquid nitrogen temperature. Photoluminescence spectra of as prepared samples were obtained using a Jobin Yvon Horiba Fluorolog-3-Tau Spectrofluorometer. UV-visible absorption measurements were performed using UV-vis spectrophotometer (Specord-200 plus UV-vis spectrophotometer, Germany) for analyzing the photocatalytic activity.

3. Results and discussions

3.1 Morphology and phase analyses

During the hydrothermal reaction, hydrothermal pressure and H⁺ ions play a crucial role in morphological changes as well as phase transition of MnO₂. The extreme hydrothermal pressure forces reactants molecules to appear in ionic forms as described below:²⁸

2MnO₄⁻ + 3NO₂⁻ + 2H⁺ → 2MnO₂ + 3NO₃⁻ + H₂O (1)

Here, permanganate ion acts as an oxidant and resource of manganese (Mn) element, whereas nitrite ions are used as a reducing agent. It is conspicuous that the stoichiometric molar ratio of permanganate to nitrite ions is 2 : 3. For proper feasibility of the hydrothermal reaction, potassium permanganate and sodium nitrate precursors are utilized in the molar ratio of 2 : 3. According to the Le Chatelier's principle, feasibility of the reaction depends on involvement of protons. The protons (H⁺ ions) needed for reaction is supplied by sulphuric acid. Modifications in amount of H⁺ ions can lead to variations in shape, size and phase of the final product. Increase in H⁺ ions decreases the reduction potential of permanganate ions based on Nernst equation.⁶⁰ In our system, decrease in reduction potential of permanganate ions is compensated by an increase in reduction potential of nitrite ions for equilibrium conditions, which further accounts for an increment in formation rate of Mn⁴⁺ ions. Therefore, in our system Mn⁴⁺ concentration is directly controlled by H⁺ ions concentration. By decreasing the acidic concentration, it was possible to reduce Mn⁴⁺ concentration or growth unit [MnO₆], resulting in formation of slimmer outlook for as synthesized material. This is evident from the FESEM (Fig. 1a) and HRTEM images (Fig. 1b and c) of sample S1 which displays nanostructures, when sample was prepared with 0.2 μL H₂SO₄. Nanostructures can be visualized to exhibit nanocacti like morphology comprising nanowires (diameters in the range of 1–10 nm) self-assembled by ultrathin sheets. The d-spacing of 0.692 nm in growth direction (110) is observed for sample S1 (Fig. 1c inset). This hints for α phase of the material which is supported by the XRD analysis. The XRD pattern of the sample S1 (Fig. 1d) prepared with 0.2 μL H₂SO₄ has major diffraction peaks at 2θ = 12.7, 18.1, 28.8, 37.4, 49.8, 60.2 corresponding to tetragonal phase of α-MnO₂ (JCPDS 44-0141). XRD patterns further indicate that subsequent formation of α-MnO₂ crystals preferably grow along (211) plane direction. EDS pattern for sample S1 is presented as inset of Fig. 1d. Absence of any impurity peaks reveals pristine nature of as prepared sample.

Fig. 1 (a) FESEM image, (b and c) HRTEM image with (inset c) d-spacing = 0.692 nm in growth direction (110) and (d) XRD pattern with (inset d) EDS pattern of sample S1 prepared at 0.2 μL of H₂SO₄. (e) FESEM image, (f and g) HRTEM image with (inset g) d-spacing = 0.311 nm in growth direction (110) and (h) XRD pattern with (inset h) EDS pattern of sample S2 prepared at 0.3 μL of H₂SO₄. (i) Crystal structure of α-MnO₂ showing [2 × 2] and [1 × 1] tunnel structure and (j) crystal structure of β-MnO₂ showing [1 × 1] tunnel structure.

When the acid concentration was increased further to 0.3 μL, there was no noticeable change in morphology. This is evident from the FESEM (Fig. 1e) and HRTEM images of S2 (Fig. 1f and g) prepared with 0.3 μL of H₂SO₄, which shows almost similar morphology to sample S1. Observed d-spacing of 0.311 nm in (110) plane growth direction is shown in Fig. 1g inset. However, in our system, this increase in H⁺ ions concentration increases formation rate of various crystal faces in growth unit due to enhancement in Mn⁴⁺ ions and thus results in phase transition of the material. XRD patterns of sample S2 (Fig. 1h) shows high intensity diffraction peaks at 2θ = 28.68, 37.33 and 56.65 corresponding to tetragonal phase of β-MnO₂ (JCPDS 24-0735). The subsequent formation of β-MnO₂ crystals preferably grow along (110) plane direction. EDS for sample S2 is shown as inset in Fig. 1h. The presence of high intensity peaks for manganese and oxygen elements and absence of any impurity peaks indicate that obtained β-MnO₂ nanocacti were in pure form with negligible impurities. Under low acidic strength, α-phase of MnO₂ comprising double chains of the [MnO₆] octahedra forming a larger [2 × 2] alongwith [1 × 1] tunnels (Fig. 1i) is favorable compared to its more stable and confined β phase counterpart consisting only [1 × 1] tunnels (Fig. 1j), accounting for higher number of Mn⁴⁺ ions or growth unit.

FESEM (Fig. 2a) and HRTEM image (Fig. 2b) shows 1D nanorods like morphology with diameters in range of about 10–40 nm for sample S3 prepared at 0.3 M H₂SO₄. The d-spacing of 0.314 nm with growth direction (310) shown as inset in Fig. 2b, suggests α-phase for the MnO₂ nanorods, which is confirmed from the XRD pattern shown in Fig. 2c. The diffraction peaks can be assigned to tetragonal phase of α-MnO₂ (JCPDS card number 44–0141). EDS pattern presented as inset in Fig. 2c rules out the presence of any impurities and further suggests for high purity of as prepared sample. The presence of nanorods instead of nanocacti has more to do with gradual addition of H₂SO₄ (dropwise addition of 0.3–0.4 M H₂SO₄ solution) compared to sudden addition of concentrated H₂SO₄ (0.2–0.3 μL) into the reacting solution. Thus, phase as well as morphology of final product can be predicted before the start of hydrothermal process by optimizing the concentration of reactants. This could be better explained using following reaction, which is supposed to occur before the hydrothermal process.

5NaNO₂ + 2KMnO₄ + 3H₂SO₄ → 5NaNO₃ + 2MnSO₄ + K₂SO₄ + 3H₂O (2)

Fig. 2 (a) FESEM image, (b) HRTEM image with (inset b) d-spacing = 0.314 nm in growth direction (310) and (c) XRD pattern with (inset c) EDS pattern of sample S3 prepared at 0.3 M H₂SO₄. (d) FESEM image, (e) HRTEM image with (inset e) d-spacing = 0.240 nm in growth direction (101) and (f) XRD pattern with (inset f) EDS pattern of sample S4 prepared at 0.4 M H₂SO₄.

Every chemical process has certain time duration for its feasibility and is evident by the formation of 1D nanorods. The sudden addition of H₂SO₄ completes the onset requirements of above reaction leading to formation of MnSO₄ compound and forces manganese ions to be available as Mn₂⁺ instead of Mn₄⁺ ions. Fortunately, with dropwise addition of H₂SO₄, the above reaction is restricted due to unavailability of required amount of SO₄²⁻ and favors the existence of Mn₄⁺ ions. As a consequence, when adequate amount of Mn₄⁺ ions are present as stabilizers then 1D morphologies (nanorods) with increased diameters of 10–40 nm are visible as compared with the slimmer 1D morphologies (nanowires with diameters in the range of 1–10 nm) observed in nanocacti (sample S1 and S2). Furthermore, when acid concentration was increased to 0.4 M H₂SO₄, similar kind of nanorods existed. It is evident form FESEM (Fig. 2d) and HRTEM image (Fig. 2e) of sample S4 prepared at 0.4 M H₂SO₄, which showcases 1D morphologies, having diameters in range of 10–40 nm. Obviously, this increased acid concentration alters phase of the material. β-phase can be conferred for the sample S4 depending on observed d-spacing of 0.24 nm in growth direction (101) as shown in inset of Fig. 2e and the XRD pattern (Fig. 2f). The major diffraction peaks observed in XRD patterns for sample S4 can be attributed to tetragonal phase of β-MnO₂ with JCPDS card number 24–0735. High purity of the as prepared sample S4 can be acknowledged by the absence of any impurity peaks in respective EDS pattern shown in inset of Fig. 2f. A similar reason as discussed earlier can be surmised for change in phase of the material from α to β phase on increasing the molar concentration from 0.3 M to 0.4 M H₂SO₄ with increase in H⁺ concentration. It is notable that β phases for the nanorods as well as nanocacti were persistent when pH value of the reacting solution was at 2, whilst α phases for both the morphologies were consistent at relatively low acidic strength of 4 pH. Phase and morphological changes involved during the synthesis of MnO₂ nanostructures at different modes of acid count is briefly drawn in Fig. 3. Concrete details concerning the in-depth cause relating the phase and morphological transformation of MnO₂ are still under investigation.

Fig. 3 Schematic showing the formation of α- and β-MnO₂ nanocacti and α- and β-MnO₂ nanorods at different reaction conditions.

Growth process of α-MnO₂ nanocacti is monitored through FESEM analysis when the hydrothermal process was carried out at different time intervals of 4, 8 and 12 h (Fig. 4a–c, respectively) using 0.2 μL H₂SO₄. The growth process starts with nucleation, when redox reaction rate of MnO₄⁻ ions to form MnO₂ is significantly increased during initial hydrothermal reaction. After 4 h of reaction, the supersaturated nuclei aggregate together to reduce interfacial energy resulting in formation of nanoparticles (Fig. 4a). When the reaction process were extended further for 8 h, then these nanoparticles aggregates further by increasing their size to minimize interfacial energies as shown in Fig. 4b. Finally at 12 h, further stabilization in the reactants molecules gave rise to the formation of nanowires self-assembled by ultrathin sheets (Fig. 4c). A brief schematic of the nanocacti growth process is portrayed in Fig. 4d.

Fig. 4 (a–c) FESEM images taken after 4, 8 and 12 h, respectively during the synthesis of sample S1 using 0.2 μL of H₂SO₄. (d) Schematic of α-MnO₂ nanocacti growth process.

FESEM images (Fig. 5a–c) show morphological status of sample prepared at 0.3 M H₂SO₄ during different time intervals. After 4 h of reaction, highly agglomerated micro or nanorods like morphologies are visible (Fig. 5a). When the reaction was extended further for 8 h, morphologies of nanowires become dominant (Fig. 5b) and individual nanowires starts getting separated. However, nanowires are still found connected with each other through ultrathin sheets. After 12 h of reaction, the ultrathin sheets lose their identity completely and ultrafine individual nanowires with 10–40 nm diameters are easily perceptible with no traces of any sheet like morphologies (Fig. 5c). A brief schematic of the nanorods growth process is presented in Fig. 5d.

Fig. 5 (a–c) FESEM images taken after 4, 8 and 12 h, respectively during the synthesis of sample S3 using 0.3 M H₂SO₄. (d) Schematic of the α-MnO₂ nanorods growth process.

3.2 Functional group analysis

Functional groups were determined using the FTIR spectroscopy. A similar trend in FTIR patterns was found for all the samples (S1–S4) as shown in Fig. 6a. The presence of metal–oxygen (Mn–O) bending modes in samples can be inferred from the common bands at about 715, 531 and 448 cm⁻¹ that are below 750 cm⁻¹. Absence of any other bands reveals the high purity of all synthesized samples. The results are in consistent with the XRD data and found in good agreement with the earlier report.⁴⁵

Fig. 6 (a) FTIR, (b) PL and (c) UV-vis spectra and (d) Tauc plot of samples S1, S2, S3 and S4 prepared at 0.2 μL, 0.3 μL, 0.3 M and 0.4 M of H₂SO₄, respectively.

3.3 Optical properties

The photo luminescence (PL) spectra (Fig. 6b) of all synthesized samples show two different emission peaks at 414 and 486 nm in visible region. Intensity of emission peaks decreases in order for samples S4, S3, S2 and S1. Sample S1 exhibited the lowest emission peak. The separation between electrons and holes directly depend upon emission peaks. This suggests that sample S1 has larger separation of electron hole pairs than all other samples which indicates for its better photocatalytic activity.

The optical absorption and energy band gap were evaluated using UV-vis absorption (diffuse reflectance spectra mode) spectra shown in Fig. 6c. Broad bands in visible region, with absorption edges of 600–900 nm are observed for as prepared samples. Absorption intensity follows a decreasing order for samples S1, S2, S3 and S4, respectively. Different bandgap gaps of 1.50, 1.52, 1.55 and 1.59 eV were calculated for the samples S1, S2, S3 and S4, respectively, using tauc's equation and corresponding tauc's plot (Fig. 6d). The lowest bandgap estimated for sample S1 can be marked as a criterion for its better photocatalytic activity.

3.4 Surface analysis

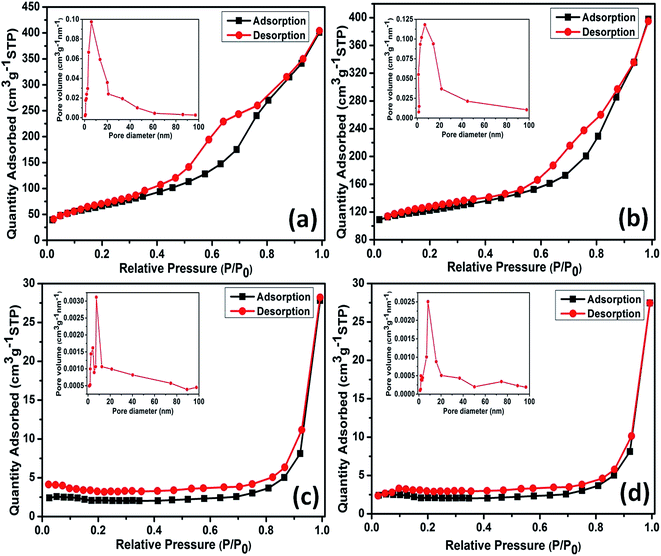
The specific textural properties of as prepared samples are presented by nitrogen (N₂) adsorption–desorption isotherms and BJH pore size distributions (PSDs) in Fig. 7a–d. A typical mesoporous kind of material property can be attributed for sample S1 as the isotherm (Fig. 7a) is distinguished as type IV with type H1 loop according to IUPAC classification.⁶¹ H1 loop resemblance can be ascribed to the presence of rigidly agglomerated 1D morphologies self-assembled by ultrathin sheets having high pore size uniformity and facile pore connectivity.⁶¹ This is in line with the FESEM and HRTEM analyses. PSD histogram for sample S1 shown in Fig. 7a inset, is narrow, which mainly cumulates at 4–9 nm with an average value of 6 nm. Specific surface area of sample S1 calculated using BET method is found to be 271 m² g⁻¹. Sample S2 also poses mesoporous kind of material property as similar isotherm representing type IV with type H1 loop is observed for S2 as shown in Fig. 7b. Specific surface area of sample S2 is estimated as 253 m² g⁻¹ by BET method. Furthermore, PSD histogram of sample S2 (Fig. 7b inset) mainly cumulates at 4–11 nm with an average value of 6.7 nm. Wider value observed for isotherms of sample S1 accounts for its high specific surface area and low pore size as compared with the S1. Similar kinds of textural properties observed for sample S1 and S2 can be assigned for their unique nanocacti like morphologies.

Fig. 7 (a–d) Nitrogen (N₂) adsorption–desorption isotherms and corresponding (inset a–d) BJH pore size distributions (PSDs) of samples S1, S2, S3 and S4 prepared at 0.2 μL, 0.3 μL, 0.3 M and 0.4 M of H₂SO₄, respectively.

On the contrary, the 1D nanorods sample S3 presents same type IV isotherm but with a type H4 loop,⁶¹ typical of mesoporous materials (Fig. 7c). This is in agreement with the FESEM and TEM analyses. As shown in Fig. 7c inset, PSD histogram of the sample S3 presents two narrow peaks mainly at 3–5 nm and 6–11 nm with an average value of 7.3 nm. Specific surface area of sample S1 calculated by BET method is found to be 37 m² g⁻¹. Likewise S3 isotherm, sample S4 also presents same type IV isotherm with a type H4 loop, typical of mesoporous materials (Fig. 7d). PSD histogram of sample S4 (Fig. 7d inset), mainly cumulates at 6–12 nm with an average value of 8.1 nm. The narrower desorption isotherm observed for S4 accounts for its low specific surface area (31 m² g⁻¹) compared to sample S3. Moreover, out of two phases α-MnO₂ nanocacti (S1) exhibited high surface area than its β counterpart (S2) and it was true for the case of α- and β-MnO₂ nanorods (S3 and S4, respectively) as well. This may be due to larger tunnels structure present in α phase which might facilitates N₂ adsorption–desorption on to the surface.

3.5 Photocatalytic performance

Fig. 8a shows absorption spectrum of CR dye over as prepared α-MnO₂ nanocacti (S1) measured at different time intervals. The characteristic absorption peak is observed at around 350 nm followed by a higher intensity absorption peak at around 500 nm, which decrease with gradual increase of irradiation time. 97% of CR degradation is achieved in 25 min of irradiation time. The absorption spectrum of MO under same conditions is shown in Fig. 8b. The characteristic absorption peak observed at around 450 nm decreases gradually with increasing irradiation time. Within 70 min of visible light irradiation time 95% of MO degradation is achieved. High degradation percentages of CR and MO dyes are achieved in certainly less time at similar conditions than the reported results.³⁹ In addition, visible light driven photocatalysts is considered to be superior to the already reported UV light driven photocatalysts.³⁹ The results suggest that α-MnO₂ nanocacti exhibit promising photocatalytic activity specially toward CR.

Fig. 8 The absorption spectrum of (a) CR and (b) MO dyes over the as prepared α-MnO₂ nanocacti (S1) measured at different time intervals. The degradation efficiency of (c) CR and (d) MO dyes with the use of different samples S1–S4 as photocatalysts.

In order to illustrate for which as synthesized samples, dyes are highly degraded, we compared degradation efficiencies of CR (Fig. 8c) and MO (Fig. 8d) with use of different samples as photocatalysts. The changes in the organic pollutant concentration under visible light irradiation are calculated as follows:

I = C/C₀ × 100% (3)

where, C₀ is the initial concentration of the organic pollutants when visible light is turned on, while real time concentration of organic pollutants under visible light irradiation is expressed by C. The relative ratio C/C₀ represents the photocatalytic efficiency with respect to irradiation time. From Fig. 8c and d, the order of photocatalytic efficiencies for as prepared samples are follows: α-MnO₂ nanocacti (S1) > β-MnO₂ nanocacti (S2) > α-MnO₂ nanorods (S3) > β-MnO₂ nanorods (S4). Obviously, α-MnO₂ nanocacti (S1) possess the highest photocatalytic efficiency among all other synthesized samples.

High surface area observed for α-MnO₂ nanocacti (S1) accounting for its high mesoporous structure is favorable for photo generated electron trapping and is most likely cause for its better photocatalytic activity than other samples. Furthermore, α-phases of nanocacti (sample S1) and nanorods (sample S3) exhibited better catalytic activity than their respective β-phase counterparts (samples S2 and S4). This may be due to presence of larger 2 × 2 tunnels as compared to the 1 × 1 tunnels in β-phase. This larger tunnel structure of α-phase can offer extra space for interstitial active sites and provides more room for electrons to get trapped thereby increasing photo-generated electron transport between the nanowires and ultrathin sheets. This can accelerate the charge separation forbidding electron–hole pair recombination. Thus stability of electron–hole pairs is assumed to be higher in α-phase.

The pseudo first order kinetics for the degradation of CR and MO is calculated through

C = C₀ exp[−kt] (A)

where ‘k’ is the degradation constant and ‘t’ is the reaction time. The calculated degradation constant for CR and MO using samples S1–S4 are 0.1125, 0.0921, 0.0721, 0.0572 and 0.0428, 0.027142, 0.0193, 0.01584 min⁻¹ respectively. The degradation constant is found to be directly dependent upon degradation percentage. The degradation constant for degradation of CR using sample S1 is higher than that of S2, S3 and S4 by 1.22, 1.56, 1.96 times. In case of MO degradation it is higher by 1.58, 2.21 and 2.70 times. Fig. 9a and b shows the linear curve fitted graph for degradation of CR using α-MnO₂ (S1) and β-MnO₂ (S2) nanocacti respectively. The linear curve fitted graph for degradation of MO using α-MnO₂ (S1) and β-MnO₂ (S2) nanocacti is presented in Fig. 9c and d.

Fig. 9 Pseudo first-order kinetics with linear curve fitting for the degradation of CR using (a) α-MnO₂ nanocacti (b) β-MnO₂ nanocacti and degradation of MO using (c) α-MnO₂ nanocacti (d) β-MnO₂ nanocacti.

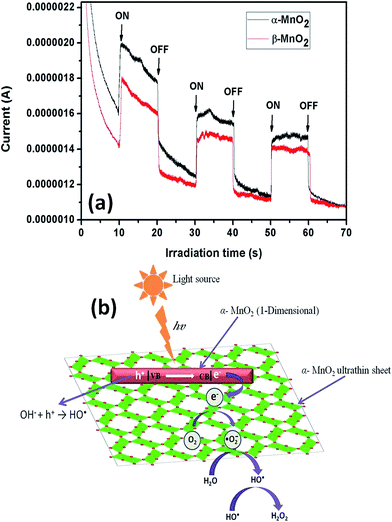
The higher photocatalytic activity of α-MnO₂ nanocacti than its β counterpart can be ascribed to the presence of higher number of photo induced electrons in α phase. This is evident from the photocurrent measurements with respect to irradiation time of α and β-MnO₂ nanocacti (Fig. 10a). Photocurrent for α-MnO₂ at 10 and 50 seconds of irradiation time is observed to be 1.11 and 1.03 times higher than β-MnO₂. This is well coordinated with above analysis.

Fig. 10 (a) Plot of photocurrent vs. irradiation time for α-MnO₂ and β-MnO₂ nanocacti. (b) A brief schematic of the plausible mechanism involved in the visible light driven photocatalysis of α-MnO₂ nanocacti (S1).

More specifically, high photocatalytic activities of samples S1 and S2 can be ascribed to enhanced electron dynamics relating to their unique morphologies. The nanowires constituting nanocacti (samples S1 and S2) have sharp edges which allow them to interact with visible light more efficiently. As a result of this electrons (e⁻) in valence band gets excited to conduction band leaving behind vacancy as hole (h⁺) in valence band. The degree of freedom for these high energy electrons gets confined in 1D tunnel structure of the nanowires. For sake of stability, these electrons intend to reduce their energy by moving into a higher dimensional (2D or 3D) structure. The ultrathin sheets being 2D or 3D structure, surrounding the nanowires attract these electrons by providing them with higher degree of freedom. This electron transition restricts photo generated electron–hole pair recombination and improves its stability which is highly beneficial for photocatalysis. The photocatalytic degradation process can be described using following equations:⁴¹

h⁺ + H₂O → HO˙ (4)

e⁻ + O₂ → O₂˙⁻ (5)

O₂˙⁻ + H₂O → HO₂˙ + HO˙ (6)

HO˙ + HO˙ → H₂O₂ (7)

Generally, h⁺ is scavenged by water molecules (H₂O) to generate hydroxyl radicals HO˙ (eqn (3)). The conduction e⁻ reacts by dissolved O₂ on surface of catalyst to form superoxide radical anions O₂˙⁻, which further reacts with water molecules to generate hydroperoxyl radical (HO₂˙) and HO˙ (eqn (4) and (5)). Two hydroxyl radicals (HO˙) further combine in pairs to form hydrogen peroxide H₂O₂ (eqn (6)). Eventually, these photogenerated radicals (O₂˙⁻ and HO˙) along with H₂O₂ oxidizes the organic pollutant and helps in degradation by forming mineralized products like CO₂, H₂O etc. Schematic diagram briefing the mechanism is illustrated in Fig. 10b.

3.6 Energy storage

The as prepared samples S1, S2, S3 and S4 were tested as anodes by constructing half cell lithium ion. The typical charge–discharge voltage curves (only selected cycles) for samples S1, S2, S3 and S4 at 1C rate in voltage range of 0.01 to 3 V (vs. Li/Li⁺) are presented in Fig. 11a–d, respectively. S1 exhibited high initial discharge capacity of about 1700 mA h g⁻¹. During second discharge a drastic loss in capacity is observed as 787 mA h g⁻¹. After 5, 10, 15, 20, 30 and 50^th cycles, specific capacities of S1 were as 537, 408, 361, 334, 307 and 300 mA h g⁻¹, respectively. There was decrease in capacity with use of sample S2, S3 and S4 as anode. The specific capacities of S2 after 2, 5, 10, 15 and 20^th cycles were 507, 448, 384, 348 and 325 mA h g⁻¹, respectively. Similarly, respective capacities of S3 were 486, 416, 376, 325 and 298 mA h g⁻¹ and for S4 were observed as 427, 410, 334, 299 and 282 mA h g⁻¹. Thus, α-MnO₂ nanocacti (S1) showed the highest capacity which deteriorates when there was phase transition to β (S2) and further decrease in capacity is observed when morphology was changed to α-MnO₂ nanorods (S3) followed by β-MnO₂ nanorods (S4). Fig. 11e shows the specific capacities during the different charge–discharge cycles. It is obvious that the capacity fades with the increase of charge–discharge cycle. However, sample S1 performs better than other samples and so its cyclic ability was monitored through extended cycling. Fortunately, a fairly constant cyclic stability is observed after 20^th cycle and even after 50 cycles α-MnO₂ nanocacti could manage a capacity of 300 mA h g⁻¹, which is considerably higher than the reported data.¹³ The drastic decrease in specific capacity may come from various factors but notably following three could be more prominent. The first is the capacity loss from the formation of solid electrolyte interface (SEI) layer which is a gel-like layer, containing ethylene oxide-based oligomers, LiF, Li₂CO₃, and lithium alkyl carbonate (ROCO₂Li), during first discharging process.⁶² The incomplete decomposition of SEI film hinders intercalation and deintercalation of Li⁺ ions on to electrode surface. This is common in all 3d transition metal oxides including CuO, NiO and Co₃O₄.⁶³ Secondly, repeated charging–discharging processes cause large volume expansion/contraction resulting in electrode pulverization. As its consequence, there is loss of inter-particle contact or particle with copper foil collector.⁴⁴ In case of nanocacti, this effect was minimized compared to nanorods. Highly porous ultrathin sheets with high surface area (271 m² g⁻¹) surrounding nanowires present in the nanocacti acts as protective layer which impedes its volume expansion and contraction thereby reducing ill effects of pulverization. Hence, better specific capacity is observed for nanocacti. Finally, the poor binding effect of electrode material with copper foil may have resulted in low electrochemical performance. From our assumption, coating of MnO₂ nanomaterial on to the copper foil using sodium alginate as binder was not so effective. The peeling off for coating was perceptible even before the assembly of coin cells which might have progressed during cycling process. Chen et al.³⁴ have reported the highest capacity for MnO₂ nanorods (even higher than its theoretical reversible value of 1404.7 mA h g⁻¹) using sodium carboxy methyl cellulose/styrene butadiene rubber (CMC/SBR, 1 : 1 by weight) as binder. Furthermore, α-MnO₂ showed better performance than β-MnO₂ counterpart. This may be due to presence of larger tunnels (2 × 2 tunnel) structure in alpha phase which might bring more space for active sites favoring intercalation and deintercalation of Li⁺ and thus help in better performance.

Fig. 11 (a–d) The typical charge–discharge voltage curves at 1C rate in the voltage range of 0.01 to 3 V (vs. Li/Li⁺) for the samples (a) S1, (b) S2, (c) S3 and (d) S4. (e) The specific capacities during the different charge–discharge cycles for samples S1–S4. (f) Nyquist plot of fresh coin cell and cell after 50 charging/discharging cycles and equivalent circuit (inset).

Briefly it can be inferred that the electrocatalytic activity is found to be directly dependent on surface area of the material. The high specific capacity of S1 can be ascribed to its large surface area. Sample S4 performs the least in energy storing mainly due to its low observable surface area. The observed surface areas of sample S2 and S3 are in intermediate and so are there specific capacities. The increased surface area enables more intercalation and deintercalation of Li⁺ ions. The high mesoporosity observed in case of as prepared nanocacti were more favorable for storing the Li⁺ ions. This might shorten the ion transport distances and provide a continuous pathway for the rapid diffusion of Li⁺ ions, thereby improving specific capacity of the electrode material.

In order to have a better understanding on charge transfer kinetics and the electrochemical performance of the sample S1 (α-MnO₂ nanocactus) upon charging/discharging cycles, electrochemical impedance (EIS) analysis of the fresh coin cell of S1 and the cell after 50 charging/discharging cycles were carried out. Fig. 11f shows the Nyquist plot obtained from the EIS measurement and the inset figure represents the equivalent circuit of the plot (fitted using Z fit software – BCS V10.37). In this circuit, R₁, R₂ and R₃ are the internal resistance of the cell known as the resistance of electrolyte, resistance at the Solid-Electrolyte Interface (SEI) and charge transfer resistance respectively; C₁ and Q₂ are associated with double-layer capacitance and constant phase elements and W₃ is the Warburg resistance. From the Nyquist plot, both the fresh cell and cycled cell (after 50 cycles) exhibits two semicircles at the high and medium frequency region along with an inclined line at the low frequency region. Among the two semicircles, the first corresponds to the resistance of the SEI film and the latter to the charge-transfer resistance at the electrolyte/electrode interface. And, the inclined line indicates the solid state diffusion resistance of Li electrode.^64,65 In comparison, the diameter of the semicircle at the higher frequency region of cycled cell is higher than the fresh cell which implies the raise in charge transfer resistance caused by the destruction of the electrode structure upon the charging/discharging cycles. Also, the increase in the solid state diffusion resistance suggest the suppressed diffusion of Li⁺ resulting in the low capacitance values. The results obtained are in line with the previous analyses.

4. Conclusions

Two different phases, α and β of MnO₂ nanocacti and nanorods were successfully synthesized following the common synthesis procedures without the use of any template, seed or other capping agents. Variations in morphologies as well as phase of as prepared samples were achieved by simply optimizing acidic content. β phase of MnO₂ was obtained at relatively high acidic strength (2 pH) as compared with α phase of MnO₂ obtained at 4 pH. The sudden addition of concentrated H₂SO₄ (0.2–0.3 μL) and dropwise addition of H₂SO₄ solution (0.3–0.4 M) during synthesis resulted in formation of nanocacti and nanorods, respectively and hence, accounts for major variations in morphologies of final products. The high specific surface area of α-MnO₂ nanocacti (271 m² g⁻¹) owing to its mesoporous structure is most likely reason for its superior photo/electro-chemical properties. The results suggest that α-MnO₂ nanocacti can be a promising photocatalyst for degradation of congo red and methyl orange dyes. The high specific capacity obtained for α-MnO₂ nanocacti make it a promising candidate for electrode material in Li-ion battery.

Acknowledgements

The work was supported by DST Nano Mission, Govt. of India, via Project No. SR/NM/NS-1062/2012. We further appreciate the aid from Science and Engineering Research Board, India, (SERB/F/4176/2015–16) for electrochemical studies.

References

1. A. L. Linsebigler, G. Lu and J. T. Yates, Chem. Rev., 1995, 95, 735–758.
2. H. Qin, W. Li, Y. Xia and T. He, ACS Appl. Mater. Interfaces, 2011, 3, 3152–3156.
3. M. Alam and D. C. Cameron, Thin Solid Films, 2000, 377, 455–459.
4. R. Abe, H. Takami, N. Murakami and B. Ohtani, J. Am. Chem. Soc., 2008, 130, 7780–7781.
5. L. Liu, Y. Li, S. M. Yuan, M. Ge, M. M. Ren, C. S. Sun and Z. Zhou, J. Phys. Chem. C, 2010, 114, 251–255.
6. J. Han, H. J. Kim, S. Yoon and H. Lee, J. Mol. Catal. A: Chem., 2011, 335, 82–88.
7. T. Gao, H. Fjellvag and P. Norby, Nanotechnology, 2009, 20, 055610.
8. J. E. Post, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3447–3454.
9. T. Zordan and L. G. Hepler, Chem. Rev., 1968, 68, 737–745.
10. V. Mathew, J. Lim, J. Kang, J. Gim, A. K. Rai and J. Kim, Electrochem. Commun., 2011, 13, 730–733.
11. G. Pistoia and A. Antonini, J. Electrochem. Soc., 1997, 144, 1553–1559.
12. S. Chen, J. Zhu and X. Wang, ACS Nano, 2010, 4, 6212–6218.
13. L. Feng, Z. Xuan, H. Zhao, Y. Bail, J. Guo, C. Su and X. Chen, Nanoscale Res. Lett., 2014, 9, 290.
14. L.-L. Yu, J.-J. Zhu and J.-T. Zhao, J. Mater. Chem. A, 2014, 2, 9353–9360.
15. W. Tang, Y. Hou, X. Wang, Y. Bai, Y. Zhu, H. Sun, Y. Yue, Y. Wu, K. Zhu and R. Hoze, J. Power Sources, 2012, 197, 330–333.
16. Y. Yang, L. Xiao, Y. Zhao and F. Wang, Int. J. Electrochem. Sci., 2008, 3, 67–74.
17. Y.-C. Chen, Y.-K. Hsu, Y.-G. Lin, Y.-K. Lin, Y.-Y. Horng, L.-C. Chen and K.-H. Chen, Electrochim. Acta, 2011, 56, 7124–7130.
18. W. Wei, X. Cui, W. Chen and D. G. Ivey, Chem. Soc. Rev., 2011, 40, 1697–1721.
19. P. Yu, X. Zhang, D. Wang, L. Wang and Y. Ma, Cryst. Growth Des., 2008, 9, 528–533.
20. V. Subramanian, H. Zhu, R. Vajtai, P. Ajayan and B. Wei, J. Phys. Chem. B, 2005, 109, 20207–20214.
21. X. Li, B. Hu, S. Suib, Y. Lei and B. Li, Biochem. Eng. J., 2011, 54, 10–15.
22. T. T. Truong, Y. Liu, Y. Ren, L. Trahey and Y. Sun, ACS Nano, 2012, 6, 8067–8077.
23. Y. Yuan, H. Li, M. Luo, S. Qin, W. Luo, L. Li and H. Yan, Water, Air, Soil Pollut., 2014, 225, 1–9.
24. Y. Hou, Y. Cheng, T. Hobson and J. Liu, Nano Lett., 2010, 10, 2727–2733.
25. J. Fei, Y. Cui, X. Yan, W. Qi, Y. Yang, K. Wang, Q. He and J. Li, Adv. Mater., 2008, 20, 452–456.
26. J. Cao, Q. Mao, L. Shi and Y. Qian, J. Mater. Chem., 2011, 21, 16210–16215.
27. W. Zhang, C. Zeng, M. Kong, Y. Pan and Z. Yang, Sens. Actuators, B, 2012, 162, 292–299.
28. J.-J. Feng, P.-P. Zhang, A.-J. Wang, Y. Zhang, W.-J. Dong and J.-R. Chen, J. Colloid Interface Sci., 2011, 359, 1–8.
29. G. Pistoia and A. Antonini, J. Electrochem. Soc., 1997, 144, 1553–1559.
30. Y. Li, Q. Zhang, J. Zhu, X. L. Wei and P. K. Shen, J. Mater. Chem. A, 2014, 2, 3163.
31. S. Bach, J. P. Pereira-Ramos and P. Willmann, Electrochim. Acta, 2011, 56, 10016–10022.
32. K. Chen, Y. Dong Noh, K. Li, S. Komarneni and D. Xue, J. Phys. Chem. C, 2013, 117, 10770–10779.
33. D. Liu, B. B. Garcia, Q. Zhang, Q. Guo, Y. Zhang, S. Sepehri and G. Cao, Adv. Funct. Mater., 2009, 19, 1015–1023.
34. J. Chen, Y. Wang, X. He, S. Xu, M. Fang, X. Zhao and Y. Shang, Electrochim. Acta, 2014, 142, 152–156.
35. H. Zhao, G. Zhang and Q. Zhang, Ultrason. Sonochem., 2014, 21, 991–996.
36. W. F. Dong, L. H. Zang and H. Li, Appl. Mech. Mater., 2013, 361, 760–763.
37. D. Zhao, X. Yang, H. Zhang, C. Chen and X. Wang, Chem. Eng. J., 2010, 164, 49–55.
38. M. Singh, D. N. Thanh, P. Ulbrich, N. Strnadova and F. Stepanek, J. Solid State Chem., 2010, 183, 2979–2986.
39. B. Yin, S. Zhang, Y. Jiao, Y. Liu, F. Qu and X. Wu, CrystEngComm, 2014, 16, 9999–10005.
40. G. Cao, L. Su, X. Zhang and H. Li, Mater. Res. Bull., 2010, 45, 425–428.
41. K. Saravanakumar, V. Muthuraj and S. Vadivel, RSC Adv., 2016, 6, 61357–61366.
42. M. Panahi-Kalamuei, K. Motevalli and M. Aliabadi, J. Mater. Sci.: Mater. Electron., 2016, 27, 4631–4635.
43. M. Xu, L. Kong, W. Zhou and H. Li, J. Phys. Chem. C, 2007, 111, 19141–19147.
44. Z. Li, Y. Ding, Y. Xiong and Y. Xie, Cryst. Growth Des., 2005, 5, 1953–1958.
45. N. Kumar, P. Dineshkumar, R. Rameshbabu and A. Sen, RSC Adv., 2016, 6, 7448–7454.
46. N. Kumar, P. Dineshkumar, R. Rameshbabu and A. Sen, Mater. Lett., 2015, 158, 309–312.
47. G. Li, L. Liang, H. Pang and H. Peng, Mater. Lett., 2007, 61, 3319–3322.
48. X. Duan, J. Yang, H. Gao, J. Ma, L. Jiao and W. Zhenglable, CrystEngComm, 2012, 14, 4196–4204.
49. W. N. Li, J. Yuan, X. F. Shen, S. Gomez-Mower, L. P. Xu, S. Sithambaram, M. Aindow and S. L. Suib, Adv. Funct. Mater., 2006, 16, 1247–1253.
50. L. Li, C. Nan, J. Lu, Q. Peng and Y. Li, Chem. Commun., 2012, 48, 6945–6947.
51. J. Cao, Q. Mao, L. Shi and Y. Qian, J. Mater. Chem., 2011, 21, 16210–16215.
52. X. C. Song, Y. Zhao and Y. F. Zheng, Cryst. Growth Des., 2007, 7, 159–162.
53. J. Fei, Y. Cu, X. Yan, W. Qi, Y. Yang, K. Wang, Q. He and J. Li, Adv. Mater., 2008, 20, 452–456.
54. D. Portehault, S. Cassaignon, E. Baudrin and J. P. Jolivet, Cryst. Growth Des., 2009, 9, 2562–2565.
55. B. B. Lakshmi, C. J. Patrissi and C. R. Martin, Chem. Mater., 1997, 9(11), 2544–2550.
56. D. Zitoun, N. Pinna, N. Frolet and C. Belin, J. Am. Chem. Soc., 2005, 127(43), 15034–15035.
57. J. C. Villegas, L. J. Garces, S. Gomez, J. P. Durand and S. L. Suib, Chem. Mater., 2005, 17(7), 1910–1918.
58. Y. Ding, X. Shen, S. Sithambaram, S. Gomez, R. Kumar, V. M. Crisostomo, S. L. Suib and M. Aindow, Chem. Mater., 2005, 17, 5382–5389.
59. M. S. Wu, J. T. Lee, Y. Y. Wang and C. C. Wan, J. Phys. Chem. B, 2004, 108, 16331–16333.
60. C. M. McShane and K.-S. Choi, J. Am. Chem. Soc., 2009, 131, 2561.
61. M. Kruk and M. Jaroniec, Chem. Mater., 2001, 13, 3169–3183.
62. J. Y. Xiang, J. P. Tu, L. Zhang, Y. Zhou, X. L. Wang and S. J. Shi, J. Power Sources, 2010, 195, 313–319.
63. J. Chen, Materials, 2013, 6, 156–183.
64. Z. Y. Sui, C. Wang, K. Shu, Q. S. Yang, Y. Ge, G. G. Wallace and B. H. Han, J. Mater. Chem. A, 2015, 3, 10403–10412.
65. L. Li, A. R. O. Raji and J. M. Tour, Adv. Mater., 2013, 25, 1–5.

---