ZnO nested shell magic clusters as tetrapod nuclei

Abstract

Although atomic clusters are generally different from bulk material in terms of their structure, they can initiate (nano)crystal formation. For ZnO, tetrapod-like nanostructures are well known; however, their nucleation model is still questionable. In this report, ZnO magic clusters were considered as seeds for the nucleation of tetrapods; these clusters were characterized via mass spectroscopy and were attributed to a series of nested shell clusters via quantum chemical calculations. Herein, these clusters were constructed as nested Goldberg polyhedra and subjected to Jahn–Teller distortion.

---

1. Introduction

Among various morphologies of ZnO nanostructures, tetrapod-like morphology, initially called fourling,¹ is well known.² The tetrapods generally have wurtzite structure of the legs, although inclusions of zinc blende phase have been found.³ Several models have been suggested to explain the nucleation of the tetrapods. Multi-twinned crystalline nuclei are most common; however, different models insist on different structures of the nucleus: wurtzite,^4–7 or zinc blende,^8–10 or hexagonal grains.¹¹ Moreover, for ZnO clusters, bonded groups of atoms, no studies have been reported on the crystalline structure of the clusters that are smaller than a few tens of atoms. Herein, these data were well-developed for small clusters that contain a few to a couple of tens of atoms as compared to those for larger clusters. Early theoretical studies^12,13 predicted the increased stability of the spheroid molecule (ZnO)₁₂, whereas experimental studies^14,15 did not report any clusters with enhanced stability, so called magic clusters with ≤20 ZnO units. Later calculations,¹⁶ which were carried out for some of the (ZnO)_n clusters in the range from n = 9 to 64, predicted the dominance of wurtzite-derived clusters over bubble-like clusters for n ≥ 26 and demonstrated the energetic advantage of the (ZnO)₆₀ onion-like cluster. It has also been reported¹⁷ that onion-like and bulk-like isomers progressively become more stable with the increasing size, whereas cage-like and tube-like structures are the most preferred structural motifs for (ZnO)_n with n = 24, 28, 36, and 48. An evolutionary algorithm has been employed for the search of stable and metastable (ZnO)_n structures for n = 1–32, and clusters for n = 12, 16, and 28 have been predicted to exhibit a relatively high stability.¹⁸ However, only the clusters of 34, 60, and 78 ZnO monomers have been found with an enhanced abundance via the experiment.¹⁹ This experiment inspired the researchers to carry out calculation to search for the structure of (ZnO)₃₄ and (ZnO)₆₀ clusters^20,21 and investigate the properties of the latter.²² The hollow cage has been nominated as the most preferred structure for (ZnO)₃₄, whereas the sodalite structural motif has been found to be the most energetically favorable structure for (ZnO)₆₀. Other studies have experimentally²³ and theoretically^24–26 reported the transition from ZnO clusters to wurtzite nanoparticles. Moreover, new structural motifs and frameworks, built of bubble-like clusters, have been considered.^26–28 However, despite the extensive efforts made in computational crystal structure prediction, a convincing link between the structure of the clusters and the particular shape of ZnO nanostructures, such as terapods, is still missing.

In this study, we present a detailed mass spectroscopy analysis of zinc oxide clusters containing up to almost 200 ZnO pairs. Inspired by the magic numbers found in the mass spectra, we constructed a series of nested shell clusters and performed a computational chemistry study on them. The proposed cluster structures explained the observed sequence of the magic numbers, predicted the composition and the structure for larger yet unexplored magic clusters, and provided the origin of ZnO tetrapods.

2. Experimental and calculation details

Time of flight mass spectroscopy

Laser ablation of an appropriate precursor material and the following time-of-flight mass spectroscopy (TOF MS) of the resultant material is an effective method for the discovery of new stable clusters.^29,30 In our study, zinc peroxide (ZnO₂) was ablated as it is an efficient precursor for zinc oxide cluster formation.³¹ Addition of alkylamines to the material for ablation was shown to increase the abundance of the magic clusters for II–VI group compounds;³² thus, octadecylamine (ODA) was used. Basically, the experimental procedure of ZnO cluster production and TOF mass spectra measurement in this study was the same as described elsewhere:¹⁹ a small drop of the suspension of zinc peroxide powder mixed with ODA was placed on the target of a Bruker Reflex III-T TOF mass spectrometer equipped with a nitrogen laser; the mass spectra of the cluster ions, either negatively or positively charged, produced by laser ablation of zinc peroxide powder mixed with octadecylamine in toluene, were obtained in the reflex mode by accumulating the signal of 500–2000 laser shots.

Calculation methods

The geometry optimization and vibrational analyses of the clusters were performed via Firefly quantum chemistry package³³ using the following methods and basis sets: Austin Model 1 (AM1) semi-empirical method;³⁴ 6-31G basis sets for oxygen³⁵ and zinc³⁶ atoms; restricted Hartree–Fock method;³⁷ density functional theory (DFT), namely, Becke's three-parameter hybrid exchange functional³⁸ coupled with the Lee–Yang–Parr nonlocal correlation functional³⁹ (B3LYP); and the second-order Møller–Plesset energy corrections (MP2).⁴⁰ The calculated structures were visualized using the wxMacMolPlt software.⁴¹ The RMSD values were calculated using the Chemcraft software.⁴²

3. Results and discussion

Analysis of the mass spectra

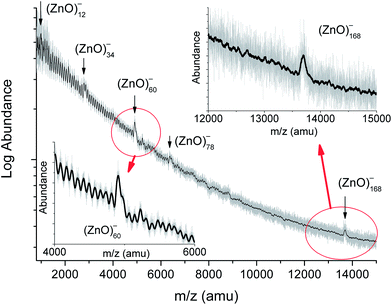
The time-of-flight mass spectrum of the negatively charged zinc oxide clusters is shown in Fig. 1, and the insets show details of the spectral features. The stoichiometric composition of the (ZnO)_n clusters was concluded from the following two findings: (i) the dominant peak in the Fourier transform spectrum (Fig. S1†) at 81.4 atomic mass units (amu) was exactly the mass of (ZnO)₁ and (ii) the extrapolation of the series to its beginning leads to the zero mass (Fig. S2†). The assignment of the cluster composition to the peaks in the spectrum was carried out via correlating the calculated isotopic patterns of the clusters in the low mass region and peak widths in the high mass region with those of the experimental spectrum (Fig. S3†). The spectrum in the mass range from 2000 to 8500 amu was similar to the reported spectrum:¹⁹ abundances of (ZnO)₃₄, (ZnO)₆₀, and (ZnO)₇₈ clusters were higher than those of their neighbors. However, the spectrum in the range of larger masses showed a distinct characteristic: the only (ZnO)₁₆₈ cluster had a notably enhanced abundance in the interval from about a hundred to two hundred ZnO pairs. The mass spectrum of the positively charged zinc oxide clusters demonstrated the same set of magic numbers (see Fig. S4†) although the peak of (ZnO)₁₆₈ cluster was hardly traceable. Addition of commonly used TOF MS matrices, namely, trifluoroacetic acid or its mixture with picolinic acid, to zinc peroxide precursor, instead of ODA, made the peak of (ZnO)₁₆₈ cluster more obvious (Fig. S5†). In the mass range below 2000 amu, (ZnO)₁₂, (ZnO)₁₄, and (ZnO)₂₂ clusters have slightly higher abundances than those of their neighbors when produced with ODA. The similarity of the mass spectra of the positively and negatively charged clusters (see Fig. 1, S4, and S5†) suggests the existence of neutral clusters with the same composition, whereas the prevalence of negatively charged (ZnO)₁₆₈ cluster indicates its high electron affinity, which resonates with the predicted high electron affinity of (ZnO)₆₀ cluster.²²

Fig. 1 The time-of-flight mass spectrum of the negatively charged zinc oxide clusters obtained by laser ablation of zinc peroxide powder mixed with octadecylamine in toluene. The gray line displays the measured signal and black line shows the smoothed spectrum (50 point adjacent averaging). The clusters of enhanced stability are pointed and labeled. Abundance is plotted on a logarithmic scale for clarity of the entire spectrum. Insets show the fragments of the spectrum in the vicinity of (ZnO)₆₀ and (ZnO)₁₆₈ cluster mass regions on a linear scale.

The structure of the magic clusters

As mass spectroscopy only provided the number of atoms that constituted the cluster, quantum chemical calculations were typically employed to find the structure of the cluster. Theoretical studies on the structure of ZnO clusters, as well as of many other inorganic clusters, were carried out after the discovery of carbon fullerenes. (ZnO)₁₂ cluster was predicted to have an enhanced stability as early as 1994,¹² and the prediction was confirmed via many calculations later.^{24,26,43–46} However, on attentively looking at the reported mass spectra,^14,15,31 a small increase in the abundance of the (ZnO)₁₂ cluster over the mean abundance of its neighbors, (ZnO)₁₁ and (ZnO)₁₃, can be observed and it was not mentioned by the authors; moreover, the current study (Fig. 1) also confirmed this fact. The larger onion-like (ZnO)₆₀ cluster also has been predicted to be stable.¹⁶ Other calculations,^21,22 however, did not suggest the onion-like structure as the most stable isomer for (ZnO)₆₀; these results were caused by suboptimal arrangement of the shells, see Fig. S6 and Table S1† for details. (ZnO)₆₀ double bubble clusters, built of (ZnO)₁₂ and (ZnO)₄₈ units as well as of analogous GaN and SiC units, have been considered as targets for enhanced electron–hole separation.^27,28,47 For other II–VI group compounds, the onion-like (ZnS)₆₀ cluster, built of (ZnS)₁₂ and (ZnS)₄₈ shells, has been theoretically suggested,⁴⁸ but only the magic numbers 13, 19, 33, and 34 (and 48 for CdSe) were observed in the mass spectra of ZnS, ZnSe, ZnTe, CdS, CdSe, and CdTe.^30,49 A recent computational study²⁶ predicted that magic number size (ZnO)_n structures are formed as single (n = 12, 16, and 36), double (n = 60, 78, and 100), and triple layer cages (n = 132 and 168); however, only some of them were actually present with an enhanced abundance in our experimental results (Fig. 1). For another well-studied binary inorganic compound, boron nitride, the enhanced stability of BN cage-like clusters of 12, 16, 28, and 60 monomers has been predicted.^50,51 A (BN)₁₂ cage, consisting of 4- and 6-membered rings, has been shown to be the most stable isomer^52,53 and is supposed to play the same role for boron nitride as C₆₀ plays for carbon.⁵² Electron microscopy shows nested BN cages⁵⁴ analogous to carbon onions.⁵⁵ In the case of carbon, the icosahedral series C₆₀, C₂₄₀, …, C_60m² has been used to simulate carbon onions,⁵⁶ whereas for BN, the orientationally ordered series starting from (BN)₁₂, namely (BN)₁₂, (BN)₄₈, …, (BN)_12m² has been considered to be non-realistic because the inter-cage distance is too small, and other series have been proposed.⁵⁴ Later calculations confirmed the relative instability of the (BN)₆₀ onion double-bubble structure.⁵⁷ On reviewing the mass spectroscopic data, it was observed that the shells of atoms principle arranges the otherwise strange-looking experimental data about magic clusters into simple geometrical sequences.⁵⁸ The principle states the enhanced stability of the clusters that have complete (closed) shells of constituting atoms.

Mathematical models of the ZnO shells

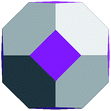
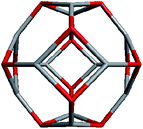
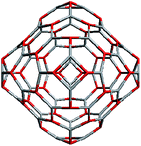
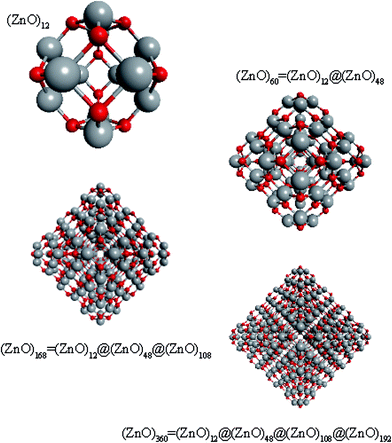
Regarding ZnO, taking into account all the abovementioned facts, we proposed the following structure for the found magic clusters (ZnO)₆₀ and (ZnO)₁₆₈. They consist of concentric nested (onion-like) shells of (ZnO)_n, n = 12m² and m = 1, 2, and 3. The first shell at m = 1 is (ZnO)₁₂, the second shell at m = 2 is (ZnO)₄₈, and the third shell at m = 3 is (ZnO)₁₀₈. The cluster (ZnO)₆₀ consists of two shells: (ZnO)₁₂ inside of (ZnO)₄₈. (ZnO)₁₆₈ cluster has three nested shells: (ZnO)₁₂, (ZnO)₄₈, and (ZnO)₁₀₈. In this way, the simple mathematical sequence (n = 12m²) exactly describes the magic numbers experimentally observed in the mass spectra. Following the sequence, the next closed atomic shell ZnO clusters were (ZnO)₃₆₀, (ZnO)₆₆₀ and so on. The calculated sizes of the clusters are listed in Table 1.

Table 1 Size of the magic (ZnO)_n nested shell clusters

Number of shells	Number of ZnO pairs, n	Diameter^a of spherical wurtzite cluster, nm	Size^b of the nested shell cluster (Th) dmin − dmax, nm
			AM1	HF/6-31G	B3LYP/6-31G	MP2/6-31G
a Diameter (nm) = (6M/πρ)^1/3, where ρ = 5600 kg m^−3 is the specific density of bulk wurtzite ZnO; M = n × MZnO is the mass of the cluster; MZnO = 81.4 amu is the mass of the (ZnO)1 unit and it is numerically equal to the molar mass of ZnO; 1 amu = 1.661 × 10^−27 kg.b dmin is the minimum distance between the opposite faces of a cluster (the diameter of the sphere inscribed into the outermost shell); and dmax is the maximum distance between the vertexes of a cluster (the diameter of the sphere circumscribed over the outermost shell).
1	12	0.82	0.49–0.66	0.47–0.61	0.47–0.62	0.48–0.63
2	60 = 12@48	1.40	0.99–1.49	0.96–1.38	0.96–1.39
3	168 = 12@48@108	1.98	1.46–2.35	1.42–2.19
4	360 = 12@48@108@192	2.55	1.95–3.22
5	660 = 12@48@108@192@300	3.12

---

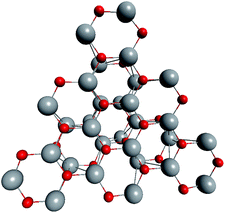
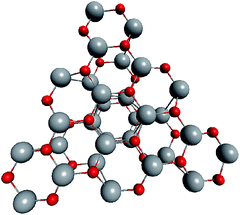
Geometrically, the sequence of (ZnO)_n, n = 12m² and m = 1, 2, 3… shells, can be described as the set of Goldberg polyhedra⁵⁹ G(a,b) of octahedral symmetry, with tetragons instead of pentagons, and a = b: G_IV(1,1), G_IV(2,2), G_IV(3,3), and so on. Unlike elementary substances, such as carbon or palladium, for describing the shells for which the Goldberg polyhedra were successfully applied,^60,61 in a binary compound, namely in ZnO, zinc and oxygen atoms were alternated in the vertices of both the tetragons and hexagons, such that each atom had three neighbors of the other element and the full octahedral O_h symmetry of the polyhedra changed to the pyritohedral T_h symmetry, whereas the octahedral shape of the polyhedra was retained. Of course, the Euler characteristic of a convex polyhedron equals 2, and the Goldberg polyhedra built of tetragons and hexagons have exactly 6 tetragonal faces. The higher stability for the shell is expected for the case of isolated tetragons,⁶² especially when they are evenly spread on the polyhedron surface, analogous to the isolated pentagon rule for buckminsterfullerenes.⁶³ It was shown⁶⁴ that equilateral convex octahedral Goldberg polyhedra do not exist for (a² + ab + b²) > 4; thus, some deformation of the polygons was expected for the second and larger shells.

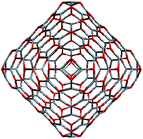
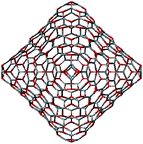
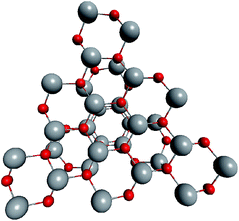
To construct the shells and to explore their geometry, Conway polyhedron notation⁶⁵ can be applied. The first shell can be presented as a truncated octahedron, tO, where t marks the operator of truncation of all the vertices and O is the abbreviation of the octahedron, which is a seed in this study. The second shell ctO can be obtained from the first shell by chamfer operator c, which introduces a new hexagonal face in place of each edge and thus transforms G(a,b) to G(2a,2b). The third shell is tktO, where k is the kis operator, which raises a pyramid on each face, and so the tk operator transforms G(a,b) to G(3a,3b). The fourth shell is cctO. Following the abovementioned rules, the Goldberg polyhedra of two and three fold numbers of a and b: cctO generates G(4a,4b), ctktO results in G(6a,6b), and so on, can be constructed. wrwtO produces a G(7a,7b) polyhedron, where w and r are the whirl and reflect operators, respectively. However, finding a combination of operators to construct the polyhedra of other prime numbers, namely, 5, 11, 13, and so on, is still a challenge. The advantage of using the Conway polyhedron notation lies in its simplicity and clearness of construction and exploration of the shells, for example, via freely available online tools.⁶⁶ The rendered polyhedra and the corresponding ZnO shells are shown in Table 2.

Table 2 Shells of ZnO in Goldberg and Conway presentations

a On-line tool^66 was used with A2 convex spherical adjustment.
Shell number, m	1	2	3	4
Number of ZnO pairs, n = 12m^2	12	48	108	192
Goldberg polyhedron	GIV(1,1)	GIV(2,2)	GIV(3,3)	GIV(4,4)
Conway notation	tO	ctO	tktO	cctO
Rendered Conway polyhedron^a
AM1 optimized Th symmetric (ZnO)n shell

---

Computational chemistry results

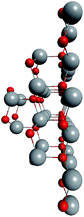
To support the suggestion of the nested shell structure of the magic ZnO clusters, quantum chemical calculations were performed. The structures of (ZnO)₁₂, (ZnO)₆₀, (ZnO)₁₆₈, and (ZnO)₃₆₀ clusters optimized at the MP2/6-31G, B3LYP/6-31G, HF/6-31G, and AM1 theory levels, respectively, are shown in Fig. 2. The highest theory level used for each cluster was restricted by feasible calculation time and software capabilities. Moreover, the degree of confidence that can be obtained at different calculation levels has been discussed hereinafter. The symmetry point group of all the shown nested shell structures is T_h.

Fig. 2 The structures of T_h symmetric (ZnO)₁₂, (ZnO)₆₀, (ZnO)₁₆₈, and (ZnO)₃₆₀ clusters optimized at MP2/6-31G, B3LYP/6-31G, HF/6-31G, and AM1 theory levels, respectively. The drawings are not to scale. Zinc atoms are shown as large gray balls and oxygen atoms are shown as small red balls.

The stationary points of the geometry optimization were found to be minimum by harmonic vibrational frequency analysis. All the frequencies are real for (ZnO)₁₂; thus, the T_h symmetric shell is indeed the minimum point of potential energy surface for this cluster. However, imaginary frequencies were found for the T_h symmetric structure of (ZnO)₆₀. Then, all the symmetry restrictions were released. Small random shifts were applied to all the atoms, the geometry was optimized, and this procedure was repeated for several thousand times using the AM1 semi-empirical method; then, a few low energy isomers were selected and optimized at the B3LYP/6-31G level. Among these, the structure lowest in energy was determined and for convenience, it was named as the C₁ symmetric structure. It had total energy 234 meV lower than that of the T_h symmetric structure, and all the vibrational frequencies were real; thus, it was indeed the minimum point of the cluster potential energy surface (PES). Visually, it is similar to the corresponding T_h symmetric structure of Fig. 2, with which it has been compared in Table S2.† The distortion of the resultant C₁ symmetric structure, compared to that of the initial T_h symmetric structure, was rather small: the root-mean square displacement (RMSD) of all the atoms was about 22.1 pm, whereas the RMSD of the atoms of the internal and the outer shells were about 5.0 pm and 20.6 pm, respectively. This structure distortion can be explained by the Jahn–Teller effect, in which symmetry reduction removes the degeneracy of the ground state and lowers the energy of the system.⁶⁷ Indeed, the T_h symmetric isomer has the triply degenerate highest occupied molecular orbital (HOMO) energy level, which is the electronic ground state, whereas the symmetry reduced C₁ symmetric isomer has the doubly degenerate HOMO energy level (see Table S3† for details). In both the cases of the T_h and C₁ symmetric isomers, the HOMO is mostly localized on the oxygen atoms of the outer shell (Fig. S7†) and therefore the HOMO degeneracy is mainly associated with the structure distortion of the outer shell. Note that contrary to the recent calculations,²⁷ where the reduced (ZnO)₆₀ double-bubble cluster symmetry has been found as C₂, our lowest energy C₁ symmetric structure of (ZnO)₆₀ cluster was very close to the C_i, C₃, and S₆ symmetry point groups: the corresponding RMSDs were 0.27, 0.42, and 0.41 pm, respectively. Geometry optimization within these symmetry restrictions slightly decreased the total energy of the cluster, but caused appearance of the imaginary frequencies (Table S3†).

To evaluate the stability of (ZnO)₆₀ with regard to the bulk material structure, the structure of the bulk wurtzite fragments of the same number of atoms was optimized, and it was found that the nested shell cluster (C₁ symmetric) had about 10.6 eV lower total energy at the HF/6-31G theory level; thus, it is much more stable than wurtzite structure for this size of ZnO clusters. Note that significant attention has been paid to find the optimal cut of the fragment from the bulk wurtzite lattice. First, thousands of randomly centered and randomly elliptical cuts were evaluated by the number of Zn–O bonds that remained within each fragment, and the fragments of the maximum number of the bonds were selected for the AM1 geometry optimization. The lowest AM1 total energy fragments were then geometry optimized ab initio, and thus the lowest HF/6-31G total energy fragment were determined (Fig. S8†).

Releasing (ZnO)₁₂ from symmetry restrictions and applying the same random displacement-optimization procedure did not lead to a lower energy structure within the precision of the calculations. The RMSD of atoms of the C₁ symmetric structure with regard to the T_h symmetric structure was barely 0.02 pm, and the HOMO energy level remained triply degenerate. Thus, (ZnO)₁₂ was not subjected to Jahn–Teller distortion most likely because of its high symmetry, analogously to C₆₀ buckminsterfullerene.

Although the T_h symmetric nested shell structure of (ZnO)₁₆₈ cluster, as shown in Fig. 2, has been found to be a stationary point of PES, the vibrational frequency analysis revealed an imaginary frequency. Therefore, a search was performed for the minimum of PES using the same procedure as described above for (ZnO)₆₀ by applying small random shifts to all the atoms, optimizing the geometry, and repeating the procedure several hundred times using the AM1 method. Surprisingly, the lowest energy structure appeared within the T symmetry point group, and it was only 70 meV lower in energy (using the HF/6-31G method) than the T_h symmetric structure. The RMSD of all its atoms with regard to the T_h structure was 33.9 pm, whereas the RMSDs of the internal (ZnO)₁₂, the intermediate (ZnO)₄₈, and the outer (ZnO)₁₀₈ shells were 10.4 pm, 32.3 pm, and 36.2 pm, respectively; same as for (ZnO)₆₀, the outer shell is the most distorted. The overall small distortion of (ZnO)₁₆₈ cluster upon its transformation from T_h to T symmetry is shown in Table S4.†

Ab initio calculation of (ZnO)₃₆₀ cluster is an exorbitant task; thus, only the semi-empirical AM1 method was used. The same random displacement-optimization procedure repeated for about a hundred times revealed that the C₁ structure was 17 eV lower in energy than the T_h symmetric structure. The RMSD of all its atoms, compared to that of T_h structure, was 56.3 pm, and the RMSDs of the shells were 43.5 pm, 53.2 pm, 53.3 pm, and 52.9 pm for (ZnO)₁₂, (ZnO)₄₈, (ZnO)₁₀₈, and (ZnO)₁₉₂, respectively. The larger RMSD values and the larger energy difference between the T_h and C₁ symmetric structures with respect to (ZnO)₆₀ and (ZnO)₁₆₈ clusters were most likely caused by the rough calculation method used. However, the geometry of the cluster, namely, its nested shell construction, did not significantly deteriorate upon symmetry reduction (see Table S5†).

Enthalpy of atomization

The enthalpy of atomization (EA) is the energy required to separate all the atoms of a cluster. Being normalized on the number of atoms or monomers, the EA is conceptually the simplest characteristic, by which the clusters of different composition (size, number of atoms or monomers) can be compared concerning their stability. The EA per ZnO pair for the nested shell ZnO clusters calculated at the feasible theory levels are presented in Table 3. Of course, only the results obtained within the same theory level could be compared. The following conclusions can be drawn. For the clusters of 12, 60, and 168 ZnO pairs, the EA increased as the number of the shells increased, as observed via both HF and DFT calculations, whereas the EA was almost constant, as observed by the semi-empirical method. Then, if ab initio methods are considered to be more reliable, even higher stability for the (ZnO)₃₆₀ cluster can be predicted because its semi-empirical results are similar to those of the smaller clusters. Moreover, all the methods suggest that (ZnO)₁₂ is less stable than the larger multi-shell clusters, which partially explains why (ZnO)₁₂ was commonly found to be a magic cluster in the calculations, but not in the mass spectra.

Table 3 The enthalpy of atomization of ZnO nested shell magic clusters^a

Cluster	Symmetry restriction	The enthalpy of atomization per ZnO pair, eV
		AM1	HF/6-31G	B3LYP/6-31G	MP2/6-31G
a ! Marks the structures, for which imaginary frequencies were found.
(ZnO)12	Th	5.832	7.612	9.686	17.172
	C1	5.832	7.612	9.686	17.172
(ZnO)60	Th	5.821	8.322!	10.375!
	C1	5.848	8.322	10.379
(ZnO)168	Th	5.800	8.604!
	C1	5.844	8.605
(ZnO)360	Th	5.785
	C1	5.832

---

Moreover, the degree of confidence that can be obtained at different calculation levels can be estimated. For the single-shell cluster (ZnO)₁₂, all the methods performed well although they showed significantly different enthalpy of atomization; thus, corresponding experimental data are necessary to evaluate them. For the multi-shell clusters, which consist of a significantly larger number of atoms, the MP2 method is extremely expensive in terms of computational resources and time, which makes it hardly applicable even for the (ZnO)₆₀ cluster. AM1 semiempirical method, which is the fastest and least demanding in terms of resources and thus applicable from the smallest up to the largest clusters, clearly demonstrated higher stability (lower total energy) for the symmetry-reduced clusters (Jahn–Teller effect), as B3LYP/6-31G does. However, AM1 may converge (sometimes) into strange structures that are obviously unstable when checked by HF or DFT methods. AM1 results can be used for fast preliminary evaluation of the cluster energies but should be checked (if possible) by the higher level methods. The HF/6-31G method showed about the same energy for both the T_h and C₁ structures and thus it hardly revealed the Jahn–Teller effect as an energy decrease but clearly indicated the unstable high-symmetry geometry (T_h) by imaginary frequencies. The vibrational frequency analysis at the AM1 level did not reveal imaginary frequencies for the high symmetry (T_h) isomers; thus, it is less applicable there.

Bond lengths

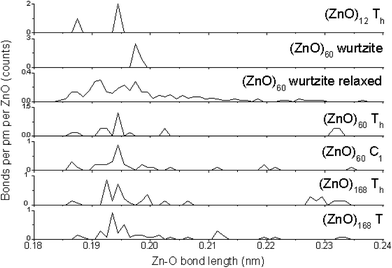
As different calculation methods provide different values of energy of a cluster, they also result in different bond lengths (see Table S6,† which lists the bond lengths in the T_h symmetric (ZnO)₁₂ cluster, which was calculated by the HF, B3LYP DFT, and MP2 theory levels using 3-21G, 6-31G, and 6-31G(3df) basis sets, as well as by the AM1 semi-empirical method). Thus, to explore the changes in bond lengths upon the number of grown shells, the same calculation method should be used for all the clusters under investigation. HF/6-31G results are available for the clusters of 12, 60, and 168 ZnO pairs. Fig. 3 shows the counted Zn–O bond length distributions for these clusters in T_h symmetric and the symmetry reduced nested shell structures and also for the fragment of 60 ZnO pairs, which was cut from the wurtzite ZnO crystal lattice, and for its relaxed geometry.

Fig. 3 Zn–O bond length distributions counted from HF/6-31G optimizations. The second panel from the top, labeled as (ZnO)₆₀ wurtzite, represents the fragment of 60 ZnO pairs, which was cut from the bulk wurtzite ZnO crystal structure, whereas the result of its geometry optimization, labeled as (ZnO)₆₀ wurtzite relaxed, is shown in the third panel.

The first obvious feature, as shown in Fig. 3, is the sharp main peak at about 0.194–0.198 nm in all the graphs, except for the relaxed wurtzite structure. This peak points to the Zn–O bond length in the bulk wurtzite crystal structure, and it is the most abundant Zn–O bond length in all the clusters. Note that it is unexpected to find this distance to be smaller for the clusters than that for the bulk; typically, the smaller the particle, the larger the interatomic distance.²³ However, in the present case, clusters instead of particles were considered, and they were different from the bulk structure and thus had shorter bonds. The relaxed wurtzite structure has very broad bond-length distribution, which suggests many bonds of unfavorable lengths, which explains the much higher total energy of this structure as abovementioned.

The second feature is the presence of bonds of about 0.23 nm, which is the intershell distance in the nested shell T_h symmetric clusters. These long bonds are energetically disadvantageous and thus the number of these bonds is significantly lower in the symmetry-reduced structures C₁ symmetric (ZnO)₆₀ and T symmetric (ZnO)₁₆₈, which have many of the inter-shell bonds of about 0.21–0.22 nm instead.

The third feature is the presence of 1/3 of the 0.187 nm (ZnO)₁₂ cluster bonds at the edges between hexagons. They are much shorter than the optimal interatomic length in the bulk wurtzite lattice. This explains the lower stability of this cluster compared with that of the larger nested shell clusters, where the relative number of these bonds is smaller.

The distributions of all Zn–O, O–O, and Zn–Zn distances in the clusters are shown in Fig. S9–S11.† These calculated fingerprints can be used for identifying the clusters using Fourier transform X-ray absorption fine structure (XAFS) experimental data when this information will be obtained for ZnO clusters of this size range (1–2 nm diameter), whereas the reported XAFS data on ZnO is for larger clusters and particles.⁶⁸

Tetrapod nucleation model

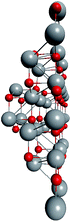
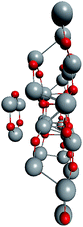
Based on the symmetry of the magic nested shell clusters, we supposed that they could be the seeds, from which ZnO tetrapods grow (Fig. 4). This can be explained as follows. (ZnO)₃ hexagons, which make triangular facets of the clusters, are energetically more favorable than (ZnO)₂ tetragons, which form quads on cluster vertexes.^13,16 The cluster growth is expected to be faster on the facets than on the vertices and thus the formation of the legs of the tetrapods can be initiated. Looking along the normal to the facet on its center, the arrangement of the hexagons of different shells corresponds to the stacking sequence along the c-axis in the wurtzite lattice although the shells are not as rippled as in the wurtzite structure, as observed when viewed perpendicular to the axis (Table 4). However, the T_h symmetric clusters, both considered above and suggested in other works,^26–28 have 8 equivalent facets, which would lead to 8 equivalent directions of growth. However, the tetrapods have only 4 legs. Thus, there must be some symmetry reduction of the clusters. The abovementioned lowering of the symmetry of (ZnO)₁₆₈ cluster from T_h to T is just as was expected: T symmetric (ZnO)₁₆₈ cluster (see Table S4†) has 4 equivalent convex and 4 equivalent concave facets.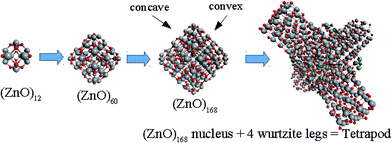

Fig. 4 A schematic for the tetrapod nucleation. The octahedral shape of (ZnO)₁₆₈ nucleus of tetrapod is guided for the eyes as black lines, and atoms of its vertices (“squares”) are marked green.

Table 4 The arrangement of the hexagons of the nested shells of (ZnO)₁₆₈ cluster of T symmetry point group (viewing along and perpendicular to the normal to the cluster facet on its center), and the stacking sequence of the wurtzite lattice (along and perpendicular to the c-axis)

	Along^a	Perpendicular^a
a The angles of view are slightly inclined for presentation clarity.
Fragment of (ZnO)168 concave facet
Fragment of (ZnO)168 convex facet
Fragment of wurtzite structure

---

To check the supposition about the nonequivalency of the facets for wurtzite leg growth, the binding energy of the adsorbed (ZnO)₃ rings (considering this as the first step of the leg formation) was compared to the concave and convex facets of the cluster. Freezing the cluster and optimizing the geometry of 4 symmetrically adsorbed (ZnO)₃ rings using the HF/6-31G theory level, the binding energy of (ZnO)₃ ring of the concave facet was found to be 1.35 eV higher than that of the convex facet. This proved that the reduced symmetry nested shell (ZnO)₁₆₈ cluster indeed has 4 equivalent preferential growth directions, and thus, it could initiate tetrapod nucleation. However, it could not be excluded that at first, some more closed shells would be formed on the cluster and only after this, the tetrapod legs would start to grow as very little information is yet known about (ZnO)₃₆₀ and larger multi-shell nested clusters.

The distortion of the nested shell clusters can also explain the experimentally observed variation of the angles between the legs of the tetrapods.^1,4,7,9,11 A fixed set of the angles can be determined by relative orientation of the hexagons of the curved cluster facets at the beginning of formation of the tetrapod legs. The broader the dispersion of the angles, the larger the nested shell clusters (3, 4, 5, … shells) at the moment of the beginning of the formation of the tetrapod legs.

Speculating on the resemblance of II–VI group compounds,⁴⁹ we may expand the proposed model of ZnO tetrapod nucleation on the other compounds of the group, namely, ZnS, ZnSe, ZnTe, CdS, CdSe, CdTe, for which the tetrapod-like structures are known.^69–73

Other confirmations of ZnO magic clusters

Note other researchers have observed evidence for the existence of these magic ZnO clusters. Van Dijken et al.⁷⁴ grew ZnO nanoparticles and observed very small ZnO clusters with a mean radius of approximately 7 Å, corresponding to about 60 molecular ZnO units. Vega-Poot et al.⁷⁵ studied the nucleation of ZnO nanoparticles and found a plateau in the absorbance spectra at 306–308 nm, which they affiliated with the mean particle diameter of ZnO nuclei of around 2.6 nm that is very close to the size of (ZnO)₃₆₀ cluster (see Table 1). Spherical clusters of the same size, about 2.5 nm, were dominant after deposition on Au or carbon substrates although their structure was found to be zinc-blende after annealing to 470 K and TEM electron beam action.⁷⁶ Ronning et al.¹¹ suggested the transition from a fullerene-like ZnO cluster to a nanometer-sized tetrahedron, however, they did not specify the fullerene-like cluster and the transition, whereas the analogous transformation of carbon onions to diamonds is well-known.⁷⁷

4. Conclusions

This report reveals a new structural motif for ZnO – the nested shell clusters. Experimental findings of mass spectroscopy, namely, the magic numbers 12, 60, and 168, matched the mathematical model of the clusters, which are constructed as concentric Goldberg polyhedra. This perfect match reasonably rules out other structural motifs for these magic clusters. Ab initio calculations supported their stability and discovered more details of their structure: multishell clusters are subjected to Jahn–Teller distortion. These symmetry reduced clusters, in particular (ZnO)₁₆₈, structurally correspond to the nuclei of the well-known ZnO tetrapods: they have tetrahedral symmetry of preferential growth directions. Moreover, the atomic arrangement of their corresponding facets is congruent with the wurtzite crystal structure, which is common for the tetrapod legs. Thus, we bridged the gap from the smallest stable atomic clusters to the particular nanostructures with atomic precision that paves the way for future research on physics and applications of ZnO clusters and nanostructures with ultimate exactness.

Acknowledgements

A. Dmytruk is thankful to Dr A. Ryabtsev for the support of the computer cluster of the Institute of Physics of NAS of Ukraine; R. Belosludov and I. Dmitruk are grateful for the support of the HITACHI SR16000-M1 supercomputing facility by the Computer Science Group and E-IMR center at the Institute for Materials Research, Tohoku University, Sendai, Japan.

References

1. M. L. Fuller, Twinning in Zinc Oxide, J. Appl. Phys., 1944, 15, 164–170.
2. M. C. Newton and P. A. Warburton, ZnO Tetrapod Nanocrystals, Mater. Today, 2007, 10, 50–54.
3. L. Lazzarini, G. Salviati, F. Fabbri, M. Zha, D. Calestani, A. Zappettini, T. Sekiguchi and B. Dierre, Unpredicted Nucleation of Extended Zinc Blende Phases in Wurtzite ZnO Nanotetrapod Arms, ACS Nano, 2009, 3, 3158–3164.
4. M. Fujii, H. Iwanaga, M. Ichihara and S. Takeuchi, Structure of Tetrapod-like ZnO Crystals, J. Cryst. Growth, 1993, 128, 1095–1098.
5. Y. Dai, Y. Zhang and Z. L. Wang, The Octa-Twin Tetraleg ZnO Nanostructures, Solid State Commun., 2003, 126, 629–633.
6. Z. Zhang, H. Yuan, Y. Gao, J. Wang, D. Liu, J. Shen, L. Liu, W. Zhou, S. Xie, X. Wang, X. Zhu, Y. Zhao and L. Sun, Large-Scale Synthesis and Optical Behaviors of ZnO Tetrapods, Appl. Phys. Lett., 2007, 90, 153116.
7. B.-B. Wang, J.-J. Xie, Q. Yuan and Y.-P. Zhao, Growth Mechanism and Joint Structure of ZnO Tetrapods, J. Phys. D: Appl. Phys., 2008, 41, 102005.
8. M. Shiojiri and C. Kaito, Structure and Growth of ZnO Smoke Particles Prepared by Gas Evaporation Technique, J. Cryst. Growth, 1981, 52, 173–177.
9. K. Nishio, T. Isshiki, M. Kitano and M. Shiojiri, Structure and Growth Mechanism of Tetrapod-like ZnO Particles, Philos. Mag. A, 1997, 76, 889–904.
10. Y. Ding, Z. L. Wang, T. Sun and J. Qiu, Zinc-Blende ZnO and Its Role in Nucleating Wurtzite Tetrapods and Twinned Nanowires, Appl. Phys. Lett., 2007, 90, 153510.
11. C. Ronning, N. G. Shang, I. Gerhards, H. Hofsäss and M. Seibt, Nucleation Mechanism of the Seed of Tetrapod ZnO Nanostructures, J. Appl. Phys., 2005, 98, 034307.
12. E. C. Behrman, R. K. Foehrweiser, J. R. Myers, B. F. French and M. E. Zandler, Possibility of Stable Spheroid Molecules of ZnO, Phys. Rev. A, 1994, 49, R1543–R1546.
13. J. M. Matxain, J. E. Fowler and J. M. Ugalde, Small Clusters of II–VI Materials: Zn_iO_i, i = 1–9, Phys. Rev. A, 2000, 62, 053201–053210.
14. A. Burnin and J. J. BelBruno, Zn_nS_m⁺ Cluster Production by Laser Ablation, Chem. Phys. Lett., 2002, 362, 341–348.
15. I. M. Kukreja, A. Rohlfing, P. Misra, F. Hillenkamp and K. Dreisewerd, Cluster Formation in UV Laser Ablation Plumes of ZnSe and ZnO Studied by Time-of-Flight Mass Spectrometry, Appl. Phys. A, 2004, 78, 641–644.
16. M. Zhao, Y. Xia, Z. Tan, X. Liu and L. Mei, Design and Energetic Characterization of ZnO Clusters from First-Principles Calculations, Phys. Lett. A, 2007, 372, 39–43.
17. B. Wang, X. Wang, G. Chen, S. Nagase and J. Zhao, Cage and Tube Structures of Medium-Sized Zinc Oxide Clusters (ZnO)_n (n = 24, 28, 36, and 48), J. Chem. Phys., 2008, 128, 144710.
18. A. A. Al-Sunaidi, A. A. Sokol, C. R. A. Catlow and S. M. Woodley, Structures of Zinc Oxide Nanoclusters: As Found by Revolutionary Algorithm Techniques, J. Phys. Chem. C, 2008, 112, 18860–18875.
19. A. Dmytruk, I. Dmitruk, I. Blonskyy, R. Belosludov, Y. Kawazoe and A. Kasuya, ZnO Clusters: Laser Ablation Production and Time-of-Flight Mass Spectroscopic Study, Microelectron. J., 2009, 40, 218–220.
20. X. Wang, B. Wang, L. Tang, L. Sai and J. Zhao, What Is Atomic Structures of (ZnO)₃₄ Magic Cluster?, Phys. Lett. A, 2010, 374, 850–853.
21. B. Wang, X. Wang and J. Zhao, Atomic Structure of the Magic (ZnO)₆₀ Cluster: First-Principles Prediction of a Sodalite Motif for ZnO Nanoclusters, J. Phys. Chem. C, 2010, 114, 5741–5744.
22. C. Caddeo, G. Malloci, F. De Angelis, L. Colombo and A. Mattoni, Optoelectronic Properties of (ZnO)₆₀ Isomers, Phys. Chem. Chem. Phys., 2012, 14, 14293–14298.
23. A. Wood, M. Giersig, M. Hilgendorff, A. Vilas-Campos, L. M. Liz-Marzán and P. Mulvaney, Size Effects in ZnO: The Cluster to Quantum Dot Transition, Aust. J. Chem., 2003, 56, 1051–1057.
24. C. R. A. Catlow, S. A. French, A. A. Sokol, A. A. Al-Sunaidi and S. M. Woodley, Zinc Oxide: a Case Study in Contemporary Computational Solid State Chemistry, J. Comput. Chem., 2008, 29, 2234–2249.
25. C. R. A. Catlow, S. T. Bromley, S. Hamad, M. Mora-Fonz, A. A. Sokol and S. M. Woodley, Modelling Nano-Clusters and Nucleation, Phys. Chem. Chem. Phys., 2010, 12, 786–811.
26. M. Chen, T. P. Straatsma, Z. Fang and D. A. Dixon, Structural and Electronic Property Study of (ZnO)_n, n ≤ 168: Transition from Zinc Oxide Molecular Clusters to Ultrasmall Nanoparticles, J. Phys. Chem. C, 2016, 120, 20400–20418.
27. M. R. Farrow, J. Buckeridge, C. R. A. Catlow, A. J. Logsdail, D. O. Scanlon, A. A. Sokol and S. M. Woodley, From Stable ZnO and GaN Clusters to Novel Double Bubbles and Frameworks, Inorganics, 2014, 2, 248–263.
28. A. A. Sokol, M. R. Farrow, J. Buckeridge, A. J. Logsdail, C. R. A. Catlow, D. O. Scanlon and S. M. Woodley, Double Bubbles: a New Structural Motif for Enhanced Electron–Hole Separation in Solids, Phys. Chem. Chem. Phys., 2014, 16, 21098–21105.
29. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, C₆₀: Buckminsterfullerene, Nature, 1985, 318, 162–163.
30. A. Kasuya, R. Sivamohan, Yu. A. Barnakov, I. M. Dmitruk, T. Nirasawa, V. R. Romanyuk, V. Kumar, S. V. Mamykin, K. Tohji, B. Jeyadevan, K. Shinoda, T. Kudo, O. Terasaki, Z. Liu, R. V. Belosludov, V. Sundararajan and Y. Kawazoe, Ultra-Stable Nanoparticles of CdSe Revealed From Mass Spectrometry, Nat. Mater., 2004, 3, 99–102.
31. A. Dmytruk, I. Dmitruk and A. Kasuya, Zinc Peroxide Precursor for ZnO Clusters, Materialwiss. Werkstofftech., 2009, 40, 265–267.
32. A. Dmytruk, I. Dmitruk, R. Belosludov, Y. Kawazoe and A. Kasuya, Laser Ablation of CdSe and ZnO: Alkylamine Assisted Formation of Magic Clusters, in NATO Science for Peace and Security Series B: Physics and Biophysics. Nanostructured Materials for Advanced Technological Applications, ed. J. P. Reithmaier, P. Petkov, W. Kulisch and C. Popov, Springer, 2009, pp. 201–206.
33. A. A. Granovsky, Firefly version 8, accessed January 20, 2017, http://classic.chem.msu.su/gran/firefly/index.html.
34. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, The Development and Use of Quantum-Mechanical Molecular-Models. 76. AM1 - a New General-Purpose Quantum-Mechanical Molecular-Model, J. Am. Chem. Soc., 1985, 107, 3902–3909.
35. W. J. Hehre, R. Ditchfield and J. A. Pople, Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257–2261.
36. V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, 6-31G* basis set for atoms K through Zn, J. Chem. Phys., 1998, 109, 1223–1229.
37. C. C. J. Roothaan, New Developments in Molecular Orbital Theory, Rev. Mod. Phys., 1951, 23, 69–89.
38. A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652.
39. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
40. C. Møller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46, 618–622.
41. B. M. Bode and M. S. Gordon, Macmolplt: a Graphical User Interface for GAMESS, J. Mol. Graphics Modell., 1998, 16, 133–138.
42. G. A. Andrienko, ChemCraft, accessed January 20, 2017, http://www.chemcraftprog.com.
43. J. M. Matxain, J. M. Mercero, J. E. Fowler and J. M. Ugalde, Electronic Excitation Energies of Zn_iO_i Clusters, J. Am. Chem. Soc., 2003, 125, 9494–9499.
44. A. C. Reber, S. N. Khanna, J. S. Hunjan and M. R. Beltrán, Cobalt Doped Rings and Cages of ZnO Clusters: Motifs for Magnetic Cluster-assembled Materials, Chem. Phys. Lett., 2006, 428, 376–380.
45. B. Wang, S. Nagase, J. Zhao and G. Wang, Structural Growth Sequences and Electronic Properties of Zinc Oxide Clusters (ZnO)_n (n = 2-18), J. Phys. Chem. C, 2007, 111, 4956–4963.
46. A. Dmytruk, On the Structure of Atomic Clusters: Selection of Calculation Methods to Match Mass Spectra, Adv. Mater. Res., 2015, 1117, 26–30.
47. M. R. Farrow, C. R. A. Catlow, A. A. Sokol and S. M. Woodley, Double Bubble Secondary Building Units Used as a Structural Motif for Enhanced Electron–Hole Separation in Solids, Mater. Sci. Semicond. Process., 2016, 42, 147–149.
48. E. Spanó, S. Hamad and C. R. A. Catlow, ZnS Bubble Clusters with Onion-like Structures, Chem. Commun., 2004, 7, 864–865.
49. V. R. Romanyuk, I. M. Dmitruk, Y. A. Barnakov, R. V. Belosludov and A. Kasuya, Ultra-Stable Nanoparticles in A_IIB_VI (A_II = Cd, Zn; B_VI = S, Se, Te) Compounds, J. Nanosci. Nanotechnol., 2009, 9, 2111–2118.
50. G. Seifert, P. W. Fowler, D. Mitchell, D. Porezag and T. Frauenheim, Boron-Nitrogen Analogues of the Fullerenes: Electronic and Structural Properties, Chem. Phys. Lett., 1997, 268, 352–358.
51. V. V. Pokropivny, V. V. Skorokhod, G. S. Oleinik, A. V. Kurdyumov, T. S. Bartnitskaya, A. V. Pokropivny, A. G. Sisonyuk and D. M. Sheichenko, Boron Nitride Analogs of Fullerenes (the Fulborenes), Nanotubes, and Fullerites (the Fulborenites), J. Solid State Chem., 2000, 154, 214–222.
52. F. Jensen and H. Toftlund, Structure and Stability of C₂₄ and B₁₂N₁₂ Isomers, Chem. Phys. Lett., 1993, 201, 89–96.
53. D. L. Strout, Structure and Stability of Boron Nitrides: Isomers of B₁₂N₁₂, J. Phys. Chem. A, 2000, 104, 3364–3366.
54. O. Stephan, Y. Bando, A. Loiseau, F. Willaime, N. Shramchenko, T. Tamiya and T. Sato, Formation of Small Single-Layer and Nested BN Cages Under Electron Irradiation of Nanotubes and Bulk Material, Appl. Phys. A, 1998, 67, 107–111.
55. D. Ugarte, Curling and Closure of Graphitic Networks Under Electron-Beam Irradiation, Nature, 1992, 359, 707–709.
56. K. G. McKay, H. Kroto and D. J. Wales, Simulated Transmission Electron Microscope Images and Characterization of Concentric Shell and Icospiral Graphitic Microparticles, J. Chem. Soc., Faraday Trans., 1992, 88, 2815–2821.
57. S. A. Shevlin, Z. X. Guo, H. J. J. van Dam, P. Sherwood, C. R. A. Catlow, A. A. Sokol and S. M. Woodley, Structure, Optical Properties and Defects in Nitride (III–V) Nanoscale Cage Clusters, Phys. Chem. Chem. Phys., 2008, 10, 1944–1959.
58. T. P. Martin, Shells of Atoms, Phys. Rep., 1996, 273, 199–241.
59. M. Goldberg, A Class of Multi-Symmetric Polyhedra, Tohoku Mathematical Journal, 1937, 43, 104–108.
60. M. Yoshida and E. Osawa, Molecular Mechanics Calculations of Giant- and Hyperfullerenes with Eicosahedral Symmetry, Fullerene Sci. Technol., 1993, 1, 55–74.
61. D. Fujita, Y. Ueda, S. Sato, N. Mizuno, T. Kumasaka and M. Fujita, Self-assembly of tetravalent Goldberg polyhedra from 144 small components, Nature, 2016, 540, 563–567.
62. P. W. Fowler, T. Heine, D. Mitchell, R. Schmidt and G. Seifert, Boron-nitrogen analogues of the fullerenes: The isolated-square rule, J. Chem. Soc., Faraday Trans., 1996, 92, 2197–2201.
63. H. W. Kroto, The Stability of the Fullerenes C_n, with n = 24, 28, 32, 36, 50, 60 and 70, Nature, 1987, 329, 529–531.
64. S. Schein and J. M. Gayed, Fourth Class of Convex Equilateral Polyhedron with Polyhedral Symmetry Related to Fullerenes and Viruses, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 2920–2925.
65. J. H. Conway, H. Burgiel and C. Goodman-Strass, The Symmetries of Things, ed. A. K. Peters, CRC Press, Taylor and Francis, New York, 2008, p. 448.
66. A. Levskaya, polyHédronisme v0.2, accessed Jan 20, 2017, http://levskaya.github.io/polyhedronisme/.
67. H. A. Jahn and E. Teller, Stability of Polyatomic Molecules in Degenerate Electronic States. I. Orbital Degeneracy, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235.
68. B. L. Caetano, C. V. Santilli, F. Meneau, V. Briois and S. H. Pulcinelli, In Situ and Simultaneous UV-vis/SAXS and UV-vis/XAFS Time-Resolved Monitoring of ZnO Quantum Dots Formation and Growth, J. Phys. Chem. C, 2011, 115, 4404–4412.
69. L. Manna, D. J. Milliron, A. Meisel, E. C. Scher and A. P. Alivisatos, Controlled Growth of Tetrapod-Branched Inorganic Nanocrystals, Nat. Mater., 2003, 2, 382–385.
70. Y.-W. Jun, S.-M. Lee, N.-J. Kang and J. Cheon, Controlled Synthesis of Multi-Armed CdS Nanorod Architectures Using Monosurfactant System, J. Am. Chem. Soc., 2001, 123, 5150–5151.
71. R. Wang and W. Liu, Synthesis and Characterization of ZnS Tetrapods and ZnO/ZnS Heterostructures, Thin Solid Films, 2012, 522, 40–44.
72. J. Hu, Y. Bando and D. Golberg, Sn-Catalyzed Thermal Evaporation Synthesis of Tetrapod-Branched ZnSe Nanorod Architectures, Small, 2005, 1, 95–99.
73. R. Xie, U. Kolb and T. Basche, Design and Synthesis of Colloidal Nanocrystal Heterostructures with Tetrapod Morphology, Small, 2006, 2, 1454–1457.
74. A. Van Dijken, E. A. Meulenkamp, D. Vanmaekelbergh and A. Meijerink, The Kinetics of the Radiative and Nonradiative Processes in Nanocrystalline ZnO Particles upon Photoexcitation, J. Phys. Chem. B, 2000, 104, 1715–1723.
75. A. G. Vega-Poot, G. Rodriguez-Gattorno, O. E. Soberanis-Dominguez, R. T. Patino-Diaz, M. Espinosa-Pesqueira and G. Oskam, The Nucleation Kinetics of ZnO Nanoparticles from ZnCl₂ in Ethanol Solutions, Nanoscale, 2010, 2, 2710–2717.
76. K. Schouteden, Y.-J. Zeng, K. Lauwaet, C. P. Romero, B. Goris, S. Bals, G. van Tendeloo, P. Lievens and C. van Haesendonck, Band Structure Quantization in Nanometer Sized ZnO Clusters, Nanoscale, 2013, 5, 3757–3763.
77. F. Banhart and P. M. Ajayan, Carbon Onions as Nanoscopic Pressure Cells for Diamond Formation, Nature, 1996, 382, 433–435.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra01610g

---