Tuning conductivity and magnetism of CuFe₂O₄ via cation redistribution

Abstract

Copper ferrite polycrystalline samples with different cation distributions are prepared via different thermal treatments. Combined studies including X-ray diffraction, PPMS, Mössbauer spectroscopy, and complex impedance spectroscopy show both conductivity and magnetism keep increasing, accompanied by an obvious phase transition from tetragonal symmetry (I4₁/amd) to cubic symmetry (Fd3̄m) as Cu²⁺ ions migrate from O_h sites to T_d sites. The changes of structural, electrical and magnetic properties due to the cation redistribution are also investigated by spin-polarized density functional theory. The simulated results indicate that the semiconducting band structure gradually transforms into a metallic band structure as Cu²⁺ ions migrate from O_h sites to T_d sites. The conductivity and magnetism will increase during the same process, which matches well with the experimental observations. This work demonstrates that the cation redistribution in copper ferrite is effective in controlling both conductivity and magnetism, which can be further exploited in applications using interacting electron/spin systems.

---

1. Introduction

Recently, ion migration of oxide materials triggered by an electric field or local heat has emerged as a promising route to novel functionalities and electronic devices.^1–3 The ion migration, especially anion (e.g., O²⁻ ions) redistribution, is vital to the nonvolatile resistive switching (RS) properties of oxide thin films, which have been extensively studied by many researchers.^4–6 Cation redistribution in oxide materials is also important due to tunable magnetic and optical properties beyond the RS effect. Spinel ferrites are among those oxide materials with tunable magnetism via cation redistribution.⁷ Lithium ferrite receives most intensive research interest due to the easy modulation of chemical states and magnetic properties through a Li⁺ ion de-intercalation/intercalation process.^8,9 Copper ferrite (CuFe₂O₄) which contains elements (Cu²⁺ ions) with a high migration rate and low activation energy (∼0.1 eV) is also an ideal candidate for ionic control of chemical states and magnetic properties.^10,11 Moreover, copper ferrite showing two phases (tetragonal spinel phase and cubic spinel phase) with large differences in physical properties differs from many spinel ferrites with only one cubic spinel phase.¹² The phase transition and physical properties of copper ferrite can also be easily modulated by cation redistribution between tetrahedral site (T_d site or A site) and the octahedral site (O_h site or B site) via thermal stimuli as previous studies indicated.^10,13 The cation redistribution of copper ferrite leading to modulation of magnetic and magneto-optical properties have been well studied.^14,15 However, few attentions have been paid to the effect of cation redistribution on the electrical properties of copper ferrite, which still remains unclear. It is also important to understand the mechanism behind cation redistribution dependent electrical properties, which could extend the applications of spinel ferrite beyond permanent magnet, magnetic recording, power handling, and millimeter wave integrated circuitry applications.

In this work, thermal treatments are used to induce cation redistribution in copper ferrite polycrystalline samples. The cation redistribution can be verified by the phase transition and change of magnetic properties. Complex impedance spectra indicate both grain conductivity and DC conductivity of copper ferrite changes dramatically as Cu²⁺ ions redistribute between O_h site and T_d site. And migration of Cu²⁺ ions from O_h site to T_d site leads to the enhancement of conductivity. To understand the mechanism of cation redistribution tunable conductivity, theoretical calculations based on spin-polarized density functional theory are also carried out. The simulated results of copper ferrite reveal that the semiconducting band structure gradually transforms into metallic band structure as Cu²⁺ ions migrate from O_h site to T_d site, which explains the increase of conductivity in the same ion migration process. This work demonstrates that the cation redistribution in copper ferrite is effective on controlling both conductivity and magnetism, which can be exploited in the applications implemented using interacting electron/spin systems.¹⁶

2. Experimental

2.1 Fabrication of CuFe₂O₄ ceramics with different cation distributions

The stoichiometric CuFe₂O₄ polycrystalline powders were synthesized though a standard solid state reaction method with starting reactants of CuO (99.99%) and Fe₂O₃ (99.99%) in the ratio of 1 : 1. The mixing powders of reactants were milled for 8 h and then calcined in air at 900 °C for 4 h. The powders were remilled for 8 h to obtain homogeneous powders. And then the powders were pressed via isostatic method into cylinders (ϕ = 8 mm, d = 1.5 mm) to obtain maximum density. Then all these cylinders were sintered in air at 1000 °C for 4 h and followed by a slowly cooling process (∼12 hours to room temperature) to obtained the pure tetragonal spinel phase of CuFe₂O₄ (T-CFO). These sintered cylinders acted as pristine samples (denoted as SC-1000 or RQ-0) for further nonequilibrium thermal treatment (using rapid quenching method). RQ-0 samples were then heated up and maintained at 500 °C, 700 °C, 900 °C for 3 hours to reach equilibrium state at the given temperatures. Then these heated samples were rapid quenched in pure water to room temperature and marked as sample RQ-500, RQ-700 and RQ-900, respectively. In this way, CuFe₂O₄ ceramics with different cation distributions were obtained.

2.2 The structural, electrical, and magnetic characterization of CFO ceramics

The structure of these slowly cooled and rapid quenched samples were investigated by means of PANalytical X'pert XRD. The magnetic hysteresis loops were recorded on a Quantum Design Physical Property Measurement System (PPMS) with magnetic field sweeping between ±2 T. The Mössbauer spectra of CFO polycrystalline samples were recorded by using a conventional constant acceleration spectrometer with a γ-ray source of 25 mCi ⁵⁷Co in palladium matrix, and the isomer shift quoted in this work was relative to that of the α-Fe. The room temperature complex impedance spectra covering wide frequency (40 Hz–110 MHz) were recorded by Agilent 4294A impedance analyzer. Temperature dependent complex impedance spectra were measured by using Agilent 4980A impedance analyzer with scanning frequency ranging from 20 Hz–2 MHz. In order to ensure electrical contacts, 100 nm thick Au electrodes were deposited at each side of cylinder samples using sputtering method.

2.3 First-principle calculations on CFO ceramics with different cation distributions

To explore the mechanism behind the cation distribution dependent electric properties in copper ferrite, the electronic structure calculations were performed by using spin-polarized DFT method as implemented in CASTEP package. A generalized gradient approximation (GGA) exchange correlation term as constructed by Perdew–Burke–Ernzerhof for solid (PBESOL) was adopted for the geometry optimization as well as electronic structure calculation. The correlated 3d orbitals of Cu and Fe atoms had been taken into account and assigned Hubbard U values of 5 eV and 4 eV, respectively, as previous studies indicated.¹⁷ The pseudopotentials used to describe the interaction between ions and electrons were Ultrasoft with cutoff energy of 500 eV and energy convergence of 1.0 × 10⁻⁶ eV per atom. The magnetic moments on the tetrahedral sites and octahedral sites were set antiparallel to each other as the initial magnetic structure.

3. Results and discussion

3.1 XRD analysis

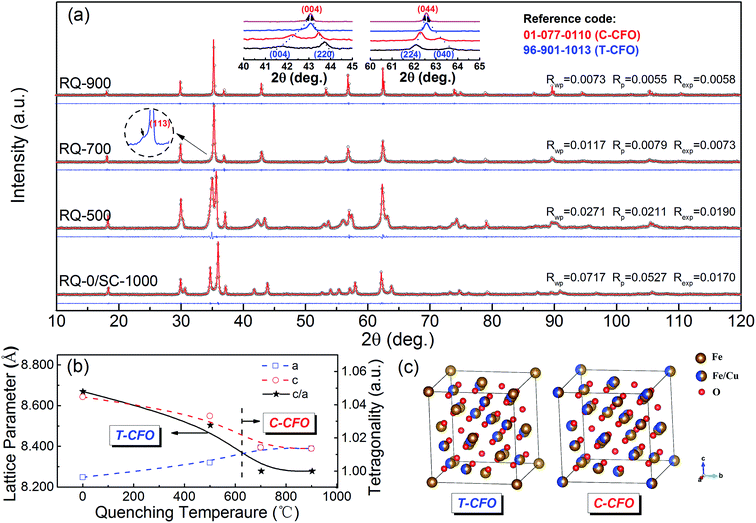
Inversion parameter λ, the occupancy ratio of the M²⁺ cations at the O_h site, was often used to evaluate cation distribution in spinel ferrites MFe₂O₄ (M = divalent transition cations, including Fe²⁺, Co²⁺, Ni²⁺, Cu²⁺, Zn²⁺ etc.). Aside from the fully normal (λ = 0, M²⁺ cations completely occupying the T_d site) and fully inverse (λ = 1, M²⁺ and Fe³⁺ cations equally distributed in the O_h site) cases, a variety of spinel ferrites possess equilibrium cation distribution with 0 < λ < 1. For CFO spinel, the decrease of inversion parameter λ can be directly observed through the XRD analysis due to the symmetry transition from I4₁/amd (tetragonal spinel phase) to Fd3̄m (cubic spinel phase) induced by the gradual migration of Cu²⁺ ions from O_h site to T_d site.¹⁰ The Jahn–Teller distortion caused by Cu²⁺ cations at O_h site can be significantly suppressed as the inversion parameter λ decreases. According to literatures, the process of cation redistribution would get enhanced and inversion parameter continuously decreases as the temperature gradually increases.^18,19 And the reverse process of cation redistribution and increased inversion parameter take place if the temperature slowly cools down. However, nonequilibrium operation including rapid quenching can freeze the T_d/O_h site occupancy formed at high temperature. Fig. 1(a) shows the XRD diffraction patterns and the full Rietveld refinement of the samples RQ-0(SC-1000), RQ-500, RQ-700, and RQ-900, illustrating the phase transition trigged by rapid quenching of CuFe₂O₄ samples from different temperatures. The XRD patterns of all CFO samples are well fitted by the full Rietveld refinement with R_wp values less than 0.08. As it can be seen from the insets I and II in the top corner of Fig. 1(a), the corresponding peaks of T-CFO gradually merge together and transform into the diffraction peaks of cubic spinel phase CuFe₂O₄ (C-CFO) as the quenching temperature (T_Q) increases. For the sample quenched from 700 °C, a small shoulder at the (113) peak can be detected, indicating that the transformation from T-CFO to C-CFO is still not completed. A very small portion remains tetragonal phase. The phase transition is completed in the sample RQ-900 quenched from 900 °C. Based on the results of structure refinements (see ESI†) on all CFO samples, the changes of the lattice parameters and the tetragonality with the increasing of T_Q are shown in Fig. 1(b). The decrease of tetragonality from 1.05 for the sample RQ-0 to 1 for the sample RQ-900 clearly demonstrates the migration of the Cu²⁺ cations from the O_h sites to the T_d sites, resulting in the decrease of inversion parameter. The site occupancies of Cu²⁺ and Fe³⁺ ions obtained from structure refinements (see ESI†) also confirm the same migration paths for Cu²⁺ cations predicted by tetragonality. Fig. 1(c) schematically shows the symmetry transition of CuFe₂O₄ from tetragonal spinel phase (T-CFO) to cubic spinel phase (C-CFO) as the inversion parameter decreases.

Fig. 1 Structural characterization by using X-ray diffraction. (a) Phase transition from tetragonal spinel phase to cubic spinel phase after rapid quenching from different temperature. (b) The change of lattice parameter and tetragonality as a function of quenching temperature. (c) Schematic view of cation distribution and symmetries of CFO.

3.2 Magnetic hysteresis loops and Mössbauer spectra

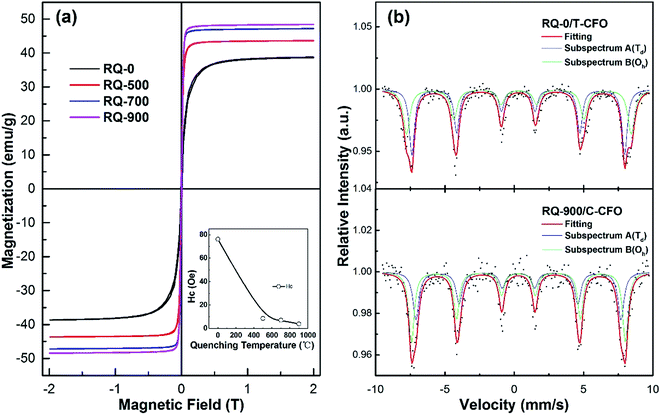
To explore the effects of the cation redistribution on magnetic properties, the room-temperature M–H hysteresis loops as well as Mössbauer spectra were measured for these samples, as shown in Fig. 2. The different degrees of cation redistribution induced by different quenching temperatures have large effect on the overall magnetic properties of CFO ceramics. The saturation magnetization M_S increases with the increasing of quenching temperature as the result of decreasing inversion parameter. The migration of Cu²⁺ ions from O_h sites to T_d sites enhances the spin imbalance among these sites.¹⁴ Besides, according to the Néel configuration for the spinel ferrite with ferrimagnetic structure, the total 1 formula unit magnetic moment of spinel ferrite can be expressed as M_S = λM_Cu²⁺ + (2 − λ) M_Fe³⁺ − (1 − λ) M_Cu²⁺ − λM_Fe³⁺ = (2 − 2λ) M_Fe³⁺ + (2λ − 1) M_Cu²⁺. As Fe³⁺ cation has much more spins than that of Cu²⁺ cation, the total magnetic moment of 1 f.u. increases with the decreasing of inversion parameter λ. The RQ-0 sample with c/a ∼1.05 shows much higher M_S with 38.81 emu g⁻¹ (shown in Table 1) than the M_S of 25.01 emu g⁻¹ (∼1700 Gs with density of 5.41 g cm⁻³) measured in T-CFO with maximum c/a of 1.06, indicating much lower inversion parameter in our sample. The coercivity of CFO is also strongly influenced by the inversion parameter, which shows tendency of decreased values as the quenching temperature increases (shown in the inset of Fig. 2(a)). The RQ-900 sample with cubic symmetry shows the coercivity of only several Oe.

Fig. 2 Magnetic properties of CFO samples characterized by PPMS and Mössbauer spectra. (a) Magnetic hysteresis loops recorded with magnetic field applied in the range between −3 T–3 T. The small inset shows the coerivities of CFO samples as a function of quenching temperature. (b) Mössbauer spectra of RQ-0 and RQ-900 samples demonstrating the cation redistribution triggered by thermal treatment.

Table 1 Saturate magnetization M_s, coercivity H_C, hyperfine fields H, isomer shifts δ, ratio of absorption area S_A/S_B, and inversion parameter λ for tetragonal spinel phase and cubic spinel phase CuFe₂O₄

Sample	Ms (emu g^−1)	HC (Oe)	H(A) (T)	δ(A) (mm s^−1)	H(B) (T)	δ(B) (mm s^−1)	SA/SB	λ
RQ-0/T-CFO	38.81	76.1	47.58	0.28	50.25	0.33	1.14	0.84
RQ-900/C-CFO	48.46	3.8	45.86	0.30	47.83	0.30	0.75	0.74

---

Mössbauer spectra of CFO recorded at room temperature, as shown in Fig. 2(b), provide direct evidence of cation redistribution and change of inversion parameter induced at high quenching temperature. The experimental data (dots), which are well-fitted by curves with red solid lines, exhibit two Zeeman sextets, as indicated by subspectrum A and B with blue and green solid lines, respectively. The hyperfine fields, isomer shifts, and linewidths of fitted curves shown in Fig. 2(b) match well with the values reported for CFO polycrystalline samples in the literature.^20,21 No quadruple splits, which are typical for nanoparticles, are detected in the spectra. The magnetic parameters obtained from both PPMS and Mössbauer measurements are listed in Table 1. Both SC-1000 (T-CFO) and RQ-900 (C-CFO) samples shows the isomer shifts δ varying in the range of 0.25–0.35, which is in accordance with the high spin state for Fe³⁺ cations.^21,22 As the measured magnetic hyperfine field H_A of subspectrum A is lower than that of subspectrum B in both samples, the subspectrum A and B can be assigned to Fe³⁺ cations occupying T_d sites and O_h sites, respectively. The occupancy of Fe³⁺ cations among T_d sites and O_h sites can be evaluated on the basis of the relative absorption area S_A and S_B, through the equation S_A/S_B = λf_A/(2 – λ)f_B, where f_A and f_B are the recoil-free fractions of Fe³⁺ cations at the T_d and O_h sites, respectively.¹⁸ The higher S_A/S_B ratio corresponds to a higher inversion parameter λ. As the λ of 0.75 is believed to be the inversion parameter boundary for T-CFO and C-CFO, it is reasonable to assume that RQ-700 sample with slight tetragonal phase possesses the λ with a value around 0.75.²³ The values of inversion parameter for other CFO samples are estimated based on the magnetization of fully inverse case (λ = 1 with M_S of 25.01 emu g⁻¹) and partial inverse case (λ = 0.75 with M_S of 47.20 emu g⁻¹ for sample RQ-700). CFO samples RQ-0, RQ-500, and RQ-900 are then roughly estimated to possess inversion parameters of 0.84, 0.79, and 0.74, respectively, which we believe to be reasonable according to previous reports and our calculations from PPMS and Mössbauer spectra.¹⁰ These estimated inversion parameters are also very close to those from structure refinement.

3.3 Complex impedance spectra

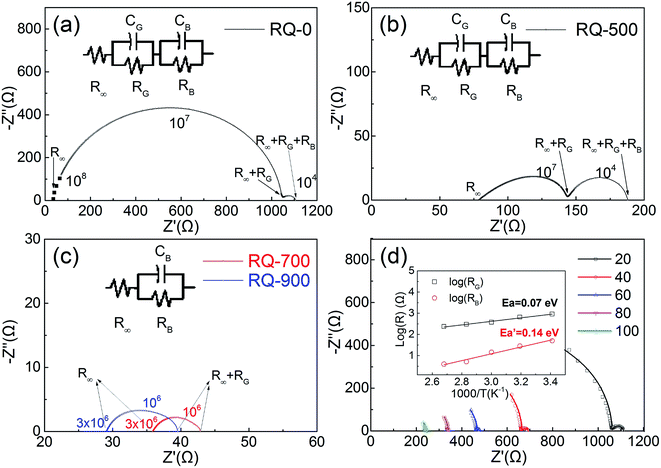
The electrical properties of CFO samples after various thermal treatments are revealed by the complex impedance spectra measured at room temperature, which are shown in Fig. 3(a)–(c). The temperature dependent complex impedance spectra were obtained by using 4980A covering 20 Hz–2 MHz (shown in Fig. 3(d)). According to Fig. 3(a)–(c), the inversion parameter has a large influence on the impedance spectra of polycrystalline CFO samples. The RQ-0 and RQ-500 samples with tetragonal spinel structure exhibit a distinct feature of two semicircles, which can be attributed to the contribution from grains and the grain boundaries, respectively. The polycrystalline structure of both samples can be characterized by an equivalent circuit model consisting of two parallel RC elements and one serial R element. In contrast, the RQ-700 and RQ-900 samples show only one semicircles in impedance spectra which can be interpreted by an equivalent circuit model consisting of one parallel RC elements and one serial R element. In the circuit models, R_G (R_B), and C_G (C_B) stand for the resistance and capacitance of the grains (grain boundaries), respectively. R₀, and R_∞ represent the DC resistance, and the resistance at optical frequency of polycrystalline CFO samples. Noting the average grain size for the RQ-0, RQ-500, RQ-700, and RQ-900 sample are around 10.8 μm, 11.6 μm, 11.5 μm, and 11.1 μm, respectively, according to the SEM investigations (see ESI†). The grain sizes show little variations after different heat treatments. The calculated values for the elements of equivalent circuits are listed in Table 2. The capacitance of grain boundary for all CFO samples are among the range of 200–3000 nF, which are in accordance with the possible interpretation for grain boundary. The grains show much smaller capacitance compared to that of grain boundary for RQ-0 and RQ-500 samples. All the polycrystalline CFO samples possessing small DC resistance (in the range of 40–1200 Ω) show semiconducting behavior. It can also be clearly seen that the DC resistance R₀ decreases (or DC conductivity σ₀ increases) as the T_Q increases (or the inversion parameter λ decreases). It is worth noting that the grain resistance R_G of the CFO samples also shows the same trend of decreasing as the inversion parameter decreases from Fig. 3(a) and (b). The disappearance of the semicircle, which corresponds to the effect of the grains in the RQ-700 and RQ-900 samples, can be understood as the result of the rapid decreasing resistance of the grains caused by the decreasing of inversion parameter. The XPS investigation on the RQ-900 sample indicates the drastic change of grain resistance is not caused by the increased concentration of Cu⁺ or Fe²⁺ cations due to the formation of oxygen vacancies during quenching process. The activation energies of the grains and the grain boundaries for the RQ-0 sample were investigated by fitting the values of R_G and R_B using above mentioned circuit model after scanning the impedance spectra from 20 °C to 100 °C (shown in Fig. 3(d)). The R–T plots are well fitted by the relation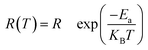, from which the activation energies for the grains and the grain boundaries are calculated as 0.07 eV and 0.14 eV, respectively, for the RQ-0 sample.

Fig. 3 The room temperature complex impedance spectra for RQ-0(a), RQ-500(b), and RQ-700/RQ-900(c) CFO samples. The equivalent circuit models are illustrated in each graph. The scanning frequencies have been marked. (d) The complex impedance spectra for RQ-0 CFO sample measured at 20 °C, 40 °C, 60 °C, 80 °C, 100 °C. The inset is the R–T plots for RQ-0 CFO sample showing the activation energies for grain (black line) and grain boundaries (red line).

Table 2 Calculated electric parameters for CFO polycrystalline samples prepared after different heat treatment

Sample	RG (Ω)	CG (nF)	RB (Ω)	CB (nF)	R∞ (Ω)	R0 (Ω)	σ0 (mS m^−1)
RQ-0	1000	0.0523	64	2784	36	1100	2.71
RQ-500	65	0.5015	42	1488	79	188	15.87
RQ-700	—	—	7	297	36	43	69.40
RQ-900	—	—	11	290	29	40	74.60

---

3.4 Theoretical calculations

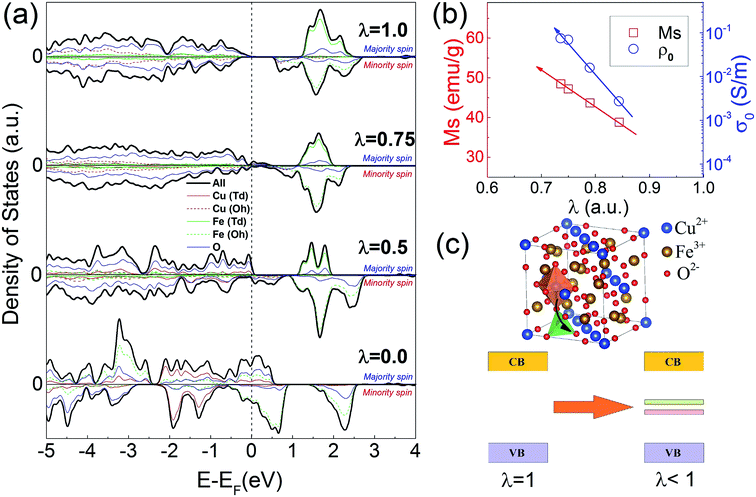
To explore the origin of cation distribution dependent conductivity in copper ferrite, the spin-resolved electronic densities of states (DOS) of copper ferrite with various inversion parameters (λ = 0, 0.5, 0.75, 1) were calculated after geometric optimization (shown in Fig. 4). All the calculations are based on a 14-atom primitive unit cell of the spinel structure for λ = 0, 0.5, 1. The geometric optimization and electronic structure calculation for CFO with λ = 0.75 are performed on a 28-atom unit cell. For the half inverse (λ = 0.5) and fully inverse (λ = 1) cases, the primitive unit cells are constructed by transposing one and two Cu²⁺ cations at the T_d site with the Fe³⁺ cations at the O_h site based on the structure of normal spinel (λ = 0), respectively.^17,24 The geometric relaxation on CFO (λ = 1) unit cell leads to a tetragonal distortion, which matches well with the structure of the fully inverse T-CFO reported in literature.¹⁰ The DOS calculated for the fully inverse CFO shows a band gap of 0.603 eV, as shown in Fig. 4(a), which shows semiconducting feature. As GGA scheme typically underestimates band gap of transition elements oxides, the calculated value of 0.603 eV is reasonable when compared with the expected band gap for CFO reported in the literatures.^15,17 After creating anti-site defect by transposing one Cu²⁺ cation (T_d site) with one Fe³⁺ cation (O_h site) in a 28-atom primitive unit cell, defect-like states emerge near the valence band maximum in CFO with λ = 0.75. Partial DOS indicates that these defect-like states are mainly attributed to the d orbitals of Cu (T_d) atoms and 2p orbitals of surrounding oxygen atoms, showing self-doping effect originating from transposition between Cu (O_h) atoms and Fe (T_d) atoms.^25,26 Fig. 4(b) illustrates the tendencies of saturation magnetization M_S and DC conductivity σ₀ as a function of inversion parameter λ. It can be seen from Fig. 4(b), both M_S and σ₀ increases with the decreasing of inversion parameter λ. The tendency of increasing DC resistivity of CFO as inversion parameter decreases matches well with the result from first-principle calculation. As we can see from the DOS of CFO with λ = 0.75, the defect-like states fill the bandgap making CFO highly conductive when compared with the scenario of fully inversed CFO (λ = 1). CFO samples with even lower inversion parameter λ may be obtained through rapid quenching from higher temperature (above 900 °C). More defect-like states fill in the energy level between 0–0.6 eV in half inverse CFO compared to that of 75% inversed CFO, which we believe will further enhance the conductivity of CFO. When the Fe (T_d) atoms are completely replaced by Cu (O_h) atoms, the electronic structure of normal CFO will change dramatically and exhibits typical metallic features. In short, the electronic properties of CFO can be significantly tuned by inversion parameter via creating defect-like density states in the bandgap, which is schematically shown in Fig. 4(c). And the semiconducting band structure gradually transforms into metallic band structure as Cu²⁺ ions migrate from O_h site to T_d site. It is worth noting that the first-principle calculations also show that for all CFO the magnetic moments between T_d site and O_h site are antiferromagnetically coupled and the magnetic moments within T_d site or O_h site are ferromagnetically coupled. The magnetic structures in the ground state for all CFO are ferrimagnetic. And based on the partial DOS analysis the density of states above Fermi level are mainly contributed by Fe³⁺ cations. The spin-resolved electronic densities of states (DOS) in Fig. 4(a) indicate the density of states above Fermi level in minority spin channel becomes more and more dominated as inversion parameter decreases, suggesting the magnetism of CFO would get enhanced as Cu²⁺ ions migrate from O_h site to T_d site.

Fig. 4 (a) The spin resolved densities of states for CFO with λ = 1.0, 0.75, 0.5, 0.0. Partial DOS show the contribution from each type of ions. (b) Saturation magnetization M_S and DC conductivity σ₀ as a function of inversion parameter λ. (c) Schematic view of Cu²⁺ ions migration from O_h site to T_d site and defect-like states created due to cation redistribution.

4. Conclusions

In summary, the CFO polycrystalline samples with different cation distributions are prepared through nonequilibrium thermal treatment. Migration of Cu²⁺ ions from O_h site to T_d site not only induces clear phase transition from tetragonal symmetry to cubic symmetry but also significantly enhance saturation magnetization and conductivity of CFO. Moreover, the first-principle calculations reveal that the self-doping effect induced by ion migration would create defect-like states in the bandgap of semiconducting fully inverse CFO and increase the conductivity of partially inverse CFO. The tunable cation redistribution in copper ferrite can be very promising for future applications implemented by using interacting electron/spin systems.

Conflict of interest

The authors declare no competing financial interest.

Acknowledgements

The work was supported by the National Natural Science Foundation of China (No: 61631166004, 61471290 and 51390472), the SRFDP-RGC Joint Research Project 2013/14 (20130201140002), and National 973 Projects of China (No. 2015CB654603 and 2015CB654903). It was also partially supported by the Fundamental Research Funds for the Central University.

References

1. H. Akinaga and H. Shima, Proc. IEEE, 2010, 98, 2237–2251.
2. J. J. Yang, D. B. Strukov and D. R. Stewart, Nat. Nanotechnol., 2013, 8, 13–24.
3. S. Menzel, U. Bottger, M. Wimmer and M. Salinga, Adv. Funct. Mater., 2015, 25, 6306–6325.
4. A. Regoutz, I. Gupta, A. Serb, A. Khiat, F. Borgatti, T. L. Lee, C. Schlueter, P. Torelli, B. Gobaut, M. Light, D. Carta, S. Pearce, G. Panaccione and T. Prodromakis, Adv. Funct. Mater., 2016, 26, 507–513.
5. S. Kumar, C. E. Graves, J. P. Strachan, E. M. Grafals, A. L. D. Kilcoyne, T. Tyliszczak, J. N. Weker, Y. Nishi and R. S. Williams, Adv. Mater., 2016, 28, 2772–2776.
6. S. K. Vishwanath and J. Kim, J. Mater. Chem. C, 2016, 4, 10967–10972.
7. Q. Wang, Y. Zhu, X. Liu, M. Zhao, M. Wei, F. Zhang, Y. Zhang, B. Sun and M. Li, Appl. Phys. Lett., 2015, 107, 063502.
8. X. J. Zhu, J. T. Zhou, L. Chen, S. S. Guo, G. Liu, R. W. Li and W. D. Lu, Adv. Mater., 2016, 28, 7658–7665.
9. S. Dasgupta, B. Das, M. Knapp, R. A. Brand, H. Ehrenberg, R. Kruk and H. Hahn, Adv. Mater., 2014, 26, 4639–4644.
10. A. M. Balagurov, I. A. Bobrikov, V. Y. Pomjakushin, D. V. Sheptyakov and V. Y. Yushankhai, J. Magn. Magn. Mater., 2015, 374, 591–599.
11. S. Dasgupta, B. Das, Q. Li, D. Wang, T. T. Baby, S. Indris, M. Knapp, H. Ehrenberg, K. Fink, R. Kruk and H. Hahn, Adv. Funct. Mater., 2016, 26, 7507–7515.
12. A. M. Balagurov, I. A. Bobrikov, M. S. Maschenko, D. Sangaa and V. G. Simkin, Crystallogr. Rep., 2013, 58, 710–717.
13. M. Desai, S. Prasad, N. Venkataramani, I. Samajdar, A. K. Nigam and R. Krishnan, J. Appl. Phys., 2002, 91, 2220–2227.
14. A. Yang, Z. Chen, X. Zuo, D. Arena, J. Kirkland, C. Vittoria and V. G. Harris, Appl. Phys. Lett., 2005, 86, 252510–252512.
15. M. Kucera and P. Brom, J. Appl. Phys., 2015, 117, 17B738–717B741.
16. F. Kagawa and H. Oike, Adv. Mater., 2016 DOI:10.1002/adma.201601979.
17. Z. Jiang, W. H. Zhang, W. F. Shangguan, X. J. Wu and Y. Teraokag, J. Phys. Chem. C, 2011, 115, 13035–13040.
18. R. G. Kulkarni and V. U. Patil, J. Mater. Sci., 1980, 15, 2221–2223.
19. K. J. Kim, J. H. Lee and S. H. Lee, J. Magn. Magn. Mater., 2004, 279, 173–177.
20. G. F. Goya, H. R. Rechenberg and J. Z. Jiang, J. Appl. Phys., 1998, 84, 1101–1108.
21. K. B. Modi, P. Y. Raval, S. V. Dulera, C. R. Kathad, S. J. Shah, U. N. Trivedi and U. Chandra, AIP Conf. Proc., 2015, 1665, 130011–130013.
22. M. Liu, M. Lu, L. Wang, S. Xu, J. Zhao and H. Li, J. Mater. Sci., 2016, 51, 5487–5492.
23. T. Mlyadai, S. Miyahara and Y. Matsuo, J. Phys. Soc. Jpn., 1965, 20, 980–984.
24. B. S. Holinsworth, D. Mazumdar, H. Sims, Q.-C. Sun, M. K. Yurtisigi, S. K. Sarker, A. Gupta, W. H. Butler and J. L. Musfeldt, Appl. Phys. Lett., 2013, 103, 082406–082409.
25. T. R. Paudel, Z. Andriy, L. Stephan, D. A. Mayeul and Z. Alex, Adv. Funct. Mater., 2011, 21, 4493–4501.
26. Y. Shi, P. F. Ndione, L. Y. Lim, D. Sokaras, T. C. Weng, A. R. Nagaraja, A. G. Karydas, J. D. Perkins, T. O. Mason and D. S. Ginley, Chem. Mater., 2014, 26, 1867–1873.

---

Footnote

† Electronic supplementary information (ESI) available: The refinement parameters for all CFO samples. Grain sizes of all CFO samples obtained by SEM and XPS investigations on RQ-900 CFO sample. See DOI: 10.1039/c7ra01765k

---