Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Preferential stabilization of HeI2 van der Waals isomers: the effect of energetics and temperature
Álvaro Valdésa and
Rita Prosmiti *b
*b
aDepartamento de Física, Universidad Nacional de Colombia, Calle 26, Cra 39, Edificio 404, Bogotá, Colombia
bInstituto de Física Fundamental (IFF-CSIC), CSIC, Serrano 123, 28006 Madrid, Spain. E-mail: rita@iff.csic.es; Tel: +34 915616800
First published on 31st March 2017
Abstract
The populations of the two different HeI2 conformers (linear and T-shaped) were calculated as a function of temperature using a simple thermodynamic model and the quantum mechanical partition functions for each conformer. Variational quantum calculations were performed for angular momentum values J up to 15, and by analyzing the rovibrational energies and functions, all states up to dissociation were assigned. On the basis of the vibrational and rotational partition functions calculations, it was found that the relative populations of the isomers have a strong dependence on the temperature. The population of the linear isomer (the most stable one according to the ab initio CCSD(T)/CBS potential used) decreases relative to that of the T-shaped, as the temperature increases, and at temperatures around 1 K the two populations are equal, with the T-shaped isomer being more abundant for higher temperatures. The temperature effect on the relative population was also investigated as a function of the difference in the binding energy values of the two isomers, including those determined from the experimental observations with the T-shaped being energetically most stable. In this case, even though the ratio of the T-shaped/linear populations decreases rapidly for temperatures below 1 K, the T-shaped isomer was the most abundant at all temperatures. The system evolves between both T-shaped and linear arrangements, with no significant changes at temperatures 1.5 K. The disagreement at low temperatures between theoretical predictions and experimental data available indicates that further refinement is still needed for controlling the isomers' formation, and various possible sources of errors are extensively discussed.
Weakly bound van der Waals (vdW) clusters have proven, by both theoreticians and experimentalists, to be suitable for investigating long-range intermolecular interactions,1–3 energy transfer mechanisms, and even microsolvation processes.4–7 There has been a significant amount of effort focused on rare gas–dihalogen complexes,1,8–28 and as a consequence new aspects of these systems emerge. For example, high-level ab initio electronic structure computations have predicted minima in the ground electronic states of such complexes at both linear and T-shaped orientations,29,30 with the final conclusion drawn, later on, from the experimental evidences on the stabilization of two isomers in the supersonic expansions,10,12,18 although they have been first observed by Levy and coworkers31 in the spectra of the HeI2. In the case of He–dihalogen, such as HeBr2, HeI2 and HeICl, the depths of the potential wells for the linear and T-shaped configurations have been found to be comparable, with the linear being the deepest one.14,29,30 By including zero-point-energy (ZPE) effects for T = 0 K, the linear isomer has been predicted to be the most stable one, with energy differences between the two conformers estimated at 3.14, 1.14 and just only 0.21 cm−1 for the HeICl, HeBr2, and HeI2, respectively.14,29,32 For the HeICl and HeBr2 complexes such values has been found in accord with experimental predictions, while in the case of the HeI2 experimental measurements support an inverse ordering in the stability of the two isomers, with the T-shaped conformer being by 0.3 cm−1 more stable than the linear one.18
Moreover, Loomis and coworkers18 have recorded LIF and complimentary action spectra for HeI2 in the I2 B–X, 20, 0 region at two different distances downstream along the expansion, corresponding to rotational temperatures of <0.09 and 1.86(2) K. By observing changes in the intensities of the T-shaped and linear features, with the linear spectral feature becoming less intense than the T-shaped peak with cooling, they have presumed18 that the linear conformer is less stable than the T-shaped one. This finding brings us back to one of the initial motivations of this series of studies, arising the question of whether there is a simple explanation for the apparent disagreement between theory and experiment on the stability of the two ground state HeI2 isomers. Although the errors in the experimental binding energy values of the two isomers are larger than the energy difference between them, it seems that the linear isomer has been measured to be the most stable one. So far, a number of spectroscopic studies have detected different isomers for such vdW clusters formed in supersonic expansions,1,10,12,18,22 with the mechanisms for their formation and the subsequent cooling via collisions remain uncertain, and probably system depended. Experimental results have shown13 that the relative populations of the isomers may change within a supersonic expansion even under conditions of temperature below 1 K. Further, investigations in similar rare gas–dihalogen complexes33–35 have also shown that the formation of isomers is controlled by thermodynamic factors, so the complexes are not kinetically trapped in different potential minima, and thus kinetic effects do not influence the relative population with respect to the equilibrium ones.
As such, an important issue to be checked is the temperature dependence of the isomers' populations in the case of the HeI2. Thus, calculations of the rovibrational states of the HeI2 (X) were performed using the ab initio CCSD(T)/CBS potential surface,32 vibrational and rotational partition functions were computed, and then the populations of the linear and T-shaped conformers were obtained via a simple thermodynamic model as a function of temperature. Apart of the temperature effect on the stability of the isomers, we also investigate the role of the difference in the binding energies of the isomers, as it has been predicted by both theory and experiment. Hence, we present how the relative populations of the two HeI2 isomers vary with the temperature, and thus with the distance from the nozzle. Such results offer additional information, since complexes with different orientations could be preferentially stabilized, and that can serve as targets for experimental and theoretical endeavors aimed to fine-tune errors in the measurements and to improve any reflecting deficiencies in the intermolecular potentials for controlling their formation. The remainder of the paper is organized as following. Next section contains three subsections, which include computational details for the variational rovibrational state calculations, description of the thermodynamic model, calculation of partition functions and relative population of the two isomers, and discussion of the results and their sensitivity to various parameters. Finally, Section 2 summarizes some conclusions of this work.
1 Computational details, results and discussion
1.1 Rovibrational states from variational calculations
The rovibrational Hamiltonian in the Jacobi (r,R,θ) coordinate system has the form36
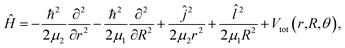 | (1) |
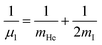 and
and 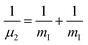 are the reduced masses, mHe = 4.00260 and mI = 126.904473 u are the atomic masses of 4He and 127I isotopes,
are the reduced masses, mHe = 4.00260 and mI = 126.904473 u are the atomic masses of 4He and 127I isotopes, ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) and ĵ are the angular momentum operators associated with the vectors R and r, respectively, leading to a total angular momentum Ĵ =
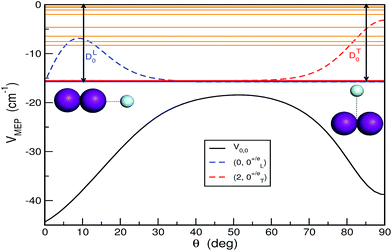
and ĵ are the angular momentum operators associated with the vectors R and r, respectively, leading to a total angular momentum Ĵ = ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) + ĵ, while Vtot(r,R,θ) = V(r,R,θ) + VI2(r), with V(r,R,θ) and VI2(r) being the ab initio CCSD(T)/CBS HeI2 and I2 ground state potentials from ref. 32. The CCSD(T)/CBS energies and structures have been further compared with experimental data for both HeI2 and I2 molecules, as well as with values from multi-reference calculations.19,32,37,38 In Fig. 1 we display the minimum energy path (MEP) of the vibrationally averaged Vv,v′(R,θ) = 〈χv(r)|V(R,θ,r)|χv′(r)〉 intermolecular vdW potential of HeI2 over the I2 χv=0 vibrational eigen functions, as a function of θ. This surface presents minima for both linear and T-shaped configurations at −44.48 and −38.93 cm−1, respectively, which are very close in energy within 5.5 cm−1, while they are separated by a isomerization barrier lying at energy of −18.43 cm−1.
+ ĵ, while Vtot(r,R,θ) = V(r,R,θ) + VI2(r), with V(r,R,θ) and VI2(r) being the ab initio CCSD(T)/CBS HeI2 and I2 ground state potentials from ref. 32. The CCSD(T)/CBS energies and structures have been further compared with experimental data for both HeI2 and I2 molecules, as well as with values from multi-reference calculations.19,32,37,38 In Fig. 1 we display the minimum energy path (MEP) of the vibrationally averaged Vv,v′(R,θ) = 〈χv(r)|V(R,θ,r)|χv′(r)〉 intermolecular vdW potential of HeI2 over the I2 χv=0 vibrational eigen functions, as a function of θ. This surface presents minima for both linear and T-shaped configurations at −44.48 and −38.93 cm−1, respectively, which are very close in energy within 5.5 cm−1, while they are separated by a isomerization barrier lying at energy of −18.43 cm−1.
The bound vdW levels, and the corresponding wave functions are calculated variationally by diagonalizing the vibrationally averaged Hamiltonian, using up to four vibrational basis functions, χv=0–3(r). For a given total angular momentum J and a parity of total nuclear coordinates inversion p, the corresponding Hamiltonian is represented as a product of radial, {fn(R)}, and angular, {Θ(JMp)jΩ}, basis functions. For the R coordinate a discrete variable representation (DVR) basis set was used based on the particle in a box eigen functions, while the angular {Θ(JMp)jΩ} basis functions are eigen functions of the parity, with M being the projection of J on the space-fixed z-axis, Ω its projection on the body-fixed z-axis, which is chosen here along the R vector.39 The Hamiltonian is represented on a finite three-dimensional basis set. The Vv,v′ potential matrix elements were evaluated for v = 0–3 values at 61 Gaussian quadrature points in r range between 2.2 to 3.5 Å. For the angular coordinate we used ortho normalized Legendre polynomials {Pj(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)} as basis functions, with up to 48 and 49 values of the diatomic rotation j, for even and odd symmetry, respectively, while for the R coordinate, a basis set of 140 DVR functions over the range from 2.85 to 15.0 Å were used, achieving a convergence of 0.0005 cm−1 in the bound state calculations.
θ)} as basis functions, with up to 48 and 49 values of the diatomic rotation j, for even and odd symmetry, respectively, while for the R coordinate, a basis set of 140 DVR functions over the range from 2.85 to 15.0 Å were used, achieving a convergence of 0.0005 cm−1 in the bound state calculations.
In Fig. 1 the bound vibrational (J = 0) states together with their angular distributions are also depicted. On the basis of the localization of their radial and angular distributions, the lowest 3 levels for n = 0, 1 and 2, were assigned to linear and T-shaped isomers, respectively. Their binding energies were calculated to be DL0 = 15.72 and DT0 = 15.51 cm−1, respectively, with the linear conformer being more stable by just 0.21 cm−1 than the T-shaped one.
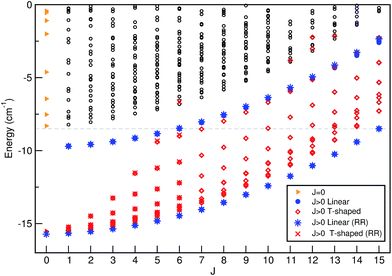
The energies of all bound levels for each J ≤ 15 are displayed in Fig. 2. As we are interested at low temperatures T ≤ 3 K, only states with J ≤ 15 are significantly populated, so only these states were evaluated. As we mentioned above for J = 0, the n = 0 and 1 states have linear He⋯I–I geometries, the n = 2 state corresponds to T-shaped ones, while the higher vibrational states present a wide spread over the θ angle. As J value increases, we observe two smooth progressions for the linear states (denoted by • symbols) corresponding initially to the two lowest levels (n = 0, 1) for J = 0 at energy of −15.72 cm−1, and to n = 1, 2 levels for J = 1 at −9.70 cm−1, respectively. In turn, for each J value the T-shaped states (denoted by ⋄ symbols) split into 2J + 1 different K rotor levels, although due to near degeneracies between states with same K value and different parities only J + 1 levels are distinguishable in Fig. 2. The energies of these levels increase and their pattern becomes congested as J increases with the K states spreading at higher energies and overlapping other rovibrational states. By comparing with the rigid rotor model energy values (denoted by * and × symbols for linear and T-shaped levels, respectively), one can observe a very similar behavior, especially at low energies.
1.2 Thermodynamic model and partition functions
The thermodynamic model employed to obtain the HeI2 isomers' populations is similar to the one described in ref. 33. In brief, relative isomers' populations were obtained from the exact formula derived directly from the standard Gibbs energies of the isomers,40 assuming that both linear and T-shaped isomers are in thermodynamic equilibrium. Thus, their relative populations, at a given temperature, are equivalent to the ratio of their partition functions (respecting entropy contributions). Moreover, as vibrational energies are greater than the rotational constants for the HeI2 in its ground electronic state, so vibrational and rotational motions are reasonably well separated, and the partition functions can be simplified to:| ZL,T(T) = ZL,Tvib(T)ZL,Trot(T) | (2) |
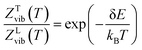 | (3) |
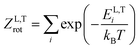 | (4) |
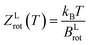 | (5) |
The rotational constant for the linear HeI2 isomer, BLrot, is obtained as the one half of the difference between the energies of the J = 1 and J = 0 calculated states. The values of 0.0301 and 0.0309 cm−1 indicate that the criterion, T ≫ θLrot = BLrot/kB = 0.043 K, is fulfilled by a factor of only 2 for the lowest temperature values reported at the experiment.18 For the T-shaped conformer, the theoretical approximation of the rotational partition function based on the asymmetric top rigid rotor is,34,41
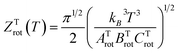 | (6) |
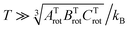 . The constants for the T-shaped rotor, ATrot = 0.2404 cm−1, BTrot = 0.0376 cm−1, and CTrot = 0.0322 cm−1, are obtained again by energy difference between the J = 1 and J = 0 T-shaped levels, indicating temperatures of T 0.095 K. In this case, one can see that the characteristic temperature is just at the lower limit of the cluster's temperature, and thus, the rotational partition functions for both linear and T-shaped states were also determined using eqn (4) by the sum over the calculated energies of the linear or T-shaped conformers for temperatures up to 5 K.
. The constants for the T-shaped rotor, ATrot = 0.2404 cm−1, BTrot = 0.0376 cm−1, and CTrot = 0.0322 cm−1, are obtained again by energy difference between the J = 1 and J = 0 T-shaped levels, indicating temperatures of T 0.095 K. In this case, one can see that the characteristic temperature is just at the lower limit of the cluster's temperature, and thus, the rotational partition functions for both linear and T-shaped states were also determined using eqn (4) by the sum over the calculated energies of the linear or T-shaped conformers for temperatures up to 5 K.
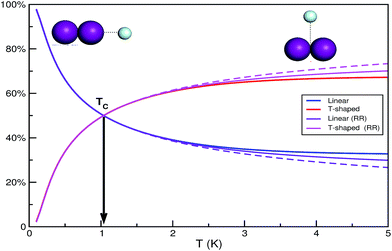
The small difference in the binding energies of the two ground state conformers together with the larger density of states for the slightly more energetic T-shaped configuration shown above, indicates the possibility of a temperature dependence populations for the linear and T-shaped conformers. Thus, the relative populations of the linear and T-shaped He⋯I2 features, ZL/ZT, are plotted in Fig. 3 as a function of temperature. It is noticeable their strong dependence on the temperature, with the population of the linear being almost 100% at low temperature, while it decreases rapidly at 66% at T = 0.5 K compared to that of 34% for the T-shaped feature by increasing temperature. The two populations become equal at TC = 1.037 K, while above this temperature there is an inversion of the population ratio of the He⋯I2 isomers. The T-shaped isomer is more abundant than the linear one, counting 61 and 65% at T = 2 and 3 K, respectively. Also in Fig. 3 the corresponding partition functions obtained from the rigid rotor (RR) model are shown for both linear and T-shaped rotors. Different type of lines correspond in the case that the second progression of linear rotor states (see Fig. 2) appears at J ≥ 1 has been included (solid line) or not (dashed line) in the calculation. One can see that no differences are obtained in the populations of the He⋯I2 isomers for temperatures below 2 K, while above this temperature the RR model diverge, slightly favoring the T-shaped abundance, and with the inclusion of the linear states' progression in the upper energy band to quantitatively affect the partition functions' ratio. We should point out that as temperature increases (T > 3 K), the rotational partition functions start to become subject to the finite number of calculated J states.
1.3 Results' discussion
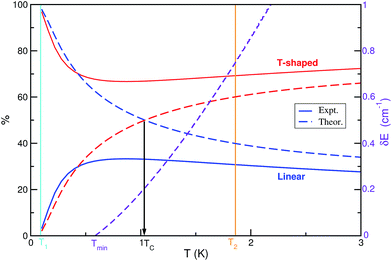
A theoretical approach based on a simple thermodynamic model including data from quantum rovibrational J ≥ 0 bound state calculations was employed to evaluate the isomers' populations as a function of temperature and to provide results on the populations' inversion of the He⋯I2 system. We should note that the relative proportion of the linear and T-shaped isomers was obtained from the corresponding vibrational and rotational partition functions. On the other hand, as we mentioned above, LIF and action spectra have been recorded18 at two different downstream distances along the expansion. The I2 (X, v = 0) rotational temperature of these spectra was estimated at 1.86(2) K and <0.09 K, respectively. They observed18 that the intensity of the linear spectral feature becomes less intense with cooling, than the T-shaped one, so the linear He⋯I2 (X, v = 0) isomer should be less stable than the T-shaped. The binding energy of the linear species has been measured18 at 16.3(6) cm−1 by the average energies of the onsets of the continuum signals of action spectra in the I2 B–X, v′-0 regions with v′ = 19, 20 and 23, while the relative binding energy of the T-shaped conformers has been measured at 0.3(2) cm−1 by recording multiple, two-photon spectra, setting18 the T-shaped binding energy to 16.6(6) cm−1. We should note that the errors reported in the experimental binding energy values for each isomer are higher than the energy difference between them, and their stability is in an inverse ordering compared to the theoretical estimates from ab initio quantum mechanical calculations. Thus, in Fig. 4 we present the relative populations of the isomers obtained from the RR model using the rotational constants from the rovibrational calculations, and the values of the experimental binding energies DT0 = 16.6 and DL0 = 16.3 cm−1. As it was expected, there is no inversion from the T-shaped to linear species. One can now see that the population of the T-shaped conformers drops down to 67% at temperatures up to 1 K, and then increases slightly to 72%. The reversed behavior occurs in the population of the linear species, with population around to 3 and 30% at the experimental temperatures of 0.09 and 1.86 K, respectively. Similar estimates for the population of each He⋯I2 (X, v = 0) isomer can be, in principle, tracked by measuring the integrated intensity of the corresponding He⋯I2 spectral feature in the recorder action spectra at the same temperatures.18 Moreover, the binding energy difference value, δE, between the two isomers is also expected to influence the value of the population's crossing temperature (see eqn (3)). Thus, on the basis of the present theoretical results on the HeI2 partition functions with the linear isomer being more stable than the T-shaped one, the lowest TC value for the convertion is Tmin = 0.58 K (see Fig. 4), corresponding to the zero energy difference between the two isomers.A key point could also be that the present theoretical results check whether only thermodynamic factors control the inversion of the populations, without taking into account kinetic effects that may change them compared to the equilibrium ones. In this vein, simulations in similar vdW systems33 have been provide insights into different collision mechanisms that could affect the inversion between the isomers even at the very low temperatures of the experimental setups. The dominant mechanism for such conversion under temperature has not been, so far, precisely determined, although for He complexes there is no evidence for kinetically trapped species in the different potential wells,13,34 that seem to behave thermodynamically in the supersonic expansion. Thus, according to the present results for the HeI2 complex the ordering and relative values of the binding energies for the two isomers still remain under consideration. Given that there is no kinetic effect, the simplest explanation to the discrepancies between the experimental and theoretical values should be the accumulation of statistical or fitting errors to the measurements, and/or convergence errors in the ab initio calculations. On the one hand, it may be useful to record spectra of the He⋯I2 vdW complex at multiple distances to the nozzle. By varying the temperature regimes within the expansion different features could be identified, and the role of the underlying interactions, as well as the effect of the thermodynamic and/or kinetic mechanisms on the complex dynamics could be then determined. On the other hand, it is clear that the energy difference between the two isomers is really very small, so ab initio calculations for improving the accuracy of the interaction should be performed. Previous CCSD(T)/CBS calculations on HeI2 (X) complex estimated differences of about 4 cm−1 in the optimized linear and T-shaped interaction energies.32 Different simple extrapolation formulas in conjunction with correlation consistent basis sets have been used. However, the spread in interaction energies from those CBS schemes,32 counting to around 1.5 cm−1, provides the uncertainty in these values, indicating that any of the CBS estimates should be seen only as an approximation of the CBS limit.42,43
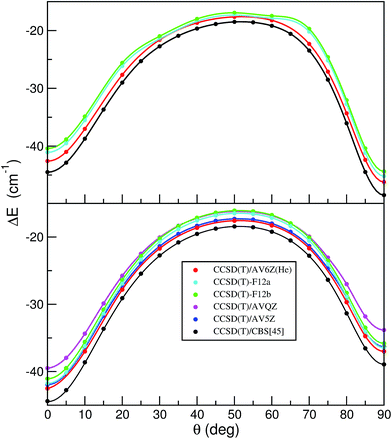
More recently explicitly correlated CCSD(T)-F12a/b methods have also been developed, providing dramatic improvements of the basis set convergence of CCSD correlation energies.44 Thus, we performed CCSD(T)-F12 calculations using the Molpro package45,46 to further check the quality of the HeI2 ab initio data and their convergence to CCSD(T)/CBS limit. In the F12 calculations specially optimized correlation consistent F12 basis sets47 were used, in conjunction with resolution of the identity complementary auxiliary basis set (OptRI), and density fitting of the Fock, exchange and other two-electron integrals (JKFit, MP2Fit).45,46 Up to now, benchmarks were usually carried out considering only equilibrium configurations. However, given the importance of the linear/T-shaped isomerization barrier in the energetics of the HeI2, as well as the small energy differences observed between the HeI2 isomers, we now consider to check the performance of the different methods and basis sets at a number of intermolecular configurations. Obviously, the most relevant for the sampling should be those in the regions along the minimum energy path between the two HeI2 potential minima. In this way, we created a set of 19 benchmark interaction energies for the HeI2 along the minimum values of the 2D V(R,θ;re) potential, and another 13 configurations corresponding to the minimum energies of the full V(R,θ,r) surface. In Fig. 5 we display the results from the CCSD(T), CCSD(T)/CSB and CCSD(T)-F12 calculations along these two minimum energy paths (see top and bottom panel, respectively). As it can be seen, the CCSD(T)/CBS data predicts deeper potential wells at both linear and T-shaped configurations, and lower isomerization barrier than the CCSD(T) results, while the CCSD(T)-F12 estimates present an opposite behavior, showing shallower wells and higher isomerization barrier compared to the CCSD(T) ones. The F12a and F12b energy values are quite similar, with the F12a closer to the CCSD(T) reference values corresponding to the calculations with the AV6Z/AV5Z-PP basis sets. We should note that the convergence of the CCSD(T)-F12 energies is quite different in the regions around the barrier and minima, showing a better performance, especially the F12a, in the configurations around the potential minima. Even though the potential energies nearby the two minima are described pretty consistently by the CCSD(T)/AV5Z/AV5Z-PP, CCSD(T)/AV6Z/AV5Z-PP and CCSD(T)-F12a calculations, the performance of the CCSD(T)-F12 around the barrier seems inconclusive, and thus no additional support for its reliability has been gained.
2 Summary and conclusions
The present work addressed the role played by temperature and energetics on the stabilization of different HeI2 isomers. Such conformers have been stabilized in supersonic expansions at varying the distance from the nozzle, and have been identified within spectral features in LIF and action spectra recorded in the I2 B–X, 20–0 region. By analyzing the intensities of the linear and T-shaped features in these spectra with cooling Loomis and coworkers18 have presumed that the linear He⋯I2 (X, v = 0) isomer should be less stable than the T-shaped. This was somewhat surprisingly when for similar He–dihalogen complexes linear species have been found, by both theory and experiment, to be most stable than the T-shaped ones. So, we calculated the population of each He⋯I2 (X, v = 0) ground state isomer as a function of temperature using a thermodynamic model and the quantum partition functions from rovibrational variational computations employing the ab initio CCSD(T)/CBS surface with J values up to 15. We chose to monitor the change in the relative populations of the linear and T-shaped isomers as temperature changes, and conversion of the linear into T-shaped He⋯I2 isomers is observed even at low temperatures, with their populations being equal at T = 1 K. We showed that above this temperature the T-shaped isomer is the more abundant. We also found that linear and T-shaped rigid rotor models offer a good description of the system especially at low energies. So, the results from the quantum partition functions were then compared with those obtained from the rigid rotor model and the experimental binding energy values of the two isomers. Such comparisons demonstrate the high sensitivity of isomers' populations on the energetics and temperature, indicating that a higher level of refinement is still needed in theoretical approaches for this system, and possible in experimental measurements and their interpretations, to reach an agreement at low temperature regime for this very weakly bound complex. In particular, even though high level ab initio calculations were performed to determine the He–I2 intermolecular interactions, several approximations, e.g. the CBS extrapolation procedure, should be still reconsidered. Given the difficulties associated with such calculations for a very weak system containing heavy atoms (such as iodine), we aimed to bracket the uncertainties of recent ab initio methods at various representative configurations. We found that the previous CBS schemes overestimate the depths for both linear and T-shaped wells, while no clear clues were came out for the energies of the isomerization barrier between them. It seems that the approximations should be improved and modifications should be introduced, while complementary information is still needed for ascertaining the importance of energetics, thermodynamic or even kinetic effects for this system. Thus, it would be extremely interesting to record HeI2 spectra in varying distances to the nozzle and temperature regimes within the expansion, that could provide additional insights in order to fine-tune errors and deficiencies for controlling the stabilization of its isomers.Acknowledgements
The authors thank to Centro de Calculo del IFF, SGAI (CSIC) and CESGA for allocation of computer time. This work has been supported by MINECO grant No. FIS2014-51933-P, by “CSIC for Development” (i-COOP) programme ref: ICOOPB20214, and by COST Actions CM1204(X-LIC) and CM1405(MOLIM).References
- A. Rohrbacher, N. Halberstadt and K. C. Janda, Annu. Rev. Phys. Chem., 2000, 51, 405–433 CrossRef CAS PubMed.
- D. Bonhommeau, N. Halberstadt and U. Buck, Int. Rev. Phys. Chem., 2007, 26, 353–390 CrossRef CAS.
- J. Beswick, N. Halberstadt and K. Janda, Chem. Phys., 2012, 399, 4–16 CrossRef CAS.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed.
- M. P. de Lara-Castells, R. Prosmiti, G. Delgado-Barrio, D. López-Durán, P. Villarreal, F. A. Gianturco and J. Jellinek, Phys. Rev. A, 2006, 74, 053201 CrossRef.
- O. Echt, T. D. Mark and P. Scheier, Handbook of Nanophysics, Vol. 2: Clusters and Fullerenes, CRC Press, Taylor and Francis Group, Boca Raton, FL, 2010 Search PubMed.
- R. Pérez de Tudela, P. Barragán, A. Valdés and R. Prosmiti, J. Phys. Chem. A, 2014, 118, 6492–6500 CrossRef PubMed.
- A. S. Miller, C.-C. Chuang, H. Fu, K. Higgins and W. Klemperer, J. Chem. Phys., 1999, 111, 7844–7856 CrossRef.
- A. Burroughs and M. Heaven, J. Chem. Phys., 2001, 114, 7027–7035 CrossRef CAS.
- A. A. Buchachenko, R. Prosmiti, C. Cunha, G. Delgado-Barrio and P. Villarreal, J. Chem. Phys., 2002, 117, 6117–6120 CrossRef CAS.
- C. Cunha, R. Prosmiti, P. Villarreal and G. Delgado-Barrio, Mol. Phys., 2002, 100, 3231–3237 CrossRef CAS.
- D. S. Boucher and R. A. Loomis, J. Chem. Phys., 2003, 118, 7233–7244 CrossRef.
- D. S. Boucher, M. D. Bradke, J. P. Darr and R. A. Loomis, J. Phys. Chem. A, 2003, 107, 6901–6904 CrossRef CAS.
- Á. Valdés, R. Prosmiti, P. Villareal and G. Delgado-Barrio, Mol. Phys., 2004, 102, 2277–2283 CrossRef.
- A. B. McCoy, J. P. Darr, D. S. Boucher, P. R. Winter, M. D. Bradke and R. A. Loomis, J. Chem. Phys., 2004, 120, 2677–2685 CrossRef CAS PubMed.
- D. S. Boucher, D. B. Strasfeld, R. A. Loomis, J. M. Herbert, S. E. Ray and A. B. McCoy, J. Chem. Phys., 2005, 123, 104312 CrossRef PubMed.
- J. P. Darr, R. A. Loomis and A. B. McCoy, J. Chem. Phys., 2005, 122, 044318 CrossRef PubMed.
- S. E. Ray, A. B. McCoy, J. J. Glennon, J. P. Darr, E. J. Fesser, J. R. Lancaster and R. A. Loomis, J. Chem. Phys., 2006, 125, 164314 CrossRef PubMed.
- A. Valdés, R. Prosmiti, P. Villarreal, G. Delgado-Barrio and H.-J. Werner, J. Chem. Phys., 2007, 126, 204301 CrossRef PubMed.
- A. Valdés, R. Prosmiti, P. Villarreal, G. Delgado-Barrio, D. Lemoine and B. Lepetit, J. Chem. Phys., 2007, 126, 244314 CrossRef PubMed.
- D. S. Boucher and R. A. Loomis, Stabilization of Different Conformers of Weakly Bound Complexes to Access Varying Excited-State Intermolecular Dynamics, Wiley, New York, 2008, vol. 138, pp. 375–420 Search PubMed.
- J. M. Pio, W. E. van der Veer, C. R. Bieler and K. C. Janda, J. Chem. Phys., 2008, 128, 134311 CrossRef PubMed.
- D. S. Boucher, J. P. Darr, D. B. Strasfeld and R. A. Loomis, J. Phys. Chem. A, 2008, 112, 13393–13401 CrossRef CAS PubMed.
- Y. Zhang, K. Vidma, D. H. Parker and R. A. Loomis, J. Chem. Phys., 2009, 130, 104302 CrossRef PubMed.
- J. M. Pio, M. A. Taylor, W. E. van der Veer, C. R. Bieler, J. A. Cabrera and K. C. Janda, J. Chem. Phys., 2010, 133, 014305 CrossRef PubMed.
- Á. Valdés, R. Prosmiti, P. Villarreal and G. Delgado-Barrio, J. Chem. Phys., 2011, 135, 054303 CrossRef PubMed.
- J. P. Darr and R. A. Loomis, Chem. Phys. Lett., 2013, 586, 34–39 CrossRef CAS.
- Á. Valdés and R. Prosmiti, J. Phys. Chem. A, 2015, 119, 12736–12741 CrossRef PubMed.
- R. Prosmiti, C. Cunha, P. Villarreal and G. Delgado-Barrio, J. Chem. Phys., 2002, 117, 7017–7023 CrossRef CAS.
- R. Prosmiti, Á. Valdés, P. Villarreal and G. Delgado-Barrio, J. Phys. Chem. A, 2004, 108, 6065–6071 CrossRef CAS.
- R. Smalley, D. Levy and L. Wharton, J. Chem. Phys., 1976, 64, 3266–3276 CrossRef CAS.
- L. Garcia-Gutierrez, L. Delgado-Tellez, A. Valdés, R. Prosmiti, P. Villarreal and G. Delgado-Barrio, J. Phys. Chem. A, 2009, 113, 5754–5762 CrossRef CAS PubMed.
- A. Bastida, J. Zúñiga, A. Requena, B. Miguel, J. A. Beswick, J. Vigué and N. Halberstadt, J. Chem. Phys., 2002, 116, 1944–1953 CrossRef CAS.
- D. S. Boucher, J. P. Darr, M. D. Bradke, R. A. Loomis and A. B. McCoy, Phys. Chem. Chem. Phys., 2004, 6, 5275–5282 RSC.
- O. Carrillo-Bohórquez, Á. Valdés and R. Prosmiti, J. Phys. Chem. A, 2016, 120, 9458–9464 CrossRef PubMed.
- J. M. Hutson, Advances in Molecular Vibrations and Collision Dynamics, JAI Press, Inc., 1991, vol. 1, pp. 1–46 Search PubMed.
- A. Kalemos, A. Valdés and R. Prosmiti, J. Phys. Chem. A, 2012, 116, 2366–2370 CrossRef CAS PubMed.
- A. Kalemos, A. Valdés and R. Prosmiti, J. Chem. Phys., 2012, 137, 034303 CrossRef PubMed.
- R. Zare, Angular momentum: understanding spatial aspects in chemistry and physics, Wiley, 1988 Search PubMed.
- Z. Slanina, Int. Rev. Phys. Chem., 1987, 6, 251–267 CrossRef CAS.
- D. A. McQuarrie, Statistical mechanics, Harper & Row, Harper's Chemistry Series, New York, 1975 Search PubMed.
- D. Feller, K. Peterson and D. Dixon, Annual Reports in Computational Chemistry, Elsevier, Amsterdam, 2016, vol. 12, ch. 2 Search PubMed.
- D. W. Schwenke, J. Chem. Phys., 2005, 122, 014107 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., MOLPRO, version 2012.1, a package of ab initio programs, 2012, http://www.molpro.net Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Computational Molecular Science, 2012, 2, 242–253 CrossRef CAS.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |