Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Triply-bonded indium![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e002.gif) phosphorus molecules: theoretical designs and characterization†
phosphorus molecules: theoretical designs and characterization†
Jia-Syun Lua,
Ming-Chung Yanga and
Ming-Der Su *ab
*ab
aDepartment of Applied Chemistry, National Chiayi University, Chiayi 60004, Taiwan. E-mail: midesu@mail.ncyu.edu.tw
bDepartment of Medicinal and Applied Chemistry, Kaohsiung Medical University, Kaohsiung 80708, Taiwan
First published on 10th April 2017
Abstract
The effect of substitution on the potential energy surfaces of triple-bonded RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR (R = F, OH, H, CH3, SiH3, NHC, SiMe(SitBu3)2 and SiiPrDis2) species was investigated, using the density functional theory (i.e., M06-2X/Def2-TZVP, B3PW91/Def2-TZVP and B97-D3/LANL2DZ+dp). The theoretical results suggest all of the triple-bonded RIn
PR (R = F, OH, H, CH3, SiH3, NHC, SiMe(SitBu3)2 and SiiPrDis2) species was investigated, using the density functional theory (i.e., M06-2X/Def2-TZVP, B3PW91/Def2-TZVP and B97-D3/LANL2DZ+dp). The theoretical results suggest all of the triple-bonded RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR molecules prefer to adopt a bent form with an angle (∠In–P–R) of about 90°. Present theoretical evidence suggests only the bulkier substituents, in particular for the strong donating groups (such as the NHC group), can greatly stabilize the In
PR molecules prefer to adopt a bent form with an angle (∠In–P–R) of about 90°. Present theoretical evidence suggests only the bulkier substituents, in particular for the strong donating groups (such as the NHC group), can greatly stabilize the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond. In addition, bonding analyses demonstrate the bonding character of such triple-bonded RIn
P triple bond. In addition, bonding analyses demonstrate the bonding character of such triple-bonded RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR compounds should be represented as
PR compounds should be represented as  . That is to say, the In
. That is to say, the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond contains one traditional σ bond, one traditional π bond, and one donor–acceptor π bond. As a consequence, the theoretical findings strongly suggest the In
P triple bond contains one traditional σ bond, one traditional π bond, and one donor–acceptor π bond. As a consequence, the theoretical findings strongly suggest the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond in acetylene analogues (RIn
P triple bond in acetylene analogues (RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR) should be very weak.
PR) should be very weak.
I. Introduction
Compounds with an E14![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E14 (E14 = Si, Ge, Sn, and Pb) triple bond are a new area in the inorganic field.1,2 In 1999, in the group of Schwarz, the first example of an acetylene analogue was prepared and detected.3 In this compound, the C
E14 (E14 = Si, Ge, Sn, and Pb) triple bond are a new area in the inorganic field.1,2 In 1999, in the group of Schwarz, the first example of an acetylene analogue was prepared and detected.3 In this compound, the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si triple bond is kinetically stabilized by the halogen ligands (F and Cl). After this, several alkyne analogues, such as RSi
Si triple bond is kinetically stabilized by the halogen ligands (F and Cl). After this, several alkyne analogues, such as RSi![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiR,4 RGe
SiR,4 RGe![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) GeR,5 RSn
GeR,5 RSn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SnR,6 and RPb
SnR,6 and RPb![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PbR7 were synthesized and structurally characterized. Besides these homologous acetylene compounds that were detected experimentally, several heteronuclear systems were also predicted theoretically.8–10 These successful examples for synthesizing the acetylene analogues give us a hint as to whether it is possible to anticipate the stability of RE13
PbR7 were synthesized and structurally characterized. Besides these homologous acetylene compounds that were detected experimentally, several heteronuclear systems were also predicted theoretically.8–10 These successful examples for synthesizing the acetylene analogues give us a hint as to whether it is possible to anticipate the stability of RE13![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E15R (E13 = group 13 elements and E15 = group 15 elements)11,12 species based on the effects of substituents, since the RE13
E15R (E13 = group 13 elements and E15 = group 15 elements)11,12 species based on the effects of substituents, since the RE13![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E15R systems are isoelectronic to the RE14
E15R systems are isoelectronic to the RE14![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E14R compound from the valence electron viewpoint.
E14R compound from the valence electron viewpoint.
If fact, research on photochemical devices based on group 13-group 15 compound semiconductor electrodes has attracted tremendous attention over the past three decades due to their potential applications in solar energy apparatuses and the simplicity of manufacturing such electronic materials.13–26 In particular, InP (indium phosphide) based semiconductors are promising for high-speed electron, optoelectronic, and photovoltaic devices due to their superior material properties and the possibility of developing various kinds of materials with heterostructures.27 It is not surprising nowadays that different types of InP-based semiconductor nanowire apparatus containing field effect transistors,28 photodetectors,29 light-emitting devices, waveguides,30 and solar cells31 have been investigated using various types of heterostructures.32–35
Although InP has already been recognized as a useful semiconductor material, no research, including both experimental and theoretical studies, concerning molecules containing the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond has been carried out. The aim of this work is therefore to explore the possible existence of a triple-bonded In
P triple bond has been carried out. The aim of this work is therefore to explore the possible existence of a triple-bonded In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P molecule given adequate substituents. It is hoped the present studies on indium
P molecule given adequate substituents. It is hoped the present studies on indium![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) phosphorus triple-bonded molecules can open up a new inorganic field in the near future.
phosphorus triple-bonded molecules can open up a new inorganic field in the near future.
II. Results and discussion
(1) Small ligands on substituted RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) PR
PR
We first used quantum-mechanical methods to examine the relative stabilities of various kinds of triple-bonded RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR molecules and the corresponding double-bonded RIn
PR molecules and the corresponding double-bonded RIn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR species utilizing the small substituted groups (R = H, F, OH, CH3, and SiH3). Three kinds of density functional theory (DFT) have been utilized to investigate the potential energy surfaces of the unimolecular rearrangement reactions. The three DFT are M06-2X/Def2-TZVP, B3PW91/Def2-TZVP and B3LYP/LANL2DZ+dp. As a result, the computational results for the potential energy surfaces concerning the 1,2-migration reactions of the model molecule, RInPR (R = F, OH, H, CH3 and SiH3), are given in Fig. 1. From Fig. 1, one may find two kinds of 1,2-shift rearrangement reactions, i.e., RIn
PR species utilizing the small substituted groups (R = H, F, OH, CH3, and SiH3). Three kinds of density functional theory (DFT) have been utilized to investigate the potential energy surfaces of the unimolecular rearrangement reactions. The three DFT are M06-2X/Def2-TZVP, B3PW91/Def2-TZVP and B3LYP/LANL2DZ+dp. As a result, the computational results for the potential energy surfaces concerning the 1,2-migration reactions of the model molecule, RInPR (R = F, OH, H, CH3 and SiH3), are given in Fig. 1. From Fig. 1, one may find two kinds of 1,2-shift rearrangement reactions, i.e., RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR → TS1 → R2In
PR → TS1 → R2In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P: and RIn
P: and RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR → TS2 → :In
PR → TS2 → :In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR2. All three DFT calculated results demonstrate the triple-bonded RIn
PR2. All three DFT calculated results demonstrate the triple-bonded RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR species are neither theoretically nor kinetically stable on the intramolecular isomerization reaction surfaces. According to the present theoretical findings, it can be concluded that the experimental detections of the triple-bonded RIn
PR species are neither theoretically nor kinetically stable on the intramolecular isomerization reaction surfaces. According to the present theoretical findings, it can be concluded that the experimental detections of the triple-bonded RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR molecules bearing the small substituents should be unlikely.
PR molecules bearing the small substituents should be unlikely.
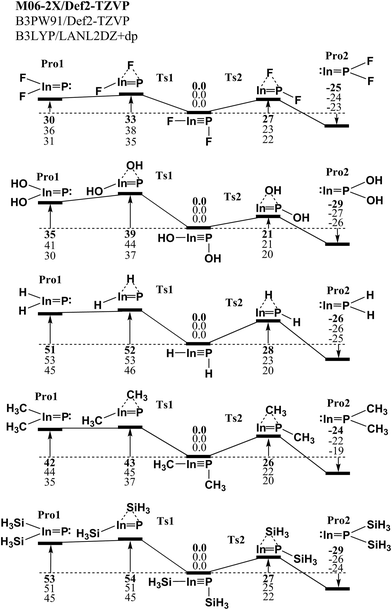 | ||
Fig. 1 The Relative Gibbs free energy surfaces for RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR (R = F, OH, H, CH3 and SiH3). These energies are in kcal mol−1 and are calculated at the M06-2X/Def2-TZVP, B3PW91/Def2-TZVP, and B3LYP/LANL2DZ+dp levels of theory. For details see the text and Table 1. PR (R = F, OH, H, CH3 and SiH3). These energies are in kcal mol−1 and are calculated at the M06-2X/Def2-TZVP, B3PW91/Def2-TZVP, and B3LYP/LANL2DZ+dp levels of theory. For details see the text and Table 1. | ||
Despite the theoretical observations given in Fig. 1 showing the triple-bonded RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR with small groups should be very difficult to form, we still examine the physical properties of such RIn
PR with small groups should be very difficult to form, we still examine the physical properties of such RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR species, whose data are collected in Table 1. From Table 1, the theoretical calculations estimate the In
PR species, whose data are collected in Table 1. From Table 1, the theoretical calculations estimate the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond distance (Å) should be in the range of 2.312–2.422, 2.303–2.412, and 2.337–2.459 for the M06-2X/Def2-TZVP, B3PW91/Def2-TZVP (in round brackets) and B3LYP/LANL2DZ+dp (in square brackets) methods, respectively. Experimentally, however, until now the In–P single bond length is reported 2.62 Å,36 which is slightly longer than the sum of the covalent radii (2.50 Å).37 In addition, all the optimized geometries demonstrate they prefer to adopt the bent structures with a vertical angle (∠In–P–R ≈ 90°), as shown in Scheme 1. The reason for having such structures can be attributed to the relativistic effect discussed earlier.38 More importantly, the three DFT calculations given in Table 1 always show the Wiberg Bond Index (WBI) of the indium–phosphorus bond is less than 2.0, meaning these RInPR species possessing the small ligands do not own the In
P triple bond distance (Å) should be in the range of 2.312–2.422, 2.303–2.412, and 2.337–2.459 for the M06-2X/Def2-TZVP, B3PW91/Def2-TZVP (in round brackets) and B3LYP/LANL2DZ+dp (in square brackets) methods, respectively. Experimentally, however, until now the In–P single bond length is reported 2.62 Å,36 which is slightly longer than the sum of the covalent radii (2.50 Å).37 In addition, all the optimized geometries demonstrate they prefer to adopt the bent structures with a vertical angle (∠In–P–R ≈ 90°), as shown in Scheme 1. The reason for having such structures can be attributed to the relativistic effect discussed earlier.38 More importantly, the three DFT calculations given in Table 1 always show the Wiberg Bond Index (WBI) of the indium–phosphorus bond is less than 2.0, meaning these RInPR species possessing the small ligands do not own the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond.
P triple bond.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR using the M06-2X/Def2-TZVP, B3PW91/Def2-TZVP (in round brackets) and B3LYP/LANL2DZ+dp (in square brackets) levels of theory
PR using the M06-2X/Def2-TZVP, B3PW91/Def2-TZVP (in round brackets) and B3LYP/LANL2DZ+dp (in square brackets) levels of theory
| R | F | OH | H | CH3 | SiH3 |
|---|---|---|---|---|---|
a The natural charge density on the central indium atom.b The natural charge density on the central phosphorus atom.c ΔEST (kcal mol−1) = E(triplet state for R–In) − E(singlet state for R–In).d ΔEST (kcal mol−1) = E(triplet state for R–P) − E(singlet state for R–P).e BE (kcal mol−1) = E(singlet state for R–P) + E(singlet state for R–In) − E(singlet for RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR).f The Wiberg bond index (WBI) for the In PR).f The Wiberg bond index (WBI) for the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P bond: see ref. 39. P bond: see ref. 39. |
|||||
In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P (Å) P (Å) |
2.413 | 2.422 | 2.312 | 2.330 | 2.313 |
| (2.402) | (2.412) | (2.303) | (2.323) | (2.311) | |
| [2.443] | [2.459] | [2.335] | [2.359] | [2.337] | |
| ∠R–In–P (°) | 179.8 | 178.5 | 179.2 | 176.3 | 176.6 |
| (178.0) | (177.3) | (179.7) | (178.3) | (177.2) | |
| [178.3] | [177.0] | [178.6] | [179.7] | [178.3] | |
| ∠In–P–R (°) | 96.54 | 99.53 | 84.95 | 102.3 | 94.76 |
| (98.80) | (101.6) | (84.30) | (104.0) | (97.59) | |
| [96.13] | [99.12] | [85.10] | [104.2] | [100.4] | |
| ∠R–P–In–R (°) | 180.0 | 179.8 | 177.3 | 178.2 | 179.7 |
| (180.0) | (179.7) | (179.9) | (179.5) | (179.2) | |
| [180.0] | [178.6] | [179.2] | [180.0] | [177.6] | |
| QIna | 1.3203 | 1.2598 | 1.0766 | 1.2088 | 0.9576 |
| (1.2181) | (1.1404) | (0.9760) | (1.0968) | (0.8590) | |
| [1.3909] | [1.3290] | [1.1458] | [1.2782] | [1.056] | |
| QPb | 0.054 | −0.030 | −0.7118 | −0.4567 | −0.8677 |
| (0.085) | (−0.031) | (−0.6597) | (−0.3983) | (−0.7972) | |
| [0.024] | [−0.008] | [−0.7054] | [−0.4721] | [−0.8762] | |
| ΔEST for In–Rc (kcal mol−1) | 84.09 | 72.79 | 87.38 | 45.18 | 32.63 |
| (86.60) | (74.05) | (86.73) | (46.44) | (35.77) | |
| [81.58] | [77.81] | [83.73] | [44.43] | [38.96] | |
| ΔEST for P–Rd (kcal mol−1) | −28.91 | −17.53 | −30.75 | −26.43 | −5.804 |
| (−33.35) | (−21.29) | (−35.49) | (−30.26) | (−8.678) | |
| [−31.76] | [−20.24] | [−33.16] | [−29.21] | [−14.46] | |
| HOMO–LUMO (kcal mol−1) | 166.5 | 154.0 | 254.0 | 142.8 | 207.7 |
| (122.9) | (111.9) | (212.0) | (104.4) | (158.4) | |
| [187.6] | [151.4] | [317.3] | [143.5] | [169.2] | |
| BEe (kcal mol−1) | 86.99 | 81.76 | 87.38 | 76.85 | 81.65 |
| (86.77) | (81.41) | (86.73) | (76.05) | (81.52) | |
| [91.57] | [92.41] | [83.73] | [77.81] | [93.90] | |
| WBIf | 1.356 | 1.344 | 1.551 | 1.494 | 1.476 |
| (1.373) | (1.360) | (1.581) | (1.524) | (1.510) | |
| [1.375] | [1.352] | [1.554] | [1.507] | [1.456] | |
(2) Large ligands on substituted R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) PR′
PR′
Since the above section concludes the RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR molecules bearing small substituents are unlikely to be stabilized from both a thermodynamic and kinetic viewpoint, we thus turn to use the bulkier substituents (R′) to attach to indium–phosphorus to stabilize such triple-bonded R′In
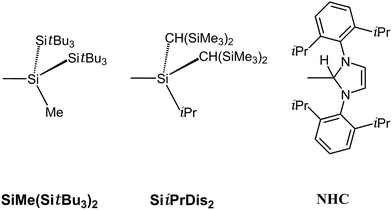
PR molecules bearing small substituents are unlikely to be stabilized from both a thermodynamic and kinetic viewpoint, we thus turn to use the bulkier substituents (R′) to attach to indium–phosphorus to stabilize such triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ compounds for the sake of being observed experimentally. As a result, three bulkier ligands (R′ = SiMe(SitBu3)2,40 SiiPrDis2,40 and NHC;41 see Scheme 2) are utilized in this work to study the effects of substituents on the stability of triple-bonded R′In
PR′ compounds for the sake of being observed experimentally. As a result, three bulkier ligands (R′ = SiMe(SitBu3)2,40 SiiPrDis2,40 and NHC;41 see Scheme 2) are utilized in this work to study the effects of substituents on the stability of triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules. Since the computed systems for the R′In
PR′ molecules. Since the computed systems for the R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ species possessing bulky ligands are so large, we thus use the B97-D3/LANL2DZ+dp42 level of theory to investigate both their chemical and physical behaviors.
PR′ species possessing bulky ligands are so large, we thus use the B97-D3/LANL2DZ+dp42 level of theory to investigate both their chemical and physical behaviors.
Again, we used the intramolecular 1,2-migration reaction to examine theoretically relative stabilities of the triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ compounds and its corresponding doubly bonded isomers (i.e., R′2In
PR′ compounds and its corresponding doubly bonded isomers (i.e., R′2In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P: and :In
P: and :In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR′2). See Scheme 3. The computational reaction enthalpies (i.e., ΔH1 and ΔH2) of Scheme 3 are collected in Table 2. It is not surprising to see the energy of the triple-bonded R′In
PR′2). See Scheme 3. The computational reaction enthalpies (i.e., ΔH1 and ΔH2) of Scheme 3 are collected in Table 2. It is not surprising to see the energy of the triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecule is apparently much lower than those of both doubly bonded isomers by at least 88.0 kcal mol−1, owing to steric overcrowding effects. Accordingly, the theoretical evidence strongly suggest the bulkier substituents can kinetically stabilize the triple-bonded R′In
PR′ molecule is apparently much lower than those of both doubly bonded isomers by at least 88.0 kcal mol−1, owing to steric overcrowding effects. Accordingly, the theoretical evidence strongly suggest the bulkier substituents can kinetically stabilize the triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules relative to the isomeric double-bonded R′2In
PR′ molecules relative to the isomeric double-bonded R′2In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P: and :In
P: and :In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR′2 species.
PR′2 species.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ at the B97-D3/LANL2DZ+dp level of theory. See also Schemes 2 and 3a
PR′ at the B97-D3/LANL2DZ+dp level of theory. See also Schemes 2 and 3a
| R′ | SiMe(SitBu3)2 | SiiPrDis2 | NHC |
|---|---|---|---|
a (1) The natural charge density on the central indium atom. (2) The natural charge density on the central phosphorus atom. (3) ΔEST (kcal mol−1) = E(triplet state for R′–In) − E(singlet state for R′–In). (4) ΔEST (kcal mol−1) = E(triplet state for R′–P) − E(singlet state for R′–P). (5) BE (kcal mol−1) = E(triplet state for R′–In) + E(triplet state for R′–P) − E(singlet for R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′). (6) See Scheme 3. (7) The Wiberg bond index (WBI) for the In PR′). (6) See Scheme 3. (7) The Wiberg bond index (WBI) for the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P bond: see ref. 39. P bond: see ref. 39. |
|||
In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P (Å) P (Å) |
2.362 | 2.337 | 2.315 |
| ∠R′–In–P (°) | 169.6 | 175.0 | 176.7 |
| ∠In–P–R′ (°) | 115.0 | 112.0 | 110.4 |
| ∠R′–In–P–R′ (°) | 177.5 | 172.47 | 176.1 |
| QIn | 1.1046 | 0.9396 | 0.9589 |
| QP | −0.9546 | −0.9363 | −0.6380 |
| ΔEST for In–R′ (kcal mol−1) | 33.93 | 29.53 | 21.84 |
| ΔEST for P–R′ (kcal mol−1) | −28.51 | −27.58 | −24.44 |
| HOMO–LUMO (kcal mol−1) | 74.96 | 72.41 | 77.66 |
| BE (kcal mol−1) | 86.51 | 84.30 | 106.2 |
| ΔH1 (kcal mol−1) | 92.07 | 90.08 | 96.14 |
| ΔH2 (kcal mol−1) | 88.35 | 89.18 | 90.43 |
| WBI | 2.263 | 2.251 | 2.174 |
According to the data from Table 2, we may use the valence-bond bonding model (Fig. 2) to interpret both bonding characters and geometrical structures of the triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules featuring the bulky substituents. First, the R′In
PR′ molecules featuring the bulky substituents. First, the R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ compound is split into two components, one is R′–In and the other is R′–P. According to the B3LYP calculations given in Table 2, it is known the R′–In fragment has the singlet ground state, while the R′–P moiety possesses the triplet ground state. As these DFT data reveal, the promotion energy from the singlet ground state to the triplet excited state for the R′–In fragment is estimated to be at least 22 kcal mol−1 and the promotion energy from triplet ground state to the singlet excited state for the R′–P fragment is evaluated to be at least 24 kcal mol−1. One may easily conclude it would be convenient for the former to jump to the triplet excited state (compared with the data shown in Table 1). As a result, the formation of the triple-bonded R′In
PR′ compound is split into two components, one is R′–In and the other is R′–P. According to the B3LYP calculations given in Table 2, it is known the R′–In fragment has the singlet ground state, while the R′–P moiety possesses the triplet ground state. As these DFT data reveal, the promotion energy from the singlet ground state to the triplet excited state for the R′–In fragment is estimated to be at least 22 kcal mol−1 and the promotion energy from triplet ground state to the singlet excited state for the R′–P fragment is evaluated to be at least 24 kcal mol−1. One may easily conclude it would be convenient for the former to jump to the triplet excited state (compared with the data shown in Table 1). As a result, the formation of the triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecule at the singlet ground state can be considered the combination of two triplet fragments, i.e., [R′–In]3 and [R′–P]3. As a consequence, from Fig. 2, the bonding scheme of the In
PR′ molecule at the singlet ground state can be considered the combination of two triplet fragments, i.e., [R′–In]3 and [R′–P]3. As a consequence, from Fig. 2, the bonding scheme of the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond in the R′In
P triple bond in the R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ species can re regarded as
PR′ species can re regarded as  , comprising one covalent σ bond, one covalent π bond and one donor–acceptor π bond. Fig. 2 shows the lone pair orbital of the R′–P moiety includes the valence s orbital of phosphorus. This, in turn, can reduce the overlap populations between the pure p–π orbital of indium and the lone pair orbital of phosphorus. Moreover, since the quantum numbers of the valence orbitals of phosphorus are quite different from those of indium, one may imagine the overlapping populations for both covalent σ bond and covalent π bond are small as well, unlike the case of the traditional C
, comprising one covalent σ bond, one covalent π bond and one donor–acceptor π bond. Fig. 2 shows the lone pair orbital of the R′–P moiety includes the valence s orbital of phosphorus. This, in turn, can reduce the overlap populations between the pure p–π orbital of indium and the lone pair orbital of phosphorus. Moreover, since the quantum numbers of the valence orbitals of phosphorus are quite different from those of indium, one may imagine the overlapping populations for both covalent σ bond and covalent π bond are small as well, unlike the case of the traditional C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond. As a consequence, one can foresee the In
C triple bond. As a consequence, one can foresee the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond should be weak. Indeed, as shown in Table 2, the WBI of the In
P triple bond should be weak. Indeed, as shown in Table 2, the WBI of the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond is estimated to be 2.16, 2.25, and 2.27 for (SiMe(SitBu3)2)–In
P triple bond is estimated to be 2.16, 2.25, and 2.27 for (SiMe(SitBu3)2)–In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P–(SiMe(SitBu3)2), (SiiPrDis2)–In
P–(SiMe(SitBu3)2), (SiiPrDis2)–In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P–(SiiPrDis2), and (NHC)–In
P–(SiiPrDis2), and (NHC)–In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P–(NHC), respectively, at the B97-D3/LANL2DZ+dp level of theory. Comparatively, the WBI of the C
P–(NHC), respectively, at the B97-D3/LANL2DZ+dp level of theory. Comparatively, the WBI of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond of acetylene is calculated to be 2.99 at the same level of theory.
C triple bond of acetylene is calculated to be 2.99 at the same level of theory.
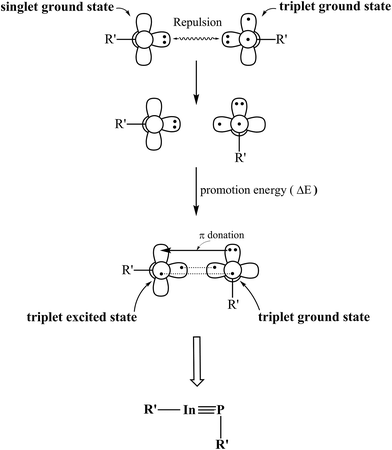 | ||
Fig. 2 The interaction model for the triply-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecule bearing the bulky substituents (R′). PR′ molecule bearing the bulky substituents (R′). | ||
Similar to the cases of the triple-bonded RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR with small ligands, the DFT computations in Table 2 predict the three R′In
PR with small ligands, the DFT computations in Table 2 predict the three R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules having bulkier substituents possess the In
PR′ molecules having bulkier substituents possess the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond distance of about 2.3 Å. Also, the calculations anticipate their structures all choose the bent geometry with the bond angle ∠In–P–R′ being closed to 110°. That is to say, the geometrical conformations of the triple-bonded R′In
P triple bond distance of about 2.3 Å. Also, the calculations anticipate their structures all choose the bent geometry with the bond angle ∠In–P–R′ being closed to 110°. That is to say, the geometrical conformations of the triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules featuring the bulky ligands are quite similar to those done earlier, as schematically illustrated in Scheme 1. The reason for having such a perpendicular angle can be, again, attributed to the relativistic effects38 as discussed earlier.
PR′ molecules featuring the bulky ligands are quite similar to those done earlier, as schematically illustrated in Scheme 1. The reason for having such a perpendicular angle can be, again, attributed to the relativistic effects38 as discussed earlier.
To obtain further insight into the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond of the R′In
P triple bond of the R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ species studied in this work, both the natural bond orbital (NBO)37 and the natural resonance theory (NRT)43 analyses were calculated, and are given in Table 3. As discussed earlier, the WBI and the NRT of three R′In
PR′ species studied in this work, both the natural bond orbital (NBO)37 and the natural resonance theory (NRT)43 analyses were calculated, and are given in Table 3. As discussed earlier, the WBI and the NRT of three R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules are all slightly above 2. That is, WBI = 2.17–2.26 and NRT = 2.13–2.25. All these values strongly imply the studied R′In
PR′ molecules are all slightly above 2. That is, WBI = 2.17–2.26 and NRT = 2.13–2.25. All these values strongly imply the studied R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules possessing the bulkier substituents have a weaker triple bond, which is quite different from acetylene with the traditional C
PR′ molecules possessing the bulkier substituents have a weaker triple bond, which is quite different from acetylene with the traditional C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond, whose WBI was calculated to be 2.99. Moreover, the NBO calculations summarized in Table 3 show for three R′In
C triple bond, whose WBI was calculated to be 2.99. Moreover, the NBO calculations summarized in Table 3 show for three R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ compounds both σ and π bonds are strongly polarized towards the phosphorus atom. For instance, in the case of (SiMe(SitBu3)2)–In
PR′ compounds both σ and π bonds are strongly polarized towards the phosphorus atom. For instance, in the case of (SiMe(SitBu3)2)–In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P–(SiMe(SitBu3)2), its σ bond contain 69.8% (P), while its π bonds involve 85.2(π⊥)% (P) and 85.1(π‖)% (P). Further, its NBO analysis of the In
P–(SiMe(SitBu3)2), its σ bond contain 69.8% (P), while its π bonds involve 85.2(π⊥)% (P) and 85.1(π‖)% (P). Further, its NBO analysis of the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P bonding interaction was computed to be as follows: π(In
P bonding interaction was computed to be as follows: π(In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P) = 0.3845(5s5p99.99)In + 0.9231(3s3p99.99)P, again revealing the dominant interaction between the (SiMe(SitBu3)2)–In and the (SiMe(SitBu3)2)–P units arises from the 5p(In) ← 3p(P) donation. Its optimized wave functions representing the In
P) = 0.3845(5s5p99.99)In + 0.9231(3s3p99.99)P, again revealing the dominant interaction between the (SiMe(SitBu3)2)–In and the (SiMe(SitBu3)2)–P units arises from the 5p(In) ← 3p(P) donation. Its optimized wave functions representing the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P π bonding orbitals are shown in Fig. 3.
P π bonding orbitals are shown in Fig. 3.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules that feature ligands (R′ = SiMe(SitBu3)2, SiiPrDis2, and NHC) at the B97-D3/LANL2DZ+dp level of theorya,b
PR′ molecules that feature ligands (R′ = SiMe(SitBu3)2, SiiPrDis2, and NHC) at the B97-D3/LANL2DZ+dp level of theorya,b
R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ PR′ |
WBI | NBO analysis | NRT analysis | |||
|---|---|---|---|---|---|---|
| Occupancy | Hybridization | Polarization | Total/covalent/ionic | Resonance weight | ||
a The value of the Wiberg bond index (WBI) for the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P bond and the occupancy of the corresponding σ and π bonding NBO (see ref. 37).b NRT; see ref. 43. P bond and the occupancy of the corresponding σ and π bonding NBO (see ref. 37).b NRT; see ref. 43. |
||||||
| R′ = SiMe(SitBu3)2 | 2.26 | σ: 1.82 | σ: 0.5492 In (sp0.85) + 0.8357 P (sp16.18) | 30.16% (In) 69.84% (P) | 2.24/1.66/0.58 | In–P: 6.53% |
| π⊥: 1.86 | π⊥: 0.3845 In (sp99.99) + 0.9231 P (sp99.99) | 14.78% (In) 85.22% (P) | In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P: 58.37% P: 58.37% |
|||
| π‖: 1.90 | π‖: 0.3856 In (sp99.99) + 0.9227 P (sp99.99) | 14.87% (In) 85.13% (P) | In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P: 35.10% P: 35.10% |
|||
| R′ = SiiPrDis2 | 2.25 | σ: 1.95 | σ: 0.4530 In (sp1.29) + 0.8915 P (sp0.97) | 20.52% (In) 79.48% (P) | 2.25/1.84/0.41 | In–P: 8.28% |
| π⊥: 1.92 | π⊥: 0.5362 In (sp1.09) + 0.8441 P (sp5.75) | 28.75% (In) 71.25% (P) | In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P: 67.75% P: 67.75% |
|||
| π‖: 1.91 | π‖: 0.4330 In (sp99.99) + 0.9014 P (sp99.99) | 18.75% (In) 81.25% (P) | In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P: 23.97% P: 23.97% |
|||
| R′ = NHC | 2.17 | σ: 1.95 | σ: 0.7060 In (sp0.07) + 0.7082 P (sp20.04) | 49.85% (In) 50.15% (P) | 2.13/1.69/0.44 | In–P: 8.53% |
| π⊥: 1.91 | π⊥: 0.4289 In (sp33.04) + 0.9111 P (sp99.72) | 14.14% (In) 85.86% (P) | In![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P: 76.52% P: 76.52% |
|||
| π‖: 1.92 | π‖: 0.4117 In (sp99.99) + 0.9113P (sp99.99) | 16.95% (In) 83.05% (P) | In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P: 14.95% P: 14.95% |
|||
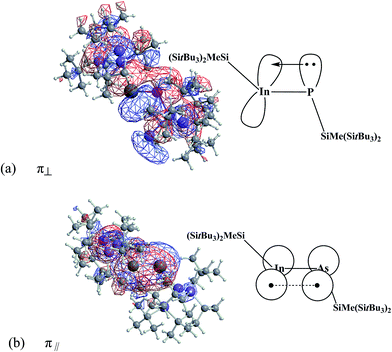 | ||
Fig. 3 The natural In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P π bonding orbitals ((a) and (b)) for (SiMe(SitBu3)2)–In P π bonding orbitals ((a) and (b)) for (SiMe(SitBu3)2)–In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P–(SiMe(SitBu3)2). Also see Fig. 2. P–(SiMe(SitBu3)2). Also see Fig. 2. | ||
Besides these, it is well established NHC is a strong donating group.41 As a result, its excellent application as a substituent for stabilizing transition-metal complexes has been unusually successful in organometallic and inorganic chemistry.41 Likewise, one may imagine the NHC ligand utilizes its lone pair orbital to donate to the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P moiety. That is to say, both the NHC → In and NHC → P donating bonds can strongly stabilize the In
P moiety. That is to say, both the NHC → In and NHC → P donating bonds can strongly stabilize the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond. Accordingly, the (NHC)–In
P triple bond. Accordingly, the (NHC)–In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P–(NHC) molecule can be considered the representation of (NHC) → In
P–(NHC) molecule can be considered the representation of (NHC) → In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P ← (NHC), which should be an exciting target for future experimental synthesis and structural characterization.
P ← (NHC), which should be an exciting target for future experimental synthesis and structural characterization.
III. Conclusion
In conclusion, the above theoretical evidence strongly support the concept both electronic and steric effects can greatly influence the relative stability of compounds involving an In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond. The present theoretical investigations indicate the small organic groups, regardless of electronegativities, cannot efficiently stabilize the In
P triple bond. The present theoretical investigations indicate the small organic groups, regardless of electronegativities, cannot efficiently stabilize the In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond. Only the bulkier substituents (R′), in particular for the strong electron-donating groups (such as NHC),41 can successfully stabilize such an In
P triple bond. Only the bulkier substituents (R′), in particular for the strong electron-donating groups (such as NHC),41 can successfully stabilize such an In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond. Besides these, the theoretical findings also reveal the bonding characters for the triple-bonded R′In
P triple bond. Besides these, the theoretical findings also reveal the bonding characters for the triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ species with the bulkier ligands can be represented as
PR′ species with the bulkier ligands can be represented as  . Additionally, the theoretical observations demonstrate the effects come from the lone pair of phosphorus elements involving the valence s character and the different radii of the valence p orbitals in the indium and phosphorus atoms can strongly influence the chemical bonding between both elements.44 As a consequence, the present theoretical results conclude once the triple-bonded R′In
. Additionally, the theoretical observations demonstrate the effects come from the lone pair of phosphorus elements involving the valence s character and the different radii of the valence p orbitals in the indium and phosphorus atoms can strongly influence the chemical bonding between both elements.44 As a consequence, the present theoretical results conclude once the triple-bonded R′In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR′ molecules featuring the bulkier groups are stabilized, their In
PR′ molecules featuring the bulkier groups are stabilized, their In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bonds should be very weak.45
P triple bonds should be very weak.45
It is hoped that the results of experimental synthesis and structural characterization will confirm these predictions.
Acknowledgements
The authors are grateful to the National Center for High-Performance Computing of Taiwan for generous amounts of computing time, and the Ministry of Science and Technology of Taiwan for the financial support. Special thanks are also due to reviewers 1 and 2 for very help suggestions and comments. Special thanks are also due to reviewers 1 and 2 for very help suggestions and comments.References
- For reviews, see: (a) P. P. Power, Chem. Rev., 1999, 99, 3463 CrossRef CAS PubMed; (b) P. Jutzi, Angew. Chem., Int. Ed., 2000, 39, 3797 CrossRef CAS; (c) M. Weidenbruch, J. Organomet. Chem., 2002, 646, 39 CrossRef CAS; (d) P. P. Power, Chem. Commun., 2003, 2091 RSC; (e) M. Weidenbruch, Angew. Chem., Int. Ed., 2004, 43, 2 CrossRef; (f) P. P. Power, Appl. Organomet. Chem., 2005, 19, 488 CrossRef CAS; (g) M. Lein, A. Krapp and G. J. Frenking, Am. Chem. Soc., 2005, 127, 6290 CrossRef CAS PubMed and references therein (h) A. Sekiguchi, M. Ichinohe and R. Kinjo, Bull. Chem. Soc. Jpn., 2006, 79, 825 CrossRef CAS; (i) P. P. Power, Organometallics, 2007, 26, 4362 CrossRef CAS and references therein (j) A. Sekiguchi, Pure Appl. Chem., 2008, 80, 447 CrossRef CAS; (k) A. Sekiguchi, R. Kinjo and M. Ichinohe, Synth. Met., 2009, 159, 773 CrossRef CAS; (l) R. C. Fischer and P. P. Power, Chem. Rev., 2010, 110, 3877 CrossRef CAS PubMed; (m) Y. Peng, R. C. Fischer, W. A. Merrill, J. Fischer, L. Pu, B. D. Ellis, J. C. Fettinger, R. H. Herber and P. P. Power, Chem. Sci., 2010, 1, 461 RSC; (n) T. Sasamori, J. S. Han, K. Hironaka, N. Takagi, S. Nagase and N. Tokitoh, Pure Appl. Chem., 2010, 82, 603 CrossRef CAS.
- For comprehensive study, for example, see: (a) A. Bino, M. Ardon and E. Shirman, Science, 2005, 308, 234–235 CrossRef CAS PubMed; (b) P. Su, J. Wu, J. Gu, W. Wu, S. Shaik and P. C. Hiberty, J. Chem. Theory Comput., 2011, 7, 121–130 CrossRef CAS PubMed; (c) E. Ploshnik, D. Danovich, P. C. Hiberty and S. Shaik, J. Chem. Theory Comput., 2011, 7, 955–968 CrossRef CAS PubMed; (d) I. Seidu, M. Seth and T. Ziegler, Inorg. Chem., 2013, 52, 8378 CrossRef CAS PubMed; (e) D. Danovich, A. Bino and S. Shaik, J. Phys. Chem. Lett., 2013, 4, 58–64 CrossRef CAS PubMed.
- For C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si, see:
(a) M. Karni, Y. Apeloig, D. Schröder, W. Zummack, R. Rabezzana and H. Schwarz, Angew. Chem., Int. Ed., 1999, 38, 331 CrossRef and related references therein
(b) D. Danovich, F. Ogliaro, M. Karni, Y. Apeloig, D. L. Cooper and S. Shaik, Angew. Chem., Int. Ed., 2001, 40, 4023 CrossRef CAS;
(c) D. Gau, T. Kato, N. Saffon-Merceron, A. D. Cozar, F. P. Cossio and A. Baceiredo, Angew. Chem., Int. Ed., 2010, 49, 6585 CrossRef CAS PubMed;
(d) N. Lühmann and T. Müller, Angew. Chem., Int. Ed., 2010, 49, 10042 CrossRef PubMed.
Si, see:
(a) M. Karni, Y. Apeloig, D. Schröder, W. Zummack, R. Rabezzana and H. Schwarz, Angew. Chem., Int. Ed., 1999, 38, 331 CrossRef and related references therein
(b) D. Danovich, F. Ogliaro, M. Karni, Y. Apeloig, D. L. Cooper and S. Shaik, Angew. Chem., Int. Ed., 2001, 40, 4023 CrossRef CAS;
(c) D. Gau, T. Kato, N. Saffon-Merceron, A. D. Cozar, F. P. Cossio and A. Baceiredo, Angew. Chem., Int. Ed., 2010, 49, 6585 CrossRef CAS PubMed;
(d) N. Lühmann and T. Müller, Angew. Chem., Int. Ed., 2010, 49, 10042 CrossRef PubMed. - For Si
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si, see:
(a) A. Sekiguchi, R. Kinjo and M. Ichinohe, Science, 2004, 305, 1755 CrossRef CAS PubMed;
(b) N. Wiberg, S. K. Vasisht, G. Fischer and P. Z. Mayer, Z. Anorg. Allg. Chem., 2004, 630, 1823 CrossRef CAS;
(c) T. Sasamori, K. Hironaka, T. Sugiyama, N. Takagi, S. Nagase, Y. Hosoi, Y. Furukawa and N. Tokitoh, J. Am. Chem. Soc., 2008, 130, 13856 CrossRef CAS PubMed.
Si, see:
(a) A. Sekiguchi, R. Kinjo and M. Ichinohe, Science, 2004, 305, 1755 CrossRef CAS PubMed;
(b) N. Wiberg, S. K. Vasisht, G. Fischer and P. Z. Mayer, Z. Anorg. Allg. Chem., 2004, 630, 1823 CrossRef CAS;
(c) T. Sasamori, K. Hironaka, T. Sugiyama, N. Takagi, S. Nagase, Y. Hosoi, Y. Furukawa and N. Tokitoh, J. Am. Chem. Soc., 2008, 130, 13856 CrossRef CAS PubMed. - For Ge
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Ge, see:
(a) M. Stender, A. D. Phillips, R. J. Wright and P. P. Power, Angew. Chem., Int. Ed., 2002, 41, 1785 CrossRef CAS;
(b) M. Stender, A. D. Phillips and P. P. Power, Chem. Commun., 2002, 1312 RSC;
(c) L. Pu, A. D. Phillips, A. F. Richards, M. Stender, R. S. Simons, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 2003, 125, 11626 CrossRef CAS PubMed;
(d) Y. Sugiyama, T. Sasamori, Y. Hosoi, Y. Furukawa, N. Takagi, S. Nagase and N. Tokitoh, J. Am. Chem. Soc., 2006, 128, 1023 CrossRef CAS PubMed;
(e) G. H. Spikes and P. P. Power, Chem. Commun., 2007, 85 RSC.
Ge, see:
(a) M. Stender, A. D. Phillips, R. J. Wright and P. P. Power, Angew. Chem., Int. Ed., 2002, 41, 1785 CrossRef CAS;
(b) M. Stender, A. D. Phillips and P. P. Power, Chem. Commun., 2002, 1312 RSC;
(c) L. Pu, A. D. Phillips, A. F. Richards, M. Stender, R. S. Simons, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 2003, 125, 11626 CrossRef CAS PubMed;
(d) Y. Sugiyama, T. Sasamori, Y. Hosoi, Y. Furukawa, N. Takagi, S. Nagase and N. Tokitoh, J. Am. Chem. Soc., 2006, 128, 1023 CrossRef CAS PubMed;
(e) G. H. Spikes and P. P. Power, Chem. Commun., 2007, 85 RSC. - For Sn
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Sn, see: A. D. Phillips, R. J. Wright, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 2002, 124, 5930 CrossRef CAS PubMed.
Sn, see: A. D. Phillips, R. J. Wright, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 2002, 124, 5930 CrossRef CAS PubMed. - For Pb
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Pb, see: L. Pu, B. Twamley and P. P. Power, J. Am. Chem. Soc., 2000, 122, 3524 CrossRef CAS.
Pb, see: L. Pu, B. Twamley and P. P. Power, J. Am. Chem. Soc., 2000, 122, 3524 CrossRef CAS. - For C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Ge, see:
(a) H.-Y. Liao, M.-D. Su and S.-Y. Chu, Chem. Phys. Lett., 2001, 341, 122 CrossRef CAS;
(b) P.-C. Wu and M.-D. Su, Dalton Trans., 2011, 40, 4253 RSC.
Ge, see:
(a) H.-Y. Liao, M.-D. Su and S.-Y. Chu, Chem. Phys. Lett., 2001, 341, 122 CrossRef CAS;
(b) P.-C. Wu and M.-D. Su, Dalton Trans., 2011, 40, 4253 RSC. - For C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Sn, see: P.-C. Wu and M.-D. Su, Inorg. Chem., 2011, 50, 6814 CrossRef CAS PubMed.
Sn, see: P.-C. Wu and M.-D. Su, Inorg. Chem., 2011, 50, 6814 CrossRef CAS PubMed. - For C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Pb, see: P.-C. Wu and M.-D. Su, Organometallics, 2011, 30, 3293 CrossRef CAS.
Pb, see: P.-C. Wu and M.-D. Su, Organometallics, 2011, 30, 3293 CrossRef CAS. - For B
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, see:
(a) P. Paetzold, Adv. Inorg. Chem., 1987, 31, 123 CrossRef CAS;
(b) P. Paetzold, in Boron Chemistry, Proceedings of the 6th International Meeting on Boron Chemistry, ed. HermanekS., World Scientific, Singapore, 1987, p. 446 Search PubMed;
(c) P. Paetzold, Pure Appl. Chem., 1991, 63, 345 CrossRef CAS;
(d) P. Paetzold, Phosphorus, Sulfur Silicon, 1994, 93–94, 39 CrossRef CAS.
N, see:
(a) P. Paetzold, Adv. Inorg. Chem., 1987, 31, 123 CrossRef CAS;
(b) P. Paetzold, in Boron Chemistry, Proceedings of the 6th International Meeting on Boron Chemistry, ed. HermanekS., World Scientific, Singapore, 1987, p. 446 Search PubMed;
(c) P. Paetzold, Pure Appl. Chem., 1991, 63, 345 CrossRef CAS;
(d) P. Paetzold, Phosphorus, Sulfur Silicon, 1994, 93–94, 39 CrossRef CAS. - For Ga
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and In
N and In![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, see: R. J. Wright, A. D. Phillips, T. L. Allen, W. H. Fink and P. P. Power, J. Am. Chem. Soc., 2003, 125, 1694 CrossRef CAS PubMed.
N, see: R. J. Wright, A. D. Phillips, T. L. Allen, W. H. Fink and P. P. Power, J. Am. Chem. Soc., 2003, 125, 1694 CrossRef CAS PubMed. - P. O'Brien and M. Green, Chem. Commun., 1998, 2459 Search PubMed.
- H. Fu and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 24, 15064 CrossRef.
- R. F. Hicks, K. Raghavachari, Q. Fu, L. Li, C. H. Li and D. C. Law, J. Am. Chem. Soc., 2002, 124, 15119 CrossRef.
- B. Johansson, M. C. Qian, M. Gothelid and S. Mirbt, Phys. Rev. B, 2003, 3, 35308 Search PubMed.
- J. W. Archer and M. G. Shen, Mic. Opt. Tec. Lett., 2004, 2, 92 CrossRef.
- J. L. Blackburn, D. C. Selmarten, R. J. Ellingson, M. Jones and A. J. Nozik, J. Phys. Chem. B, 2005, 109, 2625 CrossRef CAS PubMed.
- J. W. Archer and M. G. Shen, Mic. Opt. Tec. Lett., 2006, 2, 338 CrossRef.
- G. Shen, Y. Bando, B. Liu, C. Tang and D. Golberg, J. Phys. Chem. B, 2006, 110, 20129 CrossRef CAS PubMed.
- W. E. Buhro and F. Wang, J. Am. Chem. Soc., 2007, 129, 14381 CrossRef PubMed.
- M. M. G. Alemany, J. R. Chelikowsky, X. Huang, M. L. Tiago and L. J. Gallego, Nano Lett., 2007, 7, 1878 CrossRef CAS.
- A. Ivanisevic and H. H. Park, J. Phys. Chem. C, 2007, 111, 3710 Search PubMed.
- K. Ikejiri, Y. Kitauchi, K. Tomioka, J. Motohisa and F. Takashi, Nano Lett., 2011, 11, 4314 CrossRef CAS PubMed.
- F. Ou, B. Buchholz, F. Yi, C. Hseih, R. P. H. Chang and S.-T. Ho, ACS Appl. Mater. Interfaces, 2011, 3, 1341 CAS.
- S. Lee, E. B. Song, K. L. Wang, C. S. Yoon, Y. Shon and T. W. Kang, J. Phys. Chem. C, 2011, 115, 23564 CAS.
- K. Ikejiri, Y. Kitauchi, K. Tomioka, J. Motohisa and T. Fukui, Nano Lett., 2011, 11, 4314 CrossRef CAS PubMed.
- X. Duan, Y. Huang, Y. Cui, J. Wang and C. M. Lieber, Nature, 2001, 409, 66 CrossRef CAS PubMed.
- J. Wang, M. S. Gudiksen, X. Duan and Y. Cui, Science, 2001, 293, 1455 CrossRef CAS PubMed.
- Y. Ding, J. Motohisa, B. Hua, S. Hara and T. Fukui, Nano Lett., 2007, 7, 3598 CrossRef CAS.
- H. Goto, K. Nosaki, K. Tomioka, S. Hara, K. Hiruma, J. Motohisa and T. Fukui, Appl. Phys. Express, 2009, 2, 5004 Search PubMed.
- E. D. Minot, F. Kelkensberg, M. V. Kouwen, J. A. V. Dam, L. P. Kouwenhoven, V. Zwiller, M. T. Borgstr€om, O. Wunnicke, M. A. Verheijen and E. P. A. M. Bakkers, Nano Lett., 2007, 7, 367 CrossRef CAS PubMed.
- A. Fuhrer, L. E. Fr€oberg, J. N. Pedersen, M. W. Larsson, A. Wacker, M.-E. Pistol and L. Samuelson, Nano Lett., 2007, 7, 243 CrossRef CAS PubMed.
- V. Zwiller, N. Akopian, M. V. Weert, M. V. Kouwen, U. Perinetti, L. Kouwenhoven, R. Algra, J. Gomez Rivas, E. Bakkers, G. Patriarche, L. Liu, J.-C. Harmand, Y. Kobayashi and J. Motohisa, C. R. Phys., 2008, 9, 804 CrossRef CAS.
- P. Mohan, J. Motohisa and T. Fukui, Appl. Phys. Lett., 2006, 88, 133105 CrossRef.
- T. Douglas and K. H. Theopold, Inorg. Chem., 1991, 30, 594 CrossRef CAS.
- J. Emsley, in The Elements, Clarendon Press, Oxford, 2nd edn, 1991 Search PubMed.
- It is known that valence s orbital of phosphorus is more strongly contracted than its valence p orbitals. As a result, the valence s and p orbitals of phosphorus overlap less to form strong hybrid orbitals. One may call such a phenomenon as the “orbital non-hybridization effect” or the “inert s-pair effect”. See: (a) P. Pykk and J.-P. Desclaux, Acc. Chem. Res., 1979, 12, 276 CrossRef; (b) W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 23, 272 CrossRef; (c) P. Pykk, Chem. Rev., 1988, 88, 563 CrossRef; (d) P. Pyykk, Chem. Rev., 1997, 97, 597 CrossRef.
- The Wiberg bond index, which is used to screen atom pairs for the possible bonding in the natural bonding orbital (NBO) search, are performed with the NBO program. For details, see: http://www.chem.wisc.edu/%7Enbo5. Also, see: K. B. Wiberg, Tetrahedron, 1968, 1083 CrossRef CAS; A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1998, 88, 899 CrossRef.
- (a) K. Kobayashi and S. Nagase, Organometallics, 1997, 16, 2489 CrossRef CAS; (b) K. Kobayashi, N. Takagi and S. Nagase, Organometallics, 2001, 20, 234 CrossRef CAS; (c) N. Takagi and S. Nagase, Organometallics, 2001, 20, 5498 CrossRef CAS.
- The full name is N-heterocyclic carbene. For comprehensive reviews, see: (a) Coord. Chem. Rev. 2007, 251, 595–895 Search PubMed; (b) F. E. Hahn, Angew. Chem., Int. Ed., 2006, 45, 1348 CrossRef CAS PubMed; (c) F. E. Hahn and M. C. Jahnke, Angew. Chem., Int. Ed., 2008, 47, 3122 CrossRef CAS PubMed; (d) Chem. Rev. 2009, 109(8), 3209–3884 Search PubMed; (e) Eur. J. Inorg. Chem. 2009, 1663–2007 Search PubMed; (f) Dalton Trans., 2009, 6873–7316 Search PubMed; (g) D. Martin, M. Melaimi, M. Soleihavoup and G. Bertrand, Organometallics, 2011, 30, 5304 CrossRef CAS PubMed.
- (a) S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211 CrossRef CAS; (b) S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed; (c) D. J. Liptrot and P. P. Power, Nat. Rev. Chem., 2017, 1, 4 CrossRef.
- (a) E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 593 CrossRef CAS; (b) E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 610 CrossRef CAS; (c) E. D. Glendening, J. K. Badenhoop and F. Weinhold, J. Comput. Chem., 1998, 19, 628 CrossRef CAS.
- The most fundamental difference between indium and phosphorus elements lies in their covalent radii (1.50 Å and 106 Å, respectively). Moreover, the valence electrons for the indium and phosphorus atoms are 5s25p1 and 3s23p2, respectively. Therefore, the above information strongly suggests that the overlap populations between indium and phosphorus should be small. Indeed, our computational results given in Tables 1 and 2 demonstrate that the In
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond in such an acetylene analogues (RIn
P triple bond in such an acetylene analogues (RIn![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) PR) is really very weak.
PR) is really very weak. - After submitting this manuscript, one reviewer suggested some useful references, which are related to this work. See: (a) M. Rubin, A. Trofimov and V. Gevorgyan, J. Am. Chem. Soc., 2005, 127, 10243 CrossRef CAS PubMed; (b) O. V. Sizova, L. V. Skripnikov, A. Y. Sokolov and V. V. Sizov, Int. J. Quantum Chem., 2009, 109, 2581 CrossRef CAS; (c) F. Billes, I. Ziegler and H. Mikosch, Struct. Chem., 2015, 26, 1703 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra01295k |
| This journal is © The Royal Society of Chemistry 2017 |