Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermal wave: from nonlocal continuum to molecular dynamics†
A. H. Akbarzadeh *a,
Y. Cuib and
Z. T. Chenb
*a,
Y. Cuib and
Z. T. Chenb
aDepartment of Bioresource Engineering, McGill University, Island of Montreal, QC H9X 3V9, Canada. E-mail: hamid.akbarzadeh@mcgill.ca; Fax: +1 514 398 7990; Tel: +1 514 398 7680
bDepartment of Mechanical Engineering, University of Alberta, Edmonton, AB T6G 2G8, Canada
First published on 28th February 2017
Abstract
It is well known that the continuum model of Fourier's law of heat conduction violates the relativity theory, admits an instantaneous thermal response, and assumes a quasi-equilibrium thermodynamic condition. Transient heat transport, however, is a non-equilibrium phenomenon with a finite thermal wave speed for applications involving very low temperatures, extremely high temperature gradients, and ballistic heat transfers. Hyperbolic and phase-lag heat conduction models have enabled detection of the finite thermal wave speed in heat transport. To accommodate effects of thermomass and size-dependency of thermophysical properties on nano/microscale heat transport and to remove the theoretical singularity of temperature gradients across the thermal wavefront, a nonlocal, fractional-order, three-phase-lag heat conduction is introduced. The model is capable of simulating heat conduction phenomena in multiple spatio-temporal scales. To confirm the existence of thermal waves in nano/microscale heat transport, a molecular dynamics simulation is implemented for the heat transfer within a nanoscale copper slab. Correlating thermal responses in continuum and atomistic scales sheds light on the effect of length scale, fractional order, and phase-lags in multiscale heat transport. The multiscale simulation is of practical importance for microelectromechanical system design, photothermal techniques, and ultrafast laser-assisted processing of advanced materials.
1. Introduction
Advances in ultrafast laser-assisted manufacturing technology have enabled the fabrication of miniaturized nano/microscale devices for electronics, optics, medicine, and energy applications. Electrons and lattices, however, are not in an equilibrium state during ultrafast laser processing of metals. A non-equilibrium heat transfer model is required instead of the classical phenomenological Fourier heat conduction to evaluate the temperature rise during laser-assisted manufacturing.1,2 Laser material processing has also opened a new horizon for developing ultralight architected materials with unprecedented multifunctional properties in multiple scales (nano/micro to macro) for heat exchanging, thermal insulating, shock damping, and current collecting.3–6 Due to the broad range of applications of these types of advanced architected materials, the advanced materials could experience very low temperature or extremely high temperature gradients for which a precise heat transport model should be considered to capture temperature rise from thermal wave propagation.7,8 In addition, novel technologies like dip-in 3D direct-laser-writing optical lithography are capable of manufacturing nano/micro-architected materials in which physical properties (e.g. elastic modulus, thermal conductivity, and electrical permeability) become size-dependent, particularly for nanoscale materials.9,10 The interaction of energy carriers with domain boundaries for nanoscale devices is more pronounced than macroscale devices, leading to a lower thermal conductivity compared to the bulk value.9,11,12 This fact implies the necessity of applying a nonlocal heat transfer model for nano-devices to accommodate the contribution of thermomass and phonon scattering in heat transport. Nanomaterials with characteristic length and time comparable to the phonon mean free path and phonon relaxation time reveal phonon propagation in a wave form and not in a diffusive form found in conventional heat transport phenomena;13,14 for instance, Monte Carlo simulation has shown the thermal wave in phonon ballistic transport regime for nanofilms and graphene sheets.15,16 To better comprehend the simulation methodologies for thermal wave propagation, we first review alternative continuum heat conduction models and then introduce a new heat transport analysis through the molecular dynamics (MD) simulation.The earliest heat conduction model is the empirical Fourier's law,17 which assumes the following linear relation between heat flux (![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) and temperature gradient (
) and temperature gradient (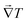 ) through thermal conductivity (k):
) through thermal conductivity (k):
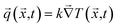 | (1) |
Because of the simplicity of Fourier's law, it has been widely used for a broad range of engineering applications. Nonetheless, Fourier's law results in a parabolic-type heat conduction equation with an infinite speed for the conductive heat transport, which contradicts the relativity theory.18 In reality, the applicability of Fourier's law for ultra-small spatial and temporal heat transport is controversial;19 experiments have reported the violation of nano/microscale heat conduction from Fourier's law. To eradicate this contradiction, Cattaneo and Vernotte (C–V)20,21 presented the first non-Fourier heat conduction theory by introducing thermal relaxation time (τCV):
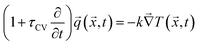 | (2) |
The C–V model leads to a hyperbolic-type heat conduction equation that predicts the experimentally proven thermal wave in heat transport. The model, however, lacks a physical basis, violates the second-law of thermodynamics, and cannot accurately describe the experimental data of heat transport.22–24 In addition, the C–V model of heat conduction overlooks the effects of microstructure on the heat transport process. To consider the non-equilibrium thermodynamics process of heat transport during the ultrafast laser heating and micro-macro interactions of heat carriers, a hyperbolic, two-step, phenomenological model was derived by Qiu and Tien25,26 by solving the Boltzmann equation. The model is appropriate for femto/picosecond laser heating since it considers three mechanisms of laser energy absorption by electrons, the transport of energy by electrons, and heating of the lattice by electron-lattice interactions. For ultrafast heating processes, Tzou27 presented a unified dual-phase-lag (DPL) heat conduction model which accounts for the microscale temporal and spatial effects of heat transport via the introduction of phase-lags of heat flux τq and temperature gradient τT:
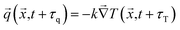 | (3) |
The phase-lags, τq and τT, are positive values and intrinsic properties of the material. The phase-lag of heat flux can be interpreted as the time delay due to the fast transient effect of thermal inertia, while the phase-lag of the temperature gradient represents the effect of phonon–electron interactions and phonon scattering during ultrafast heat transfer.28 Depending on the value of phase-lags, alternative orders of Taylor series expansion can be made to provide a series of DPL heat conduction models.29 Extending the thermoelastic model introduced by Green–Naghdi,30 Choudhuri31 proposed a three-phase-lag heat (TPL) conduction theory. The TPL heat conduction theory encompasses all the aforementioned non-Fourier heat conduction models by introducing the phase-lag of thermal displacement gradient (τυ), in addition to τq and τT:
 | (4) |
![[small upsilon, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e158.gif) = T), a field whose time derivative is the absolute temperature and has been first introduced by Helmholtz;32,33 k* (>0) represents a positive material constant characteristics of the TPL theory, and τυ is the phase-lag of thermal displacement gradient. Alternative parabolic and hyperbolic types of heat conduction can be developed by Taylor series expansion of eqn (4) with respect to time.24,29
= T), a field whose time derivative is the absolute temperature and has been first introduced by Helmholtz;32,33 k* (>0) represents a positive material constant characteristics of the TPL theory, and τυ is the phase-lag of thermal displacement gradient. Alternative parabolic and hyperbolic types of heat conduction can be developed by Taylor series expansion of eqn (4) with respect to time.24,29
The hyperbolic models of non-Fourier heat conduction can predict thermal wave propagation through a medium subjected to abrupt thermal disturbances. Nonetheless, the hyperbolic models suffer from the unrealistic singularity of temperature gradient across thermal wavefront. The fractional calculus for differentiation and integration can not only remove the thermal wave singularity but also enables the modification of existing formulation for physical processes, e.g. heat and mass transfer, in chemistry, biology, electronics, wave propagation, and chaos/fractals.34–37 Non-Fourier heat conduction models with time-fractional derivatives can be derived by Taylor series expansion of an arbitrary time-fractional order αF on the both sides of eqn (3) or (4). For instance, Ezzat et al.36,38 introduced the three-phase-lag heat conduction model with time-fractional derivatives, called fractional three-phase-lag (FTPL), by taking a Taylor series expansion on the both sides of eqn (4) and retaining terms up to 2αF-order for τq and up to the αF-order for τT and τυ as follows:
 | (5) |
All the aforementioned non-Fourier heat conduction models were based on the local/classical continuum mechanics approach. To accommodate the effect of thermomass, the distinctive mass of heat, of dielectric lattices in the heat conduction and size-dependency of thermophysical properties, Tzou9,10 has included the nonlocal (NL) behavior of heat transport in space in addition to the thermal lagging of temperature gradient and heat flux, in time. The nonlocal dual-phase-lag (NL DPL) heat conduction can be written as:
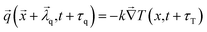 | (6) |
![[small lambda, Greek, vector]](https://www.rsc.org/images/entities/i_char_e121.gif) q is the correlating length of nonlocal heat flux. Tzou9 has shown that the correlating length
q is the correlating length of nonlocal heat flux. Tzou9 has shown that the correlating length ![[small lambda, Greek, vector]](https://www.rsc.org/images/entities/i_char_e121.gif) q has the same form of the length parameter in the thermomass model.39 Using the first-order Taylor series expansion of eqn (6) with respect to both correlating lengths and phase-lags, Tzou has developed the NL DPL heat conduction.
q has the same form of the length parameter in the thermomass model.39 Using the first-order Taylor series expansion of eqn (6) with respect to both correlating lengths and phase-lags, Tzou has developed the NL DPL heat conduction.
The aforementioned continuum heat conduction models have been applied for the heat transfer analysis in coupled multiphysics problems for media of multiple scales (from nano to macro). For example, one can consider the heat transport modelling in magneto-thermoelasticity analysis,40 hygrothermal analysis of magnetoelectroelastic composites,41,42 laser heating of gas-saturated porous media,43 femtosecond laser processing of metals,2 and non-isothermal heat flow of liquids and gas on the interface with solids.44 Beside the continuum modelling of heat transfer, MD simulation is a powerful tool for the precise modelling of molecular interactions for nano/micro scale structures and thin films.45 MD simulations with larger characteristic lengths and higher temperature ranges show better agreement with experimental data. Recent attempts for MD simulation of heat transfer have shown that the phonon heat transfer does not follow the continuum Fourier's law of heat conduction and approved the thermal wave propagation (second sound effect) in solid argon thin films and carbon nanotubes.18,46–51
In order to develop a robust heat conduction model, appropriate for multiscale heat transport and thermal wave propagation within nano/microscale to macroscale media, we first introduce in this paper (Section 2) a novel nonlocal fractional three-phase-lag (NL FTPL) heat conduction model. The NL FTPL model does not only detect thermal wave propagation and remove the discontinuity of temperature at thermal wavefront but also takes into account the size-dependency of thermophysical properties, subdiffusion or superdiffusion of heat transport, phonon–electron interaction, and the effect of thermal displacement in the ultrafast heat transport. We present in Section 3.1 series of semi-analytical solutions for continuum heat conduction in one-dimensional media with semi-infinite and finite length. The theoretical methodology can be extended to simulate thermal wave propagation in advanced materials with graded thermophysical properties. Afterwards, in Section 3.2, we implement MD simulation to approve the presence of thermal wave in nano/microscale heat transport and to confirm the validity of the introduced continuum model for heat conduction. Finally, the numerical results are presented in Section 4 to demonstrate the effect of non-Fourier heat conduction models, time-fractional order, length scale, phase-lags, material gradient, and embedded atom model (EAM) on thermal responses predicted by continuum heat conduction or MD simulation. The introduced multiscale heat conduction model can be applied to precisely simulate heat transfer in heat storage/conversion systems,52 thermal energy harvesters,53 selective laser-melting additive manufacturing,54 smart metamaterials,4,55–57 and ultralight lattices.6
2. NL FTPL model
In this section, we introduce a novel non-local, continuum mechanics model for the multiscale heat conduction analysis. On the basis of fractional calculus, nonlocal behavior, and phase-lag non-Fourier heat conduction, we introduce for the first time the nonlocal fractional three-phase-lag (NL FTPL) heat conduction model.As discussed earlier in Introduction, Tzou10 introduced a non-local model of phase-lag heat conduction called NL DPL. As an extension, a non-local three-phase-lag (NL TPL) constitutive equation for the non-Fourier heat conduction can be derived in the following form to include the effects of thermal displacement, a scalar history variable called by Green and Naghdi,58 and its associated nonlocal length in the NL DPL thermal analysis:
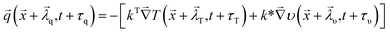 | (7) |
![[small lambda, Greek, vector]](https://www.rsc.org/images/entities/i_char_e121.gif) q,
q, ![[small lambda, Greek, vector]](https://www.rsc.org/images/entities/i_char_e121.gif) T, and
T, and ![[small lambda, Greek, vector]](https://www.rsc.org/images/entities/i_char_e121.gif) υ represent correlating nonlocal lengths of heat flux, temperature gradient, and thermal displacement gradient. The Taylor series expansion of constitutive eqn (7) with respect to either nonlocal lengths and/or phase-lags leads to alternative nonlocal phase-lag heat conduction models. Among the heat conduction constitutive equation derived from eqn (7), only those with coordinate-independent properties must be retained.59 To derive the non-local TPL heat conduction equation, the heat flux
υ represent correlating nonlocal lengths of heat flux, temperature gradient, and thermal displacement gradient. The Taylor series expansion of constitutive eqn (7) with respect to either nonlocal lengths and/or phase-lags leads to alternative nonlocal phase-lag heat conduction models. Among the heat conduction constitutive equation derived from eqn (7), only those with coordinate-independent properties must be retained.59 To derive the non-local TPL heat conduction equation, the heat flux ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) (
(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) should be eliminated between eqn (7) and the following energy equation:
,t) should be eliminated between eqn (7) and the following energy equation:
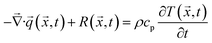 | (8) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t), ρ, cp, and
,t), ρ, cp, and 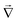 stand for the heat generation per unit time per unit volume, material density, specific heat at constant pressure, and divergence operator.
stand for the heat generation per unit time per unit volume, material density, specific heat at constant pressure, and divergence operator.
To enable the integration of subdiffusion or superdiffusion of heat transport, in addition to the effect of size-dependency of thermophysical properties and phonon–electron interaction, into the ultrafast heat conduction model, we introduce a novel nonlocal fractional three-phase-lag (NL FTPL) heat conduction model. The constitutive equation of NL FTPL heat conduction is defined as:
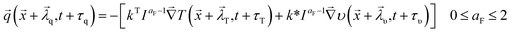 | (9) |
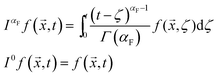 | (10) |
The NL FTPL heat conduction equation is derived by eliminating the heat flux ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) (
(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) between the energy equation (eqn (8)) and the constitutive equation (eqn (9)). For eqn (9), we implement here the second-order Taylor series expansion of λq, λT, and λυ in the space domain and the second-order Taylor series expansion of τq, τT, and τυ in the time domain to derive a general heat conduction model for NL FTPL. We take divergence and time-derivative of the subsequent constitutive equation and eliminate
,t) between the energy equation (eqn (8)) and the constitutive equation (eqn (9)). For eqn (9), we implement here the second-order Taylor series expansion of λq, λT, and λυ in the space domain and the second-order Taylor series expansion of τq, τT, and τυ in the time domain to derive a general heat conduction model for NL FTPL. We take divergence and time-derivative of the subsequent constitutive equation and eliminate  via the time-derivative of energy eqn (8) to derive the following NL FTPL heat conduction equation:
via the time-derivative of energy eqn (8) to derive the following NL FTPL heat conduction equation:
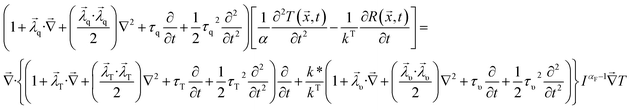 | (11) |
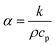 is thermal diffusivity. Depending on the values of nonlocal lengths and phase-lags as well as the order of Taylor series expansion, eqn (11) could include alternative forms of diffusive-like or wave-like NL FTPL heat conduction. Since the heat conduction equation should be coordinate-independent, and considering that
is thermal diffusivity. Depending on the values of nonlocal lengths and phase-lags as well as the order of Taylor series expansion, eqn (11) could include alternative forms of diffusive-like or wave-like NL FTPL heat conduction. Since the heat conduction equation should be coordinate-independent, and considering that ![[small lambda, Greek, vector]](https://www.rsc.org/images/entities/i_char_e121.gif) q is the only nonlocal length scale related to existing microscale/nanoscale heat transfer models, we hereafter consider merely the nonlocal length
q is the only nonlocal length scale related to existing microscale/nanoscale heat transfer models, we hereafter consider merely the nonlocal length ![[small lambda, Greek, vector]](https://www.rsc.org/images/entities/i_char_e121.gif) q, and implement the Taylor series expansion of space domain up to the first-order. As a result, the following wave-like NL FTPL for a homogenous medium is derived by simplifying the NL FTPL heat conduction equation introduced in eqn (11) which implies the first-order Taylor series expansion of λq in space and the second-order Taylor series expansion of τq and the first-order Taylor series expansion of τT and τυ in time:
q, and implement the Taylor series expansion of space domain up to the first-order. As a result, the following wave-like NL FTPL for a homogenous medium is derived by simplifying the NL FTPL heat conduction equation introduced in eqn (11) which implies the first-order Taylor series expansion of λq in space and the second-order Taylor series expansion of τq and the first-order Taylor series expansion of τT and τυ in time:
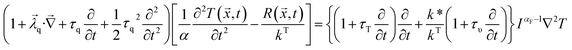 | (12) |
It is worth to recall that λ presents the length parameter in a thermomass model describing the effect of phonon gas in dielectrics,9 τq, τT, and τυ present delayed thermal responses due to the collisions of electrons and phonons, temporary momentum loss, normal relaxation in phonon scattering, and internal energy relaxation,10,24,31 and time-fractional derivative (αF) removes thermal wave singularity across thermal wavefront and is used to present the subdiffusion (0 ≤ αF < 1), normal diffusion (αF = 1), and superdiffusion phenomena (1 < αF < 2).61,64
3. One-dimensional heat conduction
To examine the propagation of thermal disturbances in a solid medium and explore the characteristics of thermal wave, we focus on the heat conduction in one-dimensional (1D) isotropic media. The solid 1D slab shown in Fig. 1, which can be finite or semi-infinite in multiple scales, is initially (t = 0) at a constant temperature T0 and is thermally disturbed from a stationary state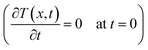 . In the absence of heat source within the slab, the surface temperature of the left side of the slab (x = 0) is suddenly raised to TWL, while the surface temperature of the right side is kept at initial temperature. The sudden temperature rise causes the propagation of thermal disturbance through the medium, which is investigated in Sections 3 and 4 via the continuum NL FTPL heat conduction model as well as the MD simulation. In this section, we first introduce the solutions for the continuum heat conduction model and then elucidate the procedure for the MD simulation of ultrafast heat transport in a nano/micro slab.
. In the absence of heat source within the slab, the surface temperature of the left side of the slab (x = 0) is suddenly raised to TWL, while the surface temperature of the right side is kept at initial temperature. The sudden temperature rise causes the propagation of thermal disturbance through the medium, which is investigated in Sections 3 and 4 via the continuum NL FTPL heat conduction model as well as the MD simulation. In this section, we first introduce the solutions for the continuum heat conduction model and then elucidate the procedure for the MD simulation of ultrafast heat transport in a nano/micro slab.
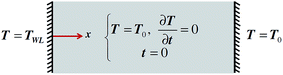 | ||
| Fig. 1 Thermal boundary and initial conditions of a 1D slab in multiple scale (from nanoscale to macroscale). | ||
3.1. Continuum NL FTPL heat conduction analysis
The solution of continuum NL FTPL heat conduction eqn (12) is sought in this section for slabs with homogenous and functionally graded (FG) properties. For the analysis, we introduce the following non-dimensional parameters:
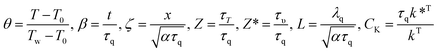 | (13) |
Presenting the numerical thermal responses in the abovementioned non-dimensional form enables us to generalize the thermal wave characteristics to both nano/microscale and macroscale materials.
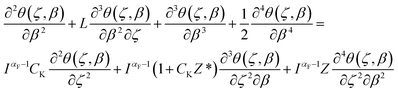 | (14a) |
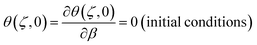 | (14b) |
| θ(0,β) = 1,θ(ζR,β) = 0 (boundary conditions) | (14c) |
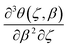 implying the negligible effect of heat flux nonlocality on the thermal responses for long-term and steady-state heat transport analysis and the reduction of thermal behavior of NL FTPL to transient Fourier heat conduction.19,24
implying the negligible effect of heat flux nonlocality on the thermal responses for long-term and steady-state heat transport analysis and the reduction of thermal behavior of NL FTPL to transient Fourier heat conduction.19,24Due to the time-dependency of transient NL FTPL heat conduction, the solution of temperature in eqn (14) is found in the Laplace domain. The Laplace transform of a temperature function θ(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) is defined as:
,t) is defined as:
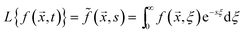 | (15) |
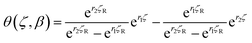 | (16) |
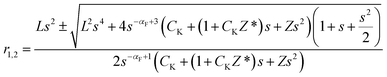 | (17) |
It is worth mentioning that the following identity has been used for the Laplace transform of Riemann–Liouville fractional integral to derive the closed-form solutions given in eqn (16):61
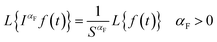 | (18) |
To retrieve temperature in the time domain, either Riemann sum approximation59 or the fast Laplace inverse transform65 can be used. For the case of a semi-infinite slab, the term associated with a positive characteristic root (r1 or r2) in the closed-form solution (eqn (16)) should be omitted to satisfy the thermal boundary condition T = T0 for locations very far from the thermal excitation (x → ∞).
The material properties of FGMs can be arbitrarily tailored through the variation of volume fraction of constituent solid components. To provide close-form solutions for transient temperature changes in the Laplace domain, we adopt the following exponential variation for thermal conductivity (k), material constant of the TPL theory (k*), and specific heat per volume (ρc) through the length of FGM slab:
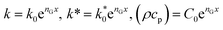 | (19) |
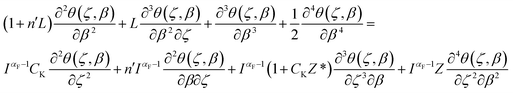 | (20) |
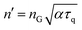 . The solution of eqn (20) in the Laplace domain leads to a closed-form solution given in eqn (16) with the modified characteristic roots as:
. The solution of eqn (20) in the Laplace domain leads to a closed-form solution given in eqn (16) with the modified characteristic roots as:
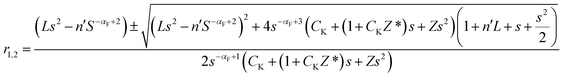 | (21) |
Temperature is then retrieved in the time domain by using a numerical Laplace inversion.
3.2. Molecular dynamics (MD) simulation for thermal analysis
In this section, we present the MD simulation of thermal wave propagation in a relatively-long nano-slab, representing the one-dimensional heat transport. The results of MD simulation enable us to observe the thermal wave propagation in nano/microscale heat transport and to compare qualitatively the MD results with those predicted in Section 3.1 by the non-Fourier, continuum, NL FTPL heat conduction model.The MD simulation is implemented by LAMMPS software package.79 The geometry of a nano-slab considered here for the MD simulation is shown in Fig. 2. The dimensions of the copper single-crystalline nano-slab are 361.5 nm (length), 7.23 nm (width), and 7.23 nm (height). To implement the MD simulation, the following steps are taken:
(1) The copper nano-slab is created by face-centred-cubic lattices.
(2) The atoms are initialized with random velocities.
(3) The nano-slab is equilibrated at room temperature 300 K for 20 picosecond (ps) under Noose–Hoover thermostat (NVT) ensembles.80 The temperatures of both hot and cool zones of the equilibrated nano-slab are fixed by rescaling their atoms at each time step.
(4) The temperature of the fixed hot zone of the nano-slab is suddenly increased to 1000 K which replicates the thermal boundary condition of continuum NL FTPL heat conduction modelling for a slab subjected to a sudden temperature rise.
The MD simulation is implemented in this paper with a time step of 1 femtosecond (fs) for a time period of 10 ps before thermal wavefront reaches the right end of nano-slab. We apply a time integration scheme which closely follows the time-reversible measure-preserving Verlet and rRESPA integrators derived by Tuckerman et al.81 The NVE integration is used to update the position and velocity of atoms at each time-step and to provide a system trajectory consistent with the microcanonical ensemble.
It is worth mentioning that heat transfer in solids is carried out by electrons and phonons. Consequently, it is critical to precisely capture the interactions among atoms and electrons in the applied atomic potential of the MD simulation. The atomic interactions are described here through the embedded atom method (EAM) potential.82 The total potential energy of the atoms is given as:
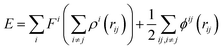 | (22) |
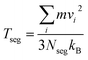 | (23) |
4. Results and discussion
The continuum and MD methodologies introduced above for a multiscale heat conduction is applied to a nano/micro-slab in order to investigate the characteristics of thermal wave propagating through a homogenous or an FGM medium. The left side of the slab suddenly experiences an increased temperature of TWL while the left side remains at the initial/environmental temperature T0. Numerical continuum and MD modelling are implemented respectively via coding in MATLAB and LAMMPS software packages. In this section, we present in detail the characteristics of thermal wave in both local/nonlocal, non-Fourier continuum heat conduction and MD heat transfer. We specifically explore the effects of alternative heat conduction models, the values of fractional-order αF, TPL parameter CK, correlation length L, phase-lag ratios Z and Z*, non-homogeneity index nG, molecular interaction, and embedded atom model on the characteristics of thermal wave.4.1. Effect of alternative continuum heat conduction models
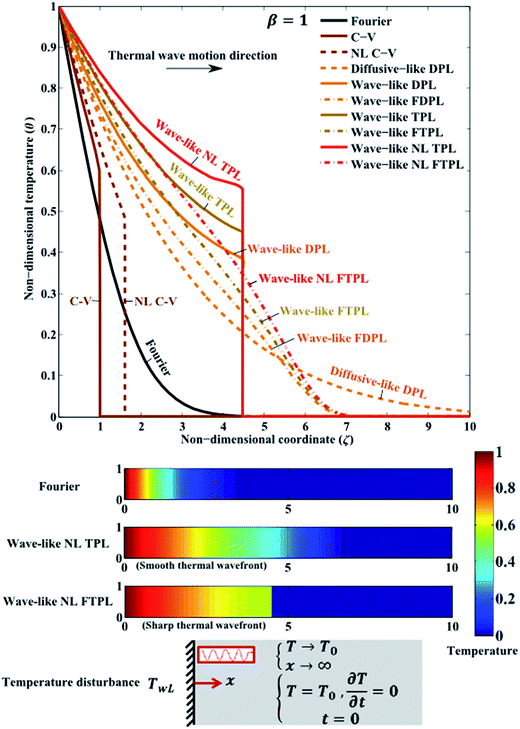
To better understand the characteristics of alternative continuum heat conduction models, temperature distribution developed within a semi-infinite slab subjected to an increased temperature of θ = 1 on its left side is depicted in Fig. 3 for 10 alternative heat conduction models at non-dimensional time β = 1. Fig. 3 compares temperature distribution at non-dimensional time β = 1 for the Fourier, C–V, nonlocal C–V (NL C–V) (L = 1), diffusive-like and wave-like DPL (Z = 10), wave-like fractional DPL (FDPL) (Z = 10, αF = 0.95), wave-like TPL (Z = Z* = 10, CK = 0.3), wave-like FTPL (αF = 0.95, Z = Z* = 10, CK = 0.3), wave-like NL TPL (L = 1, Z = Z* = 10, CK = 0.3), and wave-like NL FTPL (L = 1, αF = 0.95, Z = Z* = 10, CK = 0.3) continuum heat conduction models, all reduced from eqn (11) and (12). Except the Fourier and diffusive-like DPL heat conduction models, all heat conduction models reveal the propagation of thermal disturbance in the form of wave. However, unrealistic sharp thermal wavefront is observed in the temperature profile of C–V, NL C–V, wave-like DPL, and wave-like TPL, wave-like NL TPL heat conduction models. A sharp thermal wavefront divides the thermal response domain into the heat affected and unaffected zones and causes the discontinuity of temperature and resulting thermal strain fields. As reported by Tzou10 and confirmed by the numerical results provided in Fig. 3, the thermal wave speed of NL C–V model (CNL C–V) is higher than the C–V model (CC–V);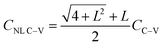 where dimensional C–V thermal wave speed is
where dimensional C–V thermal wave speed is  or
or 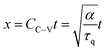 . As observed in Fig. 3, thermal wave speed of wave-like DPL (Cwave-like DPL), wave-like TPL (Cwave-like TPL), and wave-like NL TPL (Cwave-like NLTPL) are equal and their thermal wave speed can be mathematically expressed as:
. As observed in Fig. 3, thermal wave speed of wave-like DPL (Cwave-like DPL), wave-like TPL (Cwave-like TPL), and wave-like NL TPL (Cwave-like NLTPL) are equal and their thermal wave speed can be mathematically expressed as: 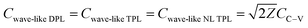 using eqn (14a).19 As a result:
using eqn (14a).19 As a result:
 | (24) |
For the assumed Z = 10 and L = 1 in Fig. 3, the thermal wavefront of the wave-like DPL, TPL, and NL TPL models is ahead of NL C–V models, all ahead of the C–V model. As mentioned above, depending on the continuum non-Fourier heat conduction model, thermal wave speed can be related to the phase-lags of temperature gradient and heat flux, thermal diffusivity, and correlating length.
It is worth mentioning that although both classical Fourier heat conduction and diffusive-like DPL models do not show a finite thermal wave speed, the thermal affected zones are not the same for these two models, as observed in Fig. 3. Further detailed analyses reveal that the diffusive-like DPL model leads to a wider affected zone compared to the classical Fourier heat conduction for Z > 1, while the thermal affected zone is narrower for Z < 1. Fig. 3 shows that the thermal behavior predicted by the wave-like NL TPL, TPL, and DPL models are similar; nonetheless, the NL TPL model predicts a higher temperature range for thermal affected zone behind the thermal wavefront location. As seen in Fig. 3, introducing time-fractional derivatives in fractional order heat conduction models of wave-like FDPL, FTPL, and NL FTPL effectively removes the singularity of temperature field around thermal wavefront because of the  term in heat conduction equation of (14a). While smooth and continuous variation of temperature is observed in the thermal response of fractional heat conduction and thermal wave speed is the same for all wave-like FDPL, FTPL, and NL FTPL models, NL FTPL model leads to a higher temperature range for thermal affected zones. As depicted in Fig. 3, the NL FTPL heat conduction model simultaneously detects thermal wave propagation, removes the discontinuity of temperature at thermal wavefront, and enables taking into account the effect of length scale and microstructural heat transport on thermal responses.
term in heat conduction equation of (14a). While smooth and continuous variation of temperature is observed in the thermal response of fractional heat conduction and thermal wave speed is the same for all wave-like FDPL, FTPL, and NL FTPL models, NL FTPL model leads to a higher temperature range for thermal affected zones. As depicted in Fig. 3, the NL FTPL heat conduction model simultaneously detects thermal wave propagation, removes the discontinuity of temperature at thermal wavefront, and enables taking into account the effect of length scale and microstructural heat transport on thermal responses.
4.2. Characteristics of NL FTPL thermal wave
In this section, we explore the effect of driving parameters of the NL FPL continuum heat conduction model on the characteristics of thermal wave propagating through the homogenous nano/micro slab. The most significant parameters of NL FTPL heat conduction are: αF, CK, L, Z, and Z*.Fig. 4 depicts the effect of the order of time-fractional derivative on the thermal behavior. As seen in this figure, αF = 1 reduces the NL FTPL model to the NL TPL heat conduction with a sharp thermal wavefront. Reducing the fractional-order αF gradually removes the discontinuity of temperature at thermal wavefront and makes wider the thermal affected zone in the back of thermal wavefront; for example, the thermal affected zone of αF = 0.8 is about 58% wider than the zone associated with αF = 0.1. Decreasing αF from 1 to 0.5 completely destroys the thermal wave and makes the temperature profile similar to the Fourier heat conduction.
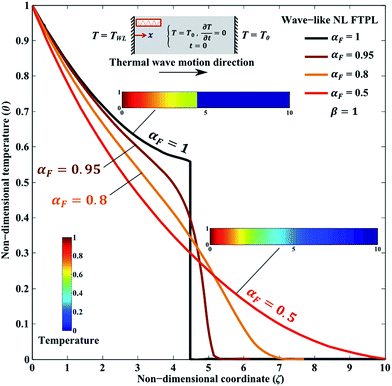 | ||
| Fig. 4 Effect of fractional order (αF) on non-dimensional temperature distribution at non-dimensional time β = 1 predicted by NL FTPL heat conduction model (L = 1, Z = 10, Z* = 10, CK = 0.3). | ||
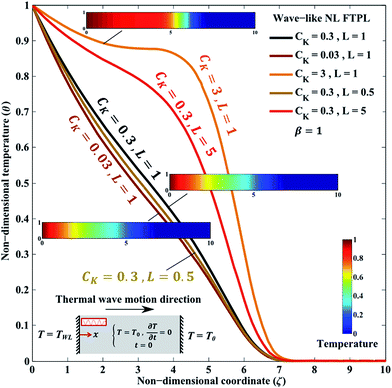
Fig. 5 shows the effect of non-dimensional TPL parameters CK and correlation length L on the temperature profile of a nano/micro-slab predicted by the wave-like NL FTPL heat conduction model with material properties of αF = 0.8 and Z = Z* = 10. Because of the application of fractional derivative αF = 0.8 in the NL FTPL heat conduction model, the sharp thermal wavefront does not appear in the temperature profile. Considering eqn (14a), it is found that CK and L similarly contribute to the NL FTPL heat conduction by respectively introducing the third-order, mixed derivatives of 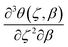 and
and 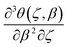 in the heat conduction differential equation. As a result, CK and L has similar effect on the temperature profile. Increasing CK and L enhances temperature in the thermal affected zone behind thermal wavefront, while the location of thermal affected zone and thermal wavefront is independent of CK and L parameters.
in the heat conduction differential equation. As a result, CK and L has similar effect on the temperature profile. Increasing CK and L enhances temperature in the thermal affected zone behind thermal wavefront, while the location of thermal affected zone and thermal wavefront is independent of CK and L parameters.
To further explore the effect of phase-lags of temperature gradient, heat flux, and thermal displacement gradient on the thermal behavior of wave-like NL FTPL model, we present in Fig. 6 the temperature profile of the nano/micro-slab at the non-dimensional time β = 1 for alternative values of phase-lag ratios Z and Z*. As mentioned earlier in Section 4.1, the thermal wave speed of wave-like NL TPL model can be estimated by  . Although this formulation is not viable for the NL FTPL heat conduction model, due to the destroyed thermal wavefront by time fractional derivatives, the formulation could still be used to approximately estimate the location of thermal affected zone. As a result, increasing the phase-lag ratio of temperature gradient to heat flux (Z) makes wider the thermal affected zone since it enhances the speed of thermal wave propagation, a phenomenon that is also observed in Fig. 6. For example, while the thermal affected zone for Z = 5 and Z* = 10 is 0 ≤ ζ ≤ 5, the affected zone is 0 ≤ ζ ≤ 7.15 for Z = 10 and Z* = 10 which confirms that the thermal affected zone of the NL FTPL heat conduction is expanded to
. Although this formulation is not viable for the NL FTPL heat conduction model, due to the destroyed thermal wavefront by time fractional derivatives, the formulation could still be used to approximately estimate the location of thermal affected zone. As a result, increasing the phase-lag ratio of temperature gradient to heat flux (Z) makes wider the thermal affected zone since it enhances the speed of thermal wave propagation, a phenomenon that is also observed in Fig. 6. For example, while the thermal affected zone for Z = 5 and Z* = 10 is 0 ≤ ζ ≤ 5, the affected zone is 0 ≤ ζ ≤ 7.15 for Z = 10 and Z* = 10 which confirms that the thermal affected zone of the NL FTPL heat conduction is expanded to 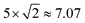 when Z is increased from 5 to 10. Opposite to Z, Z* does not alter the NL FTPL thermal wave speed and only tailors the temperature within the thermal affected zone. As shown in Fig. 6, increasing the thermal displacement to heat flux phase-lag ratio of Z* from 5 to 20 slightly enhances temperature at all locations within the thermal affected zone 0 ≤ ζ ≤ 7.15. It is worth mentioning that vanishing the value of Z (Z ≅ 0) could result in diverged and noisy temperature profiles for the NL FTPL heat conduction similar to those observed for the wave-like DPL and TPL heat conduction models.24
when Z is increased from 5 to 10. Opposite to Z, Z* does not alter the NL FTPL thermal wave speed and only tailors the temperature within the thermal affected zone. As shown in Fig. 6, increasing the thermal displacement to heat flux phase-lag ratio of Z* from 5 to 20 slightly enhances temperature at all locations within the thermal affected zone 0 ≤ ζ ≤ 7.15. It is worth mentioning that vanishing the value of Z (Z ≅ 0) could result in diverged and noisy temperature profiles for the NL FTPL heat conduction similar to those observed for the wave-like DPL and TPL heat conduction models.24
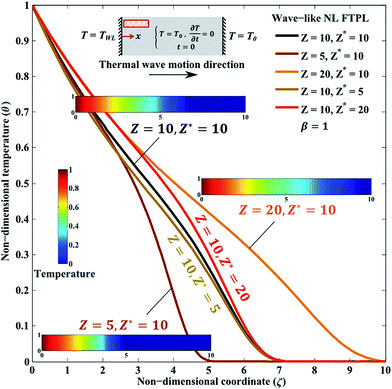 | ||
| Fig. 6 Effect of non-dimensional phase-lag ratios Z and Z* on non-dimensional temperature distribution at non-dimensional time β = 1 using NL FTPL heat conduction model (L = 1, CK = 0.3, αF = 0.8). | ||
4.3. Effect of material gradation on thermal wave
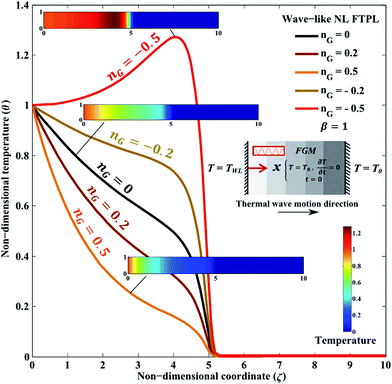
As discussed in Section 3.1.2, the microstructure of most of biological materials like bamboo, tooth, and squid beak reveals the smooth variation of properties within the material. In this section, we present the temperature profile in an exponentially graded FGM nano/micro-slab at non-dimensional time β = 1 based on the NL FTPL heat conduction model. Fig. 7 specifically depicts the effect of FGM exponential index nG (defined in eqn (19)) on the characteristics of NL FTPL thermal wave. As seen in this figure, the NL FTPL thermal wave speed is constant and independent of non-homogeneity index nG for this specific type of FGM materials; a phenomenon emanating from the absence of non-homogeneity index parameter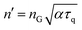 in terms of the highest order of temperature derivatives in NL FTPL differential heat conduction eqn (20). While the material gradation does not alter the thermal wave speed for this specific, exponentially graded FGM materials based on the NL FTPL model, thermal wave speed might varies within the FGM medium or be altered by the non-homogeneity index for FGM materials with an arbitrary variation of properties when it is predicted by the DPL or C–V heat conduction models.19,24,83 Fig. 7 shows that material gradation can effectively tailor temperature within the thermal affected zone, which is of significant importance for avoiding failure and fracture in composite materials used for thermal shielding against excessive thermal disturbance. Increasing the FGM exponential index nG from −0.5 to 0.5 can remarkably reduce temperature within the thermal affected zone of FGM medium. In the meantime, decreasing the FGM exponential index nG can magnify temperature at the thermal wavefront causing temperature within the FGM medium to exceed the temperature at the boundaries; for example, the maximum temperature within an FGM medium with nG = −0.5 is about 30% higher than the maximum temperature occurred within a homogenous medium nG = 0. As a result, material gradation can potentially improve the performance of advanced materials used in extreme environmental conditions if the material gradation index is selected appropriately.
in terms of the highest order of temperature derivatives in NL FTPL differential heat conduction eqn (20). While the material gradation does not alter the thermal wave speed for this specific, exponentially graded FGM materials based on the NL FTPL model, thermal wave speed might varies within the FGM medium or be altered by the non-homogeneity index for FGM materials with an arbitrary variation of properties when it is predicted by the DPL or C–V heat conduction models.19,24,83 Fig. 7 shows that material gradation can effectively tailor temperature within the thermal affected zone, which is of significant importance for avoiding failure and fracture in composite materials used for thermal shielding against excessive thermal disturbance. Increasing the FGM exponential index nG from −0.5 to 0.5 can remarkably reduce temperature within the thermal affected zone of FGM medium. In the meantime, decreasing the FGM exponential index nG can magnify temperature at the thermal wavefront causing temperature within the FGM medium to exceed the temperature at the boundaries; for example, the maximum temperature within an FGM medium with nG = −0.5 is about 30% higher than the maximum temperature occurred within a homogenous medium nG = 0. As a result, material gradation can potentially improve the performance of advanced materials used in extreme environmental conditions if the material gradation index is selected appropriately.
4.4. Characteristics of thermal wave in MD heat transfer
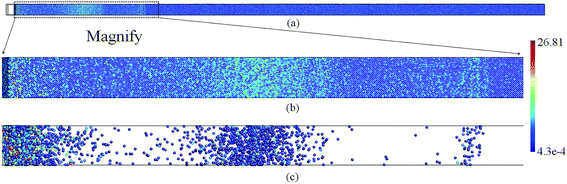
In this section, we present the MD results for heat transfer in the nano-slab described in Section 3.2 to discover the existence of thermal wave in molecular level and to compare qualitatively thermal characterizations in the molecular and continuum scales. From these perspectives, Fig. 8 presents the snapshot of the squared velocity of atoms, normalized with spatial average temperature, along the nano-slab at the instance of 4 ps after the thermal disturbance of nano-slab. Distinguished from the continuum heat transfer presented through the NL FTPL heat conduction theory, the squared velocity of each atom is depicted here to represent the “local temperature”.50 The velocity contours presented in Fig. 8 are associated with a single run of MD simulation. The velocity of each atom is non-dimensionalized by the spatial average temperature to characterize the local temperature inside the nano-slab. The value of squared velocity varies among the atoms; some of the squared velocities are extremely small compared to the mean value, while the others are the opposite. As seen in Fig. 8a and b, at t = 4 ps, only the magnified zone with a finite length have experienced a thermal disturbance while the rest of the nano-slab has almost remained in their initial condition, which implies the propagation of thermal wave along the slab length. Once an appropriate threshold is chosen for temperature, thermal wave can be better depicted with those atoms remained in the zone of interest; Fig. 8c, for example, depicts atoms with non-dimensional square velocity higher than 14.1.As seen in eqn (23), average thermodynamic temperature is related to mean square velocity of atoms. To better understand the nature of propagation of thermal disturbances in nanoscale materials, Fig. 9 shows temperature profile in a copper nano-slab at different time. The temperature profile is similar to the observed temperature in a nano argon film48 and reveals temperature evolution in a nano-slab in the form of thermal wave. The thermal wave is observed to travel from the hot surface on the left side of the nano-slab towards the cold surface on the right. Further investigation in the MD results, presented in Fig. 9, provides us with an estimate of thermal wave speed CMD = 23–25 × 103 m s−1 for a copper nano-slab. Correlating the thermal wave speed estimated by MD simulation with the speed of sharp thermal wavefront predicted by the NL C–V model,10 the correlating length λq defined in eqn (9) can be estimated as:
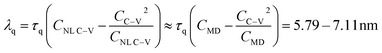 | (25) |
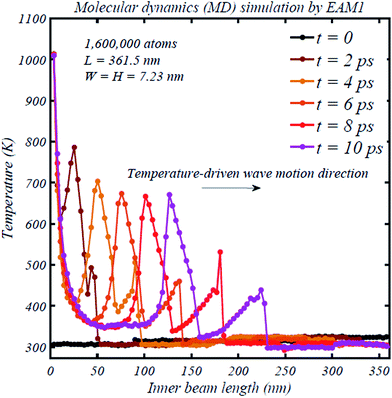 | ||
| Fig. 9 Evolution of temperature distribution in a nano-slab at different time predicted by MD simulation, which reveals the thermal wave propagation. | ||
The superficial temperature computed by eqn (23) does not distinguish between the induced thermal wave (second-sound) and mechanical (sound) wave caused by the generated thermal stress,84 which can be the reason for two peaks in the MD temperature responses (Fig. 9) a phenomenon previously observed in graphene ribbons pulsed by local heating16 and argon thin films.48 The superficial temperature shows a weakly dissipative feature. Consistent with the Monte Carlo simulation implemented in,13,14 our both MD simulation and NL FTPL continuum heat conduction modelling reveal a finite speed for the temperature-driven wave propagation. To shed lights on the coupling of thermal and mechanical waves in the abovementioned temperature-driven wave propagation, thermal wave is solely shown in Fig. A1 of Appendix by excluding the mechanical wave caused by thermal expansion induced by temperature rise in the hot zone.
Different interatomic potential can sometimes yield to dissimilar MD results.89,90 As a result, implementing an appropriate embedded atom model (EAM) is crucial for MD simulation. To confirm the robustness and reliability of thermal wave characteristics observed by MD simulation for the nano/microscale heat transport, thermal results of MD simulation are compared in Fig. 10 for a series of EAM potentials.85–88 As seen in Fig. 10, all the four tested EAM potentials show the propagation of thermal disturbance through a thermal wave. Similar to Fig. 9, two peaks presented in temperature-driven wave in Fig. 10 are due to the strong coupled thermal and mechanical waves. Except for the EAM2 potential, temperature profiles for all EAM potentials are almost identical. If the mechanical wave due to thermal expansion is removed, only one peak with appears in temperature profile presenting the thermal wave with a lower intensity compared to the temperature-driven wave including the coupled thermal and mechanical waves. As shown in Fig. A2 in Appendix, all four EAM potentials then result in almost the same thermal wave demonstrating that the discrepancy of EAM2 potential in the superficial temperature profile, presented in Fig. 10, emanates from the mechanical wave.
It is important mentioning that EAMs, opposed to Lennard-Jones type potential, consider electron effect in the potential energy. However, EAM potentials do not allow a long-distance transport of electrons, which can affect the heat transport. As an empirical derivation from first-principle methods, the EAM potential considerably improves the computational efficiency for dealing with relatively large-scale systems. To better examine the thermal transport behavior, first-principle methods like density functional theory (DFT) can be an appropriate alternative to examine in details the role that electrons play in the heat transport within nanoscale metallic materials.
5. Concluding remarks
Despite proposed alternative non-Fourier heat conduction theories for multiscale heat transfer analysis, a robust heat conduction model validated by experimental data and molecular dynamics simulation yet to be developed to accurately simulate the propagation of thermal wave in advanced materials. To address this important concern for microelectromechanical system design and laser-assisted advanced and additive manufacturing, we have introduced a novel nonlocal fractional three-phase-lag (NL FTPL) continuum heat conduction model and corroborated its prediction for thermal wave characteristics with those found by molecular dynamics simulation for nano/microscale heat transfer. The introduced wave-like NL FTPL is a non-Fourier heat conduction model which simultaneously detects thermal wave, removes temperature discontinuity at the wavefront, and incorporate the effects of size-dependency, sub/super diffusion, phonon–electron interaction, and thermal displacement in the ultrafast heat transport. The NL FTPL model considers the effects of size-dependency, subdiffusion or superdiffusion of heat transport, interaction of energy carriers (phonons and electrons), and thermal displacement on ultrafast transient heat transport through the introduction of correlation nonlocal length (λ), time-fractional derivative (αF), phase-lags of heat flux (τq), temperature gradient (τT), and thermal displacement (τυ) into the constitutive heat conduction model.To reveal the characteristics of thermal wave, semi-analytical solutions have been derived for the heat transport through homogenous and functionally graded nano/microscale one-dimensional slabs on the basis of NL FTPL continuum heat conduction. MD simulation has been implemented to compare the characteristics of thermal wave in continuum and molecular level. The MD simulation confirms the existence of thermal wave in molecular level which can also be traced through the nonlocal heat conduction model (NL FTPL), a phenomenon which requires experimental thermal testing and imaging through high-speed thermal camera to fully characterize the thermal wave specification for a wide range of materials (from metals to biological materials). The comparison of the numerical predictions of MD and nonlocal continuum heat transfer enables us to estimate the correlating length of a nano-scale copper slab as λq = 5.79–7.11 nm. A detailed MD simulation, corroborated with experimental data, is needed to quantify accurately the value of correlating length scale required for nonlocal heat conduction analysis. The multiple parameters defined in the proposed NL FTPL continuum heat conduction model not only enable tracking the thermal wave propagation with smooth thermal wavefront, but also potentially facilitate the correlation between experimental data for the ultrafast heat transport and a numerical continuum heat conduction model.
Appendix
The non-dissipative MD thermal wave by excluding mechanical wave from the temperature-driven wave propagation is shown in Fig. A1. Since the local macroscopic momentum contributes in the superficial temperature, temperature of each segment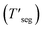 can be determined by excluding the local macroscopic momentum as:16
can be determined by excluding the local macroscopic momentum as:16
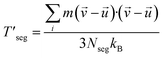 | (A1) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) is the atom velocity and
is the atom velocity and ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) is the velocity due to the local macroscopic momentum.
is the velocity due to the local macroscopic momentum.
Acknowledgements
A. H. Akbarzadeh acknowledges the financial support provided by the Natural Sciences and Engineering Research Council (NSERC) of Canada through the NSERC Discovery Grant.References
- G.-X. Wang and V. Prasad, Microscale heat and mass transfer and non-equilibrium phase change in rapid solidification, Mater. Sci. Eng., A, 2000, 292(2), 142–148 CrossRef.
- I. H. Chowdhury and X. Xu, Heat transfer in femtosecond laser processing of metal, Numer. Heat Transfer, Part A, 2003, 44(3), 219–232 CrossRef CAS.
- T. Bückmann, et al., Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography, Adv. Mater., 2012, 24(20), 2710–2714 CrossRef PubMed.
- A. Rafsanjani, A. Akbarzadeh and D. Pasini, Snapping Mechanical Metamaterials under Tension, Adv. Mater., 2015, 27(39), 5931–5935 CrossRef CAS PubMed.
- J. H. Lee, et al., 25th anniversary article: ordered polymer structures for the engineering of photons and phonons, Adv. Mater., 2014, 26(4), 532–569 CrossRef CAS PubMed.
- T. A. Schaedler, et al., Ultralight metallic microlattices, Science, 2011, 334(6058), 962–965 CrossRef CAS PubMed.
- A. Salazar, Energy propagation of thermal waves, Eur. J. Phys., 2006, 27(6), 1349 CrossRef.
- E. Marín, On thermal waves, Eur. J. Phys., 2013, 34(5), L83 CrossRef.
- D. Tzou, Nonlocal behavior in phonon transport, Int. J. Heat Mass Transfer, 2011, 54(1), 475–481 CrossRef.
- D. Tzou and Z.-Y. Guo, Nonlocal behavior in thermal lagging, Int. J. Therm. Sci., 2010, 49(7), 1133–1137 CrossRef.
- D. Li, et al., Thermal conductivity of individual silicon nanowires, Appl. Phys. Lett., 2003, 83(14), 2934–2936 CrossRef CAS.
- M. Asheghi, et al., Phonon-boundary scattering in thin silicon layers, Appl. Phys. Lett., 1997, 71(13), 1798–1800 CrossRef CAS.
- D.-S. Tang, et al., Phonon wave propagation in ballistic-diffusive regime, J. Appl. Phys., 2016, 119(12), 124301 CrossRef.
- G. Chen, Nanoscale energy transport and conversion, 2005 Search PubMed.
- D.-S. Tang, Y.-C. Hua and B.-Y. Cao, Thermal wave propagation through nanofilms in ballistic-diffusive regime by Monte Carlo simulations, Int. J. Therm. Sci., 2016, 109, 81–89 CrossRef.
- W.-J. Yao and B.-Y. Cao, Thermal wave propagation in graphene studied by molecular dynamics simulations, Chin. Sci. Bull., 2014, 59(27), 3495–3503 CrossRef CAS.
- J. B. J. Baron Fourier, The analytical theory of heat, The University Press, 1878 Search PubMed.
- M. Wang, N. Yang and Z.-Y. Guo, Non-Fourier heat conductions in nanomaterials, J. Appl. Phys., 2011, 110(6), 064310 CrossRef.
- A. Akbarzadeh and Z. Chen, Heat conduction in one-dimensional functionally graded media based on the dual-phase-lag theory, Proc. Inst. Mech. Eng., Part C, 2013, 227(4), 744–759 CrossRef.
- C. Cattaneo, Sulla conduzione del calore, in Some Aspects of Diffusion Theory, 1948 Search PubMed.
- P. Vernotte, Les paradoxes de la théorie continue de léquation de la chaleur, C. R. Hebd. Seances Acad. Sci., 1958, 246(22), 3154–3155 Search PubMed.
- M. Rubin, Hyperbolic heat conduction and the second law, Int. J. Eng. Sci., 1992, 30(11), 1665–1676 CrossRef.
- D. D. Joseph and L. Preziosi, Heat waves, Rev. Mod. Phys., 1989, 61(1), 41 CrossRef.
- A. Akbarzadeh and D. Pasini, Phase-lag heat conduction in multilayered cellular media with imperfect bonds, Int. J. Heat Mass Transfer, 2014, 75, 656–667 CrossRef.
- T. Qiu and C. Tien, Heat transfer mechanisms during short-pulse laser heating of metals, J. Heat Transfer, 1993, 115(4), 835–841 CrossRef CAS.
- T. Qiu and C. Tien, Femtosecond laser heating of multi-layer metals—I. Analysis, Int. J. Heat Mass Transfer, 1994, 37(17), 2789–2797 CrossRef CAS.
- D. Y. Tzou, The generalized lagging response in small-scale and high-rate heating, Int. J. Heat Mass Transfer, 1995, 38(17), 3231–3240 CrossRef CAS.
- D. Tzou, A unified field approach for heat conduction from macro-to micro-scales, J. Heat Transfer, 1995, 117(1), 8–16 CrossRef.
- A. Akbarzadeh, J. Fu and Z. Chen, Three-phase-lag heat conduction in a functionally graded hollow cylinder, Trans. Can. Soc. Mech. Eng., 2014, 37(4), 155–171 Search PubMed.
- A. Green and P. Naghdi, On undamped heat waves in an elastic solid, J. Therm. Stresses., 1992, 15(2), 253–264 CrossRef.
- S. R. Choudhuri, On a thermoelastic three-phase-lag model, J. Therm. Stresses., 2007, 30(3), 231–238 CrossRef.
- P. Podio-Guidugli, For a statistical interpretation of Helmholtz’thermal displacement, Continuum Mech. Thermodyn., 2016, 1–5 Search PubMed.
- H. von Helmholtz, Principien der Statik monocyclischer Systeme, J. Reine Angew. Math., 1884, 97, 111–140 Search PubMed.
- A. Dzieliński, D. Sierociuk and G. Sarwas, Some applications of fractional order calculus, Bull. Pol. Acad. Sci.: Tech. Sci., 2010, 58(4), 583–592 Search PubMed.
- M. Stiassnie, On the application of fractional calculus for the formulation of viscoelastic models, Appl. Math. Model., 1979, 3(4), 300–302 CrossRef.
- M. A. Ezzat, A. S. El Karamany and M. A. Fayik, Fractional order theory in thermoelastic solid with three-phase lag heat transfer, Arch. Appl. Mech., 2012, 82(4), 557–572 CrossRef.
- M. Žecová and J. Terpák, Heat conduction modeling by using fractional-order derivatives, Appl. Math. Comput., 2015, 257, 365–373 CrossRef.
- M. A. Ezzat, A. A. El-Bary and M. A. Fayik, Fractional fourier law with three-phase lag of thermoelasticity, Mech. Adv. Mater. Struct., 2013, 20(8), 593–602 CrossRef.
- Z.-Y. Guo and Q.-W. Hou, Thermal wave based on the thermomass model, J. Heat Transfer, 2010, 132(7), 072403 CrossRef.
- M. A. Ezzat and A. S. El Karamany, Fractional order heat conduction law in magneto-thermoelasticity involving two temperatures, Z. Angew. Math. Phys., 2011, 62(5), 937–952 CrossRef CAS.
- A. Akbarzadeh, M. Babaei and Z. Chen, Coupled thermopiezoelectric behaviour of a one-dimensional functionally graded piezoelectric medium based on C–T theory, Proc. Inst. Mech. Eng., Part C, 2011, 225(11), 2537–2551 CrossRef.
- A. Akbarzadeh and D. Pasini, Multiphysics of multilayered and functionally graded cylinders under prescribed hygrothermomagnetoelectromechanical loading, J. Appl. Mech., 2014, 81(4), 041018 CrossRef.
- N. Afrin, Y. Zhang and J. Chen, Dual-phase lag behavior of a gas-saturated porous-medium heated by a short-pulsed laser, Int. J. Therm. Sci., 2014, 75, 21–27 CrossRef.
- R. Khayat, et al., Non-Fourier effects in macro-and micro-scale non-isothermal flow of liquids and gases. Review, Int. J. Therm. Sci., 2015, 97, 163–177 CrossRef CAS.
- J. R. Lukes, et al., Molecular dynamics study of solid thin-film thermal conductivity, J. Heat Transfer, 2000, 122(3), 536–543 CrossRef CAS.
- X. Wang and X. Xu, Molecular dynamics simulation of thermal and thermomechanical phenomena in picosecond laser material interaction, Int. J. Heat Mass Transfer, 2003, 46(1), 45–53 CrossRef CAS.
- P. Chantrenne, M. Raynaud, D. Baillis and J. L. Barrat, Study of phonon heat transfer in metallic solids from molecular dynamic simulations, Microscale Thermophys. Eng., 2003, 7(2), 117–136 CrossRef CAS.
- Q. Liu, P. Jiang and H. Xiang, Molecular dynamics simulations of non-Fourier heat conduction, Prog. Nat. Sci., 2008, 18(8), 999–1007 CrossRef.
- A. Singh and E. B. Tadmor, Thermal parameter identification for non-Fourier heat transfer from molecular dynamics, J. Comput. Phys., 2015, 299, 667–686 CrossRef CAS.
- J. Shiomi and S. Maruyama, Non-Fourier heat conduction in a single-walled carbon nanotube: Classical molecular dynamics simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(20), 205420 CrossRef.
- R. N. Salaway and L. V. Zhigilei, Molecular dynamics simulations of thermal conductivity of carbon nanotubes: Resolving the effects of computational parameters, Int. J. Heat Mass Transfer, 2014, 70, 954–964 CrossRef CAS.
- Y. Li, Z. Y. Fu and B. L. Su, Hierarchically structured porous materials for energy conversion and storage, Adv. Funct. Mater., 2012, 22(22), 4634–4667 CrossRef CAS.
- M. Gueltig, et al., High frequency thermal energy harvesting using magnetic shape memory films, Adv. Energy Mater., 2014, 4(17), 1400751 CrossRef.
- Y. Li and D. Gu, Parametric analysis of thermal behavior during selective laser melting additive manufacturing of aluminum alloy powder, Mater. Des., 2014, 63, 856–867 CrossRef CAS.
- A. Akbarzadeh, et al., Electrically conducting sandwich cylinder with a planar lattice core under prescribed eigenstrain and magnetic field, Compos. Struct., 2016, 153, 632–644 CrossRef.
- A. Akbarzadeh, et al., Dynamic eigenstrain behavior of magnetoelastic functionally graded cellular cylinders, Compos. Struct., 2014, 116, 404–413 CrossRef.
- J. T. Overvelde, et al., A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom, Nat. Commun., 2016, 7, 10929 CrossRef CAS PubMed.
- A. Green and P. Naghdi, A re-examination of the basic postulates of thermomechanics, Proc. R. Soc. London, Ser. A, 1991 DOI:10.1098/rspa.1991.0012.
- D. Y. Tzou, Macro-to microscale heat transfer: the lagging behavior, John Wiley & Sons, 2014 Search PubMed.
- R. Kimmich, Strange kinetics, porous media, and NMR, Chem. Phys., 2002, 284(1), 253–285 CrossRef CAS.
- H. M. Youssef, Theory of fractional order generalized thermoelasticity, J. Heat Transfer, 2010, 132(6), 061301 CrossRef.
- Y. Z. Povstenko, Fractional heat conduction equation and associated thermal stress, J. Therm. Stresses., 2004, 28(1), 83–102 CrossRef.
- F. Mainardi and R. Gorenflo, On Mittag-Leffler-type functions in fractional evolution processes, J. Comput. Appl. Math., 2000, 118(1), 283–299 CrossRef.
- A. Suzuki, et al., Fractional diffusion modeling of heat transfer in porous and fractured media, Int. J. Heat Mass Transfer, 2016, 103, 611–618 CrossRef.
- F. Durbin, Numerical inversion of Laplace transforms: an efficient improvement to Dubner and Abate's method, Comput. J., 1974, 17(4), 371–376 CrossRef.
- T. Tan, et al., Mechanical properties of functionally graded hierarchical bamboo structures, Acta Biomater., 2011, 7(10), 3796–3803 CrossRef CAS PubMed.
- N. Rahbar and W. Soboyejo, Design of functionally graded dental multilayers, Fatigue Fract. Eng. Mater. Struct., 2011, 34(11), 887–897 CrossRef CAS.
- A. Miserez, et al., The transition from stiff to compliant materials in squid beaks, Science, 2008, 319(5871), 1816–1819 CrossRef CAS PubMed.
- F. Nogata and H. Takahashi, Intelligent functionally graded material: bamboo, Compos. Eng., 1995, 5(7), 743–751 CrossRef.
- C. Zhou, et al., Mechanical and biological properties of the micro-/nano-grain functionally graded hydroxyapatite bioceramics for bone tissue engineering, J. Mech. Behav. Biomed. Mater., 2015, 48, 1–11 CrossRef PubMed.
- U. G. Wegst, et al., Bioinspired structural materials, Nat. Mater., 2015, 14(1), 23–36 CrossRef CAS PubMed.
- L. Guo, Z. Wang and N. Noda, A fracture mechanics model for a crack problem of functionally graded materials with stochastic mechanical properties, Proc. R. Soc. London, Ser. A, 2012, 468, 2939–2961 CrossRef.
- J. Reddy and C. Chin, Thermomechanical analysis of functionally graded cylinders and plates, J. Therm. Stresses., 1998, 21(6), 593–626 CrossRef.
- S. S. Vel and R. Batra, Three-dimensional analysis of transient thermal stresses in functionally graded plates, Int. J. Solids Struct., 2003, 40(25), 7181–7196 CrossRef.
- A. Akbarzadeh, M. Abbasi and M. Eslami, Coupled thermoelasticity of functionally graded plates based on the third-order shear deformation theory, Thin-Walled Structures, 2012, 53, 141–155 CrossRef.
- B. Kieback, A. Neubrand and H. Riedel, Processing techniques for functionally graded materials, Mater. Sci. Eng., A, 2003, 362(1), 81–106 CrossRef.
- N. W. Bartlett, et al., A 3D-printed, functionally graded soft robot powered by combustion, Science, 2015, 349(6244), 161–165 CrossRef CAS PubMed.
- A. Akbarzadeh, A. Abedini and Z. Chen, Effect of micromechanical models on structural responses of functionally graded plates, Compos. Struct., 2015, 119, 598–609 CrossRef.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81(1), 511–519 CrossRef.
- M. Tuckerman, B. J. Berne and G. J. Martyna, Reversible multiple time scale molecular dynamics, J. Chem. Phys., 1992, 97(3), 1990–2001 CrossRef CAS.
- S. Foiles, M. Baskes and M. S. Daw, Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33(12), 7983 CrossRef CAS.
- M. Babaei and Z. Chen, Hyperbolic heat conduction in a functionally graded hollow sphere, Int. J. Thermophys., 2008, 29(4), 1457–1469 CrossRef CAS.
- S. Volz, et al., Transient Fourier-law deviation by molecular dynamics in solid argon, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(1), 340 CrossRef CAS.
- G. Bonny, et al., Ternary Fe–Cu–Ni many-body potential to model reactor pressure vessel steels: First validation by simulated thermal annealing, Philos. Mag., 2009, 89(34–36), 3531–3546 CrossRef CAS.
- M. Mendelev, et al., Analysis of semi-empirical interatomic potentials appropriate for simulation of crystalline and liquid Al and Cu, Philos. Mag., 2008, 88(12), 1723–1750 CrossRef CAS.
- J. Hoyt, et al., An embedded atom method interatomic potential for the Cu–Pb system, Modell. Simul. Mater. Sci. Eng., 2003, 11(3), 287 CrossRef CAS.
- J. Adams, S. Foiles and W. Wolfer, Self-diffusion and impurity diffusion of fee metals using the five-frequency model and the embedded atom method, J. Mater. Res., 1989, 4(01), 102–112 CrossRef CAS.
- C. Si, et al., Impacts of potential models on calculating the thermal conductivity of graphene using non-equilibrium molecular dynamics simulations, Int. J. Heat Mass Transfer, 2017, 107, 450–460 CrossRef CAS.
- J.-H. Zou, et al., Phonon thermal properties of graphene from molecular dynamics using different potentials, J. Chem. Phys., 2016, 145(13), 134705 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28831f |
| This journal is © The Royal Society of Chemistry 2017 |