Strong enhancement of spin–orbit splitting induced by σ–π coupling in Pb-decorated silicene

Abstract

Electronic properties and spin–orbit (SO) splitting of silicene adsorbed with Cu, Ag, Au and Pb atoms at different coverages are investigated by means of first-principles calculations. All four kinds of adatoms we studied tend to adsorb at hollow sites. The adsorption of Pb atoms enhances the hybridization of σ electrons and π electrons around the Fermi level in silicene, resulting in considerable SO splitting (∼100 meV). Only a small degree of SO splitting is achieved in NM–silicene (NM stands for noble metal atoms, i.e. Cu, Ag, and Au) systems. Our results suggest that the σ–π coupling is a very important factor for the enhancement of SO coupling in silicene. The concentration and the intrinsic SO coupling of adatoms will also affect SO splitting in these systems. All structures we studied are stable at room temperature. Our work provides an imperative understanding of the physical mechanism of enhancing SO coupling in two dimensional materials.

---

1. Introduction

The central theme of spintronics is about the spin interaction and the active manipulation of spin in solid state systems. Due to the possible applications in the electronic industry, spintronics has become an active research field. In current spintronics, the investigation of spin–orbit (SO) interaction has attracted great attention. The SO coupling connected the momentum of an electron with its spin, so that one can possibly use the external electronic field to manipulate the spin of the electron.^1–3 Moreover, many interesting phenomena are closely related to SO interaction, including the anomalous quantum Hall effect and spin quantum Hall effect,^4,5 which have been predicted in graphene, a single layer of carbon atoms in a honeycomb lattice.⁶ However, the SO interaction in pristine graphene was found to be very weak, not sufficient for practical applications.^4,7 Thus, it is very meaningful and important to study how to enhance the SO coupling and yield large SO strength in graphene. In fact, various methods have been conducted to enhance the SO coupling in graphene, such as by adsorbing impurity atoms on graphene, growing graphene on different kinds of substrates, applying an external electric field or exerting strains.^8–11

For the physicist, the important things are not only to enhance SO coupling but also to explore its physical mechanism. Castro Neto and Guinea suggested that the sp³ hybridization induced by an impurity atom could lead to a large increase of SO interaction in graphene.¹² The same mechanism also was proposed by Huertas-Hernando et al. They found the lattice deformation could enhance the hybridization of σ electrons and π electrons in graphene, leading to the increase of SO interaction.^13–15 The influence of the metal substrate on SO splitting in graphene was also investigated. Using angle-resolved photoelectron spectroscopy, Dedkov et al. observed a large Rashba splitting in an epitaxial graphene layer on top of a Ni(111) substrate.¹⁶ This Rashba effect was attributed to the combination of two effects: spin-polarization of the π band and the effective potential gradient appearing at the graphene/Ni interface. Regrettably, the remarkable Rashba splitting was not observed in the latter similar investigations.¹⁷ In addition, another mechanism about SO interaction was also raised. Marchenko et al. reported that Au intercalation at the graphene–Ni interface could create a remarkable SO splitting.¹⁸ They thought that the hybridization between C π states and Au d states was the source of the SO splitting in graphene.

To obtain a deeper insight into the physical mechanism on enhancement of the SO coupling, the further investigation is very necessary. In fact, silicene is a better material for the investigation of this mechanism. Silicene is the silicon counterpart of graphene. Those exotic features belonging to graphene such as linear energy dispersion and massless Dirac fermions are still kept in silicene,^19,20 attracting significant interest.^21–23 It is well known that the two sublattices are coplanar in graphene, whereas silicene has a buckled sheet with the two sublattices not in the same plane.²⁴ In graphene, σ orbitals and π orbitals are coupled only through the intrinsic SO coupling. Thus, the effective SO coupling is a second-order process in graphene, resulting in a rather tiny SO splitting at the Dirac point. However, due to low-buckled structure of silicene, σ orbitals and π orbitals in silicene can directly hybridize. The intrinsic effective SO coupling in silicene is a first-order process, resulting in an arrestive SO splitting at the Dirac point.^25,26 A direct band gap of 1.55 meV has been found at the Dirac point of pristine silicene by Yao group, and the gap would increase to 2.9 meV under certain pressure strain.²⁵ These investigations suggested that silicene could provide very different structural and electronic circumstances from graphene. It is very interesting to investigate the SO interaction in silicene.

The sp²–sp³ mixing hybridization in silicene causes its high surface reactivity. Lin et al. found adatoms could be much more strongly bound to silicene than to graphene.²⁷ In the present paper, we systematically study the electronic properties and SO coupling in silicene with adatoms Cu, Ag, Au and Pb within the framework of density functional theory. We know that Cu, Ag, and Au are termed as noble metal (NM) atoms, belonging to the same group. It is well known that the atomic intrinsic SO coupling is closely related to atomic number. These three kinds of adatoms we select are conducive to understand the influence of the intrinsic SO coupling on SO splitting of NM–silicene systems. In ref. 9, Ma et al. suggested the SO splitting of graphene can significantly be enhanced by Pb doping. In the past some years, Pb/Si systems has also been extensively studied, especially on Si(111) surface.^28–31 Thus, it is very meaningful to investigate the influence of Pb adsorption on electronic structures and SO splitting of silicene. Our study suggests the interaction between Pb and silicene is stronger than that between NM and silicene. Considerable spin–orbit splitting (∼100 meV) is achieved in Pb–silicene system, which can be ascribed to the enhanced σ–π coupling in silicene induced by Pb adsorption. This order of magnitude of SO splitting is sufficient for the practical applications, thus Pb decorated silicene is very promising in the spintronics.

2. Computational methods and models

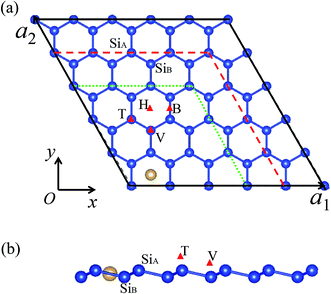
The total energy and electronic structure calculations are performed with projector augmented wave formalism based on density functional theory (DFT), as implemented in the Vienna ab initio simulation program (VASP).^32,33 The generalized gradient approximation (GGA) method with Perdew–Burke–Ernzerhof (PBE) for the exchange and correlation functional is used.³⁴ Plane waves with energy cut-off of 400 meV are used for the expansion of Kohn–Sham orbitals. The SO coupling can be included by solving the generalized Kohn–Sham equations in the relativistic DFT.^35,36 The van der Waals (vdW) interaction is considered in our calculations based on Grimme's DFT-D2 method.³⁷ Due to the hexagonal symmetry of the silicene layer, four possible adsorption positions are considered, i.e., hollow site (above the center of hexagonal), top site (on top of the upper silicon atoms), valley site (on top of the lower silicon atoms), bridge site (on top of the Si–Si bond),³⁸ for which the abbreviations ‘H’, ‘T’, ‘V’ and ‘B’ are used, as illustrated in Fig. 1. Through comparing their binding energy E_b, the relative stabilities of these sites can be measured. The binding energy is defined as E_b = E_ad + E_Si − E_total, where E_ad, E_Si, and E_total represent the total energies of a single free adatom, the clean silicene, and the M–silicene system, respectively. With this definition, a positive binding energy indicates the exothermic process. To simulate the different adsorption coverage, the supercell models are used, which consists of an (n × n, n = 3, 4, 5) primitive silicene cell and an adatom, as shown in Fig. 1a. The vacuum thickness along the z axis is no less than 15 Å, large enough to avoid the interactions between the two adjacent silicene sheets. All models are constructed based on the calculated lattice constant for (1 × 1) unitcell of 3.82 Å and the buckling distance 0.44 Å, which are in good agreement with previous theoretical values.²⁴ For geometry optimization, the internal coordinates are allowed to relax with the fixed lattice constants until the Hellmann–Feynman forces are less than 0.01 eV Å⁻¹ without SO coupling. The convergence threshold for energy is 10⁻⁶ eV. Both band structures with and without the SO coupling are calculated based on these optimized structures. The Brillouin zone integrations are performed by using Monkhorst–Pack grids³⁹ of 13 × 13 × 1, 9 × 9 × 1, 7 × 7 × 1 for (3 × 3)–(5 × 5) cells, respectively. Molecular dynamics (MD) simulations were performed to assess the stability of configurations at different temperatures.

Fig. 1 The top view (a) and side view (b) of considered adsorption sites on silicene. The symbols ‘T’, ‘V’, ‘H’, and ‘B’ express top, valley, hollow, and bridge sites, respectively. The solid black, dashed red, and dotted green lines in (a) denote the (5 × 5), (4 × 4), and (3 × 3) supercells, respectively.

3. Results and discussion

The calculated results of silicene with Cu, Ag, Au and Pb adatoms are summarized in Table 1. For all M–silicene (M = Cu, Ag, Au, Pb) systems, the H site is found to be the most stable configuration. Obviously, the binding energy is nearly independent of the adsorption coverage and increases in the order of Ag < Au < Pb < Cu. For NM atoms adsorption, this order is in good agreement with recently reported studies.⁴⁰ The binding energies for all M–silicene systems vary from the smallest value of 1.842 eV (Ag) to the largest one of 3.048 eV (Cu). Compared to the graphene, the adatoms could be much more strongly bound to silicene due to its high surface reactivity.²⁷ The obtained binding energies for Cu–graphene, Ag–graphene, and Au–graphene systems by Ding et al. are only 0.25, 0.03, and 0.16 eV, respectively.⁴¹ Interestingly, the binding energy of Ag is still the smallest, and that of Cu is still the largest even if they are adsorbed on graphene. However, the binding energies of M–silicene (M = Cu, Ag, Au, and Pb) systems are much less than those of TM–silicene.^38,42 For example, the binding energies of Ti, Fe, Co, Ni on silicene (4 × 4) supercells vary from the smallest value of 3.516 eV (Fe) to the largest one of 4.776 eV (Ni).²⁷ If silicene (6 × 6) supercells are adopted, the larger binding energies can be obtained. The binding energy can even reach 7.05 eV for W–silicene (6 × 6) system.³⁸ Obviously, the closed d shells of Cu, Ag and Au atoms result in a relative weak interaction between them and silicene, lowering the binding energies of these systems. Conversely, the open d shells of those transition metal atoms strengthen the interaction between them and silicene, resulting in the larger binding energies. For Pb–silicene systems, the relative small binding energies can be ascribed to the large Pb–Si bond lengths.

Table 1 Calculated parameters for Cu, Ag, Au, and Pb adsorbed silicene: the most stable site, binding energy E_b, the distances between the adatom and its nearest (next-nearest) Si atom d1 (d2), band gap at the Dirac point without (with) SO coupling E_g1 (E_g2)

		Site	Eb (eV)	d1 (Å)	d2 (Å)	Eg1 (eV)	Eg2 (eV)
Cu	3 × 3	H	2.878	2.40	2.66	0.180	0.178
	4 × 4		2.972	2.41	2.64	0.047	0.046
	5 × 5		3.048	2.41	2.64	0.032	0.030
Ag	3 × 3	H	1.842	2.55	2.78	0.175	0.168
	4 × 4		1.898	2.55	2.76	0.040	0.039
	5 × 5		1.920	2.56	2.75	0.026	0.026
Au	3 × 3	H	2.354	2.50	2.75	0.200	0.170
	4 × 4		2.351	2.50	2.73	0.044	0.033
	5 × 5		2.353	2.50	2.70	0.037	0.031
Pb	3 × 3	H	2.420	2.91	3.43	0.365	0.308
	4 × 4		2.528	2.96	3.23	0.269	0.236
	5 × 5		2.567	2.95	3.23	0.224	0.204

---

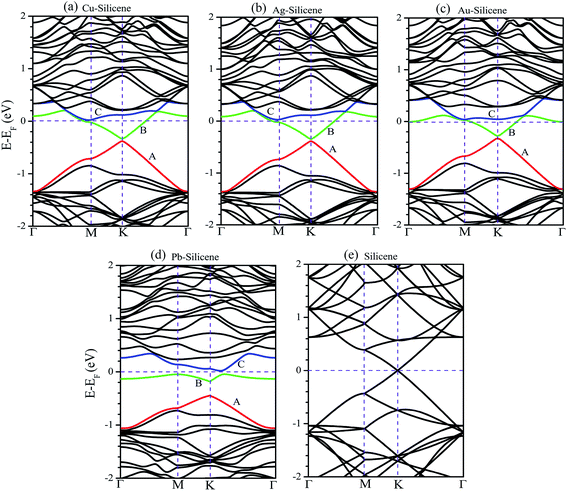
The band structures of systems without the consideration of SO coupling are shown in Fig. 2. For brevity without sacrificing generality, the only (4 × 4) supercell is selected as a representative example. The energy band of pristine silicene (4 × 4) supercell is also illustrated in Fig. 2e for comparative purpose. We first focus on the influence of NM atoms on the electronic properties of silicene. The comparison of band structures between pristine silicene (Fig. 2e) and NM–silicene systems (Fig. 2a–c) suggests that the Dirac cones are not destroyed completely by the adsorption of NM atoms, but the sites of Dirac cones shift from Fermi level (E_F) to about −0.4 eV, which is almost independent of the concentration of adatoms. That is to say, the E_F will lift when NM atoms are adsorbed on silicene, which means the direction of charge transfer is from NM atoms to silicene, leading to n-type doping.^27,40 The scenario is similar for the adsorption of other metal atoms, such as Li atom, on silicene.⁴³ On the contrary, the adsorption of non-metal atoms, such as F atom, will lower the E_F.⁴⁴ Although the shapes of Dirac cones in NM–silicene systems are almost kept, the adsorptions of NM atoms lead to the emergence of band gaps at the Dirac points, i.e., the gaps between A band and B band in Fig. 2a–d. The values of these band gaps without the consideration of SO coupling are given as ‘E_g1’ in Table 1. For each NM–silicene, it can be seen that the band gaps of NM–silicene (3 × 3) systems are significantly larger than those of (4 × 4) and (5 × 5) systems. And the band gaps of (4 × 4) systems are only slightly larger than those of (5 × 5) systems. That is to say, the band gaps at the Dirac points will reduce gradually with the decrease of the concentration of adatoms. The evolution of band structures of Pb–silicene is shown in Fig. 2d. Obviously, the influence of Pb on the properties of silicene is much stronger than that of NM atoms. In Pb–silicene (4 × 4) system, the Dirac cone has been distorted, and a band gap of 0.269 eV is opened. With the decrease of the concentration of Pb atoms, the band gaps around the Dirac points also reduce gradually. This is similar to the case of NM adsorption.

Fig. 2 The band structures of (a) Cu–silicene, (b) Ag–silicene, (c) Au–silicene, (d) Pb–silicene, and (e) pristine silicene systems without the consideration of SO coupling. Only (4 × 4) supercells are selected as representative examples.

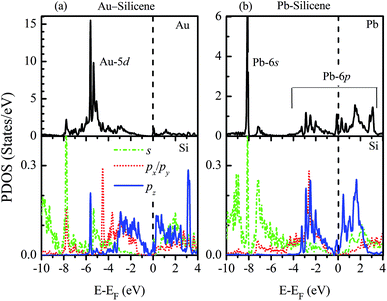
To understand how the adatoms affect the electronic properties of silicene, the partial density of states (PDOS) are plotted in Fig. 3. For the adsorption of NM atoms, the characteristic of PDOS for Cu–silicene and Ag–silicene systems is similar to that for Au–silicene, thus we only select Au–silicene as a representative system and show its PDOS in Fig. 3a. Due to the closed d shell of Au atom, the Au 5d states are located in the deep energy range of −4 eV to −7 eV. However, the Si 3p states are near the E_F, resulting in the relative weak interaction between Au atom and silicene. The scenario is different for the adsorption of Pb atoms. It can be seen from Fig. 3b that there is one perfect peak superposition between Pb 6s and Si 3s orbitals. In addition, both Pb 6p and Si 3p states are around the E_F. These features suggest the strong hybridization and interaction appear between Pb adatoms and silicene, leading to the obvious change of electronic structure in silicene.

Fig. 3 Partial densities of states of (a) Au–silicene (4 × 4) and (b) Pb–silicene (4 × 4) systems.

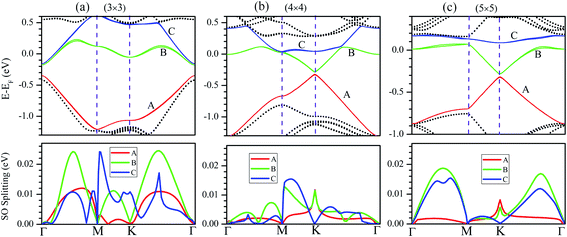
The influence of SO coupling on the band structures of M–silicene systems is further explored. First we focus on the pristine silicene. A band gap of 1.51 meV at the Dirac point is obtained in pristine silicene after the SO coupling is considered, which is in good agreement with previous result.²⁵ This gap can be regarded as an SO splitting, which is caused by lifting the degeneracy of the valence band and conduction band at K point. Moreover, the spin degeneracy of energy bands can also be lifted when the SO coupling is taken into account. In the following, we will mainly focus on this kind of SO splitting induced by lifting the spin degeneracy of bands. There are many factors that influence the SO splitting in M–silicene systems, including the concentration of adatoms, the intrinsic SO coupling, and the orbital hybridization, etc. To exclude the influence of the intrinsic SO coupling of adatoms, only the energy band structures of Au–silicene systems with SO coupling are shown in the upper three panels of Fig. 4. Here, it is worth noting that the Dirac cone (K) of silicene is folded to the Γ point due to the Brillouin zone folding of the (3 × 3) silicene supercell. However, the SO splitting can not be distinguished easily from these band structures. By analyzing the energy of each band, the absolute values of the SO splitting can be extracted. In the lower three panels of Fig. 4, we give the SO splitting of three bands around the E_F, denoted as A, B, and C in band structures. We found that the SO splitting of A bands are obviously smaller than that of B and C bands except those high symmetrical points. One can see from Fig. 3a that the A band is chiefly composed of Si p_z (π) states, while the B and C bands include not only Si p_z (π) states but also Si s, p_x and p_y (σ) states. Due to the hybridization, Au 6s states also have small contribution to the B and C bands. The strong interaction between σ states and π states occurs in B and C bands, leading to the large SO splitting. On the other hand, Fig. 4 shows the largest values of SO splitting for each band in Au–silicene (3 × 3) system is slightly larger than those in (4 × 4) and (5 × 5) systems, suggesting the concentration of adatoms also affects the SO splitting.

Fig. 4 The band structures of Au–silicene systems with the consideration of SO coupling (the upper three panels) and SO splitting of A, B and C bands (the lower three panels). (a) Au–silicene (3 × 3), (b) Au–silicene (4 × 4), and (c) Au–silicene (5 × 5).

The SO splitting of A, B and C bands around the E_F (see Fig. 2a–d) for all M–silicene (4 × 4) (M = Cu, Ag, Au, and Pb) systems are given in Fig. 5. Obviously, the values of SO splitting increase according to the order of Cu < Ag < Au < Pb, suggesting the intrinsic SO coupling of adatoms is an obvious factor that affects SO splitting. However, it is worth noting that the SO splitting of Pb–silicene system (∼100 meV) is much larger than that of Au–silicene system (∼20 meV) although the atomic number of Pb atom is only slightly larger than that of Au atom. The reason can be analyzed based on the hybridization of σ–π orbitals. As mentioned above, the strong interaction appears between Pb and silicene, and the electronic states around the E_F in silicene produce remarkable change. It can be seen from Fig. 3b that all Si s, p_x/p_y, and p_z orbitals participate in hybridization around the E_F, forming quasi-sp³ hybridization, enhancing SO splitting in Pb–silicene system. Furthermore, the hybridization between Si frontier orbitals and Pb 6p orbital is also an important source of the SO splitting. Conversely, the small SO splitting in Au–silicene systems can be ascribed to the relative weak interaction between Au and silicene as well as the small changes of electronic structures in silicene. Based on the above analysis, we can draw a conclusion that the hybridization of σ–π orbitals is a very important factor for the enhancement of SO splitting in silicene, and the intrinsic SO coupling of adatoms as well as the concentration of adatoms can also affect the SO splitting. After the SO coupling effect is considered, the Dirac cones in NM–silicene systems move toward E_F and locate at around −0.3 eV. The band gaps at the Dirac points decrease due to the SO splittings of A and B bands, especially for Pb–silicene systems (see ‘E_g2’ in Table 1). Obviously, these results suggest the SO coupling will exert an important effect on the electronic structures of silicene with heavy metal atoms.

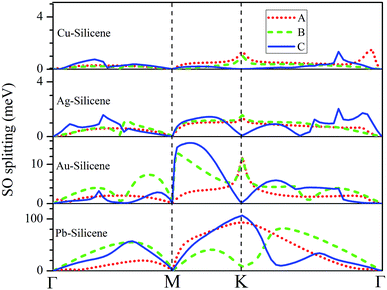Fig. 5 The SO splitting of A, B and C bands in Cu–silicene (4 × 4), Ag–silicene (4 × 4), Au–silicene (4 × 4), and Pb–silicene (4 × 4) systems. A, B and C bands are marked in Fig. 2.

Only when these systems are stable at room temperature, they are useful in spintronics device. To study the thermal stabilities of these systems at different temperatures, we carry out the molecular dynamics (MD) simulations on M–silicene (4 × 4) systems. The oscillations of M–Si bond lengths with the MD steps below 1000 K are shown in Fig. 6a. During the entire MD simulation process of 2 ps with the time step of 1 fs, no bond breaking is observed below 1000 K. On the whole, the oscillating period of M–Si bond lengths gradually increase with the rise of temperature. Once the temperature exceeds 1000 K, the adatoms will disaffiliate from silicene one after another. In Fig. 6b, we give the critical temperature of M–Si bond breaking, which is 1000 K, 1200 K, and 1200 K for Cu–silicene, Ag–silicene, and Pb–silicene, respectively. However, no bond breaking is observed in Au–silicene system even if the temperature is up to 1400 K. Surprisedly, the Si–Si bonds begin to break when the temperature is up to 1500 K, meaning the disintegration of silicene at this temperature.⁴⁵ Therefore it is meaningless to conduct MD simulations above 1500 K. Of course, the above MD simulations are not enough to find the exact critical temperature of disintegration, and they only stand for a temperature range. However, based on these results, we can confirm these M–silicene systems are stable at least at room temperature, thus they can be well applied in spintronics.

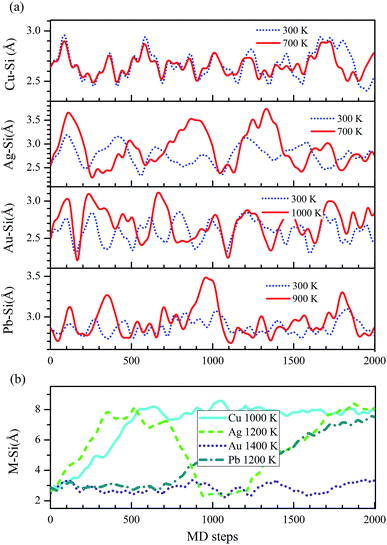Fig. 6 The changes of M–Si bond lengths in M–silicene (4 × 4) systems with the MD steps (1 fs per step). (a) Below 1000 K, (b) above 1000 K.

4. Conclusions

The spin–orbit coupling effect and electronic properties in silicene with adsorbed Cu, Ag, Au, and Pb atoms are explored based on first-principles method. For the adsorption of NM atoms on silicene, the shapes of Dirac cones in NM–silicene systems are almost kept except for the emergence of band gaps at the Dirac points. Only small spin–orbit splitting is achieved in NM–silicene systems. Different from the NM adsorption, the strong interaction between Pb and silicene can enhance the hybridization of σ electrons and π electrons around Fermi level, resulting in the remarkable change of electronic structures in silicene. Considerable spin–orbit splitting (∼100 meV) can be achieved in Pb–silicene systems due to the enhanced σ–π coupling. Based on our results, a significative conclusion can be drawn that the hybridization of σ–π orbitals is a very important factor for the enhancement of SO splitting in silicene. The concentration and the intrinsic SO coupling of adatoms can also affect the SO splitting.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (NSFC, Grant No. 11404096, U1404609, 11404098), the key Project for Education Department of Henan Province (Grant No. 16A140008), the Innovation Team of Henan University of Science and Technology (No. 2015XTD001).

References

1. I. Žutić, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323.
2. D. D. Awschalom and M. E. Flatté, Nat. Phys., 2007, 3, 153–159.
3. Z. H. Zhang, C. F. Chen and W. L. Guo, Phys. Rev. Lett., 2009, 103, 187204.
4. C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 226801.
5. Z. H. Qiao, S. A. Yang, W. X. Feng, W.-K. Tse, J. Ding, Y. G. Yao, J. Wang and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161414.
6. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
7. Y. G. Yao, F. Ye, X.-L. Qi, S.-C. Zhang and Z. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 041401.
8. D. W. Ma, Z. Y. Li and Z. Q. Yang, Carbon, 2012, 50, 297–305.
9. D. W. Ma and Z. Q. Yang, New J. Phys., 2011, 13, 123018.
10. M. Gmitra, S. Konschuh, C. Ertler, C. Ambrosch-Draxl and J. Fabian, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235431.
11. D. Marchenko, J. Sanchez-Barriga, M. R. Scholz, O. Rader and A. Varykhalov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115426.
12. A. H. Castro Neto and F. Guinea, Phys. Rev. Lett., 2009, 103, 026804.
13. D. Huertas-Hernando, F. Guinea and A. Brataas, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 155426.
14. F. Kuemmeth, S. Llani, D. C. Ralph and P. L. Mceuen, Nature, 2008, 452, 448–452.
15. J. Zhou, Q. F. Liang and J. M. Dong, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195427.
16. Y. S. Dedkov, M. Fonin, U. Rudiger and C. Laubschat, Phys. Rev. Lett., 2008, 100, 107602.
17. O. Rader, A. Varykhalov, J. Sanchez-Barriga, D. Marchenko, A. Rybkin and A. M. Shikin, Phys. Rev. Lett., 2009, 102, 057602.
18. D. Marchenko, A. Varykhalov, M. R. Scholz, G. Bihlmayer, E. I. Rashba, A. Rybkin, A. M. Shikin and O. Rader, Nat. Commun., 2012, 3, 1232.
19. L. C. Lew Yan Voon, J. J. Zhu and U. Schwingenschlögl, Appl. Phys. Rev., 2016, 3, 040802.
20. J. J. Zhao, H. S. Liu, Z. M. Yu, R. Quhe, S. Zhou, Y. Y. Wang, C. C. Liu, H. X. Zhong, N. N. Han, J. Lu, Y. G. Yao and K. H. Wu, Prog. Mater. Sci., 2016, 83, 24–151.
21. W. C. Wu, Z. M. Ao, C. H. Yang, S. Li, G. X. Wang, C. M. Li and S. Li, J. Mater. Chem. C, 2015, 3, 2593–2602.
22. W. B. Zhang, Z. B. Song and L. M. Dou, J. Mater. Chem. C, 2015, 3, 3087–3094.
23. J. Zhu and U. Schwingenschlögl, J. Mater. Chem. C, 2015, 3, 3946–3953.
24. S. Cahangirov, M. Topsakal, E. Akturk, H. Şahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
25. C. C. Liu, W. X. Feng and Y. G. Yao, Phys. Rev. Lett., 2011, 107, 076802.
26. C. C. Liu, H. Jiang and Y. G. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195430.
27. X. Q. Lin and J. Ni, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075440.
28. C. Brun, I. Hong, F. Patthey, I. Y. Sklyadneva, R. Heid, P. M. Echenique, K. P. Bohnen, E. V. Chulkov and W. D. Schneider, Phys. Rev. Lett., 2009, 102, 207002.
29. E. Ganz, F. Xiong, I. S. Hwang and J. Golovchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 7316–7319.
30. B. Slomski, G. Landolt, S. Muff, F. Meier, J. Osterwalder and J. H. Dil, New J. Phys., 2013, 15, 125031.
31. V. Yeh, L. Berbil-Bautista, C. Z. Wang, K. M. Ho and M. C. Tringides, Phys. Rev. Lett., 2000, 85, 5158–5161.
32. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
33. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. G. Theurich and N. A. Hill, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 073106.
36. A. D. Corso and A. M. Conte, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115106.
37. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
38. H. Sahin and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085423.
39. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
40. Z. Y. Ni, H. X. Zhong, X. H. Jiang, R. Quhe, G. F. Luo, Y. Y. Wang, M. Ye, J. B. Yang, J. J. Shi and J. Lu, Nanoscale, 2014, 6, 7609–7618.
41. J. Ding, Z. H. Qiao, W. X. Feng, Y. G. Yao and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195444.
42. J. Y. Zhang, B. Zhao and Z. Q. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 165422.
43. T. P. Kaloni, G. Schreckenbach and M. S. Freund, J. Phys. Chem. C, 2014, 118, 23361–23367.
44. W. W. Ju, T. W. Li, X. Y. Su, H. L. Cui and H. S. Li, Appl. Surf. Sci., 2016, 384, 65–72.
45. G. R. Berdiyorov and F. M. Peeters, RSC Adv., 2014, 4, 1133–1137.

---