Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polyelectrolyte pKa from experiment and molecular dynamics simulation†
Michael S. Bodnarchuk‡
a,
Kay E. B. Doncom‡b,
Daniel B. Wright‡b,
David M. Heyesa,
Daniele Dini*a and
Rachel K. O'Reilly *b
*b
aDepartment of Mechanical Engineering, Imperial College, South Kensington Campus, London SW7 2AZ, UK. E-mail: d.dini@imperial.ac.uk
bDepartment of Chemistry, University of Warwick, Coventry, CV4 7AL, UK. E-mail: rachel.oreilly@warwick.ac.uk
First published on 5th April 2017
Abstract
The pKa of a polyelectrolyte has been determined experimentally by potentiometric titration and computed using Molecular Dynamics (MD) constant pH (CpH) methodology, which allows the pKa of each titratable site along the polymer backbone to be determined separately, a procedure which is not possible by current experimental techniques. By using experimental results within the CpHMD method, the simulations show that the protonation states of neighbouring residues are anti-correlated so that the charges are well-separated. As found with previous simulation studies on model polyelectrolytes, the end groups are predicted to be the most acidic. CpHMD is shown to result in distinct polymer conformations, brought about by the range of protonation states changes along the polymer; this can now be used in the design of pH-responsive polymers for, amongst other applications, additive formulation and drug delivery devices.
Introduction
Stimuli-responsive polymers undergo a change in hydrophilicity in response to a particular stimulus. Incorporation of these polymers into self-assembling block copolymer systems leads to stimuli-sensitive self-assembled structures which have the propensity to undergo a morphology transition in response to the particular stimulus. Stimuli which have been investigated within the literature include, but are not limited to, temperature,1–5 pH6–8 and light.4,9 pH-responsive polymers have found uses as potential drug delivery systems,7,10–13 nanoreactors,14–18 recyclable catalysts19–21 and in controlling surface properties.22,23 Additionally, polyelectrolytes are widely used as water soluble thickeners and deliverers of specific functionality in added value products, where the acid–base equilibria can be exploited to determine performance.24–27For monomers, the acid dissociation constant, or pKa, is readily measured through titration experiments and is equal to the pH value at which equal amounts of the acid and conjugate base (or base and conjugate acid) are present. It has been reported that the pKa of the monomers can change upon polymerisation. In one example the pKa of styrenesulfonic acid was estimated, by solving the Poisson–Boltzmann equation, to increase from −0.53 for the monomer to 2.9 for polymers with degrees of polymerisation (DP) of 8–12 units.28 Often the overall pKa of the polymer is measured by titration and this value is used as a reference point for where the overall shift in amphiphilic balance will occur in some systems. Therefore the hydrophilicity is often treated as an on/off function. However, for polymers the situation is more complicated. Unlike small molecules, where the protonation of individual species occurs independently, the protonation (and hence pKa) of different sites on a polymer are directly affected by the immediate environment of that group within the molecule. Factors such as hydrophobicity of the environment,29 distribution of ionisable units30 and the ionisation state of the neighbouring units31,32 can all affect the pKa. Indeed, the pKa of acidic groups increases with increasing degree of ionisation.33 Therefore when altering the pH of a solution, in order to induce a hydrophilicity change, the polymer is not being protonated uniformly to the same extent, but rather different sites become ionised first. When considering applications, such effects may be significant. Therefore a more thorough understanding of the pKa behaviour of units within the polymer structure is advantageous.
As with polymer chains, the pKa values of the ionisable sites within a protein structure are sensitive to the immediate surrounding environment.34 Investigating accurate pKa values for different residues is important because factors such as folding, stabilisation, solubility interactions and reactivity are affected by pKa values.35–39 Using computational techniques it is possible to obtain the pKa value for each individual ionisable residue within the molecule. The software Depth Server can be used to predict the pKa, taking into account factors such as the depth of the site, accessible surface area, hydrogen bonds and electrostatic interactions.40 This is useful when considering reactivity of a particular residue at various pHs.
Determining the pKas of individual units along a polymer backbone can be experimentally challenging. Current experimental potentiometric titration techniques used to determine the pKa values of different titratable sites on the same molecule are most accurate when the pKa values are widely separated, and if this is not the case an average value is the best that can usually be achieved. This limits the ability to introduce desired functionality at an early stage of any application of molecule development.
Theoretical techniques can usefully be applied to help elucidate these issues. Quantum mechanical (QM) approaches can, in principle, be used to calculate the pKa of each titratable group in small molecules,41–45 and oligomers,46 but they are too costly to apply routinely to large molecules such as polyelectrolytes. Also the large computational demands of QM necessitate that it is used to calculate the pKa of one group at a time. This procedure does not include the effects of simultaneous protonation and deprotonation across the polyelectrolyte, and therefore limits the reliability of any such calculation.
In contrast to separated monomers in solution, the intramolecular electrostatic interactions within the polyelectrolyte molecule can restrict further ionisation unless the distance between two sites are greater than the Bjerrum length.47 When the polyelectrolyte experiences restricted ionisation, its conformation can be biased towards more elongated structures. Metropolis Monte Carlo (MC) computer simulation methods were developed in the 1990s to mimic the titration procedure using a coarse-grained representation of the polyelectrolyte molecule to determine the backbone site specific pKa values.48–50 Mean-field calculations were also carried out by Castelnovo et al. to predict the site-resolved pKa distribution along the backbone.51 The advantage of the MC method is that it performs a computationally-efficient virtual titration in which the protonated state depends on the local electrostatic environment within the molecule. However, the stochastic nature of the ionisation event and polymer chain fluctuations can limit the physical accuracy of the MC procedure unless rare-event MC moves are included. Historically, MC-based approaches could be limited in regard to the adequate sampling of new conformations arising from changing the protonation state of the polyelectrolyte. Methods such as coarse-graining52 and the use of the Wang–Landau reaction ensemble53 show great promise in circumventing such sampling issues, and their application to polymer pKa determination has yet to be fully exploited.
In this study the more recently developed classical molecular simulation method of CpHMD is used as it overcomes many of the limitations of standard MC. The protonation state changes continuously during the simulation, and the coupled time-dependent structural and conformational fluctuations are better accounted for in the process of determining the local pKa values. There are some applications in the literature of the application of this approach to polyelectrolytes, for example RNA.54
Constant-pH Molecular Dynamics simulations (CpHMD) provide a cost effective way of calculating the pKa of ionisable groups.55–60 The sampling of the protonation state of ionisable residues within a CpHMD simulation can be achieved by two methods. The first, based upon λ-dynamics,61 treats the protonation state (λi) as a continuous variable, propagated by the forces acting within the simulation.59 λi can be any value between 0 (protonated) and 1 (deprotonated), with the Hamiltonians describing the energy of the system scaled appropriately for these states. One caveat of this approach is the presence of unphysical states during the simulation (i.e. λ0.5), although biasing schemes, based upon the free energy of deprotonation of a reference compound, can help to push the simulation towards the more realistic states. Treating the protonation state of ionisable residues in a continuous manner allows for the force and energy potential to evolve naturally, although the implementation of such approaches can be challenging.
The second sampling approach treats the protonation state of the ionisable group as a discrete variable, i.e. protonated or deprotonated only.58 Periodically during the CpHMD simulation, an ionisable group is chosen randomly and an attempt is made to change its protonation state by a Monte Carlo procedure based on the pH and difference in Gibbs free energy between the molecule of interest and a reference compound (typically the monomer of the ionisable unit). Whilst such an approach can sometimes lead to a discontinuous energy potential for a large system, it is ideally suited to modelling small systems due to the speed of the method.
Regardless of sampling approach, the CpHMD method allows the pKa of each group to be determined separately, by fitting the protonation probability of a given site as a function of pH to the Henderson–Hasselbalch equation.62 The ability to vary simultaneously the protonation state of any one of the ionisable groups during the simulation allows for synergic effects between neighbouring groups to be included explicitly in the molecular simulation. This more balanced procedure offers a significant improvement in computational efficiency over the QM alternative.
Poly(glycerol methacrylate) (pGMA) is a water soluble polymer which has a wide range of applications, from protective coatings,57 to insulin delivery agents.58 The acid–base equilibria of pGMA and its related hydrophilicity are therefore of current interest. In this study the pKa of each titratable group on a reversible addition fragmentation chain transfer RAFT synthesised pGMA, is calculated using CpHMD. These data are compared with the experimental value determined by potentiometric titration.
Experimental
Materials
AIBN (2,2′-azo-bis(isobutyronitrile)) was recrystallised from methanol and stored in the dark at 4 °C. All other materials were used as received from Aldrich, Fluka, and Acros. All aqueous solutions were prepared using nanopure water (deionised water, resistance > 18 MΩ). HCl (1 M) and NaOH (1 M) were calibrated and standardised using tris(hydroymethyl) aminomethane and potassium hydrogen phthalate, respectively.Instrumentation
1H NMR spectra were recorded on a Bruker DPX-400 spectrometer in CDCl3. Chemical shifts are given in ppm downfield from TMS.Size exclusion chromatography (SEC) measurements were performed with HPLC grade solvents (Fisher), N,N-dimethylformamide (DMF) containing LiCl (1.06 gL−1) as an eluent at 40 °C and a flow rate of 1 mL min−1. The molecular weights of the synthesised polymers were calculated relative to poly(methyl methacrylate) (PMMA) standards.
Potentiometric titration30,33,63 was performed at room temperature with an automatic titrator (Mettler Toledo G20) controlled by LabX software. 40 mL of solution (approximately 1 gL−1) was used for each potentiometric titration experiment. The polymers were first dissolved at α = 1 with 1.1 excess of HCl 1 M and then back-titrated with 0.1 M NaOH. The addition of NaOH 0.1 M titrant was added at volume increments of 5–50 μl and spaced with 180 s intervals. From the raw titration data the total number of titratable units was calculated.
Synthetic procedures
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 6.10–6.20 (m, 1H,
CH2), 6.10–6.20 (m, 1H, ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2).
CH2).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 volume compared to monomer) were added to a dry ampoule containing a stirrer bar. The solution was degassed using at least 3 freeze–pump–thaw cycles, back filled with nitrogen, sealed and placed in a pre-heated oil bath at 70 °C. After 4 hours the polymerisation was quenched by liquid nitrogen. The viscous crude reaction medium was dissolved in the minimum amount of tetrahydrofuran (THF), and the polymer was precipitated into diethyl ether and filtered. The precipitation process was repeated three times to afford a bright pink polymer. Mn NMR = 5.0 kDa Mn SEC = 5.8 kDa, ĐM = 1.10. 1H NMR (400 MHz, CDCl3, 298 K): δ 0.85–1.30 (br, 3H, CH2–C–CH3), 1.90–2.20 (br, 2H, –CH2–C–CH3), 1.94 (s, 6H, end group), 2.80–2.90 (br, 2H, –CH2–CH–O–CH2), 3.20–3.30 (br, 2H, –CH2–CH–O–CH2), 3.95–4.20 (br, 1H, –CH2–CH–O–CH2), 7.41 (t, J = 8.1 Hz, 2H, end group), 7.55 (t, J = 7.4 Hz, 2H end group), 7.85 (d, J = 8.2 Hz, 1H end group).
4 volume compared to monomer) were added to a dry ampoule containing a stirrer bar. The solution was degassed using at least 3 freeze–pump–thaw cycles, back filled with nitrogen, sealed and placed in a pre-heated oil bath at 70 °C. After 4 hours the polymerisation was quenched by liquid nitrogen. The viscous crude reaction medium was dissolved in the minimum amount of tetrahydrofuran (THF), and the polymer was precipitated into diethyl ether and filtered. The precipitation process was repeated three times to afford a bright pink polymer. Mn NMR = 5.0 kDa Mn SEC = 5.8 kDa, ĐM = 1.10. 1H NMR (400 MHz, CDCl3, 298 K): δ 0.85–1.30 (br, 3H, CH2–C–CH3), 1.90–2.20 (br, 2H, –CH2–C–CH3), 1.94 (s, 6H, end group), 2.80–2.90 (br, 2H, –CH2–CH–O–CH2), 3.20–3.30 (br, 2H, –CH2–CH–O–CH2), 3.95–4.20 (br, 1H, –CH2–CH–O–CH2), 7.41 (t, J = 8.1 Hz, 2H, end group), 7.55 (t, J = 7.4 Hz, 2H end group), 7.85 (d, J = 8.2 Hz, 1H end group).| ΔG = kBT(pH − pKa,mon)ln10 + ΔGdeprot,sys − ΔGdeprot,mon | (1) |
Monomer deprotonation free energies for common ionisable amino acids come pre-calculated in AMBER; for novel ionisable units these need to be calculated manually. Consequently the first stage of the simulation was to calculate the deprotonation free energy, ΔGdeprot,mon, of the GMA monomer using classical Thermodynamic Integration (TI). TI is a method for calculating the free-energy difference between two end states, termed λ0 and λ1. In these simulations, a value of λ0 indicates that the monomer is protonated, while λ1 indicates that the monomer is deprotonated. Intermediate values of λ represent hybrids between the two end states and are used to improve the accuracy of the TI simulations. Eleven equally spaced λ-windows between 0 and 1 [0–0.09, 0.09–0.18 …1] were used to calculate the free energy, with each window simulated for 5 ns. Data was collected for the last 4 ns of the simulation. The value of ΔU/Δλ was calculated for each window (where U is the potential energy of the system) and integrated with respect to λ to find the overall free energy change between λ0 and λ1. The deprotonation free energies for the two alcohol sites on the monomer at different salt concentrations are shown in Table 1.
| Alcohol site | 0 M | 0.5 M |
|---|---|---|
| Primary | −64.1 | −44.5 |
| Secondary | −64.4 | −44.4 |
Implicit solvent constant-pH simulations were performed with AMBER 14 (ref. 67) using the same conditions as the TI simulations. The pGMA molecule was made by combining 30 titratable monomer units in the leap module of AMBER and capping it with AIBN and benzodithioate at the termini, with the small excess charge evenly distributed on one of the backbone atoms of each polymeric unit to ensure neutrality. The polymer was initially minimised in Sander, and then equilibrated for 100 ps prior to the simulation. The simulations were set up to ensure that each residue had its titration state sampled, on average, every 100 fs. Simulations were performed at every pH integer between 3 and 10, with more performed around the equivalence point of the titration. A time-step of 2 fs was used. Each constant-pH simulation was carried out for 10 ns, with the probability of one of the alcohol sites being deprotonated monitored throughout the simulation. At least four repeats were performed for each pH value to calculate the statistical uncertainty in the value of the average deprotonation probability across the polymer, α. The value of α as a function of pH was used to fit the data using the Henderson–Hasselbalch equation, shown in eqn (2), to find the pKa.
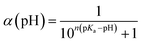 | (2) |
In eqn (2), n is the Hill coefficient which indicates whether the deprotonation of two sites are correlated (n > 1) or anti-correlated (n < 1). Both n and pKa are fitted parameters in eqn (2).
The GMA monomer, AIBN and benzodithioate groups were parameterised using the antechamber module in AMBER,67 with the partial charges assigned using the AM1-BCC model.68 Prior to simulation, minimisation was performed using the Sander module of AMBER to remove bad contacts, using an igb keyword of 1. The GAFF force-field was used to model the monomer and pGMA,69 with the Generalised-Born model of Onufriev70 (igb = 2) used to describe the implicit GB solvent model. A non-bonded cut-off of 3.0 nm and salt concentrations (NaCl) of 0 M and 0.5 M were used. The Berendsen thermostat was used with a time constant of 2.0 ps to maintain the temperature at 300 K. Bond distances were maintained constant using the SHAKE algorithm.71
Results and discussion
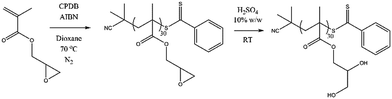
The monomer glycerol methacrylate (GMA) was chosen for study because, as previously mentioned, the polymer is water soluble and has a wide range of potential applications. Reversible addition-fragmentation chain transfer (RAFT) polymerisation techniques were used because this monomer has been shown previously to be polymerised with good control by RAFT.64 The precursor monomer, glycidyl methacrylate (GM), was first polymerised in 1,4-dioxane using a dithiobenzoate chain transfer agent (Fig. 1).65 Hydrolysis of the resulting polymer with a 10% w/w solution of H2SO4, followed by exhaustive dialysis, yielded the pGMA polymer, Mn NMR = 5.0 kDa, Mn SEC = 5.8 kDa, ĐM = 1.08 (see ESI†). 1H NMR comparison of the end group signals of the CTA with the side chain signals of the GMA group gave a degree of polymerisation (DP) of 30. The controlled character of the polymerisation was demonstrated by the narrow dispersity of the SEC trace and the good agreement between the DP obtained from 1H NMR analysis of the purified polymer and that predicted from conversion NMR.The pKa of the GMA monomer was determined experimentally to be 6.3 (see ESI†). As shown in eqn (1), one of the prerequisites to perform a CpHMD simulation is the monomer pKa (pKa,mon). Despite advances in pKa calculations of small molecules, the best accuracy for pKa estimation is typically ±0.5 pKa units. This error can be larger for molecules which can have multiple titration sites or have unusual chemical functionalities. Experimental values of the pKa,mon were used in the CpHMD simulations to give a more accurate titration profile for the polymer due to the presence of the diol. This value was used as an input in the CpHMD simulations. The pKa of the pGMA homopolymer was determined by potentiometric titration in salt-free water and in a 0.5 M NaCl solution.
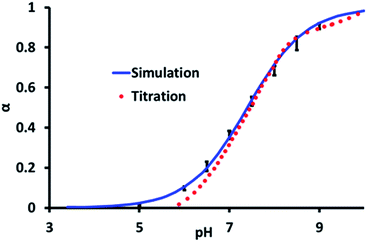
CpHMD simulations performed on the pGMA shown in Fig. 1 used the AMBER simulation package, with implicit solvent (see experimental for detailed simulation procedure). Simulations were performed at unit intervals in pH between 3 and 10 for salt concentrations of 0 and 0.5 M. The average value of the degree of ionisation, α, recorded during the simulation as a function of pH was fitted to the Henderson–Hasselbalch (HH) equation to determine the Hill coefficient and the pKa of the polymer (i.e. where α = 0.5).
The average degree of deprotonation of pGMA, as a function of pH at 0 M salt concentration determined by both experiment and simulation are plotted in Fig. 2. The predicted pKa from the CpHMD simulation is 7.4 ± 0.25, which compares favourably with the experimental titration value of 7.5 ± 0.2. The calculated Hill coefficient from the simulation, 0.67 also agrees well with the experimental titration value of 0.72. It is significant to note that the simulated curve begins to deviate from the experimental titration curve at low pH values. Experimentally, at low pH the ionic strength associated with [H]+ is increased, which contributes to an electrostatic screening effect. Landsgesell and co-workers have shown that one of the caveats of the CpHMD method is that it does not capture this pH-induced screening, which leads to a subtle deviation from the experimental curve.72
In the absence of salt the pKa of the pGMA is consistently about 1 pKa unit higher than its monomer. We attribute this to the increasing difficulty of ionising neighbouring repeat units along the pGMA chain. As the nth group along the pGMA chain becomes negatively charged it requires more energy for the n + 1th (neighbouring) group to also be ionised because of the electrostatic repulsion between the groups. The exception to this phenomenon, however, is the terminus of the polymer. As a result, the average pKa of the polymerised chain is higher than that of the monomer.
Evidence for electrostatic repulsion along the chain can be seen in Fig. 3, which shows the state of deprotonation of each titratable group along the molecule (as a colour coded map) captured at an instant in the simulation when pH = pKa, i.e. at the equivalence point of the polymer. Fig. 3 shows that a protonated site is typically found adjacent to two deprotonated sites, highlighting the synergy between adjacent units to reduce electrostatic repulsion. Indeed, no more than three adjacent deprotonated sites are ever observed in the simulation at pH = pKa. As the pH of the simulation deviates further from the polymer pKa, more protonated or deprotonated sites in proximity to each other will occur. A key advantage of the CpHMD method is that the level of detail shown in Fig. 3 cannot be derived currently from experiment. These results can therefore be used to give insights into experimental observations and trends.
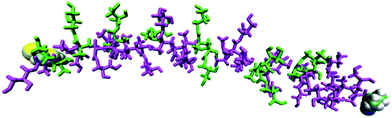 | ||
| Fig. 3 Simulated protonation state (magenta = deprotonated, green = protonated) for each site in pGMA in a 0 M salt solution at pH = 7.4. The terminal groups are shown as van der Waals spheres. | ||
One such observation is the formation of micro-domains within polyelectrolytes. Micro-domains are partly folded regions of the polymer conformation which display increased order compared to a fully-extended conformation. Their occurrence is of interest in the fields of drug-delivery and biotechnology, as they can be exploited to trap small molecules.73–75 The small molecules can be enclosed within the polymer at a certain pH value, and then released within the body under physiological pH.
It is thought that typical micro-domains result from hydrogen-bonds between triplets of titratable sites.76 In order to investigate whether pGMA is capable of forming micro-domains, the MD trajectories at pH = pKa were examined. Despite being a small polymer, the MD simulations show conformational features which are suggestive of incipient micro-domain formation. Bent or ‘hairpin’ conformations appear frequently in the simulation, and a MD representation of them can be found in Fig. 4. Radial distribution functions (RDFs) between atoms were calculated which provide another perspective on this conformational trend. The RDF between two atoms gives the probability of finding them at a set distance from each other. The hairpin conformation presented in Fig. 4 could be a consequence of favourable electrostatic attractions between triplets of ionisable sites along the polymer chain, highlighting the benefits of using CpHMD to identify protonation-conformation relationships. This should show up in the RDF between the primary O-atom of one site (n) and the primary O-atom of the n − 3rd and n + 3rd site.
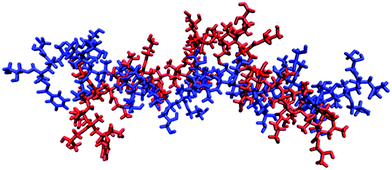 | ||
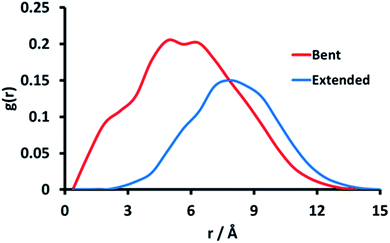
| Fig. 4 Two snapshots of the pGMA generated by simulation when it is stretched out (blue) and has a bend in the middle (red), with a solution salt concentration of 0 M. | ||
Fig. 5 shows the RDF between site 14, which is at the apex of the bending motion shown in Fig. 3, and near-adjacent sites 17 and 20 in the polymer chain. The RDFs indicate that the greatest probability of finding the O-atoms of sites 17 and 20 closest to the O-atom of site 14 is approximately 4.5 Å for the hairpin conformation, while for the extended conformation it is approximately 7 Å. Fig. 5 therefore indicates the formation of microdomain-like features, even within this relatively small pGMA 30-mer. This behaviour is reproduced for other hairpin conformations, which suggests that ionisable sites spaced 3 units apart are able to interact favourably to form small localised microdomains in pGMA.
In the simulations we also explored the effect of increasing the concentration of monovalent salt on the ionisation behaviour of the pGMA 30-mer. The predicted pKa from the CpHMD simulation at a salt concentration of 0.5 M NaCl is 7.1 ± 0.25 which again agrees well with the experimental titration value of 7.1 ± 0.2 (cf. the pKa of the pGMA at 0 M was 7.4 ± 0.25). The decrease in pKa on increasing the salt concentration from 0 to 0.5 M is consistent with an enhanced screening of the electrostatic repulsion between adjacent deprotonated units, which causes the sites to be more acidic by approximately 0.4 pKa units. Classical Debye–Hückel (DH) theory,77 can account at a mean-field level of approximation for changes from an ideal solution to an electrolyte. DH also predicts a pKa shift of ca. 0.3 units which is in excellent agreement with the CpHMD shift noted above. Of course DH theory does not provide the level of atomic detail obtained by CpHMD, which is important for resolving other issues relating to this system.
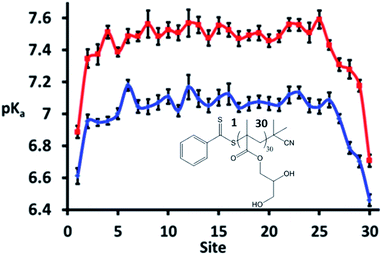
A strength of simulations that include reactions, such as the CpHMD methods, is the ability to follow specific single sites along the polymer chain. The site specific pKa is plotted in Fig. 6 and shows that the ω and α ends of the polymer (numbered sites 1 and 30 here) are more acidic than those near the centre of the molecule. This can be attributed to a reduced electrostatic repulsion from neighbouring sites in that region; the termini of the polymer are neutral, and as such it is easier to ionise units near these regions. Similar behaviour has been noted previously by Castelnovo and co-workers.51 Of note is that sites 6 to 26 have, within statistics, the same pKa value at the two salt concentrations with these pKa values slightly higher than the recorded average pKa, particularly at 0 M.
Thus it can be concluded that the average, macroscopic, pKa of a polymer recorded by experiment is not necessarily indicative of the microscopic pKa of its constituent units. The consistent microscopic pKa recorded across the polymer suggests that, at pH = pKa, the synergy seen between triplets of ionisable units is likely to be reversible and dynamic. It is foreseeable that, as the pH is varied further from the pKa, the synergy between triplets will become less reversible and more long-lived. Under these circumstances, CpHMD is ideally suited to identify these triplets; both through the MD snapshots and also the emergence of pronounced peaks and troughs in the microscopic pKas.
Conclusions
This work has used both experimental and computational procedures to study the ionisation and titration behaviour of a pGMA. One of the input requirements for a CpHMD simulation is the pKa of the ionisable monomer, which is usually known for common amino acids but less so for more unusual monomers. By using a monomer pKa which has been measured experimentally we show that CpHMD can reproduce both the experimental pKa and the titration behaviour of pGMA as a function of salt concentration, the latter being found to agree well with Debye–Hückel theory for this benchmark system.One of the strengths of CpHMD lies in its ability to calculate routinely, with modest computational resources, the pKa's of all the sites in the molecule in a single simulation in a way which incorporates the natural synergy between adjacent sites at various states of protonation. Guided by experimental input, the conformational states likely to be adopted by the real polymer at different pH values can be generated and linked to the protonation states of the units along the polymer backbone. Such detail cannot be determined by classical MD or experiment and, as briefly explored here, can be used to design pH-responsive polymers which can trap and release small molecules within micro-domains depending on the system acidity. Furthermore, this work lays the groundwork for using CpHMD to help assist in the design of new polymers78 as a guide to experimental synthesis which may enable the preparation of responsive and functional nanomaterials for applications as diverse as electronics or healthcare.
Acknowledgements
M. S. B., D. M. H., and D. D. thank the Imperial College High Performance Computing Service. (http://www.imperial.ac.uk/ict/services/teachingandresearchservices/highperformancecomputing) for providing computational resources. M. S. B. thanks BP for funding his research postdoctoral fellowship and D. B. W. thank the EPSRC and BP for the award of a CASE studentship. K. E. B. D. and R. K. OR thank the ERC (grant no. 615142) and University of Warwick for funding. D. D. also acknowledges the support of the EPSRC via the Established Career Fellowship EP/N025954/1. All data reported in this article can be made available by contacting the corresponding authors or by emailing E-mail: tribology@imperial.ac.uk.References
- M. I. Gibson and R. K. O'Reilly, Chem. Soc. Rev., 2013, 42, 7204–7213 RSC.
- R. Liu, M. Fraylich and B. Saunders, Colloid Polym. Sci., 2009, 287, 627–643 CAS.
- D. Roy, W. L. A. Brooks and B. S. Sumerlin, Chem. Soc. Rev., 2013, 42, 7214–7243 RSC.
- F. D. Jochum and P. Theato, Chem. Soc. Rev., 2013, 42, 7468–7483 RSC.
- A. O. Moughton, J. P. Patterson and R. K. O'Reilly, Chem. Commun., 2011, 47, 355–357 RSC.
- S. Dai, P. Ravi and K. C. Tam, Soft Matter, 2008, 4, 435–449 RSC.
- D. Schmaljohann, Adv. Drug Delivery Rev., 2006, 58, 1655–1670 CrossRef CAS PubMed.
- K. E. B. Doncom, C. F. Hansell, P. Theato and R. K. O'Reilly, Polym. Chem., 2012, 3, 3007–3015 RSC.
- S. Dai, P. Ravi and K. C. Tam, Soft Matter, 2009, 5, 2513–2533 RSC.
- T. Yoshida, T. C. Lai, G. S. Kwon and K. Sako, Expert Opin. Drug Delivery, 2013, 10, 1497–1513 CrossRef CAS PubMed.
- K. M. Huh, H. C. Kang, Y. J. Lee and Y. H. Bae, Macromol. Res., 2012, 20, 224–233 CrossRef CAS.
- S. Mura, J. Nicolas and P. Couvreur, Nat. Mater., 2013, 12, 991–1003 CrossRef CAS PubMed.
- O. Onaca, R. Enea, D. W. Hughes and W. Meier, Macromol. Biosci., 2009, 9, 129–139 CrossRef CAS PubMed.
- L. Zhu, Y. Shi, C. Tu, R. Wang, Y. Pang, F. Qiu, X. Zhu, D. Yan, L. He, C. Jin and B. Zhu, Langmuir, 2010, 26, 8875–8881 CrossRef CAS PubMed.
- T. Einfalt, R. Goers, I. A. Dinu, A. Najer, M. Spulber, O. Onaca-Fischer and C. G. Palivan, Nano Lett., 2015, 15, 7596–7603 CrossRef CAS PubMed.
- D. Grafe, J. Gaitzsch, D. Appelhans and B. Voit, Nanoscale, 2014, 6, 10752–10761 RSC.
- H. A. Zayas, A. Lu, D. Valade, F. Amir, Z. Jia, R. K. O'Reilly and M. J. Monteiro, ACS Macro Lett., 2013, 2, 327–331 CrossRef CAS.
- A. Lu, D. Moatsou, D. A. Longbottom and R. K. O'Reilly, Chem. Sci., 2013, 4, 965–969 RSC.
- Y. Xie, M. Wang, X. Wu, C. Chen, W. Ma, Q. Dong, M. Yuan and Z. Hou, ChemPlusChem, 2016, 81, 541–549 CrossRef CAS.
- J. Zhang, M. Zhang, K. Tang, F. Verpoort and T. Sun, Small, 2014, 10, 32–46 CrossRef CAS PubMed.
- A. Ievins, X. Wang, A. O. Moughton, J. Skey and R. K. O'Reilly, Macromolecules, 2008, 41, 2998–3006 CrossRef CAS.
- Y. Kotsuchibashi, Y. Wang, Y.-J. Kim, M. Ebara, T. Aoyagi and R. Narain, ACS Appl. Mater. Interfaces, 2013, 5, 10004–10010 CAS.
- C. de las Heras Alarcón, B. Twaites, D. Cunliffe, J. R. Smith and C. Alexander, Int. J. Pharm., 2005, 295, 77–91 CrossRef PubMed.
- N. P. Gerard, R. L. Eddy, T. B. Shows and C. Gerard, J. Biol. Chem., 1990, 265, 20455–20462 CAS.
- J.-M. Y. Carrillo and A. V. Dobrynin, Macromolecules, 2011, 44, 5798–5816 CrossRef CAS.
- Q. Liao, A. V. Dobrynin and M. Rubinstein, Macromolecules, 2003, 36, 3386–3398 CrossRef.
- D. J. Sandberg, J.-M. Y. Carrillo and A. V. Dobrynin, Langmuir, 2007, 23, 12716–12728 CrossRef CAS PubMed.
- H. Dong, H. Du, S. R. Wickramasinghe and X. Qian, J. Phys. Chem. B, 2009, 113, 14094–14101 CrossRef CAS PubMed.
- U. P. Strauss and M. S. Schlesinger, J. Phys. Chem., 1978, 82, 571–574 CrossRef CAS.
- I. Borukhov, D. Andelman, R. Borrega, M. Cloitre, L. Leibler and H. Orland, J. Phys. Chem. B, 2000, 104, 11027–11034 CrossRef CAS.
- J. D. Ziebarth and Y. Wang, Biomacromolecules, 2010, 11, 29–38 CrossRef CAS PubMed.
- H. Lee, S. H. Son, R. Sharma and Y.-Y. Won, J. Phys. Chem. B, 2011, 115, 844–860 CrossRef CAS PubMed.
- O. Colombani, E. Lejeune, C. Charbonneau, C. Chassenieux and T. Nicolai, J. Phys. Chem. B, 2012, 116, 7560–7565 CrossRef CAS PubMed.
- E. L. Mehler, M. Fuxreiter, I. Simon and B. E. Garcia-Moreno, Proteins: Struct., Funct., Bioinf., 2002, 48, 283–292 CrossRef CAS PubMed.
- F. B. Sheinerman, R. Norel and B. Honig, Curr. Opin. Struct. Biol., 2000, 10, 153–159 CrossRef CAS PubMed.
- M. Schaefer, M. Sommer and M. Karplus, J. Phys. Chem. B, 1997, 101, 1663–1683 CrossRef CAS.
- J. Kim, J. Mao and M. R. Gunner, J. Mol. Biol., 2005, 348, 1283–1298 CrossRef CAS PubMed.
- A. H. Elcock and J. A. McCammon, J. Mol. Biol., 1998, 280, 731–748 CrossRef CAS PubMed.
- Z. S. Hendsch, T. Jonsson, R. T. Sauer and B. Tidor, Biochemistry, 1996, 35, 7621–7625 CrossRef CAS PubMed.
- K. P. Tan, T. B. Nguyen, S. Patel, R. Varadarajan and M. S. Madhusudhan, Nucleic Acids Res., 2013, 41, W314–W321 CrossRef PubMed.
- N. Uddin, T. H. Choi and C. H. Choi, J. Phys. Chem. B, 2013, 117, 6269–6275 CrossRef CAS PubMed.
- W. L. Jorgensen, J. M. Briggs and J. Gao, J. Am. Chem. Soc., 1987, 109, 6857–6858 CrossRef CAS.
- W. L. Jorgensen and J. M. Briggs, J. Am. Chem. Soc., 1989, 111, 4190–4197 CrossRef CAS.
- C. Lim, D. Bashford and M. Karplus, J. Phys. Chem., 1991, 95, 5610–5620 CrossRef CAS.
- J. Ho and M. L. Coote, Theor. Chem. Acc., 2009, 125, 3–21 CrossRef.
- H. Dong, H. Du and X. Qian, J. Phys. Chem. B, 2009, 113, 12857–12859 CrossRef CAS PubMed.
- J. Landsgesell, C. Holm and J. Smiatek, J. Chem. Theory Comput., 2017, 13, 852–862 CrossRef CAS PubMed.
- M. Ullner and B. Jönsson, Macromolecules, 1996, 29, 6645–6655 CrossRef CAS.
- M. Ullner, B. Jönsson, B. Söderberg and C. Peterson, J. Chem. Phys., 1996, 104, 3048–3057 CrossRef CAS.
- M. Ullner and C. E. Woodward, Macromolecules, 2000, 33, 7144–7156 CrossRef CAS.
- M. Castelnovo, P. Sens and J.-F. Joanny, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 1, 115–125 CrossRef CAS.
- J. Baschnagel, J. P. Wittmer and H. Meyer, arXiv:cond-mat/0407717 [cond-mat.soft], 2014.
- J. Landsgesell, C. Holm and J. Smiatek, J. Chem. Theory Comput., 2017, 13, 852–862 CrossRef CAS PubMed.
- G. B. Goh, J. L. Knight and C. L. Brooks, J. Chem. Theory Comput., 2013, 9, 935–943 CrossRef CAS PubMed.
- R. Bürgi, P. A. Kollman and W. F. van Gunsteren, Proteins: Struct., Funct., Bioinf., 2002, 47, 469–480 CrossRef PubMed.
- A. Aleksandrov, S. Polydorides, G. Archontis and T. Simonson, J. Phys. Chem. B, 2010, 114, 10634–10648 CrossRef CAS PubMed.
- J. Mongan, D. A. Case and J. A. McCammon, J. Comput. Chem., 2004, 25, 2038–2048 CrossRef CAS PubMed.
- J. Mongan and D. A. Case, Curr. Opin. Struct. Biol., 2005, 15, 157–163 CrossRef CAS PubMed.
- M. S. Lee, F. R. Salsbury and C. L. Brooks, Proteins: Struct., Funct., Bioinf., 2004, 56, 738–752 CrossRef CAS PubMed.
- M. S. Bodnarchuk, D. M. Heyes, D. Dini, S. Chahine and S. Edwards, J. Chem. Theory Comput., 2014, 10, 2537–2545 CrossRef CAS PubMed.
- J. L. Knight and C. L. Brooks, J. Comput. Chem., 2009, 30, 1692–1700 CrossRef CAS PubMed.
- S. Donnini, F. Tegeler, G. Groenhof and H. Grubmüller, J. Chem. Theory Comput., 2011, 7, 1962–1978 CrossRef CAS PubMed.
- H. Lee, S. H. Son, R. Sharma and Y. Y. Won, J. Phys. Chem. B, 2011, 115, 844–860 CrossRef CAS PubMed.
- L. P. D. Ratcliffe, A. J. Ryan and S. P. Armes, Macromolecules, 2013, 46, 769–777 CrossRef CAS.
- C. S. Gudipati, M. B. H. Tan, H. Hussain, Y. Liu, C. He and T. P. Davis, Macromol. Rapid Commun., 2008, 29, 1902–1907 CrossRef CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. E. Cheatham III, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, AMBER2014, University of California, San Francisco, 2014 Search PubMed.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- A. Onufriev, D. A. Case and D. Bashford, J. Comput. Chem., 2002, 23, 1297–1304 CrossRef CAS PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- J. Landsgesell, J. Smiatek and C. Holm, 2017, arXiv:1702.04911 [cond-mat.soft].
- M. Qi, S. Duan, B. Yu, H. Yao, W. Tian and F.-J. Xu, Polym. Chem., 2016, 7, 4334–4341 RSC.
- G. Fundueanu, M. Constantin, C. Stanciu, G. Theodoridis and P. Ascenzi, J. Mater. Sci.: Mater. Med., 2009, 20, 2465 CrossRef CAS PubMed.
- S. Yamaguchi, R. Kawabata, E. Yamamoto and T. Nagamune, Polym. J., 2014, 46, 880–886 CrossRef CAS.
- J. L. Garcés, G. J. M. Koper and M. Borkovec, J. Phys. Chem. B, 2006, 110, 10937–10950 CrossRef PubMed.
- R. A. Cox, Angew. Chem., Int. Ed., 2013, 52, 7638 CrossRef CAS.
- P. Cotanda, D. B. Wright, M. Tyler and R. K. O'Reilly, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 3333–3338 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: 1H and 13C NMR spectra of the GMA monomer. Characterisation data, SEC trace and polymerisation behaviour of pGMA. See DOI: 10.1039/c6ra27785c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |