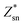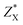Anisotropic phonon transport and lattice thermal conductivities in tin dichalcogenides SnS₂ and SnSe₂

Abstract

In recent years, layered semiconductor tin dichalcogenides, SnX₂ (X = S and Se), have received great attention owing to their wide applications in numerous fields. However, theoretical studies on their phonon transport properties and lattice thermal conductivities are very rare. Herein, we carry out comprehensive investigations on the phonon transport properties and heat transfer phenomena in tin dichalcogenides using first-principles calculations combined with the Boltzmann transport theory, and compare them with the recent popular thermoelectric materials SnS (SnSe) and widely studied typical TMD MoS₂ (MoSe₂). The obtained total thermal conductivities of SnS₂ and SnSe₂ agree well with the experimental measured values. The ultralow out-of-plane thermal conductivities of both materials may be useful for thermoelectric applications. The contributions of different phonon branches to the total lattice thermal conductivities are evaluated, and the results suggest that it would be difficult for alloying to reduce κ_L because the contribution of the optical branches is rather small compared with SnS and SnSe. Subsequently, we investigated the size dependence of the thermal conductivities and found that nanostructuring may be efficient to further reduce κ_L since the mean free paths of the dominant phonon modes are relatively long. This conclusion is consistent with recent experimental findings, where the κ_L of SnS₂ was found to evidently decrease with a decrease in the thickness of SnS₂ films. We believe that this phenomenon may also exist in SnSe₂, which may demonstrate a much better thermoelectric performance than that of SnS₂ because of its higher anharmonicity than that of SnS₂, leading to much lower thermal conductivity.

---

1. Introduction

Transition metal dichalcogenides (TMDs) (MX₂, where M denotes a transition metal and X denotes a chalcogen) are currently attracting increasing interest as a group of mostly semiconducting two-dimensional (2D) and few-layer materials that complement other 2D systems, such as graphene^1,2 or h-BN.^3,4 Among all the TMDs, tin dichalcogenides (SnS₂ and SnSe₂) (hereafter denoted as SnX₂) are more earth-abundant and environmentally-friendly. Recently, they have attracted much attention due to their great potential in a wide spectrum of applications, e.g., thin film solar cells, optoelectronic devices, field-effect transistors (FETs), lithium-ion batteries and portable electronic information storage devices.^5–12 In spite of the large amount of research on their structural, electronic and optical properties,^11–16 only limited information is now available concerning the thermoelectric performances of SnS₂ and SnSe₂.^17–19 In the recent theoretical study by B. Sun et al.,¹⁸ it was shown that the peak ZT can reach as high as 0.96 for SnS₂ and 0.88 for SnSe₂ at room temperature, which shows their potential for TE applications. Moreover, in another recent experimental study,¹⁹ the authors suggest that SnS₂ nanosheets are negatively correlated thermoelectric materials with a negative correlation between electrical and thermal conductivity, that is, as the thickness of SnS₂ decreases, s increases, whereas κ decreases. Naturally, this is an important finding since most TE materials demonstrate decreased thermal conductivity when their electrical conductivity increases. Although the lattice thermal conductivity is crucial to the thermoelectric performance of TE materials, to date, theoretical reports that discuss the lattice thermal conductivity of SnX₂ are still lacking, with the exception of one recent study¹⁸ that considered the theoretically minimum lattice thermal conductivity (κ_min). On the other hand, several of the experimentally measured values of thermal conductivity differ enormously.^19–23 Furthermore, a complete and comparative prediction and understanding of the underlying phonon transport properties of SnS₂ and SnSe₂ are key to expanding the range of their application in nanoelectronics, optoelectronics and thermoelectrics; however, thus far, the phonon transport properties of these two dichalcogenides are still less known. Therefore, it is necessary to give a detailed study of their phonon transport and accurately predict their intrinsic thermal conductivity. Another fact that should be noted is that the present materials have several similarities with SnS and SnSe, which have been recently found to display high thermoelectric efficiencies with great potential for the conversion of heat to electricity.^24,25 For example, they all are constituted of Sn and S (Se) that tend to form weak atomic bonds and usually lead to strong anharmonicity. In addition, they all have anisotropic (orthorhombic) layered structures and the interplanar van der Waals forces usually bring ultralow out-of-plane thermal conductivity. Then, the question arises of whether SnX₂ could perform well as thermal insulators similar to SnS and SnSe.

Herein, we conduct comprehensive investigations into the anisotropic phonon transport properties and intrinsic thermal conductivities of SnX₂ based on first-principles calculations. A systematic study of the lattice dynamics are performed and related properties, including Born effective charge (BEC), dielectric constant (DC) and frequencies of optical modes, together with their irreducible representation are given. Then, the lattice thermal transports of both materials are calculated by solving the phonon Boltzmann transport equation. The obtained thermal conductivities of SnS₂ and SnSe₂ are close to the experimental measured values. The contributions of each phonon branch to the total thermal conductivities, phonon lifetimes and the dependence of thermal conductivities for both materials are evaluated, and the underlying mechanism governing their diverse thermal transport behavior are analyzed and discussed in detail.

2. Computational details

First-principles calculations were performed using the density functional theory as implemented in the Vienna ab initio simulation package (VASP)^26–28 with a plane wave energy of up to 500 eV in the expansion of the electronic wave function. The local density approximation (LDA),²⁹ which is typically used for layered structures where van der Waals interactions are important, was chosen as the exchange–correlation functional of DFT. The valence electron configurations considered in this calculation are Sn (4d¹⁰5s²5p²), S (3s²3p⁴), and Se (4s²4p⁴). The internal coordinates and lattice constants were optimized until the Hellmann–Feynman forces acting on each atom became less than 10⁻³ eV Å⁻¹. The convergence for energy was chosen as 10⁻⁶ eV between two steps, and a Monkhorst–Pack k-mesh of 7 × 7 × 5 was used to sample the Brillouin zone in the structure optimization. Phonon frequencies and the corresponding thermodynamic properties were obtained using the PHONOPY³⁰ program. Moreover, an iterative self-consistent method was used for solving the phonon Boltzmann transport equation to calculate the lattice thermal conductivity with the ShengBTE³¹ code, which is based on the second-order (harmonic) and third-order (anharmonic) interatomic force constants (IFCs) combined with an iterative self-consistent algorithm to solve the BTE, and has also successfully predicted the thermal conductivities of many materials.^32–38 We used 4 × 4 × 2 supercells containing 96 atoms with 3 × 3 × 3 k-mesh for calculations of second-order and third-order IFCs for both SnS₂ and SnSe₂. In the calculations of the third-order IFCs, we considered third-order interatomic force constants up to the fourth shell of neighbors. Well-converged 20 × 20 × 11 q-meshes were used in the calculation of the lattice thermal conductivity of SnX₂.

3. Results and discussion

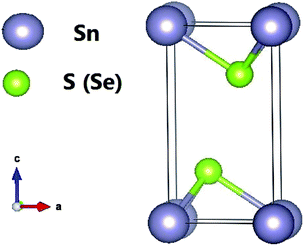
Tin dichalcogenides (SnS₂ and SnSe₂) crystallize in the hexagonal closed packed CdI₂-type structure with P3̄m1 symmetry (space group 164). They have three atoms in the unit cell, which extends over only one sandwich layer as seen in Fig. 1. The intralayer metal (Sn)–chalcogenide (S or Se) bonds are predominantly covalent in nature, whereas the layers themselves are coupled by weak van der Waals bonds. The Sn atoms provide four electrons to fill the bonding states of SnX₂ such that the oxidation states of the Sn and S (or Se) atoms are +4 and −2, respectively. Our relaxed lattice constants resulting from LDA are a = 3.63 Å and c = 5.71 Å for SnS₂, and a = 3.80 Å and c = 5.90 Å for SnSe₂, which agree well with previous ab initio calculations¹³ but are slightly underestimated compared with the experimental results.³⁹ This is reasonable because of the overbinding effect of LDA.

Fig. 1 Crystal structures of SnX₂ (X = S and Se).

3.1 Lattice dynamics properties

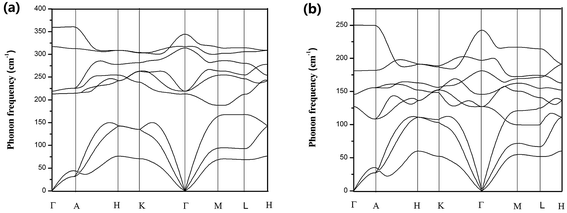
The harmonic phonon dispersions of SnX₂ as obtained from the force constants and considering the longitudinal optical–transverse optical (LO–TO) splitting are shown in Fig. 2. The LO–TO splitting is predicted by incorporating the effects of long-range Coulomb interactions based on the Born effective charges and high-frequency dielectric constants calculated by first-principles. Our calculated Born effective charges and dielectric constants are illustrated in Table 1. It is worth noting that the ionic contribution to the dielectric constant of SnS₂ along the out-of-plane (c axis) direction is very small (0.69), which indicates that SnS₂ holds more two-dimensional characteristics than SnSe₂. This is consistent with the fact that the out-of-plane thermal conductivity of SnS₂ is much lower than that of SnSe₂, which will be discussed later.

Fig. 2 Calculated phonon dispersions for (a) SnS₂ and (b) SnSe₂.

Table 1 Calculated Born effective charges, high-frequency dielectric tensors (ε^∞) and ionic contributions (ε^ion) of SnX₂ (X = S and Se)

				ε^∞	ε^ion
SnS2	In-plane	4.91	−2.50	9.12 (8.5)^40	9.91 (10.3)^40
	Out-of-plane	2.08	−1.03	7.51 (6.7)^40	0.69 (0.6)^40
SnSe2	In-plane	5.24	−2.78	16.16	12.02
	Out-of-plane	2.59	−1.33	17.78	1.15

---

In general, SnS₂ and SnSe₂ show very similar dispersion curves along different high symmetry lines except (1) the frequencies of the optical branches of SnS₂ are significantly higher, which is mainly due to the smaller atomic mass of S. (2) There exists an evident phonon gap (about 30 cm⁻¹) between the acoustic branches and optical branches for SnS₂ owing to its larger cation/anion mass ratio, whereas there is no similar gap for SnSe₂.

In comparison with the phonon dispersions of SnS and SnSe,³⁴ a big difference is that the phonon spectrum of SnS and SnSe are characterized by markedly dispersive optical phonon branches, which result in significant group velocities of the optical phonon branches, whereas there are no similar phenomena for SnS₂ and SnSe₂. Another important feature of the phonon spectra of SnX₂ is that along the Γ–A high-symmetry k-paths, the phonon dispersion curves of both materials are almost flat, particularly for SnS₂. This means that the phonon group velocities along the out-of-plane direction are very low, which can be attributed to ultra weak interactions between the layers. In fact, as revealed by Babu Ram et al.,⁴¹ the interlayer coupling of SnS₂ is much weaker than that of MoS₂.

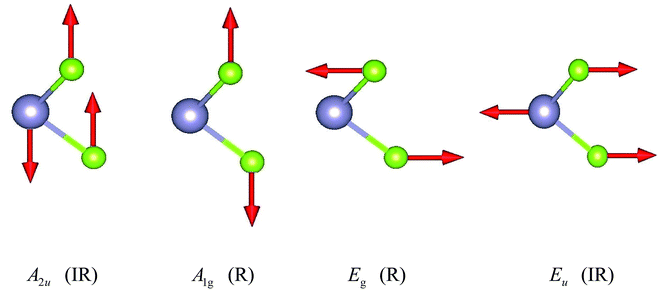
The unit cell of SnX₂ contains three atoms, and therefore there are total of nine vibrational modes. Group theoretical symmetry analysis yields the irreducible representations of the Γ-point phonon modes: Γ = A_1g + 2A_2u + E_g + 2E_u. The acoustic modes are A_2u + E_u. Thus, there are four optical modes, of which A_1g + E_g are Raman active and the other two A_2u + E_u are infrared active. Note that the double degenerate E_u mode has two orthogonal eigenvectors, which result in LO–TO splitting when the phonon propagates in the ab plane, that is, E_u(LO) and E_u(TO) modes. The electrostatic interaction between the ions pushes the longitudinal optical (LO) phonons to high frequency, whereas the transversal optical (TO) phonons are unaffected. Similarly, the LO–TO splitting effect also separate the A_2u mode into A_2u(LO) and A_2u(TO) modes. In Table 2 we list the calculated frequencies of the optical vibrational modes considering the LO–TO splitting and compare experimentally measured Raman values since the A_1g and E_g symmetries are easily distinguished experimentally.

Table 2 Calculated frequencies of the optical vibrational modes at the Brillouin zone center Γ point for SnX₂ and comparison with other reports

		A2u(LO)	A2u(TO)	A1g	Eu(LO)	Eg	Eu(TO)
SnS2	Calc^this work	358	342	317	314	210	215
	Calc^42	356	340	315	314	208	205
	Expt^39			313.9		205
SnSe2	Calc^this work	250	242	183	199	126	145
	Calc^42	248	241	186	204	113	144
	Expt^39			185.9		118.9

---

The specific oscillation patterns of the optical modes are shown in Fig. 3. We can find that E_g and E_u correspond to in-plane vibration modes, whilst A_2u and A_1g are out-of-plane vibration modes. In addition, the Raman mode A_1g and E_g species involve exclusively chalcogen atom vibrations.

Fig. 3 Irreducible representations for SnX₂ at the Brillouin zone center Γ point.

3.2 Lattice thermal conductivity

Fig. 4 shows the temperature-dependent κ_L of SnS₂ and SnSe₂ along the in-plane (a axis) and out-of-plane (c axis) directions in comparison with the experimental measured data at 300 K.^19–21 We can see that the lattice thermal conductivities decrease with an increase in temperature following the T⁻¹ relationship, which implies that the thermal conductivity is given by the anharmonic phonon–phonon interactions. In addition, the thermal conductivities of both materials are extremely anisotropic; for example, the ratio of κ^in-plane_L/κ^out-plane_L for SnSe₂ at 300 K is as large as 7.1, which is much higher than that of MoSe₂ (∼5.0)³³ and SnSe (∼2.5),³⁴ showing much larger anisotropy of the present materials. The large anisotropy between the in-plane and out-of-plane thermal conductivity is largely due to the much smaller group velocities in the c direction. This is the result of the interlayer (vdW) interactions being much weaker than the intralayer Sn-X covalent bonding. The average lattice thermal conductivity of bulk SnS₂ and SnSe₂ can be evaluated as 2/3κ^in-plane_L + 1/3κ^out-plane_L.³³ Our calculated average κ_L values at room temperature (8.2 W mK⁻¹ for SnS₂ and 5.6 W mK⁻¹ for SnSe₂) are close to the historically measured κ_L of bulk single crystals (10 W mK⁻¹ (ref. 20) for SnS₂ and 7.29 W mK⁻¹ (ref. 21) for SnSe₂ at 300 K). Although the calculated thermal conductivity for SnS₂ is much larger than the experimental value for 22 nm-thick nanosheets (4.63 W mK⁻¹),¹⁹ it is perfectly reasonable since in 2D SnS₂, the surface phonon scattering may be greatly enhanced and thus possibly decrease the lattice thermal conductivity. In comparison with other typical layer materials, the lattice thermal conductivities of SnX₂ are much larger than that of SnS (∼1.6 W mK⁻¹ (ref. 34) at 300 K calculated using the same iterative self-consistent method with the ShengBTE code and the experimental value of ∼1.7 W mK⁻¹ (ref. 43)) and SnSe (∼1.5 W mK⁻¹ (ref. 34) at 300 K calculated with the ShengBTE code and the experimental value of ∼0.67 W mK⁻¹ (ref. 24)), but greatly lower than that of MoS₂ (∼67 W mK⁻¹ (ref. 36)) at 300 K calculated with the ShengBTE code and the experimental value of 110 ± 20 W mK⁻¹ (ref. 44)) and MoSe₂ (∼60 W mK⁻¹ (ref. 33) at 300 K) calculated using the ShengBTE code.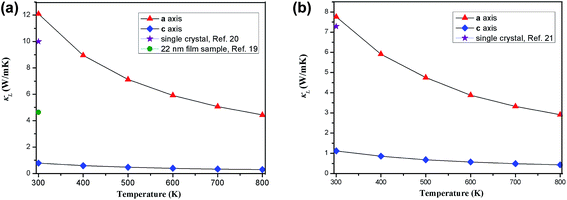

Fig. 4 Calculated temperature dependent lattice thermal conductivities of (a) SnS₂ and (b) SnSe₂ along the a axis and c axis, in comparison with the experimental data at 300 K.

What is even more important is that the out-of-plane thermal conductivities for both materials are found to be unexpectedly low; for example, the calculated room-temperature κ_L of SnS₂ along the out-of-plane direction is 0.78 W mK⁻¹, which approaches the predicted amorphous limit (0.47 W mK⁻¹)¹⁸ and is even lower than that of SnS (0.8 W mK⁻¹ along the out-of-plane direction at room temperature).³⁴ Furthermore, these values are remarkably low among most of the TMDs; for example, the calculated out-of-plane thermal conductivity using the same method for MoS₂ is 2.3 W mK⁻¹ (ref. 36) (the experimental out-of-plane thermal conductivity of bulk MoS₂ at 300 K is 1.05 W mK⁻¹ (ref. 45)) and that of WTe₂ is 1.04 W mK⁻¹.³⁸ This implies that the thermoelectric performance of SnS₂ along the out-of-plane direction may be as good as that of SnS. In fact, it is difficult to definitely say how its thermoelectric performance would be because the thermoelectric figure of merit is determined by several strongly coupled quantities and the lattice thermal conductivity is only one of them, but at least, we can conclude that the present material is a good thermal insulator in the out-of-plane direction. Unfortunately, the experimentally measured thermal conductivity values of the out-of-plane direction are not yet available in the literature.

Using the obtained thermal conductivity values of SnX₂, its thermal diffusivity can be derived from the formula α = κ_L/C_pρ (κ_L is thermal conductivity, C_p is heat capacity and ρ is density). Thermal diffusivity is one of the crucial parameters to investigate the thermal transportation process, which indicates that the rate of temperature changes and reflects the correlation between thermal conductivity and heat capacity.^46–49 The TAPP software⁵⁰ gives heat capacity values of C^S_p = 252 J kg K⁻¹ for SnS₂ and C^Se_p = 261 J kg K⁻¹ for SnSe₂ at room temperature. The density of SnX₂ is easily calculated as ρ_S = 4700 kg m⁻³ for SnS₂ and ρ_Se = 6200 kg m⁻³. Then, we derive the thermal diffusivity α_S = 6.9 × 10⁻⁶ m² s⁻¹ for SnS₂ and α_Se = 3.4 × 10⁻⁶ m² s⁻¹ for SnSe₂. Clearly, the thermal diffusivity of SnS₂ is much larger than that of SnSe₂ mainly due to its larger thermal conductivity and smaller mass density. Our calculated thermal diffusivity for SnSe₂ is close to the historically calculated value (α_Se = 5.4 × 10⁻⁶ m² s⁻¹ at 300 K);²² however, the thermal diffusivity of bulk SnS₂ was not found in the literature.

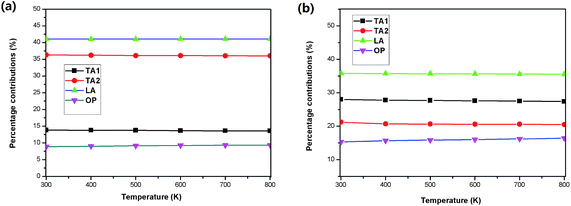
We then determined the contribution of the different phonon modes to the total lattice thermal conductivities for the two materials, as illustrated in Table 3. It is found that along the in-plane direction, the contribution of the optical branches to the total thermal conductivity at room temperature for both SnS₂ and SnSe₂ is small, whereas along the out-of-plane direction, the contribution of the optical branches is relatively large, particularly for SnS₂, where the contribution of the optical branches is as large as 22%. This may be one of the reasons for the ultralow out-of-plane thermal conductivity since the optical branches usually possess much smaller group velocities and much shorter phonon lifetimes than those of the acoustic branches. The small contributions of the optical phonons of SnX₂ is an obvious difference with SnX, for instance, the optical phonon branches contribute ∼60% to the total thermal conductivity of SnSe.³⁴ Therefore, alloying may not be an effective strategy for further reducing the κ_L of SnX₂.

Table 3 Contributions from phonon branches to the total thermal conductivity for SnX₂ at 300 K

		TA1	TA2	LA	Optic
SnS2	In-plane	16%	35%	43%	6%
	Out-of-plane	30%	24%	24%	22%
SnSe2	In-plane	14%	36%	41%	9%
	Out-of-plane	28%	22%	35%	15%

---

Furthermore, the temperature dependence of contributions from the phonon branches is plotted in Fig. 5 using SnSe₂ as an example. One can see that the contributions of all the phonon modes along the in-plane direction are very insensitive to temperature, where the percentage contributions of the acoustic phonon branches slightly decrease with an increase in temperature, and at the same time, the contribution of the optical phonon branches slightly increases with an increase in temperature. While along the out-of-plane direction, the increase tendency of the contributions of the optical branches becomes evident and reaches 16.5% at 800 K, indicating that higher frequency optical phonons are excited at higher temperatures.

Fig. 5 Temperature dependence of the percentage contributions of the phonon branches to the total lattice thermal conductivity for SnSe₂ along the (a) in-plane direction and (b) out-of-plane direction.

Considering the significant difference in the contribution of different phonon branches to the total thermal conductivity in SnX₂, it is worthwhile to examine the relaxation times of the phonon modes as functions of phonon frequency, as displayed in Fig. 6. It is found that the relaxation times of the phonon modes for SnS₂ and SnSe₂ are very close to each other. Otherwise, the relaxation times of the acoustic branch are one order of magnitude bigger than that of the optical branches, which indicates small contributions of optical phonons to the total κ_L. In comparison with SnX and MoX₂, the relaxation times of SnX₂ are much shorter than that of MoX₂, although slightly longer than that of SnX. For example, the calculated longest relaxation time of acoustic phonons for SnS₂ is about 160 ps, whilst that of MoS₂ is as large as 10⁴ ps,³⁶ and that of SnS is only about 28 ps.³⁴

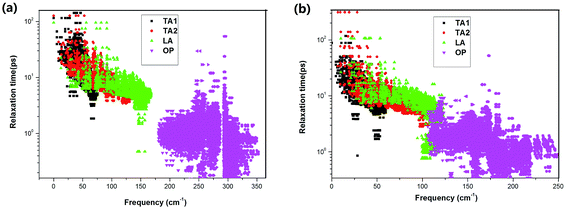Fig. 6 Frequency-dependent phonon relaxation times of the acoustic (AP) and optical phonons (OP) for (a) SnS₂ and (b) SnSe₂ at 300 K.

Since the phonon lifetimes of these two materials are comparable, what is the main mechanism that leads to the higher κ_L in SnS₂? We next calculated the phonon group velocities of SnX₂ around the Γ point. Our calculated sound velocity in the long-wavelength limit of SnS₂ is about 5060 m s⁻¹ along the in-plane direction, and that of SnSe₂ is only 4050 m s⁻¹. Thus, the conclusion is clear that it is just the relatively larger phonon group velocities combined with the higher phonon frequencies of SnS₂ that induce the much higher κ_L than SnSe₂. We also evaluated the anharmonic phase space volume P₃, that is, the number of allowed three-phonon processes of the present two compounds, which is usually used to quantify the anharmonicity of a certain material. The obtained P₃ of SnS₂ is 0.54 × 10⁻² eV⁻¹, and that of SnSe₂ is 0.83 × 10⁻² eV⁻¹; therefore it is clear that the anharmonicity of SnSe₂ is higher than that of SnS₂. In comparison with other low-conductivity compounds, the anharmonic phase space volume P₃ is slightly larger than that of Si (0.47 × 10⁻² eV⁻¹),³² but much smaller than that of SnSe (1.9 × 10⁻² eV⁻¹).³² Furthermore, the mode Grüneisen parameters are calculated as 1.18 for SnS₂ and 1.21 for SnSe₂, which also indicates that the anharmonicity of SnSe₂ is higher than that of SnS₂.

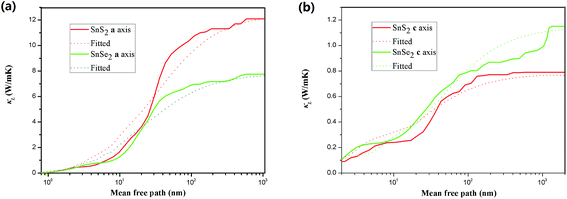
Finally, we investigate the size effects of the present materials by studying the cumulative thermal conductivity κ(l) as a function of phonon mean free path, which is defined as the thermal conductivity contributed by phonons whose mean free path l is smaller than a given value l_max. Fig. 7 shows the cumulative thermal conductivity along the a and c directions with respect to the phonon MPFs at room temperature, 300 K. It can be seen that the cumulative thermal conductivity of both materials continuously increases as MFP increases, until reaching the limit length L, which represents the longest mean free path of the heat carriers. We derived the limit lengths of L_a ∼ 585 nm and L_c ∼ 400 nm for SnS₂, and L_a ∼ 575 nm and L_c ∼ 1100 nm for SnSe₂. It should be noted that the limit lengths L of the present compounds are much larger than that of SnS and SnSe.^32,34

Fig. 7 Cumulative lattice thermal conductivity of SnX₂ along the (a) in-plane and (b) out-of-plane directions as a function of phonon MFP at room temperature. The fitted curves are plotted with dotted lines.

Then, we fitted the cumulative κ(l) for SnX₂ along the in-plane and out-of-plane directions at 300 K to a single parametric function,^51,52 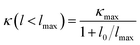, where, κ_max is the ultimate cumulated κ, l_max is the maximal MFP concerned, and l₀ is the parameter to be evaluated by the fitting. The fitted curves are plotted in Fig. 7, which reproduce the calculated data well and yield the parameter l₀ for the two materials along the in-plane and out-of-plane directions, which could be interpreted as the representative MFP (rMFP). The rMFP is helpful to study the size effect on ballistic or diffusive phonon transport, which is important for thermal design with nanostructuring. Our fitted rMFPs (l₀) for SnS₂ are 30 nm along the in-plane direction and 20 nm along the out-of-plane direction, and for SnSe₂, they are 24 nm along the in-plane direction and 38 nm along the out-of-plane direction. These values are quite larger than that of SnSe (4.30 nm along the armchair direction and 6.86 nm along the zigzag direction).³⁵ Such large representative rMFPs suggest that there are strong size effects in the phonon transport of micro-/nano-sized materials based on these two materials. Our results suggest that to reduce the lattice thermal conductivities of both materials, nanostructuring will be an effective way. This suggestion is consistent with recent experiment findings, where the κ_L of SnS₂ was found to evidently decrease with a decrease in the thickness of SnS₂ films.¹⁹ Moreover, we believe that such a phenomenon may also exist in SnSe₂, that is, this material may also be a negatively correlated thermoelectric material just like SnS₂ with a negative correlation between electrical and thermal conductivity. In addition, SnSe₂ may demonstrate a much better thermoelectric performance than that of SnS₂ because of its higher anharmonicity than that of SnS₂, leading to much lower thermal conductivity.

4. Conclusion

In summary, we have systematically investigated the anisotropic phonon transport properties and intrinsic lattice thermal conductivities for tin dichalcogenides (SnS₂ and SnSe₂) from first principles calculations. The calculated in-plane lattice thermal conductivity of SnS₂ is 12.10 W mK⁻¹, whereas that of SnSe₂ is much lower (7.76 W mK⁻¹), which mainly originates from its relatively smaller phonon group velocities combined with lower phonon frequencies. The out-of-plane thermal conductivities of both materials are found to be remarkably low (0.78 W mK⁻¹ for SnS₂ and 1.12 W mK⁻¹ for SnSe₂) due to very weak interlayer forces, which indicates their significance in thermoelectric applications. The obtained total thermal conductivities of SnS₂ and SnSe₂ agree well with experimental measured values. The phonon lifetimes of all branches are found to be much shorter in comparison with that of MoS₂ (MoSe₂) but slightly longer than that of SnS (SnSe). The contributions of the optical phonon branches to the total thermal conductivities are found to be rather small, which suggests that it would be difficult for the strategy of alloying to reduce κ_L. However, nanostructuring may be effective to further reduce κ_L since the mean free paths of the dominant phonon modes are relatively long. This conclusion is consistent with recent experiment findings, where the κ_L of SnS₂ thin films were found to be much lower than that of bulk SnS₂. Our study not only presents comprehensive investigations on the phonon transport properties of SnS₂ and SnSe₂, but also provides discussions and analyses on the origins of the diverse heat transfer phenomena, which would be of significance for further studies and applications based on these two TMDs.

Acknowledgements

This study was supported by the Natural Science Foundation of China (Grant no. 11145004 and 21363019).

Notes and references

1. J. Gu, X. Yang, Z. Lv, N. Li, C. Liang and Q. Zhang, Int. J. Heat Mass Transfer, 2016, 92, 15–22.
2. J. Gu, C. Xie, H. Li, J. Dang, W. Geng and Q. Zhang, Polym. Compos., 2014, 35, 1087–1092.
3. J. Gu, X. Meng, Y. Tang, Y. Li, Q. Zhuang and J. Kong, Composites, Part A, 2017, 92, 27–32.
4. J. Gu, C. Liang, J. Dang, W. Dong and Q. Zhang, RSC Adv., 2016, 6, 35809–35814.
5. S. Gedi, V. R. M. Reddy, B. Pejjai, C.-W. Jeon and C. Park, Appl. Surf. Sci., 2016, 372, 116–124.
6. X. Jing, D. D. Zhu, L. Wang, B. Huang, X. Huang and X. M. Meng, Adv. Funct. Mater., 2015, 25, 4255–4261.
7. X. Zhou, Q. Zhang, L. Gan, H. Li and T. Y. Zhai, Adv. Funct. Mater., 2016, 26, 4405–4413.
8. S. Song, S. L. Li, L. Gao, Y. Xu, K. Ueno, J. Tang, Y. B. Chengad and K. Tsukagoshi, Nanoscale, 2013, 5, 9666–9670.
9. F. Zhang, C. Xia, J. Zhu, B. Ahmed, H. Liang, D. B. Velusamy, U. Schwingenschlögl and H. N. Alshareef, Adv. Energy Mater., 2016, 16, 01188.
10. C. KyungMin, D. Wamwangi, M. Woda, M. Wuttig and W. Bensch, J. Appl. Phys., 2008, 103, 083523.
11. Z. Sun and H. Chang, ACS Nano, 2014, 8, 4133–4156.
12. H. Zhong, G. Yang, H. Song, Q. Liao, H. Cui, P. Shen and C. Wang, J. Phys. Chem. C, 2012, 116, 9319–9326.
13. X. He and H. Shen, Phys. B, 2012, 407, 1146–1152.
14. L. A. Burton, D. Colombara, R. D. Abellon, F. C. Grozema, L. M. Peter, T. J. Savenije, G. Dennler and A. Walsh, Chem. Mater., 2013, 25, 4908–4916.
15. S. Mandalidis, J. A. Kalomiros, K. Kambas and A. N. Anagnostopoulos, J. Mater. Sci., 1996, 31, 5975–5978.
16. A. Voznyi, V. Kosyak, A. Opanasyuk, N. Tirkusova, L. Grase, A. Medvids and G. Mezinskis, Mater. Chem. Phys., 2016, 173, 52–61.
17. A. A. Kozma, M. Y. Sabov, E. Y. Peresh, I. E. Barchiy and V. V. Tsygyka, Inorg. Mater., 2015, 51, 93–97.
18. B. Sun, Z. Ma, C. Hea and K. Wu, Phys. Chem. Chem. Phys., 2015, 17, 29844–29853.
19. M. J. Lee, J. H. Ahn, J. H. Sung, H. Heo, S. G. Jeon, W. Lee, J. Y. Song, K. H. Hong, B. Choi, S. H. Lee and M. H. Jo, Nat. Commun., 2016, 7, 12011.
20. C. Khélia, F. Maïz, M. Mnari, T. Ben Nasrallah, M. Amlouk and S. Belgacem, Eur. Phys. J.: Appl. Phys., 2000, 9, 187–193.
21. G. Busch, C. Fröhlich, F. Hulliger and E. Steigmeier, Helv. Phys. Acta, 1961, 34, 359.
22. Z. V. Borges, C. M. Poffo, J. C. de Lima, S. M. de Souza, D. M. Triches, T. P. O. Nogueira, L. Manzato and R. S. de Biasi, Mater. Chem. Phys., 2016, 169, 47–54.
23. A. A. Kozma, M. Yu. Sabov, E. Yu. Peresh, I. E. Barchiy and V. V. Tsygyka, Inorg. Mater., 2015, 51, 93–97.
24. L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377.
25. L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu and V. P. Dravid, Science, 2016, 351, 141–144.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
29. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048.
30. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
31. W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747.
32. J. Carrete, N. Mingo and S. Curtarolo, Appl. Phys. Lett., 2014, 105, 101907.
33. S. Kumar and U. Schwingenschlögl, Chem. Mater., 2015, 27, 1278–1284.
34. R. Guo, X. Wang, Y. Kuang and B. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 115202.
35. G. Qin, Z. Qin, W.-Z. Fang, L.-C. Zhang, S.-Y. Yue, Q.-B. Yan, M. Hu and G. Su, Nanoscale, 2016, 8, 11306–11319.
36. A. N. Gandi and U. Schwingenschögl, EPL, 2016, 113, 36002.
37. B. Peng, H. Zhang, H. Shao, Y. Xu, X. Zhang and H. Zhu, Ann. Phys., 2016, 528, 504–511.
38. G. Liu, H. Y. Sun, J. Zhou, Q. F. Li and X. G. Wan, New J. Phys., 2016, 18, 033017.
39. V. G. Hadjiev, D. De, H. B. Peng, J. Manongdo and A. M. Guloy, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104302.
40. Y. Kumagai, L. A. Burton, A. Walsh and F. Oba, Phys. Rev. Appl., 2016, 6, 014009.
41. B. Ram, A. Manjanath and A. K. Singh, 2D Mater., 2016, 3, 015009.
42. G. Lucovsky, J. C. Mikkelslen Jr., W. Y. Liang and R. M. White, Phys. Rev. B: Solid State, 1976, 14, 1663–1669.
43. J. Wasscher, W. Albers and C. Haas, Solid-State Electron., 1963, 6, 261.
44. J. Liu, G. M. Choi and D. G. Cahill, J. Appl. Phys., 2014, 116, 233107.
45. H. J. Goldsmid, in Semiconductors and Semimetals, ed. T. M. Tritt, Elsevier, 2001, vol. 69, p. 1.
46. V. Kishore, R. Sharma, V. K. Saraswat, N. S. Saxena, K. Sharma and T. P. Sharma, Appl. Therm. Eng., 2007, 27, 1552–1554.
47. J. M. Laskar, S. Bagavathiappan, M. Sardar, T. Jayakumar, J. Philip and B. Raj, Mater. Lett., 2008, 62, 2740–2742.
48. K. Zhou and B. Wei, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 248.
49. W. Zhai, K. Zhou, L. Hu and B. Wei, J. Chem. Thermodyn., 2016, 95, 159–163.
50. O. H. Hamilton, TAPP Software Version 2.2, E. S. Microwave Inc, Wade Court, 1990.
51. W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758.
52. G. Qin, Q.-B. Yan, Z. Qin, S.-Y. Yue, M. Hu and G. Su, Phys. Chem. Chem. Phys., 2015, 17, 4854.

---