Molecular structures of gas-phase neutral morpholine and its monohydrated complexes: experimental and theoretical approaches

Abstract

Morpholine (NH(CH₂CH₂)₂O) is a typical six-membered aliphatic heterocyclic compound. Herein, infrared plus vacuum ultraviolet (IR/VUV) single photon “soft” ionization spectroscopy was employed to study the structures of neutral morpholine and its monohydrated clusters. Theoretical calculations revealed that the structures containing equatorial-chair and axial-chair conformations were the most stable conformers in the gas phase, and this was confirmed by IR spectral analysis. Analysis of the observed and calculated spectra of the monohydrated clusters suggested that multiple conformers may co-exist in the molecular beam, and that the water molecule acts as a hydrogen donor. In the most stable structure, the hydrogen atom of the water molecule is bound to the NH group of the equatorial-chair conformer of morpholine. Moreover, the water molecules simultaneously serve as hydrogen bond donors for the NH group and interact with the CH group weakly. It is suggested that the weak intermolecular CH⋯O interaction is also responsible for the molecular stability.

---

1. Introduction

Aliphatic heterocyclic compounds have received considerable interest in recent years.^1–8 In heterocyclic compounds, the ring contains at least one other type of atom besides the carbon atoms. Heterocyclic compounds form the largest class of organic compounds, and most commonly contain nitrogen, sulfur, or oxygen atoms in addition to carbon. They are widely found in nature, and most of the important compounds related to biology are heterocyclic compounds, such as nucleic acids, certain vitamins, antibiotics, hormones, pigments, and alkaloids. In addition, the wide variety of heterocyclic compounds have various properties, some of them can be used as drugs, pesticides, herbicides, dyes, or plastics.

Morpholine is a typical six-membered aliphatic heterocyclic compound with the molecular formula NH(CH₂CH₂)₂O. It contains a heterocyclic ring that is present in many compounds of biological and pharmaceutical relevance.⁹ Most interestingly, the morpholine heterocycle contains both nitrogen and oxygen atoms. The carbon atoms adjacent to the N–H bond are saturated, ensuring sp³ hybridization at the nitrogen center, with the result that the N atom lies out of the plane defined by the four carbon atoms. This gives rise to two possible conformers where the N–H bond lies either axial or equatorial.¹⁰ We were also curious to see what would happen if a monomer provided two different acceptor sites. Morpholine is an amine as well as an ether, and each group can provide an electron pair to accept a water proton and form a hydrogen bond. Because the alkalinity of the amine group is considerably greater than that of the ether group, we expected that the N⋯H–O bonded complex would be preferred.

In general, the molecular structure of morpholine can be explored using several experimental techniques, such as NMR, IR, microwave, and Raman spectroscopy, and dipole moment and Kerr effect measurements, etc.^11–14 However, different conclusions have been reached by different groups. For instance, the axial-chair conformation of morpholine was deduced from dipole moment and Kerr effect measurements. Allinger et al. and Baldock and Katritzky,^15,16 suggested an equatorial-chair conformation. Smith and Shoulders¹⁷ could not distinguish the conformers that were present in morpholine using NMR measurements because the axial and equatorial conformations easily interconvert on the timescale of NMR spectroscopy. Baldock and Katritzky¹⁶ considered the equatorial positions to be more stable from IR measurements between the equatorial and axial conformation. Sloan and Kewley¹³ found many characteristic features for the equatorial-chair conformation from microwave spectroscopy but none for the axial-chair form. In 1989, Grabow et al.,¹⁴ repeated the microwave spectroscopy measurements for the normal and N-deuterated species at very high resolution and derived deuterium quadrupole coupling constants. The presence of two conformers was supported by Raman spectroscopy in the liquid state.^18,19 However, the details of the structure of the morpholine molecule and its hydrated clusters in the gas phase need further studies.

It is well know that Fourier transform IR (FTIR) absorption spectroscopy is one of the most effective approaches to study molecule and cluster structures, which had made massive outstanding achievements,^20–31 these include the groups of Suhm, Georges, and Asselin. In this paper, we introduce an alternative infrared absorption spectroscopy technique. Supersonic jet-laser spectroscopy is one of the most powerful tools for investigating the variety of conformers because it enables researchers to freeze conformational conversion using the ultracold, collision-free conditions in a jet.³² The frozen conformers are easily distinguished by IR dip spectroscopy, and their structures can be precisely determined. Recently, mass-selected optical spectroscopy has been widely applied in the investigation of gas-phase structures and dynamics. Combining mass-selected optical spectroscopy with the supersonic jet technique enables us to determine the geometrical structures and dynamics of molecules and clusters with high reliability. Vibrational spectroscopy in supersonic jets is an effective approach that can provide information on the geometric structures of molecules and clusters, and their intermolecular interactions.^33–38 Furthermore, the vibrational frequencies and intensities of IR absorption modes, such as modes involving OH, NH, and CH groups, are generally very sensitive probes of hydrogen bonding and other intra- and intermolecular interactions. This makes them excellent probes for the investigation of detailed aspects of the structures of biologically relevant ions, radicals, and molecules.³⁹ In addition, the extent of hydrogen bonding can be directly investigated by using IR spectroscopy to detect the OH and NH stretching modes of the relevant clusters.⁴⁰ The OH and NH vibrations are very susceptible to local perturbations and show dramatic red shifts when the OH or NH group is strongly hydrogen bonded as an acceptor group, such as the OH group of an adjacent water or alcohol molecule.^41–44

Modern quantum chemical calculations, for instance, density functional theory (DFT) and Møller Plesset second-order perturbation theoretical functional (MP2) calculations, can be used to optimize the structures and predict the energies and frequencies of monomer molecules and clusters.^19,45,46 Recently, vibrational spectroscopy combined with quantum chemical calculations was successfully applied to distinguish molecular conformers, exploring conformational equilibrium in the condensed state and assign vibrational bands.^32,47,48

In the present study, we combine IR spectroscopy with various theoretical methods to investigate the structure of morpholine and its monohydrated complexes. These structures were probed using IR spectroscopy with vacuum ultraviolet (VUV) photoionization detection.

2. Methods

2.1 Experimental methods

Liquid morpholine (>98% pure) was purchased from Aladdin-reagent company (Shanghai, China) and used without further purification. The experimental apparatus employed to record VUV/TOFMS and IR spectra has been previously described in detail,^33,49–52 and thus only a brief description is given here. Liquid morpholine is placed close to the valve body at room temperature. He (purity 99.999%) was used as the carrier gas and the stagnation pressure was about 0.1 MPa. The morpholine vapour and carrier gas mixture gas is expanded into a vacuum chamber from a pulse nozzle under supersonic flow conditions. The beam is collimated by a conical skimmer with a 1.5 mm entrance aperture at its apex, located about 3 cm from the nozzle orifice. This beam is crossed perpendicularly by a 118 nm VUV laser beam at the ion source region of a TOFMS. The vertical ionization energy (VIE) of morpholine is predicted ca. 8.27 eV, which is less than the ionizing VUV photon energy employed in this study. The counter propagating (to the VUV beam) IR laser beam is focused upstream from the molecular beam/118 nm light beam intersection point by a 40 cm focal length lens.

Generation of the VUV 118 nm laser light and the IR light was reported in previous publications.⁵⁰ The VUV radiation is generated as the ninth harmonic of the fundamental of the 1064 nm output of a Nd³⁺:YAG (yttrium aluminum garnet) laser. The fundamental 1064 nm is tripled to 355 nm, which is focused into a cell with Xe/Ar at a ratio 1 : 10 at approximately 250 Torr by a 25 cm lens. The 118 nm light generated is focused by a MgF₂ lens into the ionization region of a TOFMS. This same lens defocuses the residual 355 nm light. The 118 nm light is about 5 μJ per pulse or 10¹² photons per pulse⁵³ and the conversion efficiency is roughly 1.2 × 10⁻⁵. This light is employed for single photon ionization of the molecules and clusters in the molecular beam. Tunable IR radiation 3–5 mJ per pulse in the 2800–3800 cm⁻¹ range with a bandwidth of 2–3 cm⁻¹ (broad band mode) is generated from an optical parametric oscillator/optical parametric amplifier (OPO/OPA) system (LaserVision) pumped by the Nd:YAG fundamental and counterpropagates with respect to the VUV beam. Both the VUV and IR laser beams are perpendicular to the molecular beam and to the ion flight path of the TOFMS.

2.2 Computational methods

The calculations of geometry optimization, vibrational frequencies, all of the theoretical calculations were performed with the GAUSSIAN 03 and GAUSSIAN 09 program packages. The geometry optimizations were calculated by the DFT and MP2. The MP2 theoretical functional, which accounts for the electron correlation, can obtain more reliable results for correlation energies than the DFT method.⁴¹ Therefore, the geometry optimization and correlation energies of morpholine were predicted by MP2/6-311++G(d,p). Natural bond orbital (NBO) analyses of the monohydrated morpholine complexes were performed at the same level of theory. However, compared with the MP2 theoretical functional, the DFT method is inexpensive, and the prediction of normal-mode frequencies is reliable.^53,54 Thus, the geometries and the vibrational frequencies of the morpholine conformers were optimized at the B3LYP/6-311++G(d,p) level. In order to confirm the results, we made further theoretical calculations employing the ωB97X-D/cc-pVTZ level. The resulting relative energies are given in Table 1. Therefore, we chose the ωB97X-D/cc-pVTZ computational results for the final discussion in present report. However, we also carried out geometry optimization at MP2/aug-cc-pVTZ level for monohydrated morpholine to calculate the hydrogen bond length. The calculated geometry optimization were corrected for basis set superposition errors (BSSE) using the scheme of Boys and Bernardi counterpoise correction.

Table 1 Relative energies (E_rel/kJ mol⁻¹) calculated at the B3LYP/6-311++G(d,p), MP2/6-311++G(d,p) and ωB97X-D/cc-pVTZ levels of theory for the most stable conformers of the morpholine and its monohydrated complexes

Conformer	Erel (B3LYP)	Erel (MP2)	Erel (ωB97X-D)
Eq-chair	0	0	0
Ax-chair	4.3	4.8	3.1
Ax-boat	26	26	25
Eq-boat	30	35	32
Ma–H2O-1	0	0	0
Ma–H2O-2	6.4	4.8	6.1
Ma–H2O-3	10	7.7	12
Ma–H2O-4	25	19	22
Me–H2O-1	8.5	5.8	6.2
Me–H2O-2	12	9.6	10
Me–H2O-3	15	13	14
Me–H2O-4	30	23	24

---

3. Results and discussion

3.1 Mass spectra

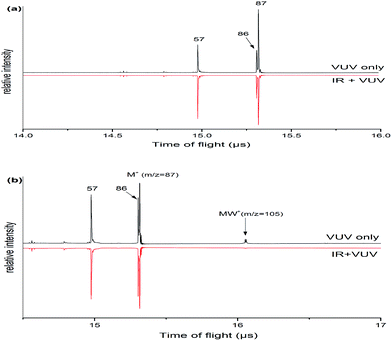
Fig. 1 shows the mass spectra of morpholine and its monohydrated clusters, which observed by using a time-of-flight mass spectrometer. Two mass spectra are superimposed in this figure: the black line represents the mass spectrum of morpholine or its monohydrated clusters that were generated with 118 nm one-photon ionization, and the red line represents the mass spectrum of morpholine or its monohydrated clusters obtained with both IR (about 3000 cm⁻¹) and 118 nm radiation. The IR probe precedes the 118 nm pulse by 50 ns. The mass peaks of the morpholine cation (m/z = 87) and the fragment cation (m/z = 86, 57) are seen in Fig. 1(a). The intensity of signals in mass channels m/z = 57 increasing with the addition of IR photons, while the mass channel m/z = 86 is not significantly enhanced. In contrast, the signals related to the parent ion (m/z = 87) are reduced in the presence of IR radiation at 2900 cm⁻¹ approximately, which corresponds to the C–H stretching modes (Fig. 1(a)). This suggests that the absorbed IR photons cause the morpholine monomer to dissociate into morpholine fragments. After absorbing IR photons, the molecule is excited to higher vibrational states and thus its fragmentation efficiency is increased. The fragment with m/z = 86 arises from the morpholine molecular lossing a H atom under single photon ionization. This dissociation is known to produce the C₄H₈NO⁺ ion and a hydrogen atom in the following steps: C₄H₉NO + hν (10.5 eV) → C₄H₈NO⁺ + H + e⁻. The signal at m/z = 57 is assigned to the loss of a CH₂O radical from the morpholine cation: C₄H₉NO + hν (10.5 eV) → C₃H₇N⁺ + CH₂O + e⁻. Fig. 1(b) shows the mass spectrum of the morpholine monohydrated clusters and its fragment ions. These fragment ions are the same as those observed in Fig. 1(a), which indicates that no new pathway involving the water molecule is opened. The IR radiation clearly causes the monohydrated clusters of the morpholine cation (MW⁺) to disappear. However, we did not observe any obvious enhancement of other smaller ion peaks. This phenomenon may be due to the relatively small content of clusters in the molecular beam, so little impact on the other ions. The infrared (IR) absorption spectrum was observed by controlling the sample concentration conditions that no larger clusters were observed. At low concentrations, the measured spectrum mainly corresponds to the original IR spectrum of the monomer or monohydrated cluster and serious distortion from larger cluster fragmentation would be mostly avoided.

Fig. 1 (a) Mass spectra of morpholine cation and fragment ions which are generated in the 118 nm light with the IR light on/off. (b) Mass spectrum of morpholine monohydrated clusters and fragment ions which are generated in the 118 nm light with the IR light on/off. Both mass spectrums were observed with a time of flight mass spectrometer.

3.2 Monomer structure

The morpholine molecule is known to exist as a chair form with the N–H bond arranged in axial and equatorial conformations in the liquid.¹⁹ Extensive studies of the conformation of neutral morpholine have been previously carried out,^10,55–58 but only few of these have been in the gas phase. Fig. 2 shows the four lowest energy conformers of the morpholine molecule, calculated at the B3LYP/6-311++G(d,p) level of theory and reoptimized at the ωB97X-D/cc-pVTZ level. Both the skew-boat and chair conformations are found to be stable, and the four conformations can be identified from the N–H bond that lies either axial or equatorial relative to the skew-boat and chair ring. As shown in Fig. 2, the chair conformers have higher symmetry and are much more stable (with a stabilization energy of about 25.06 kJ mol⁻¹) than the skew-boat conformer, which reveals that the chair conformer may be favored in the gas phase. In the chair conformer, the dihedral angle between the N–H bond and the C–N–C plane is −121.0° and 119.70° for the equatorial and axial conformations, respectively. The energy difference between the two chair conformers (equatorial and axial) is only 3.1 kJ mol⁻¹, and the equatorial conformer is more stable. This implies that chair conformers may co-exist in the gas phase. Furthermore, previous work^10,59 has identified that the boat conformers do not contribute to the IR or microwave spectra of morpholine, which demonstrates that the two chair conformers are dominant in the liquid phase. Under jet-cooled conditions, the temperature of the molecular beam is about 15 K.¹⁰ Owing to the difference in energy between two conformers, the parent molecules can be expected to freeze into two conformer forms and not interconvert freely.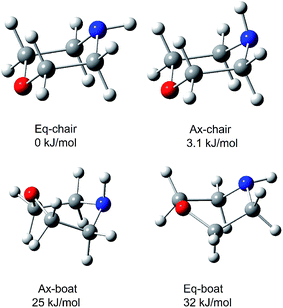

Fig. 2 The four lowest-energy structures of morpholine calculated by ωB97X-D/cc-pVTZ. The relative energy in kJ mol⁻¹ is listed above each structure.

The observed and calculated IR spectra of the neutral morpholine monomer in the range of 2600–3600 cm⁻¹ are shown in Fig. 3; this frequency range corresponds primarily to C–H and N–H stretching. The calculated spectra are based on the four conformations of neutral morpholine at the ωB97X-D/cc-pVTZ level, and the vibrational frequencies are scaled by 0.9415. Fig. 3(a) shows the observed IR spectrum of gas-phase neutral morpholine in the range of 2600–3150 cm⁻¹; the C–H stretching bands are clearly observed as slightly broadened bands at about 2820, 2848, 2907, 2939, and 2954 cm⁻¹. Theoretical calculations show that both equatorial-chair and axial-chair are the stablest structures among all of the conformers, and the spectrum calculation for the two chair conformers show good agreement with all of the observed spectral features in the studied range. In contrast, the calculated spectra for the other conformers do not reproduce the observed intense C–H stretching bands very well. The IR spectrum of neutral morpholine in the range of 3200–3500 cm⁻¹ is also show in Fig. 3(a). The frequencies of this region correspond primarily to N–H stretching vibrations. The bands attributed to the N–H stretching of the axial and equatorial conformers are observed at 3320 and 3336 cm⁻¹, respectively, and these two bands overlap at approximately 3330 cm⁻¹. Theoretical calculation results in this region show good agreement with the observed spectra (Fig. 3). Generally, the results above reveal that both of the two chair conformers may coexist in the conformational equilibrium of the gas. Hence, only the two chair conformers are considered further in this paper. Furthermore, the theoretical calculations reveal that the equatorial-chair conformer is more stable, and thus it may be more favorable in the gas phase.

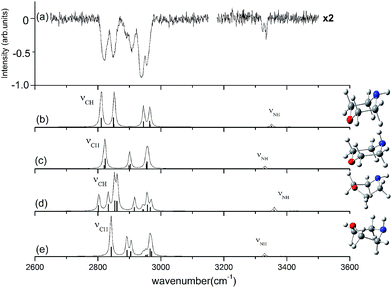Fig. 3 Observed IR spectrum of neutral morpholine and the calculated spectrum based on the optimized structure shown (ωB97X-D/cc-pVTZ). The calculated frequencies are scaled by 0.9415.

3.3 Monohydrated morpholine

Morpholine is an interesting molecule from the viewpoint of hydrogen bonding interactions owing to the presence of multiple hydrogen bonding sites. Water can serve as a hydrogen bond donor for both the NH group and the ether oxygen of morpholine, and it can also act as a hydrogen bond acceptor for the NH group. It is anticipated that monohydrated morpholine will present many different isomers. Fig. 4 shows the fully optimized geometries of the eight lowest-energy structures of neutral monohydrated morpholine. All geometries were initially optimized at the B3LYP/6-311++G(d,p) level of theory and reoptimized at the ωB97X-D/cc-pVTZ level.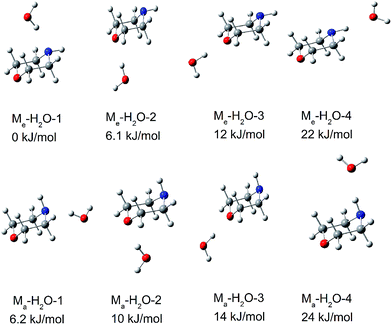

Fig. 4 The eight lowest-energy structures of morpholine monohydrated complexes calculated by ωB97X-D/cc-pVTZ. The relative energy in kJ mol⁻¹ is listed above each structure.

In the most stable structure of monohydrated morpholine, M_e–H₂O-1 (shown in Fig. 4), the morpholine molecule has an equatorial-chair conformation and the water molecule serves as a hydrogen bond donor for the NH group. The morpholine molecule also exists as the equatorial-chair conformer in M_e–H₂O-2 and M_e–H₂O-3, but the water molecule serves as a hydrogen bond donor for the ether oxygen. The calculated results reveal that the energies of M_e–H₂O-2 and M_e–H₂O-3 are about 6.1 and 12 kJ mol⁻¹ higher than that of M_e–H₂O-1 at the ωB97X-D/cc-pVTZ level, respectively. The theoretical calculations presented in Fig. 4 thus show that the monohydrated morpholine complex with the equatorial-chair conformation is more stable. Furthermore, the most stable monohydrated clusters containing equatorial and axial morpholine conformers are M_e–H₂O-1 and M_a–H₂O-1, respectively. This indicates that the water molecule preferentially serves as a hydrogen donor for the NH group in morpholine. This conclusion agrees well with the Fourier transform microwave study of Indris et al.,⁵⁷ and it reflects the large intrinsic basicity of this functional group, which is much larger than that of the ether oxygen. However, the water molecule serves as a hydrogen acceptor in the least stable complexes (M_e–H₂O-4 and M_a–H₂O-4). Therefore, there is only a low probability that the morpholine molecule serves as hydrogen donor in the monohydrated morpholine.

Fig. 5 presents the IR plus VUV spectrum recorded at 118 nm for monohydrated morpholine, together with the corresponding spectra calculated for the eight lowest-energy conformers of monohydrated morpholine. These spectra are based on the conformations optimized at the ωB97X-D/cc-pVTZ level of theory, and the vibrational frequencies were scaled by 0.9415. In the observed spectrum of monohydrated morpholine (Fig. 5(a)), a sharp intense dip peak is observed at 3714 cm⁻¹, which corresponds to the free O–H stretch of water. The two broad bands at about 3309 and 3432 cm⁻¹ must therefore result from hydrogen bonded. The feature at 3432 cm⁻¹ can be assigned to O–H stretching hydrogen bond, and the feature at 3309 cm⁻¹ to the N–H stretching hydrogen bond. These spectral features seem to indicate that the monohydrated morpholine has a ring-type structure, in which the water acts as a bridge and serves as hydrogen bond acceptor to the N–H group and a hydrogen bond donor to the ether oxygen. However, DFT and MP2 energy calculations do not support this assignment, and the geometry optimization shows that this is an unstable structure. As we can see in Fig. 5, the observed spectrum does not match very well with the simulated spectra of the monohydrated morpholine complexes that contain O–H⋯N (b, e) or O–H⋯O hydrogen bonds (c, d, f, g). However, the signals corresponding to O–H⋯N hydrogen bond stretching in simulated spectra (b) and (e) match with the signal in the observed spectrum at 3309 cm⁻¹, and those corresponding to O–H⋯O hydrogen bond stretching in (c), (d), (f), and (g) match with the signal in the observed spectrum at 3432 cm⁻¹. Therefore, we conclude that structures of monohydrated morpholine in which the water molecule behaves as a hydrogen bond donor towards the NH group and the ether oxygen co-exist in the molecular beam. The discrepancy in the calculated spectra may be explained by the anharmonic resonance with the combination and the overtone bands of lower frequency modes. In addition, the absence of an antisymmetric free OH stretch in the experimental spectrum indicates that the morpholine monohydrated clusters in which the morpholine molecule behaves as the hydrogen donor do not contribute to the IR spectrum. This is also supported by the theoretical calculations. In other words, these results imply that more than one monohydrated conformer is present in the beam, where it would be more appropriate for the morpholine molecule to behave as the hydrogen donor in the monohydrated clusters. Considering the cooling effect in the molecular beam, the low energy structures will be dominant at low temperature. Indris and coworkers employed FT microwave spectroscopy to investigate the morpholine–H₂O complex.⁵⁷ Their results demonstrate that the N⋯H–O hydrogen-bonded structure was found existing in a molecular beam, while the O⋯H–O hydrogen-bonded structure was not detected. It is worth noting that no sharp band related to free N–H stretching is seen in Fig. 5; the absence of this feature may be due to the fact that the N–H stretching signal is too weak and its position may overlap with the broad hydrogen bond signals.

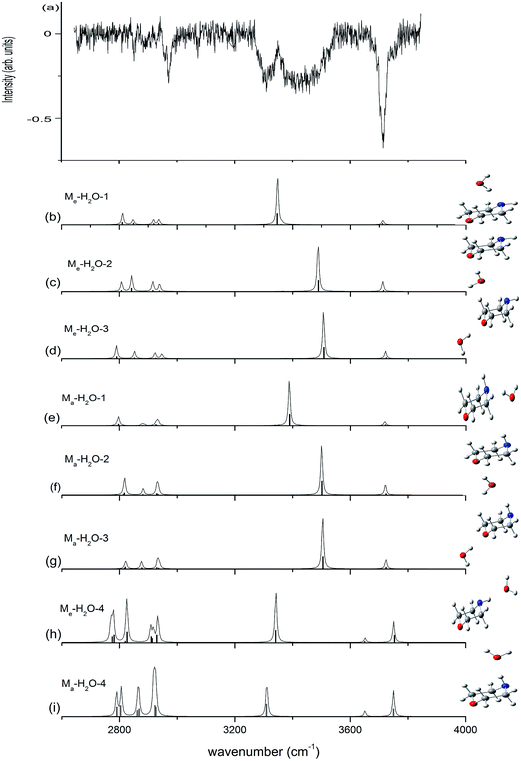Fig. 5 Observed IR spectrum of neutral monohydrated morpholine and the calculated spectrum based on the optimized structure shown (ωB97X-D/cc-pVTZ). The calculated frequencies are scaled by 0.9415.

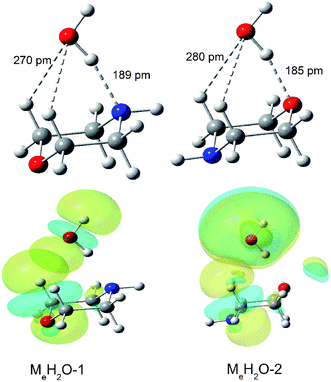
We can find that the water molecules form two different kinds of hydrogen bond (O–H⋯O and O–H⋯N) in the complexes with morpholine molecule in the spectra. And the hydrogen bond length of O–H⋯N calculated in M_e–H₂O-1 is 189 pm, which is longer than the O–H⋯O hydrogen bond in M_e–H₂O-2 (185 pm) (Fig. 6). These two hydrogen bonds attributable to strong hydrogen bonds.⁶⁰ To substantiated the spectroscopy results and estimated the interaction strength, we carried out the natural bond orbitals (NBO) calculations with MP2/6-311++G(d,p) (Pop = nbo) level. The second-order perturbation stabilization energy E(2) obtained from natural bond orbital (NBO) analysis for the n(O) → σ*(O–H) hydrogen bond interaction in M_e–H₂O-2 (48 kJ mol⁻¹) is more than the n(N) → σ*(O–H) hydrogen bond interaction in M_e–H₂O-1 (29 kJ mol⁻¹). The stabilization energy gained from the hydrogen bond interaction, denoted E(2), is a measure of the interaction strength.⁶¹ This result means that the σ* orbital of the water O–H bonds overlap better with the oxygen lone pair orbital of morpholine. As we can see in Fig. 4, the oxygen atom of morpholine acts as hydrogen bond acceptor, while the water molecule serves as a hydrogen bond donor and seems to have a weakly intermolecular interacts with the CH groups at the same time (Fig. 6) in the M_e–H₂O-2 and M_a–H₂O-2 structure. However, this phenomenon was not found in M_e–H₂O-3 and M_a–H₂O-3 structure. Furthermore, the M_e–H₂O-2 and M_a–H₂O-2 structure is more stable than M_e–H₂O-3 and M_a–H₂O-3 structure in energy respectively. This suggests that the weak intermolecular interaction C–H⋯O may be contributes to the molecular stability of the complex. The occurrence of the weak intermolecular reactions improves the relative stability of these morpholine–water complexes. To prove the existence of this interaction, the NBO diagrams shows that the oxygen lone pair orbital of water and the σ* orbital of the C–H bonds overlap in M_e–H₂O-1 and M_e–H₂O-2 structure would lead to intermolecular interaction occurring (see Fig. 6). Moreover, the second-order perturbation stabilization energies, E(2), between the nonbonding orbital and the σ* orbital (Lewis type NBO) is 0.92, 0.42 kJ mol⁻¹ in M_e–H₂O-1 and M_e–H₂O-2 respectively. And we can found that the σ* orbitals of the C–H bonds overlap with the oxygen lone pair orbitals in M_e–H₂O-1 and M_e–H₂O-2. Thus, the interactions among the oxygen lone pair orbitals and the C–H bonds are confirmed. These results imply that there are weak interactions C–H⋯O between the molecules (morpholine and water) besides the strong hydrogen bonding interactions. And this weak force may also play an important role in the intermolecular reactions and contribute to improve the relative stability of these conformations.

Fig. 6 MP2/aug-cc-pVTZ optimization for M_e–H₂O-1 and M_e–H₂O-2 and nbo plots illustrating the overlap of the σ*C–H of morpholine and the n(O) orbital of the oxygen atom in water in the morpholine–water complex: M_e–H₂O-1 and M_e–H₂O-2.

4. Conclusions

This study describes a promising spectroscopic method, in which IR/VUV photoionization vibrational spectra are combined with theoretical calculations. This technique enables us to monitor multiple vibrational modes of the different isomers of morpholine and its monohydrated complexes.

The results show that the two chair conformers (axial and equatorial) are the most stable structures among all of the conformers, which are the dominant in a supersonic expansion. The predicted IR spectra for these two conformers show good agreement with the observed spectral features. DFT and MP2 calculations show that monohydrated morpholine has several stable conformers. The obtained IR spectra suggest that multiple isomers may be formed in the expansion, and that morpholine prefers to act as the hydrogen acceptor in hydrogen bonding involving the NH group and the ether oxygen. Moreover, NBO analysis result shows that the weak intermolecular reactions CH⋯O exists in the complexes, and this weak interaction contribute to improve the relative stability of these conformations.

Acknowledgements

This work has been supported by NSFC (No. 11079020, 21273083, U1332132) grants and Guadong-NSF grants (No. S2013010016551). The scientific research foundation for State Education Ministry, the foundation for introduction of talents by the universities in Guangdong Province, and the project under scientific and technological planning by Guangzhou City.

References

1. R. Properzi and E. Marcantoni, Chem. Soc. Rev., 2014, 43, 779–791.
2. T. Eicher, S. Hauptmann and A. Speicher, The Chemistry of Heterocycles: Structures, Reactions, Synthesis, and Applications, 3rd edn, John Wiley & Sons, 2013.
3. P. Aslanidis, P. J. Cox, S. Divanidis and A. C. Tsipis, Inorg. Chem., 2002, 41, 6875–6886.
4. D. Pinto, C. M. Santos and A. M. Silva, Recent research developments in heterocyclic chemistry, ed. T. M. V. D. Pinho e Melo and A. M. d. A. Rocha, Research Signpost, Trivandrum, 2007, pp. 397–475.
5. D. E. Olson, A. Maruniak, S. Malhotra, B. M. Trost and J. Du Bois, Org. Lett., 2011, 13, 3336–3339.
6. M. Asay, C. Jones and M. Driess, Chem. Rev., 2010, 111, 354–396.
7. W. A. Herrmann, J. Schütz, G. D. Frey and E. Herdtweck, Organometallics, 2006, 25, 2437–2448.
8. Z.-G. Wang, H.-M. Sun, H.-S. Yao, Q. Shen and Y. Zhang, Organometallics, 2006, 25, 4436–4438.
9. G. Assaf, G. Cansell, D. Critcher, S. Field, S. Hayes, S. Mathew and A. Pettman, Tetrahedron Lett., 2010, 51, 5048–5051.
10. T. A. Oliver, G. A. King and M. N. Ashfold, Chem. Sci., 2010, 1, 89–96.
11. F. Riddell, Q. Rev., Chem. Soc., 1967, 21, 364–378.
12. H. Kessler, Angew. Chem., Int. Ed. Engl., 1970, 9, 219–235.
13. J. J. Sloan and R. Kewley, Can. J. Chem., 1969, 47, 3453–3462.
14. J.-U. Grabow, H. Ehrlichmann and H. Dreizler, Z. Naturforsch, 1989, 44, 833–836.
15. N. L. Allinger, J. Carpenter and F. M. Karkowski, J. Am. Chem. Soc., 1965, 87, 1232–1236.
16. R. Baldock and A. Katritzky, Tetrahedron Lett., 1968, 9, 1159–1162.
17. W. B. Smith and B. A. Shoulders, J. Phys. Chem., 1965, 69, 579–582.
18. S. SenGupta, N. Maiti, R. Chadha and S. Kapoor, Chem. Phys. Lett., 2015, 639, 1–6.
19. M. Xie, G. Zhu, Y. Hu and H. Gu, J. Phys. Chem. C, 2011, 115, 20596–20602.
20. P. Asselin, P. Soulard, M. Alikhani and J. Perchard, Chem. Phys., 2000, 256, 195–205.
21. C. Hartz, B. Wofford, A. McIntosh, R. Meads, R. Lucchese and J. Bevan, Ber. Bunsenges. Phys. Chem., 1995, 99, 447–456.
22. C. Liang, K. Hong, G. A. Guiochon, J. W. Mays and S. Dai, Angew. Chem., Int. Ed., 2004, 43, 5785–5789.
23. X. de Ghellinck d'Elseghem Vaernewijck, D. Golebiowski and M. Herman, Mol. Phys., 2012, 110, 2735–2741.
24. P. Asselin, P. Soulard, B. Madebène, M. Goubet, T. Huet, R. Georges, O. Pirali and P. Roy, Phys. Chem. Chem. Phys., 2014, 16, 4797–4806.
25. D. McNaughton, C. Evans and E. Robertson, FT-IR Spectroscopy of the CFC Replacements HFC-152a and HFC-227ea in a Supersonic Jet Expansion, Springer, 1997.
26. M. Snels, V. Horká-Zelenková, H. Hollenstein and M. Quack, Handbook of High-resolution Spectroscopy, 2011.
27. T. Häber, U. Schmitt and M. A. Suhm, Phys. Chem. Chem. Phys., 1999, 1, 5573–5582.
28. Y.-C. Lee, V. Venkatesan, Y.-P. Lee, P. Macko, K. Didiriche and M. Herman, Chem. Phys. Lett., 2007, 435, 247–251.
29. R. Petry, S. Klee, M. Lock, B. P. Winnewisser and M. Winnewisser, J. Mol. Struct., 2002, 612, 369–381.
30. A. Amrein, D. Luckhaus, F. Merkt and M. Quack, Chem. Phys. Lett., 1988, 152, 275–280.
31. M. Quack, Annu. Rev. Phys. Chem., 1990, 41, 839–874.
32. Y. Matsuda, N. Mikami and A. Fujii, Phys. Chem. Chem. Phys., 2009, 11, 1279–1290.
33. T. S. Zwier, Annu. Rev. Phys. Chem., 1996, 47, 205–241.
34. T. Ebata, A. Fujii and N. Mikami, Int. Rev. Phys. Chem., 1998, 17, 331–361.
35. U. Buck and F. Huisken, Chem. Rev., 2000, 100, 3863–3890.
36. M. A. Duncan, Int. Rev. Phys. Chem., 2003, 22, 407–435.
37. J. M. Lisy, J. Chem. Phys., 2006, 125, 132302.
38. M. Zhou, L. Andrews and C. W. Bauschlicher, Chem. Rev., 2001, 101, 1931–1961.
39. Y. Hu, J. Guan and E. R. Bernstein, Mass Spectrom. Rev., 2013, 32, 484–501.
40. J.-W. Shin and E. R. Bernstein, J. Chem. Phys., 2009, 130, 214306.
41. R. N. Pribble and T. S. Zwier, Science, 1994, 265, 75–79.
42. C. J. Gruenloh, J. R. Carney, C. A. Arrington, T. S. Zwier, S. Y. Fredericks and K. D. Jordan, Science, 1997, 276, 1678–1681.
43. Y. Hu, H. Fu and E. Bernstein, J. Chem. Phys., 2006, 125, 154306.
44. O. Kostko, L. Belau, K. R. Wilson and M. Ahmed, J. Phys. Chem. A, 2008, 112, 9555–9562.
45. I. M. Šapić, L. Bistričić, V. Volovšek, V. Dananić and K. Furić, Spectrochim. Acta, Part A, 2009, 72, 833–840.
46. G. A. Guirgis, P. M. Mazzone, D. N. Pasko, P. Klaeboe, A. Horn and C. J. Nielsen, J. Raman Spectrosc., 2007, 38, 1159–1173.
47. B. Liang, M. Zhou and L. Andrews, J. Phys. Chem. A, 2000, 104, 3905–3914.
48. E. Uggerud, Mass Spectrom. Rev., 1992, 11, 389–430.
49. Y. Hu, H. Fu and E. Bernstein, J. Phys. Chem. A, 2006, 110, 2629–2633.
50. Y. Hu, H. Fu and E. Bernstein, J. Chem. Phys., 2006, 125, 154305.
51. H. Fu, Y. Hu and E. Bernstein, J. Chem. Phys., 2006, 124, 024302.
52. Y. Hu, H. Fu and E. Bernstein, J. Chem. Phys., 2006, 124, 114305.
53. P. R. Shirhatti and S. Wategaonkar, Phys. Chem. Chem. Phys., 2010, 12, 6650–6659.
54. K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–168.
55. M. M. Vallejos, A. M. Lamsabhi, N. M. Peruchena, O. Mó and M. Yáñez, J. Phys. Org. Chem., 2012, 25, 1380–1390.
56. P. K. Sahu, A. Chaudhari and S.-L. Lee, Chem. Phys. Lett., 2004, 386, 351–355.
57. O. Indris, W. Stahl and U. Kretschmer, J. Mol. Spectrosc., 1998, 190, 372–378.
58. R. Friedel and D. McKinney, J. Am. Chem. Soc., 1947, 69, 604–607.
59. A. L. Capparelli, J. Marañon, O. M. Sorarrain and R. R. Filgueria, J. Mol. Struct., 1974, 23, 145–151.
60. G. R. Desiraju and T. Steiner, The weak hydrogen bond: in structural chemistry and biology, Oxford University Press on Demand, 2001.
61. S. D. Schrøder, J. H. Wallberg, J. A. Kroll, Z. Maroun, V. Vaida and H. G. Kjaergaard, J. Phys. Chem. A, 2015, 119, 9692–9702.

---