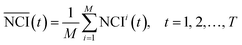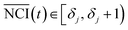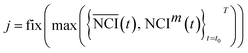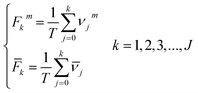Open Access Article
Open Access ArticleEdge effect detection for real-time cellular analyzer using statistical analysis
Yinghao Chena,
Shan Chena,
Tianhong Pan *a and
Xiaobo Zou
*a and
Xiaobo Zou b
b
aSchool of Electrical and Information Engineering, Jiangsu University, Zhenjiang, Jiangsu 212013, China. E-mail: thpan@live.com; Tel: +86-15805298357b
bSchool of Food and Biological Engineering, Jiangsu University, Zhenjiang, Jiangsu 212013, China
First published on 11th April 2017
Abstract
Real time cellular analyzers (RTCA) are widely used to test the cytotoxicity of chemicals. However, there are some uncontrollable factors, which are detrimental to the experimental quality. One of the fundamental issues is the edge effect. Abnormal time-dependent cellular response curves (TCRCs) are observed when the wells are located at the edge of the E-plate. In this paper, the Smirnov test was used to detect the edge effect. The average normalized cell index (NCI) of the negative control located in the inner wells was taken as the standard. Thereafter, all TCRCs were divided into several intervals, and their corresponding empirical distribution functions (EDFs) of the mean NCI and NCI located at the edge wells were calculated, and hypothesis testing was used to determine the differences of the EDFs. The experimental results evaluated the performance of the proposed algorithm. This framework provided a systematic method for edge-effect detection.
1. Introduction
To assess the hazards of industrial chemicals, consumer products, pharmaceuticals, and environmental contaminants, animal tests are generally adopted by the Globally Harmonized System (GHS) classification and human health risk assessments.1,2 However, the cost of animal experiments is high and the understanding of the mechanism of action remains limited. Cell based in vitro assay is an alternative to animal testing in safety/hazard assessments.3–6 A popular instrument in cell-based in vitro assay is the xCELLigence real-time cell analyzer (RTCA), which allows for uninterrupted, noninvasive, label-free, and real-time analysis of cells over the course of an experiment.7 It has been widely used in many different research fields, such as drug discovery, water quality monitoring, and toxicology investigations.8–12 However, although researchers use RTCA as a tool, the experimental quality is not always noted.In the RTCA experiment, the cellular response in the edge well of the E-plate is usually different from that of the inner well, especially in the E-plate ×96 and ×384 formats, which is described as the edge effect. There are two main reasons why the edge effect appears in RTCA experiments: one reason is that the evaporation of long-term incubation causes the edge effect (evaporation effect), because the evaporation efficiency of water in the edge well is higher than that in the inner well; and the other reason is that the temperature of the edge well reaches the desired incubation temperature faster than that of the inner well owing to plate stacking (temperature effect).13 To weaken the edge effect, Lundholt and Scudder14 pre-incubated newly seeded plates in ambient conditions (air at room temperature), which resulted in an even distribution of the cells in each well. However, the result of this method is not stable and would be invalid for long-term cultivation (>24 h). Furthermore, a special anti-volatile lid has been developed to restrain the edge effect,15 but the performance is limited. Malo and Hanley16 proposed a statistical method to optimize the configuration of the reference wells for reducing the positional effects of wells within plates. In a nutshell, those methods are designed to reduce the edge effect on the experimental process or device, nevertheless, they cannot completely eliminate the edge effect. Furthermore, there is no effective method to identify the edge effect.
To avoid the edge effect, researchers tend to abandon the data located at edge wells, which decreases the testing efficiency of the RTCA and will make a lot of waste, especially in E-plate ×96 formats (37.5%). Furthermore, researchers manually screen the edge effect, which is time consuming and can result in inaccuracies. In this work, the Smirnov test was used to determine the edge effect. Compared with manual selection, the proposed method is efficient and reliable.
This paper has been organized as follows: in Section 2, the problem of edge effect has been described. In Section 3, the Smirnov test was applied to identify the edge effect with related variables. In Section 4, several RTCA experiments were used to validate the proposed method. Finally, Section 5 included concluding remarks.
2. Problem statement
In this study, the xCELLigence RTCA system with E-plate ×384 formats was selected as the experimental equipment and the schematic diagram is shown in Fig. 1(a).17 The basic principle of the RTCA is to monitor the cell population changes in electrode impedance induced by the interactions between testing cell numbers and electrodes.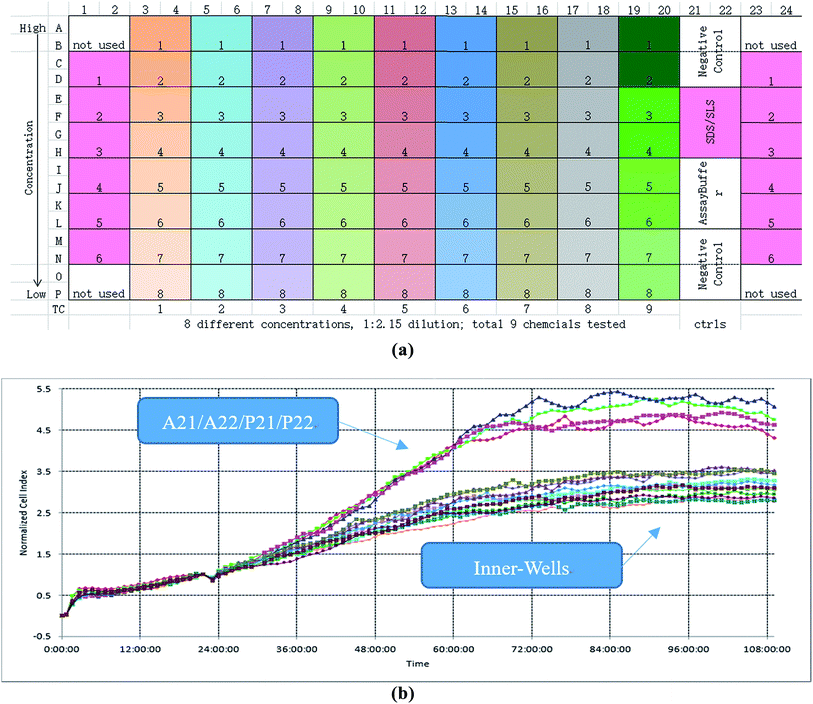 | ||
| Fig. 1 Experiment and its edge effect. (a) The schematic diagram of RTCA. (b) TCRCs of negative control. | ||
The procedure of the cytotoxicity assay is as follows: first, a certain cell line was added to each well of the ×384 E-plate and incubated in the culture medium about 24 h; second, different chemicals with different concentrations were added to the E-plate, which followed a particular protocol: the same chemical was added to every two columns of wells, and the same concentration of chemical decreasing from top to bottom was added to every two rows of wells. According to this protocol, each concentration of each chemical was repeated four times (for example, as shown in Fig. 1(a), A3, A4, B3, and B4 wells have the same culture environment; C3, C4, D3, and D4 have the same culture environment) to enhance the robustness of the experiment. An experiment lasted about 96 h. The time-dependent cellular response profiles were dynamically recorded in RTCA, which was termed the Normalized Cell Index (NCI) (shown in Fig. 1(b)). In the cell based in vitro assay, the data after the cellular exposure was important (from 24 to 96 h), so the total sampling time was 72 h.
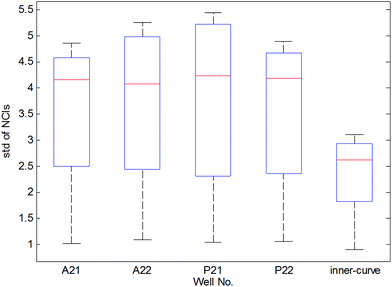
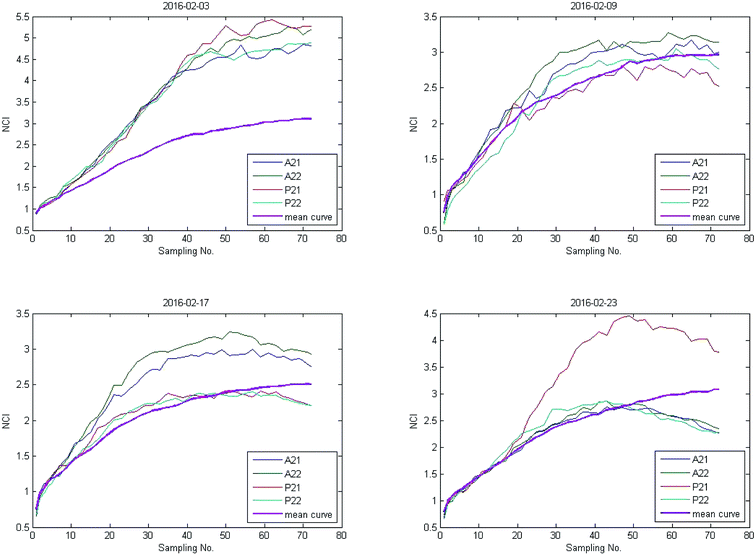
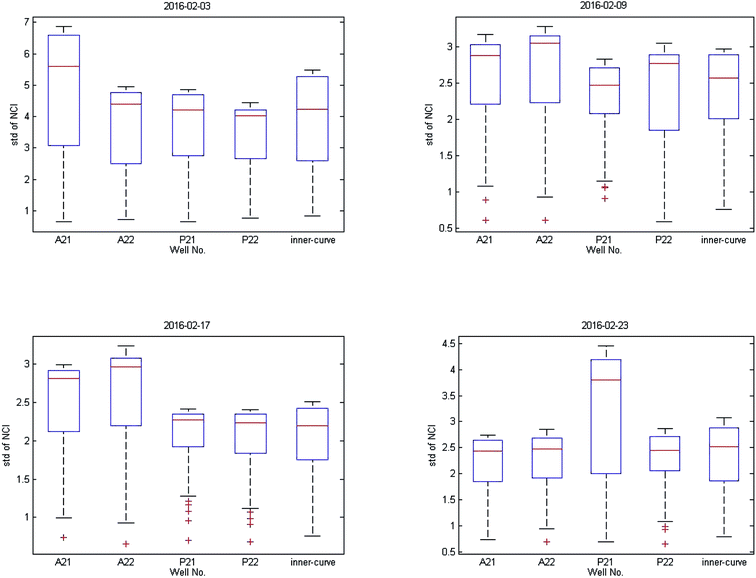
As shown in Fig. 1(b), the time-dependent cellular response curves (TCRCs) of A21/A22/P21/P22 (edge wells) were significantly different from the TCRCs of inner wells. NCIs of the inner wells were lesser than those of edge wells, this was named the edge effect. To describe the differences, the standard deviations of NCIs in the sampling interval located at edge/inner well were calculated and shown in Fig. 2. The mean NCIs of the inner wells were set as standard. The boxplots of edge wells were obviously different from those of the inner wells. As mentioned previously, the abnormal TCRCs located at the edge wells were screened manually. The automatic detection of the edge effect was the key issue in the RTCA experiment. To develop a validated method, the data of negative control were selected as examples, since cells without chemicals grow naturally in the culture medium. This eliminates the error cause by different cell growth environment.
3. Smirnov test method
To eliminate the effect of cell seeding populations, the cell index (CI) as normalized as follows:
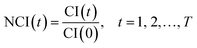 | (1) |
As shown in Fig. 1(b), the TCRCs located at inner wells were similar to each other, and different from the TCRCs located at edge wells (denoted asNCIm, m = 1, 2, 3, 4). Here, NCIs of inner wells were averaged as a standard:
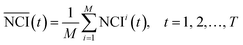 | (2) |
It is difficult to distinguish the difference between 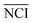 and NCIm directly, because TCRC is one type of time series. To develop a validated method, the empirical distribution of NCI was used and the range interval was set as:
and NCIm directly, because TCRC is one type of time series. To develop a validated method, the empirical distribution of NCI was used and the range interval was set as:
| {[δj, δj + 1)}j=0J | (3) |
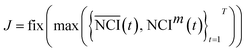 | (4) |
For each TCRC, the cumulative frequency of each interval was calculated as follows:
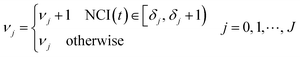 | (5) |
Through the interval segmentation and frequency accumulation, the time series NCI was transformed into independent random variables. Then the corresponding empirical distribution function (EDF) of each TCRC was computed:
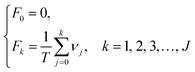 | (6) |
As a result, the EDFs of NCI of each edge-well (Fm) and mean NCI of inner wells (![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ) were obtained. The Smirnov test was used to determine whether the TCRC's EDFs of the edge wells were equal to the mean TCRC's EDFs, i.e.:
) were obtained. The Smirnov test was used to determine whether the TCRC's EDFs of the edge wells were equal to the mean TCRC's EDFs, i.e.:
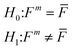 | (7) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) and Fm (m = 1, 2, 3, 4) are the EDFs of the mean TCRC and the four edge TCRCs, respectively.
and Fm (m = 1, 2, 3, 4) are the EDFs of the mean TCRC and the four edge TCRCs, respectively.
To compare the EDFs of two different samples without assuming any underlying parametric model for the sample, i.e. it is a nonparametric test,19 the Smirnov test is taken for consideration in this work.
The statistical magnitude of Smirnov test Dm was given by:
Dm = max|![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) k − Fkm| k − Fkm|
| (8) |
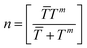 | (9) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) and Tm are the sample size of mean TCRC and TCRC of the edge well. In this work, the sample size was fixed at 72, so n = 32. α was the level of significance, in general α = 0.05 (95% confidence). The flowchart of the algorithm is illustrated in Table 1.
and Tm are the sample size of mean TCRC and TCRC of the edge well. In this work, the sample size was fixed at 72, so n = 32. α was the level of significance, in general α = 0.05 (95% confidence). The flowchart of the algorithm is illustrated in Table 1.
4. Case studies
Data from four experiments were collected from February 2016 (Fig. 3). The box plots of results are shown in Fig. 4. The average of the inner curves is shown as a bold purple curve. As shown in two figures above, in many cases it is difficult to identify the edge effect through artificial selection. In this section, experiment 1 (2016-02-03) was used as an example to show the distinguishing procedure. Using the proposed method, the significance level was set as α = 0.05 and the critical region was Dn,1−α = D36,1−0.05 = 0.22119. The calculation of the empirical distribution function is shown in Table 2. From eqn (8), the result is shown in Table 3.| Range interval | Cumulative frequency | Empirical distribution function | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| νj1 | νj2 | νj3 | νj4 | ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) j j |
Fk1 | Fk2 | Fk3 | Fk4 | ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) k k |
|
| [0,1) | 1 | 1 | 1 | 1 | 1 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| [1,2) | 14 | 13 | 15 | 15 | 20 | 0.014 | 0.014 | 0.014 | 0.014 | 0.014 |
| [2,3) | 10 | 11 | 10 | 10 | 37 | 0.208 | 0.194 | 0.222 | 0.222 | 0.292 |
| [3,4) | 10 | 11 | 10 | 10 | 14 | 0.347 | 0.347 | 0.361 | 0.361 | 0.806 |
| [4,5) | 37 | 19 | 11 | 36 | 0 | 0.486 | 0.500 | 0.500 | 0.500 | 1 |
| [5,6) | 0 | 17 | 25 | 0 | 0 | 1 | 0.764 | 0.653 | 1 | 1 |
| Edge-well | A21 | A22 | P21 | P22 |
|---|---|---|---|---|
Dm = max|![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) k − Fkm| k − Fkm| |
0.514 | 0.500 | 0.500 | 0.500 |
| Dm > D36,1−0.05 | Yes | Yes | Yes | Yes |
| Edge effect | Yes | Yes | Yes | Yes |
As shown in Table 2, the values of the statistical magnitude Dm of the four edge-well TCRCs were calculated, which were greater than the critical region D36,1−0.05 = 0.22119 (Table 3). According to the Smirnov test, hypothesis H0 was rejected. Therefore, the edge effects occurred in four edge-well TCRCs of experiment 1 and those TCRCs should be removed before the cytotoxicity assay.
The results of three other experiments are shown in Table 4. It can be seen there are many edge-effect TCRCs, which are consistent with the actual situation (Fig. 3 and 4). Therefore, the proposed method could effectively detect the edge effect.
| Experiment | Edge-well | Dm | Edge-effect |
|---|---|---|---|
| 2016-02-03 | A21 | 0.514 | Yes |
| A22 | 0.500 | Yes | |
| P21 | 0.500 | Yes | |
| P22 | 0.500 | Yes | |
| 2016-02-09 | A21 | 0.306 | Yes |
| A22 | 0.542 | Yes | |
| P21 | 0.292 | Yes | |
| P22 | 0.202 | No | |
| 2016-02-17 | A21 | 0.486 | Yes |
| A22 | 0.516 | Yes | |
| P21 | 0.186 | No | |
| P22 | 0.186 | No | |
| 2016-02-23 | A21 | 0.284 | Yes |
| A22 | 0.486 | Yes | |
| P21 | 0.284 | Yes | |
| P22 | 0.284 | Yes |
To compare the effects of different levels of significance of the experiment, another significant level was applied where α = 0.1. The corresponding critical region was D36,1−0.1 = 0.19910. The results are shown in Table 5.
| Experiment | Edge-well | Dm | Edge-effect |
|---|---|---|---|
| 2016-02-03 | A21 | 0.514 | Yes |
| A22 | 0.500 | Yes | |
| P21 | 0.500 | Yes | |
| P22 | 0.500 | Yes | |
| 2016-02-09 | A21 | 0.306 | Yes |
| A22 | 0.542 | Yes | |
| P21 | 0.292 | Yes | |
| P22 | 0.202 | Yes | |
| 2016-02-17 | A21 | 0.486 | Yes |
| A22 | 0.516 | Yes | |
| P21 | 0.186 | No | |
| P22 | 0.186 | No | |
| 2016-02-23 | A21 | 0.284 | Yes |
| A22 | 0.486 | Yes | |
| P21 | 0.284 | Yes | |
| P22 | 0.284 | Yes |
The P22 of experiment 2 (2016-02-09) was distinguished as an edge effect with α = 0.1. However, from Fig. 3, the TCRC of P22 fluctuated up and down with a mean curve in a small range, which is common when taking real cell growth into account. Therefore, in this work, it was too harsh to set α = 0.1, accordingly, in this work α = 0.05 was recommended.
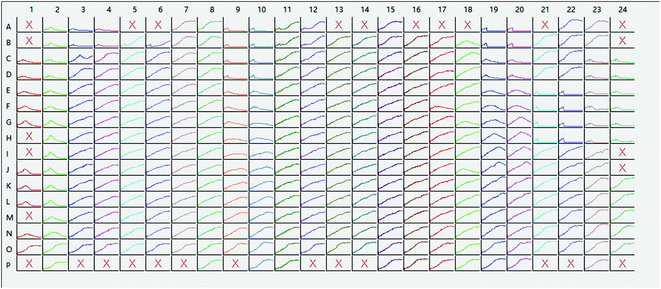
Furthermore, the wells with chemicals were also tested by using the presented Simonov test. As mentioned before, each concentration of each chemical was repeated four times, and only two inner wells were set as references. The results were shown in Table 6. Based on the proposed algorithm, the wells with edge-effect were screened out (“×” in Fig. 5) automatically, which can reduce the technician's workload and remove the careless operation.
| Edge-well | Dm | Edge-effect | Edge-well | Dm | Edge-effect |
|---|---|---|---|---|---|
| A1 | 0.514 | Yes | P1 | 0.514 | Yes |
| A2 | 0.202 | No | P2 | 0.202 | No |
| A3 | 0.186 | No | P3 | 0.306 | Yes |
| A4 | 0.186 | No | P4 | 0.486 | Yes |
| A5 | 0.306 | Yes | P5 | 0.368 | Yes |
| A6 | 0.542 | Yes | P6 | 0.368 | Yes |
| A7 | 0.202 | No | P7 | 0.486 | Yes |
| A8 | 0.202 | No | P8 | 0.202 | No |
| A9 | 0.186 | No | P9 | 0.386 | Yes |
| A10 | 0.186 | No | P10 | 0.128 | No |
| A11 | 0.070 | No | P11 | 0.128 | No |
| A12 | 0.070 | No | P12 | 0.292 | Yes |
| A13 | 0.284 | Yes | P13 | 0.292 | Yes |
| A14 | 0.486 | Yes | P14 | 0.306 | Yes |
| A15 | 0.128 | No | P15 | 0.128 | No |
| A16 | 0.284 | Yes | P16 | 0.128 | No |
| A17 | 0.306 | Yes | P17 | 0.070 | No |
| A18 | 0.306 | Yes | P18 | 0.070 | No |
| A19 | 0.128 | No | P19 | 0.070 | No |
| A20 | 0.146 | No | P20 | 0.070 | No |
| A21 | 0.514 | Yes | P21 | 0.284 | Yes |
| A22 | 0.070 | No | P22 | 0.284 | Yes |
| A23 | 0.070 | No | P23 | 0.202 | No |
| A24 | 0.486 | Yes | P24 | 0.306 | Yes |
5. Conclusion
The primary goal of this work was to develop an effective method to detect the edge effect, which can help technicians rapidly screen valid TCRCs. A standard Smirnov test was used to determine this. Although the statistical methods employed are not new, it is the first time they were applied to determine the edge effect in RTCA systems. The method effectively determined the edge effect, and reduced the risk of error by manual screening.Although the results demonstrated the effectiveness of the proposed method, future research should include the following:
● The choice of significant levels should be discussed based on the specific data, since the performance of this method is affected by the range interval;
● Other edge wells should be tested in addition to the negative control;
● Except for the TCRC of edge wells, the abnormal TCRC of inner wells with certain screening strategies should be discussed.
Acknowledgements
The work was supported by the National Nature Science Foundation of China [grant number 61273142], the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) and Foundation for Six Talents by Jiangsu Province. We also thank Xiao Xu, Xiaobo Wang and Can Jin from ACEA Biosciences Inc., David Kinniburgh and Dorothy Yu Huang from Alberta Centre for Toxicology, Weiping Zhang from Alberta Health, Biao Huang from University of Alberta (Canada) for scientific advice and technical support.References
- Organization W H., WHO human health risk assessment toolkit, chemical hazards, World Health Organization, 2010 Search PubMed.
- D. McGregor, A. Boobis and M. Binaglia, et al., Guidance for the classification of carcinogens under the Globally Harmonised System of Classification and Labelling of Chemicals (GHS), Crit. Rev. Toxicol., 2010, 40(3), 245–285 CrossRef CAS PubMed.
- F. Zucco, I. D. Angelis and E. Testai, et al., Toxicology investigations with cell culture systems: 20 years after, Toxicol. in Vitro, 2004, 18(2), 153–163 CrossRef CAS PubMed.
- T. Voskoglounomikos, J. L. Pater and L. Seymour, Clinical predictive value of the in vitro cell line, human xenograft, and mouse allograft preclinical cancer models, Clin. Cancer Res., 2003, 9(11), 4227–4239 Search PubMed.
- W. J. Pichler, Predictive drug allergy testing: an alternative viewpoint, Toxicology, 2001, 158(1–2), 31–41 CrossRef CAS PubMed.
- K. A. Houck and R. J. Kavlock, Understanding mechanisms of toxicity: insights from drug discovery research, Toxicol. Appl. Pharmacol., 2008, 227(2), 163–178 CrossRef CAS PubMed.
- Roche. xCELLigence system application note No. 16, RTCA HT instrument high throughput GPCR screening, Roche Diagnostics GmbH, Mannheim, Germany, 2011 Search PubMed.
- F. A. Atienzar, K. Tilmant and H. H. Gerets, et al., The use of real-time cell analyzer technology in drug discovery: defining optimal cell culture conditions and assay reproducibility with different adherent cellular models, J. Biomol. Screening, 2011, 16(6), 575–587 CrossRef CAS PubMed.
- T. H. Pan, B. Huang and J. Z. Xing, et al., Recognition of chemical compounds in contaminated water using time-dependent multiple dose cellular responses, Anal. Chim. Acta, 2012, 724(8), 30–39 CrossRef CAS PubMed.
- T. Zheng, X. Kuang and J. Wang, et al., Real-time cell analysis – a new method for dynamic, quantitative measurement of infectious viruses and antiserum neutralizing activity, J. Virol. Methods, 2013, 193(2), 364–370 CrossRef PubMed.
- J. Z. Xing, S. Gabos and B. Huang, et al., High-throughput quantitative analysis with cell growth kinetic curves for low copy number mutant cells, Anal. Bioanal. Chem., 2012, 404(6–7), 2033–2041 CrossRef CAS PubMed.
- L. Otero-González, R. Sierra-Alvarez and S. Boitano, et al., Application and validation of an impedance-based real time cell analyzer to measure the toxicity of nanoparticles impacting human bronchial epithelial cells, Environ. Sci. Technol., 2012, 46(18), 10271–10278 Search PubMed.
- Eli Lilly and Company and the National Institute of Health Chemical Genomics Center, Guidance for Assay Development & HTS, March 2007, Version 5, 2005 Search PubMed.
- B. K. Lundholt, K. M. Scudder and L. Pagliaro, A Simple Technique for Reducing Edge Effect in Cell-Based Assays, J. Biomol. Screening, 2003, 8(5), 566–570 CrossRef CAS PubMed.
- B. J. Foley, A. M. Drozd and M. T. Bollard, et al., Maintaining Microclimates during Nanoliter Chemical Dispensations Using Custom-Designed Source Plate Lids, JALA, 2015, 21(1), 115–124 Search PubMed.
- N. Malo, J. A. Hanley and S. Cerquozzi, et al., Statistical practice in high-throughput screening data analysis, Nat. Biotechnol., 2006, 24(2), 167–175 CrossRef CAS PubMed.
- J. Chen, T. H. Pan and B. D. Devendran, et al., Analysis of inter-/intra-E-plate repeatability in the real-time cell analyzer, Anal. Biochem., 2015, 477, 98–104 CrossRef CAS PubMed.
- T. H. Pan, H. R. Li and K. Swanand, et al., High-throughput screening assay for the environmental water samples using cellular response profiles, Ecotoxicol. Environ. Saf., 2015, 114, 134–142 CrossRef CAS PubMed.
- L. Mora-López and J. Mora, An adaptive algorithm for clustering cumulative probability distribution functions using the Kolmogorov–Smirnov two-sample test, Int. J. Expert Sys. Appl., 2015, 42(8), 4016–4021 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |