Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Surface dissimilarity affects critical distance of influence for confined water†
Aleena Alex ,
Ashwin Konanur Nagesh and
Pijush Ghosh*
,
Ashwin Konanur Nagesh and
Pijush Ghosh*
Indian Institute of Technology Madras, Chennai, TN, India-600036. E-mail: pijush@iitm.ac.in
First published on 13th January 2017
Abstract
Water at interfaces and under nano-confinement is part of many natural processes. The behavior of this water is greatly influenced by the nature of the surfaces it is in contact with and the confinement distance. The objective of this study is to understand the behaviour of confined water between dissimilar (X–Y) surfaces under varying confinement spacing. The surfaces considered were hydrophilic in nature and the combinations were considered based on crystal structure and surface energy. The critical distance of influence of mineral substrates on the water molecules was determined by applying time-averaged static properties such as interfacial layer density and orientation and dynamic properties such as diffusion. It was observed that dynamic properties provide a higher value of critical distance compared to static properties for dissimilar surface combination. The reason for this disparity is probed in terms of mineral–water and water–water interactions. The disproportion of strong and weak H-bonds was observed to be significant in determining the dynamic behaviour of interfacial layer. We applied hydrophilic surface combinations of tricalcium silicate (C3S) and dicalcium silicate (C2S) for our investigations.
1. Introduction
Mineral–water interfaces play an important role in many physical, biological and chemical systems. The nature of the substrate, such as hydrophilicity, local charge distribution and overall arrangement of atomic species leads to different density, orientation, and H-bond networking in water, both perpendicular and parallel to the surface. Two hydrophilic surfaces consisting of similar atomic species may show identical behavior in the direction perpendicular to the surface. However, the near surface two-dimensional structuring and orientational preferences of water molecules can vary significantly.Behaviour of water confined between surfaces of varying degrees of hydrophilicity has not been investigated until very recently.1–5 Most of the mineral water interaction systems deal with only single surface6,7 or similar surfaces8,9 (homogenous) on either end of the confined volume. Water density, orientation and H-bond formation of such similar surface combinations have been studied extensively. However, there are many technological and biological applications where water comes under nano-confinement between dissimilar (heterogeneous) surfaces. Few examples are atomic scale surface–lubricant interactions in nano-scale devices, cell-sorting devices and programmable self-cleaning devices. Such systems have been looked into in terms of stick-slip bridging of water molecules, varying the surface properties by controlling polarity, stiffness and head group repulsion of the surface etc. There have been several attempts in recent literature to gradually tune the surface properties such as hydrophilicity to arrive at a general theory and functional relationships between the influence of substrate properties on nano-confined water.1,2 Unlike technological systems with fixed surface separations, there are many natural systems in which water comes under nano-confinement between two dissimilar surfaces. The tricalcium silicate (C3S), dicalcium silicate (C2S)–water interface is an interesting example of that genre. C3S and C2S are the major constituents of Ordinary Portland Cement (OPC) which are responsible for strength gaining and binding properties of a cement matrix. This is a multi-particle interacting system with water confined at varying spacing between two or more surfaces of C3S and/or C2S. For many such natural systems, the properties of interfacial water are not completely understood even though molecular level studies have been conducted and promising results have been obtained in recent years.6,7,10–13 Most of these studies have given insights into single surface–water interaction. However, our study focuses on the initial few nanoseconds of the wetting stage before the hydration reaction starts. During this wetting stage, the water molecules comes in contact with the surface, lowering the surface energy, and arranges themselves with respect to the surface properties and local polarities. Mineral–water interaction between C3S/C2S–water systems during these initial stages of hydration significantly influences the overall kinetics of the hydration reaction and product formation.14,15
The natural system of calcium silicates differs from the technological nano-devices previously discussed in literature, due to the presence of a wide range of varying surface separations. This variation in confinement spacing leads to the definition of a critical distance of influence at which the presence of one surface no longer affects the properties of interfacial water on the second surface. In almost all the literature dealing with water confinement, it was reported that the substrate effect on water molecules extends only up to 1–2 nm.28,31,32 However, most of these works deal with similar surfaces on either end of confined volume. The critical distance of influence for a system with dissimilar surfaces is yet to be investigated. Hence in this work, we attempt to determine the critical distance (dc) for similar and dissimilar surface combinations by determining the static and dynamic properties of interfacial water layer.
Thus, both similar (C3S–C3S and C2S–C2S) and dissimilar (C3S–C2S) surface combinations with a confined volume of water enclosed between them, have been considered for this study. The adsorbed water molecules are found to form a layered morphology closer to the mineral surface. However, this layering is affected by the proximity and nature of the second mineral surface. It is observed that while the average static properties like density and orientation are not significantly influenced by the proximity of the second surface, the dynamic properties like diffusion coefficient and mean square displacement are found to vary even at confined spacings greater than 4 nm. Understanding the effect of surface separation on the dynamics of water under nano-confinements between similar and dissimilar surfaces is the primary motivation for this study. The observations in this sample system can be extended to several comparable organic and inorganic systems with confined water such as the swelling behaviour of clay and mechanical properties of biomaterials.16–19
2. Methods
Molecular Dynamic (MD) simulations are very useful in obtaining information on the behavior of large molecular systems. Wetting characteristics of minerals have been extensively studied using MD in order to comment on hydrophilicity/hydrophobicity.20 Using all-atom classical MD simulations, the equilibrium state of the system was approached dynamically. The atoms and molecules were allowed to move without any constraints other than those imposed by the force fields, and system variables of temperature and pressure. Statistical thermodynamics was applied to obtain ensemble averages which are in turn related to the macroscopic properties. This dynamic technique gives a better understanding of interaction mechanisms involved in the evolution of a system. All simulations were performed using Large Scale Atomic Molecular Massively Parallel Simulator (LAMMPS).21 Initial configurations were prepared using Packmol22 and visualisation and trajectory analysis were carried out using Visual Molecular Dynamics (VMD)23 software.The general model used for all the simulations was a layer of water molecules with starting density of 1 g cm−3, confined between two calcium silicate layers. The thickness of this water layer or the confinement spacing was then varied between 1–8 nm. The structures proposed by Golovastikov (1975) and Nevskii (1982)24,25 obtained from Crystallography Open-access Database (COD),26 were used for C3S and C2S (alpha) respectively. Previous investigations into the calcium silicate–water interactions have been performed with Reactive Force Field (ReaxFF) to capture the bond breaking and formation.6,7 However, in our study we employ a non-reactive forcefield as we are interested only in the wetting stage prior to the initiation of hydration. The crystal structure, chemical formula and the potential parameters for C2S and C3S have been provided as ESI.†
TIP3P model was used for the water molecule. The model applied in this study is shown in Fig. 1.
For heterogeneous system with C3S on one end and C2S on the other, application of Periodic Boundary Conditions (PBC) is slightly problematic. This is because the application of PBC will result in C3S–C2S interactions at the periodic system boundary. However, the crystal height is chosen in such a way that it is greater than non-bonded interaction cut-off distance, so that these interactions do not affect the behaviour of water molecules.
The lateral dimensions of the crystal were taken as 135 × 100 Å i.e. 10 × 10 unit cells for C3S and 14 × 18 unit cells for C2S. For both the crystals, the [1 0 0] cleavage plane was exposed to the water molecules. The energy of the cleavage planes was calculated from eqn (1).
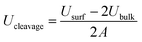 | (1) |
Surface cleavage usually requires the cleavage of covalent bonds, thus creating broken or dangling bonds on the surface. It is undesirable to have such dangling bonds because they cause excess and physically implausible polarization of charges and increased surface energy. Charge neutrality and stoichiometry is ensured in this work by selecting surface terminations appropriately and reforming any broken bond, thus preserving the SiO4 tetrahedral.
The confinement spacings used in this study correspond to the smallest pores present in hydrating cement characterized as gel pores (1–10 nm).27
It was previously reported that the effect of a crystal surface on the water layer extends up to a distance of 10–15 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 or up to the diameter of five water molecules (diameter of a single water molecule being 2.75 Å).
28 or up to the diameter of five water molecules (diameter of a single water molecule being 2.75 Å).
This value depends on the nature and atomic compositions of individual surfaces. However, the behaviour of confined water can be different. Hence, the different cases of confinement distances and surface combinations considered in this study, gives us an interesting understanding of the influence of confinement on properties such as diffusion and self-assembly of species.
A simple, non-reactive forcefield was adopted for the molecular dynamics simulations with the Coulomb and Lennard-Jones potentials accounting for the inter-atomic interactions and the harmonic bond and angle potentials accounting for the intra-atomic interactions.29,30 This forcefield has already been validated for atomistic simulations and it provides good agreement with available experimental data such as cleavage energies, X-ray structures, IR spectra and elastic modulus. The parameters were shown to accurately simulate interfaces with water, polymers, and bio-molecules. We have adopted this forcefield because it was found to have less than 10% deviation from experimental results as far as interfacial properties are concerned.
The simulations were performed in two stages. In the first stage, both the crystals, C3S and C2S, were fixed and energy minimizations were performed on the water molecules using conjugate gradient method with energy and force cut-off tolerances set close to zero (10−35). A common cut-off distance of 10 Å was fixed for coulombic and L-J pair potentials with long range Coulomb interactions accounted for using Ewald summation technique. The system was equilibrated in the NVT ensemble using Nose–Hoover thermostat, with the damping parameter for temperature set at 10 fs and integrating the Newton's equations of motion using the velocity verlet algorithm with a time step of 1 fs. In the second stage of simulation, the atoms in C2S and C3S were released allowing the movement of ions and the system was equilibrated in NPT ensemble at 300 K and 1 atm. Equilibrations were carried out for 10 ns and the quantifications were done from the atomic trajectories corresponding to the last 1 ns. Averaging of static properties was done over at least 50 time frames and dynamic properties were averaged over at least 5 repetitions.
3. Results and discussion
The structural parameters such as atomic densities of hydrogen (H) and oxygen (O) atoms across the water layer, and the orientation of H–O–H angle bisector with respect to the surface normal were determined at the first stage of simulation. Density and orientation of water molecules are classified as static properties in this work.28,31,32 Other static properties include Radial Distribution Function (RDF) and the number of hydrogen bonds per unit volume. While calculating the density and orientation of water molecules, the crystals were fixed in place in order to facilitate a more efficient analysis and clearer distinction of the near-surface water behavior. Mean Square Displacement (MSD) of water molecules, a dynamic parameter, was calculated and the diffusion behavior was observed at the second stage of simulation.The structure and dynamics of water are influenced by crystal surface, since crystal surface affects water density, orientation, and mobility (rotation and translation). Water molecules take up a layered and ordered structure near the crystal facet. Such layering has been reported extensively in the literature31–33 and has been investigated for different crystal facets like mica, talc, brucite etc. The extent of the crystal's influence on these layers and molecular arrangement within the layers is determined by the nature of crystal surface and the resulting H-bond network formed within the layer and between the adjacent layers. The near-surface water layer is referred to as the interfacial layer or the tessellated water layer.6 Using the properties of this water layer, the effect of confinement and the presence of similar and dissimilar surfaces are studied in this work.
3.1 Static properties: density and orientation
Density of water is calculated using the number density of hydrogen (H) and oxygen (O) atoms per unit volume. For bulk water with a density of 1 g cm−3, the corresponding H atom number density can be calculated as 0.066 per Å3. This density value is, however, expected to vary within the interfacial layer since its structure varies from that of bulk water in the directions both perpendicular and parallel to the confining surfaces. It is also influenced depending on the presence of similar or dissimilar surfaces on either side of the confined volume. For the C2S surface, the average number density of H atoms in water molecules over the entire surface was observed to be 8–10% lower than the same for C3S surface. In the 2-dimensional density contours, however, this value varies from one point to another on the surface. A periodic pattern of higher (red in the density contour marked as Section A and B), intermediate (yellow-Section C and D) and lower (dark blue-Section E and F) density regions are observed in the Z direction as shown in Fig. 2. The sections of higher density (Section A and B in Fig. 2) have a peak density value of 0.14 per Å3. This value is more than double the bulk water density. Water density, as observed, is significantly lower at certain other sections (Section E and F in Fig. 2) on the surface. This periodicity in the crests and troughs of water density from one point to another on the crystal surface suggests that the water molecules mimic the underlying periodicity of the atomic arrangement on the surface. The distance between two adjacent crests in the Y and Z direction in the water density profile are found to be 6 Å and 9.5 Å, respectively. This corresponds to the distance between two Ca1.5+ ions or O1− ions (part of the [SiO44−] tetrahedra) in the respective directions. There are also peaks in the density profile of intermediate amplitude ranging from 0.02–0.06 per Å3 (Section C and D in Fig. 2), the presence of which can be explained either (a) with the structured water molecules forming a secondary layer of water with slightly lower density through intermolecular H-bonds or (b) it could indicate the presence of a strong local charge in the mineral layer immediately below the surface (e.g. sub-surface oxygen in Fig. 2).The properties of confined water are influenced by surface similarity. This is because the water molecules closer to one crystal surface may come under the influence of the second crystal surface and this competition between first and second surfaces determines the structure of water. These two surfaces can be similar or dissimilar. This helps us to define a critical distance dc beyond which, the presence of a second crystal surface does not influence the properties of the interfacial water layer of the first. Both similar and dissimilar surface combinations namely C3S–C3S (X–X), C2S–C2S (Y–Y) and C3S–C2S (X–Y), are considered in this study.
In C3S–C3S and C2S–C2S combinations, the interfacial layer density was determined as 0.075 per Å3 and 0.068 per Å3 respectively for confinements greater than 2 nm. The density profile is symmetrical in the direction perpendicular to the surface. For dissimilar surface combination (C3S–C2S), at higher confinements (>2 nm), the density profile is asymmetrical and the interfacial layer behavior for the respective crystal surfaces was same as that of similar surface combinations.
For all the surface combinations, the critical distance dc was estimated as 2 nm. This indicates that beyond 2 nm, the interfacial layer water density is no longer affected by the presence of a second surface. The density profile in Fig. 3 shows the variation in the interfacial layer water density with respect to the confinement spacing d. At d = 1 nm the density values are lesser by 20–40% compared to the same at higher confinements (d > 2 nm). However, for C2S–C2S system, the reduction is only 5%. The reduction is greater for the dissimilar surface system than the similar one. At low confinement spacing, the entire water volume can be treated as an interfacial layer and thus no water behaves as bulk water between the two mineral surfaces. This water forms H-bond bridging between the two surfaces as shown in Fig. 5. For a confinement spacing of 1 nm, the C2S–C2S surface combination shows minimum deviation (Δ1) from interfacial layer density and the C2S–C3S system shows the maximum deviation (Δ2). This clearly indicates that for the same underlying substrate, besides the confinement spacing, the behavior of interfacial layer is influenced by the nature of the second surface. Fluctuations in water density have been identified in literature as an indication of hydrophobic nature of the substrate.3–5 H-Density near the C2S surface shows a sudden dip from 0.068 per Å3 to 0.0425 per Å3 in the presence of C3S at a separation of 1 nm (Fig. 3). This indicates a cavity formation near the C2S surface in the presence of C3S at close proximity. It implies that the otherwise hydrophilic C2S surface behaves like a hydrophobic surface in the presence of C3S at 1 nm.
Orientation is calculated with respect to the angle θ formed between the H–O–H angle bisector and the normal to the crystal surface. The probability distribution of θ, P(θ) vs. cos(θ) for interfacial layer water molecules under different confinements is plotted in Fig. 4. It is observed that the orientation profile of the interfacial layer is indistinguishable after a distance of 2 nm. Hence, as quantified from the two static properties in this study, the critical distance (dc) after which surface-1 no longer perturbs the properties of water molecules of surface-2 is 2 nm.
In Fig. 4, the near surface orientation shows bias at certain angles for the C3S and C2S surface as opposed to bulk water which gives a uniform distribution of probability at all orientations. This is a result of reorientation of water molecules on the crystal facet depending on the underlying molecular arrangement and the local charge fields. However, this orientation is also distorted at confinements lesser than 2 nm. It is observed that all the orientation profiles of the first crystal surface have major peaks biased towards the left. Orientations of the interfacial layer near the second surface with respect to the first surface-normal results in an inverted curve biased towards the right. Hence, as we bring the second surface closer, the interfacial layer is influenced by surface-2 resulting in the shift of probability distribution from left to right. The shift is observed at confinement d = 1 nm for all the C2S–C3S surface combinations.
Another important observation from the study of molecular structure of water on the mineral facet is the existence of two or more layers (layer 1 and layer 2) with varying predominant orientations as shown in Fig. 5. Interfacial layer at C2S shows preferential bias at 120° and 60°. This particular bias results from a combination of causes. The local arrangement of ionic species in the crystal forms H-bonds with the first or primary layer of water aligning the water molecules at 120° (layer 1). These aligned water molecules form the secondary layer through water–water H-bonds with the water layer above aligning the layer at 60° (layer 2). These secondary layers also indicate a transition from the structured interfacial layer to the randomly oriented bulk water. Such primary and secondary layers of water are responsible for the multiple peaks of varying intensity in the orientation probability distribution (Fig. 5). Even though such layers are observed in the orientation profile of C3S, they cannot be distinguished visually because of the closely packed atomic arrangement in the crystal. The formation of these layers can be attributed to (a) the “hard-wall” effect or the excluded volume effect,34 which creates a geometric constraint on the crystal facet preventing the solvent molecule from penetrating into the crystal and (b) the electrostatic forces of attraction between the solute and solvent species. This phenomenon is similar to that observed during the hydration of a crystal solute in bulk water as in the case of C3S/C2S in cement mortar.
3.2 Dynamic properties: Mean Square Displacement (MSD) and diffusion behavior
Mean Square Displacement (MSD) is a measure of translation mobility of the molecules. Self-diffusion coefficient of a particle can be related to the mean square displacement using Einstein's relation as in eqn (2).
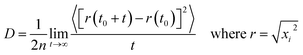 | (2) |
The term inside 〈 〉 denotes the ensemble average of MSD. ‘n’ denotes the dimensionality of the system and ‘t’ denotes time. For all the calculations in this study, the dimensionality is taken to be 3 (i = 1, 2, 3) and the total time considered is 1 ns. The slope of the MSD vs. time plot gives the self-diffusion coefficient.
The orientation profiles indicate the existence of two or three distinct water layers near the crystal facet and a gradual transition to the bulk liquid. Each facet of mineral influences the water molecules to form such oriented layers which behave differently from bulk water. Here, the confined volume of water was divided into volumes of 3 Å thicknesses to estimate its dynamic properties. The thickness was chosen to ensure that at least one layer of water molecules (diameter = 2.75 Å) was present in the divided volume. The layers were fixed and the diffusion coefficient was calculated based on water molecules that were present in the layer at a particular point of time. Once a molecule goes out of the layer it was no longer considered for further estimations. Thus, essentially, even though the 3-D diffusion coefficient is estimated, it gives the required interfacial molecular mobility or the planar (2-D) mobility, ignoring the movement in perpendicular direction.
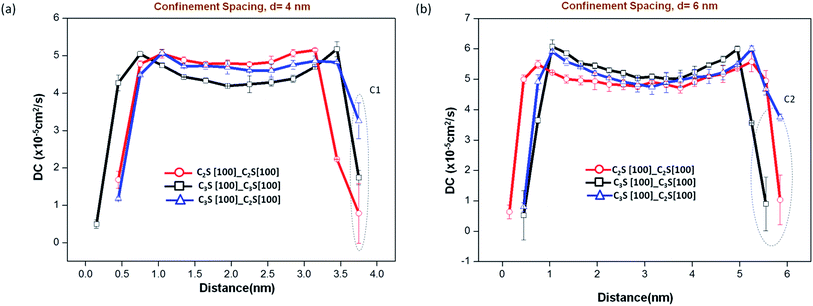
The variation of diffusion coefficient (DC), over the entire volume of water, for confinement spacing ranging from 2 nm to 8 nm for all the three C2S–C3S surface combinations are provided in Fig. 6. For 1 nm confinement, the value ranges in the order of 10−7 cm2 s−1 for all the three surface combinations. This is two orders of magnitude less than the bulk water DC which suggests that these molecules are almost immobile. This is consistent with the observation made earlier where at 1 nm spacing the water between the two crystals forms a bridging layer (Fig. 5). These bridges are held in place by strong electrostatic force exerted by both mineral surfaces on water molecules due to the Ca–Ow and Ob/Onb–Hw interactions. The mineral also imposes a geometric constraint in the direction perpendicular to its surface arresting the motion of water molecules.
At lower confinement spacings of 2 and 4 nm, a reduced value of DC is observed for water molecules in all the layers. Eventually, for confinements greater than 4 nm the DC value of bulk water in the middle of the confined volume stabilizes to the reported value of DC for TIP3P type water.35 This decrease in DC value at lower confinement spacing can be attributed to the excluded volume effect as discussed in the previous section.
For the entire range of confinement spacings, similar surface combinations (C2S–water–C2S and C3S–water–C3S) show symmetric behavior, with the interfacial layer diffusion coefficient significantly lesser than that of bulk water. The reduction of DC value at the interfacial layer indicates that the layer is temporarily stabilized, preventing further dissociation and intermigration of species. The far-surface water in higher confinements approaches bulk water behavior. However, the water molecules in the system with dissimilar surfaces on either end of the confined volume, shows stabilization in one end (C3S), and higher mobility close to bulk water in the other end (C2S) (C1 and C2 in Fig. 6). For an ideal case when there is sufficient separation between the two confining surfaces we would expect that the value of DC at the stabilized interfacial layer to be lower than 2 × 10−5 cm2 s−1. However, dissimilar surface combinations, with spacings as large as 8 nm, does not show this reduction at the C2S end. The mobility of interfacial layer water molecules at this end is consistently higher than the corresponding value in the similar surface combination. Hence the C3S–C2S critical distance of influence is greater than 8 nm.
The analysis of static properties in the previous sections had suggested that for confinement spacing greater than 2 nm, interfacial layer of surface-1 is not affected by the presence of surface-2. However, from the DC values obtained, we make a different observation. The mobility of interfacial layer water molecules is affected by the second surface at confinement spacing above 2 nm. Hence, the critical distance of influence of the surfaces is also higher. The extent of this influence or the value of critical distance (dc) depends on the nature of the two surfaces. In our study, the presence of C3S causes the water molecules from the interfacial layer of C2S to get continuously exchanged with the solution (bulk water) thus increasing its mobility. However, interestingly during this exchange, it maintains its orientation and density so that this phenomenon is not reflected in the static properties as measured earlier.
The study was repeated with C2S [1 1 0] surface with Ucleavage = 0.51 J m−2, energy value comparable to the C3S [1 0 0] cleavage surface energy of 0.54 J m−2. The increase in the value of diffusion coefficient with confinement distance is observed here as well. However, the two cleavage planes of the same crystal C2S, exhibits different interfacial layer characteristics, in the presence of a dissimilar surface. At a confinement spacing of 2 nm, with C3S [1 0 0] as surface 1, at the C2S [1 1 0] end the DC value reduces to 1.4 × 10−5 cm2 s−1 whereas for C2S [1 0 0] the value increases to 4.6 × 10−5 cm2 s−1 (C3 in Fig. 7). This suggests that, in addition to the dissimilarity of the surfaces, the difference in cleavage energy also contributes in determining the critical distance. It is possible to derive a functional relationship between cleavage energy of the surface and interfacial layer diffusion coefficient. However, in order to do this, certain number of surface combinations needs to be studied and their static and dynamic properties need to be quantified. This is, at present, beyond the scope of this work.
3.3 H-Bond and RDF analysis
Detailed H-bond analysis of water molecules associated with the interfacial layers of C3S and C2S surfaces and the bulk was made in order to understand the mechanism responsible for the different water behavior in these layers (Fig. 8). Hydrogen bonds were divided into strong, medium and weak36–38 depending on the donor (D)–acceptor (A) spacing (dH) and D–H⋯A angle (ϕ). A dH spacing <2.5 Å and ϕ < 20° is classified as a strong H-bond. It was observed that strong H-bonds are not present in bulk water. However, in the interfacial layer of C3S and C2S, strong H-bonds constitute approximately 10% of all the bonds. H-Bonds of medium strength defined as 2.5 ≤ dH < 3.2 (Å) and 20° ≤ ϕ < 30° constitutes 55% of all bonds in the interfacial layer of both surfaces and 67% of all bonds in bulk water. This limiting distance of 3.2 Å corresponds to the minima of Ow–Ow Radial Distribution Function (RDF) as observed in Fig. 10. Hence it accounts for maximum number of water molecules being present in this state for all three cases. The remaining H-bonds with 3.2 ≤ dH < 4.0 (Å) and 30° ≤ ϕ < 40° are classified as weak H-bond. At dH ≥ 4 Å and ϕ ≥ 40°, H-bonds are assumed to be broken. Number of H-bonds presented here is normalized to the number of water molecules present in each layer to allow reasonable comparison between different systems.Average H-bonds per water molecule is found to be 3.72 and 3.11 for interfacial water layer of C3S and C2S respectively. This is consistent with the higher density in C3S interfacial layer as observed in the density profile. Interfacial layer associated with C3S was found to have maximum number of strong and medium H-bonds. In order to quantitatively estimate the relative bond intensities, we define two parameters α and β as in eqn (3) and (4):
 | (3) |
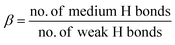 | (4) |
It is a relative measure of mobility of water molecules or the ease of breaking of H-bonds. The value of α is estimated to be 0.180 and 0.195 for interfacial layer water molecules of C3S and C2S respectively. This implies that the strong/medium bond ratio does not vary significantly between the two systems. However the value of β was estimated to be 1.47 for C3S and 1.20 for C2S. From diffusion characteristics, it is observed that in the presence of C3S, water molecules from the interfacial layer of C2S show higher kinetic energy and increased mobility. The reason for this increase is the 18% higher β value of C3S compared to that of C2S. A higher β value indicates higher number of medium H-bonds compared to weak H-bonds. Thus, for surfaces with lower β value, the interfacial layer of water molecules is more likely to get exchanged with the bulk because weak H-bonds are easier to break. This is what happens in the case of interfacial layer associated to C2S [1 0 0] and a possible reason for the higher mobility of water molecules in this layer.
Two factors can be attributed towards the formation and characteristic behavior of the interfacial water layer (i) water–water interaction and (ii) mineral–water interaction. We observe that there is a higher percentage of strong and medium H-bonds in the interfacial layer, while strong bonds are absent in the bulk water layer above. This indicates that the strong bonds are formed between the water and the crystal surface. In order to break it down further, the dynamics of different H-bonded pairs of donor and acceptor groups is investigated. We follow the hydrogen bond dynamics of water molecules within themselves (Ow–Ow H-bonds) and with the bonded and non-bonded polar oxygen atoms on the crystal surfaces (Ob–Ow and Onb–Ow H-bonds). An H-bond is defined using the same geometric definition as stated previously and we ignore the weak bonds in this section as we are interested in the dynamics of strong and medium bonds. The structural relaxation of hydrogen bonds was characterized using interrupted and continuous auto-correlation functions defined as in eqn (5).
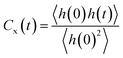 | (5) |
The auto-correlation function is then fitted to a multi-exponential function of the form given by eqn (6).
 | (6) |
Lifetime of H-bond is calculated as given in eqn (7).
 | (7) |
The variation in lifetime of hydrogen bonds for heterogeneous and homogenous surface combinations is given in Fig. 9. All potential combinations of donor and acceptor pairs were considered. Onb–Ow and Ob–Ow are the H-bonds formed with the non-bonded and bonded oxygens on the surface of the crystal. It should be noted that non-bonded oxygens are absent in C2S. Water–water H-bonds are represented by Ow–Ow interactions. H-Bond lifetime for the different combinations reduces in the order Onb–Ow (C3S) > Ob–Ow (C3S) > Ob–Ow (C2S) > Ow–Ow (water layers). From the values of H-bond lifetimes it is clear that surface–water H-bonds are certainly more significant in determining the properties of interfacial water than water–water H-bonds. The Onb–Ow donor acceptor pair on the C3S surface has the largest lifetime of 37.48 ps with the homogenous surface combination. However, this lifetime doubles to 71.07 ps for the heterogeneous surfaces. This shows that in the presence of a second surface of lower polarity and hydrophilicity on the other end, the lifetime of hydrogen bond increases on the first surface. The reverse is also true. In the presence of a surface of larger polarity on the other end of the confined water volume, as in the case of Ob–Ow donor–acceptor pairs on C2S surface, the lifetime reduces from 7.22 for the homogenous surface combination to 6.36 ps for the heterogeneous surface combination. This reduction in lifetime of crystal-water H-bond, however, leads to a nominal increase in lifetime of Ow–Ow H-bonds on the first water layer above C2S surface from 0.21 ps to 0.47 ps. Thus the increase in diffusion coefficient observed at the C2S surface, in the presence of C3S on the other end of the confined water volume is due to this breakage of surface–water H-bonds rather than water–water H-bonds.
It is observed that the proportion of strong H-bonds in the interfacial layer is less than 15% even though this layer shows higher density. In addition, the calcium ions and the bonded and non-bonded oxygen ions in the crystal are well coordinated with the oxygen and hydrogen atoms in the water molecule (Fig. 10) indicating strong electrostatic interactions between these oppositely charged species. Hence, we can conclude that in the interfacial layer the electrostatic interaction between the crystal ions and water molecules are more predominant than the water–water interaction. In C3S, the non-bonded oxygen atoms show higher coordination with the hydrogen in water molecules. The surface reactive sites causes the water molecules to move away from each other, thus preventing them from forming strong H-bonds. This electrostatic interaction with reactive sites is reflected in the Ow–Ow/RDF of water confined in 1 nm (Fig. 10) where all the water molecules form part of the interfacial layer. The RDF plot shows multiple peaks at regular intervals, indicating that there is a periodic arrangement of water molecules on the mineral facet. This also agrees with the observations made on the two dimensional near-surface density profiles in Section 3.1. The argument is further strengthened by the fact that the peaks are at positions 6 Å and 9 Å corresponding to the inter-atomic spacing in C2S.
 | ||
| Fig. 10 Ow–Ow/RDF for (a) C3S and (b) C2S for confinement spacing ranging from 1 to 8 nm. Onb–Hw, Ca–Ow, Ob–Hw RDFs for (c) C3S and (d) C2S. | ||
4. Conclusions
In this work, the effect of surface dissimilarity on the critical distance of influence on confined water was examined by determining static and dynamic properties. Critical distances become important when modeling particle–particle interaction at higher length scales. Critical distance determined from time averaged static properties or by using similar surfaces is significantly smaller than the value obtained taking into account the dynamics of the system and with dissimilar surfaces. Static analysis suggests that the critical distance of influence is less than 2 nm. However, the dynamics of interfacial water layer suggests that dc could be greater than 8 nm. It is absolutely essential to analyze both similar and dissimilar surface combinations in order to properly understand this disparity. It was also observed that water forms two or more specifically-oriented layers above the crystal surface. These layers are characterized by varying dynamics of water. The layered structure of water, which is evident from the density and orientation profiles, is a combined effect of the surface-specific hydrogen bonding, organization of the solvent molecules and the disorganization due to the thermal motion and kinetic energy of the molecules. The separation distance between the two surfaces which confines the water molecules also plays an important role in their organization. The additional mobility of the interfacial layer of C2S surface in the presence of C3S is due to (a) the medium to weak H-bond disproportion (lower β value) and (b) the higher number of reactive sites on the C3S surface due to the presence of non-bonded oxygen atoms. This is further validated by the larger H-bond lifetime of Onb–Ow donor acceptor pair. H-Bond dynamics also substantiates that surface–water interaction dominates water–water interactions in determining interfacial layer characteristics. It is possible to develop a functional relationship between properties such as the surface energy, polarity etc. of two competing surfaces and interfacial water characteristics and critical distances. This provides scope for future studies and developments to generalize these observations for any two arbitrary surface combinations.Acknowledgements
Supercomputing facility used for simulations at PG Senapathy Centre for Computing Resource, Indian Institute of Technology, Madras is greatly acknowledged. The authors also wish to acknowledge the support from Department of Science and Technology (DST), India for the financial support through Project File Number SB/S3/CEE/017/2015.References
- M. Kanduč, A. Schlaich, E. Schneck and R. R. Netz, Langmuir, 2016, 32, 8767–8782 CrossRef PubMed.
- W. Chen, A. S. Foster, M. J. Alava and L. Laurson, Phys. Rev. Lett., 2015, 114, 095502 CrossRef PubMed.
- S. N. Jamadagni, R. Godawat and S. Garde, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 147–171 CrossRef CAS PubMed.
- S. R. Accordino, J. M. M. de Oca, J. A. R. Fris and G. A. Appignanesi, J. Chem. Phys., 2015, 143, 154704 CrossRef PubMed.
- N. Giovambattista, P. J. Rossky and P. G. Debenedetti, Annu. Rev. Phys. Chem., 2012, 63, 179 CrossRef CAS PubMed.
- H. Manzano, E. Durgun, I. López-Arbeloa and J. C. Grossman, ACS Appl. Mater. Interfaces, 2015, 7, 14726–14733 CAS.
- E. Durgun, H. Manzano, P. V. Kumar and J. C. Grossman, J. Phys. Chem. C, 2014, 118, 15214–15219 CAS.
- M. Zokaie and M. Foroutan, RSC Adv., 2015, 5, 39330–39341 RSC.
- H. Kumar, C. Dasgupta and P. K. Maiti, RSC Adv., 2015, 5, 1893–1901 RSC.
- Q. Wang, H. Manzano, Y. Guo, I. Lopez-Arbeloa and X. Shen, J. Phys. Chem. C, 2015, 119, 19869–19875 CAS.
- D. Hou, T. Zhao, H. Ma and Z. Li, J. Phys. Chem. C, 2015, 119, 1346–1358 CAS.
- P. A. Bonnaud, Q. Ji, B. Coasne, R. M. Pellenq and K. J. Van Vliet, Langmuir, 2012, 28, 11422–11432 CrossRef CAS PubMed.
- H. Manzano, S. Moeini, F. Marinelli, A. C. Van Duin, F. J. Ulm and R. J. M. Pellenq, J. Am. Chem. Soc., 2012, 134, 2208–2215 CrossRef CAS PubMed.
- J. J. Thomas, H. M. Jennings and J. J. Chen, J. Phys. Chem. C, 2009, 113, 4327–4334 CAS.
- K. L. Scrivener and A. Nonat, Hydration of Cementitious Materials, Present and Future, Cem. Concr. Res., 2011, 41, 651–665 CrossRef CAS.
- N. T. Skipper, G. Sposito and F. R. C. Chang, Clays Clay Miner., 1995, 43, 294–303 CAS.
- J. A. Stammen, S. Williams, D. N. Ku and R. E. Guldberg, Biomaterials, 2001, 22, 799–806 CrossRef CAS PubMed.
- S. R. Schmidt, D. R. Katti, P. Ghosh and K. S. Katti, Langmuir, 2005, 21, 8069–8076 CrossRef CAS PubMed.
- P. Ghosh, D. R. Katti and K. S. Katti, Biomacromolecules, 2007, 8, 851–856 CrossRef CAS PubMed.
- A. C. van Duin and S. R. Larter, Org. Geochem., 2001, 32, 143–150 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- N. I. Golovastikov, Sov. Phys. Crystallogr., 1975, 20, 441–445 Search PubMed.
- A. M. Il'Inets, N. N. Nevskii, V. V. Ilyukhin, M. Y. Bikbau and N. V. Belov, Sov. Phys. Dokl., 1982, 27, 906 Search PubMed.
- S. Grazulis, D. Chateigner, R. T. Downs, A. T. Yokochi, M. Quiros, L. Lutterotti, E. Manakova, J. Butkus, P. Moeck and A. Le Bail, J. Appl. Crystallogr., 2009, 42, 726–729 CrossRef CAS PubMed.
- M. B. Pinson, E. Masoero, P. A. Bonnaud, H. Manzano, Q. Ji, S. Yip, J. J. Thomas, M. Bazant, K. J. VanVliet and H. M. Jennings, Phys. Rev. Appl., 2015, 064009 CrossRef.
- A. G. Kalinichev, J. Wang and R. J. Kirkpatrick, Cem. Concr. Res., 2007, 37, 337–347 CrossRef CAS.
- R. K. Mishra, R. J. Flatt and H. Heinz, J. Phys. Chem. C, 2013, 117, 10417–10432 CAS.
- R. K. Mishra, L. Fernández-Carrasco, R. J. Flatt and H. Heinz, Dalton Trans., 2014, 43, 10602–10616 RSC.
- J. Wang, A. G. Kalinichev and R. J. Kirkpatrick, Geochim. Cosmochim. Acta, 2006, 70, 562–582 CrossRef CAS.
- J. Wang, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2009, 113, 11077–11085 CAS.
- A. G. Kalinichev, P. Padma Kumar and R. James Kirkpatrick, Philos. Mag., 2010, 90, 2475–2488 CrossRef CAS.
- L. Cheng, P. Fenter, K. L. Nagy, M. L. Schlegel and N. C. Sturchio, Phys. Rev. Lett., 2001, 156103 CrossRef CAS PubMed.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- C. L. Perrin and J. B. Nielson, Annu. Rev. Phys. Chem., 1997, 48, 511–544 CrossRef CAS PubMed.
- G. A. Jeffrey and S. Takagi, Acc. Chem. Res., 1978, 11, 264–270 CrossRef CAS.
- G. R. Desiraju, Acc. Chem. Res., 1991, 24, 290–296 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra25758e |
| This journal is © The Royal Society of Chemistry 2017 |