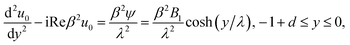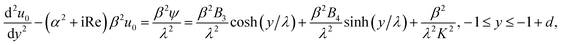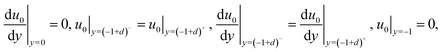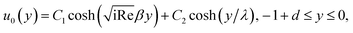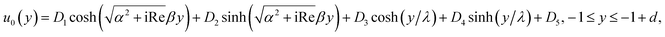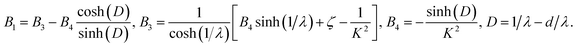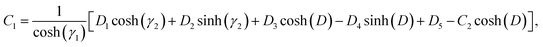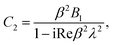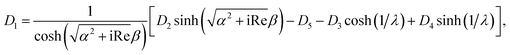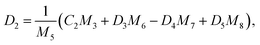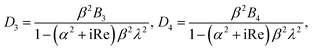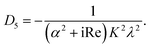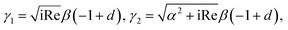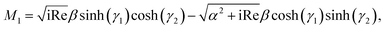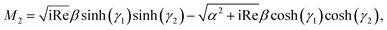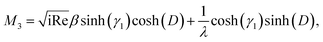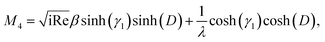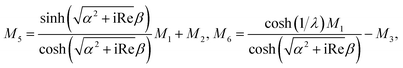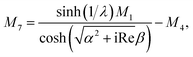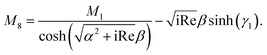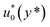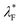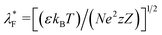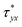DOI:
10.1039/C6RA24930B
(Paper)
RSC Adv., 2017,
7, 782-790
Transient alternating current electroosmotic flow of a Jeffrey fluid through a polyelectrolyte-grafted nanochannel
Received
9th October 2016
, Accepted 15th November 2016
First published on 3rd January 2017
Abstract
The purpose of this study is to investigate the flow of viscoelastic fluid through a slit polyelectrolyte-grafted (PE-grafted) nanochannel under applied alternating current (AC) electric field. The PE-grafted nanochannel (also called a soft nanochannel) is represented by a rigid surface coated by a polyelectrolyte layer (PEL) in a brush-like configuration. By solving linearized Poisson–Boltzmann equations and momentum equations, analytical solutions regarding electrical potentials and transient electroosmotic flow (EOF) velocities are derived under appropriate boundary conditions in the decoupled regime of the PE-grafted nanochannel, where the thickness of the PEL is independent of the electrostatic effects triggered by polyelectrolyte charges. We compare the distributions of EOF velocities between PE-grafted and rigid nanochannels. A good agreement with each other is found when the thickness of the PEL is very small. However, the velocity for PE-grafted nanochannels is larger than that for rigid ones. The influences of pertinent dimensionless parameters on the EOF velocities in PE-grafted nanochannels are discussed in detail. The results indicate that the EOF velocity amplitude for PE-grafted nanochannels increases with the thickness of the PEL. Increasing the relaxation time enhances the oscillation of the EOF velocity profiles, yet increasing the retardation time dampens the oscillation. Furthermore, increasing the oscillating Reynolds number Re results in a more obvious oscillating phenomenon of the EOF velocity, together with a weakening amplitude of oscillation. The conclusions have theoretical significance for biofluid-based microfluidic transport systems.
1. Introduction
The theory of electrokinetics in microelectromechanical systems (MEMS) is of utmost importance in analyzing many chemical, biological and medical devices.1,2 Lately, the electrokinetic transport in micro-nano channels has received remarkable attention due to its variety of practical applications. Electroosmotic flow (EOF) is an important electrokinetic phenomenon and has become very attractive in the industrial and biomedical areas. When solid surfaces contact with electrolyte solution, it will cause charge exchange at the solid–liquid interface so as to form the electrical double layer (EDL). When an electric field is applied tangentially to the electrolyte solution, an electric field force acts on the excess counter-ions in the diffuse layer of the EDL. Then the excess counter-ions will migrate under the electric field force, carrying the liquid with them by viscosity, resulting in the electroosmotic flow.3
A rigid nanochannel, in which the inner walls are covered by a layer of polyelectrolyte materials in the form of polyelectrolyte brushes (PE-brushes),4–6 is denoted as polyelectrolyte-grafted (PE-grafted) nanochannel (or soft nanochannel). Polyelectrolyte layer (PEL), containing both electrolyte ions and fixed charge density of ions, is also called fixed charge layer (FCL). It is assumed that electrolyte ions can penetrate into the PEL. Meanwhile, the existing of fixed charge density of ions will result in a drag force on the fluid flow within PEL. Some studies on the electrokinetic theory in soft nanochannel have been reported.7–13 Keh and Ding14 presented an analytical solution about the steady electrokinetic flow in a long uniform soft capillary tube or slit. The results show that the direction and the magnitudes of EOF velocity are governed by the fixed charge density inside the surface polymer layer. Chanda et al.15 investigated the streaming potential and electrochemomechanical energy conversion efficient in soft nanochannel and compared them with those in the rigid nanochannel under the linearization of the Poisson–Boltzmann equation. They found that energy conversion efficient and streaming potential of soft nanochannel are always upper than those of rigid nanochannel except for the particular case of large drag parameter. Chen and Das16 obtained the streaming potential and electroviscous effects in the soft nanochannel without considering Debye–Hückel approximation. Therefore, they provided a deeper and wider theory for electrokinetic phenomenon in soft nanochannel.
In the previous literatures, many investigations on EOF in microchannels have been reported.17–43 Oliveira and Pinho44 presented analytical solutions of Phan-Thien–Tanner (PTT) fluid in fully developed channel and pipe. The results indicated that the wall shear stress of PTT fluid is substantially smaller than the corresponding value of Newtonian or upper-convected Maxwell fluid. The transient behavior of electroosmotic flow under direct current (DC) or alternating current (AC) electric field in a rectangular curved microtube was discussed by Luo.45 Chakraborty and Ray46 obtained the analytical expression of mass flow rate in circular microchannel under the pulsating electric fields. Wang47 presented an analytical solution for the electroosmotic flow in a semicircular microchannel under the Debye–Hückel approximation. The analytical solution of the time periodic electroosmotic flow of Maxwell fluid through a rectangular microchannel was derived by Jian et al.48 under the Debye–Hückel approximation. Beyond the assumption of linearization approximation, Yang et al.49 studied the time and space development of EOF in a slit channel. Time periodic electroosmotic flow of Jeffrey fluids between two micro-parallel plates was examined by Liu et al.,50 semi-analytical solutions are obtained by using the method of separation of variables. Transient electroosmotic flow of Oldroyd-B fluids in a narrow capillary tube was studied by Zhao et al.,51 analytical solutions for electric potential and transient velocity are derived. And the effects of relaxation time and retardation time on the oscillation of the velocity are pointed out.
Recently, Matin and Ohshima52 presented the analysis of the flow about Newtonian fluid driven by combined electroosmotic and pressure through a soft nanochannel. Li et al.53 investigated the time periodic electroosmotic flow (EOF) of an electrolyte solution through a slit soft nanochannel under applied AC electric field. The results indicated that oscillation of velocity is restricted within the region near the PEL–electrolyte interface for higher oscillating Reynolds number Re. The study of non-Newtonian fluids has gained great interest due to their extensive applications in industry. Materials that do not obey the Newtonian law of viscosity are non-Newtonian fluids. Complex fluids like polymer solutions, colloids, and cell suspensions, which are made of long chain molecules and behave obvious non-Newtonian characteristics, are non-Newtonian fluids. The most common and simplest model of non-Newtonian fluids is Jeffrey fluid which has time derivative instead of convected derivative in the constitutive equation. It should be noted that Jeffrey fluid model is a general viscoelastic model including relaxation time λ1 and retardation time λ2. It includes the classical viscous Newtonian fluid as a special case for λ1 = 0, λ2 = 0, and the Maxwell fluid for λ1 ≠ 0, λ2 = 0. In addition, Jeffrey fluid model was used to describe the blood flow through a tapered artery.54,55 However, there seems almost no report about the transient EOF of viscoelastic fluid through a PE-grafted nanochannel. The present paper is to investigate the transient EOF of Jeffrey fluid through a PE-grafted nanochannel under an external imposed AC electric field. We obtain the analytical solutions of EOF velocity in the PE-grafted nanochannel under Debye–Hückel approximation, and discuss the influences of pertinent dimensionless parameters on the EOF velocity.
2. Mathematical formulation
The unsteady EOF of the incompressible Jeffrey fluid driven by external imposed AC electric field through a PE-grafted nanochannel of height 2h, as illustrated in Fig. 1, is investigated. We assume that the channel height 2h is much smaller than the channel length L and width W, i.e., 2h ≪ L, W. We take a two-dimensional coordinate system where x*-axis is placed at the middle of two plates. The bottom plate is located at y* = −h, and the top plate is located at y* = h. Therefore, the system only depends on y*. It is assumed that the PE-grafted nanochannel is represented as a rigid one covered by PEL of thickness d*, containing positively charged FCL ions, and we suppose that the thickness of PE-brushes is smaller than the half height of nanochannel. Due to the symmetry of channel and electrolyte solution, we only consider the half of the channel (−h ≤ y* ≤ 0).
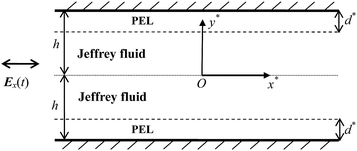 |
| | Fig. 1 Schematic of Jeffrey fluid driven by AC electric field in PE-grafted nanochannel. | |
2.1 Distribution of the electrostatic potential
According to the electrostatic theory, the distribution of electrical potential ψ* in the EDL can be described by the following Poisson–Boltzmann equations in decoupled regime6,56 of PE-grafted nanochannel, where the thickness of PEL is independent of the electrostatic effects triggered by polyelectrolyte charges.| |
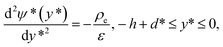 | (1a) |
| |
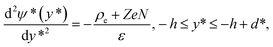 | (1b) |
where −h ≤ y* ≤ −h + d* denotes the PEL region, ε is the dielectric constant of the electrolyte liquid which is assumed to be identical both inside and outside PEL,16 ρe = −2ezn0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(ezψ*/(kBT)) is the free charge density in the electrolyte, e is the elementary electronic charge, z is the absolute value of the ionic valence, n0 is the number concentration of electrolyte solution, kB and T are the Boltzmann constant and temperature. Z and N are the valence and the ionic number concentration of the FCL ions. It is assumed that the electrical potential is small compared with the thermal energy of the ions, that is, exp[±(ezψ*)/(kBT)] can be replaced by 1 ± (ezψ*)/(kBT), then eqn (1a) and (1b) become
sinh(ezψ*/(kBT)) is the free charge density in the electrolyte, e is the elementary electronic charge, z is the absolute value of the ionic valence, n0 is the number concentration of electrolyte solution, kB and T are the Boltzmann constant and temperature. Z and N are the valence and the ionic number concentration of the FCL ions. It is assumed that the electrical potential is small compared with the thermal energy of the ions, that is, exp[±(ezψ*)/(kBT)] can be replaced by 1 ± (ezψ*)/(kBT), then eqn (1a) and (1b) become| |
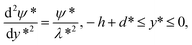 | (2a) |
| |
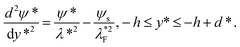 | (2b) |
In eqn (2a) and (2b), λ* = [(εkBT)/(2n∞e2z2)]1/2 is the EDL thickness, 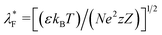 is the equivalent EDL thickness inside PEL and ψs = kBT/ez. The corresponding boundary conditions are
is the equivalent EDL thickness inside PEL and ψs = kBT/ez. The corresponding boundary conditions are
| |
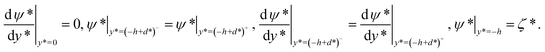 | (3) |
To make a direct comparison between the PE-grafted and rigid nanochannels, the last boundary condition in eqn (3) gives the wall electrical potential ζ* at the interface of PEL and wall, which is different from previous boundary condition.15,16,52 Introducing the following dimensionless variations ψ = ψ*/ψs, y = y*/h, d = d*/h, λ = λ*/h and 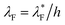 , we obtain the following equations and boundary conditions about the dimensionless electrical potential ψ
, we obtain the following equations and boundary conditions about the dimensionless electrical potential ψ
| |
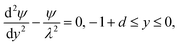 | (4a) |
| |
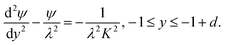 | (4b) |
| |
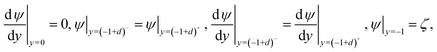 | (5) |
here
K =
λF/
λ represents the ratio of the characteristic thickness of the mobile charges in the bulk electrolyte to that in the FCL.
ζ =
ζ*/
ψs is the dimensionless wall electrical potential at the PEL-wall interface. The solutions of
eqn (4a) and
(4b) under the boundary conditions
(5) are
| |
ψ(y) = B1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh(y/λ), −1 + d ≤ y ≤ 0, cosh(y/λ), −1 + d ≤ y ≤ 0,
| (6a) |
| |
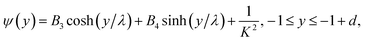 | (6b) |
2.2 Distribution of the velocity field
We assume that the pressure gradient along the axial direction is ignored. When an external electric field Ex(t) is applied, a pure EOF of Jeffrey fluid through a PE-grafted nanochannel is governed by the modified momentum equations, i.e.,| |
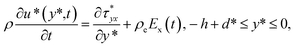 | (7a) |
| |
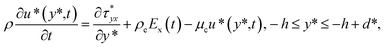 | (7b) |
where u*(y*,t) is the axial velocity, t is time, Ex(t) is the applied AC electric field, ρeEx(t) is the electric field force, ρ is the fluid density, μc is the drag coefficient within PEL, 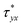 is the stress tensor which satisfies the constitutive equation of the Jeffrey fluid.
is the stress tensor which satisfies the constitutive equation of the Jeffrey fluid.| |
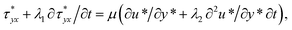 | (8) |
where λ1 is the relaxation time, λ2 is the retardation time, μ is the zero shear rate viscosity. Generally, the retardation time is smaller than the relaxation time.57 When the relaxation time λ1 and the retardation time λ2 tend to zero, eqn (8) reduces to the constitutive equation of the Newtonian fluid. We assume that AC electric field and the EOF velocity of Jeffrey fluid can be written in the following complex forms:| |
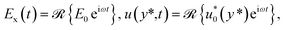 | (9) |
where ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) {} denotes the real part of a complex number, E0 is the amplitude of the applied AC electric field and
{} denotes the real part of a complex number, E0 is the amplitude of the applied AC electric field and 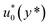 is the complex amplitude of EOF velocity, i is the imaginary number unit and ω is the oscillating angular frequency of the applied AC electric field. Combining eqn (7a), (7b) and (8), eliminating stress tensor
is the complex amplitude of EOF velocity, i is the imaginary number unit and ω is the oscillating angular frequency of the applied AC electric field. Combining eqn (7a), (7b) and (8), eliminating stress tensor 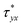 , it yields:
, it yields:| |
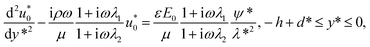 | (10a) |
| |
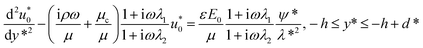 | (10b) |
Boundary conditions are given by
| |
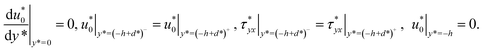 | (11) |
In above boundary conditions, the first condition represents the symmetric velocity about x* axis. The second and third conditions imply the continuity for the velocity and shear stress at the interface of the FCL–electrolyte. No-slip condition of the velocity is satisfied in the last condition. Notice that the continuous condition for the shear stress reduces to the condition 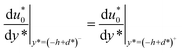 . In fact, substituting eqn (9) into (8), dividing by λ1, we obtain
. In fact, substituting eqn (9) into (8), dividing by λ1, we obtain
| |
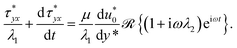 | (12) |
Then, by integrating eqn (12) and assuming that the fluid is in unstressed state at t = −∞, we get the expression of shear stress
| |
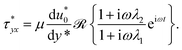 | (13) |
Dimensionless velocity is introduced by 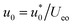 , where Ueo = εE0ψs/μ denotes steady Helmholtz–Smoluchowski EOF velocity of Newtonian fluid. eqn (10a) and (10b) and corresponding boundary conditions (11) in the dimensionless form are
, where Ueo = εE0ψs/μ denotes steady Helmholtz–Smoluchowski EOF velocity of Newtonian fluid. eqn (10a) and (10b) and corresponding boundary conditions (11) in the dimensionless form are
| |
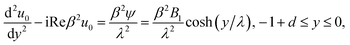 | (14a) |
| |
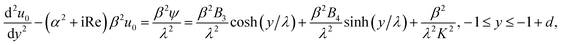 | (14b) |
| |
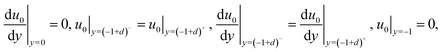 | (15) |
where Re =
ρωh2/
μ is oscillating Reynolds number,
α2 =
μch2/
μ is dimensionless drag parameter, and
β2 = (1 + i
ωλ1)/(1 + i
ωλ2). The solutions of
eqn (14a) and
(14b) are
| |
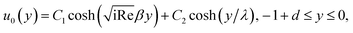 | (16a) |
| |
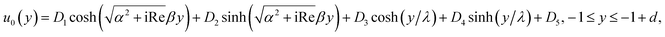 | (16b) |
where
We use the following notations in the above coefficients:
3. Results and discussions
Analytical solutions are derived for the transient EOF of Jeffrey fluid through a PE-grafted nanochannel. Next, we will discuss the influences of pertinent parameters (d, K, λ, Re, λ1ω, λ2ω, ωt) on the EOF velocity. In practical engineering problems, typical parameters are taken as follows: the half height of the channel is h ∼ 100 nm, ρ ∼ 1.06 × 103 kg m−3, μ ∼ 10−3 kg (m−1 s−1), the AC electric field frequency changes from 0 to 400 MHz, then the angle frequency ω is from 0 to 2.5 × 109 s−1. The oscillating Reynolds number Re varies from 0 to 25 due to Re = ρωh2/μ. In addition, according to the previous studies,15,16,52 we let α = 1, d/λ ≤ 1. Generally speaking, the retardation time λ2 is smaller than the relaxation time λ1, and λ1 should be smaller than the oscillating period of the electric field,50 that is, λ2ω < λ1ω ≤ 2π. In the following figures, letters S and R represent the PE-grafted and rigid nanochannels, respectively. The meanings of all symbols in the present paper are listed in Table 1.
Fig. 2 provides the variation of the dimensionless electrical potential ψ with dimensionless distance y for different values of the K, d and ζ when λ = 0.1. In Fig. 2a, K = 0.1, 1 and 10, d = 0.1 and 0.05, ζ = 1. It is shown that the parameter K = λF/λ should be taken larger than 1 to ensure the validity of Debye–Hückel linearization. In the following discussion, we always let K ≥ 1. If the thickness of PEL in the PE-grafted nanochannel is very small (d = 0.01), Fig. 2b compares the electrical potential in PE-grafted and rigid nanochannels when K = 1, 10 and ζ = 1, 0.8. It is observed that coincident profiles of electrical potential for PE-grafted and rigid nanochannels are plotted under the same wall electrical potential.
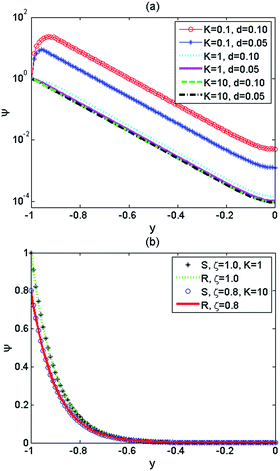 |
| | Fig. 2 Variation of the dimensionless electrical potential ψ with dimensionless distance y for different values of the d and K when λ = 0.1 (a) in the PE-grafted nanochannel (d = 0.10, 0.05, ζ = 1), (b) the comparison between PE-grafted and rigid nanochannel (d = 0.01, ζ = 1.0, 0.8, K = 1, 10). | |
Fig. 3 compares the velocity amplitude u0(y) for Newtonian, Jeffrey and Maxwell fluids in PE-grafted and rigid nanochannels at different values of PEL thickness d when λ = 0.1, K = 1, ζ = 1, Re = 8 (d = 0.01 in Fig. 3a and d = 0.1 in Fig. 3b). Noted that λ1ω = 0, λ2ω = 0; λ1ω = 2π, λ2ω = 0.5π and λ1ω = 2π, λ2ω = 0 correspond to Newtonian fluid; Jeffrey fluid and Maxwell fluid, respectively. When the thickness of PEL in the PE-grafted nanochannel is very thin (d = 0.01), the profiles of velocity amplitude for the PE-grafted nanochannel agree very well with those for the rigid nanochannel (see Fig. 3a). However, for thick PEL thickness (d = 0.1), the velocity in the PE-grafted nanochannel is substantially larger than that in the rigid nanochannel whenever the values of λ1ω and λ2ω (see Fig. 3b). Among them, the increment of velocity for Maxwell fluid (λ1ω = 2π, λ2ω = 0) is more obvious than Newtonian and Jeffrey fluids. Under the influence of AC electric field, negative values maybe emerge in the EOF velocity profile, which mean the backflow of the fluid.
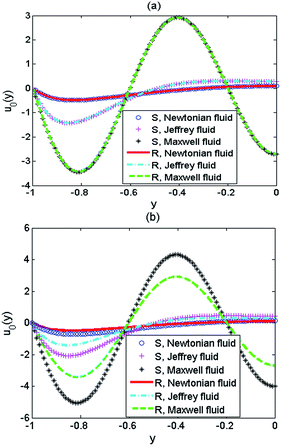 |
| | Fig. 3 Comparison of the velocity amplitude for Newtonian, Maxwell and Jeffrey fluids in PE-grafted and rigid nanochannels (λ = 0.1, K = 1, ζ = 1, Re = 8) at different values of d: (a) d = 0.01, (b) d = 0.1. For Newtonian fluid λ1ω = 0, λ2ω = 0; for Jeffrey fluid λ1ω = 2π, λ2ω = 0.5π; for Maxwell fluid λ1ω = 2π, λ2ω = 0. | |
Fig. 4 illustrates the velocity amplitude u0(y) at different values of d, λ and K when Re = 1, ζ = 1, λ1ω = 2π, λ2ω = 0.5π. In Fig. 4a, d = 0.01, 0.05 and 0.10, λ = 0.10, K = 1; in Fig. 4b, d = 0.10, λ = 0.10, 0.15, 0.20, K = 1, 10. As shown in the figure, the velocity amplitude increases with d, but decreases with λ and K. Physically, in the PE-grafted nanochannel, PEL is a layer comprising polyelectrolyte materials, which contains both electrolyte ions and fixed charge density of positive ions. Under the action of an applied electric field, an increase in the thickness of the PEL (d) accompanies the increment of the cations, and therefore promotes the fluid flow. The increase of the EDL thickness (λ) means the augmentation of ionic density inside the EDL, which indicates the accumulation of the ions and leads to a high resistance in the fluid flow, together with the decline of the velocity. The increase of parameter K (K = λF/λ) corresponds to the decrease of electrical potential ψ due to low ionic concentration inside the PEL, therefore, the velocity would decrease with K according to the dimensionless momentum eqn (14a) and (14b).
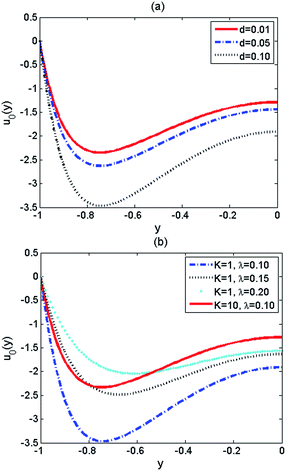 |
| | Fig. 4 Dimensionless velocity amplitude u0(y) at different values of d, λ and K when Re = 1, ζ = 1, λ1ω = 2π, λ2ω = 0.5π (a) d = 0.01, 0.05, 0.10, λ = 0.10, K = 1, (b) d = 0.10, λ = 0.10, 0.15, 0.20, K = 1, 10. | |
Fig. 5 and 6 describe the effects of the relaxation time and retardation time on the velocity amplitude u0(y) of the Jeffrey fluid for different oscillating Reynolds number Re (0.5, 3, 10, and 25) in the PE-grafted nanochannel. In Fig. 5, different values of relaxation time λ1ω (0.1π, 0.5π, π, 2π) are discussed, and Fig. 6 considers different retardation time λ2ω (0.1π, 0.3π, 0.5π). It can be observed from Fig. 5 and 6, with the increase of the oscillating Reynolds number Re, the velocity profiles gradually present oscillating characteristic, and the oscillating amplitude of velocity tends to be lessening whether at high or low values of relaxation time and retardation time. It is pointed out that near the region of EDL and the interface of liquid–PEL, the oscillation phenomenon of the velocity becomes particularly obvious for large oscillating Reynolds number Re. And yet, the EOF velocities are almost zero at the region far away from the EDL (see Fig. 5c and d and 6c and d). Physically, it is because that the diffusion time is much longer than the oscillating period in the case of high oscillating frequency. Therefore, the velocities near the centre of the channel are almost zero. Furthermore, according to profiles of velocity amplitude in Fig. 5 and 6, the velocity increases with λ1ω due to large elastic effect. However, the profile of velocity decreases with λ2ω due to large retard effect of Jeffrey fluid. Therefore, the increase of relaxation time enhances the oscillation of EOF velocity. On the contrary, the increase of retardation time dampens the oscillation.
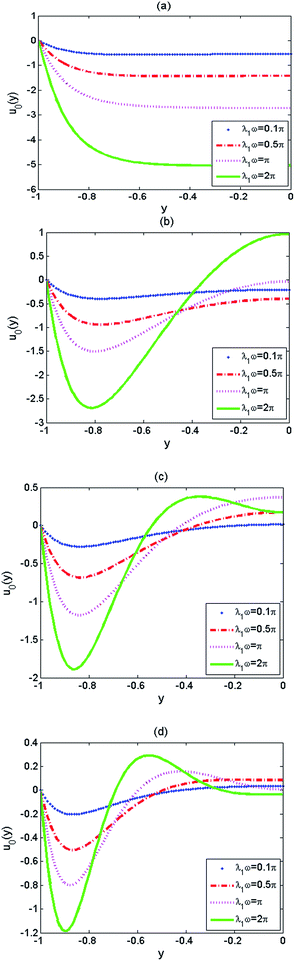 |
| | Fig. 5 Dimensionless velocity amplitude u0(y) at different values of λ1ω (λ1ω = 0.1π, 0.5π, π, 2π) when d = 0.1, λ = 0.1, K = 1, ζ = 1 and λ2ω = 0.5π corresponding to (a) Re = 0.5, (b) Re = 3, (c) Re = 10, (d) Re = 25. | |
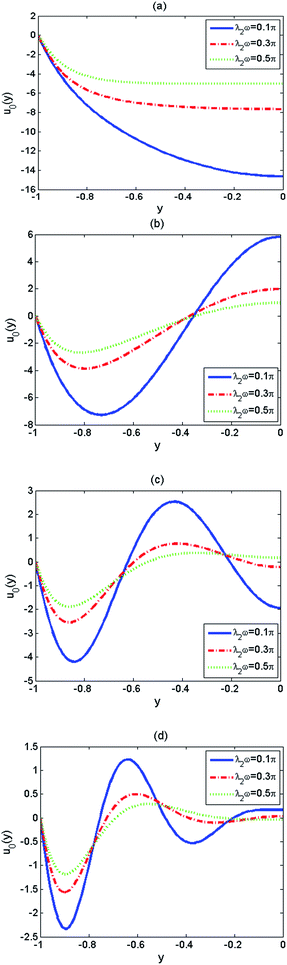 |
| | Fig. 6 Dimensionless velocity amplitude u0(y) at different values of λ2ω (λ2ω = 0.1π, 0.3π, 0.5π) when d = 0.1, λ = 0.1, K = 1, ζ = 1 and λ1ω = 2π corresponding to (a) Re = 0.5, (b) Re = 3, (c) Re = 10, (d) Re = 25. | |
Table 1 List of symbols
| Symbol |
Meaning |
| d* |
Thickness of PEL (m) |
| d |
Dimensionless thickness of PEL |
| Ex(t) |
AC electric field (V m−1) |
| E0 |
Amplitude of AC electric field (V m−1) |
| e |
Elementary electronic charge (C) |
| h |
Half height of soft nanochannel (m) |
| i |
Imaginary number unit |
| K |
Ratio of characteristic thickness, K = λF/λ |
| kB |
Boltzmann constant (J K−1) |
| L |
Length of the soft nanochannel (m) |
| N |
Ionic number concentration of the FCL ions (m−3) |
| n0 |
Number concentration of electrolyte solution (m−3) |
| Re |
Oscillating Reynolds number, Re = ρωh2/μ |
| R |
Rigid nanochannel |
| S |
Soft nanochannel (PE-grafted nanochannel) |
| T |
Temperature (K) |
| t |
Time (s) |
| u*(y*,t) |
Axial velocity for soft nanochannel (m s−1) |
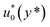 |
Amplitude of velocity for soft nanochannel (m s−1) |
| u0(y) |
Dimensionless amplitude of velocity for soft nanochannel |
| ur(y,t) |
Dimensionless axial velocity for rigid nanochannel |
| ur0(y) |
Dimensionless amplitude of velocity for rigid nanochannel |
| Ueo |
Helmholtz–Smoluchowski velocity of Newtonian fluids (m s−1) |
| W |
Width of the soft nanochannel (m) |
| x*, y* |
Coordinates |
| x, y |
Dimensionless coordinates |
| Z |
Valence of the FCL ions |
| z |
The absolute value of the ionic valence |
| α |
Dimensionless drag parameter, α2 = μch2/μ |
| β |
Dimensionless parameter, β2 = (1 + iωλ1)/(1 + iωλ2) |
| ψ* |
Electrical potential (V) |
| ψ |
Dimensionless electrical potential |
| ψr(y) |
Electrical potential for rigid nanochannel (V) |
| ψs |
Characteristics of electrical potential (V), ψs = kBT/ez |
| ε |
Dielectric constant (N m−1) |
| ρe |
Free charge density (C m−3), ρe = −2ezn0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(ezψ*/kBT) sinh(ezψ*/kBT) |
| λ* |
Thickness of EDL (m), λ* = [(εkBT)/(2n∞e2z2)]1/2 |
| λ |
Dimensionless thickness of EDL |
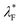 |
Equivalent EDL thickness inside PEL (m), 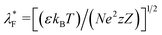 |
| λF |
Dimensionless equivalent EDL thickness inside PEL |
| ζ* |
Wall electrical potential at the interface of PEL and wall (V) |
| ζ |
Dimensionless wall electrical potential |
| ρ |
Fluid density (kg m−3) |
| μc |
Drag coefficient within PEL |
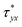 |
Stress tensor of Jeffrey fluid (N m−2) |
| λ1 |
Relaxation time (s) |
| λ2 |
Retardation time (s) |
| μ |
Zero shear rate viscosity (kg (m−1 s−1)) |
| ω |
Oscillating angular frequency of the applied AC electric field (s−1) |
The variation of transient velocity with time is an important characteristic of unsteady electroosmotic flow. Fig. 7 depicts the EOF velocity profiles u(y,t) of the Jeffrey fluid as a function of time (t) for different oscillating Reynolds number Re (0.5, 3, 10, and 25) in the PE-grafted nanochannel. From Fig. 7, it is evident that for lower oscillating Reynolds number, the flow can extend to the whole PE-grafted nanochannel. However, with the increasing of oscillating Reynolds number, near the interface of liquid–PEL, the oscillating characteristic of velocity become obvious gradually. In the case of large oscillating Reynolds number, EOF velocity far away from the interface of liquid–PEL almost maintains zero at any time. These phenomena for Jeffrey fluid are similar to those for Newtonian fluid in the PE-grafted.53
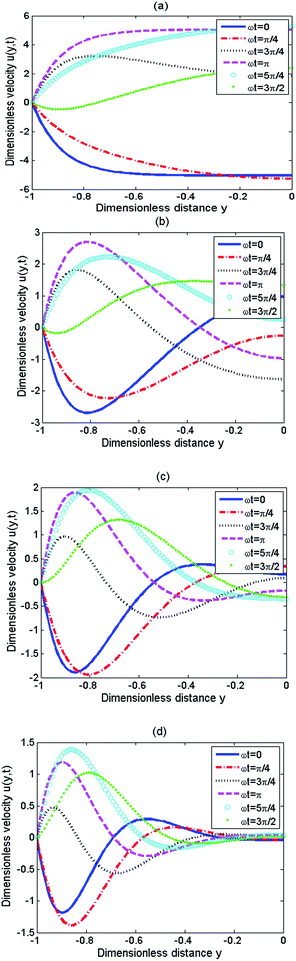 |
| | Fig. 7 Dimensionless velocity u(y,t) at different values of ωt (ωt = 0, π/4, 3π/4, π, 5π/4, 3π/2) when d = 0.1, λ = 0.1, K = 1, ζ = 1 and λ1ω = 2π, λ2ω = 0.5π corresponding to (a) Re = 0.5, (b) Re = 3, (c) Re = 10, (d) Re = 25. | |
4. Conclusions
An analytical transient EOF of Jeffrey fluid under external applied AC electric field in a PE-grafted nanochannel is presented in this work. Based on the Debye–Hückel approximation, we arrive at the analytical solutions involving the momentum equations and the constitutive equation of the Jeffrey fluid. By comparing the electrical potentials and EOF velocities between PE-grafted and rigid nanochannels, it can be found that electrical potentials and EOF velocities in PE-grafted nanochannel with thin PEL are in excellent agreement with those in rigid nanochannel. In PE-grafted nanochannel, the PEL has the positive role of increasing the velocity amplitude. However, the amplitude of EOF velocity decreases with EDL thickness λ and parameter K. Moreover, with the increase of oscillating Reynolds number Re, the oscillating phenomenon of EOF velocity becomes obvious, and the weakening amplitude of oscillation is observed. In the case of high oscillating frequency, the EOF velocities are almost zero at the region far away from the interface of liquid–PEL. It is observed that relaxation time of Jeffrey fluid enhances the oscillation of velocity. However, the retardation time dampens the oscillation of velocity. The results have theoretical significance for biofluids-based microfluidic transport system.
Acknowledgements
The work was supported by the National Natural Science Foundation of China (Grant No. 11472140, 11362012), the Natural Science Foundation of Inner Mongolia Autonomous Region of China (Grant No. 2016MS0106), the Inner Mongolia Grassland Talent (Grant No. 12000-12102013).
References
- H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381 CrossRef.
- T. Bayraktar and S. B. Pidugu, Int. J. Heat Mass Transfer, 2006, 49, 815 CrossRef CAS.
- R. J. Hunter, Zeta potential in colloid science, Academic Press, New York, 1981 Search PubMed.
- Y. B. Zhulina, V. A. Pryamitsyn and O. V. Borisov, Polym. Sci. U.S.S.R., 1989, 31, 205 CrossRef.
- S. T. Milner, Science, 1991, 251, 905 CrossRef CAS PubMed.
- S. Das, M. Banik, G. Chen, S. Sinha and R. Mukherjee, Soft Matter, 2015, 11, 8550 RSC.
- E. Donath and E. Voigt, J. Colloid Interface Sci., 1986, 109, 122 CrossRef CAS.
- H. Ohshima and T. Kondo, J. Colloid Interface Sci., 1990, 135, 443 CrossRef CAS.
- E. Donath, P. Kuzmin, A. Krabi and A. Voigt, Colloid Polym. Sci., 1993, 271, 930 CAS.
- H. J. Keh and Y. C. Liu, J. Colloid Interface Sci., 1995, 172, 222 CrossRef CAS.
- J. H. Wu and H. J. Keh, Colloids Surf., A, 2003, 212, 27 CrossRef CAS.
- J. F. L. Duval and H. P. van Leeuwen, Langmuir, 2004, 20, 10324 CrossRef CAS PubMed.
- H. C. Ma and H. J. Keh, J. Colloid Interface Sci., 2007, 313, 686 CrossRef CAS PubMed.
- H. J. Keh and J. M. Ding, J. Colloid Interface Sci., 2003, 263, 645 CrossRef CAS PubMed.
- S. Chanda, S. Sinhab and S. Das, Soft Matter, 2014, 10, 7558 RSC.
- G. Chen and S. Das, J. Colloid Interface Sci., 2015, 445, 357 CrossRef CAS PubMed.
- D. Burgreen and F. R. Nakache, J. Phys. Chem., 1964, 68, 1084 CrossRef.
- S. Levine, J. R. Marriott, G. Neale and N. Epstein, J. Colloid Interface Sci., 1975, 52, 136 CrossRef.
- C. Yang, D. Li and J. H. Masliyah, Int. J. Heat Mass Transfer, 1998, 41, 4229 CrossRef CAS.
- S. Arulanandam and D. Li, Colloids Surf., A, 2000, 161, 89 CrossRef CAS.
- S. Chakraborty, Int. J. Heat Mass Transfer, 2006, 49, 810 CrossRef.
- Y. J. Kang, C. Yang and X. Y. Huang, J. Colloid Interface Sci., 2002, 253, 285 CrossRef CAS PubMed.
- H. K. Tsao, J. Colloid Interface Sci., 2000, 225, 247 CrossRef CAS PubMed.
- A. Sharma and S. Chakraborty, Int. J. Heat Mass Transfer, 2008, 51, 4875 CrossRef CAS.
- A. M. Afonso, M. A. Alves and F. T. Pinho, J. Non-Newtonian Fluid Mech., 2009, 159, 50 CrossRef CAS.
- S. Dhinakaran, A. M. Afonso, M. A. Alves and F. T. Pinho, J. Colloid Interface Sci., 2010, 344, 513 CrossRef CAS PubMed.
- S. Chakraborty and A. K. Srivastava, Langmuir, 2007, 23, 12421 CrossRef CAS PubMed.
- Y. Jian, L. Yang and Q. Liu, Phys. Fluids, 2010, 22, 042001 CrossRef.
- S. Das and S. Chakraborty, AIChE J., 2007, 53, 1086 CrossRef CAS.
- S. Das, K. Subramanian and S. Chakraborty, Colloids Surf., B, 2007, 58, 203 CrossRef CAS PubMed.
- C. C. Chang and C. Y. Wang, Electrophoresis, 2008, 29, 2970 CrossRef CAS PubMed.
- N. Scales and R. N. Tait, J. Chem. Phys., 2006, 125, 094714 CrossRef PubMed.
- D. Erickson and D. Li, Langmuir, 2003, 19, 5421 CrossRef CAS.
- Q. Liu, Y. Jian and L. Yang, J. Non-Newtonian Fluid Mech., 2011, 166, 478 CrossRef CAS.
- X. X. Li, Z. Yin, Y. J. Jian, L. Chang, J. Su and Q. S. Liu, J. Non-Newtonian Fluid Mech., 2012, 187–188, 43 CrossRef CAS.
- P. Dutta and A. Beskok, Anal. Chem., 2001, 73, 5097 CrossRef CAS.
- H. J. Keh and H. C. Tseng, J. Colloid Interface Sci., 2001, 242, 450 CrossRef CAS.
- Y. J. Kang, C. Yang and X. Y. Huang, Int. J. Eng. Sci., 2002, 40, 2203 CrossRef.
- W.-J. Luo, J. Colloid Interface Sci., 2006, 295, 551 CrossRef CAS PubMed.
- B. Gheshlaghi, H. Nazaripoor, A. Kumar and M. Sadrzadeh, RSC Adv., 2016, 6, 17632 RSC.
- G. C. Shit, A. Mondal, A. Sinha and P. K. Kundu, Colloids Surf., A, 2016, 489, 249 CrossRef CAS.
- L. Martínez, O. Bautista, J. Escandón and F. Méndez, Colloids Surf., A, 2016, 498, 7 CrossRef.
- J. Marroquin-Desentis, F. Méndez and O. Bautista, Fluid Dynam. Res., 2016, 48, 035503 CrossRef.
- P. J. Oliveira and F. T. Pinho, J. Fluid Mech., 1999, 387, 271 CrossRef.
- W.-J. Luo, J. Colloid Interface Sci., 2004, 278, 497 CrossRef CAS PubMed.
- S. Chakraborty and S. Ray, Phys. Fluids, 2008, 20, 083602 CrossRef.
- C. Y. Wang, Y. H. Liu and C. C. Chang, Phys. Fluids, 2008, 20, 3105 Search PubMed.
- Y. Jian, Q. Liu and L. Yang, J. Non-Newtonian Fluid Mech., 2011, 166, 1304 CrossRef CAS.
- C. Yang, K. T. Ooi, T. N. Wong and J. H. Masliyah, J. Colloid Interface Sci., 2004, 275, 679 CrossRef PubMed.
- Q. Liu, Y. Jian and L. Yang, Phys. Fluids, 2011, 23, 102001 CrossRef.
- M. Zhao, S. Wang and S. Wei, J. Non-Newtonian Fluid Mech., 2013, 201, 135 CrossRef CAS.
- M. H. Matin and H. Ohshima, J. Colloid Interface Sci., 2015, 460, 361 CrossRef CAS PubMed.
- F. Li, Y. Jian, L. Chang, G. Zhao and L. Yang, Colloids Surf., B, 2016, 147, 234 CrossRef CAS PubMed.
- N. S. Akbar and S. Nadeem, Commun. Theor. Phys., 2012, 57, 133 CrossRef CAS.
- R. Ellahi, S. U. Rahman and S. Nadeem, Phys. Lett. A, 2014, 378, 2973 CrossRef CAS.
- G. Chen and S. Das, J. Phys. Chem. B, 2015, 119, 12714 CrossRef CAS PubMed.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport phenomena, John Wiley & Sons, Inc., New York, 2nd edn, 2001 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
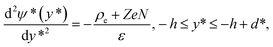
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(ezψ*/(kBT)) is the free charge density in the electrolyte, e is the elementary electronic charge, z is the absolute value of the ionic valence, n0 is the number concentration of electrolyte solution, kB and T are the Boltzmann constant and temperature. Z and N are the valence and the ionic number concentration of the FCL ions. It is assumed that the electrical potential is small compared with the thermal energy of the ions, that is, exp[±(ezψ*)/(kBT)] can be replaced by 1 ± (ezψ*)/(kBT), then eqn (1a) and (1b) become
sinh(ezψ*/(kBT)) is the free charge density in the electrolyte, e is the elementary electronic charge, z is the absolute value of the ionic valence, n0 is the number concentration of electrolyte solution, kB and T are the Boltzmann constant and temperature. Z and N are the valence and the ionic number concentration of the FCL ions. It is assumed that the electrical potential is small compared with the thermal energy of the ions, that is, exp[±(ezψ*)/(kBT)] can be replaced by 1 ± (ezψ*)/(kBT), then eqn (1a) and (1b) become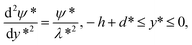
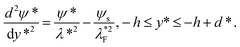
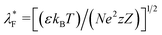 is the equivalent EDL thickness inside PEL and ψs = kBT/ez. The corresponding boundary conditions are
is the equivalent EDL thickness inside PEL and ψs = kBT/ez. The corresponding boundary conditions are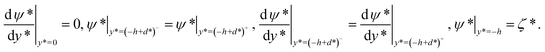
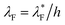 , we obtain the following equations and boundary conditions about the dimensionless electrical potential ψ
, we obtain the following equations and boundary conditions about the dimensionless electrical potential ψ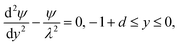
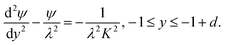
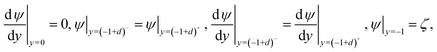
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh(y/λ), −1 + d ≤ y ≤ 0,
cosh(y/λ), −1 + d ≤ y ≤ 0,
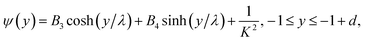
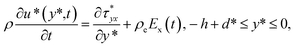
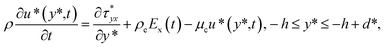
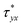 is the stress tensor which satisfies the constitutive equation of the Jeffrey fluid.
is the stress tensor which satisfies the constitutive equation of the Jeffrey fluid.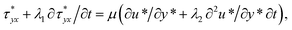
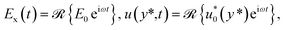
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) {} denotes the real part of a complex number, E0 is the amplitude of the applied AC electric field and
{} denotes the real part of a complex number, E0 is the amplitude of the applied AC electric field and 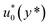 is the complex amplitude of EOF velocity, i is the imaginary number unit and ω is the oscillating angular frequency of the applied AC electric field. Combining eqn (7a), (7b) and (8), eliminating stress tensor
is the complex amplitude of EOF velocity, i is the imaginary number unit and ω is the oscillating angular frequency of the applied AC electric field. Combining eqn (7a), (7b) and (8), eliminating stress tensor 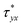 , it yields:
, it yields: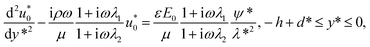
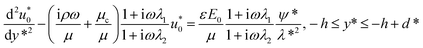
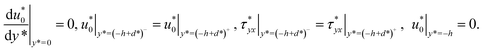
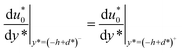 . In fact, substituting eqn (9) into (8), dividing by λ1, we obtain
. In fact, substituting eqn (9) into (8), dividing by λ1, we obtain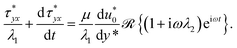
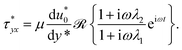
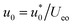 , where Ueo = εE0ψs/μ denotes steady Helmholtz–Smoluchowski EOF velocity of Newtonian fluid. eqn (10a) and (10b) and corresponding boundary conditions (11) in the dimensionless form are
, where Ueo = εE0ψs/μ denotes steady Helmholtz–Smoluchowski EOF velocity of Newtonian fluid. eqn (10a) and (10b) and corresponding boundary conditions (11) in the dimensionless form are