Drop-on-demand microdroplet generation: a very stable platform for single-droplet experimentation

Abstract

This paper reports the performance of drop-on-demand piezo-activated microdroplet generation investigated using microdroplet cavity enhanced fluorescence spectroscopy. Aqueous microdroplets, doped with a fluorescent dye, exhibit fluorescence spectra that are dominated by cavity resonances (termed whispering gallery modes) that, when analysed using Mie theory, allow for the determination of the radius of each microdroplet. The effect of controlled changes in the square-wave droplet generator voltage waveform on droplet size is investigated as well as the size reproducibility of successive microdroplets. Furthermore, using custom square-wave waveforms, microdroplet radii spanning ∼10 to 30 μm are produced from the same droplet dispenser. These non-standard waveforms do not sacrifice the reproducibility of microdroplet generation with <1% size variation. Tuning the single square-wave pulsewidths induces predictable changes in the microdroplet radius and steps on the order of tens of nanometers are detectable. With finer voltage adjustments the microdroplet size is essentially tunable. These results confirm the extremely high stability and reproducibility of on-demand microdroplet generation and that precise size control is possible, rendering them suitable platforms for many applications in fundamental and applied research in areas including mass spectrometry, aerosol investigations and liquid-phase chemistry.

---

Introduction

Free liquid microdroplets are present in many environments including clouds, ocean sprays, fuel sprays and medical nebulizers. As the surface-to-volume ratio of a microdroplet is relatively large and comprises a significant liquid volume, the chemistry and physical properties of microdroplet ensembles are intriguing but challenging to study. In the laboratory, the controlled production of single microdroplets allows for convenient study of liquid-phase processes and provides a useful means of transporting small portions of liquid in a reproducible manner. The focus of this article is drop-on-demand generation (DoD) of free liquid microdroplets. DoD techniques are distinguished here from sprays and vibrating orifice generators that produce higher numbers of droplets per second which, while having their own virtues, are generally not suited for the precise delivery of microdroplets one at a time at low repetition rates. One advantage of precision DoD generation is that every newly arriving microdroplet is a fresh chemical system, allowing chemical and physical changes to be studied with no cross-contamination between microdroplets.¹

The DoD dispensers typically operate when a potential is applied in a short pulse (∼30 μs) to a piezoelectric crystal that surrounds a liquid filled capillary. This pulse briefly compresses the capillary and causes a small portion of liquid to exit the nearby capillary orifice.^2–4 The size of the resulting liquid droplet is generally determined by the capillary inner diameter, the characteristics of the applied potential pulse (including pulsewidth and amplitude), in addition to the physical properties of the liquid (e.g. viscosity and surface tension). Employing more complex voltage-pulse waveforms can markedly change the droplet size.^3–6 Tuning droplet size by controlling the fluid pressure has been demonstrated.⁷

DoD droplet dispensers most are commonly deployed in inkjet printing platforms as they offer great control over droplet delivery timing and liquid volume.^8,9 Inkjet printing exploits the droplet stream generated from the dispenser to deposit a thin layer of liquid onto a substrate and is commonly implemented, for example, in the generation of graphics,¹⁰ deposition of biomaterials^11,12 and fabrication of electronic circuits.¹³ In order to achieve a clean and even thin-layer on the substrate the droplets must be highly reproducible and most commercial inkjet dispensers having droplet size reproducibility of ∼1%.¹⁴ This suggests that DoD dispensers may be well-suited as platforms for fundamental physical and chemical single droplet studies.

A notable application of DoD microdroplet generation is in coupling with mass spectrometry with several groups incorporating different desorption and ionization strategies. A groundbreaking example is the “soft” laser desorption of ions from single microdroplets delivered into vacuum environments.^15–19 In these experiments, single aqueous microdroplets are launched into the low pressure (10⁻⁴ to 10⁻⁵ Torr) source region of a mass spectrometer and ions are desorbed when a pulsed IR laser, tuned to a vibrational absorption band of water (∼2.9 μm), irradiates the droplet. Using microdroplets in this case ensures that the vacuum chamber is not overloaded with unnecessary solvent so that the source region pressure is minimized, and, furthermore, the laser pulse overlaps entirely with the liquid sample. These gentler laser desorption conditions enabled the detection of intact biological-relevant non-covalent complexes.¹⁶ Importantly, as the volume of each microdroplet is on the order of 50 pL, extremely small amounts of chemical sample are consumed. In other experiments, microdroplets have been used to introduce samples to mass spectrometers at atmospheric pressure using a needle-probe electrospray configuration¹ to investigate laser photochemistry in single microdroplets, one droplet at a time. Another example strategy injects single microdroplets into an inductively coupled plasma source for elemental analysis.^18,20 High-precision generation of microdroplets has also been exploited for calibration of water-vapor isotope spectrometry,²¹ ionic liquid deposition,²² the study of coalescence dynamics and mixing²³ and the isolation of single biological cells.²⁴ The production of metal droplet in an on-demand fashion is also well studied.^25–27

This paper reports the performance of commercially available microdroplet generators using single-droplet cavity-enhanced fluorescence spectroscopy. This cavity-enhanced emission, collected from single droplets one at a time, provides highly-precise details of droplet radius. First, it is demonstrated that generation of droplets is highly reproducible, affording a very stable and predictable platform for experiments of microdroplet systems. Secondly, the size of droplets can be altered from a single droplet dispenser, without sacrificing the stability and performance of the droplet generation. And thirdly, that the droplet size is smoothly “tunable” over a narrow size-distribution.

Experimental

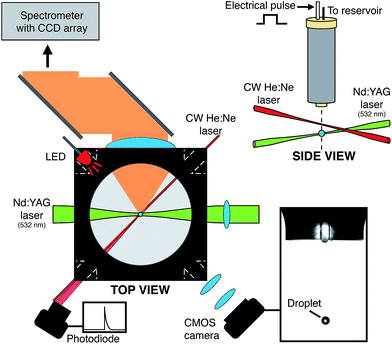
All measurements presented in this paper were performed on the experimental setup shown schematically in Fig. 1. A microdroplet dispenser was held centrally within a 6-way chamber by a x, y, z translatable mount. This chamber (LC6W, Thorlabs) facilitates the alignment of input lasers and optics. The commercially available microdroplet dispenser (MICRODROP, MD-K-140), with an orifice diameter of 50 μm, was supplied with a voltage pulse, typically square shaped, provided by a signal generator (HAMEG 2525) and amplifier (Krohn-Hite. Model #7602). The liquid sample reservoir was open to ambient pressure with no active pressure control. As will be detailed below, more complex pulse waveforms are possible. Each pulse produces a single droplet with droplet generation frequency ranging from ∼1 Hz to ∼1 kHz. In this study, aqueous droplets were generated at a frequency of 10 Hz to match the optimum laser pulse repetition rate. Typically the square-wave pulsewidth ranges from 30–80 μs with an amplified potential ranging from 50–150 V (V_0-P). The rise and fall time of the voltage pulse is approximately 7 ns. Working operating parameters, particularly the voltage and the pulsewidth, are highly dependent on the properties of the dispensed liquid.

Fig. 1 Experimental schematic of optics and laser inputs relative to the droplet location.

The exit region of the droplet generator was monitored using an imaging setup that comprised a CMOS camera (DCC1645C, Thorlabs) and light-emitting diode (LED) (500 mcd, λ_max = 660 nm) with the dispenser positioned in between (shown in Fig. 1). Driven by a voltage pulse (3 V amplitude, 4 μs pulse-length) from a digital delay generator (DG645, Stanford Research Systems), the LED illuminated the droplet dispenser tip region at a controllable delay. The LED was pulsed for every droplet and the light was collected and collimated using a lens (f = 75 mm), then focused (f = 200 mm) onto the CMOS camera, producing bright-field images that were viewed on a computer at a rate of 10 frames per second, matching the droplet generation frequency. By controlling the LED emission pulse timing, the early moments of the droplet formation can be inspected ensuring that the droplet production was stable during measurements. A 532 nm (±10 nm) notch rejection filter was positioned in front of the CMOS camera to eliminate elastically scattered light from the pulsed laser (λ = 532 nm) while allowing for detection of fluorescence emission.

After formation, a microdroplet falls ∼3 mm before passing through a continuous wave He : Ne laser beam (Thorlabs HRP020-1, 632.8 nm, 2 mW) that was focused by a lens (f = 100 mm, D = 1′′). As the droplet traversed the He : Ne beam, elastically scattered light was collected by a lens (f = 75 mm, D = 1′′) and focused onto an amplified photodiode (Thorlabs, DET36A/M). A 632.8 nm line-pass filter ensured only He : Ne scattered light was detected by the photodiode. This scattered light signal triggered a digital delay generator (DG645, Stanford Research Systems) that in turn, dictated the timing of the spectrometer CCD exposure and read-out, the pulsing of a Nd : YAG laser (Minilite II, Continuum) and the aforementioned LED. After the triggering of the delay generator, at a controlled delay (typically 300 μs) the droplet was irradiated a single pulse from a Nd : YAG laser operating on the second harmonic (λ = 532 nm, ca. 1 kJ cm⁻² at focal point). Prior to irradiating the droplet, the Nd : YAG laser pulse passed through beam expansion optics. The expansion was performed using a Keplerian beam expander providing a 4× increase in beam waist. This expansion reduces the final beam waist of the laser when ultimately focused at the droplet (∼10⁻⁶ cm²). To ensure each single droplet was irradiated at the same point in its fall time, this triggering and timing was crucial.

In these experiments, droplets were aqueous and contained a fluorescent dye, Rhodamine 6G (Sigma-Aldrich, 10 μM). After laser illumination, emitted light from the droplet was collected orthogonal to the excitation laser by a 2-inch lens (f = 60 mm) that collimated the collected light and directed it towards a spectrometer (Shamrock 500, Andor, 1200 lines per mm grating) via two broadband mirrors (D = 2′′) and then through a second 2-inch lens that was selected to best match the spectrometer's numerical aperture (f/6). Prior to entering the spectrometer the light passed through a 532 nm notch rejection filter that removed elastically scattered laser light. The spectrometer was equipped with a TE-cooled (−70 °C) open-electrode CCD detector (Newton, Andor). The CCD signal was processed using a custom LabView control program. Using this arrangement, single droplet laser emission spectra were collected one droplet at a time without fail.

Fluorescence and Raman spectra collected from single microdroplets are known to exhibit fine-structure peaks that correspond to microcavity resonances, often referred to as morphology dependent resonances (MDRs) or whispering gallery modes (WGMs), due to optical feedback within the microdroplet.^28–31 The WGM wavelength locations are dependent on the droplet radius and refractive index. As is well known, fitting the measured WGM wavelength locations using Mie theory allows for the extraction of droplet radius and refractive index with very good accuracy.^28–35 In the current experiments, to ascertain the radius of each droplet, the fluorescence spectrum was subjected to a peak picking routine to determine the location of the sharp peaks that correspond to WGMs. The WGMs are initially assigned guesses for polarity (TE or TM), mode order and mode number.^{28,32,34,36–38} The radius and dispersion corrected refractive index were then fitted to best match the theoretical WGM positions to those observed experimentally. The reported uncertainties on these fitted quantities are reported as one standard deviation (1σ) as determined from the least-squares fitting routine (Levenberg–Marquardt). Then mode assignments were iterated to determine the overall best fit. The iterative procedure follows the general algorithm of Eversole et al.^28,39 In this study, the droplets were rather large and this ultimately limits the accuracy of the analysis.⁴⁰ Notwithstanding this limitation, the intention here is to demonstrate the precision and reproducibility of the droplet generation technique and to monitor controllable changes in droplet size.

Results

Voltage-pulse waveform and droplet size

As a general guide, the size of the emitted microdroplet from the DOD dispenser is about the same as the dispenser's orifice diameter.³ In practice, the droplet size depends on a range of variables including the physical properties of the solvent, the temperature and the characteristics of the voltage waveform applied to the piezoelectric crystal. In the following section it will be shown that different droplet sizes are obtainable by changing the waveform applied to the dispenser and it is also demonstrated that these alternate waveforms provide excellent reproducibility and stability.

Fig. 2 shows five voltage waveforms applied to the droplet dispenser and corresponding fluorescence spectrum from a single representative droplet. The size reproducibility of droplets generated from these corresponding waveforms will be examined below. The waveforms are ordered A–E to correspond to the smallest to largest droplet diameter. The waveform parameters are provided in Table S1 of the ESI.† All waveforms have a 0 V starting baseline. The waveform labeled C in Fig. 2 is the standard square-wave pulse and the typical operating parameters for aqueous solutions range from 70–150 V_0-P amplitude and 35–80 μs pulse length. Waveforms A, B, D and E are examples of alternate pulse-shapes inspired by Chen and Basaran⁴ and the fitted droplet diameters are shown alongside the corresponding waveform in Fig. 2. As the droplets are labeled with the fluorescent dye Rhodamine 6G, fluorescence is collected over 560–590 nm. The spectra display sharp optical resonances—the WGMs—that are used to calculate the droplet size and refractive index.^{28,30,33,35,36}

Fig. 2 Voltage waveforms applied to the microdroplet dispenser, the corresponding measured single microdroplet diameters and representative single droplet fluorescence spectra are shown to the right. Waveform parameters are provided in Table S1 of the ESI.†

From A through E, the average spacing between the WGMs (the free-spectral range) in the single-droplet fluorescence spectra decreases and is consistent with an increasing droplet size. For each case, A–E, the WGM assignments, fitted radii and refractive index terms are included in the ESI (Table S2†). As mentioned above it is known that for large droplets and WGM measurements by standard CCD spectrometers there are limits to fitting the dispersion corrected refractive index terms and the radius as all unconstrained parameters.⁴¹ Nevertheless, the fitted radii are in good accord with optical images that are also acquired (where the droplet diameter can be roughly measured in image “pixels”).

The bright-field images shown in Fig. S1 (ESI†) depict shadow images of single microdroplets corresponding to each waveform (A–E) in Fig. 2. In each image, the dispenser capillary tip, elastically scattered light from the He : Ne trigger laser and droplet fluorescence emission are all visible. The change in microdroplet size from A–E is clear from the images in Fig. S1† and the image pixel numbers provided in the ESI (Table S2†). All images are taken using the same optical arrangement and are therefore directly comparable.

It is not apparent to us that there is a clear overall systematic trend between the waveform and the ultimate droplet size but suffice to say that the pulsewidths tend to be overall longer for larger droplets.

In Fig. 2, the fitted radii reveal that there is an appreciable range in droplet size. Thus, with a single droplet dispenser, with a fixed capillary orifice size, one can achieve a range of droplet radii, in this case from ∼10 to 30 μm. This corresponds to droplet volumes ranging from 4 to 113 pL; spanning two orders of magnitude. It will be illustrated below that these alternate waveforms provide very stable droplet streams. Furthermore that reproducible size steps are achievable in addition to smooth “tuning” of the droplets' radii.

Stability and reproducibility

An important factor to consider when tweaking the waveform applied to a DOD dispenser is the effect on stability—where stability is characterised here by the consistent success of droplet production, consistency in droplet size and reproducible droplet velocity/trajectory. These stability factors of droplet generation are vital for measurements where many single droplet experiments (1000+) are averaged together.^1,42 The tracking of WGM positions can be used to detect and measure subtle changes in droplet sizes on the precision of nanometers.^28,31,43 Fig. 3 shows an intensity plot of single fluorescence emission spectra measured for 1500 consecutive single droplets and is a portion of an overall set of 5000 consecutive droplets. These droplets are produced using the waveform labeled C in Fig. 2. The two single spectra in Fig. 3 (top) compare a single droplet emission spectrum to the average of all 1500 spectra. The FWHM peakwidth of the single droplet spectrum is 0.09 nm compared to 0.20 nm for the average of 1500. This broadening is attributed to random variations in the WGM peak positions, as the peakshape in the averaged spectrum are Gaussian-like distributions. The largest shot-to-shot variations detected are ∼0.5 nm shifts in WGM position and this is equivalent to ∼20 nm change in droplet radius, ∼0.1% of the radius, recalling that the droplet radius in this case is ∼21 μm. The results in Fig. 3 reveal that the standard square-wave waveform yields highly reproducible droplets with very small random size variation (<0.2%) and no detectable systematic drift.

Fig. 3 Single microdroplet spectra from droplets generated by waveform C (Fig. 2). The average of 1500 consecutive droplets is shown (red, top), with a single representative microdroplet spectrum (black). The intensity plot shows 1500 consecutive single microdroplet fluorescence spectra stacked to track the WGM positions over time. The inset (right) shows an expansion of the WGM at ∼574.8 nm.

Using the same analysis, the stability and reproducibility of the alternate waveforms are now investigated. Fig. 4 shows a series of 1500 single droplets produced from waveform A. As previously shown, waveform A can be implemented to generate droplets significantly smaller than the 50 μm exit orifice diameter of the dispenser. As the case in Fig. 3, the positions of the WGMs in the fluorescence spectra are tracked for each droplet over the course of the measurement. The spacing between the WGM peak positions is comparatively large as the droplets are significantly smaller. For this case A, the droplet size is extremely stable, within the limits of our spectral resolution (0.043 nm per pixel, where a WGM shift of 0.043 nm would correspond to a ∼2 nm change in droplet radius for a ∼10 μm radius droplet), with only a few outlying spectra over the course of the measurement. The random fluctuations are just discernable in the zoom trace on the 571.2 nm WGM peak in Fig. 4. The largest fluctuations observed here are shifts on the order of ±0.3 nm, which corresponds to a 12 nm change in radius. Fig. 4 also compares a single droplet spectrum to the average of the 1500 spectra shown. It shows that the reproducibility is such that the FWHM of the single droplet spectrum is essentially identical to the 1500 droplet average and presumably limited by the spectral resolution of the measurement, meaning that any random radius fluctuations are on average <2 nm.

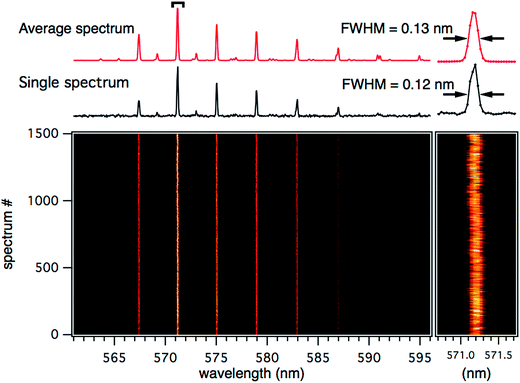Fig. 4 Single microdroplet spectra from droplets generated by waveform A (Fig. 2). The average of 1500 consecutive droplets is shown (red, top), with a single representative microdroplet spectrum (black). The intensity plot shows 1500 consecutive single microdroplet fluorescence spectra stacked to track the WGM positions over time. The inset (right) shows an expansion of the WGM at ∼571.2 nm.

For larger droplets, the reproducibility is also very good. For waveform E, 1500 single droplets were tracked and compared in the same way and these data are included in the ESI (Fig. S2†). As the microdroplets produced from this waveform are much larger than the previous examples, the observed spacing between the WGMs is much smaller. The WGM positions have similar stability to the previous waveform examples although this set of spectra exhibits some systematic drifting. The possible cause of drift might be temperature change experienced by the droplet generator—these are not temperature controlled droplet dispensers (although these are available). Although this systematic drift is clearly detectable, the actual droplet size drift is quite small, equating to ∼30 nm in radius over the course of the measurement (equivalent to ∼0.25 pL volume change).

These results demonstrate that the complex waveforms presented in this study can produce droplet trains that have excellent reproducibility, with size stability is within <0.2%.

Size stepping and tuning

We have shown that altering the pulse waveform allows access to a large range of droplet sizes from the one dispenser with excellent reproducibility. The next section demonstrates that smaller size steps are possible, measurable and predictable. Fig. 5 shows fluorescence spectra from an experiment where single-droplet WGMs are tracked as the square-wave pulsewidth is incrementally increased by 100 ns steps. The initial pulsewidth for this experiment was 37.1 μs, finishing at 38.1 μs to cover a total change of 1 μs. The inset in Fig. 5 shows the pulsewidth value corresponding to the spectra. The WGM peaks exhibit clear shifts towards longer wavelengths and this is due to the droplet size increasing, as the pulsewidth is incrementally increased.

Fig. 5 Single droplet fluorescence spectra showing WGM positions as the droplet generation pulse width is systematically stepped. The microdroplet generator pulse is a square wave pulse ranging from 37.1 to 38.1 μs as indicated on the right panel. Every 50 droplets the pulse width is increased by 100 ns as shown on the right where the pulse width is plotted along side the spectrum number.

The droplet size for each step in Fig. 5 was calculated using the Mie theory fitting routine—in this case the refractive index terms are held constant. By plotting the fitted radii at each increment against the voltage pulsewidth (Fig. 6) a linear trend is apparent. This measurement was repeated nine times (Fig. 6 displays one iterant). The average radius change was measured to be 17.3 ± 2.3 nm (1σ) per 100 ns pulsewidth increment. This result can be recast as a size-change coefficient: 0.173 ± 0.023 nm ns⁻¹.

Fig. 6 Calculated microdroplet radius at each voltage pulse width. Each pulse width step is an increment of 100 ns.

This procedure was then repeated for different pulsewidth increments (50–400 ns). When all these data are plotted against the pulsewidth step-size, the relative radius change also follows a linear trend (Fig. 7). These data were fitted using a linear regression, shown by the solid line in Fig. 7 with a gradient of 0.172 ± 0.015 nm ns⁻¹ (1σ), which is the same size-change coefficient, within the uncertainty, as the measured change in radius per nanosecond of pulse width for the 100 ns increment measurement (0.173 ± 0.023 nm ns⁻¹). The larger error bars for the larger step sizes in Fig. 7 arise from a smaller sample size in those measurements.

Fig. 7 Measured relative changes in microdroplet radius induced by steps in the applied voltage pulse width.

When the same measurement was performed using 10 ns increments, shown in Fig. 8, no resolvable steps were resolved within our spectral resolution (0.043 nm per pixel). However, over the whole 1 μs range, after 100 steps of 10 ns, an overall 4.8 nm shift in WGM position is measured. There is the ultimate appearance of smoothly tuning the droplet size. This total shift in WGM peak position is the same total shift that is observed in the 100 ns increment set (Fig. 5). The size-change coefficient is calculated in this case as 0.179 nm ns⁻¹. This shows that by varying the driving waveform provided to DOD dispensers, one can not only access large changes in the resulting droplet radius and also finely and controllably tune the droplet radii with good precision (below <10 nm). We also note that these data described in Fig. 7 were acquired over many experimental days from the same stock solution. As all size change-coefficients are the same, there is good predictability in the size change as the voltage pulsewidth is changed.

Fig. 8 Consecutive single droplet fluorescence spectra showing WGM location over 5000 single microdroplets as the voltage pulse width is systematically increased. The dye-doped droplets were generated using a standard square wave pulse (PW = 37.1–38.1 μs). After 50 droplets the pulse width has increased by 10 ns as shown by the inset showing the pulse width change vs. spectrum number.

Conclusion

The conclusions of this study can be summarised as follows:

• A DoD microdroplet dispenser with ∼50 μm diameter orifice can produce droplets with radii ranging ∼10 to 30 μm (∼5 to 110 pL) by altering the shape of the waveform. Very stable droplet streams were recorded by monitoring WGM present in the fluorescence emission of dye-labeled microdroplets. Droplet size reproducibility was deemed excellent with <1% size variation measured for each waveform presented.

• By controlling the pulsewidth of the square-wave pulse it is possible to change the droplet size, stepwise, in discrete and reproducible increments. A linear relationship was established between the voltage pulse-width and the measuring shift in droplet radius, with a size-change coefficient of 0.173 ± 0.023 nm ns⁻¹.

• Finally, it is shown that it is possible to smoothly “tune” microdroplet size by scanning the pulsewidth of the square wave pulse in nanosecond increments.

In a temperature controlled laboratory, with relatively slow temperature variations on the order of 0.1 °C, we assume that any changes in the physical properties of the liquid sample (viscosity, surface tension and density) negligibly affect the observed droplet shot-to-shot size fluctuations – temperature drifts may be more of an issue for longer timescale systematic deviations in droplet size. It is likely that the main variable affecting shot-to-shot variability in droplet size is the voltage of the square-wave pulse. Voltage fluctuations of less than a percent are likely to affect the droplet size distribution. But, as is evident from Fig. 4, the production of micrometer diameter droplets can have an extremely narrow size distribution. A companion, systematic study of the voltage response would be desirable but maintaining stable voltages and precisely/reproducibly altering the applied voltage is significantly more difficult in practice than stepping the applied pulse-width. For broader application in inkjet printing, first-drop reliability and careful priming of the system prior to first-drop generation, would need to be carefully considered.

Ultimately, we have shown that microdroplet DoD generators are a very stable and convenient way to deliver small portions of liquid with very high levels of reproducibly and that microdroplet size can be altered—either by a large or small extent—by manipulation of the pulse waveforms. These alterations in the waveform do not sacrifice the reproducibility of microdroplet generation. A final point to note is that these single droplets are typically on the order of 50 pL volume—therefore millions of single droplets can be dispensed with only a few mL of solvent consumed.

Acknowledgements

The authors are grateful for the financial support of the Australian Research Council through the Discovery program (DP1094135 and DP120102922). Internal funding support from the University of Wollongong is also gratefully acknowledged. We are thankful to Prof Mark Buntine (Curtin University) and Prof Tim Schmidt (UNSW) for their generous loaning of equipment during the initial stages of this work.

References

1. P. J. Tracey, B. S. Vaughn, B. J. Roberts, B. L. Poad and A. J. Trevitt, Anal. Chem., 2014, 86, 2895–2899.
2. P. Ben-Tzvi and W. Rone, Microsyst. Technol., 2010, 16, 333–356.
3. A. A. Castrejón-Pita, J. R. Castrejón-Pita and G. D. Martin, Rev. Sci. Instrum., 2012, 83, 115105.
4. A. U. Chen and O. A. Basaran, Phys. Fluids, 2002, 14, L1–L4.
5. T. M. Liou, C. Y. Chan and K. C. Shih, Microfluid. Nanofluid., 2010, 8, 575–586.
6. H. Y. Gan, X. C. Shan, T. Eriksson, B. K. Lok and Y. C. Lam, J. Micromech. Microeng., 2009, 19, 8.
7. R. M. Verkouteren and J. R. Verkouteren, Langmuir, 2011, 27, 9644–9653.
8. G. D. Martin, S. D. Hoath and I. M. Hutchings, J. Phys.: Conf. Ser., 2008, 105, 012001.
9. B. Derby, Annu. Rev. Mater. Res., 2010, 40, 395–414.
10. L. T. Creagh and M. McDonald, MRS Bull., 2003, 28, 807–811.
11. E. A. Roth, T. Xu, M. Das, C. Gregory, J. J. Hickman and T. Boland, Biomaterials, 2004, 25, 3707–3715.
12. T. Boland, T. Xu, B. Damon and X. Cui, Biotechnol. J., 2006, 1, 910–917.
13. H. Sirringhaus, T. Kawase, R. H. Friend, T. Shimoda, M. Inbasekaran, W. Wu and E. P. Woo, Science, 2000, 290, 2123–2126.
14. R. M. Verkouteren and J. R. Verkouteren, Anal. Chem., 2009, 81, 8577–8584.
15. M. Cernescu, T. Stark, E. Kalden, C. Kurz, K. Leuner, T. Deller, M. Gobel, G. P. Eckert and B. Brutschy, Anal. Chem., 2012, 84, 5276–5284.
16. N. Morgner, H. D. Barth and B. Brutschy, Aust. J. Chem., 2006, 59, 109–114.
17. N. Morgner, T. Kleinschroth, H. D. Barth, B. Ludwig and B. Brutschy, J. Am. Soc. Mass Spectrom., 2007, 18, 1429–1438.
18. K. Shigeta, H. Traub, U. Panne, A. Okino, L. Rottmann and N. Jakubowski, J. Anal. At. Spectrom., 2013, 28, 646–656.
19. K. Komatsu, T. Nirasawa, M. Hoshino-Nagasaka and J.-y. Kohno, J. Phys. Chem. A, 2016, 120, 1495–1500.
20. O. Borovinskaya, S. Gschwind, B. Hattendorf, M. Tanner and D. Gunther, Anal. Chem., 2014, 86, 8142–8148.
21. R. Q. Iannone, D. Romanini, S. Kassi, H. A. J. Meijer and E. R. T. Kerstel, J. Atmos. Ocean Tech., 2009, 26, 1275–1288.
22. V. J. Cadarso, J. Perera-Nunez, A. Mendez-Vilas, L. Labajos-Broncano, M. L. Gonzalez-Martin and J. Brugger, J. Mater. Res., 2014, 29, 2100–2107.
23. J.-y. Kohno, M. Kobayashi and T. Suzuki, Chem. Phys. Lett., 2013, 578, 15–20.
24. S. Moon, Y. G. Kim, L. S. Dong, M. Lombardi, E. Haeggstrom, R. V. Jensen, L. L. Hsiao and U. Demirci, PLoS One, 2011, 6, 10.
25. J. Luo, L. Qi, Y. Tao, Q. Ma and C. W. Visser, Int. J. Mach. Tool. Manufact., 2016, 106, 67–74.
26. J. Luo, L.-H. Qi, J.-M. Zhou, X.-H. Hou and H.-J. Li, J. Mater. Process. Technol., 2012, 212, 718–726.
27. S.-Y. Zhong, L.-H. Qi, J. Luo, H.-S. Zuo, X.-H. Hou and H.-J. Li, J. Mater. Process. Technol., 2014, 214, 3089–3097.
28. J. D. Eversole, H. B. Lin, A. L. Huston, A. J. Campillo, P. T. Leung, S. Y. Liu and K. Young, J. Opt. Soc. Am. B, 1993, 10, 1955–1968.
29. J. P. Reid, H. Meresman, L. Mitchem and R. Symes, Int. Rev. Phys. Chem., 2007, 26, 139–192.
30. R. Symes, R. M. Sayer and J. P. Reid, Phys. Chem. Chem. Phys., 2004, 6, 474–487.
31. G. Chen, M. M. Mazumder, R. K. Chang, J. C. Swindal and W. P. Acker, Prog. Energy Combust. Sci., 1996, 22, 163–188.
32. R. K. Chang and A. J. Campillo, Optical processes in microcavities, World Scientific Publishing Co. Pty. Ltd., 1996.
33. C. C. Lam, P. T. Leung and K. Young, J. Opt. Soc. Am. B, 1992, 9, 1585–1592.
34. T. C. Preston and J. P. Reid, J. Opt. Soc. Am. A, 2015, 32, 2210–2217.
35. J. R. Probert-Jones, J. Opt. Soc. Am. A, 1984, 1, 822–830.
36. J. F. Owen, R. K. Chang and P. W. Barber, Aerosol Sci. Technol., 1982, 1, 293–302.
37. J. Popp, M. Trunk, M. Lankers, I. Hartmann, K. Schaschek and W. Kiefer, J. Raman Spectrosc., 1997, 28, 531–536.
38. R. Symes and J. P. Reid, Phys. Chem. Chem. Phys., 2006, 8, 293–302.
39. A. J. Trevitt, P. J. Wearne and E. J. Bieske, J. Aerosol Sci., 2009, 40, 431–438.
40. R. M. Sayer, R. D. B. Gatherer, R. J. J. Gilham and J. P. Reid, Phys. Chem. Chem. Phys., 2003, 5, 3732–3739.
41. R. D. B. Gatherer, R. M. Sayer and J. P. Reid, Chem. Phys. Lett., 2002, 366, 34–41.
42. B. S. Vaughn, P. J. Tracey and A. J. Trevitt, Chem. Phys. Lett., 2012, 551, 134–138.
43. R. J. Hopkins, R. Symes, R. M. Sayer and J. P. Reid, Chem. Phys. Lett., 2003, 380, 665–672.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra08472a

---