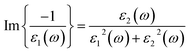Optical fingerprints and electron transport properties of DNA bases adsorbed on monolayer MoS₂

Abstract

Electronic, optical and transport properties of DNA nucleobase adsorbed on monolayer MoS₂ has been investigated using density functional theory. A significant polarization in MoS₂ has been observed upon DNA nucleobase adsorption. The nucleobase origin of the modulation in the electronic properties is clearly captured in the simulated STM measurements. The electronic transport through conjugate systems allows the clear distinction of nucleobases from one another. The modulation in electron energy loss spectra and transport properties of pristine MoS₂ has been observed on nucleobase adsorption which could serve as a fingerprint for realization of next generation DNA sequencing devices. We believe that these results also bring out the possibility of fabrication of MoS₂ based biosensors for selective detection of DNA bases in real long-chain DNA molecules.

---

1. Introduction

The interface between bio-systems and nano-materials is emerging as the most important tool for detection of various biomolecules.^1–4 In particular, the development of cost-effective, efficient and selective detection in next generation bio-sensing devices is “need of the hour”. Numerous studies have been made to explore the applications of graphene-based devices for DNA biosensing.^1,5–7 Graphene shows high flexibility, transparency, and device scalability but still offers lower sensitivity to biosensing due to the lack of a band gap.^8,9

Conventionally, metal oxides have been commonly used in sensing devices.^10,11 However, the poor sensitivity and high temperature operability in metal oxide devices; researchers have been investigating in new alternative materials such as silicene, CNT, MoS₂ etc. for sensing applications.^12–17 MoS₂ has been found to have the potential to overcome the material-dependent shortcomings for biosensing applications.⁸ Two dimensional (2D) layered transition metal dichalcogenides (TMDs) offer high surface-to-volume ratio and semiconducting properties which are essential for sensing applications.^18–20

Particularly, MoS₂-based TMDs monolayers, due to its exotic electronic and transport properties, remain a testing ground for sensing applications^19,21,22 e.g. the photoluminescence spectra (PL) of MoS₂ reveals the possibility of optical biosensors;¹⁹ modulation in PL due to the presence of DNA base could serve as a fingerprint for selective optical biosensing;¹⁹ nano-pore in pristine MoS₂ results in fast detection of DNA bases;¹⁷ MoS₂ based biomedical sensor shows promise to detect DNA origami, tumor necrosis factor-alpha (TNF-a) molecules etc.^21–25

The detection of a single nucleotide is the key idea for identification of disease for the personalized medication.²⁶ Therefore, it is important to understand the interaction of biomolecules with the materials used for sensing. The exploration of optical response and transport properties of DNA bases and MoS₂ conjugate system still need deep understanding.

In the present work, efforts have been devoted to explore the interaction of four DNA nucleotides namely adenine (A), thymine (T), cytosine (C) and guanine (G) with MoS₂ using first principles electronic structure theory. Theoretical insight about the optical response and electron transport properties of the considered nano-bio composite systems are investigated.

2. Simulation details

First principle calculations were performed within the framework of DFT as implemented in SIESTA code.^27,28 To account for electron–ion interactions, we have used well tested Troullier Martin, norm conserving, relativistic pseudo-potential^29–31 in fully separable Kleinman and Bylander form. The exchange and correlation energies were treated within the generalized gradient approximation (GGA) with PBE functional. In addition, we also used a nonlocal correlation energy functional (vdW-DF1) to account for van der Waal interaction.^32,33 The double-ζ polarized (DZP) numerical atomic orbital basis set with the confinement energy 30 meV has been used to expand the Kohn–Sham orbitals. A 200 Ry mesh cutoff has been used for reciprocal space expansion of the total charge density.

We have employed 7 × 7 supercell in our calculations. In the direction perpendicular to the monolayer, a distance of nearly 25 Å has been kept between repeated units to eliminate an interaction between adjacent monolayers, making it an effective 2D layer. The Brillouin zone was sampled using 5 × 5 × 1 Monkhorst–Pack of k-points. Optical calculations were carried out using 33 × 33 × 3 optical mesh with 0.2 eV optical broadening. A 150 unoccupied states have been used to obtain optical spectra.

The pristine monolayer with 147 atoms, and DNA nucleobases (A, T, C and G) were fully relaxed, thereafter, atomic forces were minimized to determine the preferred orientation and optimum height of the planar base of the molecule relative to the surface of the MoS₂ monolayer. The determination of the minimum total energy configuration was then followed by a 360° rotation of the base molecules in steps of 30° to probe the dependence of the energy on the orientation of the base molecules with respect to the underlying 2D-MoS₂.

3. Results and discussion

We took a single layer of MoS₂ having optimized lattice constant reported in our previous studies^29,34 for the (7 × 7) supercell. In order to determine the optimized structure, nucleobase has been placed parallel to monolayer with Mo atom at center of nucleobase hexagon. The in-plane orientation of nucleobase is expected to be more stable because geometry of the interacting species plays an important role in noticeable interaction which usually favors planarity of the two components. The optimized structures have been presented in Fig. 1. It has been found in structural optimization that the base molecule favors flat configuration which is in agreement with previously reported studies.^1,2,35 The stability of relaxed structure has been obtained by calculating binding energy as follows:

E_b = E_{nucleobase+MoS2} − (E_nucleobase + E_MoS2)

Fig. 1 Optimized ball and stick model of A, T, C and G adsorbed MoS₂ monolayer with GGA-PBE functional.

where E_{MoS2+nucleobase} is total energy of MoS₂ with absorbed molecule and E_nucleobase, E_MoS2 are total energies of nucleobase and pristine MoS₂. The obtained binding energy and the optimum height with respect to monolayer have been tabulated in Table 1. The optimum height is defined as the vertical distance between the center of mass of the molecule and the top S-layer of the MoS₂ layer. Note that negative magnitude of value of E_b indicates the physisorption of nucleobase on monolayer MoS₂. Interestingly we find increase in optimum height of nucleobase on MoS₂ within vdW-DF1 functional as compared to GGA-PBE functional. Binding is found to be more negative in vdW-DF1 calculations as compared to GGA-PBE method. The binding energies obtained with vdW-DF1 method are in good agreement with the previously reported values.³⁵ The magnitude of the calculated binding energy exhibits the following order: guanine > adenine/cytosine > thymine for both GGA-PBE and vdW-DF1 functionals. The difference in our calculated and previously reported binding energy might be due to difference in optimized height and preferred orientation of nucleobase on MoS₂ in equilibrium state (Table 1).

Table 1 The calculated (average) distance between molecule and monolayer (〈R_{molecule−MoS2}〉), binding energy (E_b) of DNA nucleobase with MoS₂ monolayer and electronic band gap of pristine MoS₂ & composite system

System	〈Rmolecule−MoS2〉 (Å)			Eb (eV)			Band gap (eV)
	Our calculation		Others^35	Our calculation		Others^35
	GGA-PBE	vdW-DF1		GGA-PBE	vdW-DF1
Pristine MoS2	—	—	—	—	—	—	1.60
Adenine + MoS2	3.51	3.74	3.53	−0.20	−0.54	−0.82	1.26
Thymine + MoS2	3.49	3.73	3.64	−0.19	−0.51	−0.75	1.58
Cytosine + MoS2	4.00	3.61	3.52	−0.20	−0.53	−0.74	1.30
Guanine + MoS2	3.37	3.66	3.55	−0.27	−0.60	−0.90	1.03

---

In order to gain further insight about the interactions of biomolecules with monolayer MoS₂, the charge density difference analysis has been performed (Fig. 2). The charge density difference profiles have been obtained as

Δρ = ρ_{nucleobase+MoS2} − (ρ_nucleobase + ρ_MoS2)

where ρ_{nucleobase+MoS2} is the total charge density of nucleobase adsorbed MoS₂ and ρ_nucleobase, ρ_MoS2 are total charge density of isolated nucleobase and pristine MoS₂ respectively. MoS₂ monolayer gets considerably polarized on the adsorption of nucleobase (Fig. 2) with redistribution of electronic charge. The polarization in case of guanine adsorbed MoS₂ is stronger as compared to other three nucleobase (A, T and C) resulting in larger magnitude of binding energy. Though considerable polarization is there; Mulliken charge transfer analysis does not show a noticeable charge transfer between nucleobase and MoS₂ forming conjugate system. The Mulliken charge transfer analysis shows that the change in total charge of the nucleobase is quite small (<10⁻³ e) upon adsorption. A similar inference has been drawn for the nucleobase adsorption on BNNT and MoS₂.^2,35 However, we find that most of the charge redistribution occurs on the upper S-layer of MoS₂ due to its proximity to nucleobase.

Fig. 2 Side and top views of charge density difference profiles for adenine (a and b), thymine (c and d), cytosine (e and f), and guanine (g and h) adsorption MoS₂. Green and red color depicts charge accumulation and depletion respectively. Isosurface value is set at 14 × 10⁻⁵ e Å⁻³.

3.1 Electronic structure

The electronic band structure of pristine MoS₂ exhibit semiconducting nature with band gap of 1.60 eV which is in good agreement with the previously reported DFT calculation^36–38 and experimentally measured values.^39,40 On the examination of molecules adsorbed electronic band structure of MoS₂, new molecular states emerged in the band gap region (Fig. 3) introducing n-type doping effect. The appearance of these energy states leads to decrease in energy band gap (Table 1). The decrease in band gap is maximum (35.62%) for guanine + MoS₂ and minimum (1.25%) for A + MoS₂ as compared to pristine MoS₂.

Fig. 3 Electronic band structure for pristine and A, T, C & G adsorbed monolayer MoS₂. The Fermi level is set at 0 eV.

The appearance of molecular levels is further confirmed by atom projected density of states as shown in Fig. 4. The major contribution in the valance band and the conduction band originates from Mo orbital's in the vicinity of valance band maxima and conduction band minima. The presence of finite density of states due to atoms of the nucleobase in the vicinity of VBM confirms the nucleobase origin of the impurity states. DOS of C and N are more pronounced in adenine and guanine adsorbed MoS₂, on the other hand, oxygen DOS dominates in thymine and cytosine adsorbed MoS₂ (Fig. 4(a–d)).

Fig. 4 Atom projected density of states for nucleobase adsorption on MoS₂ (a) adenine–MoS₂ (b) thymine + MoS₂ (c) cytosine + MoS₂ (d) guanine + MoS₂. The magnified PDOS in the vicinity of valance band is presented in inset of the respective figure.

A comparative analysis of the energy level diagram and corresponding PDOS of pristine nucleobase (Fig. S1 and S2†) and composite system (Fig. 3 and 4) gives clear signatures of energy level offset which essentially leads to decrease in the band gap. The relative alignment of valance band and conduction band could be quantified in terms of the band offset. The band offset (or energy level offset) can also be measured experimentally by using STM and μ-XPS in terms of valance band offset (VBO) and conduction band offset (CBO)⁴¹ which can be utilized as a tool for biosensing. We define VBO as ΔE_v = E_nucleobase − E_{nucleobase+MoS2} and CBO ΔE_c = E_MoS2 − E_{nucleobase+MoS2} respectively. The VBO and CBO have been tabulated in Table 2. The negative (positive) values indicate the upward (downward) shift in valance band maxima (conduction band minima). Larger value of offset gives indication of modulation in band gap which in principle is the cause of decrease in band gap to a large extent in guanine + MoS₂.

Table 2 Valance band and conduction band offset for nucleobase adsorbed MoS₂

System	Valance band offset (eV)	Conduction band offset (eV)
Adenine + MoS2	−0.45	0.34
Thymine + MoS2	−0.15	0.14
Cytosine + MoS2	−0.35	0.45
Guanine + MoS2	−0.24	0.46

---

3.2 Optical properties

In order to exploit inherent direct band character of pristine MoS₂ which provides an effective way to detect various biomolecules by recording the change in PL spectra,¹⁹ it is important to look for the modulation in optical response of nucleobase + MoS₂ systems for selective optical biosensing. For materials with a hexagonal layered symmetry, dielectric properties can be calculated with an electric vector E perpendicular to the c-axis and parallel to c-axis. The influence of nucleobase adsorption of MoS₂ in terms of the in-plane (E⊥c) and out-of-plane (E‖c) real & imaginary part of dielectric function (ε₁ and ε₂) and electron energy loss spectra is shown in Fig. 5. Peak positions in imaginary part (ε₂) and loss spectra of pristine MoS₂ and nucleobase adsorbed MoS₂ for E⊥c and E‖c axis have been tabulated in Table 3.

Fig. 5 Imaginary part (ε₂), real part (ε₁) of dielectric function and electron energy loss (EEL) spectra for nucleobase adsorbed MoS₂ for E⊥c and E‖c axis. Inset shows the magnified view of real part of dielectric function.

Table 3 Peak positions in imaginary part (ε₂) and loss spectra of pristine MoS₂ and nucleobase adsorbed MoS₂for E⊥c and E‖c axis

System	ε2 (eV)		Loss spectra (eV)
	E⊥c	E‖c	E⊥c	E‖c
Pristine MoS2	2.70, 2.88 (ref. 42)	5.23	3.19, 5.38, 7.48	6.42, 7.02, 8.29
Adenine + MoS2	2.70	5.06	3.19, 5.34, 6.87	6.36, 7.02, 8.23
Thymine + MoS2	2.70	5.06	3.19, 5.34, 6.89	6.36, 7.02, 8.23
Cytosine + MoS2	2.70	5.06	3.19, 5.37, 6.91	6.36, 7.02, 8.27
Guanine + MoS2	2.70	5.06	3.19, 5.31, 6.86	6.36, 7.02, 8.19

---

A pronounced peak at 2.70 eV indicating interband transition in imaginary part of dielectric function (ε₂) for in-plane polarization, which is in close agreement with the experimentally measured value of 2.88 eV.⁴² The ε₂ shows noticeable blue shift of 0.17 eV (Table 3) in out-of plane polarization (E‖c) for nucleobase conjugate system as compared to pristine MoS₂. The peak in the imaginary part of dielectric function remains unaltered with nucleobase adsorption. At higher energy range, marginal modulation has been found in ε₂, on nucleobase adsorption for both in-plane and out-of-plane polarization.

Furthermore, in real part (ε₁) the x-axis from negative to positive corresponds to the collective excitations of electrons. It can be seen in Fig. 5 that ε₁ in in-plane polarization cuts the zero axis from the negative y-axis at 3.05, 7.45 eV and at 6.33 eV for out-of-plane polarization (E‖c) in pristine MoS₂ while for nucleobase MoS₂ complexes ε₁ cuts the zero axis between 5.34 and 5.41 eV (UV region) as far as the parallel and perpendicular polarization is concerned.

Plasmons play a large role in the optical properties of metals and semiconductors. Light of frequencies below (above) the plasma frequency is reflected (transmitted) by a material because the electrons in the material screen (not fast to screen) the electric field of the light. The sharp peaks in the EEL function are associated with the existence of plasma oscillations. EELS has been calculated from dielectric functions using the expression:

where ε₁ and ε₂ are real and imaginary parts of dielectric function. EEL show small modulation in low energy plasmons while high energy plasmonic features are significantly modulated for both in-plane and out-of-plane polarization indicating contribution of π and σ electrons. In case of in-plane polarization a low intensity peak appears around 5.34 eV upon nucleobase adsorption. The peaks in EEL in the vicinity of 7 eV are blue shifted by ∼0.58 eV on nucleobase adsorption as compared to pristine MoS₂. These peaks are associated with the collective excitation of electrons. For out-of-plane polarization a significant modulation occurs upon nucleobase adsorption (Fig. 5). A fairly sharp peak at 6.36 eV and low intensity sharp peak at 7.02 eV and ∼8.20 eV has been found for E‖c which can be attributed to the surface plasmons propagated along c-axis. This significant modulation of EEL spectra of nucleobase + MoS₂ conjugate system could serve as benchmark for developing optical sensors. Note that, optical response can be recorded by ellipsometry measurement in experimental situation.

3.3 STM topographical analysis and tunneling current characteristics

The expected π-orbitals overlap between the DNA nucleobase and MoS₂ in planer alignment of molecules offer the favorable condition for the STM experiments. STM topographical images are known for providing the important structural and electronic information. A STM like topograph have been obtained within Tersoff and Hamann approximation^43,44 as implemented in WSxM Code.⁴⁵ The simulated STM measurements have been performed at biasing of ±1.5 eV between sample and tip. The STM topographical images for the nucleobase adsorbed MoS₂ is presented in Fig. 6. The bright spots in the images indicate that the larger magnitude of tunneling current in forward bias which originates from the nucleobase due to presence of occupied energy states of nucleobase in the vicinity of valance band maxima (Fig. 3). The faded CB topograph show typical features of the un-occupied states. The STM topography reveals that cytosine (guanine) offers maximum (minimum) number of occupied states in VB while adenine (cytosine) offers maximum (minimum) unoccupied states in CB. These distinct features originating from individual bases could serve as fingerprints for selective detection of nucleobase in STM experiments.

Fig. 6 Simulated STM-like topographical images of DNA nucleobase adsorbed on MoS₂ for valance band (VB) and conduction band (CB) at biasing of ±1.5 eV between sample and tip.

Next, we looked at the tunneling current characteristics of the nucleobase adsorbed MoS₂ within STM like setup shown in Fig. S3 of ESI.† In the STM-like setup, a tip is modeled by a cage-like Au₁₃ cluster. The Bardeen, Tersoff and Hamann (BTH) formalism of electron tunneling was used to calculate the tunneling current in this model setup.⁴⁶ The biasing is defined as forward bias (or positive bias) when the sample is connected to the positive potential with electrons flowing from tip to sample. The tip is kept at a distance of 4 Å above the nucleobase which describes the non bonding tip sample configuration (Fig. S3†). It is worth mentioning here that the choice of the tip and sample separation defines the magnitude of current as tunneling current is directly proportional to the convolution of DOS between the tip and sample, although the tunneling characteristics remain the same.

The tunneling current characteristics for pristine and nucleobase + MoS₂ system have been shown in Fig. 7. We find a rise in tunneling current at a small forward bias of ∼0.7 V for guanine and cytosine adsorbed MoS₂. We find the tunneling current more pronounced at ∼1 V which is lower than the value reported by Tanaka et al.⁴⁷ It is interesting to note that the magnitude of tunneling current increases in negative bias as compared to positive bias which can be attributed to the larger number of unoccupied states in the functionalized monolayers (Fig. 3 and 4). This rise in tunneling current in forward (reverse) bias is attributed to the VB (CB) band offset (Table 2). Note that the rise in tunneling current from zero magnitude depends on the amount of offset taking place upon nucleobase adsorption as far as the type of nucleobase adsorption is concerned.

Fig. 7 The tunneling current characteristics of A, T, C, G adsorbed MoS₂ and pristine MoS₂. The distance of separation between tip and sample has been taken as 4 Å.

3.4 Current–voltage characteristics

Furthermore, the electron transport through the nucleobase–MoS₂ system has been explored with in equilibrium transport theory as implemented in GOLLUM code.⁴⁸ It uses the DFT generated Hamiltonian as an input and generate the s-matrix and associated physical quantities such as current. The whole device setup is divided into left electrode (LE), scattering region (SR) and right electrode (RE) as shown in Fig. S4.† The applied finite voltage to the electrode change the incoming and outgoing electron distribution and hence Hamiltonian. The modified DFT Hamiltonian can be expressed in the following form:⁴⁹
where, the matrices H_L, H_R are Hamiltonian for left and right lead, H_LM, H_RM are interaction Hamiltonian between leads and extended molecule; H_M[ρ] represents non equilibrium density matrix derived Hamiltonian; μ (=eV/2) represents the change in energy levels of electrodes; S represents the corresponding overlap matrix blocks between electrode and extended molecule. It is worth mentioning here that the finite bias effects on H_M[ρ] are accounted by aligning and de-aligning the molecular orbital's at extended molecular region with shifted electrode energy levels (due to biasing). Therefore, this enables GOLLUM to introduce essential non-equilibrium effects within equilibrium transport theory. Thus the current voltage characteristics (I–V) computed from equilibrium equation
where, G = e/h is the unit of quantum conductance and T(E) is the transmission probability of electron with energy E passing from one electrode to another. Note that STM measurements provide the possibility to probe the electronic structure on a scale unobtainable with other methods on the other hand transport characteristics mimic the possibility of the model in realization of actual devices like FET for sensing application.

The current–voltage (I–V) characteristics for the pristine and nucleobase adsorbed MoS₂ is depicted in Fig. 8. An I–V characteristic of pristine MoS₂ is almost flat with in the small bias indicating its semiconducting nature. The magnitude of current increases with the increase in applied bias for the pristine as well as the nucleobase + MoS₂ complexes. The magnitude of current with applied bias is more in nucleobase + MoS₂ complexes as compared to pristine MoS₂. The higher magnitude of current in nucleobase complex is due to increase in number of open channels (transmission coefficients) conjugate system as compared to pristine MoS₂ (Fig. S5†).

Fig. 8 The current–voltage (I–V) characteristics of pristine MoS₂ and A, T, C, G adsorbed MoS₂.

Note that the polarization of the pristine MoS₂ caused by the DNA nucleobase (Fig. 2) might be the principle cause of small current with in lower bias region. Therefore, these results clearly offer a way to utilize MoS₂-based device for DNA sensor.

4. Conclusions

First principle calculations have been carried out for the pristine and nucleobase adsorbed MoS₂ using SIESTA code. Following can be concluded from the study:

• DNA nucleobase are weakly physisorbed on pristine MoS₂ monolayer.

• MoS₂ monolayer is considerably polarized upon the adsorption of nucleobase.

• Adsorption of nucleobase leads to offset in the energy levels of pristine nucleobase and MoS₂ upon adsorption which causes modification of effective band gap in pristine MoS₂.

• The electronic energy band gap is reduced to maximum of 35.62% in guanine + MoS₂ complex as compared to pristine MoS₂.

• EEL of nucleobase + MoS₂ conjugate system is blue shifted by ∼0.58 eV as compared to pristine MoS₂.

• The simulated STM measurements give the distinct features for individual nucleobase in STM topograph and tunneling current characteristics.

• Electron transport characteristics (I–V) show large magnitude of current in nucleobase + MoS₂ complexes as compared to pristine MoS₂ monolayer indicating the possibility of MoS₂ for the selective detection of nucleobase.

In nutshell, our study reveals MoS₂ monolayer to be strong candidate for the selective bio-sensing of nucleotides.

Acknowledgements

The authors wish to thank Prof. Ravindra Pandey, Michigan Technological University, for his motivation to carry out this work and discussions that proved fruitful. Helpful discussions with Dr Brij Mohan and Rajesh Thakur are highly acknowledged. Munish Sharma wishes to acknowledge the DST, Govt. of India, New Delhi for providing the financial support in the form of INSPIRE Fellowship. CVRAMAN, high performance computing cluster (provided by FIST, DST, Govt. of India, New Delhi) at Physics Department, Himachal Pradesh University has been used to obtain results presented in this paper.

References

1. T. Ahmed, S. Kilina, T. Das, J. T. Haraldsen, J. J. Rehr and A. V. Balatsky, Nano Lett., 2012, 12, 927–931.
2. S. Gowtham, R. H. Scheicher, R. Pandey, S. P. Karna and R. Ahuja, Nanotechnology, 2008, 19, 125701.
3. T. Kuila, S. Bose, P. Khanra, A. K. Mishra, N. H. Kim and J. H. Lee, Biosens. Bioelectron., 2011, 26, 4637–4648.
4. Y. Shao, J. Wang, H. Wu, J. Liu, I. A. Aksay and Y. Lin, Electroanalysis, 2010, 22, 1027–1036.
5. C. Sathe, X. Zou, J.-P. Leburton and K. Schulten, ACS Nano, 2011, 5, 8842–8851.
6. S. Meng, P. Maragakis, C. Papaloukas and E. Kaxiras, Nano Lett., 2007, 7, 45–50.
7. D. Fu and L.-J. Li, Nano Rev., 2010, 1, 5354.
8. D. Sarkar, W. Liu, X. Xie, A. C. Anselmo, S. Mitragotri and K. Banerjee, ACS Nano, 2014, 8, 3992–4003.
9. X. Gan and H. Zhao, Sens. Mater., 2015, 27, 191–215.
10. C.-S. Chou, Y.-C. Wu and C.-H. Lin, RSC Adv., 2014, 4, 52903–52910.
11. S.-W. Fan, A. K. Srivastava and V. P. Dravid, Sens. Actuators, B, 2010, 144, 159–163.
12. B. Liu, L. Chen, G. Liu, A. N. Abbas, M. Fathi and C. Zhou, ACS Nano, 2014, 8, 5304–5314.
13. S. Mukhopadhyay, S. Gowtham, R. H. Scheicher, R. Pandey and S. P. Karna, Nanotechnology, 2010, 21, 165703.
14. Z. Wang, H. He, W. Slough, R. Pandey and S. P. Karna, J. Phys. Chem. C, 2015, 119, 25965–25973.
15. R. G. Amorim and R. H. Scheicher, Nanotechnology, 2015, 26, 154002.
16. S. K. Vashist and J. H. Luong, Carbon, 2015, 84, 519–550.
17. A. B. Farimani, K. Min and N. R. Aluru, ACS Nano, 2014, 8, 7914–7922.
18. G. Korotcenkov, J. Mater. Sci. Eng. B, 2007, 139, 1–23.
19. K. Kalantar-Zadeh and J. Z. Ou, ACS Sens., 2016, 1(1), 5–16.
20. M. Sharma, P. Jamdagni, A. Kumar and P. K. Ahluwalia, AIP Conf. Proc., 2016, 1731, 140045.
21. K. Liu, J. Feng, A. Kis and A. Radenovic, ACS Nano, 2014, 8, 2504–2511.
22. H. S. Kim and Y.-H. Kim, Biosens. Bioelectron., 2015, 69, 186–198.
23. X. Zhang, M. Rahman, D. Neff and M. L. Norton, Beilstein J. Nanotechnol., 2014, 5, 501–506.
24. J. Lee, P. Dak, Y. Lee, H. Park, W. Choi, M. A. Alam and S. Kim, Sci. Rep., 2014, 4, 7352.
25. H. Nam, B.-R. Oh, M. Chen, S. Wi, D. Li, K. Kurabayashi and X. Liang, J. Vac. Sci. Tech. B, 2015, 33, 06FG01.
26. D. A. Wheeler, M. Srinivasan, M. Egholm, Y. Shen, L. Chen, A. McGuire, W. He, Y.-J. Chen, V. Makhijani and G. T. Roth, Nature, 2008, 452, 872–876.
27. P. Ordejón, E. Artacho and J. M. Soler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, R10441.
28. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
29. M. Sharma, A. Kumar, P. Ahluwalia and R. Pandey, J. Appl. Phys., 2014, 116, 063711.
30. M. Sharma, P. Jamdagni, A. Kumar and P. Ahluwalia, Phys. E, 2015, 71, 49–55.
31. N. Kumar, M. Sharma, J. Sharma and P. Ahluwalia, Indian J. Phys., 2015, 89, 143–150.
32. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
33. G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102.
34. M. Sharma, G. Loh, G. Wang, R. Pandey, S. P. Karna and P. Ahluwalia, RSC Adv., 2016, 6, 38499–38504.
35. H. Vovusha and B. Sanyal, RSC Adv., 2015, 5, 67427–67434.
36. M. Hosseini, M. Elahi, M. Pourfath and D. Esseni, J. Phys. D: Appl. Phys., 2015, 48, 375104.
37. T. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235407.
38. H. Ramakrishna Matte, A. Gomathi, A. K. Manna, D. J. Late, R. Datta, S. K. Pati and C. Rao, Angew. Chem., 2010, 122, 4153–4156.
39. A. Splendiani, L. Sun, Y. Zhang, T. Li, J. Kim, C.-Y. Chim, G. Galli and F. Wang, Nano Lett., 2010, 10, 1271–1275.
40. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805.
41. M.-H. Chiu, C. Zhang, H.-W. Shiu, C.-P. Chuu, C.-H. Chen, C.-Y. S. Chang, C.-H. Chen, M.-Y. Chou, C.-K. Shih and L. J. Li, Nat. Commun., 2015, 6, 7666.
42. Y. Li, A. Chernikov, X. Zhang, A. Rigosi, H. M. Hill, A. M. van der Zande, D. A. Chenet, E.-M. Shih, J. Hone and T. F. Heinz, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 205422.
43. J. Tersoff and D. Hamann, Phys. Rev. Lett., 1983, 50, 1998.
44. R. M. Feenstra, J. A. Stroscio and A. Fein, Surf. Sci., 1987, 181, 295–306.
45. I. Horcas, R. Fernández, J. Gomez-Rodriguez, J. Colchero, J. Gómez-Herrero and A. Baro, Rev. Sci. Instrum., 2007, 78, 013705.
46. D. Tománek and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 8327.
47. H. Tanaka and T. Kawai, Nat. Nanotechnol., 2009, 4, 518–522.
48. J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. Bailey and K. Gillemot, New J. Phys., 2014, 16, 093029.
49. V. M. García-Suárez and J. Ferrer, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125446.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra10008b

---