Mechanistic studies for dirhodium-catalyzed ring expansion reactions

Abstract

The mechanisms for dirhodium-catalyzed ring expansion reactions of azide tethered methylenecyclopropanes and their analogues were systematically investigated by DFT calculations. The calculation results indicate that the dirhodium catalyst is essential for generating a reactive Rh₂–nitrene intermediate having radical character; however, it is not essential for controlling final product selectivities. For substrates involving a three-membered ring, the experimentally obtained C–N bond formation product is a thermodynamically favored product. In contrast, for substrates having a larger ring, the kinetically favored product is the main product. The DFT calculations presented here account for previous experimental findings, and throw light on other dirhodium-catalyzed reactions involving nitrene or carbene intermediates.

---

Introduction

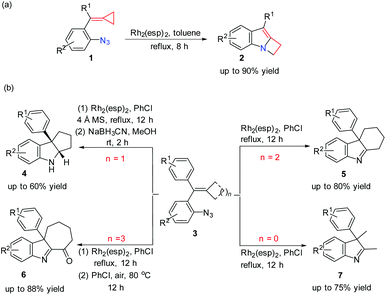
The rhodium-catalyzed reactions involving rhodium–carbenoid chemistry, represent one of the most commonly used and efficient methods in organic synthesis.¹ The dirhodium complexes (Rh₂L₄) as catalysts have been widely utilized in a variety of transformations, including a saturated C–H bond-activation/C–N bond-forming reaction,² cascade cyclopropanation/skeletal rearrangement reactions,³ ylide formations,⁴etc. It has become widely identified that the nature of the rhodium–carbenoid intermediates generated in these transformations has a major impact on the reaction outcome. Besides commonly recognized rhodium–carbenoid intermediates, some Rh₂–nitrene active intermediates can undergo single-electron-transfer (SET) to generate Rh₂(III,II)–nitrene radical intermediates, which exhibit different reactive properties. Du Bois's group^2b,e and Berry's group⁵ reported that the SET can take place between nitrene and a dirhodium(II) dimer, resulting in Rh₂(III,II) species which is the catalyst resting state in intramolecular amination reactions. Zhang's group have carried out theoretical studies on the mechanism for the Rh₂-catalyzed intramolecular C–H amination involving a triplet mixed-valent Rh₂(III,II) nitrene radical via the SET oxidation of the Rh₂(II,II) dimer.⁶ However, these Rh₂(III,II) nitrene radical intermediates are scarcely reported and studied in other types of reactions.

Very recently, our group reported a ring expansion of azide tethered methylenecyclopropanes (MCPs) 1 catalyzed by a dirhodium complex, giving indole fused azetidines 2 (Scheme 1(a)); moreover, we also found that the reactions of 3 having different sized rings or without rings under rhodium catalysis would go different directions to give related products 4–7 (Scheme 1(b)).⁷ Preliminary DFT calculations on the key reaction steps indicated that the cyclization and SET pathways are probably controlled by a designed radical clock with respect to the reactions of substrate 1.⁷

Scheme 1 Dirhodium-catalyzed ring expansion reactions of azide tethered MCPs and azide-styrenes.

Although previous experimental and preliminary theoretical results indicated that Rh₂(III,II) nitrene radical intermediates play a role in these reactions, several mechanistic questions still remain unanswered: How is the Rh₂(III,II) nitrene radical intermediate formed? What is the role of the catalyst in each of the reaction steps? What is the origin for the product selectivity? With the aim to improve our understanding of the reaction mechanism and to account for the influence of the ring size in the substrate for product selectivity in this dirhodium-catalyzed reaction, we carried out more detailed theoretical studies via DFT calculations. Herein, we would like to report our theoretical results on the reaction mechanism of the dirhodium-catalyzed reaction of azide tethered MCPs.

Computational methods

All of the calculations were performed with the Gaussian 09 software package.⁸ The geometries of all minima and transition states have been optimized using the BPW91 pure functional,⁹ with the 1997 Stuttgart relativistic small-core effective core potential (Stuttgart RSC 1997 ECP)¹⁰ for the Rh atom, augmented with a 4f function [ζ_f(Rh) = 1.350],¹¹ and the 6-31G(d) basis set for other atoms (denoted as BSI). The BPW91 pure functional used here was tested previously and demonstrated the reliable prediction of the singlet–triplet energy difference (E_st) of the dirhodium–nitrene species after comparison with the more accurate CCSD(T) method.¹² The dispersion corrections were considered in affecting the overall energy profile, however, they did not influence the relative stabilities for all species in the test reaction (for details, see the ESI†).¹³ The stabilities of the Kohn–Sham wave functions were confirmed by stability analyses¹⁴ for all of the stationary points along the reaction pathways at the BPW91/BS1 level. The subsequent frequency calculations on the stationary points were carried out at the same level of theory to ascertain the nature of the stationary points as minima or first-order saddle points on the respective potential energy surfaces. All transition states were characterized by one and only one imaginary frequency pertaining to the desired reaction coordinate. The intrinsic reaction coordinate (IRC) calculations¹⁵ were carried out at the same level of theory to further authenticate the transition states. Thermochemical corrections to 298.15 K have been calculated for all minima from unscaled vibrational frequencies obtained at this same level. The solvent effect was estimated by the IEFPCM method with radii and non-electrostatic terms for the SMD solvation model¹⁶ in toluene (ε = 2.3741) or chlorobenzene (ε = 5.6968). Solvation single-point computations utilized a basis set (denoted as BSII) consisting of the 6-311++G(d,p) basis set for C, H, N and O atoms and the same Stuttgart basis set as in BSI for the Rh atoms were performed based on the gas phase optimized structures.

The solvation Gibbs free energies for all stationary points shown in Schemes 3–9, were estimated as G_solv = E_solv(SMD-calculated) + ΔG_{corr_gas}, where E_solv(SMD-calculated) refers to the solvation single point energy and ΔG_{corr_gas} refers to the thermal correction to the free energy of the solute in the gas phase.

Scheme 2 Proposed reaction mechanism.

Scheme 3 Solvation Gibbs free energy profiles for catalyzed and uncatalyzed N₂ extrusion.

Scheme 4 Solvation Gibbs free energy profiles for the reaction of 1a having a three-membered ring.

Scheme 5 Solvation Gibbs free energy profiles for generation of product 2a without the Rh₂(esp)₂ catalyst.

Scheme 6 Solvation Gibbs free energy profiles for the reaction of 3a having a four-membered ring.

Scheme 7 Solvation Gibbs free energy profiles for generation of product 4a without the Rh₂(esp)₂ catalyst.

Scheme 8 Solvation Gibbs free energy profiles for the reaction of 3b having a five-membered ring.

Scheme 9 Solvation Gibbs free energy profiles for generation of product 5a without the Rh₂(esp)₂ catalyst.

Results and discussion

Proposed reaction pathways

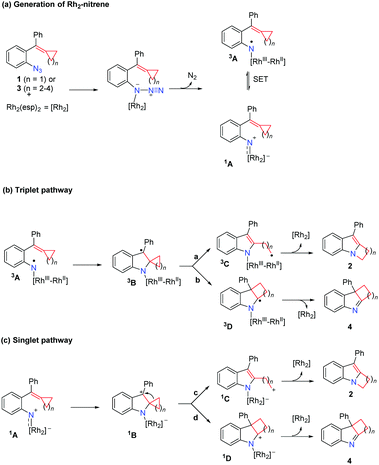
A plausible reaction mechanism is proposed in Scheme 2. Coordination of azide 1 or 3 to the Rh₂(esp)₂ complex and extrusion of N₂ gives the Rh₂–nitrene ¹A; intramolecular single electron transfer (SET) can take place, resulting in the species ³A which has the nitrogen centered radical's character (Scheme 2(a)). The following reaction can undergo the triplet pathway starting from the species ³A (Scheme 2(b)) or the singlet pathway starting from the species ¹A (Scheme 2(c)). For substrate 1 (n = 1), the reaction is proposed to proceed via the triplet pathway (path a) to give rise to product 2 together with the regeneration of the Rh₂(esp)₂ catalyst. As for substrate 3 (n = 2–4), the reactions are proposed to proceed via the singlet pathway, and do not undergo ring-opening to give intermediate ¹C (path c) and the intermediate ¹B undergoes a concerted 1,2-alkyl shift via path d to afford the corresponding 3H-indole product 4 and regenerates the Rh₂(esp)₂ catalyst.

DFT calculations have been frequently used to investigate the mechanisms for Rh-catalyzed reactions and their related reactions.¹⁷ Herein, DFT calculations are employed to investigate the detailed mechanism and the influence of ring size on product selectivity. Two parts are presented by the following mechanistic studies. First, employing typical substrates and Rh₂(esp)₂, the formation of key Rh₂–nitrene intermediate and its character are investigated and discussed in detail. Then, we investigated close-shell singlet and open-shell triplet pathways for the Rh₂-catalyzed ring expansion of azide tethered MCPs and azide-styrene, and rationalized the product selectivity affected by the ring size of the substrate.¹⁸

Generation of Rh₂–nitrene intermediate and its character

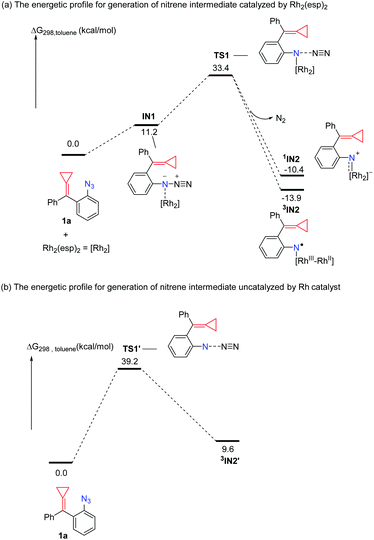
As for a variety of Rh-catalyzed reactions, the first generation of nitrene intermediate is important, and how the Rh catalyst plays its role in the formation of a nitrene intermediate also attracts a lot of interest. We first examined both Rh-catalyzed and uncatalyzed N₂ extrusion to generate a nitrene intermediate (Scheme 3). We focus our initial mechanistic studies using the substrate 1a. As shown in Scheme 3, the Rh-catalyzed pathway is initiated from the formation of the complex IN1. Passing through the transition state TS1, the nitrenoid intermediate IN2 is generated, where ¹IN2 and ³IN2 are denoted as singlet and triplet multiplicity, respectively. The computed barrier for N₂ extrusion is 22.2 kcal mol⁻¹ for the Rh₂(esp)₂ catalyzed pathway (Scheme 3(a)), which is consistent with other Rh-catalyzed N₂ extrusion processes for nitrene intermediate generation.¹⁹ The transition state TS1′ on the pathway in the absence of the Rh₂(esp)₂ catalyst is located 5.8 kcal mol⁻¹ above transition state TS1 (Scheme 3(b)). It should be noted here that without the bound Rh₂(esp)₂, only triplet nitrene ³IN2′ is stable. In the Rh-catalyzed process, the formation of a nitrene intermediate is an exothermic process; in contrast, the formation of a nitrene intermediate is an endothermic process for the pathway without the Rh catalyst. The calculation results indicate that the rhodium catalyst plays a critical role to decrease the energy barrier and makes the generation of nitrene intermediate thermodynamically favorable. For other substrates 3 bearing a four-membered ring or five-membered ring, we obtained similar results (for details, see the ESI†). Thus, the rhodium catalyst is an essential factor for the generation of the Rh₂–nitrene intermediate.

Once the Rh₂–nitrene intermediate IN2 was formed, its character attracted our attention since several experimental and theoretical reports show that some types of Rh₂–nitrene intermediates had radical character.^2b,e,5,6 In this case, the ³IN2 with a triplet state is more stable than the ¹IN2 with a singlet state by 3.5 kcal mol⁻¹, thus, the triplet state is preferred for the Rh₂–nitrene IN2. The optimized structure of ³IN2 at the BS1 level is shown in Fig. 1 and the spin densities on nitrogen and rhodium atoms are also shown in Fig. 1. Based on spin densities and MO analysis, two unpaired electrons reside in the N atom and dirhodium centers, respectively, which indicates that the Rh²⁺/Rh²⁺ dimer tends to undergo a facile one-electron oxidation when combined with related reagents,²⁰ leading to the Rh₂–nitrene ³IN2 having a mixed-valent Rh²⁺/Rh³⁺ dimer and a N radical character.

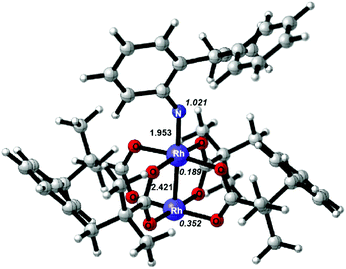Fig. 1 Optimized structure at the BS1 level for the Rh₂–nitrene ³IN2; key bond lengths (Å) and spin densities on nitrogen and rhodium atoms (in italics) are indicated.

Theoretical investigations on the origins of product selectivity

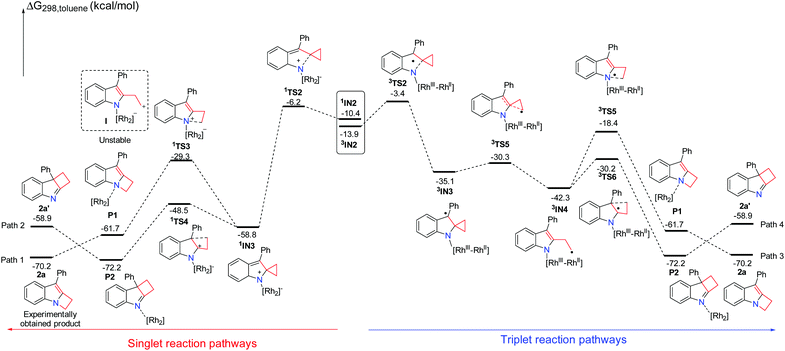
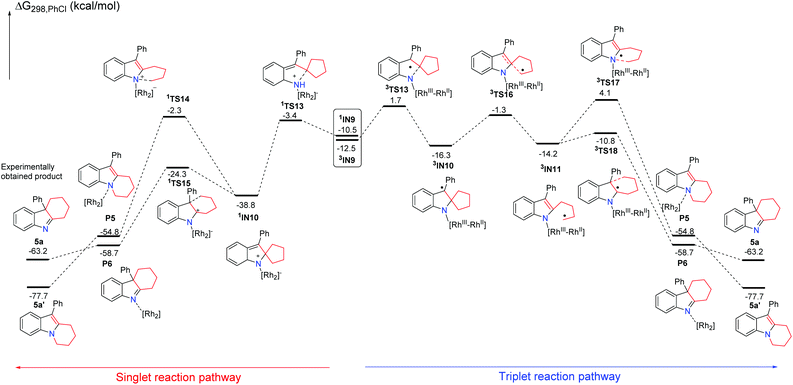
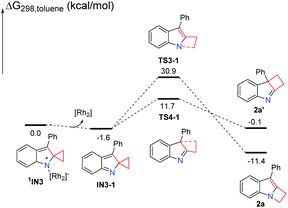
A plausible mechanism for this reaction is suggested in Scheme 2. In order to understand the detailed mechanism and rationalization of product chemoselectivity, we first investigated the possible singlet reaction pathways and triplet pathways using substrate 1a by DFT calculations, and the computed solvation free energy profiles for both singlet and triplet pathways are shown in Scheme 4, respectively. As depicted in Scheme 4, the singlet pathways (paths 1 and 2) are generally favored over the triplet pathways (paths 3 and 4). Although the triplet state ³IN2 is more favored, the ring-closure singlet transition state ¹TS2 is 2.8 kcal mol⁻¹ lower than that of the corresponding transition state ³TS2. Passing through the ring-closure singlet transition state ¹TS2, the formed intermediate IN3 is also a preferred singlet state, since the singlet state ¹IN3 is much more stable than its corresponding triplet state ³IN3 by 23.7 kcal mol⁻¹. Once the intermediate ¹IN3 is generated, it can directly undergo a concerted 1,2-alkyl shift either via¹TS3 to form a C–N bond or via¹TS4 to form a C–C bond, resulting in a product complex P1 or P2. The C–N bond formation transition state ¹TS3 is located 19.2 kcal mol⁻¹ above the C–C bond formation transition state ¹TS4, which indicates that the C–C bond formation step is kinetically favored. Cleavage of product complex P1 or P2 generates the corresponding product 2a or 2a′. The product 2a is 11.3 kcal mol⁻¹ lower than product 2a′, and it is also an experimentally obtained product. The results presented in Scheme 4 predict that the kinetic controlled product 2a′ should be obtained, which cannot account for the experimental product formation. We have tried to locate the intermediate I shown in Scheme 4, however, it is unstable and always collapses to intermediate ¹IN3. This result shows that the intermediate ¹IN3 directly undergoes a concerted 1,2-alkyl shift and does not pass the ring-opening step and then cyclization. However, we indeed used TEMPO to trap an intermediate in previous experiments.⁷ We investigated the ring-opening step on the triplet pathway, and located the stable ring-opening intermediate ³IN4. Starting from ¹IN3, a barrier of 28.5 kcal mol⁻¹ is required to generate the intermediate ³IN4, which is slightly lower than a barrier of 29.5 kcal mol⁻¹ for the formation of product 2a. Thus, the generation of the intermediate ³IN4 is a competitive step with the formation of product 2a, and the intermediate ³IN4 could be trapped by TEMPO. From the intermediate ³IN4, the following cyclization triplet pathways are calculated as shown in Scheme 4. The triplet transition states ³TS5 and ³TS6 are located above ¹TS3 and ¹TS4 by 10.9 kcal mol⁻¹ and 18.3 kcal mol⁻¹, respectively. Therefore, the singlet pathways (paths 1 and 2) are still more favored.

We have demonstrated that the rhodium catalyst is the essential factor for generation of the Rh₂–nitrene intermediate. After the Rh₂–nitrene intermediate is formed and undergoes ring-closure to form a stable intermediate, the question is whether the rhodium catalyst plays a dominant role in the following steps. We sequentially calculated the reaction pathways without the rhodium catalyst starting from the intermediate ¹IN3 (Scheme 5). Releasing the rhodium catalyst, the intermediate IN3-1 is formed. The intermediate IN3-1 without the bound rhodium catalyst can also undergo a 1,2-alkyl shift to yield corresponding products. The C–N bond formation transition state TS3-1 is located 19.2 kcal mol⁻¹ above the C–C bond formation transition state TS4-1, which is similar to the situation for the reaction steps with the rhodium catalyst. A barrier of 32.5 kcal mol⁻¹ for the formation of product 2a is higher than the barrier of 29.5 kcal mol⁻¹ for this same step with the rhodium catalyst by 3.0 kcal mol⁻¹. This result indicates that the rhodium catalyst is not essential for the following ring expansion step once the indole moiety is formed. These results are consistent with our previous experimental observations that the product 2a could be obtained at a higher reaction temperature in the absence of the rhodium catalyst.⁷ We noticed that the formation of product 2a′ is an endothermic process, which is a reversible step. Thus, the thermodynamic favored product 2a can be obtained at high temperature, which can explain the experimental product formation. Overall, the rhodium catalyst is more crucial for generating the important reactive intermediates, but it does not play a dominant role in controlling the final product selectivity.

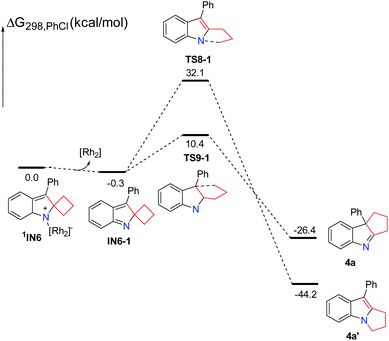
Next, we focus our attention on this Rh-catalyzed ring expansion reaction with respect to the substrates having a larger ring. As for the substrate 3a having a four-membered ring, the possible singlet reaction pathways and triplet pathways are investigated theoretically, and the computed solvation free energy profiles for both singlet and triplet pathways are shown in Scheme 6. Generally speaking, the singlet pathways are favored over the triplet pathways, which is similar to the reaction employing substrate 1a having a three-membered ring. In this case, the Rh₂–nitrene intermediate ³IN5 with the triplet state is also more stable. The free energy difference (ΔG_st = G_singlet(¹IN5) − G_triplet(³IN5)) between the singlet and triplet is 2.1 kcal mol⁻¹ which is smaller than that of their analogues having a three-membered ring (ΔG_st = G_singlet(¹IN2) − G_triplet(³IN2) = 3.5 kcal mol⁻¹) by 1.4 kcal mol⁻¹. In a similar manner, the ring-closure singlet transition state ¹TS7 is 4.9 kcal mol⁻¹ lower than the corresponding transition state ³TS7. Passing through the ring-closure singlet transition state ¹TS7, the generated intermediate IN6 is also a preferred singlet state, since the singlet state ¹IN6 is much more stable than its corresponding triplet state ³IN6 by 21.5 kcal mol⁻¹. After the intermediate ¹IN6 is yielded, it can directly undergo a concerted 1,2-alkyl shift either via¹TS8 to form a C–N bond or via¹TS9 to form a C–C bond, resulting in a product complex P3 or P4, respectively. The C–N bond formation transition state ¹TS8 is located 22.7 kcal mol⁻¹ above the C–C bond formation transition state ¹TS9, which is higher than the energy gap (19.2 kcal mol⁻¹) between ¹TS3 and ¹TS4, indicating that the barrier for C–N bond formation is more difficult to overcome with respect to the substrate 3a having a four-membered ring. Cleavage of the product complex P3 or P4 generates the corresponding product 4a or 4a′. Although the product 4a is 18.1 kcal mol⁻¹ higher than product 4a′, the product 4a is the experimentally obtained product. Probably, the energy barrier of 33.6 kcal mol⁻¹ for the C–N bond formation step is relatively high due to the steric hindrance between the increased carbon chain and the Rh₂(esp)₂ catalyst, which is difficult to overcome under the standard reaction conditions. This probably accounts for why only product 4a is obtained experimentally. Thus, the formation of product 4a is a kinetically controlled process. We also calculated the four-membered ring-opening step on the triplet pathway, and located the stable ring-opening intermediate ³IN7.²¹ However, the barrier of 36.8 kcal mol⁻¹ to generate the intermediate ³IN7 is much higher than the barrier of 10.9 kcal mol⁻¹ for producing 4a, and it is also higher than a barrier of 33.6 kcal mol⁻¹ for the formation of product 4a′. Based on the calculation results, the generation of the radical intermediate ³IN7 requires to overcome a barrier of 36.8 kcal mol⁻¹ starting from the intermediate ¹IN6, which is not a competitive step with the formation of product 4a. This result also agrees with the experimental findings that the radical intermediate ³IN7 could not be trapped by TEMPO. From the radical intermediate ³IN7, the following cyclization triplet pathways are also calculated as shown in Scheme 6. The triplet transition states ³TS11 and ³TS12 are located above ¹TS8 and ¹TS9 by 10.4 kcal mol⁻¹ and 15.6 kcal mol⁻¹, respectively. Therefore, the singlet pathways are still more favored with respect to the formation of product 4a. For comparison, we sequentially calculated the reaction pathways without the rhodium catalyst starting from the intermediate ¹IN6 (Scheme 7). Releasing the rhodium catalyst, the intermediate IN6-1 is formed. The intermediate IN6-1 without the bound rhodium catalyst can also undergo a 1,2-alkyl shift to yield the corresponding products. The C–N bond formation transition state TS8-1 is located 21.7 kcal mol⁻¹ above the C–C bond formation transition state TS9-1, which is similar to the situation for the reaction step with the rhodium catalyst. A barrier of 10.7 kcal mol⁻¹ for the formation of the experimentally obtained product 4a is slightly lower than the barrier of 10.9 kcal mol⁻¹ for this same step with the rhodium catalyst. This result also indicates that the rhodium catalyst is not essential for the ring expansion step once the indole moiety is formed. In this case, the formation of product 4a is highly exothermic, which cannot be reversible. Thus, the kinetic controlled product 4a should be obtained, which agrees with the experimental findings.

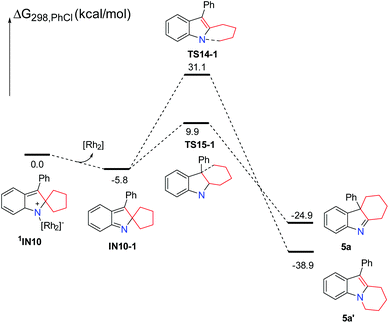
Subsequently, using the substrate 3b having a five-membered ring, the possible singlet reaction pathways and triplet pathways are also investigated theoretically, and the computed solvation free energy profiles for both singlet and triplet pathways are shown in Scheme 8. The singlet pathways are favored over the triplet pathways again, which is similar to the reaction employing the other substrates. For the substrate 3b, the corresponding Rh₂–nitrene intermediate ³IN9 with the triplet state is also more stable than its singlet state. The free energy difference (ΔG_st = G_singlet(¹IN9) − G_triplet(³IN9)) between the singlet and triplet is 2.0 kcal mol⁻¹ which is slightly smaller than that of their analogues having a four-membered ring (ΔG_st = G_singlet(¹IN5) − G_triplet(³IN5) = 2.1 kcal mol⁻¹) by 0.1 kcal mol⁻¹. The ring-closure singlet transition state ¹TS13 is 5.1 kcal mol⁻¹ lower than the corresponding transition state ³TS13. Passing through the ring-closure singlet transition state ¹TS13, the generated intermediate IN10 is also a preferred singlet state, since the singlet state ¹IN10 is much more stable than its corresponding triplet state ³IN10 by 22.5 kcal mol⁻¹. After the intermediate ¹IN10 is yielded, it can directly undergo a concerted 1,2-alkyl shift either via¹TS14 to form a C–N bond or via¹TS15 to form a C–C bond, resulting in a product complex P5 or P6, respectively. The C–N bond formation transition state ¹TS14 is located 22.0 kcal mol⁻¹ above the C–C bond formation transition state ¹TS15, which is almost same as the energy gap (22.7 kcal mol⁻¹) between ¹TS8 and ¹TS9 and higher than the energy gap (19.2 kcal mol⁻¹) between ¹TS3 and ¹TS4, indicating that the barrier for the C–N bond formation is also difficult to overcome with respect to the substrate 3b having a five-membered ring. Cleavage of product complex P5 or P6 generates the corresponding product 5a or 5a′. Although the product 5a is 14.5 kcal mol⁻¹ higher than product 5a′, the product 5a is the experimentally obtained product. It is notable that the energy barrier of 36.5 kcal mol⁻¹ for the C–N bond formation step is even higher than that (33.6 kcal mol⁻¹) of its analogue with the four-membered ring. The calculated results reveal that the longer carbon chain makes the C–N bond formation step more difficult to occur, probably due to the steric hindrance between the increased carbon chain and the Rh₂(esp)₂ catalyst. These results probably explain why only product 5a was obtained and the thermodynamically stable product 5a′ was not obtained in previous experiments. Thus, the formation of product 5a is also a kinetically controlled process. As for the substrate 3b having a five-membered ring, the stable ring-opening intermediate ³IN11 ²² with the triplet state can be located. However, the barrier of 37.5 kcal mol⁻¹ to generate the intermediate ³IN11 is much higher than the barrier of 14.5 kcal mol⁻¹ for producing 5a, and it is slightly higher than a barrier of 36.5 kcal mol⁻¹ for the formation of product 5a′. Based on the calculation results, the generation of the radical intermediate ³IN11 requires to overcome a barrier of 37.5 kcal mol⁻¹ starting from intermediate ¹IN10, which is not a competitive step with the formation of product 5a. This result can also explain the experimental finding that the radical intermediate ³IN11 could not be trapped by TEMPO. From the radical intermediate ³IN11, the following cyclization triplet pathways are also calculated as shown in Scheme 8. The triplet transition states ³TS17 and ³TS18 are located above ¹TS14 and ¹TS15 by 6.4 kcal mol⁻¹ and 13.5 kcal mol⁻¹, respectively. Therefore, the singlet pathways are more favored with respect to yielding product 5a again. In a similar manner, we calculated the reaction pathways without the rhodium catalyst starting from the intermediate ¹IN10 (Scheme 9). Upon dissociation of the rhodium catalyst, the intermediate IN10-1 is formed. The intermediate IN10-1 without the bound rhodium catalyst can also undergo a 1,2-alkyl shift to yield the corresponding products. The C–N bond formation transition state TS14-1 is located 21.2 kcal mol⁻¹ above the C–C bond formation transition state TS15-1, which is similar to the situation for the reaction step with the rhodium catalyst. A barrier of 15.7 kcal mol⁻¹ for the formation of experimentally obtained product 5a is slightly higher than the barrier of 14.5 kcal mol⁻¹ for the same step with the rhodium catalyst. This result again indicates that the rhodium catalyst is not essential for the ring expansion step once the indole moiety is formed. In this case, the formation of product 5a is also highly exothermic, which cannot be reversible. Thus, the kinetic controlled product 5a should be accessed, which is in line with the experimental findings.

Summary and conclusions

Based on systematic theoretical studies, we have disclosed the detailed reaction mechanism for the dirhodium-catalyzed ring expansion reactions of azide tethered MCPs and azide-styrenes. The mechanistic scheme we favor on the basis of the results described above can be generally summarized as the following steps: (1) complexation of the azide substrate by the dirhodium catalyst, (2) extrusion of N₂ to form a Rh₂–nitrene intermediate which has radical character, (3) electrocyclic ring closure to form the indoline ring, (4) concerted 1,2-alkyl shift to form ring expansion products and (5) dissociation of the catalyst. The dirhodium catalyst plays an important role in step 2 to generate the critical Rh₂–nitrene intermediate, and, it is also clearly to catalyze the following steps, however, it is not as important as that in step 2. For substrate 1a involving a three-membered ring, the experimentally obtained C–N bond formation product 2a is a thermodynamically favored product; moreover, the three-member-ring-opening step on the triplet pathway is a competitive process with the formation of the main product, thus a radical reaction intermediate can be trapped by TEMPO. In contrast, for substrates 3a and 3b having a larger ring, the reaction barriers for the formation of favored thermodynamic products are pretty high, thus the kinetically favored C–C bond formation products are obtained. In these cases, the ring-opening step on the triplet pathway is not a competitive process with the formation of the main product; therefore, the corresponding radical reaction intermediates cannot be trapped by TEMPO. Our findings are in line with the recent report by Driver and Tantillo,^19b which also demonstrates that the rhodium catalyst is crucial for generating the initial reactive intermediate, but not essential for controlling product selectivities in the Rh₂(II)-catalyzed reaction. The theoretical studies presented here deepened our understanding of the reaction mechanism of dirhodium-catalyzed ring expansion reactions of azide tethered MCPs and azide-styrenes, which are helpful for understanding other related dirhodium-catalyzed reactions involving nitrene or carbene intermediates.

Acknowledgements

We thank the financial support from the National Basic Research Program of China (973)-2015CB856603, and the National Natural Science Foundation of China (21372250, 20472096, 21372241, 21361140350, 20672127, 21421091, 21121062, 21302203, 20732008 and 21572052). We are grateful for the facility support from Shanghai Supercomputer Center.

Notes and references

1. For recent reviews on rhodium-catalyzed transformations, see: (a) H. M. L. Davies and S. J. Hedley, Chem. Soc. Rev., 2007, 36, 1109–1119; (b) H. M. L. Davies and Y. Lian, Acc. Chem. Res., 2012, 45, 923–935; (c) A. Padwa, Chem. Soc. Rev., 2009, 38, 3072–3081; (d) Y. Jiang, R. Sun, X.-Y. Tang and M. Shi, Chem. – Eur. J., 2016, 22, 17910–17924.
2. For selected reports on Rh-catalyzed C–H bond-activation/C–N bond-forming reaction, see: (a) C. G. Espino, K. W. Fiori, M. Kim and J. Du Bois, J. Am. Chem. Soc., 2004, 126, 15378–15379; (b) K. W. Fiori and J. Du Bois, J. Am. Chem. Soc., 2007, 129, 562–568; (c) J. J. Fleming and J. Du Bois, J. Am. Chem. Soc., 2006, 128, 3926–3927; (d) D. N. Zalatan and J. Du Bois, J. Am. Chem. Soc., 2008, 130, 9220–9221; (e) D. N. Zalatan and J. Du Bois, J. Am. Chem. Soc., 2009, 131, 7558–7559; (f) D. E. Olson and J. Du Bois, J. Am. Chem. Soc., 2008, 130, 11248–11249.
3. For selected reports on Rh-catalyzed cascade cyclopropanation/skeletal rearrangement reactions, see: (a) C.-E. Kim, S. Park, D. Eom, B. Seo and P. H. Lee, Org. Lett., 2014, 16, 1900–1903; (b) S. Rajasekar and P. Anbarasan, J. Org. Chem., 2014, 79, 8428–8434; (c) R.-Q. Ran, J. He, S.-D. Xiu, K.-B. Wang and C.-Y. Li, Org. Lett., 2014, 16, 3704–3707; (d) S. W. Kwok, L. Zhang, N. P. Grimster and V. V. Fokin, Angew. Chem., Int. Ed., 2014, 53, 3452–3456; (e) E. E. Schultz, V. N. G. Lindsay and R. Sarpong, Angew. Chem., Int. Ed., 2014, 53, 9904–9908; (f) Y. Tian, Y. Wang, H. Shang, X. Xu and Y. Tang, Org. Biomol. Chem., 2015, 13, 612–619; (g) Y.-S. Zhang, X.-Y. Tang and M. Shi, Org. Chem. Front., 2015, 2, 1516–1520; (h) T. Miura, T. Nakamuro, C.-J. Liang and M. Murakami, J. Am. Chem. Soc., 2014, 136, 15905–15908.
4. For selected reports on Rh-catalyzed ylide formations, see: (a) H. J. Jeon, D. J. Jung, J. H. Kim, Y. Kim, J. Bouffard and S. Lee, J. Org. Chem., 2014, 79, 9865–9871; (b) X. Lei, L. Li, Y.-P. He and Y. Tang, Org. Lett., 2015, 17, 5224–5227; (c) D. J. Lee, J. Shin and E. J. Yoo, Chem. Commun., 2014, 50, 6620–6622; (d) A. Boyer, Org. Lett., 2014, 16, 1660–1663; (e) Y.-S. Zhang, X.-Y. Tang and M. Shi, Chem. Commun., 2014, 50, 15971–15974; (f) J. He, Y. Shi, W. Cheng, Z. Man, D. Yang and C.-Y. Li, Angew. Chem., Int. Ed., 2016, 55, 4557–4561.
5. (a) K. P. Kornecki and J. F. Berry, Chem. – Eur. J., 2011, 17, 5827–5832; (b) K. P. Kornecki and J. F. Berry, Eur. J. Inorg. Chem., 2012, 562–568; (c) K. P. Kornecki and J. F. Berry, Chem. Commun., 2012, 48, 12097–12099.
6. X. Zhang, Z. Ke, N. J. DeYonker, H. Xu, Z.-F. Li, X. Xu, X. Zhang, C.-Y. Su, D. L. Phillips and C. Zhao, J. Org. Chem., 2013, 78, 12460–12468.
7. K. Chen, Z.-Z. Zhu, J.-X. Liu, X.-Y. Tang, Y. Wei and M. Shi, Chem. Commun., 2016, 52, 350–353.
8. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford CT, 2009.
9. (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100; (b) J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter, 1996, 54, 16533–16539.
10. (a) U. Steinbrenner, A. Bergner, M. Dolg and H. Stoll, Mol. Phys., 1994, 82, 3–11; (b) A. Henglein, J. Phys. Chem., 1993, 97, 5457–5471; (c) M. Kaupp, P. v. R. Schleyer, H. Stoll and H. Preuss, J. Chem. Phys., 1991, 94, 1360–1366.
11. W. H. Lam, K. C. Lam, Z. Lin, S. Shimada, R. N. Perutz and T. B. Marder, Dalton Trans., 2004, 1556–1562.
12. (a) X. Lin, C. Zhao, C.-M. Che, Z. Ke and D. L. Phillips, Chem. – Asian J., 2007, 2, 1101–1108; (b) X. Lin, Y. Xi and J. Sun, Comput. Theor. Chem., 2012, 999, 74–82; (c) X. Lin, J. Sun, Y. Xi and B. Pang, Comput. Theor. Chem., 2011, 963, 284–289; (d) R. Lorpitthaya, Z.-Z. Xie, K. B. Sophy, J.-L. Kuo and X.-W. Liu, Chem. – Eur. J., 2010, 16, 588–594; (e) R. Lorpitthaya, Z.-Z. Xie, J.-L. Kuo and X.-W. Liu, Chem. – Eur. J., 2008, 14, 1561–1570.
13. The energy profile for the reaction of 1a was also investigated at the B3PW91-D3/BS1//BPW91/BS1 level, including dispersion corrections. For details, see the ESI.†.
14. (a) R. Seeger and J. A. Pople, J. Chem. Phys., 1977, 66, 3045–3050; (b) R. Bauernschmitt and R. Ahlrichs, J. Chem. Phys., 1996, 104, 9047–9052.
15. (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368; (b) H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924; (c) H. P. Hratchian and H. B. Schlegel, J. Chem. Theory Comput., 2005, 1, 61–69.
16. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
17. (a) X. Hong, B. M. Trost and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 6588–6600; (b) X. Xu, P. Liu, A. Lesser, L. E. Sirois, P. A. Wender and K. N. Houk, J. Am. Chem. Soc., 2012, 134, 11012–11025; (c) T. J. L. Mustard, P. A. Wender and P. H.-Y. Cheong, ACS Catal., 2015, 5, 1758–1763; (d) P. Liu, L. E. Sirois, P. H.-Y. Cheong, Z.-X. Yu, I. V. Hartung, H. Rieck, P. A. Wender and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 10127–10135; (e) T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586; (f) Y. Park, S. Ahn, D. Kang and M.-H. Baik, Acc. Chem. Res., 2016, 49, 1263–1270; (g) R. N. Straker, Q. Peng, A. Mekareeya, R. S. Paton and E. A. Anderson, Nat. Commun., 2016, 7, 10109.
18. Attempts to investigate the open-shell singlet pathways have also been made, however, the intermediates and transition states on open-shell singlet pathways always collapsed to a close-shell singlet state.
19. (a) Q. Zhang, C. Wu, L. Zhou and J. Li, Organometallics, 2013, 32, 415–426; (b) J. G. Harrison, O. Gutierrez, N. Jana, T. G. Driver and D. J. Tantillo, J. Am. Chem. Soc., 2016, 138, 487–490.
20. For recent examples of metal-based carbene or nitrene radicals, see: (a) T. Bach, B. Schlummer and K. Harms, Chem. Commun., 2000, 287–288; (b) T. Bach, B. Schlummer and K. Harms, Chem. – Eur. J., 2001, 7, 2581–2594; (c) M. P. Doyle, Angew. Chem., Int. Ed., 2009, 48, 850–852; (d) H. Lu, W. I. Dzik, X. Xu, L. Wojtas, B. de Bruin and X. P. Zhang, J. Am. Chem. Soc., 2011, 133, 8518–8521; (e) V. Lyaskovskyy, A. I. O. Suarez, H. Lu, H. Jiang, X. P. Zhang and B. de Bruin, J. Am. Chem. Soc., 2011, 133, 12264–12273; (f) L.-M. Jin, X. Xu, H. Lu, X. Cui, L. Wojtas and X. P. Zhang, Angew. Chem., Int. Ed., 2013, 52, 5309–5313; (g) L.-M. Jin, H. Lu, Y. Cui, C. L. Lizardi, T. N. Arzua, L. Wojtas, X. Cui and X. P. Zhang, Chem. Sci., 2014, 5, 2422–2427; (h) J. Zhang, J. Jiang, D. Xu, Q. Luo, H. Wang, J. Chen, H. Li, Y. Wang and X. Wan, Angew. Chem., Int. Ed., 2015, 54, 1231–1235.
21. The corresponding intermediate ¹IN7 with the singlet state is unstable, and cannot be located.
22. The corresponding intermediate ¹IN11 with the singlet state is also unstable, and cannot be located.

---

Footnote

† Electronic supplementary information (ESI) available: Electronic energies, enthalpies, free energies, and solvation free energies (in Hartrees) and archive entries including Cartesian coordinates for all of the relevant species depicted in Schemes 3–9. See DOI: 10.1039/c6qo00713a

---