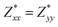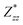Unusual phonon behavior and ultra-low thermal conductance of monolayer InSe†
Hangbo
Zhou
,
Yongqing
Cai
,
Gang
Zhang
 * and
Yong-Wei
Zhang
* and
Yong-Wei
Zhang
Institute of High Performance Computing, A*STAR, Singapore 138632. E-mail: zhangg@ihpc.a-star.edu.sg
First published on 29th November 2017
Abstract
Monolayer indium selenide (InSe) possesses numerous fascinating properties, such as high electron mobility, quantum Hall effect and anomalous optical response. However, its phonon properties, thermal transport properties and the origin of its structural stability remain unexplored. Using first-principles calculations, we show that the atoms in InSe are highly polarized and such polarization causes strong long-range dipole–dipole interaction (DDI). For acoustic modes, DDI is essential for maintaining its structural stability. For optical modes, DDI causes a significant frequency shift of its out-of-phase vibrations. Surprisingly, we observed that there were two isolated frequency regimes, which were completely separated from other frequency regimes with large frequency gaps. Within each frequency regime, only a single phonon mode exists. We further reveal that InSe possesses the lowest thermal conductance among the known two-dimensional materials due to the low cut-off frequency, low phonon group velocities and the presence of large frequency gaps. These unique behaviors of monolayer InSe can enable the fabrication of novel devices, such as thermoelectric module, single-mode phonon channel and phononic laser.
Introduction
Since the discovery of graphene in 2004, two-dimensional (2D) materials have attracted extensive research interest.1 Due to their reduced dimension, 2D materials exhibit interesting electronic properties and can potentially play key roles in the fabrication of next-generation nano-electronic devices. Recently, indium selenide (InSe), a layered metal chalcogenide semiconductor, has entered the spotlight. Bulk InSe exhibits a small electron effective mass2 and a high electron mobility at room temperature.3 Two-dimensional InSe has been theoretically predicted4 and then experimentally synthesized via mechanical exfoliation.5 A thickness-dependent bandgap has also been reported.6–8 Very recently, a high carrier mobility has been observed in monolayer InSe-based field-effect transistors.5Unlike unary 2D materials such as graphene or phosphorene, InSe is a polar material due to the substantial charge transfer between indium and selenium atoms, leading to the formation of dipoles. Recently it has been shown that these dipoles cause an unusual interaction with external molecules.9 In principle, the relative motion of dipoles generates a macroscopic electric field, which creates the interaction between dipoles. Such dipole–dipole interaction (DDI) is mediated via an electric field and hence, it decays slowly with distance, signifying a long-range interaction. Due to the weak dielectric screening effect, such long-range interaction is expected to be more pronounced in an atomic thin sheet than in its bulk counterpart.10 For example, long-range interaction due to DDI has been demonstrated to be responsible for the anomalous frequency shift of the optical E2g1 mode observed in few-layer MoS2 and WS2.10,11
For bulk InSe, the phonon properties have been examined both experimentally12–14 and theoretically.13,15 The long-range interaction causes LO–TO splitting near the Γ point.13,15 Such long-range interaction is expected to be much stronger in monolayer InSe due to its weaker dielectric permittivity.16 Therefore, it would be interesting to understand the effects of DDI on its structural stability, phonon and thermal transport properties.
In this study, by using first-principles calculations and phonon dispersion analysis, we show that the long-range DDI in monolayer InSe not only affects the optical modes of vibrations, but also plays a critical role in stabilizing the acoustic vibrations. Furthermore, we found that there exist two isolated frequency regimes in monolayer InSe that are completely separated from other regimes with frequency gaps. For each of these regimes, only a single phonon mode exists. This behavior is unique and absent in all other known 2D materials. We further show that the lattice thermal conductance of InSe is extremely low, only 10% of that of graphene, implying that it has potential for thermoelectric application.
Theoretical and computational methods
In order to examine the phonon properties of InSe, we first obtained the interatomic force constants (IFCs) using the first-principles calculation in the framework of density functional perturbation theory (DFPT).17 There exist two methods to evaluate real-space IFCs using DFPT: the small displacement method and the linear response method. The small displacement method calculates the energy variance due to a small displacement of an atom in real space, while keeping the other atoms frozen in a supercell. This method assumes that the IFCs outside the supercell boundary vanish. Hence, for a system exhibiting a long-range interaction, it requires a large supercell, which makes it computationally intensive. The recent development of the mixed-space approach allows its application to polar materials.18 However, it remains computationally challenging.The linear response method provides an efficient alternative to evaluate phonons for polar materials.19–22 It evaluates the dynamic matrix at a finite grid of reciprocal (wave-vector, q) space, and then uses Fourier transformation to get real-space IFCs. In principle, the IFCs obtained from a smooth dynamic matrix through Fourier transformation decay exponentially with distance. This is acceptable for materials with only short-range interaction, but insufficient for DDI because the IFCs of DDI decay follow an inverse power law with distance. In fact, due to the long-range interaction, dynamic matrix exhibits non-analytical behavior near the Γ point (q → 0). This non-analytical term cannot be directly treated by Fourier transformation. Fortunately, the non-analytical term caused by DDI can be explicitly evaluated using the Born effective charge tensor and dielectric constants.20 Therefore, a commonly-adopted strategy is to subtract the non-analytical term from the dynamic matrix before performing Fourier transformation. Then, we can obtain the real-space IFCs based solely on the short-range interaction. In order to consider the long-range interaction, the IFCs caused due to DDI should be explicitly added back to the short-range IFCs in real space.
The DDI-induced IFCs between two atoms at distance d in anisotropic materials are given by20
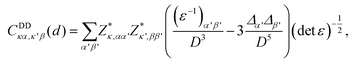 | (1) |
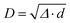 , where ε is the dielectric constant. From this expression, we can observe that the DDI-induced IFCs obey a 1/D3 decay. This DDI interaction is the long-range interaction. In contrast, the short-range interaction, which decays at least exponentially, refers to the chemical bonding between the atoms. A complete description of these interactions can be found in ref. 17 and 22.
, where ε is the dielectric constant. From this expression, we can observe that the DDI-induced IFCs obey a 1/D3 decay. This DDI interaction is the long-range interaction. In contrast, the short-range interaction, which decays at least exponentially, refers to the chemical bonding between the atoms. A complete description of these interactions can be found in ref. 17 and 22.
In a lattice, the contribution of DDI to the dynamic matrix can be evaluated using the Ewald summation technique.20 By setting the Ewald parameter to infinity, the Ewald summation is simplified to contain only the reciprocal summation term, described as22
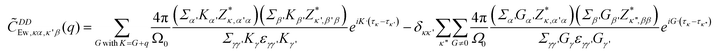 | (2) |
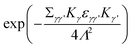 is multiplied to each term on the right hand side of eqn (2) in order to introduce a cut-off.22 The Ewald parameter Λ should be large enough, so that the result is independent of it. In the limit q → 0, we can find that
is multiplied to each term on the right hand side of eqn (2) in order to introduce a cut-off.22 The Ewald parameter Λ should be large enough, so that the result is independent of it. In the limit q → 0, we can find that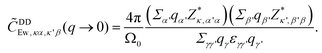 | (3) |
The above expression exhibits a non-analytical feature near the Γ point (q → 0). This expression is commonly employed to evaluate the frequency splitting between the longitude-optical (LO) modes and the transverse-optical (TO) modes caused by DDI.17,22
In this study, we use Quantum ESPRESSO23 to calculate the phonon properties, in which the linear response method is implemented. The functional of local density approximation and the electron–ion interaction with a norm-conserving pseudopotential parametrized with the Martins–Troullier method are used with a cut-off energy of 70 Ry. The Brillouin zone is sampled with 15 × 15 × 1 for the conventional cell of monolayer, and a vacuum slab with a thickness of 16 Å is adopted. All the atomic structures are fully relaxed until the forces are smaller than 1 × 10−5 eV Å−1. The convergent test is described in ESI.† From the first-principles calculation, we obtained the dynamic matrix.20,22 Starting from the dynamic matrix, we performed our analysis through the following three procedures:
Procedure (1): Only considering short-range interaction
We subtracted the long-range contribution (eqn (2)) from the dynamic matrix in the reciprocal space, which left only the short-range contribution.22 We then performed Fourier transformation to obtain the short-range IFCs in real space. This step was carried out using the Quantum ESPRESSO package. We further calculated the phonon dispersion by only considering the short-range interaction.
Procedure (2): Including long-range interaction in the reciprocal space
We interpolated the short-range contribution of dynamic matrix in the reciprocal space, and then added back the long-range contribution using eqn (2) to obtain the dispersion relation. This method was routinely carried out to calculate the phonon dispersion relation using the Quantum ESPRESSO package.
Procedure (3): Including long-range interaction in the real space
By using eqn (1), we added the long-range IFCs (real space) to the short-range IFCs in a much longer range (up to a 100 × 100 supercell) to obtain full IFCs in real space.22 Next, we performed Fourier transformation to obtain the dispersion relation.
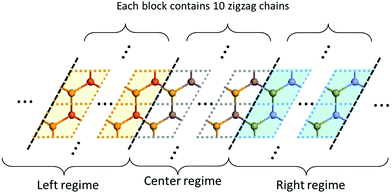
The full IFCs, calculated from procedure (3) by taking the long-range interaction into account, allowed us to calculate the thermal transport properties of InSe using the non-equilibrium Green's function (NEGF) technique as illustrated in ref. 24. In the NEGF frame, we partitioned the material into blocks along the transport direction. The blocks further fit into left, central and right regions as shown in Fig. 1. In the transverse direction of each block, the material remains periodic and thus, we can transform it to the reciprocal space to obtain Cll′κα,κ′β(q), where l,l′ are block indices. Here, we neglected the inelastic scattering, and then the central retarded Green's function was obtained via Gr(ω,q) = [(ω + iη)2M − C(q) − ΣrL(ω,q) − ΣrR(ω,q)]−1, where M is the mass matrix, C(q) is the IFCs written in matrix form and ΣrL(R) is the retarded self-energy of the left (right) region. The self-energies can be evaluated from the IFCs of the left (right) region.25 The mode-dependent transmission function can be obtained as Ξ[ω,q] = Tr[Gr(ω,q)ΓL(ω,q)Ga(ω,q)ΓR(ω,q)], where ΓL(R) = i(ΣrL(R) − [ΣL(R)]†) and Ga(ω,q) = [Gr(ω,q)]†. The frequency dependent transmission function per unit area was obtained from the mode-dependent transmission function after integrating over the Brillouin zone, 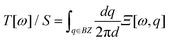 , where d is the thickness of the material and S is the cross section area for a unit cell. Once the transmission function was known, the thermal conductance per area was calculated as
, where d is the thickness of the material and S is the cross section area for a unit cell. Once the transmission function was known, the thermal conductance per area was calculated as 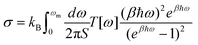 , where kB is the Boltzmann constant, β = 1/(kBT) is the inverse temperature and ωm is the cut-off frequency.
, where kB is the Boltzmann constant, β = 1/(kBT) is the inverse temperature and ωm is the cut-off frequency.
Results and discussion
Crystal structure and dipole–dipole interaction
Monolayer InSe consists of four covalently bonded atomic planes in a Se–In–In–Se sequence. Monolayer InSe has two phases, namely, α-InSe and β-InSe. Their respective atomic structures are shown in Fig. 2. The relaxed lattice constant is 3.93 Å for both phases. The thickness is estimated to be 7.57 Å for α-InSe and 7.64 Å for β-InSe, which were calculated as the buckling height plus two radii of Se atoms.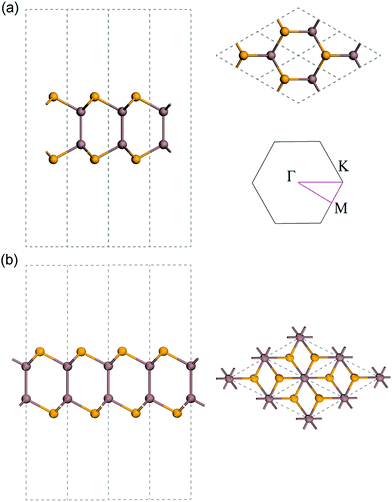 | ||
| Fig. 2 Atomic structure of (a) α-InSe and (b) β-InSe from side view and top view. The inset shows its Brillouin zone and the high symmetry points. | ||
Considering the similarities between the two phases of InSe, we choose to present the phonon and thermal properties of α-InSe in the main text, while the similar properties of β-InSe are provided in ESI† for comparison. Hence, in the following, the abbreviation InSe refers to monolayer α-InSe unless otherwise indicated.
Through DFPT calculation, we obtain the Born effective charge and dielectric constant. The results are summarized in Table 1. We found that the relative dielectric constant is isotropic within the InSe plane, but apparently weaker in the perpendicular direction (εxx = εyy = 3.88 and εzz = 1.55). Here, z refers to the direction perpendicular to the plane of the InSe sheet. As expected, the dielectric constant is much smaller than those of bulk γ-InSe (εxx = εyy = 6.2 and εzz = 4.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26) due to quantum confinement effects. The calculated Born effective charge is
26) due to quantum confinement effects. The calculated Born effective charge is 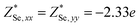 ,
, 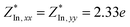 and
and 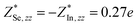 , where e (positive) is elementary charge. The charge transfer in the z direction is almost 10 times smaller than that in the xy plane. As all the 2D layered materials are highly anisotropic in the in-plane and out-of-plane directions, the dipole–dipole interactions should also be highly anisotropic. A thorough understanding of this issue requires the proper treatment of the dispersive interactions between the layers and an accurate treatment of the long-range correlation energy beyond the semi-local treatment used in the normal DFPT method. Indeed, a recent attempt has been made on this issue to separate the correlation energy into short-range and long-range terms.27 This method would allow a better description of many-body contributions to the correlation energy.
, where e (positive) is elementary charge. The charge transfer in the z direction is almost 10 times smaller than that in the xy plane. As all the 2D layered materials are highly anisotropic in the in-plane and out-of-plane directions, the dipole–dipole interactions should also be highly anisotropic. A thorough understanding of this issue requires the proper treatment of the dispersive interactions between the layers and an accurate treatment of the long-range correlation energy beyond the semi-local treatment used in the normal DFPT method. Indeed, a recent attempt has been made on this issue to separate the correlation energy into short-range and long-range terms.27 This method would allow a better description of many-body contributions to the correlation energy.
| Atom | ε xx | ε zz | C xx (≈Cyy) | C zz | |||||
|---|---|---|---|---|---|---|---|---|---|
| Short range | Long range | Short range | Long range | ||||||
| InSe | Se | 2.33 | 0.27 | 3.88 | 1.55 | 0.12435 | 0.04191 (25%) | 0.13694 | −0.00274 (2%) |
| In | −2.33 | −0.27 | 0.11421 | 0.04113 (27%) | 0.22758 | −0.00269 (1%) | |||
| MoS2 | Mo | 1.34 | 0.14 | 5.35 | 1.38 | 0.58493 | 0.03591 (6%) | 0.64287 | −0.00294 (<1%) |
| S | −0.67 | −0.07 | 0.26426 | 0.00890 (3%) | 0.33810 | −0.00073 (<1%) | |||
To make a parallel comparison, we calculated the corresponding parameters of monolayer molybdenum disulfide (MoS2) using the same procedures. We selected MoS2 because the charge transfer between Mo and S atoms also results in the formation of dipoles. The values are also shown in Table 1. It turns out that the dielectric constant of InSe is smaller than that of MoS2 in the in-plane direction (εxx = εyy = 5.35 in MoS2), while it is comparable in the perpendicular direction (εzz = 1.38 in MoS2). Moreover, the Born effective charge of InSe is much larger than that of MoS2 (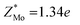 and
and 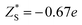 ). The values of the parameters of MoS2 are close to those in the literature.28,29 Both features indicate that InSe possesses a much stronger in-plane dipole–dipole interaction than MoS2, according to eqn (1).
). The values of the parameters of MoS2 are close to those in the literature.28,29 Both features indicate that InSe possesses a much stronger in-plane dipole–dipole interaction than MoS2, according to eqn (1).
To quantitatively describe the effects of DDI on the crystal structure, we calculated the long-range self-interaction. The self-interaction is the net restoring force constant applied to an atom upon a small displacement of itself at each direction (Cxx, Cyy and Czz). It measures the strength of the interatomic interaction at each direction. To investigate the DDI effect, we separated the self-interaction into a short-range part due to the covalent bond and a long-range part due to the DDI. As shown in Table 1, for monolayer InSe, the strength of the long-range interaction in the in-plane direction accounts for 25–27% of the total self-interaction, while this ratio is only 3–6% for monolayer MoS2. This demonstrates that DDI plays a significant role in the in-plane interatomic interactions in monolayer InSe.
Acoustic phonons and crystal stabilities
The phonon dispersion relation of InSe is shown in Fig. 3. Panels (a), (b) and (c) are obtained through the procedures (1), (2) and (3), respectively. Panels (d), (e) and (f) are zoomed-in plots of panels (a), (b) and (c), respectively. Panel (c) agrees with the previous calculations of the phonon dispersion relation.4,30 If DDI is not taken into consideration, an immediate but important observation is that the frequencies of all the acoustic modes become imaginary as illustrated by the negative frequencies in panel (a). Imaginary modes in the dispersion relation imply that the system is not stable. Previous studies suggested that 2D materials are prone to imaginary frequencies near the Γ point, indicating the instability against long-wavelength vibration.31 These conventional imaginary frequencies can be eliminated via on-site potentials, for example, by introducing the van der Waals interaction with substrates. For instance, the structural instability of silicene and borophene can be greatly suppressed with substrate support. However, for InSe, the imaginary frequencies span the entire Brillouin zone, implying that in the absence of DDI, even the unit cell itself is unstable against vibration. These imaginary frequencies disappear once the long-range contribution (DDI) is added back, either through reciprocal space using eqn (2) (panel b) or real space using eqn (1) (panel c). To make a parallel comparison, we have used the same procedures to calculate the phonon dispersion of monolayer MoS2, and the results are shown in ESI.† It was found that the imaginary frequency is absent even if the DDI is not taken into consideration. It is noted that a previous calculation on monolayer hexagonal boron–nitride also did not show any imaginary frequencies when DDI was not considered.32 Hence, we can conclude that unlike MoS2 and h-BN, long-range interaction plays an essential role in the structural stability of monolayer InSe. Without the long-range interaction, the acoustic vibrations are divergent and destroy lattice structure.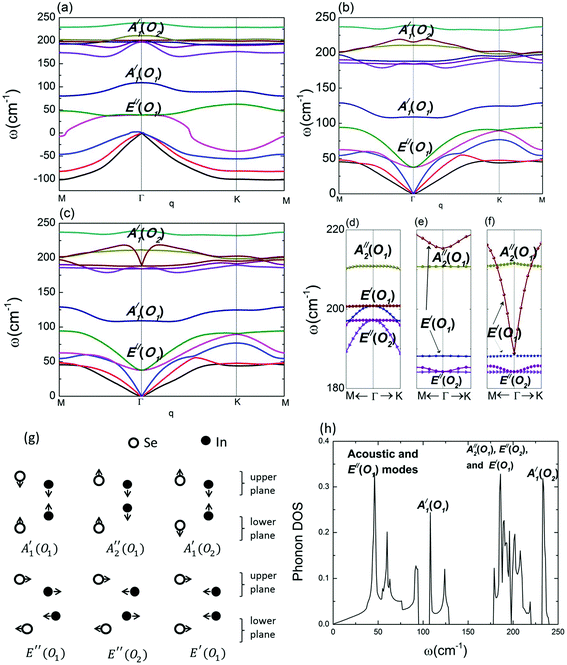 | ||
| Fig. 3 (a) and (d) The dispersion relation of InSe evaluated from the short-range interaction. The dipole–dipole interaction is not considered. (b) and (e) The dispersion relation of InSe evaluated by considering both short-range and long-range interatomic force constants due to dipole–dipole interaction in the reciprocal space, according to eqn (2). (c) and (f) The dispersion relation of InSe evaluated by considering both short-range and long-range interatomic force constants due to dipole–dipole interaction in the real space, according to eqn (1). The dipole–dipole interaction up to the 100th nearest neighbor unit cell at each direction is taken into account. (g) Illustration of atomic displacements for each optical vibration mode in the long-wavelength limit. (h) Phonon density of states corresponding to the phonon dispersion in (b). | ||
Optical phonons and frequency shifts
In addition to the acoustic modes, we found that the optical modes were also strongly affected by the dipole–dipole interaction. The vibration patterns of optical modes12 are listed in panel (g). We used O1 and O2 to distinguish two optical modes that belonged to the same symmetric group. These vibration modes are identified by their respective eigenstates at each frequency. To facilitate the discussion about the oscillation modes, we divided monolayer InSe into two planes, the upper plane and the lower plane, as shown in panel (g). By comparing panel (a/d) and panel (b/e), we observe that for the out-of-plane modes, A′1(O1), A′′2(O1) and A′1(O2), the effect of long-range interaction is not significant near the Γ point. Thus is because the charge transfer in the z direction is too small to produce a visible restoring force along the z-axis. However, beyond the Γ point, the effect of long-range interaction becomes significant. For example, in panel (a) (without DDI), the frequency of A′1(O1) mode decreases from Γ point to K point, but increases once DDI is included (panel (b)). This is because the different vibration phases between the neighboring unit cells change the interatomic distance within each plane, and thus substantially strengthen the in-plane DDI effect. Similar analysis is also applied to the E′′(O1) modes. As the E′′(O1) modes are vibration modes between the upper-plane and the lower-plane, the in-phase DDI is weak, leading to a small change in the frequency at the Γ point. However, the out-of-phase vibration strengthens DDI within each plane, resulting in a stronger effect beyond the Γ point.DDI has strong effects on the in-plane modes E′′(O2) and E′(O1), even at the Γ point (Fig. 3d and e). An important feature of these two vibration modes is that they change the In–Se bond length within each Se–In plane. Such reconfiguration of atomic positions tends towards a pairwise form. In the pairwise system, DDI is able to reduce the total energy. This explains the observation that the energy of the E′′(O2) mode decreases from 197 cm−1 (without DDI) to 184 cm−1 (with DDI) at the Γ point. In addition to the significant effect on the absolute value of the E′′(O2) mode at the Γ point, DDI also induces LO–TO splitting in the E′(O1) mode. LO–TO splitting is a phenomenon where the energies of LO and TO modes become different at the Γ point due to the presence of an electric field generated by the relative motion of atoms in the dipoles. This causes the band splitting in the dispersion relation diagram. In panel (e), we observe that the energies of the E′(O1) modes at different vibrational polarizations have a gap of 27 cm−1 (3.3 meV). This strong LO–TO splitting is about ten times that observed in monolayer MoS2 (Table 1, ref. 9). Such splitting is absent in panel (d) where only the short-range interaction is considered.
The phonon dispersion predicted from procedure (2) is performed by adding DDI in reciprocal space. This result can be reproduced by adding DDI in real space (procedure 3). As shown in Fig. 3(c), dispersion of all the phonon modes is the same as that shown in Fig. 3(b) except for the E′(O1) mode near the Γ point. By comparing panel (e) and panel (f), we observe that the only difference between them is the E′(O1) modes near the Γ point. It shows the degeneracy at the zone center and a finite slope at each side of the LO dispersion. These features agree with the theoretical prediction of optical dispersion for 2D materials.33
Fig. 3(h) presents the phonon density of states (DOS) of InSe. Interestingly, the A′1(O1) and A′1(O2) modes themselves occupy an individual peak in the DOS in the frequency ranges of 110–130 cm−1 and 230–240 cm−1, respectively. Such phenomenon is peculiar in the family of 2D materials. In other 2D materials, although there could exist a frequency gap between acoustic and optical modes (such as stanene24 and phosphorene34), at each frequency regime, the contribution to DOS always comes from a mixture of various vibration modes. However, InSe exhibits a distinct characteristic, such that once the phonons are in these two isolated frequency regimes, their vibration modes are specified and unique. In other words, in these two regimes, only a single phonon mode can be occupied. Hence, it can be possible to fine-tune the atomic vibration by using frequency control. Such unusual behavior can render possible applications in phononic laser, single-mode phonon channel or nanomechanical oscillator.
Thermal transport properties
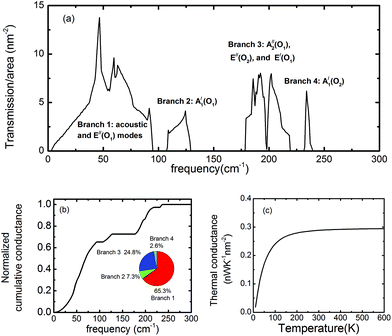
While the thermal conductivity of InSe has been studied in the diffusive regime based on the Boltzmann transport equation,35 the thermal transport properties of InSe in the ballistic regime have not yet been studied. Hence, we focused our attention on the ballistic transport regime in the wave picture of phonon transmission probabilities. The phonon transmission function obtained from the NEGF technique is shown in Fig. 4(a). In the calculation, the long-range IFCs taken into account are up to the 10th nearest neighbor unit cells at each direction, while the short-range IFCs are up to the 4th nearest neighbor unit cells. The transmission function exhibits four branches, with three frequency gaps in between, which are located exactly at the same frequency regimes as the DOS. However, in contrast to DOS, the major contribution of the transmission function is from Branch-1, which comprises the acoustic modes and the low frequency optical E′′(O1) mode. The peaks of the optical modes in the transmission function are suppressed, indicating that the group velocities of those optical phonons are small. This is further evidenced by investigating the normalized cumulative thermal conductance, which is defined as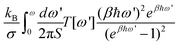 . It is a quantity to measure the contribution to the thermal conductance from phonons within the frequency regime of 0 ∼ ω. From Fig. 4(b), we can observe that at room temperature, the low frequency modes contribute significantly to the thermal transport. Quantitatively, the inset shows that Branch-1 (consisting of acoustic and E′′(O1) modes) contributes 65.3% of the total thermal conductance, while Branch-4 (the highest frequency A′1(O2) mode) only contributes 2.6%. The step-like feature in the cumulative thermal conductance diagram reflects the presence of three frequency gaps. The temperature-dependent thermal conductance is shown in Fig. 4(c). At room temperature, the thermal conductance already saturates. The thermal conductance at room temperature is 0.29 nW K−1 nm−2, which is remarkably smaller than that of graphene36 (4.1 nW K−1 nm−2), MoS2 (1.28 nW K−1 nm−2),37 phosphorene (0.76–1.08 nW K−1 nm−2)34 and stanene (0.39 nW K−1 nm−2).24 One reason for such small thermal conductance is the heavy atomic mass, resulting in a low cut-off frequency. Moreover, the presence of multiple and wide frequency gaps and the small group velocity of the optical modes are the other factors that further suppress the thermal conductance. Therefore, InSe exhibits great potential to achieve high thermoelectric performance by taking advantage of its high electron mobility7 and the low phonon thermal conductance revealed in this study.
. It is a quantity to measure the contribution to the thermal conductance from phonons within the frequency regime of 0 ∼ ω. From Fig. 4(b), we can observe that at room temperature, the low frequency modes contribute significantly to the thermal transport. Quantitatively, the inset shows that Branch-1 (consisting of acoustic and E′′(O1) modes) contributes 65.3% of the total thermal conductance, while Branch-4 (the highest frequency A′1(O2) mode) only contributes 2.6%. The step-like feature in the cumulative thermal conductance diagram reflects the presence of three frequency gaps. The temperature-dependent thermal conductance is shown in Fig. 4(c). At room temperature, the thermal conductance already saturates. The thermal conductance at room temperature is 0.29 nW K−1 nm−2, which is remarkably smaller than that of graphene36 (4.1 nW K−1 nm−2), MoS2 (1.28 nW K−1 nm−2),37 phosphorene (0.76–1.08 nW K−1 nm−2)34 and stanene (0.39 nW K−1 nm−2).24 One reason for such small thermal conductance is the heavy atomic mass, resulting in a low cut-off frequency. Moreover, the presence of multiple and wide frequency gaps and the small group velocity of the optical modes are the other factors that further suppress the thermal conductance. Therefore, InSe exhibits great potential to achieve high thermoelectric performance by taking advantage of its high electron mobility7 and the low phonon thermal conductance revealed in this study.
Conclusion
By performing first-principles calculations, we observed that InSe possesses a large Born effective charge and weak dielectric screening, resulting in a strong long-range dipole–dipole interaction in comparison with other 2D polar materials, such as MoS2. The DDI causes significant shifts in the lattice vibrational frequency of InSe. Without the DDI contribution, the frequencies of the acoustic modes become imaginary, implying that DDI is essential to maintaining the stability against acoustic vibrations. For the optical modes, we observed that the frequency shift is not significant near the Γ point but is more pronounced for the out-of-phase vibration modes, where the interatomic distances between Se and In atoms are altered. Through vibrational mode analysis, we show that two out-of-plane optical modes of InSe occupy an individual frequency regime that is completely separated from other vibration modes by frequency gaps. This unique feature, which is absent in all other 2D materials, enables its applications in phononic lasers and nanomechanical oscillators for mode control. Using the NEGF technique, we observed that the thermal conductance of InSe is 0.29 nW K−1 nm−2, which is much lower than that of any other 2D semiconductors like phosphorene, MoS2 or even stanene. The multiple frequency gaps and the small group velocity of the optical modes are the possible reasons that cause the ultra-low thermal conductance. Considering its high electron mobility and low phonon thermal conductance, InSe exhibits promising potential in thermoelectric applications.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported in part by a grant from the Science and Engineering Research Council (152-70-00017). The authors gratefully acknowledge the financial support from the Agency for Science, Technology and Research (A*STAR), Singapore and the use of computing resources at the A*STAR Computational Resource Centre, Singapore.References
- A. K. Geim and I. V. Grigorieva, van der Waals heterostructures, Nature, 2013, 499, 419–425 CrossRef CAS PubMed.
- E. Kress-Rogers, R. J. Nicholas, J. C. Portal and A. Chevy, Cyclotron resonance studies on bulk and two-dimensional conduction electrons in InSe, Solid State Commun., 1982, 44, 379–383 CrossRef CAS.
- A. Segura, F. Pomer, A. Cantarero, W. Krause and A. Chevy, Electron scattering mechanisms inn-type indium selenide, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 5708–5717 CrossRef CAS.
- L. Debbichi, O. Eriksson and S. Lebegue, Two-Dimensional Indium Selenides Compounds: An Ab Initio Study, J. Phys. Chem. Lett., 2015, 6, 3098–4103 CrossRef CAS PubMed.
- D. A. Bandurin, A. V. Tyurnina, G. L. Yu, A. Mishchenko, V. Zólyomi and S. V. Morozov, et al., High electron mobility, quantum Hall effect and anomalous optical response in atomically thin InSe, Nat. Nanotechnol., 2017, 12, 223–227 CrossRef CAS PubMed.
- G. W. Mudd, S. A. Svatek, T. Ren, A. Patanè, O. Makarovsky and L. Eaves, et al., Tuning the Bandgap of Exfoliated InSe Nanosheets by Quantum Confinement, Adv. Mater., 2013, 25, 5714 CrossRef CAS PubMed.
- S. Lei, L. Ge, S. Najmaei, A. George, R. Kappera and J. Lou, et al., Evolution of the Electronic Band Structure and Efficient Photo-Detection in Atomic Layers of InSe, ACS Nano, 2014, 8, 1263 CrossRef CAS PubMed.
- M. Brotons-Gisbert, D. Andres-Penares, J. Suh, F. Hidalgo, R. Abargues and P. J. Rodríguez-Cantó, et al., Nanotexturing To Enhance Photoluminescent Response of Atomically Thin Indium Selenide with Highly Tunable Band Gap, Nano Lett., 2016, 16, 3221 CrossRef CAS PubMed.
- Y. Cai, G. Zhang and Y.-W. Zhang, Charge Transfer and Functionalization of Monolayer InSe by Physisorption of Small Molecules for Gas Sensing, J. Phys. Chem. C, 2017, 121, 10182 CAS.
- A. Molina-Sánchez and L. Wirtz, Phonons in single-layer and few-layer MoS2 and WS2, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155413 CrossRef.
- C. Lee, H. Yan, L. E. Brus, T. F. Heinz, J. Hone and S. Ryu, Anomalous Lattice Vibrations of Single- and Few-Layer MoS2, ACS Nano, 2010, 4, 2695 CrossRef CAS PubMed.
- F. E. Faradev, N. M. Gasanly, B. N. Mavrin and N. N. Melnik, Raman scattering in some III-VI layer single crystals, Phys. Status Solidi B, 1978, 85, 381 CrossRef CAS.
- C. Ulrich, M. A. Mroginski, A. R. Goñi, A. Cantarero, U. Schwarz and V. Muñoz, et al., Vibrational Properties of InSe under Pressure: Experiment and Theory, Phys. Status Solidi B, 1996, 198, 121 CrossRef CAS.
- M. Jouanne, C. Julien, R. Beserman and M. Balkanski, Resonant Raman scattering of Li intercalated InSe, Phys. Scr., 1988, 38, 471 CrossRef CAS.
- M. Balkanski, P. G. Da Costa and R. F. Wallis, Electronic energy bands and lattice dynamics of pure and lithium-intercalated InSe, Phys. Status Solidi B, 1996, 194, 175 CrossRef CAS.
- D. Wu, A. J. Pak, Y. Liu, Y. Zhou, X. Wu and Y. Zhu, et al., Thickness-Dependent Dielectric Constant of Few-Layer In2Se3Nanoflakes, Nano Lett., 2015, 15, 8136 CrossRef CAS PubMed.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- Y. Wang, S.-L. Shang, H. Fang, Z.-K. Liu and L.-Q. Chen, First-principles calculations of lattice dynamics and thermal properties of polar solids, npj Comput. Mater., 2016, 2, 16006 CrossRef.
- P. Giannozzi, S. de Gironcoli, P. Pavone and S. Baroni, Ab initio calculation of phonon dispersions in semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 7231 CrossRef CAS.
- X. Gonze, J. C. Charlier, D. C. Allan and M. P. Teter, Interatomic force constants from first principles: The case of α-quartz, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 13035 CrossRef CAS.
- X. Gonze, First-principles responses of solids to atomic displacements and homogeneous electric fields: Implementation of a conjugate-gradient algorithm, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10337 CrossRef CAS.
- X. Gonze and C. Lee, Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355 CrossRef CAS.
- G. Paolo, B. Stefano, B. Nicola, C. Matteo, C. Roberto and C. Carlo, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- H. Zhou, Y. Cai, G. Zhang and Y.-W. Zhang, Quantum thermal transport in stanene, Phys. Rev. B, 2016, 94, 045423 CrossRef.
- J.-S. Wang, J. Wang and J. T. Lü, Quantum thermal transport in nanostructures, Eur. Phys. J. B, 2008, 62, 381 CrossRef CAS.
- O. Madelung, U. Rössler and M. Schulz, Indium selenide (InSe) dielectric constant, in Non-Tetrahedrally Bonded Elements and Binary Compounds I, ed. O. Madelung, U. Rössler and M. Schulz, Springer Berlin Heidelberg, Berlin, Heidelberg, 1998, pp. 1–3 Search PubMed.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, Long-range correlation energy calculated from coupled atomic response functions, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- Q. C. Sun, X. S. Xu, L. I. Vergara, R. Rosentsveig and J. L. Musfeldt, Dynamical charge and structural strain in inorganic fullerenelikeMoS2nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205405 CrossRef.
- C. Ataca, M. Topsakal, E. Aktürk and S. Ciraci, A Comparative Study of Lattice Dynamics of Three- and Two-Dimensional MoS2, J. Phys. Chem. C, 2011, 115, 16354 CAS.
- V. Zólyomi, N. D. Drummond and V. I. Fal'ko, Electrons and phonons in single layers of hexagonal indium chalcogenides fromab initiocalculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205416 CrossRef.
- Z. W. Tan, J.-S. Wang and C. K. Gan, First-Principles Study of Heat Transport Properties of Graphene Nanoribbons, Nano Lett., 2011, 11, 214 CrossRef CAS PubMed.
- D. Sánchez-Portal and E. Hernández, Vibrational properties of single-wall nanotubes and monolayers of hexagonal BN, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 235415 CrossRef.
- T. Sohier, M. Gibertini, M. Calandra, F. Mauri and N. Marzari, Breakdown of Optical Phonons’ Splitting in Two-Dimensional Materials, Nano Lett., 2017, 17, 3758 CrossRef CAS PubMed.
- Z.-Y. Ong, Y. Cai, G. Zhang and Y.-W. Zhang, Strong Thermal Transport Anisotropy and Strain Modulation in Single-Layer Phosphorene, J. Phys. Chem. C, 2014, 118, 25272 CAS.
- A. S. Nissimagoudar, J. Ma, Y. Chen and W. Li, Thermal transport in monolayer InSe, J. Phys.: Condens. Matter, 2017, 29, 335702 CrossRef PubMed.
- Y. Xu, X. Chen, B.-L. Gu and W. Duan, Intrinsic anisotropy of thermal conductance in graphene nanoribbons, Appl. Phys. Lett., 2009, 95, 233116 CrossRef.
- Y. Cai, J. Lan, G. Zhang and Y.-W. Zhang, Lattice vibrational modes and phonon thermal conductivity of monolayer MoS2, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035438 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr07779c |
| This journal is © The Royal Society of Chemistry 2018 |