Random positioning of nucleosomes enhances heritable bistability
Heli
Tan
ab,
Tuoqi
Liu
a,
Jiajun
Zhang
a and
Tianshou
Zhou
*a
aSchool of Mathematics, Sun Yat-Sen University, Guangzhou 510275, P. R. China. E-mail: mcszhtsh@mail.sysu.edu.cn
bSchool of Mathematics and Computational Science, Xiangtan University, XiangTan 411105, P. R. China
First published on 3rd November 2016
Abstract
Chromosomal regions are often dynamically modified by histones, leading to the uncertainty of nucleosome positions. Experiments have provided evidence for this randomness, but it is unclear how it impacts epigenetic heritability. Here, by analyzing a mechanic model at the molecular level, which considers three representative types of nucleosomes (unmodified, methylated, and acetylated) and dynamic nucleosome modifications, we find that in contrast to the equidistance partition of nucleosomes, random partition can significantly enhance heritable bistability. Moreover, the more “chaotic” the nucleosome positions are, the better the heritable bistability is, in contrast to the previous view. In both cases of nucleosome positioning, heritable bistability occurs only when the total nucleosome number is beyond a threshold, and it depends strongly on the allocation rate that enzymes regulate transitions between different nucleosome types. Thus, we conclude that random positioning of nucleosomes is an unneglectable factor impacting heritable bistability. A point worth mentioning is that our model established on a master equation can easily be extended to include other more complex processes underlying dynamic nucleosome modifications.
1. Introduction
Cells have the ability to pass on genetic information to their descendants from their ancestors. Such a genetic memory is mainly encoded in the DNA sequence in the genome of each cell, where nucleic acids provide the high stability and accurate heritability necessary for memory on evolutionary timescales. In contrast, cell epigenetic memory involves temporal signals that set the cell into one of several alternative regulatory states. These heritable states must be not only stable over time but also inherited through cell division. A surprising fact is that although modified dynamically by a number of histones, chromosomal regions can still adopt stable and heritable alternative states without changing the DNA sequence.1–10 With the development of experimental technologies, more detailed molecular mechanisms underlying epigenetic heritability have been uncovered. It is important to develop mathematical models to reveal how epigenetic heritability is generated.Epigenetic mechanisms can be roughly divided into two classes: one class involves cis-specific and DNA-associated differences. For this class, the best understood example is alternative DNA methylation.11–14 The other class is determined by circuits of diffusible and trans-acting factors that can exist in alternative regulatory states through positive feedback.15–17 The best understood examples include stable alternative induction states of the lac operon18 and the phage lambda CI-Cro switch.19 In contrast to the former class, which is mostly clearly identified when the alternative states can coexist within the same cell,20 the latter class, which is more common in prokaryotic and eukaryotic cells and is therefore a major class of epigenetic mechanisms, has not been well identified. This paper will focus on the latter.
As a consequence of epigenetic mechanisms, heritable bistability may be complicated by various nucleosome modifications. It is known that nucleosomes can carry various chemical modifications (e.g., acetylation and methylation) at different amino acid positions on different histones, potentially endowing a large information capacity with each nucleosome. Specific additions and removals of these nucleosome modifications are carried out by several classes of enzymes such as histone acetyltransferases (HATs), histone methyltransferases (HMTs), histone deacetylases (HDACs), and histone demethylases (HDMs)21 (we will limit our discussion to the catalytic roles of these four enzymes in this paper). Importantly, positive feedback can arise due to the corresponding modification reactions, e.g., positive feedback is formed if nucleosomes carry a particular modification recruit enzymes, which in turn catalyze similar modification of neighboring nucleosomes.2 Enzyme recruitment leads to stochastic transitions between distinct types of nucleosomes. However, since some enzymes such as HATs, HDACs, and HMTs are known to associate in vitro or in vivo with histones of the type that they are capable of producing,22–25 this makes a cluster of nucleosomes still able to be kept in particular modification states. Annunziato suggested that these states are inherited through DNA replication,26–28 based on the fact that nucleosomes on the parental DNA strand are distributed to both daughter strands and the enzymes recruited by these parental nucleosomes may then establish the pattern of parental modification on the newly deposited nucleosomes.
Furthermore, the positions of nucleosomes are important factors affecting a number of vital biological processes.29–34 In fact, the eukaryotic genome is packaged into chromatin, which consists of a basic repeating unit of nucleosomes arranged in regularly spaced arrays. DNA sequence is not the sole determinant of nucleosome positioning since proteins often compete with nucleosomes for binding to specific DNA regulatory sites,35–37 and ATP-dependent chromatin remodelers actively displace nucleosomes.38–40 Small et al.41 developed an experimental method to examine nucleosome positions in single cells, and revealed significant heterogeneity of nucleosome configurations within a population and complexity of nucleosome positioning as well as its role in regulating gene expression. In spite of this, the exact positions of nucleosomes are not known. In this paper, we will consider random positioning of nucleosomes, focusing on its effects on epigenetic heritability.
Experimental evidence supports the fact that nucleosome positions can impact heritable bistability, but this impact was neglected in previous studies. In order to reveal the mechanism of epigenetic cell memory, Dodd et al.2 proposed a stochastic model, which assumed that in the recruitment reaction, any nucleosome can act on any other nucleosome in the region, and thus one kind of modification can “jump” over differently modified nucleosomes. Such jumping might be facilitated by a higher-order chromatin structure, by DNA-looping or by more complex processes. However, this model only considers that nucleosome positions are equidistance in a finite region. Until now, it seems to us that no one has investigated how random positioning of nucleosomes influences heritable bistability. In addition, some previously proposed models took into consideration the fact that contacts between nucleosomes decrease with increasing distance between them on the DNA, and utilized a power law to quantify this contact, i.e., assuming that the probability of contact is proportional to 1/d1.5, where d represents the distance between two neighboring nucleosomes.42,43 In this paper, we also adopt such a power-law contact model to quantify the impact of one nucleosome on another nucleosome adjacent to it.
In summary, heritable bistability is necessary for cells of identical genomes to maintain distinct functional identities important for multi-cell organisms, factors influencing this bistability are diverse, and the positions of nucleosomes are not fixed but random. To our knowledge, there has been no systematic analysis of how dynamic nucleosome modifications including nucleosomes' random positioning affect heritable bistability. In addition, although it is known from other systems that positive feedback (or double-negative feedback) is a necessary rather than a sufficient condition for bistability,16,44 it is not clear whether this is real for heritable bistability. In this paper, we will develop a mechanic model for epigenetic systems that have the potential to generate heritable bistability. This model, which considers not only nucleosome modification reactions but also nucleosome positioning (random or deterministic), can find its prototype in the silenced mating-type locus of the fission yeast Schizosaccharomyces pombe.2,45 Using this model, we examine how heritable bistability is generated, focusing on the effect of nucleosomes' random positioning. Through analysis, we found that random positioning of nucleosomes can strengthen heritable bistability in contrast to equal positioning, that there is a critical value of the total nucleosome number such that heritable bistability occurs only when the total nucleosome number is beyond this threshold, and that heritable bistability depends heavily on a rate between enzyme allocations. We emphasize that our mathematical model is established in terms of a chemical master equation, so it has many advantages, e.g., our model is easily extended to include more complex nucleosome modifications, thus being convenient for further studies.
2. Results
2.1 Heritable bistability occurs only when the total nucleosome number is beyond a threshold
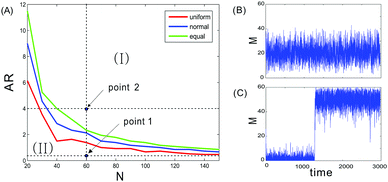
We denote N as the total number of nucleosomes, which are distinguished as three distinct types of nucleosomes, unmodified, methylated, and acetylated, with the corresponding numbers denoted by u, m and a, respectively. Since no experimental data allow us to estimate the size of this total number, we let it change in a finite interval. Here, we investigate how the total nucleosome number affects heritable bistability. The numerical results are shown in Fig. 1. From this figure, we observe that heritable bistability can occur only when the total nucleosome number is beyond a critical value. More precisely, there is a threshold of the total nucleosome number, denoted by Ncritical, such that heritable bistability can emerge as N > Ncritical. It should be noted that this critical number depends on the allocation rate between enzymes (AR), which is defined as the ratio of the probability for the active recruited processes over that for four noisy conversions between the recruited enzymes. Calculation indicates that the larger this ratio is, the smaller Ncritical required for the occurrence of heritable bistability. Correspondingly, if the total number of nucleosomes is fixed, then there is a critical allocation rate for enzymes, denoted by ARcritical, such that the steady-state probability distribution of the methylated nucleosome number, denoted by P(m), is bimodal for AR > ARcritical.Fig. 1 also shows the effect of nucleosome position on heritable bistability. We compare three representative cases of nucleosome positioning: the first case is that the distance between any two neighboring nucleosomes is equal (denoted by d the common distance), the second case is that the distance between two neighboring nucleosomes follows a uniform distribution with mean d, and the third case is that the distance between two neighboring nucleosomes follows a normal distribution also with mean d. From the left panel of Fig. 1, we observe that the bistable region for uniform distribution is larger than the one for normal distribution, which is larger than that for equal distance. This is because the line for uniform distribution is located below that for normal distribution whereas the latter is located below that for equal distance. This observation indicates that for a given allocation rate, the stronger the randomness of the distance between two neighboring nucleosomes is, the more easily heritable bistability is generated.
In addition, we also observe from the left diagram of Fig. 1 that the allocation rate between enzymes is an important factor affecting heritable bistability if the nucleosome number is fixed. In the next subsection, we will further investigate how this factor impacts heritable bistability from different angle points.
We also demonstrate time evolutions of the methylated nucleosome number in the right diagram of Fig. 1, where panels (B) and (C) correspond, respectively, to two points indicated in the left diagram of Fig. 1. These time evolutions correspond to the case where the nucleosome positions follow the normal distribution. This demonstration is mainly used to verify the correctness of the divided regions for bimodality and unimodality.
Throughout the following, we will fix the total number of nucleosomes at some value (e.g., N = 60) to characterize heritable bistability from two aspects: dwell time and epigenetic landscape. In each case, we will focus on the effects of the nucleosomes' random positions. Before that, we examine the effect of the allocation rate between enzymes on heritable bistability and compare the results obtained in three cases of nucleosome positioning.
2.2 Effect of nucleosome positions on heritable bistability
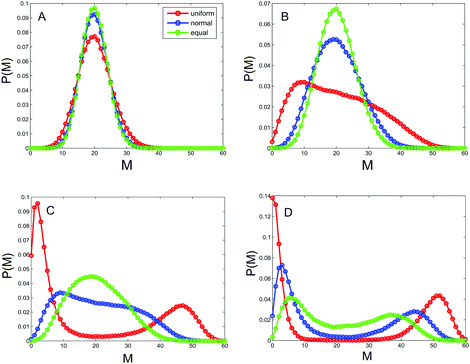
As pointed out above, the allocation rate between enzymes that regulate transitions between different types of nucleosomes describes the noise in the underlying system on the one hand, and can be used to convey the relative activities of the positive-feedback and noise-conversion processes on the other hand. Therefore, this rate is an important parameter of the system. In order to show how the rate affects heritable bistability, we calculate the distribution of the methylated nucleosome number P(m) according to eqn (9) in the Methods section. The results are shown in Fig. 2, where 4 representative values of allocation rate are used and the total number of nucleosomes is fixed at N = 60. From this figure, we first observe that P(m) is unimodal for small values of AR, e.g., AR = 1/9, but bimodal for large values of AR, e.g., AR = 1. Similar phenomena are also observed for the steady-state distribution of the unmodified nucleosome number, denoted by P(u), and for the steady-state distribution of the acetylated nucleosomes, denoted by P(a). Data are not shown here. In fact, we have a more general conclusion: if the total number of nucleosomes is fixed, then the larger the allocation rate is, the more apparent the heritable bistability will become.A more important point is one we observe from Fig. 2, that different ways of nucleosome positioning leads to different effects of the allocation rate on heritable bistability. Specifically, three positioning ways cannot create heritable bistability for a small allocation rate (e.g., less than 3/7). With the gradual increase of the allocation rate (AR increases from 1/9 to 7/3), heritable bistability occurs first in the case of uniformly distributed distances, then in the case of normally distributed distances, and finally in the case of equal distances. In other words, the uniform distribution of nucleosome positions creates heritable bistability more easily than the normal distribution that creates heritable bistability more easily than the equal distribution. This implies that the random positions of nucleosomes promote heritable bistability in contrast to the deterministic positions, which is one main conclusion of this paper. In the next subsection, we will further verify this conclusion.
2.3 Effect of nucleosome positions on dwell time
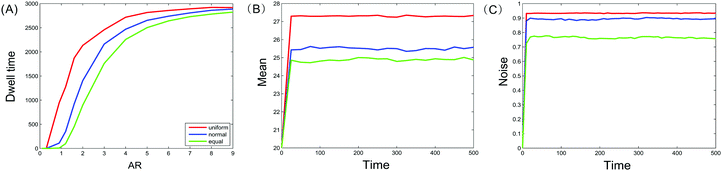
In general, dwell time measures how long a moving particle stays at some state. Since our model considers three different types of nucleosomes and assumes that their positions are random, we naturally examine how random positions affect the dwell times of these nucleosomes. Specifically, we will investigate and compare the influence of three kinds of distance distributions (two kinds of them are generated by uniform and normal distributions, the other kind is assumed as equidistance) on the total time that methylated and acetylated nucleosomes dwell at m = 0 or a = 0 (note that these states correspond to the limit case of bistability, i.e., the “strongest” bistability). The numerical results are shown in Fig. 3(A). In addition, we investigate and compare the influence of three kinds of distance distributions on the time evolutions of the mean methylated nucleosome and the noise in the methylated nucleosome, respectively, referring to Fig. 3(B) and (C).From Fig. 3(A), we first observe that the total times that methylated and acetylated nucleosomes dwell at m = 0 or a = 0 in three cases of distances are increasing functions of the allocation rate AR, and these functions are all convex, referring to Fig. 3(A). Second, the line corresponding to the case of uniform distribution is above the line corresponding to the case of normal distribution, which is above the line corresponding to the equidistance case. This implies that random nucleosome positions prolong the total resident time in contrast to equidistance. Furthermore, since the distances that follow uniform distribution are more uniformly distributed than those that follow normal distribution, the more “chaotic” the distances are, the longer is the time that the methylated or acetylated nucleosomes dwell at m = 0 or a = 0. These results are interesting on the one hand, and are in accordance with those obtained in the previous subsection on the other hand.
From Fig. 3(B), we observe that the line for the time evolution of the mean methylated nucleosome in the case of uniform distribution is above the line in the case of normal distribution, which is above the line in the equidistance case. This indicates that the more “chaotic” the distances between nucleosomes are, the larger is the mean number of methylated nucleosomes. Similarly, we observe from Fig. 3(C) that the line for the time evolution of the methylated nucleosome noise in the case of uniform distribution is above the line in the case of normal distribution, which is above the line in the equidistance case. This also indicates that the more “chaotic” the distances between nucleosomes are, the higher is the methylated nucleosome noise. By comparing Fig. 3(B) and (C), we find a counterintuitive phenomenon since the larger the mean is, the smaller the noise should be. In addition, we observe from Fig. 3(B) and (C) that there are sudden changes at the first time. Additionally, we point out that the results obtained by theoretical prediction [see eqn (10)] are in accordance with those obtained by numerical calculation (data are not shown) by noting b1,0 = 〈m〉 (see Section 3 for the definition of b1,0).
2.4 Effect of nucleosome positions on epigenetic landscape
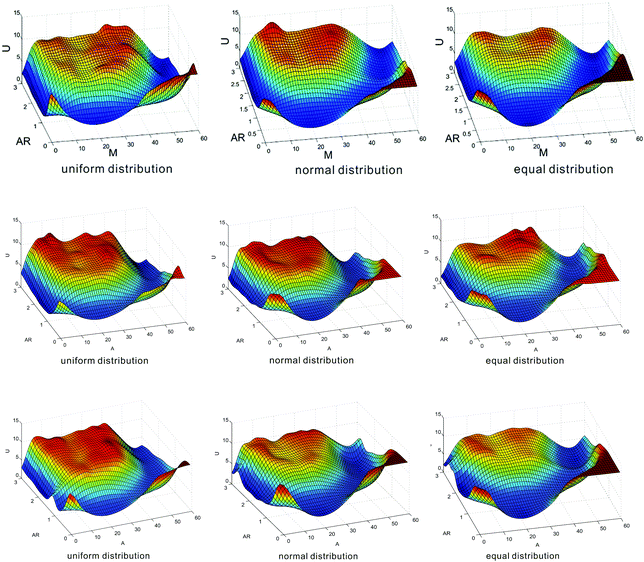
As an alternative description of heritable bistability, epigenetic landscape can give us a more intuitive understanding in contrast to the above descriptions. Such landscape describes that the state of a cell develops on some potential energy surface, and a state is maintained when the cell is caught at a particular valley for a long time. In this subsection, we investigate how nucleosome positions affect epigenetic landscape. For this, we consider three cases of nucleosome distances: two kinds of distances are generated by uniform and normal distributions and the other kind of distance is equal, and compare the numerical results on the effects of mean nucleosome distances on epigenetic landscapes in these three cases.We define epigenetic landscape function U(m) as U(m) = −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(m), where P(m) represents the steady-state probability distribution of the methylated nucleosome number. We plot the dependence relationship of U(m) on both m and AR, and thus obtain Fig. 4, where three cases of distance distribution are shown: nucleosome distances of one kind follow uniform distribution, nucleosome distances of another kind follow normal distribution, and nucleosome distances of the other kind are equidistance. In Fig. 4, the deep blue area corresponds to low values of epigenetic landscape whereas the red area to high values. These three kinds of nucleosome distances can result in transitions from unimodal to bimodal peaks. For example, if the mean distance is set at d = 10 (in unit dp) (corresponding to the first row of Fig. 4), then the transition from the navy blue area to the light blue area (i.e., the transition from monostability to bistability) takes place at AR ≈ 0.5 for uniform distribution, at AR ≈ 0.9 for normal distribution, and at AR ≈ 1.2 for equidistance, indicating that the order for the easy occurrence of bistability is from the uniform distribution of distances to the normal distribution of distances and to equidistance. Similar phenomena exhibit in the case of acetylation, referring to the third row of Fig. 4 from which we observe that the shape of epigenetic landscape is basically similar to that in the case of methylation. These observations further verify from the view point of epigenetic landscape that random nucleosome positions result in heritable bistability more easily than equidistance on the one hand, and the more “chaotic” the nucleosome distances, the better (or the more robust) the bistability on the other hand.
P(m), where P(m) represents the steady-state probability distribution of the methylated nucleosome number. We plot the dependence relationship of U(m) on both m and AR, and thus obtain Fig. 4, where three cases of distance distribution are shown: nucleosome distances of one kind follow uniform distribution, nucleosome distances of another kind follow normal distribution, and nucleosome distances of the other kind are equidistance. In Fig. 4, the deep blue area corresponds to low values of epigenetic landscape whereas the red area to high values. These three kinds of nucleosome distances can result in transitions from unimodal to bimodal peaks. For example, if the mean distance is set at d = 10 (in unit dp) (corresponding to the first row of Fig. 4), then the transition from the navy blue area to the light blue area (i.e., the transition from monostability to bistability) takes place at AR ≈ 0.5 for uniform distribution, at AR ≈ 0.9 for normal distribution, and at AR ≈ 1.2 for equidistance, indicating that the order for the easy occurrence of bistability is from the uniform distribution of distances to the normal distribution of distances and to equidistance. Similar phenomena exhibit in the case of acetylation, referring to the third row of Fig. 4 from which we observe that the shape of epigenetic landscape is basically similar to that in the case of methylation. These observations further verify from the view point of epigenetic landscape that random nucleosome positions result in heritable bistability more easily than equidistance on the one hand, and the more “chaotic” the nucleosome distances, the better (or the more robust) the bistability on the other hand.
We also investigate the effects of mean nucleosome distances on epigenetic landscape. Here, we show only a set of numerical results in the second row of Fig. 4, where the mean distance is set as d = 15. We observe that the transition from monostability to bistability takes place at AR ≈ 1.1 for uniform distribution, at AR ≈ 1.6 for normal distribution, and at AR ≈ 2.0 for equidistance. By comparing the diagrams in the first row and those in the second row of Fig. 4, we find that the mean nucleosome distances leading to bistability do not remarkably change the shape of the epigenetic landscape but different distance distributions result in different occurrences of bistability.
3. Methods
We first make assumptions for nucleosomes and their modification events, then establish a chemical master equation that incorporates the effect of (deterministic or random) nucleosome positions and use the binomial moment method that we previously developed46 to solve this master equation, and finally perform numerical calculations to show the influence of nucleosomes' positioning on heritable bistability.3.1 Hypotheses based on experimental evidence
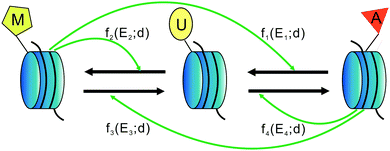
First, we assume that there are only three types of nucleosomes: unmodified, methylated, and acetylated (called U-type, M-type and A-type nucleosomes in this paper), though other types of nucleosomes are possible. These three distinct nucleosome types may be defined by different kinds of modifications. In addition, although nucleosomes carry two copies of each histone, here we ignore the role of hetero-modified nucleosomes. It should be pointed out that the total number of nucleosomes is not known exactly, since no experimental evidence allows us to estimate this number. In Section 2.1 of Results, we have shown how the total nucleosome number impacts heritable bistability.Second, we hypothesize that there are two different kinds of conversions: one is the so-called “recruited conversion”, namely, nucleosomes are actively interconverted by modifying and demodifying enzymes (HMTs, HDACs, HDMs, and HATs) that are recruited by the modified nucleosomes. It is this recruitment that forms the positive feedback necessary for the generation of heritable bistability. For clarity, we include four symmetrical positive feedback loops in the schematic shown in Fig. 5 and describe all active recruited processes in terms of one-rate parameter k+ that is absorbed in some functions fi. The other is the so-called “noisy conversion”, that is, nucleosomes are interconverted in a recruitment-independent manner. This “noise” in the system can be considered as due primarily to the activity of modifying enzymes that are either free or attached to nucleosomes beyond the region boundaries. In the absence of further information and for analysis simplicity, we also conclude four possible noise conversions in Fig. 5 with one-rate parameter k− that is also absorbed in some functions fi. We find that it is the ratio of the recruited and noise conversions that is critical in the system, so an independent noise parameter is not needed.
Third, we suppose that the nucleosome positions are random. In fact, no experimental evidence supports that they are fixed. In ref. 2 and 47 the authors theoretically studied how heritable bistability is generated in a simplified model, but they ignored the effects of nucleosome positions. Small et al.41 described an experimental technique to determine nucleosome positioning in single cells by virtue of the ability of the nucleosome to protect DNA from methylation, and showed that nucleosome positioning has assignable impacts on gene expression.
Finally, we assume that the rates of interconversion reactions at each nucleosome across the DNA region are the same (that is, homogeneous) with regard to nucleosome positions, although heterogeneity exists possibly in some systems, e.g., in the Schizosaccharomyces pombe mating-type system.45 However, our model can easily incorporate such heterogeneity.
3.2 Quantifying the effect of nucleosome positions
Given N nucleosomes in total, i.e., m + u + a = N, where m, u and a represent the numbers of M-type, U-type and A-type nucleosomes, respectively, we assume that these nucleosomes are randomly distributed in a finite DNA line and their positions are ordered from 1 to N. We denote by d1 the distance of the first nucleosome position from the second nucleosome, by dN−1 the distance of the final nucleosome position from the N − 1 nucleosome, and by di the distance between the ith and the (i + 1)th nucleosomes, where i = 2, 3,…,N − 2. Furthermore, we assume that only the two nearest neighbors of a nucleosome in the middle impact the type of this nucleosome (from one type to another type) if the nucleosome is not located at the end, and that only one nucleosome (at both ends) impacts the nucleosome type otherwise.Now, we quantify how one nucleosome influences another nucleosome. For this, we introduce a quantifier (denoted by ω), which is a function of distances between nucleosomes. For every nucleosome located in the middle of the region, we use ωi = 1/(di−1)p + 1/(di)p with i = 2, 3,…,N − 1 to quantify how its two neighbors impact this nucleosome, whereas for two nucleosomes located at the boundary, we use ω1 = 1/(d1)p and ωN = 1/(dN)p to quantify this kind of impact, where p is a positive parameter (since this parameter does not influence our qualitative conclusion, we will set p = 1.5 in our analysis. See ref. 2 for a reason of this setting). In the case that all di are deterministic, we assume that they are equal and denote by d the common distance. In the case that the distances are random, we assume that they are generated through some distribution with the mean d. In this paper, we consider only two common distributions: uniform and normal. Note that the larger the distances are, the smaller is the influence, so this setting of distances is in accordance with intuition.
Next, we consider the total impact, which is defined as
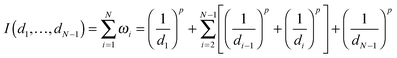 | (1) |
3.3 Mathematical model
Let U, M and A represent U-type, M-type, and A-type nucleosomes, respectively. According to the above hypotheses and for convenience of modeling, we list reactions for transitions between nucleosome types as follows: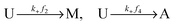 | (2a) |
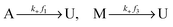 | (2b) |
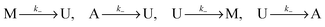 | (3) |
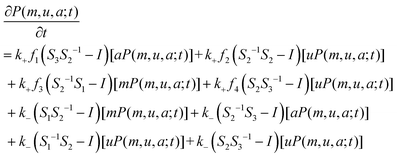 | (4) |
When writing eqn (4) based on reactions, we do not consider the constraint on the total number of nucleosomes. If this total number is fixed, i.e., if m + u + a = N, then we can eliminate a variable from eqn (4). It should be noted that in some particular cases or under specific constraints (in fact, no experimental evidence supports that all the reactions listed in eqn (2) and (3) take place simultaneously. Rather, it is possible that only parts of them occur), eqn (4) can be reduced to simpler forms. Moreover, the reduced equations can have particular meanings, e.g., if only the reactions in eqn (2a) occur (this is equal to the case in which enzymes HDAC and HDM do not exist or equally we set f1 = 0 and f3 = 0), this corresponds to the modification process (the corresponding model is called the modification model); if only the reactions in eqn (2b) occur (this is equal to the case in which enzymes HMT and HAT do not exist or equally we set f2 = 0 and f4 = 0), this corresponds to the demodification process (the corresponding model is called the demodification model); if they occur simultaneously, the corresponding model is called the standard model.
Without loss of generality and by combining the above setting of nucleosome positions, we assume that transition rates for the four recruited conversions are given by f1 = f2 = mωi, and f3 = f4 = aωi, where ωi represents the distance impact factor (see Section 2.2) and can be generated by a distribution, i = 1,…,N. When one single ωi is used to quantify the distance influence on nucleosomes, we call the corresponding case a distance-based pathway for convenience. Thus, we have N such pathways in total. For the ith pathway, we denote by Pi(m,u,a;t) the corresponding joint probability distribution governed by eqn (4).
We introduce another impact factor, which is defined as the ratio of the one-rate parameter for recruited conversion over that for noisy conversion, that is, AR = k+/k−, to describe the noise in the system. For convenience, we call this factor the allocation rate, which can be used to convey the relative activities of the positive-feedback and noise-conversion processes. It should be noted that for a given AR, the actual ratio between the recruited and noisy conversions may vary, depending on the numbers of the three nucleosome types. Since there are no experimental data to estimate the value of AR, we let it change in a large range, e.g., 0 < AR < 100, so that the results to be obtained can include various biological possibilities.
Finally, the constraint m + u + a = N can eliminate one variable from eqn (4), resulting in
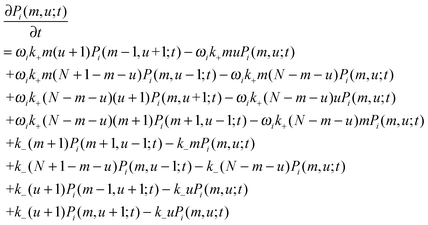 | (5) |
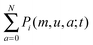 or the marginal distribution of Pi(m,u,a;t).
or the marginal distribution of Pi(m,u,a;t).
3.4 Solving the master equation using a binomial moment method
In general, analytically solving a master equation like eqn (5) is very difficult since there is no efficient method available. Here, we introduce the binomial moment approach that we developed previously,46 to solve eqn (5). In general, binomial moments of a distribution are defined as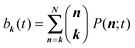 | (6) |
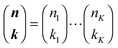 with
with 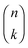 being a common binomial coefficient. Black letters represent a vector or matrix hereafter. In our case, the corresponding symbols in eqn (6) become n = (m,u), k = (k1,k2) and N = (N,N,N). With this definition, eqn (5) can be transformed into the following so-called binomial moment equations
being a common binomial coefficient. Black letters represent a vector or matrix hereafter. In our case, the corresponding symbols in eqn (6) become n = (m,u), k = (k1,k2) and N = (N,N,N). With this definition, eqn (5) can be transformed into the following so-called binomial moment equations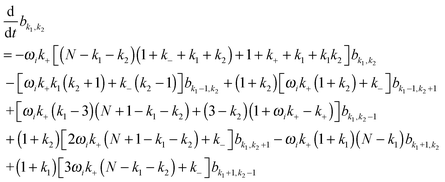 | (7) |
Once all binomial moments bk(t) are found either analytically or numerically, we can reconstruct the distribution using these known bk(t). In fact, we have the following general reconstruction formula:
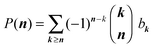 | (8) |
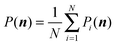 | (9) |
In addition, we can calculate the noise in nucleosomes according to the first two binomial moments, where the noise is defined as the ratio of the variance over the square of the mean. For example, for the methylated nucleosome M, the corresponding noise, denoted as ηM, can be expressed as
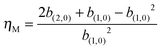 | (10) |
Similarly, we can give formulae for calculating the noise in the number of unmodified nucleosomes.
3.5 Calculating epigenetic landscape functions
First, we can reconstruct the steady-state joint distribution P(m,u) of u (representing the number of unmodified nucleosomes) and m (representing the number of methylated nucleosomes) using steady-state binomial moments obtained from eqn (7).Then, we calculate the potential landscape function Q(m,u) that is defined as Q(m,u) = −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(m,u) using P(m,u) obtained by the binomial moment method.
P(m,u) using P(m,u) obtained by the binomial moment method.
Third, we calculate U(m) = −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(m), where P(m) is the marginal distribution of P(m,u). Note that the landscape function U(m) should depend on the parameter AR (representing the allocation rate between enzymes that regulate transitions between different types of nucleosomes) since P(m,u) and further P(m) are all functions of AR.
P(m), where P(m) is the marginal distribution of P(m,u). Note that the landscape function U(m) should depend on the parameter AR (representing the allocation rate between enzymes that regulate transitions between different types of nucleosomes) since P(m,u) and further P(m) are all functions of AR.
4. Discussion
As the basic unit of chromatin, nucleosomes play an important role in the control of gene expression. Nucleosome positions have generally been determined by examining bulk populations of cells and then correlating with the overall gene expression. Apparently, this measurement method cannot tell us the exact positions of nucleosomes. In particular, because of dynamic modification by various enzymes, nucleosome positions should not be fixed but may be randomly partitioned in a finite region. On the other hand, chromosomal regions can adopt stable and heritable alternative states resulting in bistable gene expression without the accompanying changes in the DNA sequence. These heritable states must be both stable over time and inherited through cell division. Until now, it is unclear how heritable bistability is correlated with nucleosome positions. In this paper, we have developed a stochastic and mechanic model for dynamic nucleosome modification, which is mathematically described using a chemical master equation. This model considers several key factors associated with epigenetic cellular memory, such as conversions between recruited enzymes, positive feedback due to the recruitment of enzymes, different types of nucleosomes, and nucleosome positions. Interestingly, we have found that in contrast to the deterministic positions of nucleosomes, the random positions can enhance heritable bistability, and can even induce transitions from unimodality to bistability or vice versa. This finding is opposite to the previous view, namely that equal positioning of nucleosomes facilitates heritable bistability in contrast to random positioning.2The mechanism of how bistability is generated has been extensively investigated, especially in prokaryotes. Bistability in higher eukaryotes has also been obtained using, e.g., chimeric proteins derived from the viral protein VP16,49 but not using the endogenous genes under the physiological conditions considered here. The increasing knowledge about epigenetic mechanisms disagrees with a bistable model. In fact, extensive combinatorial possibilities of the dozens of histone modifications per nucleosome may produce very complex and fine-tuned outputs, very far away from the bistable model. Therefore, it is possible that random nucleosomal positioning enhances heritable epigenetic bistability, as shown in this paper. However, this random positioning can be deleterious for multistability situations which fit better with the behavior of endogenous genes in eukaryotes under physiological conditions and further investigations are needed.
In contrast to the existing related models, our proposed stochastic model for dynamic nucleosome modification has advantages in many aspects. We expect that this model can be extended relatively easily to include other nucleosome modification schemes, for example the 3-state model,50–52 and that our model can also be extended in a straightforward manner to include more than 3 types of nucleosomes, and the spatial positioning of nucleosomes,53–55 as well as heterochromatin resulting from the interaction between, e.g., histone H3/H4 N-termini and SIR3/SIR4 proteins.56
Our binomial moment approach is more powerful than the mean field approach57 in the sense that it allows one to explore probability distributions as well as epigenetic landscapes.58–61 The method can also deal with cases where the epigenetic system does not conform to a potential energy surface. For example, noise associated with cell divisions can be included in systems with double negative feedback between repressors, such as the CI-Cro feedback loop in the lysis-lysogeny switch of phage lambda.62
Our results are consistent with recent observations in mammalian cells in which increased cell division rates accelerated stochastic transitions between epigenetic states.63 This is because in our case, such acceleration means that the external impact (e.g., from random positioning of nucleosomes) is increased, leading to the enhancement of heritable bistability.
Finally, we argue two points: (1) our model considers the fact that the impact of nucleosome positions enters the model in a linear fashion, but nonlinearly entering manners are possible in real cases; (2) if more than 3 types of nucleosomes are considered, then multimodality may take place, depending on the cooperative role of nucleosome positions and the unique parameter—the allocation rate between enzymes regulating transitions between different types of nucleosomes.
Author contributions
Conceived and designed the experiments: HL, JJ, TQ and TS. Analyzed the data: HL and TQ. Wrote the paper: TS and HL.Acknowledgements
This work was supported by grants 91530320, 91230204 and 11475273 from the Natural Science Foundation of P. R. China and grant 2014CB964703 from the Science and Technology Department, P. R. China.References
- L. Bintu, J. Yong, Y. E. Antebi, K. Mccue, Y. Kazuki, N. Uno, M. Oshimura and M. B. Elowitz, Science, 2016, 351, 720–724 Search PubMed.
- I. B. Dodd, M. A. Micheelsen, K. Sneppen and G. Thon, Cell, 2007, 129, 813–822 CrossRef CAS PubMed.
- B. T. Wakimoto, Cell, 1998, 93, 321–324 Search PubMed.
- J. Veening, W. K. Smits and O. P. Kuipers, Annu. Rev. Microbiol., 2008, 62, 193–210 CrossRef CAS PubMed.
- A. J. E. Gordon, J. A. Halliday, M. D. Blankschien, P. A. Burns, F. Yatagai and C. Herman, PLoS Biol., 2009, 7, e1000044 Search PubMed.
- D. M. Bond and D. C. Baulcombe, Trends Cell Biol., 2014, 24, 100–107 Search PubMed.
- R. Jaenisch and A. Bird, Nat. Genet., 2003, 33, 245–254 Search PubMed.
- D. Cortázar, C. Kunz, J. Selfridge, T. Lettieri, Y. Saito, E. MacDougall, A. Wirz, D. Schuermann, A. L. Jacobs, F. Siegrist, R. Steinacher, J. Jiricny, A. Bird and P. Schär, Nature, 2011, 470, 419–423 Search PubMed.
- R. Lund, E. Närvä and R. Lahesmaa, Nat. Rev. Genet., 2012, 13, 732–744 Search PubMed.
- P. Sarkies and J. E. Sale, Trends Genet., 2012, 28, 118–127 Search PubMed.
- Z. X. Chen and A. D. Riggs, Biochem. Cell Biol., 2005, 83, 438–448 Search PubMed.
- A. Meissner, T. S. Mikkelsen, H. Gu, M. Wernig, J. Hanna, A. Sivachenko, X. L. Zhang, B. E. Bernstein, C. Nusbaum, D. B. Jaffe, A. Gnirke, R. Jaenisch and E. S. Lander, Nature, 2008, 454, 766–770 Search PubMed.
- P. A. Jones, Nat. Rev. Genet., 2012, 13, 484–492 Search PubMed.
- K. D. Hansen, W. Timp, H. C. Bravo, S. Sabunciyan, B. Langmead, O. G. Mcdonald, B. Wen, H. Wu, Y. Liu, D. Diep, E. Briem, K. Zhang, R. A. Irizarry and A. P. Feinberg, Nat. Genet., 2011, 43, 768–775 Search PubMed.
- R. Thomas and M. Kaufman, Chaos, 2001, 11, 170–179 Search PubMed.
- J. E. Jr. Ferrell, Curr. Opin. Cell Biol., 2002, 14, 140–148 Search PubMed.
- W. K. Smits, O. P. Kuipers and J. W. Veening, Nat. Rev. Microbiol., 2006, 4, 259–271 Search PubMed.
- J. M. Vilar, C. C. Guet and S. Leibler, J. Cell Biol., 2003, 161, 471–476 Search PubMed.
- A. B. Oppenheim, O. Kobiler, J. Stavans, D. L. Court and S. Adhya, Annu. Rev. Genet., 2005, 39, 409–429 Search PubMed.
- K. L. Arney, S. Erhardt, R. A. Drewell and M. A. Surani, Int. J. Dev. Biol., 2001, 45, 533–540 Search PubMed.
- R. J. Klose, E. M. Kallin and Y. Zhang, Nat. Rev. Genet., 2006, 7, 715–727 Search PubMed.
- R. H. Jacobson, A. G. Ladurner, D. S. King and R. Tjian, Science, 2000, 288, 1422–1425 Search PubMed.
- D. J. Owen, P. Ornaghi, J. Yang, N. Lowe, P. R. Evans, P. Ballario, D. Neuhaus, P. Filetici and A. Travers, EMBO J., 2000, 19, 6141–6149 Search PubMed.
- L. N. Rusche and J. Rine, Genes Dev., 2001, 15, 955–967 Search PubMed.
- G. Schotta, A. Ebert, V. Krauss, A. Fischer, J. Hoffmann, S. Rea, T. Jenuwein, R. Dorn and G. Reuter, EMBO J., 2002, 21, 1121–1131 Search PubMed.
- A. T. Annunziato, J. Biol. Chem., 2005, 280, 12065–12068 Search PubMed.
- P. M. J. Burgers, J. Biol. Chem., 2009, 284, 4041–4045 Search PubMed.
- B. M. Wendel, C. T. Courcelle and J. Courcelle, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 16454–16459 Search PubMed.
- T. C. Wu and M. Lichten, Science, 1994, 263, 515–518 Search PubMed.
- Z. Zhang, K. Shibahara and B. Stillman, Nature, 2000, 408, 221–225 Search PubMed.
- J. R. Lipford and S. P. Bell, Mol. Cell, 2001, 7, 21–30 CrossRef CAS PubMed.
- Y. Field, Y. Fondufemittendorf, I. K. Moore, P. A. Mieczkowski, N. Kaplan, Y. Lubling, J. D. Lieb, J. Widom and E. Segal, Nat. Genet., 2009, 41, 438–445 Search PubMed.
- F. H. Lam, D. J. Steger and E. K. O'Shea, Nature, 2008, 453, 246–250 Search PubMed.
- M. Han and M. Grunstein, Cell, 1988, 55, 1137–1145 Search PubMed.
- T. Wasson and A. J. Hartemink, Genome Res., 2009, 19, 2101–2112 Search PubMed.
- D. Aran, S. Sabato and A. Hellman, Genome Biol., 2013, 14, R21 Search PubMed.
- L. Elnitski, R. C. Hardison, J. Li, S. Yang, D. L. Kolbe, P. Eswara, M. J. Oconnor, S. Schwartz, W. Miller and F. Chiaromonte, Genome Res., 2003, 13, 64–72 Search PubMed.
- B. R. Cairns, Nature, 2009, 461, 193–198 Search PubMed.
- C. R. Clapier and B. R. Cairns, Annu. Rev. Biochem., 2009, 78, 273–304 Search PubMed.
- C. Alen, N. A. Kent, H. S. Jones, J. M. Osullivan, A. Aranda and N. J. Proudfoot, Mol. Cell, 2002, 10, 1441–1452 Search PubMed.
- E. C. Small, L. Q. Xi, J. P. Wang, J. Widom and J. D. Licht, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E2462–E2471 Search PubMed.
- L. Ringrose, S. Chabanis, P. Angrand, C. P. Woodroofe and A. F. Stewart, EMBO J., 1999, 18, 6630–6641 Search PubMed.
- K. Rippe, Trends Biochem. Sci., 2001, 26, 733–740 Search PubMed.
- J. Lewis, J. M. Slack and L. Wolpert, J. Theor. Biol., 1977, 65, 579–590 Search PubMed.
- S. I. Grewal and S. C. Elgin, Curr. Opin. Genet. Dev., 2002, 12, 178–187 Search PubMed.
- J. J. Zhang and T. S. Zhou, Biophys. J., 2014, 106, 479–488 Search PubMed.
- M. A. Micheelsen, N. Mitarai, K. Sneppen and I. B. Dodd, Phys. Biol., 2010, 7, 026010 Search PubMed.
- J. J. Zhang, Q. Nie and T. S. Zhou, J. Chem. Phys., 2016, 144(19), 018620 Search PubMed.
- K. Nalley, S. A. Johnston and T. Kodadek, Proteolytic turnover of the Gal4 transcription factor is not required for function in vivo, Nature, 2006, 442, 1054–1056 Search PubMed.
- O. Bar-Nur, H. A. Russ, S. Efrat and N. Benvenisty, Cell Stem Cell, 2011, 9, 17–23 Search PubMed.
- M. B. Zerihun, C. Vaillant and D. Jost, Phys. Biol., 2015, 12, 026007 Search PubMed.
- D. Jost, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 010701 Search PubMed.
- B. R. Zhou, H. Q. Feng, H. Kato, L. Dai, Y. D. Yang, Y. Q. Zhou and Y. W. Bai, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19390–19395 Search PubMed.
- J. Z. Kelemen, P. Ratna, S. Scherrer and A. Becskei, PLoS Biol., 2010, 8, e1000332 Search PubMed.
- T. Sexton, E. Yaffe, E. Kenigsberg, F. Bantignies, B. Leblanc, M. Hoichman, H. Parrinello, A. Tanay and G. Cavalli, Cell, 2012, 148, 458–472 Search PubMed.
- A. Hecht, T. Laroche, S. Strahlbolsinger, S. M. Gasser and M. Grunstein, Cell, 1995, 80, 583–592 Search PubMed.
- D. Davidrus, S. Mukhopadhyay, J. L. Lebowitz and A. M. Sengupta, J. Theor. Biol., 2009, 258, 112–120 Search PubMed.
- J. E. Jr. Ferrell, Curr. Biol., 2012, 22, R458–R466 Search PubMed.
- A. Godino, S. Jayanthi and J. L. Cadet, Epigenetics, 2015, 10, 574–580 Search PubMed.
- A. D. Goldberg, C. D. Allis and E. Bernstein, Cell, 2007, 128, 635–638 Search PubMed.
- M. P. Washburn, Y. Zhao and B. A. Garcia, Mol. Cell. Proteomics, 2016, 15, 753–754 Search PubMed.
- E. Aurell and K. Sneppen, Phys. Rev. Lett., 2002, 88, 048101 Search PubMed.
- J. Hanna, K. Saha, B. Pando, J. van. Zon, C. J. Lengner, M. P. Creyghton, A. van Oudenaarden and R. Jaenisch, Nature, 2009, 462, 595–601 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |