Open Access Article
Open Access ArticleProbing oligomerization of amyloid beta peptide in silico†
L.
Dorosh
 ab and
M.
Stepanova‡
*abc
ab and
M.
Stepanova‡
*abc
aDepartment of Electrical and Computer Engineering, University of Alberta, Edmonton, Alberta, Canada. E-mail: ms1@ualberta.ca; mariastepanova@missouristate.edu
bNational Research Council of Canada, Edmonton, Alberta, Canada
cDepartment of Physics, Astronomy, and Materials Science, Missouri State University, Springfield, MO, USA
First published on 4th November 2016
Abstract
Aggregation of amyloid β (Aβ) peptide is implicated in fatal Alzheimer's disease, for which no cure is available. Understanding the mechanisms responsible for this aggregation is required in order for therapies to be developed. In an effort to better understand the molecular mechanisms involved in spontaneous aggregation of Aβ peptide, extensive molecular dynamics simulations are reported, and the results are analyzed through a combination of structural biology tools and a novel essential collective dynamics method. Several model systems composed of ten or twelve Aβ17–42 chains in water are investigated, and the influence of metal ions is probed. The results suggest that Aβ monomers tend to aggregate into stable globular-like oligomers with 13–23% of β-sheet content. Two stages of oligomer formation have been identified: quick collapse within the first 40 ns of the simulation, characterized by a decrease in inter-chain separation and build-up of β-sheets, and the subsequent slow relaxation of the oligomer structure. The resulting oligomers comprise a stable, coherently moving sub-aggregate of 6–9 strongly inter-correlated chains. Cu2+ and Fe2+ ions have been found to develop coordination bonds with carboxylate groups of E22, D23 and A42, which remain stable during 200 ns simulations. The presence of Fe2+, and particularly Cu2+ ions, in negatively charged cavities has been found to cause significant changes in the structure and dynamics of the oligomers. The results indicate, in particular, that formation of non-fibrillar oligomers might be involved in early template-free aggregation of Aβ17–42 monomers, with charged species such as Cu2+ or Fe2+ ions playing an important role.
Introduction
The unique ability of proteins to adopt different conformations and to selectively and tightly bind other molecules determines their diverse functions, but the same ability can also cause protein misfolding and aggregation. Toxic protein aggregates have been implicated in amyloidosis diseases, including Alzheimer's disease (AD), Parkinson's disease (PD), amyotrophic lateral sclerosis (ALS), and transmissible spongiform encephalopathies (TSE).1,2 Since the plaques and fibrils of the amyloid β (Aβ) peptide were found in the brains of patients suffering from Alzheimer's disease, the amyloid (cascade) hypothesis emerged in the early 90s stating that the Aβ peptide fibrils are responsible for the pathology of AD.3 However, subsequent evidence was collected towards an alternative toxic oligomer hypothesis suggesting that smaller, soluble amyloid oligomers known as “seeds” or toxic pre-fibrillar aggregates, rather than mature plaques and fibrils, determine neurodegeneration in AD and other protein misfolding diseases.4–8 For example, polyclonal antibodies were found to suppress the toxicity of many soluble oligomers from different proteins (indicating common structural features), but they did not bind to mature fibrils.7 Recent experimental studies indicate in particular that Aβ42 oligomers, rather than fibrils, bind to lipid membranes causing damage to them.9 Experiments on misfolded Aβ peptide, α-synuclein, and transthyretin also suggest that amyloidogenic cytotoxicity may share a common mechanism unrelated to the specific sequence.1 Structure-based screening of compounds that bind to amyloid fibers (BAFs) allowed the finding of BAFs, which decrease Aβ peptide toxicity but not its fibrillation propensity.10 Another hypothesis suggests that plaques may play a role in the trapping of toxic oligomers converting them into a more inert form.11,12 This in turn suggests that a dynamic equilibrium may exist in the transition state between the two species, highlighting the importance of understanding detailed molecular mechanisms behind their interactions at various stages of aggregation.Specifically for Aβ peptide, monomers are found in a soluble form and are largely unstructured, with a partial α-helical13 or β-strand14 structure. They are believed to acquire β content when they aggregate.13 The term oligomer is used to describe many aggregated species, from low-molecular-weight (less than eight units) to high-molecular-weight species of various symmetries. The term protofibril usually denotes a β-sheet rich heterogeneous kinetic intermediate arising before a mature fibril structure is formed. Stable entities, which serve as nuclei for aggregation when introduced to a solution containing Aβ monomers, are known as seeds.15
Two types of Aβ peptide fragments, known as P3 (Aβ17–40/42) and P4 (Aβ1–40/42), can be derived from the amyloid precursor protein (APP) by two mutually exclusive proteolytic pathways via cleavage by α-/γ- and β-/γ-secretases, respectively.16 These fragments are believed to form small and mobile neurotoxic oligomers. Other fragments, such as Aβ1–16 or Aβ25–35, have also been studied, however only P3 and P4 peptides have been associated with neuroinflammation.16 Neurotoxic effects of P3 activated through a specific signal transduction pathway were also reported.17 Although P3 was absent or sparse in aged non-AD brains, insoluble diffuse deposits of P3 were found in nervous and vesicular systems associated with AD pathology.18,19 Diffuse non-fibrillar deposits consisting mainly of Aβ17–42 were also found in the gray and white matter and leptomeningeal/cortical vessels of AD patients after vaccination against fibrillar Aβ42.20 It was concluded that solubilized Aβ peptides from such deposits may ultimately have cascading toxic effects on cerebrovascular, gray and white matter tissues.20 As a potential mechanism, the membrane-destabilising properties of the C-terminal domain of Aβ peptide have been hypothesized.21
In the cerebrospinal fluid of non-demented controls about one-half of the Aβ end at amino acid 40, 16% end at amino acid 38, and 10% end at amino acid 42.22 Increased production rates of Aβ42 in comparison to Aβ40 have been found in AD patients, and it is therefore associated with AD synaptic changes.23 Due to the more exposed hydrophobic residues of Aβ1–42, this construct tends to aggregate faster than Aβ1–40.24 Also, an increased proportion of Aβ42:Aβ40 has been shown to enhance synaptotoxicity.25 Aβ1–42 dimers, tetramers, hexamers, and dodecamers have been detected in ion mobility spectroscopy-MS in vitro experiments.26,27 Multiples of Aβ1–42 hexamers have also been observed.27,28 A recent study of the early stages of aggregation29 suggests that monomeric Aβ1–40 and Aβ1–42 peptides tend to coalesce into largely unstructured globules from 15 nm in diameter, which slowly grow larger until a sharp transition occurs to nucleation and growth of β-rich fibrillar structures. Formation of the fibrils was found to be faster in the Aβ1–42 peptide than in the Aβ1–40 peptide. Cell toxicity tests have indicated that the most toxic species is formed during the early stage of aggregation when unstructured globules are observed, leading to a hypothesis that the globules themselves represent the toxic species.29 A very recent high-resolution atomic force microscopy study showed specifically that soluble oligomers of Aβ42, rather than Aβ40, quickly become dominant oligomers with the propensity of seed and protofibrillar structure formation in aggregation experiments in vitro.30 Also, it has been demonstrated31 that Aβ fragments 24–34, 25–35, and 26–36 alone may form oligomeric structures resembling cylinders and β-barrels.
It is believed that toxic Aβ oligomers can interact with cell membranes, cause oxidative stress, and increase the amount of transition metal ions, which in turn may lead to cell death.7,32 Since metal ions have been found in high concentrations in the senile plaque core and rim in AD brains,33–35 the Aβ and APP were even identified as Al/Cu/Zn/Fe metalloproteins. Three N-terminal histidine residues H6, H13, and H14, and a tyrosine residue Y10 have been identified as the main high-affinity Cu2+ coordinating residues.36–41 However, deprotonated main-chain amide groups or carboxylate groups D1, E3, D7, E11, E22, and D23, as well as methionine M35, are also expected to play a role in the transient coordination of metal ions.36–38,41 Studies suggest that a large region involving the N-terminal and the adjacent area36 might be involved in the coordination of Cu2+ ions, whereas Zn2+ might interact with the central region around residues 26–28.39,42 Experimental studies on the possible role of metal ions in the aggregation are also in the pipeline. Metal chelation was shown to dissolve amyloid aggregates, thereby reversing Aβ aggregation.34 Moreover, rapid acceleration of Aβ oligomer aggregation dynamics was observed in experiments in the presence of Zn and Al, whereas Cu and Fe showed limited propensity for Aβ aggregation.33–35,43 Cu and Zn prevented Aβ from forming fibrils,44 however Zn promoted the formation of small globular aggregates, while Cu produced poorly-structured micro-aggregates.45 However, a different research group46 found that Cu inhibits Aβ aggregation by competing with Zn for histidine residues.
Broader aspects of electrostatic, hydrophobic, and other non-covalent interactions on Aβ aggregation have been studied extensively.47–50 Protofibril formation is believed to be driven by hydrophobic, aromatic and steric interactions, with folds 21–30 playing an important role. Strong evidence that aromatic interactions from the phenylalanine and tyrosine rings play an important role in amyloid formation has been reported.51 These interactions are complemented by electrostatic interactions, particularly the hydrogen bond V21–K28 and the salt bridge E22/23–K28. A recent four-dimensional electron microscopy study52 indicates that forces responsible for amyloid stability are highly anisotropic, and that the inter-backbone hydrogen bonding network within β-sheets is 20 times more rigid than side-chain interactions.
Overall, the body of literature addressing the Aβ peptide structure, aggregation, and associated toxicity has increased exponentially over the last two decades, APP thereby becoming “the most studied protein in the 21st century”.53 However, despite the significant progress, detailed mechanisms of toxic oligomer (seed) formation, and their exact structure remain elusive. Complementary to the experimental studies, molecular dynamics (MD) simulations and other computational models provide important insights into the detailed atomistic mechanisms of Aβ peptide misfolding, aggregation, and fibril growth.50,54–57 Thus, many computational works study the structure and dynamics of Aβ peptide monomers58–63 using disordered amyloid peptide constructs and/or known NMR structures of insoluble fibril fragments as the initial structure models. The early stages of oligomerization were also investigated, particularly addressing dimers62,64–66 and other small size oligomers.49,67–72 Such computational studies allowed identification of the dock and lock mechanism of fibril formation, U-shape topology of β-sheet-turn-β-sheet motif of the peptide, clarification of the role of water in aggregation, elucidation into how Aβ peptide protofibrils might be solvated, and what may affect their stability. Recently, Aβ dodecamers have been constructed from monomers utilizing a docking algorithm, and their structural evolution has been analyzed.73 After 4 ns of MD simulations, the dodecameric Aβ complexes have been found to be stable within the hydrophobic core, albeit not entirely ordered.73 The mechanisms of Aβ oligomer interaction with cell membranes are not yet obvious, however they might play a role due to their ability to form membrane pores (ion channels). Simulations74 have shown that Aβ17–42 peptides can indeed form ion channels in the lipid bilayer, and that these ion channels might be blocked by Zn2+ ions. Simulation studies also indicate75 that binding of Zn2+ ions to individual Aβ peptide molecules may significantly change their conformational distribution. Binding of Cu2+ ions by the monomeric Aβ peptide has been investigated using MD simulations as well.76 The study suggests that binding of Cu2+ ions in the H13–H14 region of Aβ1–42 in solution may be accompanied by coordination of the ions by carboxyl groups D1, E3, and E22 via electrostatic attraction.
Molecular dynamics sampling of conformational space for Aβ1–42 peptide oligomers is computationally expensive. In particular, all-atom simulations of Aβ multimers containing the flexible N-terminal region Aβ1–16 would exhibit a substantially slower aggregation process in comparison to shorter chains,54 urging the development and application of various cost-reduction methods, or using shorter fragments of the peptide. Some works use coarse-grained models, such as the discrete MD with a four bead peptide model.24,77–79 In a recent discrete dynamics study utilizing a novel coarse-grained force field PRIME20, several pathways of Aβ17–42 aggregation from disordered oligomers to protofilaments have been identified, including U-shaped, O-shaped and S-shaped “seeds”.80 However, application of discrete dynamics was shown to strongly enhance hydrogen bonding in proteins, resulting in overestimated β-content in comparison to fully atomistic MD.62 Other works have applied an implicit solvent coarse grained model with an optimized potential for an efficient structure prediction (OPEP) force field, when the backbone is described in all-atom representation, and side-chains are represented by centroids with different van-der-Waals radii associated.81 To speed up folding simulations, high-temperature MD simulations have also been used.82,83 Other strategies for enhanced sampling include replica exchange MD (REMD),84 Hamiltonian temperature REMD,85 meta-dynamics86 and bias-exchange meta-dynamics.87,88 These methods allow accelerated sampling, study of the folding and aggregation, and reduction in the size of the studied systems. However, this is achieved at the expense of lower resolution and a strong dependence on the choice of force fields89 raising questions on the reliability of the predictions utilizing accelerated MD sampling, considering the demonstrated importance of the force fields in MD simulations.56,90,91
An alternative approach uses partially misfolded constructs as initial structures for all-atom explicit-water MD simulations. In the absence of reliable structural information on the oligomeric/seed state, the usage of existing Aβ peptide protofilaments allows one to address the dynamics of β-rich constructs directly without long simulations of the transition to such constructs. In particular, several published MD simulations49,67,92–94 used a hydrogen/deuterium-exchange NMR-derived structure 2BEG of the Aβ17–42 pentamer or its individual chains92 as the initial model. The model helped to investigate template induced conformational changes,93 stability of annular intermediates,94 or fibril elongation.95 Broader aspects of template-assisted aggregation have been addressed in recent review articles50,54,55 and references therein. A slight limitation of starting simulations from an experimentally derived fibril fragment structure is the focus on the existing in-register parallel β-sheet aggregates which usually do not disintegrate spontaneously, neither do they form alternative anti-parallel constructs during MD simulations. Nevertheless, extensive simulations of protofilament-derived constructs in an explicit solvent provide valuable information on the stability of these structures, and allow prediction of new rotated forms96 which can be seen as potential candidates for Aβ seed structures. Recently, new Aβ peptide structures were published, such as the octamer of D23N mutant Aβ17–40 fragments,48 the Aβ1–40 nonameric fibril fragment,97 and the Aβ1–42 peptide dimers with face-to-face packing.98 Computational modeling studies using these new constructs can be expected to provide further insights into the molecular dynamics of Aβ peptide aggregates. Various descriptors have been utilized to analyze the fibril stability. These include, for example, the number of side-chain to side-chain hydrogen bonds, the volume packing fraction within the fibril fragment, and the frustration index;99 the geometrical distance between the planes of the core and the side-chains in vertical and horizontal directions;100 as well as stability landscapes utilizing the binding free energies with a dipolar solvent model.101
In this work, we report extensive fully atomistic MD simulations of several model systems composed of ten to twelve Aβ17–42 peptides in water with the addition of Cu2+ and Fe2+ ions. We use multiple randomly positioned monomers from a protofibril model92 for our initial constructs, and an explicit water model for the solvent. Oligomers from the C-terminal fragment Aβ17–42, also known as P3, which mainly contain hydrophobic residues, may be expected to drive the processes of aggregation and fibrillation.49,67 They are found in diffuse deposits associated with AD16,17,19 and are known to be toxic.16,17,20 Although it is clear that electrostatic interactions should be important for the process of aggregation of Aβ17–42 fragments, the influence of common charge-bearing compounds such as metal ions has not been investigated yet in a MD simulation of the aggregation. Even though the fragment Aβ17–42 does not contain the main metal binding site, the possible influence of transient coordination through carboxyl groups begs for a better understanding. We investigate the evolution of these multimeric systems starting from initially random orientations of the Aβ peptide chains, specifically focusing on the changes in their secondary structure content and interatomic contacts. To the best of our knowledge, this is the first report describing the evolution of large (containing more than 6 units) multimeric Aβ peptide systems from initially random orientations down to the formation of more compact oligomeric aggregates, as observed from all-atom MD simulations in explicit solvent. To analyze the dynamic stability of various constructs, we use a novel essential collective dynamics (ECD) method that our group has developed and applied to analyze a number of biomolecular systems.102–110
Methods
Modeling structures
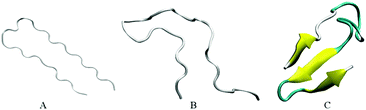
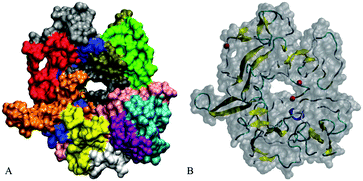
Our initial structures comprise randomly positioned monomeric Aβ peptide fragments 17LVFFAEDVGSNKGAIIGLMVGGVVIA42. For these monomer units, we used the coordinates of chains A–E of an N-terminally truncated Aβ17–42 experimentally derived pentamer from PDB ID 2BEG,92,111 see Fig. 1(A). To prepare the control monomer system, chain C from 2BEG.pdb was extracted from the complex, minimized in a vacuum, solvated in a single point charge extended (SPCE) water box, and counterions Na+/Cl− were added to the system (see Table 1, system A1). Next, using Accelrys VS112 and VMD113 packages, we have built a system containing ten monomers out of two sets of monomeric Aβ17–42 units from 2BEG.pdb, by randomly rotating and shifting the units against each other with a minimal distance of 5 Å, so that none of the units were in contact with each other. Then, we minimized these ten randomly positioned units in vacuum and added solvent and counterions (see Table 1, system A2). The Aβ17–42 decamer system was NPT simulated in a SPCE water box for 50 ns. In order to probe the formation of multiples of hexamers as seen in experiments,26,27 water molecules and ions were removed from the decamer system and two more monomer units were added, randomly rotated and distanced by at least 5 Å from the other units (see Table 1, system A3). The resulting dodecameric system was also minimized in a vacuum, solvated in a SPCE water box, and electro-neutralized. The sites bearing negative charges, with predominantly exposed carboxylate groups of E22 and D23 of different chains, were identified in system A3 using Accelrys Discovery Studio Visualizer,112 and Cu2+ or Fe2+ ions were added to these sites resulting in systems A4a, A5a, and A6a (Table 1). To collect statistics on systems dynamics, we ran additional control simulations for each of the systems A4a, A5a, and A6a, as listed in Table 1 and Table S1 (ESI†). The same starting coordinates of atoms and changed seed numbers when random-generating the initial Maxwell distributions of atom velocities were used in the additional simulations, which are labeled as “b”, “c”, and so on. In systems A5 and A6 all the metal ions were positioned in negatively charged cavities. In system A4a and the corresponding controls two Cu2+ ions were positioned in negatively charged cavities, and the third Cu2+ ion was positioned outside at a distance of approximately 7 Å from the surface of the oligomer.| System | Details of preparation | |
|---|---|---|
| A1a, A1b | Aβ monomer | Two systems, chains C and D from 2BEG.pdb92 |
| A2 | Aβ17–42 (10) decamer, random chain position | Based on 2BEG.pdb coordinates, monomers rotated by random angles and shifted by random distances of 5–7 Å against each other |
| A3 | Aβ17–42 (12) dodecamer | Based on A2 after 50 ns with two monomers added at random positions |
| A4a–A4e | Aβ17–42 dodecamer with 3 Cu2+ ions | Based on A3 with three Cu2+ ions added |
| A5a–A5e | Aβ17–42 dodecamer with 6 Cu2+ ions | Based on A3 with six Cu2+ ions added to negatively charged sites |
| A6a–A6e | Aβ17–42 dodecamer with 6 Fe2+ ions | Based on A3 with six Fe2+ ions added to negatively charged sites |
All systems A4–A6 were minimized in vacuum, then water and Na+/Cl− counterions were added. Minimizations, equilibrations and production MD simulations on systems A1–A6 were carried out using the GROMACS v4.5.3 package.114 The optimized potentials for liquid simulation (OPLS) force fields115 were used for the peptide molecules and ions. Subsequent solvent minimizations involved decreasing position restraints on non-hydrogen protein atoms, as well as heating with Berendsen thermostats and NVT-equilibration.
Molecular dynamics simulations
The production MD simulations, and also the last equilibration step, were conducted at a temperature of 310 K and a pressure of 1 atm with isotropic pressure coupling (NPT ensemble), and bond lengths restrained with the linear constant solver (LINCS) algorithm with a fourth order of expansion. These simulations were performed for 200 ns for systems A2, A3, A4a–e, A5a–e, and A6a–e (see Table S1, ESI†). 1 fs time steps were used, and snapshots were saved every 20 fs in order to analyze the essential collective dynamics. Additional details of system preparation and simulations have been described elsewhere.108Structural analysis of the trajectories, including assessment of the secondary structure, calculations of RMSD, the number of hydrogen bonds and salt bridges, the radii of gyration, distance maps, and solvent accessible areas, has been done using GROMACS package scripts114 and the VMD package.113 For graphical representation, the VMD and Accelrys VS packages were utilized.
Essential collective dynamics (ECD)
The essential collective dynamics (ECD) method allows identification of persistent dynamic correlations in macromolecules from short fragments of MD simulation trajectories. According to the statistical–mechanical framework,102,107 macromolecular dynamics can be described using generalized Langevin equations (GLE) with essential collective coordinates defined by applying principal component analysis (PCA) on MD trajectories. More specifically, short fragments of MD trajectories (usually from the last 20 ns of a production run) are analyzed. A fragment represents a temporal sequence of atomic positions,![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) i(t) = {xi(t), yi(t), zi(t)}, i = 1, 2,…, N, i(t) = {xi(t), yi(t), zi(t)}, i = 1, 2,…, N, | (1) |
Cij = 〈(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) i(t) − 〈 i(t) − 〈![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) i〉)( i〉)(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) j(t) − 〈 j(t) − 〈![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) j〉)〉, j〉)〉, | (2) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) k
= {Ek1, Ek2,… Ek3N}, k = 1, 2,…, K.
k
= {Ek1, Ek2,… Ek3N}, k = 1, 2,…, K.
| (3) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) k = { k = {![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k1, k1, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k2,… k2,…![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) kN}, k = 1, 2,…, K. kN}, k = 1, 2,…, K. | (4) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ki denote triplets of direction cosines {
ki denote triplets of direction cosines {![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ki,x,
ki,x,![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ki,y,
ki,y,![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ki,z} of eigenvectors
ki,z} of eigenvectors ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) k relative to the x, y, and z degrees of freedom for the atom i = 1, 2,…, N in 3N-dimensional configuration space.102Eqn (4) is equivalent to eqn (3) with the only difference being that the 3N direction cosines defining each eigenvector are grouped into N triplets, such that each triplet is associated with one atom in the protein. It has been shown102,107 that such triplets of direction cosines can be used to evaluate dynamical coupling (correlation of motion) between atoms of the protein, to find out which of the atoms move coherently. For this purpose, a set of N vectors is constructed as follows:107
k relative to the x, y, and z degrees of freedom for the atom i = 1, 2,…, N in 3N-dimensional configuration space.102Eqn (4) is equivalent to eqn (3) with the only difference being that the 3N direction cosines defining each eigenvector are grouped into N triplets, such that each triplet is associated with one atom in the protein. It has been shown102,107 that such triplets of direction cosines can be used to evaluate dynamical coupling (correlation of motion) between atoms of the protein, to find out which of the atoms move coherently. For this purpose, a set of N vectors is constructed as follows:107![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i = { i = {![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1i, 1i,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2i,… 2i,…![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) Ki}, i = 1, 2,..., N. Ki}, i = 1, 2,..., N. | (5) |
dij = |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i − i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j|, i, j = 1, 2,..., N, j|, i, j = 1, 2,..., N, | (6) |
A suite of dynamic descriptors, such as the protein's dynamic domains;102 main-chain flexibility profiles;103 and main-chain/backbone and side-chain pair correlation maps,106,109 have been derived within the ECD framework, extensively validated, and successfully applied to analyze the dynamics of proteins and protein–ligand and protein–nanoparticle complexes.103–106,108–110 Importantly, the ECD method does not require exhaustive sampling of the conformational space in order to draw accurate predictions. Short sub-nanosecond segments of MD trajectories are usually sufficient for compatibility of the predictions with NMR experiments representing significantly longer time regimes.102,103,105–107
In this work we assess the dynamics of Aβ aggregates using ECD dynamic domains, main-chain flexibility profiles, and backbone/side-chain correlation maps. The dynamic domains, which represent relatively rigid parts of the structure that move coherently, are identified through a clustering procedure described in detail in ref. 102. The ECD main chain flexibility descriptor 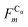 for the Cα atom in residue m is defined as the distance between the projected image of this Cα atom,
for the Cα atom in residue m is defined as the distance between the projected image of this Cα atom, 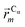 , and the centroid over the images of all Cα atoms,
, and the centroid over the images of all Cα atoms, 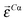 :103
:103
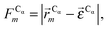 | (7) |
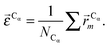 | (8) |
Results and discussion
Multiple solvated Aβ17–42 monomers form stable β-sheet containing oligomers
Two independent 20 ns simulations of Aβ monomers (system A1) were conducted. As Fig. 1 shows, individual solvated monomer units initially adopt a random-coil conformation without a β-structure. In one of two trajectories for the monomer system, a three-fold anti-parallel β-sheet involving residues 18–20, 33–35, and 39–41 was detected during 26% of the simulation time (see Fig. 1C and Table 2), consistent with the propensity of the Aβ17–42 monomers to form β-sheets reported earlier.66 However, for another monomer system we observed mainly random coils with a transient β-content present for only 2.3% of the time. The formation of metastable β-strands close to the C-terminus of Aβ monomers has been observed earlier in numerous modeling studies, such as ref. 56, 61, 62, 116, and 117, for example.| Chain | System | |||||
|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4a | A5a | A6a | |
| A | 18–20, 33–35, 39–41 | 32–34 | 18–19, 31–34 | 29–34, 39–40 | 31–33 | 18–19, 29–32 |
| B | 18–20, 25–26, 34–37, 39–41 | 18–20, 25–26, 34–37, 39–41 | 18–19, 25–26, 34–41 | 18–20, 25–26, 35–37, 39–41 | 19–20, 37–40 | |
| C | 32–33 | 32–33 | 18–19, 32–33 | 32–35 | 32–36 | |
| D | 19–23, 31–36 | 18–22, 35–38 | 19–22, 31–36 | 19–20, 35–36 | 19–21, 34–36 | |
| E | 18–21, 35–38 | 18–21 | 18–21, 39–40 | 18–21 | 18–22, 32–37 | |
| F | 33–34 | 33–35 | 31–34 | 33–35 | 33–37 | |
| G | 26–27, 31–32, 40–41 | 18–19, 26–27, 31–32, 36–37, | 26–27, 31–32, 40–41 | 26–27, 31–32, 40–41 | 26–27, 31–32 | |
| H | 18–19, 28–29, 37–38 | 18–19, 37–38 | 18–19, 37–38 | 18–19 | 18–19, 37–38 | |
| I | 39–41 | 18–20, 34–35, 39–41 | 18–20, 39–41 | 18–20, 39–41 | ||
| J | 20–21, 32–34, 40–41 | 32–35 | 32–35, 37–38 | 32–35 | 32–35 | |
| K | 34–35, 40–41 | 29–34 | 32–35 | 18–20, 36–39 | ||
| L | 34–35 | 32–39 | 34–37 | 19–24, 34–38 | ||
In particular, β-sheet or β-hairpin motifs involving residues from regions 18–20, 30–32, and 39–41 have been observed.61,62,117 Our finding of β-sheet locations (see Table 2 and Fig. S2, ESI†) is in good agreement with these studies. Some modeling works also report a significant α-helical content, especially in the N-terminal region of Aβ monomers.61,62,118 The fact that we do not observe α-helices in this work may be attributed to the absence of an N-terminal region in Aβ17–42, and the force fields used.56
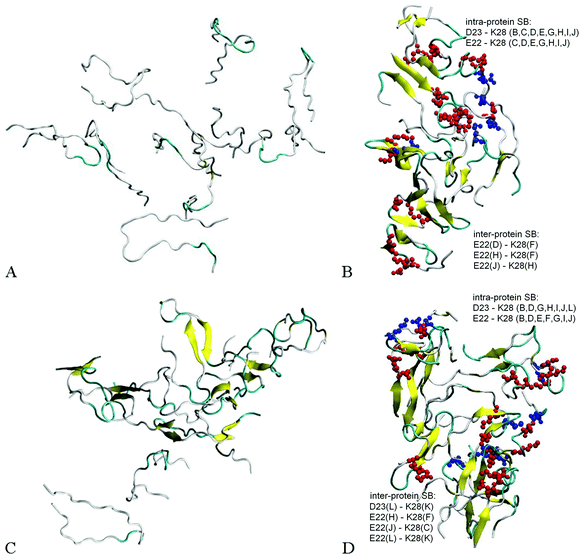
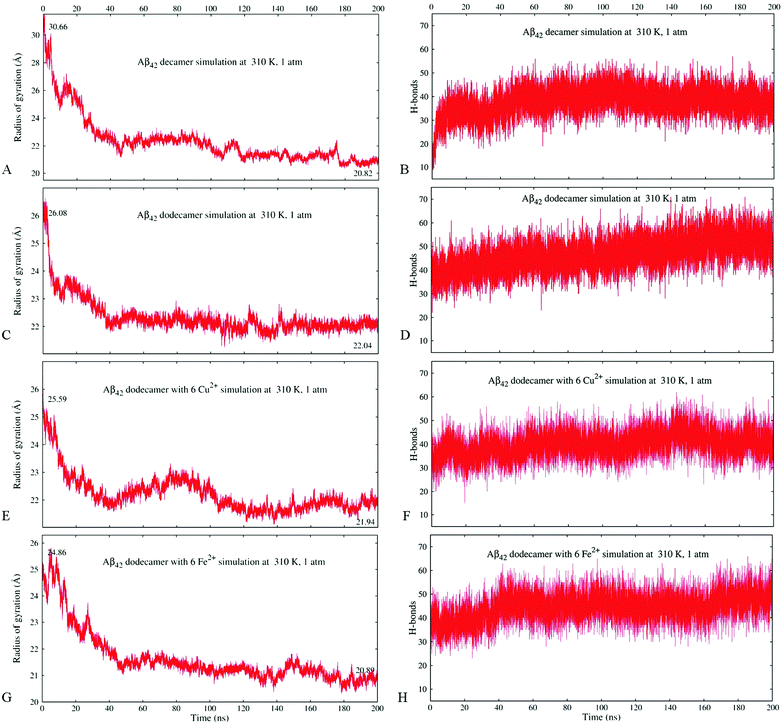
Fig. 2A and B illustrate the structure of system A2, composed of ten randomly positioned Aβ17–42 monomers in water, before and after the 200 ns MD simulation, respectively. As evident from Fig. 2A, no β-structures were present in any of the chains initially. However, the decamer started aggregating already during the 0.2 ns NPT equilibration stage. This involved a rapid decrease of inter-chain separations and the development of numerous side-chain contacts for the first 20–40 ns. Since the Aβ17–42 peptide is comprised of mostly hydrophobic residues, the aggregation was accompanied by expulsion of water molecules from the inter-chain space within 40 ns of the simulation. The distance maps in Fig. S1 (ESI†) show the mean smallest distances between side-chain atoms (above the diagonal) and main-chain atoms (below the diagonal). As one can see from Fig. S1A–C (ESI†), about 80% of the closest inter-atomic contacts that we observe at 200 ns were developed over the first 60 ns of the simulation. Further contact formation was relatively slow. As one could expect, somewhat shorter distances are observed between side-chain atoms in comparison to the main chain. Fig. 3A shows the time dependence of the gyration radius of the decamer A2; Fig. S2(B) (ESI†) shows the secondary structure evolution; Table 2 lists stable β-strands identified during 200 ns of the simulation; and the third row in Table 3 summarizes the various structural changes observed for this system. Overall in the course of a 200 ns simulation of the decamer, the radius of gyration has decreased from 30.66 Å to 20.82 Å, and a compact oligomer formed that contained both parallel and anti-parallel β-sheets. Often, although not always, stable β-strands are found in regions 18–21 and 31–41, where the monomeric system A1 also developed β-content during a 20 ns simulation (Fig. 1C and Fig. S2, ESI† and Table 2). Overall, as Table 3 shows, the β-content of system A2 increased from 3.7% to 20% in the course of 100 ns, and then decreased to 12.8% after 200 ns. This is accompanied by a pronounced increase in the number of inter-peptide and intra-peptide hydrogen bonds (HBs), as Fig. 3B illustrates. During the first 100 ns of the molecular dynamics run, the decamer A2 developed 27 pairs of HBs, in addition to the existing 14 pairs of HBs which were already formed during the equilibration. However, during the next 100 ns the decamer lost some of these HBs, so that 36 bonds remained by the end of the 200 ns simulation (see Table 3 and Fig. 3B). We attribute this to a redistribution of hydrogen bonding with the solvent during the simulations. System A2 also developed 18 salt bridges (SBs) involving acidic residues E22 or D23 and the basic residue K28 in the course of 200 ns of simulations.
| Hydrogen bonds | Salt bridges | α-helix content, % | β-sheet content, % | Isolated bridge content, % | Radius of gyration, Å | ||
|---|---|---|---|---|---|---|---|
| A2 | 10-mer | 14–41–36 | 18 | 0–0–0 | 3.7–20.0–12.8 | 2.2–3.7–5.7 | 30.66–21.76–20.82 |
| A3 | 12-mer | 39–47–50 | 18 | 0–0–0 | 12.6–15.6–19.4 | 5.6–7.1–7.4 | 26.08–22.13–22.05 |
| A4a | 12-mer + 3 Cu ions | 36–45–51 | 16 | 0–0–0 | 14.3–17.5–23.3 | 5.0–4.0–4.1 | 28.39–21.71–21.48 |
| A5a | 12-mer + 6 Cu ions | 35–40–41 | 19 | 0–0.03–0.2 | 14.5–15.9–13.3 | 4.6–6.5–6.5 | 25.59–22.28–21.94 |
| A6a | 12-mer + 6 Fe ions | 38–46–51 | 13 | 0–0–0 | 9.9–20.0–19.7 | 6.5–4.6–5.2 | 24.86–21.22–20.89 |
Dodecamer systems A3–A6 were built by adding two Aβ17–42 monomers to the decameric system A2 after 50 ns of the simulation. As an example, Fig. 2C shows the initial configuration of the dodecameric system A3. Fig. 2D and 4A and B illustrate the structures of systems A3, A5a, and A6a, respectively, after 200 ns, and Fig. 3C–H show the evolution of the gyration radii and HB numbers.
Since the initial structures for dodecamers A3–A6 were composed of a partially aggregated decamer with two additional chains distanced by more than 5 Å, the initial sizes of systems A3–A6 were slightly higher than the size of system A2, whereas the number of initial HBs in these systems was equal to the final number of HBs in system A2 after 50 ns (see Table 3). Similarly to system A2, the dodecamer systems A3–A6 have decreased in size, developed hydrogen bonds and maintained salt bridge networks during the simulations. Remarkably, the β-sheet content increased in most cases in comparison to the initial composite structure. The locations where stable β-content is found involve residues 18–21 and 31–41, similarly as for the decamer (Table 2). The dodecamer structures were formed from decamers after 50 ns of simulations, when 37 HBs were present. After 200 ns of simulations, the number of hydrogen bonds increased reaching a total of 41–51 bonds. However, no significant change in the number of salt bridges was observed in dodecamers A3 and A5a. Interestingly, dodecamer A5a with six Cu2+ ions developed one SB more than dodecamer A3 without ions, but with less HBs and less β-sheet content; whereas dodecamer A6a with six Fe2+ ions exhibited less SBs than A3, but showed an almost similar number of HBs and similar β-sheet content (see Table 3 and Fig. 4). Overall, acidic residues E22 and D23 and the basic residue K28 were often involved in inter-molecular or intra-molecular salt bridges for all Aβ systems, although in the system A6a with six Fe2+ ions some of the bridges were disrupted.
Peptide aggregation involves rapid collapse and slow relaxation stages
As mentioned in the previous section, a rapid decrease in inter-chain separation in Aβ oligomers has been observed during the first 20–60 ns of the MD simulations, followed by longer, slower structural changes. The corresponding time dependencies for the radius of gyration for the Aβ17–42 decamer (A2) and the dodecamer (A3) shown in Fig. 3A and C, respectively, exhibit two distinct phases. A quick collapse of the decamer occurs within the first 40 ns, followed by a slower relaxation afterwards. The dependence of the number of hydrogen bonds on time for decamer A2 depicted in Fig. 3B exhibits a quick increase followed by a slower trend to saturation, compatible with the described two-stage process of aggregation, however a slight decrease follows after approximately 100 ns. In contrast, the dependence of the number of HBs in dodecamer A3 shows a smooth increase with time throughout the entire 200 ns of simulation (Fig. 3D). Fig. S3(A and C) (ESI†) compares the evolution of the radius of gyration of systems A5a (A) and A6a (C) with the corresponding control simulations, which exhibit similar trends, although one can see some variations in the gyration radius for these systems.All systems studied show significant fluctuations of the radius of gyration typical for MD (see Fig. 3 and Fig. S3, ESI†). In dodecamers A5 and A6 with six Cu2+ or Fe2+ ions the fluctuations are especially pronounced. Unlike the other systems, dodecamer A5a with six Cu2+ ions exhibits wave-like expansions and contractions (Fig. 3E) accompanied by well-discernible waves in the number of HBs. The average number of HBs in system A5a after 200 ns is lower than that in system A3 (Fig. 3F). When six Fe2+ ions are added to the Aβ dodecamer instead of Cu2+ ions, the resulting system A6a develops a similar number of HBs as dodecamer A3 without ions. It also shows a milder expansion–contraction variation in the gyration radius than system A5a. Fig. S3(B and D) (ESI†) compares the HB numbers of systems A5a (B) and A6a (D) with the control simulations. The resulting amount of HBs built would be approximately the same in all simulations for both systems.
Fig. S4 (ESI†) shows a typical solvent-accessible surface representation of systems A3a, A5a, and A6a at 70 ns and at 200 ns. The control systems A5 and A6 (not shown) exhibit similar trends as in Fig. S4(B–E) (ESI†). While systems without ions and those with copper ions develop more compact, oval-like shapes, systems with iron ions tend to form more developed surfaces. Since in the initial constructs the Aβ monomers were placed at a distance from each other, all oligomers initially contained cavities and channels formed by connecting two or more peptide chains. However, most of the channels have disappeared completely or transformed into cavities in the course of the relaxation stage, or in approximately 30–40 ns. By 70 ns and thereafter, only a few cavities are found in the A5 and A6 systems.
Overall, the radius of gyration of the initial quasi decameric system A2 of 30.66 Å decreased to 20.82 Å after 200 ns (Fig. 3A), whereas an initially more compact dodecamer A3 decreased its gyration radius from 26.08 Å down to 22.05 Å (Fig. 3C). The dodecamer with six Fe2+ ions A6a developed an even more compact structure (20.89 Å) than the dodecamer with six Cu2+ ions A5a (21.94 Å) as Fig. 3E and G illustrate. In dodecamers A3, A5a, and A6a, their radius of gyration has largely stabilized after 80–120 ns, however their hydrogen bonding systems continued to develop throughout the entire 200 ns of the simulations (Fig. 3D, F, and H).
Cu2+ and Fe2+ ions develop coordination bonds with negatively charged groups of Aβ17–42
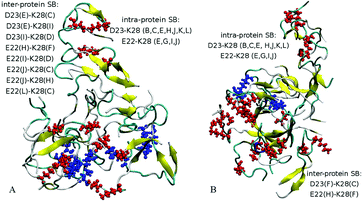
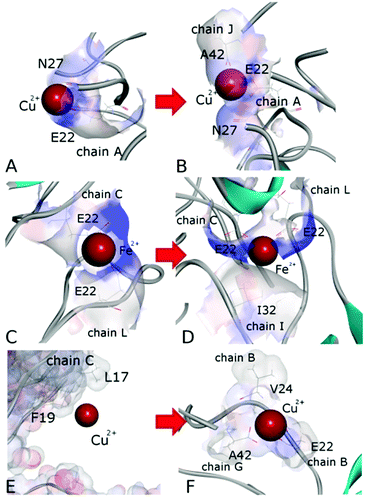
Detailed close-up images of copper/iron ions in systems A5a and A6a are shown in Fig. 5A–D and Fig. S5 (ESI†). In all the systems we observe transient coordination bonds of the ions with carboxylate groups E22, D23, and A42 via electrostatic interactions in the aqueous environment. In systems A5a and A6a, as well as in the corresponding controls, all six ions were positioned in negatively charged cavities, all of which happened to be close to at least one acidic side-chain E22. These ions started forming coordination bonds with neighboring carboxylate groups immediately during equilibration. In system A5a and the corresponding controls, six copper ions initially developed bonds with carboxylate groups of E22 in negatively charged cavities of the oligomer. In the course of production simulations the initial bonding of each copper ion to at least one E22 group was preserved, and additional bonds with groups from the same or other chains were formed.For example, the Cu2+ ion shown in Fig. 5A developed a bond with the carboxylate group of E22 from chain A in system 5Aa after equilibration. As Fig. 5B shows, after 200 ns of production simulations this ion remained bound to E22 of chain A, and additionally developed a bond with the C-terminal carboxyl group of A42 of chain J. An example of different Cu2+ ions from system A5a is illustrated in Fig. S5A and B (ESI†). This ion was initially bound to E22 of chain C in close proximity to E22 of chain L (Fig. S5A, ESI†), whereas after 200 ns simulations it was additionally bound to A42 from chains L and E, while the remaining bound to E22 of chain C (Fig. S5B, ESI†). Fe2+ ions in system A6a and the corresponding controls A6b and A6c exhibit a similar coordination pattern. After equilibration they were mainly bound to carboxylate groups of E22. Most of the ions remained in the same bonding positions during the entire production run. However, as the oligomers aggregated and became more compact, slight re-arrangements of the coordination occurred in most cases. As Fig. S5C and D (ESI†) illustrate, a Fe2+ ion from system 6Aa has retained its initial coordination bonding to E22 of chain F and D23 of chain H. However, the amide group of the hydrophobic residue I31 of chain L has moved closer to the ion by the end of the 200 ns simulation, and formed a van der Waals bond. In the example shown in Fig. 5C and D, an Fe2+ ion that was initially in contact with E22 of chain C and with E22 of chain L has been approached by the amide group of I32 from chain I during the simulations, and developed a close van der Waals bond. Overall, in both systems, A5 and A6, the majority of the metal coordination bonds were formed with carboxylate groups of E22 and D23 and the C-terminal carboxyl group of A42, often from different chains. After 200 ns of production simulations, six Cu2+ ions in system A5a had a total of 14 such bonds, and six Fe2+ ions in system A6a had 13 bonds. Out of these, 7 bonds of Cu2+ ions and 8 bonds of Fe2+ ions were with E22. Overall, bonds with E22 occurred roughly twice as often as bonds with D23 or A42. We did not observe any substantial differences between Cu2+ and Fe2+ coordination bonding to Aβ17–42 oligomers.
A similar behaviour was also observed for two Cu2+ ions positioned in negatively charged cavities in system A4a (see Fig. S6E and F, ESI†) as well as in the corresponding controls. The third Cu2+ ion, which was positioned at a distance from the surface of chain C in oligomer A4a (Fig. 5E), has traveled along the periphery of the oligomer until it developed a coordination bond with the carboxyl group of the C-terminal residue A42 of chain G after the first 10 ns of production simulation. This bond remained stable for the subsequent 190 ns of the simulation, and another bond with E22 of chain B was also established, resulting in the ion remaining positioned between chains B and G (Fig. 5E) at a distance of approximately 37 Å from its initial location. In three out of four similar control systems, Cu2+ ions positioned distantly also developed coordination bonds, yet at different locations. In the first and third control systems, A4b and A4d, the ion was bound to E22 of chain A at a distance of 28–29 Å from its initial location, and in the fourth system, A4e, the ion was bound to A42 of chains G and F at a distance of 32 Å from its initial location. In the second control system, A4c, the ion did not bind to any group of the oligomer, and remained in solution. We attribute the relocations of these ions primarily to random-walk occurring until they develop a coordination bond with a negatively charged group.
Remarkably, in our simulations all metal ions have developed coordination bonds with multiple residues of the Aβ17–42 oligomers, and retained most of these bonds in the absence of the N-terminal metal binding site. Furthermore, we observe a coordination of the ions by similar groups, especially E22, which was found to move into the coordination sphere of Cu2+ when it was bound in the N-terminal site of the Aβ1–42 monomer.76 Also, consistent with previously published simulations,76 we do not observe a coordination of metal ions by M35.
ECD analysis of Aβ oligomers reveals a strong impact of secondary and tertiary structures on the dynamics
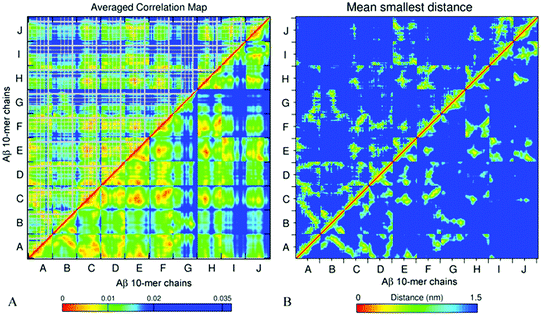
The essential collective dynamics analysis (ECD) has been performed on the modelled systems utilizing trajectory fragments from the last 20 ns of the simulations. The essential collective dynamics theory uses a set of principal eigenvectors of the covariance matrix to describe correlations between pairs of atoms in the system. The number of eigenvectors required to sample the total displacement with a given accuracy (principal components) defines the essential dimensionality of the system. Fig. S7 (ESI†) shows a dependence of the percentage of the total displacement sampled by the principal components as a function of the number of components, in average over a hundred 0.2 ns long segments of MD trajectories for systems A2–A6. It can be seen that 20 principal components sample more than 97% of the displacement for all the systems.We used 20 principal eigenvectors to determine ECD correlations of motion between main-chain and side-chain atoms (see the Methods section) in the systems considered. Fig. 6A shows the side-chain (above the diagonal) and backbone (below the diagonal) correlations in decamer A2 averaged over 100 0.2 ns long segments from 180–200 ns of the simulation, and Fig. 6B shows the corresponding mean distances for comparison (the colors were intentionally selected to match the correlation maps). The comparison of side-chain and main-chain correlations indicates a pronounced similarity. In most cases, stronger correlations of side-chains were found in regions where backbone correlations were also stronger. As the correlation map indicates, units A–F, H, and most of the N-ter of units I and J have formed a coherently moving sub-aggregate. The areas of strongest pair correlations (colored in red and orange) often include stable β-sheet formation. In particular hydrophobic residues V18–A21, which are often implicated in β-sheets, tend to exhibit strong inter-unit correlations. In turn, strong correlations can also be seen between units that are located close to each other according to the distance map, for example, units F and H. Units G and C-ter of units I and J exhibit the weakest correlations with the rest of the oligomer. According to Table 2 and Fig. S2 (ESI†), unit I of system A2 also forms little β-structure, and according to Fig. 2B, this unit does not form inter-chain salt bridges. Contrarily, units G and J form three stable β-strands each. However, in the weakly correlated units, β-sheets are located within the units, rather than across different units. Unit G also does not exhibit inter-chain salt bridges (Fig. 2B). In units B, D, E, G, H, K, and L, an “X”-shaped pattern of intra-chain correlations is visible, which is related to the antiparallel hairpin-like bending of these units.
From comparison of the pair correlation map with the distance map for system A2 (Fig. 6A and B) it is evident that residues located in close proximity to each other also tend to develop strong correlations, as one could expect. However, Fig. 6A also shows strong correlations between some of the residues positioned distantly from each other, such as for example, units B and C, or units J and A. This can be explained by non-direct interactions between the residues mediated by water or other residues, which, in turn, allow those residues to move coherently.
Pair correlations and the mean smallest distance maps of dodecamer A3 (Fig. S8, ESI†) show trends similar to decamer A2. As described in the Methods section, the dodecamer was obtained by adding two units to A2. These added units, denoted as K and L in Fig. S8 (ESI†), form close contacts and strong correlations with units E, I and J. Strong dynamic coupling in the sub-aggregate composed of units A–F, H, I and J is observed in the dodecamer in a similar manner to system A2. Some of the correlations, especially involving units I and J, have increased and new correlations, primarily with unit L, have formed extending the strongly correlated sub-aggregate.
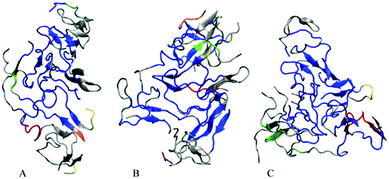
In order to visualize the strongest correlations in the oligomers more explicitly, we have identified the largest coherently moving domains within the same ECD framework (see the Methods section). Fig. 7 depicts major dynamic domains in decamer A2 as well as in dodecamers A3 and A5a mapped onto the corresponding tertiary structures. For each of the oligomers, the largest dynamic domain is shown in a blue color. As one can see from the figure, in the three systems the largest domain of correlated motion occupies the central part of the oligomer, whereas smaller domains and off-domain parts are located primarily in the peripheral regions. The domain colored blue is clearly the largest in dodecamer A3, where the domain also contains more β-structures than in the other two systems. For the dodecamer with six copper ions, A5a, the second and third largest domains (colored in red and green, respectively) involve more residues than in the two systems without ions. For system A5a, the largest domain is slightly smaller than in the two other systems.
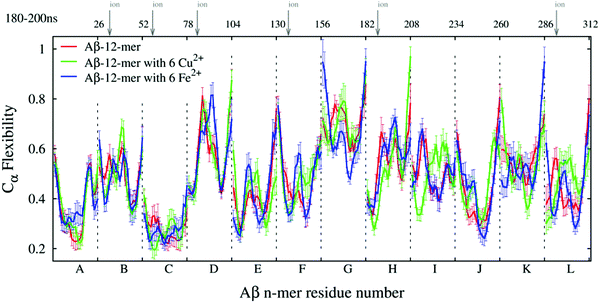
The ECD flexibility profiles of dodecamers A3, A5a, and A6a are presented in Fig. 8. Since in these systems unit L is located in the closest proximity to two other units K and J, its flexibility is somewhat lower than that of unit K. Overall, units D, G, H and K are positioned on the periphery of the oligomer, and therefore most of them show relatively high flexibility. In contrast, units A, B, C, E and F are located in the central part of the oligomer, and they show relatively low flexibility in all three systems. In systems A5a and A6a that contain ions, the flexibilities of units B, C, F, and L are somewhat lower in areas where ions are located, but other regions may have an increased flexibility.
In globular proteins with a stable secondary structure, high levels of the ECD flexibility descriptor usually correspond to flexible loops as well as termini, whereas most of the flexibility minima indicate α-helices or β-sheets.103–106,108 Consistent with this, Fig. 8 shows an increase in main-chain flexibility at the terminal regions of the twelve units. A comparison of positions of the main-chain flexibility minima in Fig. 8 with the positions of stable β-strands in Table 2 reveals a significant, although not a complete overlap. As can be seen from Table 2 and Fig. S2 (ESI†), system A3 exhibits a total of 24 stable β-strands, and systems A5a and A6a develop 19 stable β-strands each. Out of these, 15 β-strands in each system A3 and A6a, and 14 β-strands in system A5a are located in the immediate proximity to main-chain flexibility minima. In particular, β-strands located in regions 18–21 and 31–37 are often associated with the minima of flexibility. For example, a minimum around residue 19 of unit H in all three systems indicates a β-strand, which also affects the flexibility of the adjacent units F and J, which are in direct contact with it. However, not all stable β-strands can be associated with the flexibility minima. For nine β-strands in A3, seven β-strands in A5a, and three β-strands in A6a, no proximal flexibility minima were identified. We attribute this to an occasional increase in the overall mobility of the short peptide chains, such as for example, several β-strands in positions 39–41 close to C-termini. In turn, not all of the main-chain flexibility minima seen in Fig. 8 can be associated with stable β-structures. In particular, some of the flexibility minima are found at positions 23–24 and 29–31 adjacent to residues 22, 23, and 28, which are often involved in salt bridges. The formation of salt bridges seems to be accompanied by a build-up of steric constraints on the neighboring residues, which explains the observed decrease in flexibility.
Fig. 9 presents ECD pair correlation maps (panels A and C) and distance maps (panels B and D) of Aβ oligomers A5a and A6a averaged over 100 segments of the last 20 ns (180–200 ns) of the corresponding trajectories. The correlation maps show both side-chain correlations (above the diagonal) and backbone correlations (below the diagonal). Similarly to decamer A2 and dodecamer A3, stronger correlations of side-chains are found in regions where backbone correlations are also stronger.
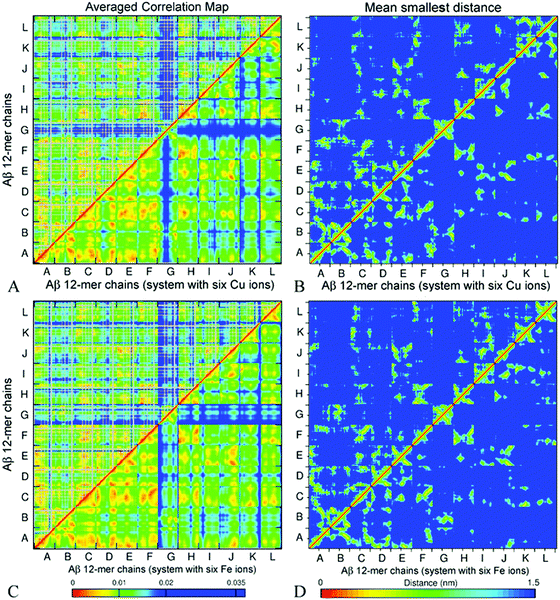 | ||
| Fig. 9 Side chain (above the diagonal) and backbone (below the diagonal) ECD correlation maps (A and C), and the mean smallest distance maps calculated using GROMACS software (B and D) for dodecamer A5a (A and B) and dodecamer A6a (C and D). The color schemes are as in Fig. 6. | ||
Fig. 9B and D represent averaged distance maps over the set of conformations for the time interval of 180–200 ns. As in systems A2 and A3, the strongest pair correlations shown in red and orange colors in Fig. 9A and C have a lot in common with the corresponding contact distance maps, however distant correlations are also observed. This implicates that residues in immediate proximity tend to move coherently in many cases, although mediated indirect interactions are also present.
For both dodecamers with the ions added, strong inter-chain correlations involving units A–F are evident from Fig. 9A and C, similar to the observations in systems A2 and A3. Units H, I, J, and L exhibit strong inter-chain correlations with C, E, and F in both systems, however these correlations tend to be stronger in dodecamer A6a, with Fe ions, than in dodecamer A5a with Cu ions (Fig. 9A and C). In both dodecamers, unit G exhibits low correlations with the rest of the oligomer (Fig. 9A and B), which is consistent with its relatively high flexibility (Fig. 8). In the MD trajectories, this chain was also found to be the most weakly bound. When compared with the ion-free dodecameric system A3 (Fig. S8, ESI†), systems A5a and A6a exhibit a build-up of close intern-chain contacts of several units. In both ion-containing systems, unit C developed more contacts with K and H, as chains K and H shifted towards an ion around chain C; unit D in turn developed more contacts with E; and the latter additionally developed more contacts with H and I (Fig. 9B and D, and Fig. S8B, ESI†). With the exception of contacts of C with K and E with I in system A5a, this build-up of additional contacts was accompanied by an increase in the corresponding inter-chain correlations shown in Fig. 9A and C, and Fig. S8A (ESI†). At the same time, both systems A5a and A6a exhibit an increase in correlations of units H with F and K in the absence of a pronounced increase in their contacts. In both ion-containing systems, units C and H exhibit the most extensive increase of inter-chain contacts or correlations, especially with E, F, K, and L. The peripheral chain L, however, lost both its contacts and correlations with units E, I, J, and K upon addition of the ions. Another notable loss in correlation in comparison to system A3 occurred between units J and E in both the A5a and A6a dodecamers. However, an overall increase in inter-chain contacts and/or in correlations prevails over the losses. Most chains that have shown changes in dynamics in comparison with the ion-free dodecamer either were in close proximity to the initial ion positions (such as units C and H), or developed coordination bonds with ions during simulations (for example, F, E, and L). The inter-chain correlation data suggest that the presence of ions may promote the shifting of neighbouring chains closer towards ion locations, tending to increase the inter-chain dynamical coupling.
Similarly to the case of systems A2 and A3, in dodecamers A5a and A6a, units A–F and H are strongly inter-correlated. Significant parts of units I, J, K, and L also show pronounced inter-chain correlations. The regions that tend to be β-populated are also often associated with stronger intra-chain and inter-chain correlations in the oligomers. For example, in A5a, residues 30–35 of unit K which accommodate a stable β-strand, exhibit pronounced inter-chain correlations with C, F, H, and L. In particular, strong correlations are observed between residues 33–40 of unit K and residues 30–38 of unit L (Fig. 9A), where β-sheets were found (Table 2 and Fig. S2, ESI†). In A6a, β-populated regions of unit K also show strong correlations with other units. A similar tendency is also clearly seen in unit L for both systems A5a and A6a. Strong correlations of unit A with units F and J were found for A6a, while for A5a the correlations were less pronounced. Correlation maps also show strong correlations for the mostly hydrophobic residues L34–A41 and F19–A21, which are often β-populated.
Overall, from comparison of Fig. 6A, 9A, and C, and Fig. S8 (ESI†), it is evident that the dodecamers exhibit more pronounced inter-chain correlations than those observed in decamer A2.
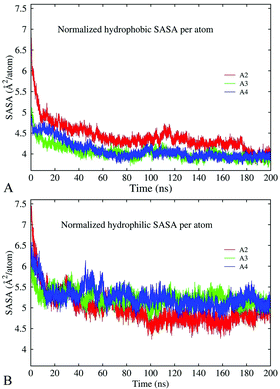
Hydrophobic and hydrophilic interactions influence the stability and morphology of the oligomers
The results discussed above indicate that hydrophobic and electrostatic interactions are strongly implicated in oligomer formation. To characterize these interactions, we have calculated changes in the total solvent-accessible surface area (SASA) of hydrophobic and hydrophilic groups in decamer A2, dodecamer A3 without ions, and dodecamer A4a with three Cu ions along 200 ns MD trajectories. In the case of the Aβ17–42 peptide, hydrophilic groups involve N- and C-terminal charged atoms, asparagine, aspartic acid, glutamic acid, lysine, and serine. The remaining 16 residues are considered to be hydrophobic. The normalized per-atom SASAs for the hydrophobic and hydrophilic groups are depicted in Fig. 10A and B, respectively. The figures show that both hydrophobic and hydrophilic exposures have decreased in the course of simulations in all the constructs. In decamer A2, the SASA of the hydrophilic groups was slightly higher at the beginning of the simulation, and after 200 ns it decreased to less than the SASA of the hydrophobic groups. This is consistent with the general trend for hydrophilic groups to remain exposed to the solvent, and for hydrophobic groups to become buried. Since decamer A2 was initially less compact than the dodecamers, the initial SASA of system A2 is higher than those of A3 and A4a. However, at the end of the 200 ns simulation, the SASA of all three systems has stabilized at the same level in average. In dodecamers A3 and A4a, the fraction of hydrophobic exposed area is slightly lower than that in decamer A2 until 180 ns of the simulation, after which the exposures adopt similar values. A significant portion of the hydrophobic exposure, approximately 57%, is due to valine and isoleucine residues (Fig. S9, ESI†). For example, a slight increase in the hydrophobic side-chain SASA of dodecamer A4a over the last 20 ns of the simulation was caused by the exposure of isoleucine and phenylalanine.Fig. 11 demonstrates the conformation for dodecamer A4a with three Cu2+ ions after 195.5 ns of the simulation. After approximately 30 ns of the production run, due to the connection of chains one channel has formed in the central region in close proximity to the copper ion bound to E22 of chain C, and another channel has formed in a peripheral region. The channels' widths varied subsequently. By the end of a 200 ns run, the dodecamer adopted an asymmetrical doughnut-like shape with a large channel in the central part and a smaller one in the peripheral region, as Fig. 11 shows. According to Table 3, the β-content in this dodecamer is higher than that in the other systems considered. One can see from Fig. 11 that locations of channels in the structure coincide with the positions of copper ions. This suggests that copper ions may compete with the development of salt bridges and other bonds in the oligomer, thereby creating favorable conditions for the development of channels in the oligomers. Distinct from the other dodecamers, in A4a, unit G is better correlated with the rest of the oligomers, while unit D and the central part of unit H are less correlated, as the correlation map in Fig. S10 (ESI†) shows. All chains are well-intertwined together: unit C (dark grey color in Fig. 11A) is located in the central part of the oligomer, and is covered with unit A (blue), which in turn is overlapped by unit B (red). Unit H (green) is connected to units A, F (brown) and G (light grey). Unit J (pink) is in contact with unit C (dark grey) and unit L (purple), which in turn is in contact with unit K (cyan). Unit I (white) is bound to unit E, and in turn to unit J. Unit D (orange) is located between units A and E (yellow) and has the smallest inter-chain interaction area, as well as the largest solvent exposure.
Control systems A4b, A4c, and A4d have developed less symmetrical yet compact, slab-like oligomers with channels or cavities in similar locations to those in A4a (Fig. S11, ESI†). In both systems a cavity or channel was close to two of the ions, whose positions were also similar across system 4a. However, the channels are narrower than in system A4a at similar simulation times. Overall, the described evolution of solvent accessible surfaces suggests that coordination bonds of metal ions may affect the oligomer compactness at the slow relaxation stage. As the chains slowly change their position, cavities and holes tend to form in close proximity to the ion location.
Conclusions
The molecular dynamics simulations reported in this work indicate that Aβ17–42 peptides tend to form compact oligomers in an aquatic environment. Consistent with recent experimental findings,29 our modeling results suggest that aggregation of 10–12 Aβ monomers tends to produce stable globular-like, largely unstructured oligomers without a pronounced long-range alignment of the units. After 200 ns of the simulations, the oligomers exhibited 13–23% β-sheet content. Stable β-strands were often found in regions 18–21 and 31–41 of the peptide chains, which are compatible with full-length simulations of Aβ monomers.62 Both parallel and anti-parallel β-sheets were observed.Two stages of oligomer formation have been identified in the course of the 200 ns MD simulations, a quick collapse within the first 40 ns and slow relaxation afterwards. The collapse stage is characterized by a quick decrease of inter-chain separation, disappearance of most cavities and channels, development of numerous inter-chain contacts, and a build-up of the β-sheet content. Formation of hydrogen bonds and salt bridges, and expulsion of water from the inter-chain space, followed by burial of the hydrophobic side chains appear to be the main driving forces of the first stage. The subsequent relaxation stage involves a slow decrease of the gyration radius. In the decamer system, this was accompanied by a partial decrease in the β-sheet content.
The essential collective dynamics analysis of the Aβ oligomers indicates that motion of some units is more strongly inter-correlated than others. Coherently moving sub-aggregates of 6–9 units have been detected, most of which are located in the central part of the oligomers. This agrees with the size of oligomers seen in experiments on Aβ1–42 aggregation in vitro, which have been hypothesized to be building blocks of larger toxic complexes.119 Although strong inter-chain correlations were often found in the vicinity of stable β-sheets, this was not always the case. Chains located close to each other in the tertiary structure were often found to move coherently in the absence of stable β-content. Main-chain flexibility of the oligomers exhibited similar trends as in globular proteins.103,105,106,108 This includes increased flexibility at terminal regions of the units, and minima of the flexibility in the vicinity of stable β-strands and salt bridges.
Coordination bonding of Cu2+ and Fe2+ ions involving carboxylate groups of E22, D23 and A42 was found for all simulated oligomers. Once formed, the coordination bonds remained stable during our simulations. Cu2+ and Fe2+ bonding does not prevent Aβ17–42 from forming compact non-fibrillary oligomers, indicating that the disruption of Aβ1–42 fibril formation previously seen in experiments44 involves different mechanisms than those observed during the early stages of Aβ17–42 aggregation. The presence of Cu2+ and Fe2+ ions in negatively charged cavities of dodecameric oligomers was often found to result in decreased main-chain flexibility in the areas close to the ions, as well as in stronger inter-chain correlations. In the case of Fe2+ ions, this was accompanied by a slightly less compact oligomer with stronger inter-chain dynamic correlations. In one of the trajectories for the oligomer with six Cu2+ ions added, pronounced wave-like expansion and contraction of the oligomer were observed at the slow relaxation stage, accompanied by a variation in the number of hydrogen bonds. Dramatic changes were observed in the dodecamer containing three Cu2+ ions. This dodecamer has repeatedly developed channels or cavities across several control simulations. In one simulation, this aggregate adopted a doughnut-like shape with a large channel in the central part and a smaller one in a peripheral region. Both channels were located close to a Cu2+ ion, suggesting that the ions might compete for the development of bonds in the oligomer, thereby facilitating the formation of channels.
Acknowledgements
The authors thank Johnathan Mane, John Mohan, Nataraj Pagadala, Oliver Stueker, Bilkiss Issack, Taras Fito, Mark Berjanskii, and Nikolay Blinov for their programming contributions and stimulating discussions. Molecular images were created using the VMD package113 and Discovery Studio Visualizer v4.0.112 Simulations were carried out using the NINT-NRC computational cluster and WestGrid and Compute Canada resources. Support of the work by Alberta Prion Research Institute is gratefully acknowledged (APRI Project 201300006).Notes and references
- M. Bucciantini, E. Giannoni, F. Chiti, F. Baroni, L. Formigli, J. Zurdo, N. Taddei, G. Ramponi, C. M. Dobson and M. Stefani, Nature, 2002, 416, 507–511 Search PubMed
.
- B. Caughey and P. T. Lansbury, Annu. Rev. Neurosci., 2003, 26, 267–298 Search PubMed
.
- J. A. Hardy and G. A. Higgins, Science, 1992, 256, 184–185 Search PubMed
.
- S. Baglioni, F. Casamenti, M. Bucciantini, L. M. Luheshi, N. Taddei, F. Chiti, C. M. Dobson and M. Stefani, J. Neurosci., 2006, 26, 8160–8167 Search PubMed
.
- I. Benilova, E. Karran and B. De Strooper, Nat. Neurosci., 2012, 15, 349–357 Search PubMed
.
- J. Hardy and D. J. Selkoe, Science, 2002, 297, 353–356 Search PubMed
.
- R. Kayed, E. Head, J. L. Thompson, T. M. McIntire, S. C. Milton, C. W. Cotman and C. G. Glabe, Science, 2003, 300, 486–489 Search PubMed
.
- C. A. McLean, R. A. Cherny, F. W. Fraser, S. J. Fuller, M. J. Smith, K. Beyreuther, A. I. Bush and C. L. Masters, Ann. Neurol., 1999, 46, 860–866 Search PubMed
.
- T. L. Williams, B. R. G. Johnson, B. Urbanc, A. T. A. Jenkins, S. D. A. Connell and L. C. Serpell, Biochem. J., 2011, 439, 67–77 Search PubMed
.
- L. Jiang, C. Liu, D. Leibly, M. Landau, M. Zhao, M. P. Hughes and D. S. Eisenberg, eLife, 2013, 2, e00857 Search PubMed
.
- R. J. Castellani, H. Lee, S. L. Siedlak, A. Nunomura, T. Hayashi, M. Nakamura, X. Zhu, G. Perry and M. A. Smith, J. Alzheimers Dis., 2009, 18, 447–452 Search PubMed
.
- A. L. Lublin and S. Gandy, Mt. Sinai J. Med., 2010, 77, 43–49 Search PubMed
.
- Y. Fezoui and D. B. Teplow, J. Biol. Chem., 2002, 277, 36948–36954 Search PubMed
.
- C. Wu and J.-E. Shea, PLoS Comput. Biol., 2013, 9, e1003211 Search PubMed
.
- A. Jan, D. M. Hartley and H. A. Lashuel, Nat. Protoc., 2010, 5, 1186–1209 Search PubMed
.
- A. M. Szczepanik, D. Rampe and G. E. Ringheim, J. Neurochem., 2001, 77, 304–317 Search PubMed
.
- W. Wei, D. D. Norton, X. Wang and J. W. Kusiak, Brain, 2002, 125, 2036–2043 Search PubMed
.
- E. Gowing, A. E. Roher, A. S. Woods, R. J. Cotter, M. Chaney, S. P. Little and M. J. Ball, J. Biol. Chem., 1994, 269, 10987–10990 Search PubMed
.
- L. S. Higgins, G. M. Murphy, L. S. Forno, R. Catalano and B. Cordell, Am. J. Pathol., 1996, 149, 585–596 Search PubMed
.
- R. L. Patton, W. M. Kalback, C. L. Esh, T. A. Kokjohn, G. D. Van Vickle, D. C. Luehrs, Y.-M. Kuo, J. Lopez, D. Brune, I. Ferrer, E. Masliah, A. J. Newel, T. G. Beach, E.
M. Castaño and A. E. Roher, Am. J. Pathol., 2006, 169, 1048–1063 Search PubMed
.
- T. Pillot, M. Goethals, B. Vanloo, C. Talussot, R. Brasseur, J. Vandekerckhove, M. Rosseneu and L. Lins, J. Biol. Chem., 1996, 271, 28757–28765 Search PubMed
.
- M. Bibl, M. Gallus, V. Welge, S. Lehmann, K. Sparbier, H. Esselmann and J. Wiltfang, Proteomics: Clin. Appl., 2012, 6, 163–169 Search PubMed
.
- L.-F. Lue, Y.-M. Kuo, A. E. Roher, L. Brachova, Y. Shen, L. Sue, T. Beach, J. H. Kurth, R. E. Rydel and J. Rogers, Am. J. Pathol., 1999, 155, 853–862 Search PubMed
.
- B. Urbanc, L. Cruz, S. Yun, S. V. Buldyrev, G. Bitan, D. B. Teplow and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17345–17350 Search PubMed
.
- K. Pauwels, T. L. Williams, K. L. Morris, W. Jonckheere, A. Vandersteen, G. Kelly, J. Schymkowitz, F. Rousseau, A. Pastore, L. C. Serpell and K. Broersen, J. Biol. Chem., 2012, 287, 5650–5660 Search PubMed
.
- S. L. Bernstein, N. F. Dupuis, N. D. Lazo, T. Wyttenbach, M. M. Condron, G. Bitan, D. B. Teplow, J.-E. Shea, B. T. Ruotolo, C. V. Robinson and M. T. Bowers, Nat. Chem., 2009, 1, 326–331 Search PubMed
.
- G. Bitan, M. D. Kirkitadze, A. Lomakin, S. S. Vollers, G. B. Benedek and D. B. Teplow, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 330–335 Search PubMed
.
- G. P. Gellermann, H. Byrnes, A. Striebinger, K. Ullrich, R. Mueller, H. Hillen and S. Barghorn, Neurobiol. Dis., 2008, 30, 212–220 Search PubMed
.
- J. Luo, S. K. T. S. Wärmländer, A. Gräslund and J. P. Abrahams, Biochemistry, 2014, 53, 6302–6308 Search PubMed
.
- N. J. Economou, M. J. Giammona, T. D. Do, X. Zheng, D. B. Teplow, S. K. Buratto and M. T. Bowers, J. Am. Chem. Soc., 2016, 138, 1772–1775 Search PubMed
.
- T. D. Do, N. E. LaPointe, R. Nelson, P. Krotee, E. Y. Hayden, B. Ulrich, S. Quan, S. C. Feinstein, D. B. Teplow, D. Eisenberg, J.-E. Shea and M. T. Bowers, J. Am. Chem. Soc., 2016, 138, 549–557 Search PubMed
.
- M. P. Lambert, A. K. Barlow, B. A. Chromy, C. Edwards, R. Freed, M. Liosatos, T. E. Morgan, I. Rozovsky, B. Trommer, K. L. Viola, P. Wals, C. Zhang, C. E. Finch, G. A. Krafft and W. L. Klein, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 6448–6453 Search PubMed
.
- A. I. Bush, Trends Neurosci., 2003, 26, 207–214 Search PubMed
.
- J. Dong, C. S. Atwood, V. E. Anderson, S. L. Siedlak, M. A. Smith, G. Perry and P. R. Carey, Biochemistry, 2003, 42, 2768–2773 Search PubMed
.
- L. M. Sayre, G. Perry, P. L. Harris, Y. Liu, K. A. Schubert and M. A. Smith, J. Neurochem., 2000, 74, 270–279 Search PubMed
.
- L. Hou and M. G. Zagorski, J. Am. Chem. Soc., 2006, 128, 9260–9261 Search PubMed
.
- C. Hureau, Y. Coppel, P. Dorlet, P. L. Solari, S. Sayen, E. Guillon, L. Sabater and P. Faller, Angew. Chem., Int. Ed., 2009, 48, 9522–9525 Search PubMed
.
- T. Miura, K. Suzuki, N. Kohata and H. Takeuchi, Biochemistry, 2000, 39, 7024–7031 Search PubMed
.
- C. S. Atwood, R. C. Scarpa, X. Huang, R. D. Moir, W. D. Jones, D. P. Fairlie, R. E. Tanzi and A. I. Bush, J. Neurochem., 2000, 75, 1219–1233 Search PubMed
.
- V. A. Streltsov, S. J. Titmuss, V. C. Epa, K. J. Barnham, C. L. Masters and J. N. Varghese, Biophys. J., 2008, 95, 3447–3456 CrossRef CAS PubMed
.
- Y. Miller, B. Ma and R. Nussinov, Coord. Chem. Rev., 2012, 256, 2245–2252 Search PubMed
.
- J. Danielsson, R. Pierattelli, L. Banci and A. Gräslund, FEBS J., 2007, 274, 46–59 Search PubMed
.
- D. Drago, S. Bolognin and P. Zatta, Curr. Alzheimer Res., 2008, 5, 500–507 Search PubMed
.
- M. Mold, L. Ouro-Gnao, B. M. Wieckowski and C. Exley, Sci. Rep., 2013, 3, 1256 Search PubMed
.
- M. Innocenti, E. Salvietti, M. Guidotti, A. Casini, S. Bellandi, M. L. Foresti, C. Gabbiani, A. Pozzi, P. Zatta and L. Messori, J. Alzheimers Dis., 2010, 19, 1323–1329 Search PubMed
.
- K. Suzuki, T. Miura and H. Takeuchi, Biochem. Biophys. Res. Commun., 2001, 285, 991–996 Search PubMed
.
- B. Moores, E. Drolle, S. J. Attwood, J. Simons and Z. Leonenko, PLoS One, 2011, 6, e25954 Search PubMed
.
- W. Qiang, W.-M. Yau, Y. Luo, M. P. Mattson and R. Tycko, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4443–4448 Search PubMed
.
- G. Reddy, J. E. Straub and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11948–11953 Search PubMed
.
- J.-E. Shea and B. Urbanc, Curr. Top. Med. Chem., 2012, 12, 2596–2610 Search PubMed
.
- E. Gazit, FASEB J., 2002, 16, 77–83 Search PubMed
.
- A. W. P. Fitzpatrick, G. M. Vanacore and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2015, 201502214 Search PubMed
.
- N. G. Franco R, J. Neurol. Neurol. Disord., 2014, 1, 103 Search PubMed
.
- G. Wei, N. Mousseau and P. Derreumaux, Prion, 2007, 1, 3–8 Search PubMed
.
- A. Morriss-Andrews and J.-E. Shea, Annu. Rev. Phys. Chem., 2015, 66, 643–666 Search PubMed
.
- L. Tran and T. Ha-Duong, Peptides, 2015, 69, 86–91 Search PubMed
.
- J. Nasica-Labouze, P. H. Nguyen, F. Sterpone, O. Berthoumieu, N.-V. Buchete, S. Coté, A. De Simone, A. J. Doig, P. Faller, A. Garcia, A. Laio, M. S. Li, S. Melchionna, N. Mousseau, Y. Mu, A. Paravastu, S. Pasquali, D. J. Rosenman, B. Strodel, B. Tarus, J. H. Viles, T. Zhang, C. Wang and P. Derreumaux, Chem. Rev., 2015, 115, 3518–3563 Search PubMed
.
- M. Yang and D. B. Teplow, J. Mol. Biol., 2008, 384, 450–464 Search PubMed
.
- M. Ito, J. Johansson, R. Strömberg and L. Nilsson, PLoS One, 2011, 6, e17587 Search PubMed
.
- Y.-S. Lin, G. R. Bowman, K. A. Beauchamp and V. S. Pande, Biophys. J., 2012, 102, 315–324 Search PubMed
.
- N. G. Sgourakis, Y. Yan, S. McCallum, C. Wang and A. E. Garcia, J. Mol. Biol., 2007, 368, 1448–1457 Search PubMed
.
- B. Barz and B. Urbanc, PLoS One, 2012, 7, e34345 Search PubMed
.
- D. J. Rosenman, C. Wang and A. E. García, J. Phys. Chem. B, 2016, 120, 259–277 Search PubMed
.
- A. Huet and P. Derreumaux, Biophys. J., 2006, 91, 3829–3840 Search PubMed
.
- B. Tarus, J. E. Straub and D. Thirumalai, J. Mol. Biol., 2005, 345, 1141–1156 Search PubMed
.
- B. Urbanc, L. Cruz, F. Ding, D. Sammond, S. D. Khare, S. V. Buldyrev, H. E. Stanley and N. V. Dokholyan, Biophys. J., 2004, 87, 2310–2321 Search PubMed
.
- N. Blinov, L. Dorosh, D. Wishart and A. Kovalenko, Biophys. J., 2010, 98, 282–296 Search PubMed
.
- N.-V. Buchete, R. Tycko and G. Hummer, J. Mol. Biol., 2005, 353, 804–821 Search PubMed
.
- N.-V. Buchete and G. Hummer, Biophys. J., 2007, 92, 3032–3039 Search PubMed
.
- A. Kahler, H. Sticht and A. H. C. Horn, PLoS One, 2013, 8, e70521 Search PubMed
.
- D. Thirumalai, G. Reddy and J. E. Straub, Acc. Chem. Res., 2012, 45, 83–92 Search PubMed
.
- J. J. Valle-Delgado, M. Alfonso-Prieto, N. S. de Groot, S. Ventura, J. Samitier, C. Rovira and X. Fernàndez-Busquets, FASEB J., 2010, 24, 4250–4261 Search PubMed
.
- S. L. Gallion, PLoS One, 2012, 7, e49375 Search PubMed
.
- H. Jang, F. T. Arce, S. Ramachandran, R. Capone, R. Azimova, B. L. Kagan, R. Nussinov and R. Lal, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6538–6543 Search PubMed
.
- W. Li, J. Zhang, Y. Su, J. Wang, M. Qin and W. Wang, J. Phys. Chem. B, 2007, 111, 13814–13821 Search PubMed
.
- D. F. Raffa and A. Rauk, J. Phys. Chem. B, 2007, 111, 3789–3799 Search PubMed
.
- J. M. Borreguero, B. Urbanc, N. D. Lazo, S. V. Buldyrev, D. B. Teplow and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6015–6020 Search PubMed
.
- S. Yun, B. Urbanc, L. Cruz, G. Bitan, D. B. Teplow and H. E. Stanley, Biophys. J., 2007, 92, 4064–4077 Search PubMed
.
- B. Urbanc, M. Betnel, L. Cruz, G. Bitan and D. B. Teplow, J. Am. Chem. Soc., 2010, 132, 4266–4280 Search PubMed
.
- M. Cheon, C. K. Hall and I. Chang, PLoS Comput. Biol., 2015, 11, e1004258 Search PubMed
.
- S. Santini, N. Mousseau and P. Derreumaux, J. Am. Chem. Soc., 2004, 126, 11509–11516 Search PubMed
.
- N. Ferguson, R. Day, C. M. Johnson, M. D. Allen, V. Daggett and A. R. Fersht, J. Mol. Biol., 2005, 347, 855–870 Search PubMed
.
-
A. R. Lam Ng, PhD thesis, Boston University, 2008, p. 80
.
- A. Baumketner and J.-E. Shea, J. Mol. Biol., 2007, 366, 275–285 Search PubMed
.
- R. Laghaei, N. Mousseau and G. Wei, J. Phys. Chem. B, 2011, 115, 3146–3154 Search PubMed
.
- A. Barducci, M. Bonomi, M. K. Prakash and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4708–E4713 Search PubMed
.
- L. E. Buchanan, E. B. Dunkelberger, H. Q. Tran, P.-N. Cheng, C.-C. Chiu, P. Cao, D. P. Raleigh, J. J. de Pablo, J. S. Nowick and M. T. Zanni, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19285–19290 Search PubMed
.
- S. Piana and A. Laio, J. Phys. Chem. B, 2007, 111, 4553–4559 Search PubMed
.
- P. H. Nguyen, M. S. Li and P. Derreumaux, Phys. Chem. Chem. Phys., 2011, 13, 9778–9788 Search PubMed
.
- W. M. Berhanu, F. Yaşar and U. H. E. Hansmann, ACS Chem. Neurosci., 2013, 4, 1488–1500 Search PubMed
.
- J. A. Lemkul and D. R. Bevan, J. Phys. Chem. B, 2010, 114, 1652–1660 Search PubMed
.
- T. Lührs, C. Ritter, M. Adrian, D. Riek-Loher, B. Bohrmann, H. Döbeli, D. Schubert and R. Riek, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17342–17347 Search PubMed
.
- W. Xi, W. Li and W. Wang, J. Phys. Chem. B, 2012, 116, 7398–7405 Search PubMed
.
- J. Zheng, H. Jang, B. Ma and R. Nussinov, J. Phys. Chem. B, 2008, 112, 6856–6865 Search PubMed
.
- W. Han and K. Schulten, J. Am. Chem. Soc., 2014, 136, 12450–12460 Search PubMed
.
- A. De Simone and P. Derreumaux, J. Chem. Phys., 2010, 132, 165103 Search PubMed
.
- J.-X. Lu, W. Qiang, W.-M. Yau, C. D. Schwieters, S. C. Meredith and R. Tycko, Cell, 2013, 154, 1257–1268 Search PubMed
.
- M. Schmidt, A. Rohou, K. Lasker, J. K. Yadav, C. Schiene-Fischer, M. Fändrich and N. Grigorieff, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11858–11863 Search PubMed
.
- J. H. Choi, C. Govaerts, B. C. H. May and F. E. Cohen, Proteins, 2008, 73, 150–160 Search PubMed
.
- Q. Van Vuong, Z. Bednarikova, A. Antosova, P. D. Q. Huy, K. Siposova, N. A. Tuan, M. S. Li and Z. Gazova, Med. Chem. Commun., 2015, 6, 810–822 Search PubMed
.
- M. R. Smaoui, F. Poitevin, M. Delarue, P. Koehl, H. Orland and J. Waldispühl, Biophys. J., 2013, 104, 683–693 Search PubMed
.
- M. Stepanova, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 051918 Search PubMed
.
- N. Blinov, M. Berjanskii, D. S. Wishart and M. Stepanova, Biochemistry, 2009, 48, 1488–1497 Search PubMed
.
- K. Barakat, B. B. Issack, M. Stepanova and J. Tuszynski, PLoS One, 2011, 6, e27651 Search PubMed
.
- K. P. Santo, M. Berjanskii, D. S. Wishart and M. Stepanova, Prion, 2011, 5, 188–200 Search PubMed
.
- B. B. Issack, M. Berjanskii, D. S. Wishart and M. Stepanova, Proteins: Struct., Funct., Bioinf., 2012, 80, 1847–1865 Search PubMed
.
- A. Potapov and M. Stepanova, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 020901(R) Search PubMed
.
- L. Dorosh, O. A. Kharenko, N. Rajagopalan, M. C. Loewen and M. Stepanova, PLoS Comput. Biol., 2013, 9, e1003114 Search PubMed
.
- O. Stueker, V. A. Ortega, G. G. Goss and M. Stepanova, Small, 2014, 10, 2006–2021 Search PubMed
.
- L. Dorosh, N. Rajagopalan, M. C. Loewen and M. Stepanova, FEBS Open Bio, 2014, 4, 496–509 Search PubMed
.
- F. C. Bernstein, T. F. Koetzle, G. J. Williams, E. F. Meyer, M. D. Brice, J. R. Rodgers, O. Kennard, T. Shimanouchi and M. Tasumi, Eur. J. Biochem., 1977, 80, 319–324 Search PubMed
.
- Accelrys Discovery Studio Visualiser, BIOVIA.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 Search PubMed
.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 Search PubMed
.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 Search PubMed
.
- C. Wu, M. M. Murray, S. L. Bernstein, M. M. Condron, G. Bitan, J.-E. Shea and M. T. Bowers, J. Mol. Biol., 2009, 387, 492–501 Search PubMed
.
- S. Côté, P. Derreumaux and N. Mousseau, J. Chem. Theory Comput., 2011, 7, 2584–2592 Search PubMed
.
- S. Kim, T. Takeda and D. K. Klimov, Biophys. J., 2010, 99, 1949–1958 Search PubMed
.
- I. A. Mastrangelo, M. Ahmed, T. Sato, W. Liu, C. Wang, P. Hough and S. O. Smith, J. Mol. Biol., 2006, 358, 106–119 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6mb00441e |
| ‡ Current address: Department of Electrical and Computer Engineering, University of Alberta; 11-203 Donadeo Innovation Centre for Engineering, 9211-116 Street NW, Edmonton, Alberta, Canada T6G 1H9. Tel: +1-780-492-3332. |
| This journal is © The Royal Society of Chemistry 2017 |