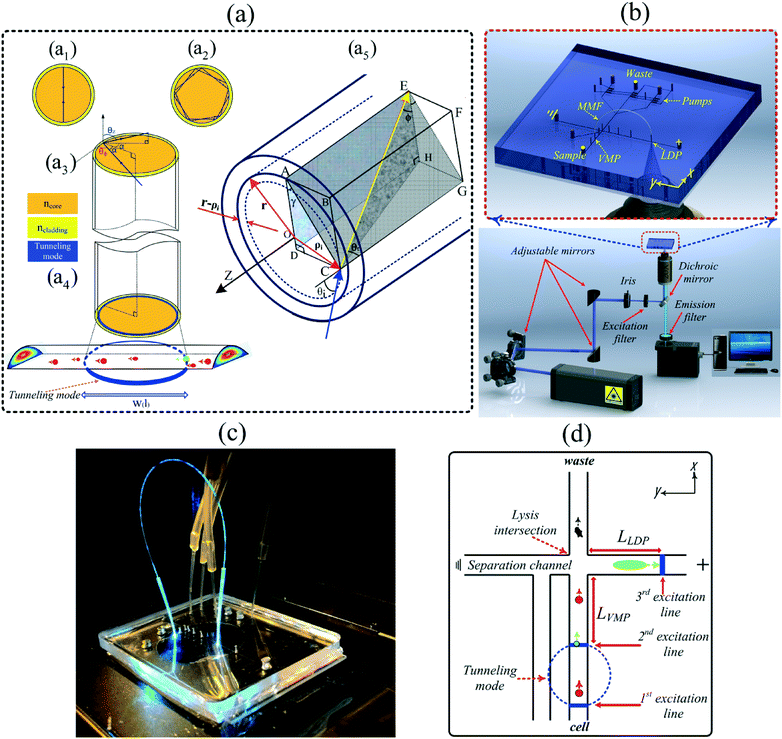
Out-of-plane integration of a multimode optical fiber for single particle/cell detection at multiple points on a microfluidic device with applications to particle/cell counting, velocimetry, size discrimination and the analysis of single cell lysate injections†
Jalal
Sadeghi‡
ab,
Damith E. W.
Patabadige‡
a,
Anne H.
Culbertson
a,
Hamid
Latifi
b and
Christopher T.
Culbertson
 *a
*a
aDepartment of Chemistry, Kansas State University, Kansas, 66506, USA. E-mail: culbert@ksu.edu
bLaser & Plasma Research Institute, Shahid Beheshti University, Evin, Tehran, 1983963113, Iran
First published on 24th November 2016
Abstract
In this paper a single particle/cell-tracking microfluidic device that integrates an out-of-plane multimode optical fiber (OP-MMF) is reported. This OP-MMF is used to generate three excitation light-lines and three detection spots using only one excitation source and one detector. It takes advantage of an optical tunneling mode to create two excitation lines in a microfluidic channel emanating from a single fiber end. This method was used to accurately count particles/cells and perform velocity measurements and size discrimination. The velocity and size distributions of 5, 7, and 10 μm fluorescently labeled polystyrene beads were determined using the OP-MMF. Additionally, this method was used to analyze cell lysates with the third excitation line in the separation channel. The OP-MMF setup accurately detected an intact cell twice ∼2 mm prior to lysis, determined its velocity, and detected the injected cell lysate 3 mm downstream of the injection point in the separation channel. Using this setup, the velocity of cells entering the lysis intersection and the absolute migration times of fluorescently labeled analytes injected into the separation channel were determined in an automated fashion. This method enabled us to determine a lysing/injection efficiency coefficient (K) using signals from the injected lysate signal and from the intact cell before lysing. K provided a reliable measurement of the amount of cell lysate that was injected into the separation channel. The approach reported here could be used in the future to track particles, cells or droplets in a variety of existing microfluidic devices without the need for multiplexed masks, layers, bulky optical elements or complex optical designs.
Introduction
Interest in microfluidic devices for the analysis of cells and particles continues to increase due, in large part, to the flexibility in being able to design the channel manifold to perform a variety of operations on the cells as they are transported through the channels.1–5 Often, this transport is controlled through the generation of pressure differentials in the channels which creates a hydrodynamic flow. The flow profile in the channel, therefore, is parabolic in nature with the highest flow velocity in the center of the channel and the lowest velocity along the walls.6 Cells or particles are, therefore, transported at different velocities depending upon their axial location in the channel. These velocity differences can cause issues and uncertainties with the transport and manipulation of particles/cells in these devices. Therefore, simple, inexpensive and easy-to-implement methods to characterize the exact nature of this flow and to monitor it in real time, could substantially improve the ability to track, transport, and manipulate particles/cells in microfluidic devices. Such capabilities are especially relevant in flow cytometry techniques where cell sorting, cell counting, cell trapping and cell lysis operations are implemented.4,5,7 Many different techniques to measure cell velocities on microfluidics devices have been developed.8,9 For example, particle image velocimetry (PIV) is used for real-time deformability cytometry10 or for the direct measurement of velocity fields in experimental systems.11 A specially designed optical space-time coding method using a spatially patterned mask has also been reported for determining cell velocity.12,13 The mask modulates the optical forward scattering or fluorescent emission propagating toward the detectors. Cell tracking information has also been obtained using a mathematical signal processing algorithm from time-domain modulated signals.13 Finally, the creation of a structured light intensity pattern without using a patterned mask has been used to measure cell velocities. For this method a spatial light modulator (SLM) was used in place of a patterned optical mask.14,15 In addition to velocity information, several of these methods can also be used to determine the average size of the cells/particles.16–18 Both theoretical and experimental studies have revealed a correlation between equilibrium position/velocity of cells/particles in the channels and their size as a function of channel cross section geometry, flow profiles and Reynolds numbers regimes.19,20 While useful, these optical detection methods are difficult to implement, mathematically complex and/or the spatial distance needed between particles to avoid interference is relatively large. For simple velocimetry measurements creating 2 detection spots in close proximity (i.e. <1 mm) to measure cell velocity is difficult and requires the use of multiple detectors. Therefore a simpler, less expensive method to obtain this information would be highly useful.12We recently reported a method to incorporate 2 detection points in close proximity on a microfluidic device using an optical fiber bridge.21 In this system, light was focused into a microfluidic channel to form one detection point using an epi-illumination system. A short length of optical fiber was inserted 30 μm above the channel at this detection point. The focused light from the epi-illumination system was also coupled into the fiber. The other end of the fiber was placed at another location 30 μm above a channel in the channel manifold. The light from the fiber then created a second excitation spot in the channel, and thus a second detection point, using only one excitation source and one detector. While the system could create 2 detection spots in close proximity (∼1–2 mm) for velocity determinations, an even closer set of detection points was desired. In addition, the excitation spot size (118 μm) was larger than desired and limited the spatial resolution. In order to decrease the distance between the detection spots and create narrower excitation lines, a rarely used optical fiber light propagation method has been employed and will be reported in this paper. As explained in more detail below, tunneling modes were created in a multimode optical fiber resulting in a ring of excitation light emanating from the end of the fiber. When this fiber was placed above the channel, 2 excitation lines were formed as shown in Fig. 1. These lines were narrow (∼8 μm wide) and only ∼110 μm apart. The velocities of cells and particles passing through the 2 points could easily be determined. In comparison to the methods mentioned above, cell/particle excitation-emission using an out-of-plane multimode optical fiber (OP-MMF) has several advantages. First, the high spatial resolution generated by the narrow (∼8 μm) excitation lines can significantly decrease particle/cell detection overlap problems. This is in contrast to other methods such as the spatially patterned mask that has a detection length of 980 μm and thus requires a much larger spatial separation of particles in the channels.13 Second, a high signal to noise ratio (S/N) is generated from the concentrated excitation beam intensity, and the narrow field of view of the fluorescence collection minimizes environmental stray light. Third, the OP-MMF detection point can be moved easily, compared to the use of in situ fabricated fixed planer waveguides.22–26 Fourth, the functionally rectangular excitation beam of the OP-MMF, in comparison to the focused circular beams of a microscopic epi-illumination system, can cover the whole channel width. Finally, the OP-MMFs have low light attenuation, have high throughput data handling capacities, are flexible, and are cost effective.
In actuality, with this system, 3 detection points are created as the end of the fiber into which the excitation light was coupled was situated above a detection point also (Fig. 1b–d). With this optical setup the efficiency of cell lysis and the efficiency of cell lysate injection were determined in a microfluidic single cell analysis device. As cells enter the lysis intersection they are axially distributed throughout the channel cross section. As such, they will have different velocities due to the parabolic nature of the hydrodynamic flow. These varying velocities mean that the time over which the cell is exposed to the electric field used to lyse the cell will also vary. If the cells enter the lysis intersection too quickly they are either not lysed or only partially lysed, as their interaction time with the electric field is limited. This can result in partial injections of the cellular content and thus can generate misleading results and conclusions because of the biased nature of the injections. This 3 detection point technique allows one to characterize the maximum velocity that a cell can enter into the intersection and still be completely lysed and the lysate completely injected. This technique can be used to characterize the flow in a microfluidic manifold, or be employed in any experiment in order to provide real-time feedback on how well the system is functioning.
In this paper the theory behind the optical fiber tunneling mode is developed and the usefulness of this light propagation mode to create two closely spaced excitation lines is shown. With this OP-MMF configuration, the velocity distributions for 3 different sizes of particles were measured and a correlation between particle size and the average particle velocity was developed. Lastly, using this device, the relationship between the cell velocity entering the lysis intersection and the efficiency of cell lysis and lysate injection into a separation channel was demonstrated.
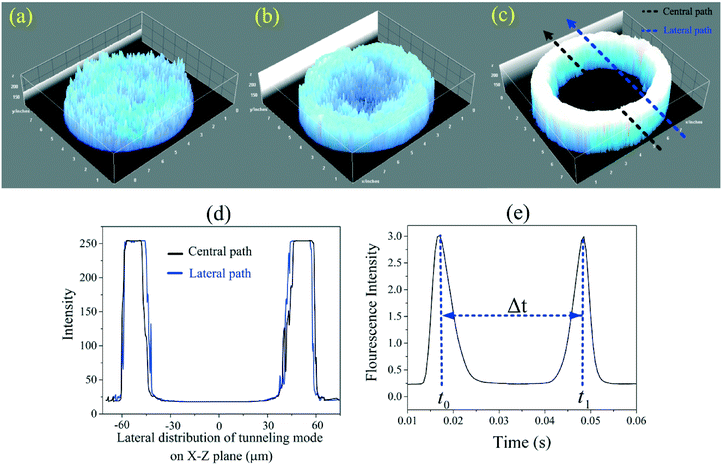
Characterization of the optical fiber light modes
According to optical waveguide theory, optical modes in a waveguide can be divided into two classes: guiding modes (bound rays) and leaky modes (refracting rays).27 Guiding modes propagate along the waveguide via total internal reflection (TIR), while leaky modes completely disappear within an extremely short distance. However, in cylindrical multimode waveguides, such as large core multimode optical fibers (MMF), a third class of modes arise that are distinct from both guiding and leaky modes; these modes are called tunneling modes (i.e. tunneling rays).28 A MMF can propagate light via hundreds of guiding modes and the interference of these modes at the fiber output usually generates a random speckle pattern (Fig. 2a).15 However, under specific optical conditions when laser light is focused into MMF input, tunneling modes can be excited and travel to the other end of the fiber resulting in a ring-like output pattern as illustrated in Fig. 2c.The general ray paths and mode regions valid for all rays propagating along the MMF can be defined by the spherical polar angles θφ and θz, where angle θφ is the azimuthal propagation angle and θz represents the longitudinal propagation angle, i.e. the angle between the ray and the optical axis. Bound rays are only defined by θz while tunneling rays are defined by both θφ and θz. Unlike bound rays, which are confined within the critical angle, θc, given by 0 ≤ θz < θc, tunneling rays are confined within the ranges given by θc ≤ θz ≤ π/2 and αc ≤ α ≤ π/2 where αc = sin−1(ncladding/ncore), θc = cos−1(ncladding/ncore) where the angle of incidence, α, is depicted in Fig. 1(a3) and given by cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = sin
α = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θz
θz![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θφ. In contrast to bound rays which cross the fiber axis (Fig. 1(a1)), tunneling rays never cross the fiber axis (Fig. 1(a2)).29
θφ. In contrast to bound rays which cross the fiber axis (Fig. 1(a1)), tunneling rays never cross the fiber axis (Fig. 1(a2)).29
In general, tunneling rays have larger losses than bound rays, but under certain conditions the overall power detected at the fiber end may be in the same range as that for bound rays. Finding the excitation power of different rays requires the evaluation of eqn (1) which represents summation over all rays
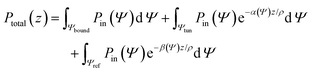 | (1) |
In order to evaluate this second term so that the power attenuation of the tunneling rays can be determined, two arbitrary parameters of L and D are defined by eqn (2a) and (2b)
 | (2a) |
D = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L L | (2b) |
For most tunneling rays of interest, the attenuation factor α(ψ)z/ρ from the 2nd term can be written in the following form
 | (3) |
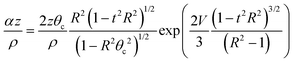 | (4) |
R = (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θz/θc) θz/θc) | (5a) |
t = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θφ θφ | (5b) |
| V is large (≥190) | (5c) |
Here g(R,t) can become large for a small number of rays with very large R values and t ∼ 0. For instance, when the rays are excited by a diffuse, Lambertian light source, over 90% of tunneling rays have R < 5 and g(R,t) < 29. In our optical configuration with a 488 nm laser source and MMF with θc ≈ 11.5 and ρ = 52.5 μm the vast majority of rays have g(R,t) ≈ 1. This results in the tunneling rays being divided into two different classes: f(R,t)L < 1 which leads to rays being greatly attenuated and f(R,t)L > 1 in which the rays are propagated with no attenuation. This allows us to explicitly determine an effective domain for tunneling rays with low attenuation. To determine this domain we must solve f(R,t)L = 1 in (R,t) space. For real values of t, the upper limits Rb and tb on R and t, respectively are:
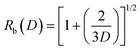 | (6) |
 | (7) |
 | (8) |
Values of R and t smaller than the values given by eqn (6) and (7) satisfy f(R,t)L > 1 and thus should be minimally attenuated. Eqn (5a), and (5b), can then be used to optimize the input angle to maximize excitation power. Several fiber techniques have been developed to generate such ring-like patterns while employing several polarization dependent higher-order modes.30 Since these mode generations involve several hybrid modes propagating at different phase velocities, the intensity distribution will vary strongly along the fiber (Fig. 1(a5)). Unlike higher-order guiding modes, a tunneling mode as a stable pattern is bounded between two specific rings. Therefore, the width of ring-like pattern depends on the rings' radii. As indicated in Fig. 1(a3) and (a5) and according to eqn (4) to (8), rays can be launched from anywhere ρi across the core surface under the incidence angle of θi. One such ray (yellow arrow), lying in the plane of ACGE, shows the maximum space that can be occupied between the first ring with a radius of ρi in a fiber core with a radius of r. Here r − ρi is the width of the ring-like pattern. In this paper, we show how the tunneling rays can be used as the dominant excitation rays in comparison to bound rays with application to single cell measurements in microfluidic devices.
Materials and methods
Reagents and materials
Dow corning Sylgard 184 silicone elastomer kits were purchased from Ellsworth adhesives (Germantown, WI). SU-8 2010 photoresist was obtained from MicroChem (Westborough, MA). AZ P4620 photoresist was acquired from AZ Electronic Materials (Branchburg, NJ). Silicon wafers (100 mm P(100) 1–10 ohm cm SSP 500um Prime Grade single side polished) were purchased from University Wafer (Boston, MA). 6-Carboxyfluorescein diacetate (6-CFDA, ∼95%) was obtained from Sigma-Aldrich (Saint Louis, MO). Yellow-green fluorescent polystyrene latex microbeads (5, 7 and 10 μm) were purchased from Magsphere Inc. (Pasadena, CA). Deionized water was generated using 18 Mohm Millipore Synthesis A10 system (Billerica, MA, USA). A length of multimode optical fiber (0.22 NA, core Ø105 μm) was acquired from Thorlabs Inc. (Newton, NJ).Cell culturing
T-lymphocytes obtained from Clone E6-1 cell line (ATCC TIB-152 American Type Culture Collection, Rockville, MD, USA) were cultured as described previously.31Microchip fabrication
The two-layer PDMS microchip was fabricated as previously reported.31 Briefly, master molds for the microfluidic channel manifold and the microvalve/pump manifold were created using AZ-P 4620 photoresist and SU8-2010 photoresist, respectively. The micropump manifold was molded in a 5 mm thick layer of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS, and the microfluidic channel layer was molded in a 50 μm thick layer of 30
1 PDMS, and the microfluidic channel layer was molded in a 50 μm thick layer of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS separately. The micropump control valves were 22 μm high and the effective surface area between the pump and channel layer was 100 μm × 200 μm. The channels in the bottom layer were 18 μm high. The gap between micropumps and fluidic channels was 32 μm. Detailed dimensions of the device are given in the ESI.†
1 PDMS separately. The micropump control valves were 22 μm high and the effective surface area between the pump and channel layer was 100 μm × 200 μm. The channels in the bottom layer were 18 μm high. The gap between micropumps and fluidic channels was 32 μm. Detailed dimensions of the device are given in the ESI.†
Optical detection system and generation of optical fiber tunneling modes
A 105/125 μm multimode fiber (MMF) (Thorlabs FG105UCA, N.A. = 0.22) was used to generate tunneling modes with a uniform irradiance distribution.29 As illustrated in Fig. 1(b), several optical elements (i.e. elliptical mirrors and an iris diaphragm) were used to direct the beam into the rear port of a commercial inverted Nikon TS-100 microscope (Nikon Instruments, Inc., Melville, NY) and control the incidence angle (α) of the rays into the optical fiber. A 20× microscope objective (NA = 0.45) and Z-axis control (i.e. focusing knob) were used to control the laser spot size of a laser beam. Also, the stage upon which the microchip sat was equipped with a translational controller knob to adjust the optical incidence position (ρi2 = X2 + Y2) at the MMF end face. The objective lens had an effective working distance of 7.4 mm with focal length of 9 mm. The beam with a diameter of 8 μm was focused into the incident point (on the separation channel) with the following characteristics of 40 ≤ ρi < 52.5, 78° ≤ α < 90°, 11.5° ≤ θz < 90°.The fiber was bridged between the velocity measuring point (VMP) in the cell handling channel and the lysate detection point (LDP) in the separation channel. As shown in Fig. 1(c), a few millimeter long pipette tip was used as a clamp in order to hold the ends of the optical fibers in place and to adjust the X, Y and Z positions of the both ends of the MMF's relative to the channels as previously described.21 Over the 1 cm length of the nozzle, the cone diameter tapered from 1 mm down to 300 μm which was suitable for fiber clamping. The excitation source was a 488 nm line from a multiline argon-ion laser (MellesGriot Laser Group, Carlsbad, CA). The focused excitation beam from the 20× microscope objective could be easily coupled into the bridged fiber at the LDP. The fiber then transmitted the excitation light via tunneling to create the VMP. The tunneling mode and microchannel junction made two uniform light-lines that perpendicularly covered the channel width (Fig. 1(a4) and (d)).
At the VMP, intact fluorescently labeled cells could be excited two times at shown in Fig. 1d. resulting in two sharp emission spikes (Fig. 2e). After the cell was lysed at the intersection, the lysate was electrophoretically injected into the separation channel and the fluorescently labeled substrate electrophoretically transported down the separation channel, where the third focused beam excited the cell lysate (LDP) and caused the third emission spike (Fig. 4a–c). Two sharp emission spikes due to the fiber's backward collection, and the third emission spike were all detected by the same photomultiplier tube (Hamamatsu Instruments, Bridgewater, NJ) attached to the trinocular port of the microscope.
Sample preparation
Jurkat cells were loaded with 6-carboxyfluorescein diacetate (6-CFDA) as previously reported.31 Briefly, 50 μL of 2 mM 6-CFDA in a DMSO stock solution was aliquoted and introduced into a cell culture flask such that the final concentration of the fluorescent dye was 50 μM. Cells were then incubated for 20 min at 37 °C in a 5% CO2 environment. After incubation, the cells were centrifuged for 3 min at 2000 rpm. The supernatant was then removed and the cell pellet was resuspended in a warm, sterile PBS solution. The centrifugation/resuspension process was repeated two more times to minimize the fluorescent background from the non-loaded dye.The fluorophore (carboxyfluorescein diacetate; CFDA) was used to label cells. This species is cell permeable and non-fluorescent in nature. After passively diffusing onto the cells, the CFDA is hydrolysed by intracellular esterases and the fluorescent product (carboxyfluorescein; CF) is formed. All live cells are labeled. Due to the hydrophilic nature of the product, it is trapped inside the cells and stable for significant time period (>1 h) as previously reported.31
Five, 7 and 10 μm diameter green fluorescent (480/501 nm) polystyrene latex beads (Magsphere Inc., Pasadena, CA) were separately prepared in 10 mM sodium borate solutions such that the final concentration of each solution was 1 × 104 beads per mL. Also, a mixture of each size of beads was prepared in same manner such that concentration of each type was 3 × 103 beads per mL.
Microchip operation – bead experiments
All of the microfluidic channels were filled with 10 mM sodium borate solution at pH = 7.2. A sample of polystyrene beads was placed in the sample reservoir. Fluid flow between the sample reservoir and the waste reservoir was generated using the 3 peristaltic pumps that were integrated with the three parallel fluidic channels.31 Stable and consistent hydrodynamic flow was generated using multilayer soft lithographic valves integrated into the device. This device has been previously characterized in terms of long-term stability and flow rates and showed no experimentally measurable changes in flow over a >80 min time period while continuously pumping cells.31 In addition, when flow rate changes were introduced intentionally, the flow rates were reproducible for a given actuation frequency and pressure, and they could be controlled precisely over a wide range of particle/cell velocities.Microchip operation – cell experiments
Single cell manipulation was performed as previously reported.31 Briefly, all of the fluidic channels were filled with a separation buffer that contained 2% BSA (w/v), 20% acetonitrile (v/v), 40 mM sodium borate, 2 mM SDS and 0.2% tween 20 (w/v). Fluorescently labeled Jurkat cells were introduced into sample reservoir. Single cells were then driven towards waste reservoirs using the peristaltic pumps at an average flow rate of 5 nL s−1. As each cell reached the lysing intersection, they were automatically lysed with a constant electric field (∼700 V cm−1) that was applied across the 5 cm long separation channel. The flow rate was finely adjusted so that cell debris were rejected towards waste reservoir and charged fluorescently labeled analytes were injected into the separation channel. The intact cell was detected just prior to lysing using the fiber bridge (zero detection point), and the lysate was detected 2 mm downstream of the lysis intersection directly using the epi-illumination system.Results and discussion
Particle velocimetry
Particle velocimetry is based on the measurement of the velocity (V) of a particle between 2 detection points. In other words, the velocity of a cell is acquired by dividing the distance between the two points (Wl) by the time elapsed between the two recorded signals (Δt), i.e. V = Wl/Δt where, Wl is defined as the external diameter of the expanded tunneling mode at the mid-plane of the channel. According to the beam divergence principle,32 the beam diameter at a position l, as shown in Fig. 1(a4), can be found from | (9) |
As performed in our previous work21 the collection efficiency of the emitted light into the fiber bridge at the ZDP which was calculated to be <94% while the actual coupling efficiency for the fiber was determined to be 45 ± 5%. Unlike the coupling efficiency, the ratio of effective excitation intensities depends on the optical modes. According to the optical dispersion principle, the 105 μm multimode fiber used in the experiments reported here produced expanded light spots with diameter of 118 μm at the mid-plane of the microfluidic channel, which was ∼45 μm from the end of the fiber. Based on the modal field distribution, for the same input power, the ratio of the effective excitation intensity between guiding (Ieff(G)) and tunneling (Ieff(T)) modes can be derived as,
 | (10) |
Determination of particle size and velocity
The ability of the tunneling optical fiber bridge detection setup to both determine particle size and velocity was examined using fluorescently labeled polystyrene particles of different sizes. The initial assay was performed using a suspension of particles that were 5, 7, and 10 μm in diameter at approximately equal concentrations. As shown in Fig. 3(a), the fluorescent signals can be divided easily into three groups based upon the size of the fluorescent beads. The relative standard deviations (RSDs) for the 5, 7, and 10 μm diameter beads were determined to be 5.1%, 6.9%, and 7.8%, respectively. These values were close to the RSD values of 10% reported by the manufacturer and most likely a more accurate assessment of the size distribution for the particular batches used.The minimum interval between cells/particles/samples that can be distinguished using the tunneling excitation and detection scheme can be determined using the resolution equation, Rs = Δt/4σ.34 In this equation Δt is the time difference between two particles passing between the excitation lines from the fiber optic, σ is the average standard deviation of the width of the two spikes, and 4σ is used as the baseline width of a spike. For the experiment reported in Fig. 3, the average baseline width of the particles was 4σ = 0.0008 s so the minimum temporal spacing of the cells must be >0.8 ms. In comparison, the minimum spacing between particles for guiding modes is ∼4 ms.
The scatter plot in Fig. 3(b) shows the fluorescent intensity as a function of the velocity of the mixture. For each particle size, the average and standard deviation of the velocity was determined as well as the spread of the velocities and are reported in Table 1. The low velocity standard deviation (SD) for the 10 μm population indicated that particle velocities were close to the mean velocity which reflected the confinement of this population to the central portion of the microchannel. In contrast, the high velocity-SD of the 5 μm population indicated that they were spread out over a wider area of microchannel and thus sampled a wider range flow streams in the parabolic fluid flow profile.
| Mean particle diameter μm | Mean velocity mm s−1 | Maximum velocity mm s−1 | Standard deviation mm s−1 | Particle count # |
|---|---|---|---|---|
| 10.2 | 4.5 | 6.0 | 0.5 | 794 |
| 7.0 | 6.6 | 15.8 | 2.4 | 805 |
| 5.1 | 7.2 | 21.5 | 3.1 | 945 |
For many applications of particle velocimetry, the particles used to measure the flow are several orders of magnitude smaller than the channel's dimensions in order not to perturb the flow.13 The lateral dimensions of the microfluidic channel manifolds used for precisely moving cells/particles, however, are generally only slightly larger than the cells/particles themselves. Under these conditions, the particles significantly affect the flow profile in their proximity. Therefore, larger particles experience more inertial migration, or in other words, the mean velocity of smaller particles is higher. As shown by the results in Table 1, the mean velocity of particles in microfluidic channels can be utilized to discriminate the various particle populations. The 10 μm population, the 7 μm population and the 5 μm population can be clearly distinguished by means of the measured velocity. The mean velocity of the 10 μm population was 4.5 mm s−1 and thus slower than the 7 μm population with a mean velocity of 6.6 mm s−1 and again slower than the mean velocity of the 5 μm population with 7.2 mm s−1.
Optimization of cell lysis and lysate injection
In this experiment, the optical fiber bridge was used to create 3 detection points – 2 defined by the tunneled light emanating from the optical fiber to measure cell velocity prior to lysis, and one in the separation channel 2 mm downstream of the lysis intersection to detect the injected lysate.According to the electroporation principle, thousands of nanopores are formed when a cell is exposed to an electric field thus permeabilizing the membrane. If the intensity and duration of the electric field exposure are sufficient, the cell membrane is irreversibly compromised leading to cell lysis. Conversely, if electroporation is generated using low electric fields and short exposure times, the pores can reseal themselves after the field is removed.35,36
For this device, the duration of the exposure of the cell to the electric field is determined by the velocity of the cell entering the lysis intersection and, therefore, cell velocity should affect the lysing and lysate injection efficiency. A secondary parameter that also affects cell lysis is cell size,37 with small cells less susceptible to lysing than large ones under the same electroporation conditions. Both the electric field exposure time (via cell velocity measurements) and cell size effects (via intact cell fluorescence) can be measured using the OP-MMF device. Fig. 4(b) shows typical electropherograms of 8 separated cells obtained from an experiment where hundreds of cells were examined. Three distinct peaks from each cell were easily detected (Fig. 4(a)). Two first sharp peaks (magnified in the inset Fig. 4(a)) are from the intact cell at the VMP as discussed in the previous section for determination of size and velocity. From the information shown in the electropherogram (Fig. 4c) the cell velocity (VC = W1(t1 − t0)−1), the absolute migration time of the lysate (ΔtL = t3 – t2) and the lysate velocity (VL = LLDP(t3 − t2)−1) can be determined. Qualitatively, the effect of cell velocity on the efficiency of lysate injection can clearly be seen in Fig. 4c. The electropherograms from the 8 individual cells in this figure are arranged based on the intact cell velocity from 1.1 mm s−1 to 8 mm s−1. These cells were all approximately the same size as judged by their signal at the VDP to eliminate any possible cell size effects. Images of cell lysate injection efficiency as a function of both velocity and size can be found in ESI† Fig. S1.
In order to quantitatively measure the efficiency of injection (K) of the lysate from any cell, the ratio of the amount of the injected lysate (peak area, AL) at the LDP to the maximum fluorescent signal from the intact cell (I) from the VDP was determined as shown in eqn (11)
| K = αAL/I | (11) |
Conclusion
In this work, a simple, fast and cost effective technique to determine the velocity of particles/cells in a high throughput manner was reported. A microfluidic platform with an integrated 10 cm long out-of-plane multimode optical fiber (OP-MMF) was used to create three excitation/detection spots between any two arbitrary points using only a single excitation source and detector. The ability to transmit light through the multimode optical fiber via tunneling modes was utilized to create two excitation/detection lines in the channel at the end of the fiber. These 2 lines were used to monitor particle velocity and determine average particle size. To demonstrate the capability of this system, the velocity and size distributions of 5, 7, and 10 μm fluorescently labeled polystyrene beads were determined. Finally, a third detection point at the end of the fiber, where the excitation light was coupled into the fiber, was used to detect the lysate from the cells whose velocity was determined at the other end of the fiber. With this design, the absolute migration times for cell lysates were measured. This allowed the characterization of migration time and lysate injection efficiency parameters that could not be previously determined. In the future, this device could be coupled with a variety of integrated and tunable microlenses to more easily generate tunneling modes for better emission, optical trapping, and other optofluidic applications.23–26Acronyms
| VMP | Velocity measuring point |
| LDP | Lysate detection point |
| OP-MMF | Out-of-plane multimode optical fiber |
Acknowledgements
This research was funded by NSF grants CHE-1411993 and CBET-1656968.References
- M. G. Roper, Anal. Chem., 2015, 88, 381–394 CrossRef PubMed.
- A. K. Price and C. T. Culbertson, Anal. Chem., 2007, 79, 2614–2621 CrossRef CAS PubMed.
- A. K. Price and B. M. Paegel, Anal. Chem., 2015, 88, 339–353 CrossRef PubMed.
- C. T. Culbertson, T. G. Mickleburgh, S. A. Stewart-James, K. A. Sellens and M. Pressnall, Anal. Chem., 2014, 86, 95–118 CrossRef CAS PubMed.
- D. E. Patabadige, S. Jia, J. Sibbitts, J. Sadeghi, K. Sellens and C. T. Culbertson, Anal. Chem., 2016, 88, 320–338 CrossRef PubMed.
- J. Sadeghi, A. H. B. Ghasemi and H. Latifi, Lab Chip, 2016, 16, 3957–3968 RSC.
- M. E. Piyasena, P. P. Austin Suthanthiraraj, R. W. Applegate Jr., A. M. Goumas, T. A. Woods, G. P. Lopez and S. W. Graves, Anal. Chem., 2012, 84, 1831–1839 CrossRef CAS PubMed.
- J. Oakey, R. W. Applegate Jr, E. Arellano, D. D. Carlo, S. W. Graves and M. Toner, Anal. Chem., 2010, 82, 3862–3867 CrossRef CAS PubMed.
- J. P. Golden, J. S. Kim, J. S. Erickson, L. R. Hilliard, P. B. Howell, G. P. Anderson, M. Nasir and F. S. Ligler, Lab Chip, 2009, 9, 1942–1950 RSC.
- O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold, D. Klaue, S. Girardo, S. Pagliara, A. Ekpenyong, A. Jacobi, M. Wobus, N. Toepfner, U. F. Keyser, J. Mansfeld, E. Fischer-Friedrich and J. Guck, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- M. Travagliati, S. Girardo, D. Pisignano, F. Beltram and M. Cecchini, Anal. Chem., 2013, 85, 8080–8084 CrossRef CAS PubMed.
- T.-F. Wu, Z. Mei and Y.-H. Lo, Lab Chip, 2012, 12, 3791–3797 RSC.
- C. Sommer, S. Quint, P. Spang, T. Walther and M. Bassler, Lab Chip, 2014, 14, 2319–2326 RSC.
- T. Cizmar, M. Mazilu and K. Dholakia, Nat. Photonics, 2010, 4, 388–394 CrossRef CAS.
- S. Bianchi and R. Di Leonardo, Lab Chip, 2012, 12, 635–639 RSC.
- B. Chun and A. J. C. Ladd, Phys. Fluids, 2006, 18, 031704 CrossRef.
- L. Zeng, Copyright (C) 2016 American Chemical Society (ACS). All Rights Reserved., 2007.
- L. Zeng, F. Najjar, S. Balachandar and P. Fischer, Phys. Fluids, 2009, 21, 033302 CrossRef.
- K. J. Humphry, P. M. Kulkarni, D. A. Weitz, J. F. Morris and H. A. Stone, Phys. Fluids, 2010, 22, 081703 CrossRef.
- J. Zhou and I. Papautsky, Lab Chip, 2013, 13, 1121–1132 RSC.
- D. E. W. Patabadige, J. Sadeghi, M. Kalubowilage, S. H. Bossmann, A. H. Culbertson, H. Latifi and C. T. Culbertson, Anal. Chem., 2016, 88, 9920–9925 CrossRef CAS PubMed.
- I. Rodríguez-Ruiz, T. N. Ackermann, X. Muñoz-Berbel and A. Llobera, Anal. Chem., 2016, 88, 6630–6637 CrossRef PubMed.
- Y. C. Seow, A. Q. Liu, L. K. Chin, X. C. Li, H. J. Huang, T. H. Cheng and X. Q. Zhou, Appl. Phys. Lett., 2008, 93, 084101 CrossRef.
- Y. C. Seow, S. P. Lim and H. P. Lee, Microfluid. Nanofluid., 2011, 11, 451 CrossRef.
- Y. C. Seow, S. P. Lim and H. P. Lee, Lab Chip, 2012, 12, 3810–3815 RSC.
- Y. Yang, A. Q. Liu, L. K. Chin, X. M. Zhang, D. P. Tsai, C. L. Lin, C. Lu, G. P. Wang and N. I. Zheludev, Nat. Commun., 2012, 3, 1662 Search PubMed.
- A. W. Snyder and J. Love, Optical waveguide theory, Springer Science & Business Media, 2012 Search PubMed.
- J. Ma and W. J. Bock, Opt. Express, 2007, 15, 16457–16470 CrossRef PubMed.
- J. Ma, W. J. Bock and A. Cusano, Opt. Express, 2009, 17, 7630–7639 CrossRef CAS PubMed.
- Y. Ma, Characterization of Higher Order Modes in Optical Fibers, Erlangen Scientific Press, Friedrich Alexander Univ., 2009 Search PubMed.
- D. E. W. Patabadige, T. Mickleburgh, L. Ferris, G. Brummer, A. H. Culbertson and C. T. Culbertson, Electrophoresis, 2016, 37, 1337–1344 CrossRef CAS PubMed.
- B. E. Saleh, M. C. Teich and B. R. Masters, J. Biomed. Opt., 2008, 13, 9901 CrossRef.
- D. Wu, J. Xu, L.-G. Niu, S.-Z. Wu, K. Midorikawa and K. Sugioka, Light: Sci. Appl., 2015, 4, e275 CrossRef CAS.
- S. C. Jacobson and C. T. Culbertson, Microfluidics: Some Basics, in Separation Methods in Microanalytical Systems, ed. J. P. Kutter and Y. Fintschenko, CRC Press, Boca Raton, FL, 2006, pp. 19–64, ISBN 0-8247-2530-1 Search PubMed.
- M. A. McClain, C. T. Culbertson, S. C. Jacobson, N. L. Allbritton, C. E. Sims and J. M. Ramsey, Anal. Chem., 2003, 75, 5646–5655 CrossRef CAS PubMed.
- H.-Y. Wang and C. Lu, Chem. Commun., 2006, 3528–3530, 10.1039/b605722e.
- N. Bao, T. T. Le, J.-X. Cheng and C. Lu, Integr. Biol., 2010, 2, 113–120 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6lc01161f |
| ‡ These authors contributed equally to the paper. |
| This journal is © The Royal Society of Chemistry 2017 |