The effect of colloidal aggregates on fat crystal networks

Abstract

We investigate the role of a colloidal model system in the crystallization and network formation of lipids. This system consists of fractal fumed silica aggregates. We look at the influence of different solid fat concentrations and fumed silica concentrations on the resulting gel network. Oscillatory rheology shows that the addition of silica to fat-in-oil gels does not significantly affect the magnitude of the storage modulus within the linear viscoelastic region. Interestingly, the range of this region is increased. Differential scanning calorimetry shows that the presence of silica leads to slightly earlier crystallization, though no significant effect on the melting profile of the formed network is found. Based on these observations, we propose that composite gel network structures have been formed. These results show that we have created reduced solid fat alternatives with similar rheological behaviour and thermal properties as the full-fat systems through the addition of colloidal silica.

---

1 Introduction

Fats are a fundamental part of our diet: as an energy source, a supply of essential fatty acids and a carrier for fat-soluble vitamins.^1,2 Fats are also building blocks in food products like butter and chocolate, which are structured by three-dimensional networks of solid fat crystals.³ Many of the properties of foods like texture and spreadability, can be directly related to these microscopic crystals.^4,5 For example, the snap of chocolate and the way it melts in the mouth can be linked to the fat crystals and the way they interact with each other.

Although the links between dietary fat and health risks are still debated,⁶ there has been a drive by food manufacturers to remove or reduce the amount of saturated fat in their products. This has directed research into a reduction in the amount of fat whilst trying to retain the desirable properties that consumers look for in their products.^7–9 One approach focuses on replacing the solid fat with other substances like waxes^10,11 to form organogels, whilst others look at forming novel structures like ‘aqueous-organic’ bigels,¹² gel-in-oil-in-gel structured emulsions¹³ or quiescent water-in-oil Pickering emulsions.¹⁴

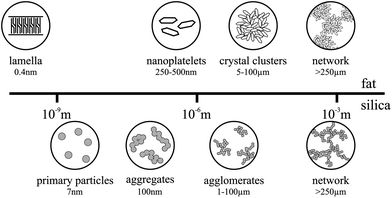
A number of studies have been undertaken to fully understand the different levels of structure in fat crystal networks, which have been recently summarized by Acevedo et al.,¹⁵ shown in Fig. 1. X-ray crystallography has shown various possible conformations for triglyceride molecules including a chair and tuning fork configuration.^16,17 In these conformations, the triglyceride molecules can self-assemble to form lamella structures, which then stack to form nanoplatelets. These lamellae and nanoplatelets can be observed and quantified by a novel technique of cold solvent extraction prior to cryogenic TEM imaging.¹⁸ It is thought that these nanoplatelets aggregate in a fractal manner to form crystal clusters.^19–21 This has been investigated in depth recently using computer simulation and ultra-small angle X-ray scattering (USAXS).^22–26 The lengthscale of these clusters can range from roughly 5–100 μm depending on the crystallization conditions, with smaller clusters being formed at faster cooling rates. These clusters then loosely pack to form chains and eventually a 3D fat network through the system.

Fig. 1 The different levels of structure in the fat¹⁵ and silica networks.²⁷

Fumed silica is a type of colloidal silicon dioxide, which is used in the food industry as an anti-caking and anti-foaming agent (E551). We are using it here as a model to manipulate the fat crystal network. Fumed silica is formed by a flame hydrolysis process using silicon tetrachloride (SiCl₄).²⁷ This process produces non-porous, spherical primary particles which then, due to the residual heat from the production process, fuse together irreversibly to form fractal aggregates. These aggregates have silanol (Si–OH) groups on their surface and so they are able to bond via hydrogen bonds to form larger agglomerates and finally a network spanning the entire system,²⁸ see Fig. 1. Unlike the fat, the silica network does not melt or break down with heat at the temperatures used in our experiments, but it is affected by shear which can break down the network back to the aggregate level.²⁷

This study investigates the interaction between fumed silica aggregates and fat crystal networks. We are using tripalmitin fat (PPP) in soybean oil as a simplified model system for fat structured products, which are made up of a continuous liquid oil phase structured by a three-dimensional fat crystal network. In particular, we measure a range of samples prepared at different fat–silica ratios to determine the effect of silica on the fat crystal networks. Our ultimate aim is to use edible colloidal particles to guide the design of lower fat foods that have thermal and mechanical properties which are not significantly different from their full fat counterparts.

This paper is organised as follows. In the next section we will detail the materials and methods used in these experiments. In section 3 we discuss the oscillatory rheology data which probes the structure of fat crystal networks. This is followed by the differential scanning calorimetry (DSC) results for the crystallization and melting behaviour of these systems. Finally we use these results along with polarised light microscopy to identify the different types of gelled structures and to suggest a picture of how the colloidal silica interacts with the fat crystal network in section 4.

2 Experimental methods

2.1 Chemicals

Tripalmitin fat (≥85% pure) and soybean oil were purchased from Sigma Aldrich and used without further purification. We used Aerosil 300 fumed silica with a primary particle diameter of 7 nm and a BET specified surface area of 300 m² g⁻¹ from Evonik Industries AG.

2.2 Sample preparation

Soybean oil and silica were mixed in the required proportions with an Ultra Turrax mixer at 13 000 rpm for 5 minutes. Solid tripalmitin was then added and the samples were heated in an oven at 100 °C for 40 minutes with regular shaking by hand to ensure the samples were properly mixed. All samples were then sealed and stored in a refrigerator at 8 °C until use. Before each experiment the bulk samples were melted in an oven at 100 °C until completely liquid.

A range of samples containing only fat in oil was prepared at 2.5 wt%, 5 wt%, 7.5 wt%, 10 wt%, 12.5 wt%. In order to investigate the effect of the fat–silica ratio a second batch of samples was produced at the same fat concentrations, all containing 2 wt% of silica. This produced samples with fat–silica ratios of 1.25 : 1, 2.5 : 1, 3.75 : 1, 5 : 1 and 6.25 : 1. We also prepared samples containing 1 wt%, 2 wt%, 3 wt%, 4 wt% and 5 wt% silica in oil without fat. For all samples, the weight percentages (wt%) are given with respect to the total sample.

Due to the fractal nature of the fumed silica aggregates, they are able to occlude a large amount of oil leading to much higher effective volume fractions,²⁸ therefore we have chosen to work with mass percentages. However it is possible to determine approximate volume fractions by using the densities for the materials used. The density of soybean oil at 25 °C is reported by Sigma Aldrich as 0.92 g mL⁻¹ and the density of fumed silica is 2.2 g cm⁻³.²⁷ The density of supercooled tripalmitin is quoted as 0.8901 g cm⁻³ at 47 °C;²⁹ although this is above the melting point for the α polymorph, we can use this as a rough estimate. Therefore, for a typical sample of 5 wt% fat and 2 wt% silica in soybean oil, we have approximately 5.2 vol% fat and 0.8 vol% silica.

For the formation of the fat crystal networks we used non-isothermal crystallization, which is a better model for real processes used in industry. It is also difficult to conduct truly isothermal crystallization since it is not experimentally possible to achieve infinitely large cooling rates.

2.3 Rheology

Approximately 1.5 ml of melted sample was dispensed onto the peltier plate of the rheometer. An AR-G2 controlled stress rheometer from TA Instruments was used with a 60 mm plate geometry and a 500 μm gap. Once on the rheometer, the samples were heated to 100 °C and sheared at 50 rad s⁻¹ for 3 minutes to destroy both fat crystal memory and any structures formed by the silica during storage. The samples were subsequently left to equilibrate for 2 minutes before taking a 5 minute oscillatory time sweep to measure the amount of structure in the system.

Then they were cooled from 100 °C to 10 °C at a rate of 10 °C min⁻¹ with the geometry held static to avoid any shear-induced crystallization. Next, the samples were immediately brought to 25 °C min⁻¹ at a rate of approximately 28 °C min⁻¹ (the highest possible rate) and a second time sweep was done for 15 minutes to measure the formation of the network. These time sweeps confirmed that the system had stopped evolving before any measurements were taken.

For the oscillatory stress sweep measurements, the oscillatory stress amplitude ranged from 0.01 Pa to 1000 Pa. For the temperature ramp measurements, we raised the temperature from 25 °C to 100 °C at 20 °C min⁻¹ with an oscillatory stress amplitude of 0.3 Pa. Once at 100 °C, we carried out a time sweep measurement over 5 minutes. The frequency for all experiments was held at 2π rad s⁻¹. Each experiment was repeated three times and the arithmetic mean is presented with the error bars corresponding to plus and minus one standard deviation.

We used oscillatory experiments to measure the shear storage and loss moduli, G′ and G′′ respectively. In the stress sweep experiments we started with small amplitude oscillatory shear stresses and then gradually moved up to larger stresses, which allowed for the determination of the linear viscoelastic region (LVR), the range of stresses within which the structure had a linear response to the applied stress. This method meant we were able to probe the networks present in the samples without damaging them under the applied stresses.^30,31

2.4 Differential scanning calorimetry

The melted sample was sheared at 9600 rpm with an Ultra Turrax mixer for 5 minutes. Roughly 10 mg of the sample solutions was weighed out directly into stainless steel pans, which were then hermitically sealed. All the data was collected on a heat flux Q20 DSC from TA Instruments that was calibrated with an indium sample at 10 °C min⁻¹.

The samples were heated to 100 °C and held for 10 minutes to ensure that all crystal memory was destroyed before cooling at a rate of 10 °C min⁻¹ down to 10 °C. The samples were brought to 25 °C at a rate of 25 °C min⁻¹ and held isothermal for 15 minutes. DSC data (not shown) confirmed that the system had stopped changing before we took any measurements.

Melting was measured by ramping the temperature from 25 °C to 100 °C at a rate of 20 °C min⁻¹. The sample was held at 100 °C to destroy any remaining crystal memory and then crystallized for a second time at 10 °C min⁻¹ down to −20 °C. We found that for some samples the first crystallization was not complete by 10 °C and so the crystallization peak was not fully obtained. On the second crystallization we were able to collect the entire peak and we were also able to see if there were any effects of reheating the samples.

All experiments were repeated three times and the arithmetic mean is presented with the error bands corresponding to plus and minus one standard deviation.

2.5 Polarised light microscopy

The melted sample was sheared at 9600 rpm with an Ultra Turrax mixer for 5 minutes, then 7.5 μl was pipetted directly onto a glass slide on a Linkam PE120 peltier stage at 100 °C. The sample was covered with a second glass slide, which had also been heated on the peltier stage. The sample was held at 100 °C for 10 minutes before being cooled at 10 °C min⁻¹ down to 10 °C. The temperature was then raised to 25 °C at the fastest rate possible (20 °C min⁻¹) and the images were captured. All images (1280 × 1024 pixels) were taken using a Zeiss Axio Observer inverted microscope with a 10× objective, crossed polarisers and a black and white PixeLINK camera. Polarised light microscopy was used because the fat crystals are birefringent and so we were able to obtain high contrast images. Nine images were taken for each sample.

To obtain the typical lengthscale, L, in the images we calculated the squared magnitude of the two dimensional discrete Fourier transform. This was then radially averaged to obtain the structure factor, I(k), where I is the intensity of the image and k is the wavevector. The typical lengthscale in the system is given by L = 2π/k_max, where k_max is the wavevector at the point of maximum intensity. In order to improve the statistics, each image was partitioned into twenty 255 × 255 pixel tiles before the analysis; a lengthscale larger than the approximate fat crystal lengthscale.

3 Results

3.1 Rheology

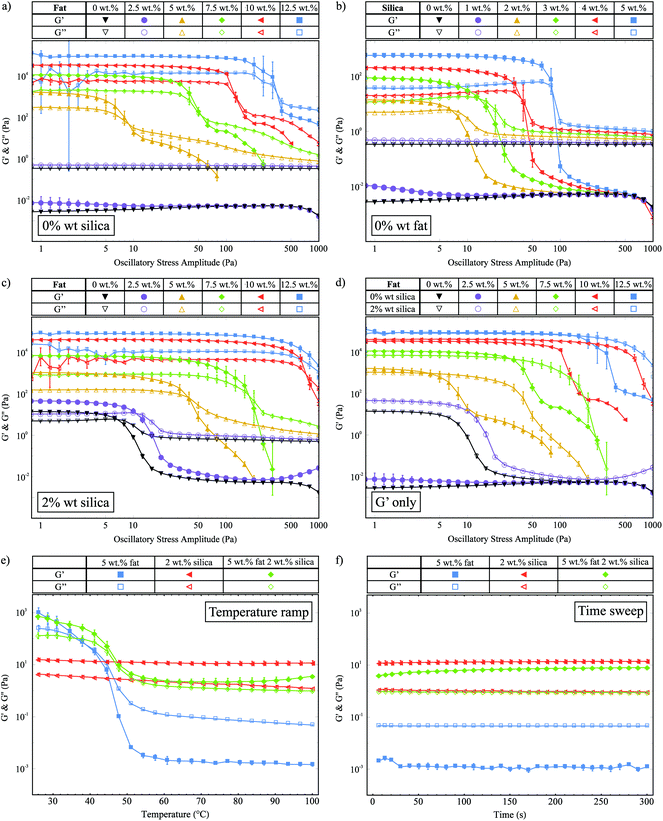
We use oscillatory stress sweeps to measure G′ and G′′ to characterize the solid- and liquid-like properties of the fat crystal networks. Fig. 2a shows G′ and G′′ against the oscillatory stress, for samples with increasing fat concentration and 0 wt% silica. There are clearly two different regimes: the high fat (≥5 wt% fat) and the low fat (<5 wt% fat) regime. In the low fat regime we see that 2.5 wt% fat is not enough to make a stress-transmitting network: G′′ is greater than G′. For the samples with 5 wt% fat and above, we see that a network is formed (G′ > G′′) and that G′ increases with fat concentration, which means that a stronger network is formed. We also observe that the linear viscoelastic region (LVR) continues to higher stresses for higher fat concentrations, which means they can withstand greater amounts of stress before they are irreversibly deformed.

Fig. 2 Stress sweep data for (a) fat samples with 0 wt% silica. (b) Silica samples with 0 wt% fat. (c) Fat samples with 2 wt% silica. (d) A comparison of G′ values for fat in oil samples with and without silica present. (e) Temperature ramp data for 5 wt% fat, 2 wt% silica and 5 wt% fat with 2 wt% silica. (f) Time sweep data taken immediately after the temperature ramp.

Fig. 2b shows the stress sweep data for samples containing different concentrations of silica and 0 wt% fat. As with the fat samples, this graph shows that there is a minimum required amount of silica necessary to create a network, which lies between 1 wt% and 2 wt%. Samples with more than 2 wt% silica show an increase in G′ and an increase in the range of the LVR as a function of silica concentration. This behaviour is similar to that seen in Fig. 2a.

Fig. 2c shows G′ and G′′ against oscillatory stress for samples of increasing fat concentration containing 2 wt% silica. In the high fat regime, we observe that G′ increases with the fat concentration which is similar to the samples without silica shown in Fig. 2a. In the low fat regime, in the presence of 2 wt% silica both 0 wt% (▼) and 2.5 wt% fat (●) samples now form stress-transmitting networks, as demonstrated by the presence of a linear region. For all samples, we also see that the length of the LVR increases with the fat concentration.

In Fig. 2d we replot the data from Fig. 2a and c, showing only the G′ values for samples with and without silica, to allow for easier comparison of the magnitudes of G′. In the high fat regime (≥5 wt% fat), we observe that the silica does not have a significant effect on the magnitude of G′. This is to be expected since at the higher fat concentrations the fat–silica ratio is the largest. However, the silica does significantly affect the range of the linear region, to the extent where the LVR is increased up to similar stresses as fat samples with higher fat concentrations. For example, the sample with 5 wt% fat and 2 wt% silica (Δ) has a similar LVR range as the sample with 7.5 wt% fat and 0 wt% silica (◆). Similar results are also seen for the higher fat concentrations. This result is a key example of samples with less solid fat exhibiting macroscopic rheological properties similar to samples with higher fat contents due to the silica present. In the low fat regime (≤5 wt%), we see that upon the addition of silica, the samples go from being liquid-like to viscoelastic gels. We believe that these are predominantly silica networks, since we know that both 0 wt% fat and 2.5 wt% fat are insufficient to create stress-transmitting fat networks as shown in Fig. 2a. Therefore, in the remainder of this paper we shall not consider the 2.5 wt% fat samples, since our focus is on the manipulation of fat crystal networks.

We observed a strong power law relationship between the storage modulus and concentration for all systems studied, plots of ln(G′) against ln(mass fraction) produced gradients of 4.22 (R² = 0.999) for the fat-only system, 3.92 (R² = 0.994) for the silica-only system, and 4.71 (R² = 0.997) for the mixed fat–silica system. Models of fat crystal networks describe this concentration dependence in terms of fractal dimensions and propose the relationship G′ ∼ ϕ^1/(d−D), where ϕ is the mass fraction, d is the Euclidean dimension (d = 3 in this case) and D is the fractal dimension.^19–21,32 Using this relationship, we extract fractal dimensions of 2.76 (fat-only), 2.74 (silica-only) and 2.79 (mixed fat–silica) illustrating that the networks are geometrically very similar.

Within this fractal model, depending on which is stronger of the inter- and intra-fat crystal bonds, systems can be separated into two regimes, the strong-link and weak-link regime respectively. A characteristic of the weak-link regime is that the limit of linearity increases with increasing concentration, which we observe for the fat crystal networks both with and without silica. This is consistent with previous studies on fat crystal networks,^20,21 and it means that as the fat crystal networks are deformed under the applied stress, the inter-fat crystal bonds break before the crystal clusters themselves are destroyed.

In Fig. 2e we show G′ and G′′ as a function of temperature for samples with 5 wt% fat, 2 wt% silica and both 5 wt% fat and 2 wt% silica. The 5 wt% fat sample (■) melts between 45 °C and 50 °C and we see a large decrease in G′ which crosses over with G′′ to give a liquid at higher temperatures. The 2 wt% silica sample (◀) is solid-like over the whole temperature range, with a small decrease in G′ as a function of temperature. The storage and loss moduli values at 25 °C for the 5 wt% fat with 2 wt% silica sample (◆) are very similar to those of the 5 wt% fat sample, suggesting that they are made up of the same fat network. The decrease in G′ due to melting also occurs at a similar temperature. However unlike the pure fat sample, there is no crossover with G′′ and the sample remains solid-like. This behaviour must be due to the silica present, but by comparison with the pure silica sample the measured G′ value is 5 times lower (11.1 Pa and 2.2 Pa measured at 70 °C). This indicates that it is not the same silica network present.

Fig. 2f shows G′ and G′′ as a function of time, for the same samples as in Fig. 2e, which were collected immediately after the temperature ramp. This plot shows that the G′ value for the 5 wt% fat with 2 wt% silica sample (◆) recovers over time to a similar value as the pure silica network (◀).

3.2 Differential scanning calorimetry

Next, we performed DSC experiments to collect crystallization and melting data, but also to determine whether there are any effects of reheating the samples. For these experiments, the samples were cooled, then heated and cooled a second time. For samples both with and without silica, the crystallization curves were not significantly different on the first and second crystallizations (data not shown). This confirms that we are starting each experiment from a valid reference point that is not affected by crystal memory or sample history.

Fig. 3a shows the exothermic crystallization curves for samples both with and without silica for the second crystallization process. All curves have been rescaled with the fat concentrations and have been translated in the y-direction for clearer interpretation. Pure soybean oil and the 2 wt% silica sample do not show any peaks for crystallization or melting (data not shown), which means that both soybean oil and silica do not go through any phase transitions at the temperatures of these experiments. In Fig. 3a we can see that as the fat concentration increases the crystallization onset temperature increases; this is due to the amount of supercooling which is directly linked to concentration, and acts as a driving force for crystallization.

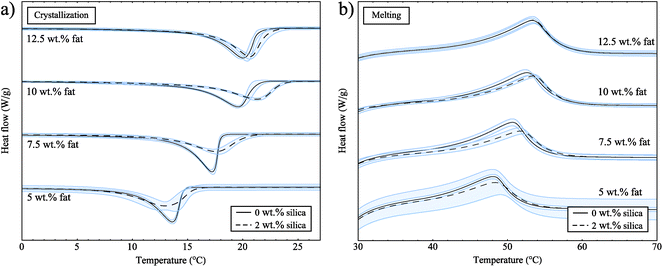Fig. 3 (a) Crystallization curves for samples both with and without silica. (b) Melting curves for samples both with and without silica. These curves have been rescaled with the fat concentrations.

From the data in Fig. 3a we also observe that crystallization occurs at slightly higher temperatures in the presence of silica. For heterogeneous nucleation, seeds or defects provide a surface to facilitate the nucleation of a substance. With a suitable surface present, the barrier to nucleation is decreased leading to earlier crystallization, reducing the amount of supercooling observed and bringing the crystallization temperature closer to the melting temperature. If the fat was nucleating on the surface of the silica, we would expect to see a larger effect due to the very large surface area of the silica aggregates (300 m² g⁻¹). The small shift we observe might be due to an excluded volume effect; the fat can not occupy the same space as the silica and so the volume available to the fat is reduced. This means that the effective concentration of the fat in the oil is increased.

In Fig. 3b we show the endothermic melting peaks for samples both with and without silica. From these data we see that the melting temperature is not notably different in the presence of 2 wt% silica for all of the fat concentrations studied. A study on the non-isothermal crystallization of tripalmitin mixtures³³ has shown that for cooling rates above 0.5 °C min⁻¹ the α polymorph is formed. The melting temperatures of the different tripalmitin polymorphs are reported as 44.7 °C (α), 55.7 °C (β′) and 65.9 °C (β).³ This suggests that the α polymorph is formed under the conditions of our experiment and the melting endotherms in Fig. 3b are consistent with this result. Furthermore, this clearly shows that the presence of silica does not change the polymorphic form of the crystals.

4 Discussion

In this section we bring together the obtained results to elucidate the different types of structures we have produced. The simplest system in this study is pure soybean oil, which is a liquid. Below we shall discuss the remaining samples and the different behaviours between them.

4.1 Suspensions

For both pure fat and pure silica systems we found the minimum required amount of solid to form a stress-transmitting network. Below these threshold values the samples are suspensions of solids in a continuous liquid phase and show overall liquid-like behaviour (G′′ > G′). For fat, this amount is found between 2.5 wt% and 5 wt% and for silica this lies between 1 wt% and 2 wt%. However, although the amount of solid present is insufficient to create a network, it does have a significant effect on the magnitudes of both G′ and G′′. The loss modulus is equal to the product of the viscosity and the frequency of oscillations (G′′ = ηω), and since the frequency is fixed for these experiments, the presence of the solids increases the effective viscosity of these suspensions.

4.2 Single component gels

The pure fat (5–12.5 wt% fat) and pure silica samples (2–5 wt% silica) both form gel networks within the oil. Both the fat networks and the silica networks show an increase in G′ and the range of the LVR with increasing amounts of solids present. This means that the strength of the networks and the amount of connectivity increases and they can be pushed further.

4.3 Composite gels

Composite gel networks, made of both fat and silica, form in the high fat regime with 2 wt% silica present. From the rheological data, shown in Fig. 2a and b, we know that both the fat and the silica are capable of forming networks at these concentrations. The fat crystals form in the presence of a silica network: the initial rheological time sweep data (not shown) taken at 100 °C show an increase in G′ for samples containing 2 wt% silica after the preshearing step. This means that before the experiments were carried out, the silica had already started to form a network.

There are various possible scenarios as the fat crystallizes within this silica network. One possibility is that, as the fat crystallizes, it encapsulates the silica within the crystals and clusters to form a mixed network. Another scenario is that they could form a bicontinuous, interpenetrating network structure where both networks co-exist within the sample volume unperturbed by the other. Alternatively, the silica network could be pushed out and rearranged by the fat crystal clusters as they grow.

From a comparison of the data with and without silica, we see that the magnitude of G′ within the linear region is not significantly different in the presence of silica. This indicates that we are measuring the same fat crystal network structure in both cases made up of the same primary units and the same interactions between them. This then suggests that the silica has not been included into the fat crystal clusters to form a mixed network.

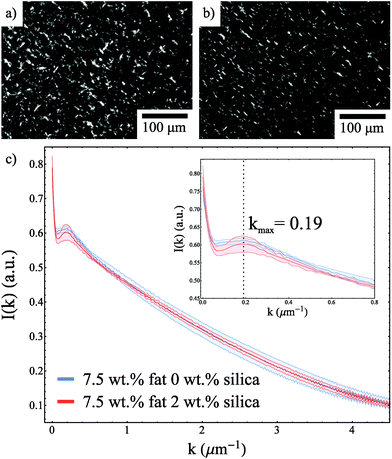
The fact that the DSC melting endotherms are not significantly different in the presence of silica is also consistent with the formation of the same fat network. Moreover, Fig. 4a and b show polarised light microscopy images for 7.5 wt% fat samples with and without silica and the presence of silica did not cause a significant difference in the observed structure. This is supported by Fig. 4c, which shows the structure factor for both samples. These curves overlap within the error of the measurements and show a k_max value of 0.19 μm⁻¹ which corresponds to a typical lengthscale of 33 μm.

Fig. 4 Polarised light microscopy images of 7.5 wt% fat samples (a) with 0 wt% silica and (b) with 2 wt% silica. (c) Structure factors for 7.5 wt% fat samples with and without 2 wt% silica. The inset is a magnification of the data around the peak.

A comparison from Fig. 2d of G′ values for the 5 wt% fat sample (▲), the lowest concentration to form a fat network, with the 0 wt% fat 2 wt% silica sample (∇) shows a difference of two orders of magnitude within the linear region. This means that the fat networks are significantly stronger than the network formed with 2 wt% silica. Therefore, we believe that as the fat crystals grow, they move and rearrange the existing, weaker silica network. The fact that the G′ values for the fat networks are almost unchanged by the presence of silica indicates that the fat networks grow unhindered by the silica network.

The temperature ramp data given in Fig. 2e shows that as the fat network melts, we can measure the structure of the silica aggregates. We see that they give a lower storage modulus to the silica network formed in the absence of fat. This suggests that they have a different structure and the network has been rearranged by the fat. However, although the silica network has been rearranged and weakened, it is still solid-like (G′ > G′′). Therefore we believe that as the fat crystal clusters grow they push out and rearrange the silica network so that there is a layer of silica particles on the surface of the fat crystal cluster chains resulting in a composite gel network. This layer of silica is continuous and so once the fat melts, it is still possible to measure a solid-like response from the silica.

The rheology data also shows that in the presence of silica the LVR is extended. This means that the silica is delaying the breakdown of the fat network under the applied shear. When higher stresses are applied to the fat network some chains will break forming weak points in the gel, from where the entire network will unzip. We believe that the added colloidal silica stabilizes these weak points by dissipating the energy around the weak spots over a much larger area, in a similar manner to that observed by Sun et al.³⁴ In this model we do not expect a change in the G′ value, but we do anticipate an increase in the linear region.

5 Conclusions

In this study we have identified the minimum amount of required solids for fat and silica networks to form in soybean oil. We have also identified some of the different types of structures seen. The rheology data has shown that as the fat crystallizes, it rearranges the existing silica network resulting in a composite gel network. These samples have almost the same G′ values but an extended linear viscoelastic region. We have shown that it is possible to use fumed silica aggregates to create lower fat systems with similar macroscopic thermal and rheological properties. This system could also be extended to model chocolate which is a semi-solid suspension of sugar and cocoa particles in a continuous fat phase.

Acknowledgements

This work was partially funded by Unilever. We thank Rob Style for many useful discussions.

References

1. P. C. Calder, J. Parenter. Enteral Nutr., 2015, 39, 18S–32S.
2. N. Kono and H. Arai, Traffic, 2015, 16, 19–34.
3. A. G. Marangoni and L. H. Wesdorp, Structure and properties of fat crystal networks, CRC Press, 2012.
4. I. Heertje, Food Struct., 2014, 1, 3–23.
5. S. S. Narine and A. G. Marangoni, Food Res. Int., 1999, 32, 227–248.
6. S. J. Baum, P. M. Kris-Etherton, W. C. Willett, A. H. Lichtenstein, L. L. Rudel, K. C. Maki, J. Whelan, C. E. Ramsden and R. C. Block, J. Clin. Lipidol., 2012, 6, 216–234.
7. M. A. Rogers, Food Res. Int., 2009, 42, 747–753.
8. M. Pernetti, K. F. van Malssen, E. Flöter and A. Bot, Curr. Opin. Colloid Interface Sci., 2007, 12, 221–231.
9. A. R. Patel and K. Dewettinck, Food Funct., 2016, 7, 20–29.
10. H.-S. Hwang, S. Kim, K. O. Evans, C. Koga and Y. Lee, Food Struct., 2015, 5, 10–20.
11. C. D. Doan, D. Van de Walle, K. Dewettinck and A. R. Patel, J. Am. Oil Chem. Soc., 2015, 92, 801–811.
12. A. Patel, B. Mankoč, M. B. Sintang, A. Lesaffer and K. Dewettinck, RSC Adv., 2015, 5, 9703–9708.
13. A. R. Patel, P. Dumlu, L. Vermeir, B. Lewille, A. Lesaffer and K. Dewettinck, Food Hydrocolloids, 2015, 46, 84–92.
14. T. S. Skelhon, N. Grossiord, A. R. Morgan and S. A. Bon, J. Mater. Chem., 2012, 22, 19289–19295.
15. N. C. Acevedo and A. G. Marangoni, Annu. Rev. Food Sci. Technol., 2015, 6, 71–96.
16. L. H. Jensen and A. J. Mabis, Nature, 1963, 197, 681–682.
17. L. Jensen and A. Mabis, Acta crystallogr., 1966, 21, 770–781.
18. N. C. Acevedo and A. G. Marangoni, Cryst. Growth Des., 2010, 10, 3327–3333.
19. R. Vreeker, L. Hoekstra, D. Den Boer and W. Agterof, Colloids Surf., 1992, 65, 185–189.
20. S. S. Narine and A. G. Marangoni, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 1908.
21. S. S. Narine and A. G. Marangoni, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 6991.
22. D. A. Pink, B. Quinn, F. Peyronel and A. G. Marangoni, J. Appl. Phys., 2013, 114, 234901.
23. F. Peyronel, J. Ilavsky, G. Mazzanti, A. G. Marangoni and D. A. Pink, J. Appl. Phys., 2013, 114, 234902.
24. B. Quinn, F. Peyronel, T. Gordon, A. Marangoni, C. B. Hanna and D. A. Pink, J. Phys.: Condens. Matter, 2014, 26, 464108.
25. F. Peyronel, B. Quinn, A. G. Marangoni and D. A. Pink, J. Phys.: Condens. Matter, 2014, 26, 464110.
26. D. A. Pink, F. Peyronel, B. Quinn, P. Singh and A. G. Marangoni, J. Phys. D: Appl. Phys., 2015, 48, 384003.
27. Basic characteristics of AEROSIL® fumed silica: Technical bulletin fine particles 11, Evonik Industries AG technical report.
28. S. R. Raghavan, H. J. Walls and S. A. Khan, Langmuir, 2000, 16, 7920–7930.
29. L. Phipps, Nature, 1962, 193, 541–542.
30. R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, New York, 1999, vol. 150.
31. J. Mewis and N. J. Wagner, Colloidal suspension rheology, Cambridge University Press, 2012.
32. W.-H. Shih, W. Y. Shih, S.-I. Kim, J. Liu and I. A. Aksay, Phys. Rev. A, 1990, 42, 4772.
33. C. Himawan, W. MacNaughtan, I. A. Farhat and A. G. Stapley, Eur. J. Lipid Sci. Technol., 2007, 109, 49–60.
34. J.-Y. Sun, X. Zhao, W. R. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. Suo, Nature, 2012, 489, 133–136.

---