Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the nanosecond proton dynamics in phosphoric acid–benzimidazole and phosphoric acid–water mixtures†
Jan-Patrick
Melchior‡
 *a and
Bernhard
Frick
*a and
Bernhard
Frick
 b
b
aMax Planck Institute for Solid State Research, Heisenbergstraße 1, 70569 Stuttgart, Germany
bInstitut Laue-Langevin, 71, avenue des Martyrs, CS 20156, F-38042 Grenoble, France
First published on 22nd September 2017
Abstract
The unique proton conduction mechanism of phosphoric acid is important for the functions of complex phosphate containing biological and technological systems (e.g. phospholipid membranes and polybenzimidazole phosphoric acid membranes for high-temperature PEM fuel cells). In neat phosphoric acid structural proton diffusion, i.e. proton hopping between phosphoric acid molecules, is superimposed onto hydrodynamic diffusion of the molecules in the viscous liquid. In this study we separate the two dynamic contributions on the nanosecond timescale for the model systems phosphoric acid–water and phosphoric acid–benzimidazole. We demonstrate that 1H NMR dipolar relaxation measurements are controlled by hydrodynamic diffusion for the investigated conditions, while 17O NMR quadrupolar relaxation measurements reflect local proton displacement as part of structural diffusion. Quasielastic neutron scattering (QENS) applying high resolution backscattering spectroscopy (nBSS) confirms structural proton diffusion measurements using PFG-NMR in phosphoric acid–benzimidazole mixtures at different concentrations. With increasing benzimidazole content proton diffusion coefficients on the nanosecond scale decrease, thus following the trend of reduced hydrogen bond network frustration. The momentum transfer (Q) dependence of the width of the QENS spectra indicates the jump diffusion mechanism and can be scaled to a master plot both for different temperatures and different benzimidazole contents. This indicates a fundamentally unchanged structural proton diffusion process, however, with a lower probability of occurrence for successful intermolecular proton transfer with increasing benzimidazole content. Results of this work enable a better separation of different diffusion processes on short timescales also in more complex phosphoric acid containing systems.
Introduction
Neat nominally dry phosphoric acid (H3PO4, PA) in the liquid state is the compound with the highest intrinsic proton conductivity1 due to its unique structural proton diffusion mechanism, i.e., fast proton transfer between different phosphate species.2–6 The proton transport properties of phosphoric acid and more complex phosphate containing systems are important in biology7–10 and technology.11–16 Prominent examples are proton transport along the aqueous cytoplasmic side of phospholipid membranes,7,8 phosphorylation of polyphosphates (e.g. adenosine diphosphate) in the metabolism of living organisms,9,10 and the conduction behavior of phosphoric acid containing membranes for application in fuel cells6,11–14 and electrochemical hydrogen pumping.16Structural diffusion of protons is also known to occur in other hydrogen bonded liquids, e.g., in water17,18 and diverse molten heterocycles such as imidazole,19,20 but phosphoric acid's structural diffusion mechanism constitutes a special case. Phenomenologically, phosphoric acid shows the highest intrinsic proton conductivity, with a high contribution of up to 97% by structural proton diffusion to the acid's overall conductivity.2,5 Remarkably, this conductivity does not increase with the addition of any base or acid6,21–24 as observed for water and heterocycles. In contrast, except for the addition of water,5,25–28 the addition of bases, and to a lesser extent acids, reduces the proton conductivity of phosphoric acid.
Structural diffusion in neat phosphoric acid is actually facilitated by the rapid intermolecular proton transfer and hydrogen bond formation reactions within a highly viscous environment.27,29 Both proton transfer and hydrogen bond formation reactions are a consequence of the acid's frustrated hydrogen bond network (there is a severe imbalance of potential proton donors and acceptors) and the strength of its highly polarizable hydrogen bonds.4 The recently proposed mechanism explains in a natural way phosphoric acid's high conductivity, its reduction through additives,5,6,23 and the striking observation that decreasing viscosity goes along with decreasing proton conductivity for the series of phosphorous oxoacids: phosphoric acid (H3PO4)–phosphonic acid (H3PO3)–phosphinic acid (H3PO2).30 This observation is at odds with the so-called Walden rule,31 relating viscosity and equivalent conductivity. It therefore questions viscosity arguments to explain conductivity trends in phosphoric acid based systems32 and underlines the peculiar nature of proton conductivity in neat phosphoric acid.
On the picosecond scale details of the structural proton diffusion mechanism have recently been investigated through ab initio MD simulations4,23,33,34 for neat acid and for mixtures of acid with the Brønsted base imidazole (see Fig. 1). It was shown that reduced frustration and density of the hydrogen bonded network negatively affect structural proton diffusion coefficients. Structural conductivity results only through fast proton exchange between phosphoric acid molecules, but not through the much slower exchange with any other molecule, e.g. (benz)imidazole.5,6 In our recent work on proton dynamics on the millisecond scale, where the model system phosphoric acid–benzimidazole is discussed in light of the application of polybenzimidazole phosphoric acid (PBI-PA) membranes in high-temperature PEM fuel cells, the predictions from picosecond timescale MD simulations were confirmed in that the activation energy of structural proton transport is unaffected by reduced frustration. Previous studies on the nanosecond and millisecond dynamics of protons in phosphoric acid containing systems (PBI-PA membranes,22,35–37 phosphoric acid water mixtures25,38), however, show contradictory results with a large variety of reported activation energies. Yet, none of the reported references attempt the discrimination between hydrodynamic and structural contributions to the proton dynamics. Activation energies obtained from 1H T1-relaxation measurements at different water contents,25 for example, deviate from activation energies of 1H pulsed field gradient (PFG)-NMR diffusion measurements (millisecond scale) and from activation energies obtained from conductivity measurements.5,25,39 Previous quasielastic neutron scattering (QENS) experiments applying backscattering2,40,41 provided only model based activation energies, e.g., applying a jump diffusion model. This technique was so far used to obtain spatial information on proton dynamics by fixing diffusion coefficients in the said model to values obtained through PFG-NMR.
 | ||
Fig. 1 Experimental timescales of measurement techniques for proton dynamics of phosphoric acid in the literature and in this study. Here proton dynamics is measured on the nanosecond scale in neat phosphoric acid and mixtures with water or benzimidazole. In the literature ab initio molecular dynamics (CPMD) simulations are described for neat phosphoric acid,4 neat di-phosphoric acid,34 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of phosphoric acid and water,33 and 1 1 mixtures of phosphoric acid and water,33 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures of phosphoric acid and imidazole.23 QENS measurements of neat phosphoric acid are previously reported on different spectrometers2,40,41 and are compared and re-evaluated here. PFG-NMR measurements for pure phosphoric acid and phosphoric acid water mixtures can be found in our recent work5 and earlier publications.2,25,38 PFG-NMR and 1H NMR lineshape analysis of exchange on the millisecond scale in phosphoric acid–benzimidazole mixtures are shown in our recent work.6 2 mixtures of phosphoric acid and imidazole.23 QENS measurements of neat phosphoric acid are previously reported on different spectrometers2,40,41 and are compared and re-evaluated here. PFG-NMR measurements for pure phosphoric acid and phosphoric acid water mixtures can be found in our recent work5 and earlier publications.2,25,38 PFG-NMR and 1H NMR lineshape analysis of exchange on the millisecond scale in phosphoric acid–benzimidazole mixtures are shown in our recent work.6 | ||
In the present study, with the model systems phosphoric acid–water and phosphoric acid–benzimidazole, we distinguish between structural diffusion and hydrodynamic diffusion on the nanosecond timescale exploiting the different underlying physics of the techniques 17O relaxation NMR,421H relaxation NMR, and high resolution neutron backscattering spectroscopy (nBSS).43,44 These techniques are reviewed in more detail in the methodology and results sections. Implications on how proton transport in phosphoric acid and more complex phosphate containing systems is affected by additives are presented in the discussion section.
Methodology
NMR relaxometry
Relaxation of the nuclear magnetization in NMR is due to fluctuations in the strength of the local magnetic field at the nucleus. The local magnetic field is governed by a number of direct or indirect interactions between different nuclei, nuclei and electrons, electric field gradients, or the applied magnetic field B0.45 Fluctuations in the strength of the field are then a result of fluctuations in either the coupling constants of such interactions or the distances of interacting nuclei, i.e. motion of nuclei with respect to each other which can be described by a pair- (for two interacting nuclei) or auto-correlation function with a thermally activated correlation time τc.For s = 1/2 nucleus 1H the dominating interaction causing relaxation is often the direct dipole dipole interaction. Correlation times τc for a local motion can be calculated from relaxation rates through the Bloembergen–Purcell–Pound (BPP) theory.46
For the s = 5/2 nucleus 17O the dominating interaction causing relaxation is the quadrupolar interaction of the nucleus quadrupolar moment with the electric field gradient caused by electronic anisotropy of the atomic shell.42,47,48 In water49,50 and H3PO4 fluctuations of the electric field gradient mainly control the relaxation times. Here such fluctuations are caused by displacements of protons in the vicinity of the oxygen molecules, i.e., transfer of protons inside a hydrogen bond connecting two oxygen atoms. Historically the first proton transfer rates between water molecules have been obtained exploiting this effect.49,50 Furthermore, H2O and H3PO4 oxygen resonances can be clearly separated in 17O NMR experiments enabling independent relaxation measurements with generally fast relaxation rates. From such measurements at different temperatures activation energies of the displacement of protons with respect to oxygen for H3PO4 and H2O can be calculated.
Quasielastic neutron scattering (QENS)
QENS experiments yield information on the time and space self-correlation of scattering particles in cases where the incoherent scattering of the investigated system dominates as here. This renders additional information on the distances and geometry of proton dynamics through the momentum transfer (Q) dependence of the quasi elastic line broadening of the energy spectra and the Q-dependence of the intensities.43,51 The technique is predominately sensitive to the motion of H-atoms in phosphorus oxoacids41 on timescales intermediate to existing simulations for H3PO44,23 and the existing PFG-NMR measurements.2,5,6,25 In phosphate containing systems QENS has e.g. recently been used to study the proton diffusion in solid CsH2PO4,52 the electrode reaction of phosphoric acid fuel cells53 and neat phosphoric acid from solid to melt.2,40,41 For CsH2PO4 it was pointed out by Ishikawa et al. that 1H NMR relaxation, 1H PFG-NMR and QENS assess different aspects of proton dynamics in phosphates.52 Establishing a similar systematics for the liquid system we extend and partially re-measure previously published data for phosphoric acid which were recorded by high resolution nBSS on IN16 at the ILL,41 re-evaluate the old data and compare them to new data recorded on the nBSS spectrometer IN16B. In contrast to previous studies2,41 our present QENS data are analyzed without model constraint, i.e., we obtain diffusion coefficients, which are not a priori fixed to values obtained through PFG-NMR on the millisecond scale.2,41Experimental
Sample preparation
Samples have been prepared as described in our previous publications on transport in phosphoric acid water mixtures and phosphoric acid benzimidazole mixtures.5,6 Water contents are in the following given with respect to P2O5 as λ = [H2O]/[P2O5] (with λ = 3 corresponding to H3PO4·0H2O or 100 wt% H3PO4 (aq.)).For phosphoric acid water mixtures, samples with phosphoric acid contents between 85 and 99 wt% H3PO4 (aq.) (λ = 4.92–3.1) were prepared by adding corresponding amounts of bi-distilled water to nominally dry crystalline phosphoric acid as obtained by centrifuging crystalline phosphoric acid (Aldrich, >99.999%).2,5,54 For higher water contents 85 wt% H3PO4 (aq.) (Merck VLS selectipur) was diluted with bi-distilled water. All concentrations were controlled and verified by acid/base titration using a 877 plus Titrino by Metrohm.
17O enriched samples for PFG-NMR measurements were prepared inside NMR tubes by adding 10% 17O enriched water (Enritech NW 17–20 Batch 179501) to nominally dry phosphoric acid. Samples had to be equilibrated for up to one month in order to ensure a homogeneous distribution of the 17O tracer over aqueous and phosphate species. This long equilibration time is controlled by the rate of the condensation/hydrolysis reaction which actually increases with increasing water content.
For phosphoric acid (benz)imidazole mixtures, nominally dry phosphoric and dry benzimidazole (Fluka, purum >98%) or imidazole (Merck, >99%) powder were respectively mixed by weight in a glovebox under dry nitrogen atmosphere and slight heating (50–80 °C) in sealed glass vials. In the following the samples are named according to the molar ratio of phosphoric acid (PA) to benzimidazole (BI) or imidazole (Imi), e.g. 3 mol H3PO4 per 1 mol BI is named 3PA1BI, 6 mol H3PO4 per 1 mol BI is named 6PA1BI, etc. (see also ref. 6). The resulting viscous liquids were either filled in a homemade aluminium QENS sample holder (see the ESI†) lined with 25 μm Teflon foil, or in a 5 mm NMR tube with a screw lid (Deutero Duran S300). Dead volume above the NMR sample was filled with a glass filler and the tube was closed with its lid inside the nitrogen atmosphere and subsequently heat sealed outside the glove box.
NMR
1H and 17O NMR measurements have been performed using a Bruker Avance III 400 spectrometer equipped with a diff60 gradient probe and a Bruker temperature control unit at a magnetic field of 9.4 T corresponding to a proton resonance frequency of 400 MHz. Spin–lattice T1 relaxation measurements have been performed using an inversion recovery pulse sequence. 1H NMR spin lattice T1 relaxation times were recorded in the temperature range T = −30 to 160 °C. Short 17O NMR T1 relaxation times could only be recorded at high temperatures (T > 100 °C).As 1H nuclear magnetic spin–lattice T1 relaxation is dominated by homonuclear interactions25,52 temperature dependent 1H relaxation rates have been evaluated by the BPP equation46
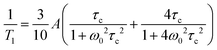 | (1) |
For temperature dependent 17O T1 relaxation rates no extrema in 1/T1 can be found at the used magnetic field (9.4 T). H3PO4 and H2O resonances are clearly separated and temperature relaxation rates are obtained independently for both resonances and for 17O enriched and non-enriched samples at different water contents.
QENS
QENS experiments were carried out on two nBSS instruments at the Institute Max von Laue–Paul Langevin, Grenoble, the high resolution backscattering instrument IN16B55,56 and its predecessor IN1644 (previously published data41). Both instruments have a very high energy resolution below 1 μeV even for large momentum transfer Q (Qmax ∼ 1.9 Å−1). IN16 had a narrower energy transfer range of ±15 μeV compared to IN16B which also has an order of magnitude increased neutron flux in comparison to its predecessor, enabling faster measurements with higher neutron count statistics and a slightly higher energy resolution (0.75 μeV). With its extended energy transfer range of ±30 μeV and improved signal to noise ratio the spectra recorded on IN16B allow for a more detailed analysis than the previously recorded spectra on IN16.Nominally dry samples were filled in flat sample holders containing a 25 μm Teflon liner as described above. The holders were placed in a standard ILL orange cryofurnace and measured on IN16B in its initial configuration with the Si(111) monochromator and 6 old IN16 large angle analysers in backscattering (6.271 Å). The flat samples of thickness 0.45 mm (total scattering probability for perpendicular orientation <13%) were oriented in transmission geometry with the slab direction towards the scattering angle of 135°. For all spectral data standard corrections for background scattering of the instrument and the sample holder containing a Teflon liner and for absorption and self-shielding were applied using the LAMP software.57,58 A similarly treated vanadium reference was used to correct for detector and analyser sensitivity. In addition the data were subsequently normalized to the integral over the elastic peak using a low temperature run of the same sample. More details concerning the data correction can be found in the ESI.†
Spectra were then fitted in LAMP in different ways applying simple model functions convoluted with the experimental resolution function. In previous studies of phosphoric acid at different temperatures it was already noted that scattering data (IN16) can be described by a broad background and a single Lorentzian peak.41 We apply here the same fit model to all samples: a single Lorentzian peak adding a flat background (model ‘LorBg’, where the background accounts for fast motions outside of the instrumental window). Different fit models with additional elastic or Lorentzian components are compared for neat phosphoric acid in the ESI.†
The model ‘LorBg’ describes the experimental data of PA quite well. For the other samples fits with ‘LorBg’ are not of the same quality at the lower temperatures, but still acceptable (see ESI†). We argue that the ‘LorBg’ model captures the average spectral relaxation time for all temperatures, detectors and samples and it shows the least correlation among different fit parameters. Therefore we restrict here the discussion mainly to the ‘LorBg’ model and plan for a more refined evaluation of the neutron data in a future publication combining nBSS and TOF data. The resulting fit parameters are summarized in the ESI† and the Q-dependence of the fitted linewidth for all samples and temperatures is discussed in the following.
For continuous (Fickian) diffusion the HWHM of the Lorentzian follows a HWHM ∼ DQ2 law, i.e. a straight line is obtained plotting HWHM versus Q2 with the diffusion coefficient proportional to its slope for low values of Q. At higher Q values the continuous diffusion approximation is no longer valid and the width of the QENS spectra depends on details of short range proton motion. The HWHM thus can often be described by jump models, which approach the limiting behavior ∼DQ2 at low Q and a Q-independent 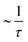 plateau at high Q, where τ is the residence time in between jumps.
plateau at high Q, where τ is the residence time in between jumps.
For a random motion with distinct jump length distributions (ρ(r)) and correlation time τ a number of models exist which describe the HWHM at large Q in a slightly different way.51,59,60 For example, Hall and Ross61 showed the dependence of HWHM on Q for a symmetric Gaussian distribution of jump length to be
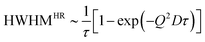 | (2) |
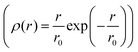 of jump length r around an expectation value r0 showed the dependence to be
of jump length r around an expectation value r0 showed the dependence to be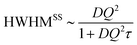 | (3) |
The Singwi–Sjölander model has been used in earlier work to obtain τ with diffusion coefficients fixed to values obtained in PFG-NMR. This approach is often applied because the Q-values in the n-scattering experiment typically do not reach very low Q values (>0.1 Å−1) and also because the observed linewidth at small Q is susceptible to broadening by multiple scattering. In the present study diffusion coefficients D are obtained through a free fit of a HWHM ∼ DQ2 law at low Q, motivated by the new interpretation of NMR data as discussed here. We comment on the jump diffusion models59,62 and investigate a series of different model systems including neat phosphoric acid and mixtures with benzimidazole at a few temperatures from which we deduce the activation energy for D(T). A similar activation energy is also obtained in a model independent approach by a temperature scaling of the linewidth over a wider Q-range. We comment on which aspects of proton dynamics are accessed in QENS of phosphoric acid based systems on nBSS.
Results
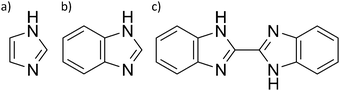
To separate different dynamic processes present in phosphoric acid on the nanosecond timescale a number of model systems are investigated for which the millisecond timescale proton dynamics has already been reported. The model systems include mixtures of phosphoric acid at different water contents and nominally dry phosphoric acid mixtures with Brønsted bases imidazole, benzimidazole, or bisbenzimidazole (Fig. 2).5,6 The choice of additives allows for general conclusions but is also directly related to the application of phosphoric acid containing systems, i.e., phosphoric acid soaked polybenzimidazole membranes as fuel cell electrolytes in high-temperature PEM fuel cells.11–13,15,16 The performance of such fuel cells is known to depend on the ratio of phosphoric acid to polybenzimidazole and the humidification, i.e., the water content, of anode and cathode stream. Those performance changes are related to differences in the membrane's water permeability,63 proton conductivity,11 electroosmotic water drag64 and, especially under dry conditions, acid redistribution65 in the membrane. In light of the fuel cell application the interactions of phosphoric acid with water and the Brønsted bases benzimidazole and imidazole have been investigated in our recent works.5,6 The common feature of the model systems is that protonation of the additives reduces the frustration in the acid's hydrogen bonded network, resulting in a reduction of the measured values for structural diffusion on the millisecond timescale.5,6 Here data for the nanosecond dynamics obtained through a selection of measurement techniques (1H relaxation NMR, 17O relaxation NMR, high resolution backscattering QENS) are presented.1H NMR T1 relaxation measurements
1H nuclear magnetic relaxation in phosphoric acid based systems is governed by the motion of protons relative to each other and temperature dependent measurements of spin–lattice T1 relaxation times can be used to obtain the correlation time τc of that local Brownian motion.46 Jeffrey et al. indicate a correlation between viscosity and 2H spin–lattice relaxation times in D3PO4 containing gels66 and a clear relation of relaxation rates to viscosity and hydrodynamic diffusion has been shown for ionic liquid electrolytes.67 To obtain the relation of 1H spin–lattice T1 relaxation times to the nanosecond timescale dynamics of phosphoric acid further considerations and data from different measurement techniques are necessary. This is due to the acid's additional intrinsic fast proton exchange and other difficulties inherent to the relaxation measurements, i.e., multiple relaxation routes, etc.52 In the following we argue that fast proton exchange as part of structural diffusion occurs at rates much too fast to considerably influence relaxation at the used magnetic field and temperatures and show the relation of 1H NMR T1 relaxation and hydrodynamic diffusion.For H3PO4 at different water contents close to the nominally dry case 1H NMR spin–spin T1 relaxation measurements with a distinct BPP-type temperature dependence of the T1 relaxation rates that allow for calculation of correlation times τc have already been reported by Aihara et al.25 The authors report a slight increase of the activation energy of τc towards lower nominal water contents and different activation energies for lower and higher temperatures. Spin–spin (T2) relaxation related linewidth measurements for phosphoric acid at different water contents, on the other hand, have mostly been discussed in terms of vitrification.39,68,69 For technical polybenzimidazole–phosphoric acid membranes both 1H spin–lattice (T1) relaxation measurements and spin–spin (T2) relaxation related linewidth measurements are reported in the literature, but are more ambiguous to evaluate22,35–37,70 than such measurements conducted on model systems with more controlled composition. In the membranes chemical effects of benzimidazole on relaxation and/or dynamics overlap with the effects of water on relaxation. Water contents in the hygroscopic membranes, actually, are notoriously difficult to control and the membranes’ water uptake depends on the used polymer and the often unclear ratio of phosphoric acid to benzimidazole groups.6 Despite the large body of work dealing with a vast number of different chemistries of the polymer backbone of polybenzimidazole–phosphoric acid membranes and the known dependence of the membranes’ conductivity on relative humidity11 there is no consensus in the literature to investigate and compare membranes at specific water contents. To our knowledge, no work treats membranes containing nominally dry phosphoric acid, which is most likely due to the described challenges in controlling such conditions for variable polymer architectures and PA contents.
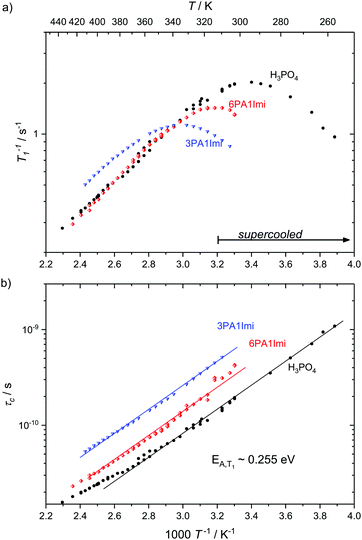
Here we present temperature dependent 1H spin–lattice relaxation rates and corresponding correlation times τc for phosphoric acid–benzimidazole and phosphoric acid–imidazole mixtures (Fig. 3 and 4) with a controlled water content (nominally dry) in comparison to the neat acid. All relaxation times have been obtained through an inversion recovery sequence with a single exponential recovery of the magnetization with time. A maximum in 1/T1versus temperature is found for all samples and correlation times τc are calculated therefrom through the BPP method. A slight upturn of ln(τc) from a linear dependence in 1/T is reported at high temperatures, similar to that observed by Aihara et al.25 This deviation from Arrhenius behavior is often associated with the fragile glass transition. In the case of phosphoric acid, however, temperature dependent changes in composition (a higher molar fraction of water) can also lead to the observed deviations from Arrhenius behavior. Viscosity is reduced disproportionately through increased condensation of phosphoric acid molecules (2H3PO4 ⇄ H4P2O7 + H2O) at higher temperatures5 and the therefore increased molar fraction of water. Water possibly also provides an additional relaxation route for magnetization. At low temperatures when the acid is supercooled and compositions in terms of molar fractions of water are often “frozen in”,29 deviations from Arrhenius behavior can indeed not be seen and low temperature data are suggested to be more reliable for obtaining activation energies.
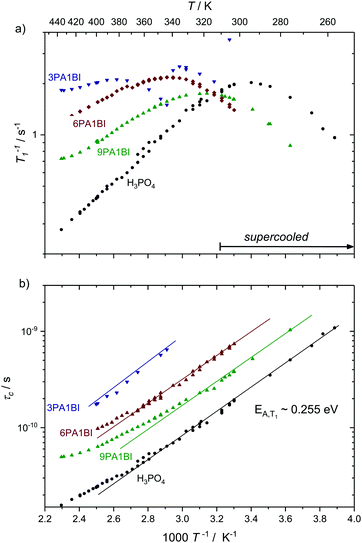 | ||
| Fig. 4 (a) 1H T1 relaxation rates for neat H3PO4 and nominally dry mixtures of phosphoric acid with benzimidazole (9PA1BI, 6PA1BI, 3PA1BI) and (b) the correlation times calculated therefrom through the BPP method. The activation energy is almost identical for all samples, with noted deviations at high temperatures (see the text). Sections of the temperature range where the samples have been cooled below the melting point of crystalline H3PO4 are marked. Deviations from Arrhenius behavior in τc are due to increasing concentration of condensation products and contributions to T1 from exchange of protons between phosphoric acid and benzimidazole.71 | ||
For mixtures of phosphoric acid with imidazole the activation energy from T1 relaxation of phosphoric acid's 1H resonance stays unchanged and deviations from the Arrhenius behavior of τc occur at higher temperatures. The explanation for that shift lies in the lower molar fraction of the condensation product water in the sample containing (benz)imidazole, which reduces condensation through reduction of the hydrogen bonded network's frustration by deprotonation of the acid.6
For mixtures of phosphoric acid with benzimidazole the activation energy from T1 relaxation of phosphoric acid's 1H resonance also stays unchanged. However, there is a considerable decrease in viscosity and T1 data at high temperatures slightly deviate from the BPP behavior. Those deviations are a consequence of the exchange of protons between phosphoric acid and benzimidazole on the millisecond timescale which we have reported previously.6 This exchange on the millisecond scale, however, does not affect the correlation times of proton dynamics inside phosphoric acid as it is on a completely different timescale (millisecond regime) than the dynamics causing relaxation in the used magnetic field (nanosecond regime). Since the exchange occurs on the same timescale as the relaxation rates themselves the increase in 1/T1 at higher temperatures is a mere artifact in the relaxation rate brought about through combination of relaxation of protons as part of benzimidazole and as part of phosphoric acid.71 Nevertheless, it is possible to evaluate relaxation data with the BPP model in a given temperature range and extrapolate undisturbed phosphoric acid relaxation rates from the data set.
Interestingly, the temperature dependence of these extrapolated data for the correlation times τc again reveals virtually unchanged activation energies for the dynamic process. Through comparison with 31P diffusion data (see Fig. 5), we ascertain that this process is indeed associated with hydrodynamic diffusion rather than fast structural proton diffusion. A close relation between the correlation times τc and the hydrodynamic diffusion coefficients (31P diffusion data), as it was previously shown to exist in ionic liquids,67 is indeed reported for neat phosphoric acid and PA-(benz)imidazole systems with low (benz)imidazole contents. For those samples hydrodynamic diffusion on the millisecond scale and the nanosecond correlation times from 1H relaxation measurements not only exhibit the same temperature dependence, but also the dynamics are reduced by exactly the same factors upon addition of (benz)imidazole—the two dynamic data sets scale with a power law with an exponent of almost one (see Fig. 5). This shows that as in some ionic liquids 1H T1 relaxation indeed is associated with the hydrodynamic diffusion of the molecules67 rather than structural proton diffusion, as sometimes assumed in the literature. It needs to be emphasized, though, that this relation strictly only holds for low benzimidazole contents and for imidazole, which has similar diffusion coefficients to the phosphate species. For a high benzimidazole content the influence of benzimidazole both on relaxation and on diffusion coefficients leads to deviations. It should also be pointed out that the strong correlation between τc from T1 relaxation measurements and hydrodynamic phosphate diffusion does not extend to a correlation between T2 relaxation and viscosity. Temperature dependent T2 relaxation and viscosity measurements are established methods to obtain the glass transition temperature. As pointed out by multiple authors the techniques, however, yield deviating results for the case of H3PO4.39,68,69
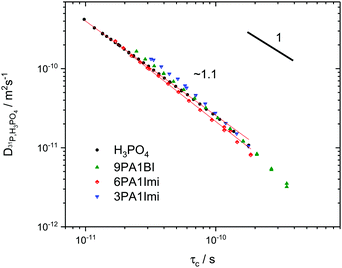 | ||
| Fig. 5 Double logarithmic plot of ortho-phosphoric acid diffusion coefficients as measured by 31P PFG NMR5,6,72versus correlation times from 1H relaxation NMR at the respective same temperature for phosphoric acid and phosphoric acid-(benz)imidazole mixtures.25 The exponent ∼1 indicates fundamental similarity of the underlying dynamic process, i.e., 1H relaxometry accesses the dynamic modes on the nanosecond scale which are related to hydrodynamic diffusion measured through 31P PFG NMR on the millisecond scale (see the text). | ||
17O NMR T1 relaxation measurements
To assess structural diffusion on the nanosecond scale more clearly 17O NMR relaxation measurements are used. Having shown that 1H NMR dipole relaxation is related to hydrodynamic diffusion, it is important to emphasize that 17O NMR relaxation occurs through a different route, i.e., fluctuations in the strength of the quadrupolar interaction (see Experimental). Such fluctuations are caused through distortions of the electric field gradient, highly dependent on the hydrogen bonds around the 17O nucleus.42,47,48 Displacements of hydrogen atoms bound to oxygen therefore are the dominant reason for relaxation of 17O nuclear magnetization,49,50 which is therefore highly dependent on the proton transfer events that are part of structural diffusion.H3PO4 and H2O resonances in the 17O NMR spectra of phosphoric acid water mixtures are separated (Fig. 6a) and allow for an individual and temperature dependent analysis of relaxation rates, i.e., the analysis of proton displacement in the vicinity of H3PO4 and H2O oxygen atoms (Fig. 6b). Measurements of H2O 17O NMR relaxation rates in non-17O-enriched samples are, however, limited to water contents higher than λ = [H2O]/[P2O5] = 4, as the signal intensity otherwise becomes too low. Nevertheless, a clear trend in activation energies obtained from temperature dependent relaxation measurements is apparent (Fig. 6b). The activation energy of H2O 17O NMR relaxation goes through a pronounced maximum between λ = 4 (H3PO4·0.5H2O) and λ = 4.5 (H3PO4·0.75H2O), but is virtually identical to the H3PO417O relaxation rate's activation energy for λ > 5 (H3PO4·1H2O). The plateau of activation energies reported below λ = 4 (H3PO4·0.5H2O), on the other hand, corresponds to the activation energy found for structural diffusion of protons on the millisecond scale in nominally dry phosphoric acid.5 The direct measurement of the activation energy of proton displacement between two phosphoric acid molecules through 17O NMR thus also confirms the validity of the methods through which the diffusion coefficients of structural proton diffusion on the millisecond scale were obtained in our previous works.5,6 It can be inferred that no other effects than those directly affecting the proton transfer reaction interfere with structural diffusion, i.e. effects on longer timescales than those investigated here.
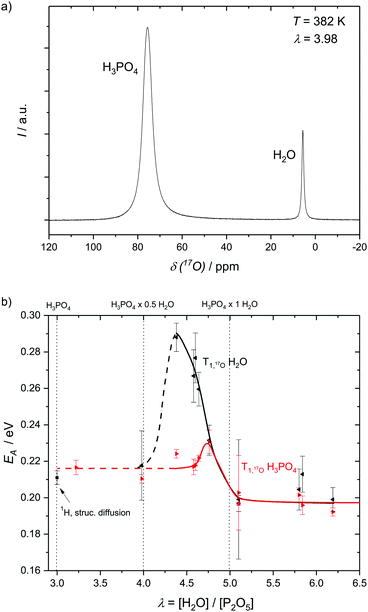 | ||
| Fig. 6 (a) 17O NMR spectrum showing the resonances of H3PO4 and H2O and (b) the activation energies as obtained from the resonances with respect to relaxation rates at different water contents λ = [H2O]/[P2O5]. The activation energies of H3PO417O relaxation reach a plateau at low water contents at EA ∼ 0.218 eV which roughly corresponds to the activation energy of millisecond structural diffusion5 and at water contents higher than λ = 5 for which H3PO4–H3PO4 structure diffusion is no longer present. Water 17O relaxation activation energy goes through a pronounced maximum at medium water contents (see the text). | ||
It has previously been shown that structural diffusion breaks down with increasing water contents in phosphoric acid–water.5 The decoupling of activation energies of H3PO4 and H2O 17O relaxation in Fig. 6b shows that, indeed, no relevant fast exchange of protons takes place between H3PO4 and H2O. Proton displacement from H2O has a much higher activation energy at intermediate water contents, for which more H3PO4 molecules than water molecules are accessible. At water contents higher than λ = 5 (1H2O·1H3PO4) hydrodynamic diffusion governs activation energies of 17O NMR relaxation for both H2O and H3PO4 and the activation energies equalize again.
Quasielastic neutron scattering (QENS)
The discussed NMR techniques provide information on activation energy or correlation times, but do not contain spatial information on the diffusion process of protons. To obtain additional spatial information especially on the structural diffusion process of protons in nominally dry H3PO4 quasielastic neutron scattering data have previously been recorded using different backscattering spectrometers.2,41 In those works line-broadening is reported, which could at higher temperatures be described by a single Lorentzian function.In this work QENS spectra are recorded at the IN16B backscattering spectrometer at the ILL in Grenoble for different mixtures of phosphoric acid and benzimidazole or bisbenzimidazole (see Fig. 2). In particular mixtures of phosphoric acid with benzimidazole (3PA1BI, 6PA1BI) and bisbenzimidazole (6PA1BisBI) are investigated over a temperature range T = 300 K to T = 430 K. Those systems are chosen as the Brønsted base benzimidazole is fully protonated by the acid and both hydrodynamic and structural proton diffusion are reduced.6 Additionally, it has already been shown that benzimidazole and phosphoric acid exchange protons with average residence times in the millisecond regime,6 which is out of range for nBSS and therefore should show up as an additional elastic signal. This is in contrast to phosphoric acid water mixtures for which the degree of protonation of water changes with water concentration and for which hydrodynamic proton diffusion is actually increased through highly mobile aqueous species and weaker hydrogen bonds.5 All existing neutron scattering studies of polybenzimidazole–phosphoric acid membranes have been conducted at unspecified high water contents73,74 for which a considerable contribution of phosphoric acid's structural diffusion process can no longer be expected and which exceeds the water contents of operating high-temperature PEM fuel cells.5,6
Despite slow hydrodynamic diffusion of phosphate species being visible in 31P PFG-NMR measurements no major contribution from slow proton motion is seen in the QENS spectra of PA, which would show up as an additional elastic signal, except if being convoluted with a faster type of motion. The reason is that proton dynamics is in fact ‘decoupled’ from the hydrodynamic motion of the phosphate species as all protons contribute to structural diffusion through very fast exchange of protons between the slowly diffusing phosphate species. The consequences of that fast exchange for measurements of the nanosecond scale proton dynamics is discussed in this study. Delicate details of dynamics of the hydrogen bonded network and thus of single proton jumps are, however, beyond the scope of this study.
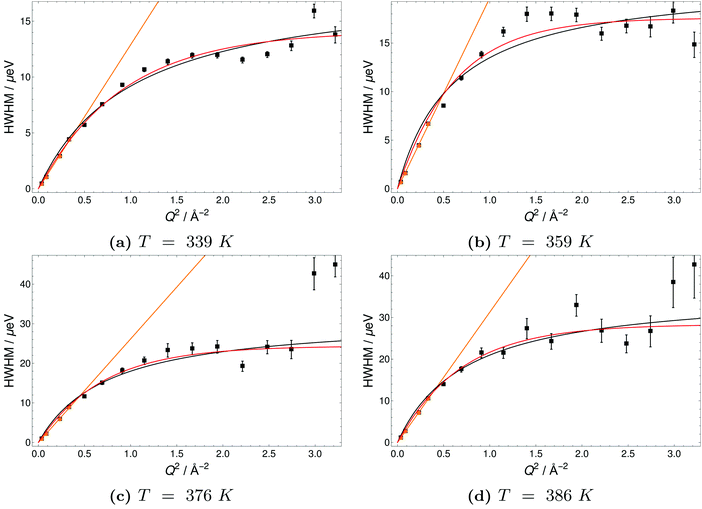
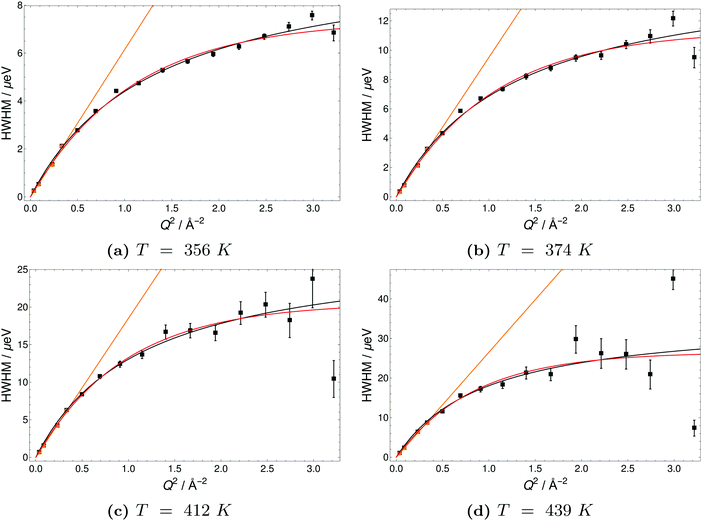
All data were fitted with different simple models as mentioned in the Experimental section and the results are discussed in the ESI.† For neat PA the simplest model ‘LorBg’, a single Lorentzian plus a flat background, describes the data pretty well, as can be judged from the figures in the ESI.† There the total fit curves for ‘LorBg’-fits at different temperatures (T = 339 K: Fig. SI-QENS 1; T = 386 K: Fig. SI-QENS 3, ESI†) are shown in conjunction with fit components for individual detectors (T = 339 K: Fig. SI-QENS 2; T = 386 K: Fig. SI-QENS 5, ESI†). For 6PA1BI the fits with ‘LorBg’ are still acceptable, but not quite as good at all detectors. For higher BI contents the discrepancy between the simple ‘LorBg’ fit and the QENS spectra increases further, which we take as a sign of the expected appearance of a slower dynamic component related to BI dynamics (see the ESI†).
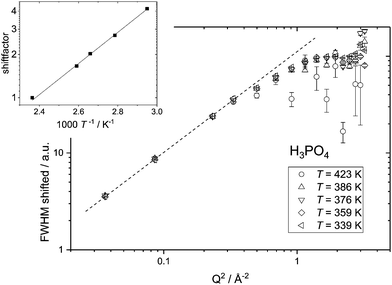
Independent of a specific diffusion model the FWHM data resulting from the ‘LorBg’ fits for PA are tested in a plot of its log(FWHM) versus log(Q2). From such plots it becomes evident that the FWHM increase with Q is nearly parallel at different temperatures. Thus, a masterplot can be constructed through multiplication of FWHM(T) for different temperatures with a Q-independent scaling factor (Fig. 7). The scaling factors are calculated from a Q-average of the FWHM data in the low-Q region (0.19 < Q < 0.58 Å−1) with Tref = 423 K as reference temperature. Except for unreliable data points at high Q for the highest temperature T = 423 K, where FWHM is as wide as the instrument energy window, there is good data superposition in all the Q-range, i.e. all scaled FWHM values fall on the same master curve. The Q-dependence of this master curve shows the characteristics of a jump model with the FWHM at the lowest Q-values following a ∼DQ2 behavior and the FWHM at high Q becomes virtually Q-independent. We take the mastercurve as a proof that the same single dynamic process on the nanosecond time scale is probed by IN16B for all investigated temperatures. This observation is in line with the initial reasoning (see above) that contributions of hydrodynamic phosphate diffusion will not show up in the QENS spectra due to the ‘decoupling’ of fast proton motion from its hydrodynamic background already on the nanosecond timescale of IN16B.
The activation energy for the single continuous dynamic process can be derived when plotting the shift factors against the inverse temperature and fitting an Arrhenius temperature dependence (inset to Fig. 7) results in an activation energy of EA ∼ 0.21 eV. This value varies slightly with the temperature range taken into account for the fit and with the Q-range for which an average of FWHM is chosen for calculating the scaling factors. From the variation in the activation energy values based on scaling factors for different Q-ranges a systematic error of 0.03 eV is calculated (see the ESI†).
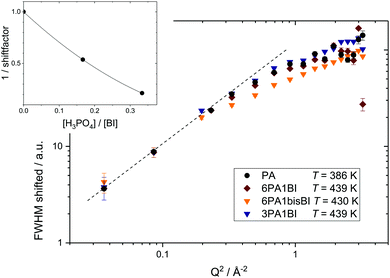
Similar master plots are possible for all other samples and are reported in the ESI.† For phosphoric acid–benzimidazole mixtures the scaled FWHM for low temperatures and for low Q values do not exactly match the master curve. This is possibly due to additional dynamic processes in the assessed energy window, which seem to contribute more strongly at low temperatures. The additional contribution at lower T most likely stems from the protons of the (bis)benzimidazole molecules and indeed increases with the benzimidazole content. The contribution of BI in the spectra, however, could so far not be isolated through the fit models discussed in the Experimental section and in the ESI.† This is partly due to the large background which includes fast processes present in neat PA and the mixtures and needs to be further investigated through measurements on shorter timescales. In the meantime the dominating dynamic process found in both PA and the mixtures is discussed, taking into account that artefacts of the dynamics of benzimidazole can affect the accuracy of the data analysis for mixtures with a high benzimidazole content. Indeed, for the most viscous sample 3PA1BI (see ESI†), the activation energy found from the scaling factor (EA = 0.29 ± 0.03 eV) deviates strongly from that for neat PA. For the samples 6PA1BI (EA = 0.21 ± 0.05 eV) and 6PA1bisBI (EA = 0.23 ± 0.01 eV) the same trend is visible with increasing errors and deviations from the activation energy found for neat PA.
Interestingly, a combined master plot of high temperature FWHM data versus Q2 of all samples (Fig. 8) can be produced. Much in the same way as shown in Fig. 9 for a single sample the FWHM data of different samples can be scaled to the reference data set of PA at T = 423 K to fall on one single master curve. This reveals that the dynamic process, probed for neat PA, is not fundamentally altered by the addition of benzimidazole. From this master-plot we can conclude that the addition of benzimidazole simply reduces the dynamics of the measured process. The inset of Fig. 8 shows the respective scaling factors as a function of benzimidazole content expressed through the ratio of phosphoric acid per mol benzimidazole ([H3PO4]/[BI]).
The Q-dependence of the line broadening is investigated in more detail by fitting the jump diffusion models described above. Again fit parameters from the ‘LorBg’ fits are analysed and some examples of the half-width-at-half-maximum (HWHM) versus the momentum transfer squared (Q2) are plotted for PA in Fig. 9 and for 6PA1BI in Fig. 10 (for a complete overview, see the ESI†). The data sets are compared to HR and SS jump diffusion models and a HWHM ∼ DQ2 law. While the jump diffusion models fit the low Q range HWHM reasonably well, the models deviate at high Q values and depending on the model reach slightly different plateau values for HWHM. However, as already discussed, at high Q and high temperatures the respective HWHM values also reach the maximum energy transfer window of IN16B and a possible correlation with the fitted flat background has to be taken into account. Therefore data for PA and 6PA1BI in the high Q regime must be assessed carefully as their Q dependence is prone to artefacts. Considering this we cannot conclude if the SS- or HR-model agrees better with the data. In the following we compare the diffusion coefficients obtained through the HWHM ∼ DQ2 law fits to the HWHM belonging to the first 4 Q values with the NMR diffusion data. At low Q, and especially at low temperatures interestingly, neither the total proton diffusion coefficient, nor the hydrodynamic diffusion coefficient from our own PFG-NMR measurements5,6 describe the HWHM's Q-dependence through a DQ2 law.
The temperature dependence of diffusion coefficients obtained by QENS through fits of the HWHM ∼ DQ2 law and fits of the two different jump diffusion models are virtually identical. The activation energy for the diffusion coefficients differs only slightly within the error bars from that of the scaling factors for the master plot (see Fig. 7). Interestingly, it is also virtually identical to the temperature dependence of structural diffusion as calculated from PFG-NMR (Fig. 11) for neat phosphoric acid and for 6PA1BI. The activation energies are furthermore virtually identical to that of the proton displacement around oxygen as obtained through 17O relaxation NMR (see Fig. 5b). This indicates that the three techniques assess the same dynamic process, i.e., proton structural diffusion.
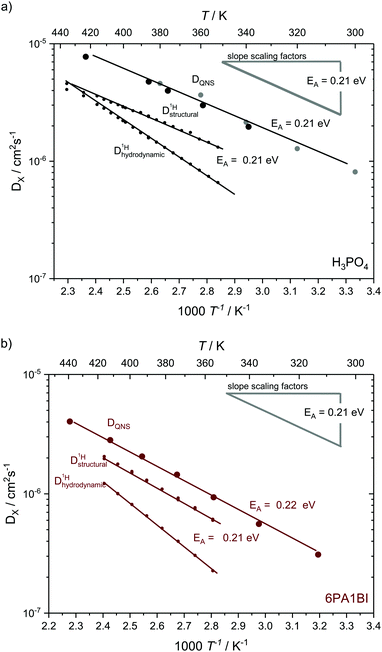 | ||
| Fig. 11 Temperature dependent diffusion coefficients as obtained from QENS through Q2 – proportionality fitting at low Q in comparison to structural and hydrodynamic proton diffusion5,6 from NMR for (a) for neat H3PO4 and (b) 6 mol H3PO4 per 1 mol BI. The temperature dependences the scaling factors is added as grey line. Diffusion data for neat H3PO4 include measurements at IN16B (larger black points) and reevaluated data from previous IN16 (gray points) measurements.41 The temperature dependence of diffusion coefficients obtained through QENS is virtually identical to that of structural diffusion coefficients calculated from different PFG-NMR measurements and very much different from the temperature dependence of hydrodynamic proton diffusion coefficients (see text). | ||
Discussion
In this study, dynamics on the nanosecond timescale has been investigated for different model systems containing phosphoric acid and water or phosphoric acid and the Brønsted base benzimidazole, thus further bridging the gap between experimental studies of proton dynamics on the millisecond timescale and ab initio molecular dynamics simulations of the sub-picosecond dynamics. In recent millisecond timescale studies structural diffusion coefficients were separated from the hydrodynamic background through investigation of the individual contributions of different phosphate species, water and the benzimidazole to proton diffusion and conductivity.5,6 The general effect that the contribution of structural diffusion to conductivity decreases with increasing temperature7 was explicitly shown. The contribution of vehicle conductivity increases with temperature for phosphoric acid which also explains the reported higher isotope (hydrogen/deuterium) effects on conductivity at very low temperatures.75 Here it is shown how through the choice of measuring technique different aspects of the dynamic processes can also be identified on the nanosecond timescale. In detail, structural diffusion, i.e., fast intermolecular proton transfer, was investigated using 17O NMR relaxation measurements at different water contents and using backscattering quasielastic neutron scattering at different levels of the benzimidazole content in phosphoric acid benzimidazole mixtures. Aspects of hydrodynamic diffusion on the nanosecond scale, on the other hand, have been investigated using 1H NMR relaxation measurements (see Fig. 12).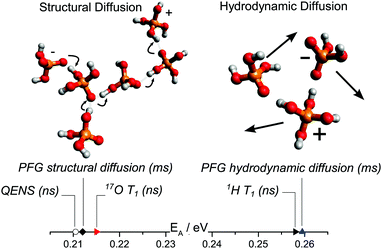 | ||
| Fig. 12 Activation energy obtained through different techniques separating structural and hydrodynamic diffusion. In our previous work6 structural and hydrodynamic diffusion have been separated on the millisecond timescale through a combination of PFG-NMR measurements of 31P, 1H and 17O (see text). The activation energies obtained through QENS and 17O NMR T1 relaxation measurements of proton dynamics on the nanosecond timescale are virtually identical to those of millisecond scale structural diffusion coefficients obtained through PFG NMR.6 The activation energy obtained from 1H T1 relaxation measurements (nanosecond timescale), on the other hand, is similar to that obtained from hydrodynamic diffusion coefficients on the millisecond scale. | ||
Correlation times obtained through 1H-NMR relaxation measurements are fundamentally related to the hydrodynamic transport of ortho-phosphoric acid molecules measured on the millisecond timescale using 31P-PFG-NMR. This explains the previously reported differences in the temperature dependence of 1H-PFG-NMR measurements and the relaxation measurements. The two techniques in fact measure different dynamical processes for the same magnetic field and temperature range. While the diffusion coefficients obtained through 1H-PFG-NMR contain long range hydrodynamic contributions of the host molecules and contributions of intermolecular proton transfer (structural diffusion), intermolecular proton transport is too fast to considerably affect the 1H-NMR relaxation. The 1H-NMR relaxation process is dominated by local reorientations of the molecules which are a prerequisite for long range hydrodynamic transport. For the data shown in Fig. 5, the hydrodynamic diffusion of phosphoric acid molecules on the millisecond scale and the nanosecond correlation times from 1H relaxation measurements, the dynamics is indeed reduced by the same factors upon addition of (benz)imidazole with virtually identical activation energies for the nanosecond and millisecond dynamics. At a higher benzimidazole content, however, interactions with the benzimidazole molecules influence the relaxation of phosphoric acid protons considerably, which makes it difficult to isolate their exact dynamics from such measurements.
Relaxation in 17O-NMR, on the other hand, is dominantly quadrupolar and therefore sensitive to displacements of protons around the oxygen ions of both H3PO4 and H2O in phosphoric acid with different water contents P2O5·λH2O. The measurements confirm that the activation energy for proton displacement around H3PO4 is the same as that of effective structural diffusion calculated on the millisecond timescale and that of the diffusion coefficients directly measured using QENS (see Fig. 12). It is furthermore shown that the activation energy of displacing protons from H3PO4 oxygens and H2O oxygens is not identical at increased water contents (λ ∼ 4.5) and that with further increasing water content intermolecular proton transfer becomes negligible. This observation is in accordance with the breakdown of structural conductivity described in our recent publication,5 which had already been assigned to weakening of the hydrogen bonds and a general decrease of frustration in the hydrogen bonded network through deprotonation of H3PO4.6
The measurement principles of QENS are in stark contrast to that of the NMR techniques. While in earlier PFG-NMR measurements the diffusion of different chemical species is distinguished and the relaxation NMR in this study assesses different aspects of dynamics independent of spatial assignments, the QENS signal contains contributions from all protons, and provides direct spatial information and the principal possibility of distinguishing different types of dynamic processes. The QENS timescale in this study (nanosecond range) does, however, not reach the sub-picosecond timescale on which proton transfer events occur according to recent ab initio simulations4,23,34 and our yet unpublished neutron TOF data. The dynamic process visible in the nanosecond window can therefore not be related to a single proton transfer event between two phosphates. On the nanosecond timescale protons, on average, have already undergone multiple such transfer events resulting in a proton diffusion coefficient which is already decoupled from the much slower hydrodynamic diffusion of the phosphate species and means that the hydrodynamic diffusion of the phosphate species does not contribute to the QENS signal on the nanosecond scale.
The application of a jump diffusion model to QENS linewidth data, assuming a single proton transfer event, in earlier works resulted in a far too high proton “jump length” (290 pm),2,40 well above the measured distances between two phosphoric acid molecules (260 pm)76 and far above the distance of two proton sites found in simulations as the average jump length of a proton within a hydrogen bond connecting two phosphoric acid molecules (63 pm).33 More recently the state of the art quasi elastic neutron scattering investigations of neat phosphoric acid from the solid to the melt conducted on the IN16 spectrometer at the Institute Laue Langevin temperature reported temperature dependence of this jump length (110–360 pm).41 In all cases the diffusion coefficients used to deduce the jump length in the literature were those of direct 1H-PFG-NMR, which are measured on the millisecond scale and contain contributions from both hydrodynamic and structural diffusion.
In this study, QENS data are analyzed self-consistently and independent of input parameters from other measurement techniques. Through high resolution backscattering QENS it is shown that indeed different dynamic processes contribute to the QENS spectra previously reported for neat H3PO4 and for phosphoric acid–benzimidazole mixtures. Especially fast processes present in both the neat acid and the mixtures cause a broad background, that needs to be analyzed in conjunction with QENS measurements of those faster timescales. For phosphoric acid–benzimidazole mixtures also the slow hydrodynamic diffusion of benzimidazole6 influences the QENS spectra. The respective ratios at which the different dynamic processes contribute to the QENS signal depend on the dynamic window of the spectrometer and the differences in the respective dynamic processes that in turn are temperature dependent. The influence of benzimidazole diffusion makes it harder to isolate the phosphoric acid dynamics for high benzimidazole containing mixtures. However, through a model free approach (see Fig. 7) it is shown that in the energy range of IN16B a single process dominates the QENS spectra for neat phosphoric acid at all recorded temperatures and that the same process dominates the QENS spectra for phosphoric acid–benzimidazole mixtures especially at higher temperatures.
The process dominating the QENS spectra has been identified through comparison of activation energies as proton structural diffusion and it is confirmed that 17O spin–lattice relaxation measurements, PFG-NMR and QENS actually assess different aspects of the same structural diffusion process. Analysis of the QENS linewidth in the Q range and temperature range where a single dynamic process dominates the signal shows that the structural diffusion process does not fundamentally change through addition of benzimidazole. Addition of benzimidazole rather reduces the linewidth of the quasielastic peak with a scaling factor constant for each benzimidazole content (inset Fig. 8). Consequently, the respective diffusion coefficients for nanosecond structural diffusion are reduced with increasing benzimidazole content (Fig. 12).
Diffusion coefficients for nanosecond proton dynamics and the model independent scaling factors, actually, confirm trends reported for the structural diffusion coefficients calculated from earlier PFG-NMR measurements. In those PFG-NMR measurements the influence of benzimidazole on the measurements has been corrected for and the obtained structural diffusion coefficients are also reduced upon addition of benzimidazole while their activation energy remains identical. In combination with the new nanosecond timescale data these results imply that the mechanism of structural proton transport is neither changed through the additive, nor that any influences on structural proton diffusion exist on timescales higher than the nanosecond regime. The data reported in this work confirm that intermolecular proton transport and all rate limiting steps of structural diffusion take place on the picosecond timescale, as found in ab initio molecular dynamics simulations. The general decrease of the diffusion coefficients, i.e., a decrease of the entropic prefactor, for structural proton diffusion according to the simulations is associated with a decreased probability of formation of protonic defects (autodissociation). Such defects are a consequence of frustrated protons (i.e., protons covalently bound to an oxygen atom, which are at the same time in a hydrogen bond to another molecule, hence reducing the charge density at the oxygen and hydrogen site). The frustrated protons react with oxygens along polarized chains of phosphate species connected through strong hydrogen bonds. Such chains form through thermally activated polarization fluctuations. This fluctuation means rattling of hydrogen atoms between different phosphate molecules. Successful transfer of a hydrogen atom, however, additionally relies on the depolarization of the chain through the described reaction with the frustrated protons. As a consequence of this sequence of events charges are separated at opposite sides of the chain in that one phosphoric acid molecule is deprived of a hydrogen atom (H2PO4−) and the other one contains additional hydrogen (H4PO4+). With a reduced density of frustrated protons the probability of occurrence for a successful proton transfer event naturally is reduced. On higher timescales (i.e. nanosecond and millisecond) this results in reduced diffusion coefficients in comparison to the neat acids.
The difference in diffusion coefficients of 3PA1BI and 6PA1BisBi, which have the same number of imidazole molecules, either indicates an additional minute effect of viscosity or it is indicative of different accessibility, or basicity of nitrogen sites of benzimidazole in comparison to those of bisbenzimidazole. Such aspects, relating to the configuration of the larger molecules, are important for the design of polybenzimidazole membranes and are actually subject of computational studies of bisbenzimidazole in different configurations.77 Further experimental studies of the difference of bisbenzimidazole and benzimidazole in phosphoric acid are necessary but beyond the scope of this work.
Conclusions
In this study it is argued which dynamic processes on the nanosecond timescale dominate the results of 17O NMR relaxation, 1H NMR relaxation, and high resolution backscattering quasi elastic neutron scattering (QENS) in phosphoric acid containing systems. 1H NMR relaxation rates are dominated by hydrodynamic diffusion at the applied magnetic field and in the investigated temperature range, as structural diffusion is indeed too fast to considerably affect the dipolar relaxation of the protons. Relaxation times are increasingly affected by other effects than pure hydrodynamic diffusion of the phosphates with increasing benzimidazole content in benzimidazole phosphoric acid mixtures. 17O NMR relaxation rates, on the other hand, provide access to the activation energies of proton displacement as part of structural diffusion, as the nuclei's quadrupolar relaxation is dominated by short range fluctuations of its electric field gradient caused through changes of covalent oxygen proton bonds to hydrogen bonds. The extracted activation energies show that structural diffusion in phosphoric acid water mixtures takes place solely between phosphoric acid molecules. In fact structural diffusion breaks down towards increasing water contents, confirming the result of recent combined electrochemical transference, impedance, and NMR diffusion studies.5 High resolution backscattering QENS measurements of phosphoric acid return a signal for scattering at all protons but quasielastic line broadening is dominated by the fast proton exchange as part of structural diffusion as this proton dynamics is decoupled from the hydrodynamic diffusion of the phosphate species. At low temperatures and high benzimidazole contents in benzimidazole phosphoric acid mixtures the average broadening becomes increasingly affected by scattering at benzimidazole's protons, which do not take part in the structural proton diffusion process. Nevertheless, this technique enables a direct measurement of the influence of benzimidazole's proton acceptor sites on structural diffusion, structural diffusion coefficients and its activation energy on the nanosecond scale. For mixtures of nominally dry phosphoric acid and the Brønsted base benzimidazole it was found that with increasing base content the structural proton diffusion coefficients are reduced while the activation energy for this process in phosphoric acid remains unaltered. The overall decrease of structural proton diffusion has been explained in a recent ab initio molecular dynamics simulation as a result of a reduced density of frustrated hydrogen bonds that reduces the probability of occurrence of successful proton transfer reactions on the picosecond scale.23 Our recent experimental studies confirmed reduced frustration through addition of (benz)imidazole and showed reduced structural diffusion coefficients on the millisecond timescale, as well as, reduced conductivity as a consequence.6 The present work connects the two previous studies and indicates that all effects leading to reduced structural proton dynamics are already present on the nanosecond timescale and all influences of Brønsted bases on structural proton dynamics of phosphoric acid (as present in technologically important polybenzimidazole phosphoric acid membranes) are those reported in the simulation work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Klaus-Dieter Kreuer for initiating the project, valuable discussions, and reading the manuscript. We acknowledge continuous interest and financial support by Prof. J. Maier. JPM highly acknowledges discussions about NMR relaxation with Günter Majer. We thank Alexander Gulledge and Brian Benicewicz (University of South Carolina) for providing the bisbenzimidazole. We further thank Michael G. Marino and Andreas Wohlfarth for assistance with sample preparation and Markus Appel for technical support in conducting the QENS experiments. JPM kindly acknowledges financial support from the Bundesministerium für Bildung und Forschung and Energie Baden Württemberg EnBW (project PSUMEA-2 No. 03SF0473).References
- K. D. Kreuer, S. J. Paddison, E. Spohr and M. Schuster, Chem. Rev., 2004, 104, 4637–4678 CrossRef CAS PubMed.
- T. Dippel, K. D. Kreuer, J. C. Lassègues and D. Rodriguez, Solid State Ionics, 1993, 61, 41–46 CrossRef CAS.
- N. N. Greenwood and A. Thompson, J. Chem. Soc., 1959, 3864–3867 RSC.
- L. Vilčiauskas, M. E. Tuckerman, G. Bester, S. J. Paddison and K. D. Kreuer, Nat. Chem., 2012, 4, 461–466 CrossRef PubMed.
- J.-P. Melchior, K. D. Kreuer and J. Maier, Phys. Chem. Chem. Phys., 2017, 19, 587–600 RSC.
- J.-P. Melchior, G. Majer and K. D. Kreuer, Phys. Chem. Chem. Phys., 2017, 19, 601–612 RSC.
- K. D. Kreuer, Chem. Mater., 1996, 8, 610–641 CrossRef CAS.
- J. Heberle, J. Riesle, G. Thiedmann, D. Oesterhelt and N. A. Dencher, Nature, 1994, 370, 379–382 CrossRef CAS PubMed.
- F. H. Westheimer, Science, 1987, 235, 1173–1178 CAS.
- M. W. Bowler, M. J. Cliff, J. P. Waltho and G. M. Blackburn, New J. Chem., 2010, 34, 784–794 RSC.
- J. S. Wainright, J. T. Wang, D. Weng, R. F. Savinell and M. Litt, J. Electrochem. Soc., 1995, 142, L121–L123 CrossRef CAS.
- Q. Li, J. O. Jensen, R. F. Savinell and N. J. Bjerrum, Prog. Polym. Sci., 2009, 34, 449–477 CrossRef CAS.
- M. Molleo, T. Schmidt and B. Benicewicz, in Fuel Cells, ed. K. D. Kreuer, Springer New York, 2013, pp. 391–431 Search PubMed.
- E. Quartarone, S. Angioni and P. Mustarelli, Materials, 2017, 10, 687 CrossRef PubMed.
- Q. Li, D. Aili, H. A. Hjuler and J. O. Jensen, High Temperature Polymer Electrolyte Membrane Fuel Cells – Approaches, Status, and Perspectives, Springer International Publishing, Cham, Heidelberg, New York, Dordrecht, London, 2016 Search PubMed.
- K. Fishel, G. Qian, G. Eisman and B. C. Benicewicz, in High Temperature Polymer Electrolyte Fuel Cells – Approaches, Status, and Perspectives, ed. J. O. Jensen, H. A. Hjuler and Q. Li, Springer International Publishing, Cham, Heidelberg, New York, Dordrecht, London, 2016, ch. 24, pp. 527–540 Search PubMed.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- M. Tuckerman, K. Laasonen, M. Sprik and M. Parrinello, J. Chem. Phys., 1995, 103, 150–161 CrossRef CAS.
- K. D. Kreuer, A. Fuchs, M. Ise, M. Spaeth and J. Maier, Electrochim. Acta, 1998, 43, 1281–1288 CrossRef CAS.
- W. Münch, K. D. Kreuer, W. Silvestri, J. Maier and G. Seifert, Solid State Ionics, 2001, 145, 437–443 CrossRef.
- R. A. Munson and M. E. Lazarus, J. Phys. Chem., 1967, 71, 3245–3248 CrossRef CAS.
- A. Schechter and R. F. Savinell, Solid State Ionics, 2002, 147, 181–187 CrossRef CAS.
- L. Vilčiauskas, M. E. Tuckerman, J.-P. Melchior, G. Bester and K. D. Kreuer, Solid State Ionics, 2013, 252, 34–39 CrossRef.
- A. Bozkurt, M. Ise, K. D. Kreuer, W. H. Meyer and G. Wegner, Solid State Ionics, 1999, 125, 225–233 CrossRef CAS.
- Y. Aihara, A. Sonai, M. Hattori and K. Hayamizu, J. Phys. Chem. B, 2006, 110, 24999–25006 CrossRef CAS PubMed.
- D.-T. Chin and H. Chang, J. Appl. Electrochem., 1989, 19, 95–99 CrossRef CAS.
- D. I. MacDonald and J. R. Boyack, J. Chem. Eng. Data, 1969, 14, 380 CrossRef CAS.
- A. Smith and A. W. C. Menzies, J. Am. Chem. Soc., 1909, 31, 1191–1194 CrossRef.
- R. A. Munson, J. Phys. Chem., 1964, 68, 3374–3377 CrossRef CAS.
- L. Vilčiauskas, C. C. de Araujo and K. D. Kreuer, Solid State Ionics, 2012, 212, 6–9 CrossRef.
- P. Walden, Z. Phys. Chem., 1906, 55, 207–249 CAS.
- Y. L. Ma, J. S. Wainright, M. H. Litt and R. F. Savinell, J. Electrochem. Soc., 2004, 151, A8–A16 CrossRef CAS.
- L. Vilčiauskas, PhD thesis, Universität Stuttgart, 2012.
- R. A. Krueger, L. Vilčiauskas, J.-P. Melchior, G. Bester and K. D. Kreuer, J. Phys. Chem. B, 2015, 119, 15866–15875 CrossRef CAS PubMed.
- A. Schechter, R. F. Savinell, J. S. Wainright and D. Ray, J. Electrochem. Soc., 2009, 156, B283 CrossRef CAS.
- J. R. P. Jayakody, S. H. Chung, L. Durantino, H. Zhang, L. Xiao, B. C. Benicewicz and S. G. Greenbaum, J. Electrochem. Soc., 2007, 154, B242–B246 CrossRef CAS.
- S. Suarez, N. K. A. C. Kodiweera, P. Stallworth, S. Yu, S. G. Greenbaum and B. C. Benicewicz, J. Phys. Chem. B, 2012, 116, 12545–12551 CrossRef CAS PubMed.
- S. H. Chung, S. Bajue and S. G. Greenbaum, J. Chem. Phys., 2000, 112, 8515–8521 CrossRef CAS.
- Y. Wang, N. A. Lane, C.-N. Sun, F. Fan, T. A. Zawodzinski and A. P. Sokolov, J. Phys. Chem. B, 2013, 117, 8003–8009 CrossRef CAS PubMed.
- J.-C. Lassègues and D. Cavagnat, Phys. B, 1992, 180–181, 645–650 CrossRef.
- B. Frick, L. Vilčiauskas, P. P. Deen and S. Lyonnard, Solid State Ionics, 2013, 252, 26–33 CrossRef CAS.
- I. P. Gerothanassis and C. G. Tsanaktsidis, Concepts Magn. Reson., 1996, 8, 63–74 CrossRef CAS.
- B. Frick and D. Neumann, in Neutrons in Soft Matter, ed. T. Imae, T. Kanaya, M. Furusaka and N. Torikai, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2011, ch. 7, pp. 183–202 DOI:10.1002/9780470933886.ch7.
- B. Frick, in Neutron and X-Ray Spectroscopy, ed. F. Hippert, E. Geissler, J. L. Hodeau, E. Lelièvre-Berna and J.-R. Regnard, Springer Netherlands, 2006, pp. 483–527 DOI:10.1007/1-4020-3337-0.
- M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, John Wiley & Sons Ltd, Chichester, 2nd edn, 2007 Search PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- I. P. Gerothanassis, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 56, 95–197 CrossRef CAS PubMed.
- I. P. Gerothanassis, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 57, 1–110 CrossRef CAS PubMed.
- S. Meiboom, J. Chem. Phys., 1961, 34, 375 CrossRef CAS.
- Z. Luz and S. Meiboom, J. Am. Chem. Soc., 1964, 86, 4768 CrossRef CAS.
- M. Bée, Quasielastic Neutron Scattering, Adam Hilger, 1988 Search PubMed.
- A. Ishikawa, H. Maekawa, T. Yamamura, Y. Kawakita, K. Shibata and M. Kawai, Solid State Ionics, 2008, 179, 2345–2349 CrossRef CAS.
- M. Khaneft, O. Holderer, O. Ivanova, W. Lüke, E. Kentzinger, M. S. Appavou, R. Zorn and W. Lehnert, Fuel Cells, 2016, 16, 406–413 CrossRef CAS.
- K. D. Kreuer, W. Weppner and A. Rabenau, Solid State Ionics, 1981, 3–4, 353–358 CrossRef CAS.
- B. Frick, E. Mamontov, L. V. Eijck and T. Seydel, Z. Phys. Chem., 2010, 224, 33–60 CrossRef CAS.
- J.-P. Melchior and B. Frick, 2013, DOI:10.5291/ILL-DATA.9-11-1631.
- LAMP, the Large Array Manipulation Program, http://www.ill.eu/data_treat/lamp/the-lamp-book/.
- D. Richard, M. Ferrand and G. J. Kearley, J. Neutron Res., 1996, 4, 33–39 CrossRef.
- H. Jobic and D. N. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS.
- H. Jobic, in Recent Advances in Gas Separation by Microporous Ceramic Membranes, Membrane Science and Technology, ed. N. K. Kanellopoulos, Elsevier, 2000, vol. 6, pp. 109–137 Search PubMed.
- P. L. Hall and D. K. Ross, Mol. Phys., 1981, 42, 673–682 CrossRef CAS.
- K. S. Singwi and A. Sjölander, Phys. Rev., 1960, 119, 863–871 CrossRef CAS.
- U. Reimer, J. Ehlert, H. Janssen and W. Lehnert, Int. J. Hydrogen Energy, 2016, 41, 1837–1845 CrossRef CAS.
- D. Weng, J. S. Wainright, U. Landau and R. F. Savinell, J. Electrochem. Soc., 1996, 143, 1260–1263 CrossRef CAS.
- H. Becker, L. N. Cleemann, D. Aili, J. O. Jensen. and Q. Li, Electrochem. Commun., 2017, 82, 21–24 CrossRef CAS.
- K. R. Jeffrey, G. Z. Zukowska and J. R. Stevens, J. Chem. Phys., 2003, 119, 2422–2431 CrossRef CAS.
- K. Hayamizu, in Ionic Liquids – Classes and Properties, ed. S. T. Handy, InTech, 2011, ch. 10, pp. 209–236 DOI:10.5772/24099.
- B. Ellis, Nature, 1976, 263, 674–676 CrossRef CAS.
- H. R. Corti, F. J. Nores-Pondal and C. A. Angell, Phys. Chem. Chem. Phys., 2011, 13, 19741–19748 RSC.
- S. Wasmus, A. Valeriu, G. D. Mateescu, D. A. Tryk and R. F. Savinell, Solid State Ionics, 1995, 80, 87–92 CrossRef CAS.
- D. E. Woessner, in Enceclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, John Wiley & Sons, Ltd, 2007, pp. 4018–4028 Search PubMed.
- K. D. Kreuer, Solid State Ionics, 2000, 136–137, 149–160 CrossRef CAS.
- O. Holderer, O. Ivanova, B. Hopfenmüller, M. Zamponi, W. Maier, A. Majerus, W. Lehnert, M. Monkenbusch and R. Zorn, Int. J. Hydrogen Energy, 2014, 39, 21657–21662 CrossRef CAS.
- O. Ivanova, W. Lüke, A. Majerus, M. Krutyeva, N. K. Szekely, W. Pyckhout-Hintzen, M.-S. Appavou, M. Monkenbusch, R. Zorn, W. Lehnert and O. Holderer, J. Membr. Sci., 2017, 533, 342–350 CrossRef CAS.
- M. Heres, Y. Wang, P. J. Griffin, C. Gainaru and A. P. Sokolov, Phys. Rev. Lett., 2016, 117, 156001 CrossRef CAS PubMed.
- R. H. Tromp, S. H. Spieser and G. W. Neilson, J. Chem. Phys., 1999, 110, 2145–2150 CrossRef CAS.
- K. Shirata and S. Kawauchi, J. Phys. Chem. B, 2015, 119, 592–603 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp04116k |
| ‡ Current address: Oak Ridge National Laboratory, 1 Bethel Valley Road, Oak Ridge, TN 37831, USA. E-mail: melchiorj@ornl.gov |
| This journal is © the Owner Societies 2017 |